Keywords

1 Introduction

Fractional-order calculus was not especially popular in previous decades when its concepts have a lot of attention in various scientific fields, including more accurate system modeling and automatic control assignment [1, 2]. Utilising the notion of non-integer order should be more appropriate step because real-life processes appear to be fractional [3, 4]. The fractional-order calculus is the generalisation of the classical calculus, where the order of integration and differentiation is not an integer index [5]. There have been some reports on non-integer calculus, applied to various areas of the applications, e.g.: bioengineering [6], physics [7, 8], chaos theory [9], control systems [1, 10, 11] and fractional signal processing [12, 13].

It is clear that the rise of interest in the fractional calculus domain is related to the increasing availability of high-performance and advanced computational tools. Fractional order calculus was applied in robotics and automation, taking into account system identification and automatic control [2]. The control performance assessment has a large influence on the economic aspect of the real-life processes. It was reported that conventional PID controller, in industrial applications, is worse than fractional order PID controller according to the tuning flexibility [14].

For fractional order system analysis one of existing packages for non-integer order modeling and controller synthesis tasks, such as CRONE, Ninteger or FOMCON [15], can be employed. Above packages are implemented in Matlab environment and have effective tools for solving various fractional order problems and can be easily connected with other Matlab facilities (e.g. simulation of models in Simulink environment utilising graphical interface).

The non-integer order differentiation is equivalent to infinite dimensional filter that is why the selection of appropriate approximation factors is very important. The goal of this study is to verify fitting the Outsaloup filter to the fractional inertial model approximation in a specified narrow frequency range. The proper Oustaloup’s approximation could be then used for modelling the non-integer order differentiation operator in an integer order state-space form. The fractional order control problem would be then reformulated to solve optimal input signal design task [16, 17]. For non-integer order system modeling in frequency and time domains the Fomcon toolbox was utilised [15].

2 Fractional Calculus

The idea of the differentiation operator is a fundamental tool in the study of the ordinary differential equations. Fractional calculus is a special case of integration and differentiation to non-integer order operator \( {}_{a}D_{t}^{\alpha } \) as follows:

$$ {}_{a}D_{t}^{\alpha } = \left\{ {\begin{array}{*{20}l} {\frac{{d^{\alpha } }}{{dt^{\alpha } }}} \hfill & {\Re \left( \alpha \right) > 0} \hfill \\ 1 \hfill & {\Re \left( \alpha \right) = 0,} \hfill \\ {\int\limits_{a}^{t} {\left( {d\tau } \right)^{ - \alpha } } } \hfill & {\Re \left( \alpha \right) < 0} \hfill \\ \end{array} } \right. $$
(1)

where: a, t - denote the limits of the process and α is the set for all complex numbers.

There are different definitions of the fractional derivative operator [1].

The Riemann-Liouville fractional derivative (α > 0) of a function f(t) is defined as:

$$ {}_{a}D_{t}^{\alpha } \,f\left( t \right) = \frac{{d^{\alpha } \,f\left( t \right)}}{{dt^{\alpha } }} = \frac{1}{{\varGamma \left( {m - \alpha } \right)}}\left( {\frac{d}{dt}} \right)^{m} \int\limits_{a}^{t} {\frac{f\left( \tau \right)}{{\left( {t - \tau } \right)^{\alpha + 1 - m} }}d\tau ,} $$
(2)

where: Γ(·) stands for Euler’s gamma function and \( m - 1 < \alpha \le m,m\,{ \in }\,{\text{N, for }}\alpha \, \in \,(0,\,1\rangle . \) Such a definition can also be reformulated to fractional-order derivative in the form:

$$ {}_{a}D_{t}^{\alpha } \,f\left( t \right) = \frac{{d^{\alpha } \,f\left( t \right)}}{{dt^{\alpha } }} = \frac{1}{{\Gamma \left( {1 - \alpha } \right)}}\frac{d}{dt}\int\limits_{a}^{t} {\frac{f\left( \tau \right)}{{\left( {t - \tau } \right)^{\alpha } }}d\tau ,} $$
(3)

The Laplace transform of the Riemann-Liouville derivative (2) for a = 0 is:

$$ L\left\{ {{}_{0}D_{t}^{\alpha } f\left( t \right)} \right\} = s^{\alpha } F\left( s \right) - \sum\limits_{k = 1}^{m} {s^{k - 1} f^{{\left( {a - k} \right)}} \left( {0^{ + } } \right)} , $$
(4)

where: \( F\left( s \right) = L\left\{ {f\left( t \right)} \right\}. \)

The Caputo’s definition of fractional-order derivative (α > 0) is defined as follows:

$$ {}_{a}D_{t}^{\alpha } \,f\left( t \right) = \frac{{d^{\alpha } \,f\left( t \right)}}{{dt^{\alpha } }} = \frac{1}{{\varGamma \left( {m - \alpha } \right)}}\int\limits_{0}^{t} {\frac{{f^{\left( p \right)} \left( \tau \right)}}{{\left( {t - \tau } \right)^{\alpha + 1 - m} }}d\tau ,} $$
(5)

where: \( f^{\left( m \right)} \left( t \right) = \left( {{{d^{m} } \mathord{\left/ {\vphantom {{d^{m} } {dt^{m} }}} \right. \kern-0pt} {dt^{m} }}} \right)f\left( t \right),\,\,m - 1 < \alpha \le m. \) This definition for \( \alpha \in (0,\,1\rangle \) can be reformulated to fractional-order derivative in the following form:

$$ {}_{a}D_{t}^{\alpha } \,f\left( t \right) = \frac{{d^{\alpha } \,f\left( t \right)}}{{dt^{\alpha } }} = \frac{1}{{\varGamma \left( {1 - \alpha } \right)}}\int\limits_{0}^{t} {\frac{f\left( \tau \right)}{{\left( {t - \tau } \right)^{\alpha } }}d\tau } . $$
(6)

The Laplace transform of the Caputo derivative (5) for a = 0 is:

$$ L\left\{ {{}_{0}D_{t}^{\alpha } f\left( t \right)} \right\} = s^{\alpha } F\left( s \right) - \sum\limits_{k = 1}^{m} {s^{\alpha - k} \,f^{{\left( {k - 1} \right)}} \left( {0^{ + } } \right)} . $$
(7)

It was reported that for real functions, the fractional-order derivative from the Riemann-Liouville and Grünwald-Letnikov definitions are identical [10].

Finally, the Grünwald-Letnikov definition would be considered:

$$ {}_{a}D_{t}^{\alpha } \,f\left( t \right) = \mathop {\lim }\limits_{h \to 0} \frac{1}{{h^{\alpha } }}\sum\limits_{j = 0}^{k} {\left( { - 1} \right)^{j} \left( {\begin{array}{*{20}c} \alpha \\ j \\ \end{array} } \right)\,} f\left( {t - jh} \right), $$
(8)

where: \( \omega_{j}^{\alpha } = \left( { - 1} \right)^{j} \left( {\begin{array}{*{20}c} \alpha \\ j \\ \end{array} } \right) \) describes polynomial factors, which can be received recursively from:

$$ \omega_{0}^{\alpha } = 1,\omega_{j}^{\alpha } = \left( {1 - \frac{\alpha + 1}{j}} \right)\omega_{j - 1}^{\alpha } ,\;j = 1,2, \ldots , $$
(9)

Utilising Eq. (9) the fractional-order derivative (8) can be suitably modified as:

$$ {}_{a}D_{t}^{\alpha } \,f\left( t \right)\,{ \approx }\frac{1}{{h^{\alpha } }}\sum\limits_{j = 0}^{k} {\omega_{j}^{\alpha } } \,f\left( {t - jh} \right), $$
(10)

where a = 0, t = kh is the step number and h is the step duration. The Laplace transform assuming zero initial conditions of derivative (8) with \( \alpha \,{ \in }\,{\text{R}}^{ + } \) is as follows [1]:

$$ L\left\{ {{}_{0}D_{t}^{\alpha } f\left( t \right)} \right\} = s^{\alpha } F\left( s \right). $$
(11)

Linear fractional-order continuous-time SISO dynamic system can be expressed by a fractional-order differential equation [1, 2]:

$$ \sum\limits_{k = 0}^{n} {a_{k} D_{t}^{{\alpha_{i} }} y\left( t \right) = \sum\limits_{k = 0}^{m} {b_{k} D_{t}^{{\beta_{i} }} u\left( t \right),} } $$
(12)

where: a k , b k are real numbers. The discrete-time version for various orders one can find in [18]. Applying the Laplace transform to (12) with zero initial conditions the input-output description of the fractional-order system can be expressed in the transfer function form:

$$ G\left( s \right) = \frac{Y\left( s \right)}{U\left( s \right)} = \frac{{b_{m} s^{{\beta_{m} }} + b_{m - 1} s^{{\beta_{m - 1} }} + \ldots + b_{0} s^{{\beta_{0} }} }}{{a_{n} s^{{\alpha_{n} }} + a_{n - 1} s^{{\alpha_{n - 1} }} + \ldots + a_{0} s^{{\alpha_{0} }} }}. $$
(13)

The transfer function (13) is commensurate order if all orders of the fractional operator s are integer multiples of base order q in such a way: \( q\,{ \in }\,{\text{R}}^{ + } ,\,0 < q < 1,\,\alpha_{k} ,\beta_{k} = kq. \) The above continuous-time transfer function can be modified to give to the pseudo-rational function H(λ) in the form:

$$ H\left( \lambda \right) = \frac{{\sum\limits_{k = 0}^{m} {b_{k} \lambda^{k} } }}{{\sum\limits_{k = 0}^{n} {a_{k} \lambda^{k} } }}, $$
(14)

where: λ = s q. Using the pseudo-rational notation a fractional-order linear time-invariant system can be easily expressed by a state-space model given by:

$$ \begin{aligned} {}_{0}D_{t}^{\alpha } x\left( t \right) & = Ax\left( t \right) + Bu\left( t \right), \\ y\left( t \right) & = Cx\left( t \right) + Du\left( t \right). \\ \end{aligned} $$
(15)

For system parameters identification purposes the difference equation representing input-output dynamic of the system is more convenient than the state-space description. However the state-space model notation provides of multiple input and multiple output (MIMO) fractional-order systems representation.

3 Oustaloup Filter to Approximation of Fractional-Order Operators

The potentiality of approximating the fractional-order plant model by an integer-order one is presented in [1]. For linear fractional-order model identification purposes the Oustaloup filter method, which is often used in practical applications, should be considered. We focus our attention on the classical Oustaloup approximation algorithm. To solve the problem of approximation of a fractional differentiator or a fractional integrator the following equations should be used:

$$ s^{\alpha } \approx K\prod\limits_{k = 1}^{N} {\frac{{s + \omega_{k}^{{\mathbf{'}}} }}{{s + \omega_{k} }},} $$
(16)

where: poles, zeros and gain of the filter can be obtained from:

$$ \omega_{k}^{{\mathbf{'}}} = \omega_{b} \cdot \omega_{u}^{{{{\left( {2k - 1 - \alpha } \right)} \mathord{\left/ {\vphantom {{\left( {2k - 1 - \alpha } \right)} N}} \right. \kern-0pt} N}}} , $$
(17)
$$ \omega_{k} = \omega_{b} \cdot \omega_{u}^{{{{\left( {2k - 1 + \alpha } \right)} \mathord{\left/ {\vphantom {{\left( {2k - 1 + \alpha } \right)} N}} \right. \kern-0pt} N}}} , $$
(18)
$$ K = \omega_{h}^{\alpha } , $$
(19)
$$ \omega_{u} = \sqrt {\frac{{\omega_{h} }}{{\omega_{b} }}} , $$
(20)

where: N is the order of approximation and (ω b , ω h ) is the expected frequency fitting range. The order of the resulting filter is 2N + 1, taking into account a higher orders of N the resulting approximation should be more accurate.

The Oustaloup filter provides very good approximation results of fractional operators in an expected fitting range and a wide orders interval. Thus, for the fractional order operators where α ≥ 1 the following equation should be adopted:

$$ s^{\alpha } = s^{n} s^{\gamma } , $$
(21)

where: n = α – γ indicates the integer part of α and s γ is evaluated according to (16) utilising Oustaloup filter method.

4 Problem Formulation

To illustrate the properties of the above approach to fractional-order system parameter estimation, using the Oustaloup filter, we have selected FOMCON toolbox, which provides time-domain and frequency-domain non-integer order system analysis, as well as system stability checking [15]. The goal of this study is to verify the accuracy of the Oustaloup filter to the fractional inertial system transfer function parameters estimation in a specified frequency range ω = [ω b , ω h ] and order of the filter 2N + 1.

To justify the idea of this approach to integer model parameter estimation, an inertial object was selected as:

$$ G\left( s \right) = \frac{k}{{s^{\alpha } T + 1}},\,\alpha > 0. $$
(22)

The fractional-order linear time invariant system can be then described by the following single input, single output state-space model:

$$ \begin{aligned} {}_{0}D_{t}^{\alpha } \,x\left( t \right) & = Ax\left( t \right) + Bu\left( t \right), \\ y\left( t \right) & = x\left( t \right), \\ \end{aligned} $$
(23)

with assumed values of the matrix parameters: A = −1, B = 1 and zero initial conditions. The specified wide bandwidth would cause a large computational burden as N is increased. Therefore, the choice of N is based on following rule:

$$ N = \log \left( {\omega_{h} } \right) - \log \left( {\omega_{b} } \right). $$
(24)

The results of the Oustaloup filter approximation of the fractional transfer function (22) for different values α from the interval 0.5 ≤ α ≤ 1.9 and arbitrary selected bandwidth ω = [10−1, 101] with N= 2 according to (24), are displayed by transfer functions G o (s) given by:

$$ G\left( s \right) = \frac{1}{{s^{0.5} + 1}},\,G_{o} (s) = \frac{{0.24s^{5} + 3.14s^{4} + 11.5s^{3} + 14.48s^{2} + 6.26s + 0.76}}{{s^{5} + 9.4s^{4} + 25.98s^{3} + 25.98s^{2} + 9.4s + 1}}, $$
(25)
$$ G\left( s \right) = \frac{1}{{s^{0.7} + 1}},\,G_{o} (s) = \frac{{0.17s^{5} + 2.38s^{4} + 9.57s^{3} + 13.21s^{2} + 6.27s + 0.83}}{{s^{5} + 8.65s^{4} + 22.78s^{3} + 22.78s^{2} + 8.65s + 1}}, $$
(26)
$$ G\left( s \right) = \frac{1}{{s^{0.99} + 1}},\,G_{o} (s) = \frac{{0.09s^{5} + 1.52s^{4} + 6.97s^{3} + 11.01s^{2} + 5.97s + 0.91}}{{s^{5} + 7.49s^{4} + 17.99s^{3} + 17.99s^{2} + 7.49s + 1}}, $$
(27)
$$ G\left( s \right) = \frac{1}{{s^{1.3} + 1}},\,G_{o} (s) = \frac{{0.50s^{5} + 5.97s^{4} + 19.95s^{3} + 22.91s^{2} + 9.04s + 1}}{{s^{6} + 9.54s^{5} + 22.88s^{4} + 39.91s^{3} + 28.88s^{2} + 9.54s + 1}}, $$
(28)
$$ G\left( s \right) = \frac{1}{{s^{1.5} + 1}},\,G_{o} (s) = \frac{{0.32s^{5} + 4.13s^{4} + 15.14s^{3} + 19.05s^{2} + 8.24s + 1}}{{s^{6} + 8.56s^{5} + 23.19s^{4} + 30.27s^{3} + 23.19s^{2} + 8.56s + 1}}, $$
(29)
$$ G\left( s \right) = \frac{1}{{s^{1.7} + 1}},\,G_{o} (s) = \frac{{0.20s^{5} + 2.86s^{4} + 11.48s^{3} + 15.85s^{2} + 7.52s + 1}}{{s^{6} + 7.72s^{5} + 18.71s^{4} + 22.96s^{3} + 18.71s^{2} + 7.72s + 1}}, $$
(30)
$$ G\left( s \right) = \frac{1}{{s^{1.9} + 1}},\,G_{o} (s) = \frac{{0.02s^{5} + 1.97s^{4} + 49.18s^{3} + 289.6s^{2} + 402.9s + 112.2}}{{s^{6} + 35.9s^{5} + 260s^{4} + 487.5s^{3} + 465.4s^{2} + 417s + 112.2}}. $$
(31)

As it can be seen the resulting filters can be displayed in the Laplace domain, as reasonable approximations of the non-integer order operators. Additionally, this method exhibit practical property: it has zeros and poles interlaced on the negative real axis of the s plane, and the length between following poles and zeros decreases as the estimation is improved by increasing the order of the polynomials’ numerator and denominator, as it is displayed in Fig. 6.

5 The Experimental Results for Time and Frequency Domains

The time-domain simulation of the evaluated model of the fractional system, utilising step input signal, is based on the Grünwald-Letnikov definition shown in Eq. (8). The solution of the numerical problem (22) is performed utilising modified Grünwald-Letnikov definition [2]:

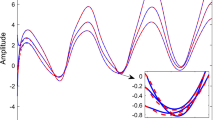
$$ y_{t} = \frac{1}{{\sum\limits_{i = 0}^{n} {\frac{{a_{i} }}{{h^{{\alpha_{i} }} }}} }}\left[ {u_{t} - \sum\limits_{i = 0}^{n} {\frac{{a_{i} }}{{h^{{\alpha_{i} }} }}\sum\limits_{j = 1}^{t/h} {\omega_{j}^{{\left( {\alpha_{j} } \right)}} y_{t - jh} } } } \right], $$
(32)

where h = 0.01 is the numerical step-size. The frequency-domain simulation is executed by replacing s = jω. This substitution was applied to Eqs. (25), (27), (29–31) to obtain frequency domain diagrams. In order to verify the stability of the approximated systems we obtained a step responses (at t = [0, t end ] with dt = 0.1) and Bode diagrams (for frequency axis range ω = [10−3, 102] and N = 2) shown in Figs. 1, 2, 3, 4 and 5.

Fig. 1.
figure 1

Step and frequency responses comparison for inertial (α = 0.5) system

Full size image
Fig. 2.
figure 2

Step and frequency responses comparison for inertial (α = 0.99) system

Full size image
Fig. 3.
figure 3

Step and frequency responses comparison for inertial (α = 1.5) system

Full size image
Fig. 4.
figure 4

Step and frequency responses comparison for inertial (α = 1.7) system

Full size image
Fig. 5.
figure 5

Step and frequency responses comparison for inertial (α = 1.9) system

Full size image

The Figs. 1, 2, 3, 4 and 5 show the Oustaloup filter step responses compared with the exact fractional inertial model step responses and frequency plots (Bode diagrams) of the real plant and obtained approximations.

Stability of the non-integer order state-space system (15) should be established from the following inequality:

$$ \left| {\arg \left( {{\text{eig}}\left( A \right)} \right)} \right| > \alpha \frac{\pi }{2}, $$
(33)

where: 0 < α < 1 is the fractional state-space system commensurate order and eig(A) describes the eigenvalues of the related matrix A. If this requirement is satisfied, then the system is stable [19]. The fractional order state-space system (23) is stable because the eigenvalue of the matrix A equals −1.

The plot shown in Fig. 6 indicates pole and zero maps of the approximated transfer functions for selected values of α. The plot shows that poles of the Oustaloup filters are in the left half-plane, and therefore the approximated models are stable.

Fig. 6.
figure 6

Pole and zero maps of the approximated systems for different values of α

Full size image

The quality of approximation of the fractional inertial system in the response space can be expressed by following errors and factors:

$$ \Delta y^{(w)} = \left| {y - \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{y} } \right|, $$
(34)
$$ e^{\left( w \right)} = \frac{\Delta y}{\left| y \right|} \cdot 100\% \,;\,y \ne 0, $$
(35)
$$ M = \sqrt {\frac{1}{n}\sum\limits_{w = 1}^{n} {\left( {\Delta y} \right)^{2} } } , $$
(36)
$$ R^{2} = \frac{{\sum\limits_{w = 1}^{n} {\left[ {\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{y}^{\left( w \right)} - \bar{y}} \right]^{2} } }}{{\sum\limits_{w = 1}^{n} {\left[ {y^{\left( w \right)} - \bar{y}} \right]^{2} } }}, $$
(37)

where Δy (w), e (w), M and R 2 are respectively: absolute error, relative error, root-mean-square error and coefficient of determination. The comparison of the performance indices for Oustaloup filter approximation are displayed in Table 1.

Table 1. The comparision of the approximation errors and factors.
Full size table

The estimated transfer functions parameters and obtained indices show high accuracy of the Oustaloup filter approximation. The slight fitting errors could be observed in the range of fractional order from the interval 0.9 ≤ α ≤ 1.7.

In some applications, a zero-pole transfer functions (25–31) as a result of fractional order systems approximation are not helpful. Instead of this, the state-space realisation (23) is desirable. The examples of the approximated integer order state-space matrices for α = 0.5 and α = 1.5 are given by:

$$ \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{A} = \left[ {\begin{array}{*{20}c} {{ - 9} . 4} & { - 26.0} & { - 26.0} & { - 9.4} & { - 1.0} \\ {1.0} & 0 & 0 & 0 & 0 \\ 0 & {1.0} & 0 & 0 & 0 \\ 0 & 0 & {1.0} & 0 & 0 \\ 0 & 0 & 0 & {1.0} & 0 \\ \end{array} } \right],\,\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{B} = \left[ {\begin{array}{*{20}c} 1 \\ 0 \\ 0 \\ 0 \\ 0 \\ \end{array} } \right],\,\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{C} = \left[ {\begin{array}{*{20}c} {0.9} & {5.3} & {8.2} & {4.0} & {0.5} \\ \end{array} } \right],\,\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{D} = \left[ {0.2} \right], $$
$$ \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{A} = \left[ {\begin{array}{*{20}c} { - 8.6} & { - 23.2} & { - 30.3} & { - 23.2} & { - 8.6} & { - 1.0} \\ {1.0} & 0 & 0 & 0 & 0 & 0 \\ 0 & {1.0} & 0 & 0 & 0 & 0 \\ 0 & 0 & {1.0} & 0 & 0 & 0 \\ 0 & 0 & 0 & {1.0} & 0 & 0 \\ 0 & 0 & 0 & 0 & {1.0} & 0 \\ \end{array} } \right],\,\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{B} = \left[ {\begin{array}{*{20}c} 1 \\ 0 \\ 0 \\ 0 \\ 0 \\ 0 \\ \end{array} } \right],\,\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{C} = \left[ {\begin{array}{*{20}c} {0.3} & {4.1} & {15.1} & {19.0} & {8.2} & {1.0} \\ \end{array} } \right]. $$

A step responses of the fractional inertial system (22) in the time duration t = [0, 30] seconds with a step size of h = 0.01 are obtained utilising the Grünwald-Letnikov method (32). The step responses for α ≤ 1 are aperiodic (Fig. 7), however conventional first order inertial system step response can be observed for α = 1. The step responses are oscillating for non-integer system orders α ≥ 1.

Fig. 7.
figure 7

Step responses comparison for inertial system with different order values α

Full size image

6 Conclusions

In this paper the accuracy of the approximation of the Outsaloup filter yielding transfer functions for a given fractional-order inertial model have been verified. The results of the Oustaloup filter approximation of the non-integer inertial model for different values α from the interval 0.5 ≤ α ≤ 1.9 and arbitrary selected narrow bandwidth ω = [10−1, 101] was presented. The simulation results in time and frequency domains confirm high accuracy of the Oustaloup estimation to the selected frequency range and order. The comparison of the performance indices for the Oustaloup approximation model and original plant shows a slight fitting errors for fractional order from the interval 0.9 ≤ α ≤ 1.8. The pole and zero diagrams show that for different values of α, obtained integer order models are stable. The choice of the approximation method depends on established requirements (e.g. accurate frequency behavior or precise time response). The proper Oustaloup’s approximation can be utilised for modelling the fractional order operator in an integer order state-space form. Then, it is possible to use one of the existing optimal control packages to solve fractional order optimal input problem.