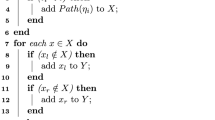Abstract
ABE (Attribute-based encryption) is capable of fine-grained data encryption, and thus has been studied for secure cloud data sharing. While a number of efforts have been dedicated to resolving the user revocation issue in the multi-user cloud data sharing setting, the trust assumption placed upon the cloud server is still high. In this work, we identify the necessity of achieving verifiability of cloud decryption in the proxy-assisted user revocation approach, so as to weaken the trust assumption on the cloud server. We further formulate a model for the system, and present two independent constructions following the formulation. Experimental results show the practicality of our proposed schemes.
Access this chapter
Tax calculation will be finalised at checkout
Purchases are for personal use only
Similar content being viewed by others
Notes
- 1.
Let’s assume to achieve 80-bit security: \(G_T\) could be instantiated such that \(|G_T| = 512, \ell _0 = 160, \epsilon _{\hbar } = 2^{-80}\), then \(|G_T| -\ell _0 - 2\log (1/\epsilon _{\hbar }) = 512 - 160 - 160 = 192\). It is thus more than enough to enable 160-bit block cipher, which can work in an appropriate mode to encrypt message of an arbitrary length.
References
An, J.H., Dodis, Y., Rabin, T.: On the security of joint signature and encryption. In: Knudsen, L.R. (ed.) EUROCRYPT 2002. LNCS, vol. 2332, pp. 83–107. Springer, Heidelberg (2002). doi:10.1007/3-540-46035-7_6
Attrapadung, N., Imai, H.: Attribute-based encryption supporting direct/indirect revocation modes. In: Proceedings of the IMA International Conference on Cryptography and Coding, pp. 278–300 (2009)
Blaze, M., Bleumer, G., Strauss, M.: Divertible protocols and atomic proxy cryptography. In: Nyberg, K. (ed.) EUROCRYPT 1998. LNCS, vol. 1403, pp. 127–144. Springer, Heidelberg (1998). doi:10.1007/BFb0054122
Boneh, D., Ding, X., Tsudik, G., Wong, C.M.: A method for fast revocation of public key certificates and security capabilities. In: Proceedings of the USENIX Security (2001)
Bellare, M., Namprempre, C.: Authenticated encryption: relations among notions and analysis of the generic composition paradigm. In: Okamoto, T. (ed.) ASIACRYPT 2000. LNCS, vol. 1976, pp. 531–545. Springer, Heidelberg (2000). doi:10.1007/3-540-44448-3_41
Bethencourt, J., Sahai, A., Waters, B.: Ciphertext-policy attribute-based encryption. In: Proceedings of IEEE S&P (2007)
CAESAR: Competition for Authenticated Encryption: Security, Applicability, and Robustness. http://competitions.cr.yp.to/caesar.html
Chen, Y., Jiang, L., Yiu, S.M., Au, M., Xuan, W.: Fully-RCCA-CCA-Secure ciphertext-policy attribute based encryption with security mediator. In: Proceedings of the 16th International Conference on Information and Communications Security, ICICS 2014 (2014)
Cloud Security Alliance: Security guidance for critical areas of focus in cloud computing (2009). http://www.cloudsecurityalliance.org
Dodis, Y., Ostrovsky, R., Reyzin, L., Smith, A.: Fuzzy extractor: how to generate strong keys from biometrics and other noisy data. SIAM J. Comput. 38(1), 97–139 (2008)
Network, E., Agency, I.S.: Cloud computing risk assessment. http://www.enisa.europa.eu/act/rm/_les/deliverables/cloud-computing-risk-assessment
Gartner: Don’t trust cloud provider to protect your corporate assets, 28 May 2012. http://www.mis-asia.com/resource/cloud-computing/gartner-dont-trust-cloud-provider-to-protect-your-corporate-assets
Green, M., Hohenberger, S., Waters, B.: Outsourcing the decryption of ABE ciphertexts. In: Proceedings of the USENIX Security (2011)
Goyal, V., Pandy, O., Sahai, A., Waters, B.: Attribute-based encryption for fine-grained access control of encrypted data. In: Proceedings of the ACM CCS 2006 (2006)
Hohenberger, S., Waters, B.: Online/Offline attribute-based encryption. In: Krawczyk, H. (ed.) PKC 2014. LNCS, vol. 8383, pp. 293–310. Springer, Heidelberg (2014). doi:10.1007/978-3-642-54631-0_17
Jiang, T., Chen, X., Li, J., Wong, D.S., Ma, J., Liu, J.K.: Towards secure and reliable cloud storage against data re-outsourcing. Future Gener. Comp. Syst. 52, 86–94 (2015)
Lai, J., Deng, R.H., Guan, C., Weng, J.: Attribute-based encryption with verifiable outsourced decryption. IEEE Trans. Inf. Forensics Secur. 8(8), 1343–1354 (2013)
Liang, K., Au, M.H., Liu, J.K., Susilo, W., Wong, D.S., Yang, G., Yu, Y., Yang, A.: A secure and efficient ciphertext-policy attribute-based proxy re-encryption for cloud data sharing. Future Gener. Comp. Syst. 52, 95–108 (2015)
Liang, K., Susilo, W., Liu, J.K.: Privacy-preserving ciphertext multi-sharing control for big data storage. IEEE Trans. Inf. Forensics Secur. 10(8), 1578–1589 (2015)
Liu, Z., Wong, D.S.: Practical attribute based encryption: traitor tracing, revocation, and large universe. https://eprint.iacr.org/2014/616.pdf
Liu, J., Wan, Z., Gu, M.: Hierarchical attribute-set based encryption for scalable, flexible and fine-grained access control in cloud computing. In: Proceedings of the 7th Information Security Practice and Experience Conference, ISPEC 2011 (2011)
Ostrovsky, R., Sahai, A., Waters, B.: Attribute-based encryption with non-monotonic access structures. In: Proceedings of ACM CCS 2007, pp. 195–203 (2007)
Qin, B., Deng, R.H., Liu, S., Ma, S.: Attribute-based encryption with efficient verifiable outsourced decryption. IEEE Trans. Inf. Forensics Secur. 10(7), 1384–1393 (2015)
Sahai, A., Seyalioglu, H., Waters, B.: Dynamic credentials and ciphertext delegation for attribute-based encryption. In: Proceedings of Advances in Cryptology, Crypto 2012, pp. 199–217 (2012)
Waters, B.: Ciphertext-policy attribute-Based encryption: an expressive, efficient, and provably secure realization. In: Proceedings of Practice and Theory in Public Key Cryptography, PKC 2011, pp. 53–70 (2011)
Wang, G., Liu, Q., Wu, J.: Hierarhical attribute-based encryption for fine-grained access control in cloud storage services. In: Proceedings of ACM CCS 2010 (2010)
Wang, S., Zhou, J., Liu, J.K., Yu, J., Chen, J., Xie, W.: An efficient file hierarchy attribute-based encryption scheme in cloud computing. IEEE Trans. Inf. Forensics Secur. 11(6), 1265–1277 (2016)
Wang, S., Liang, K., Liu, J.K., Chen, J., Yu, J., Xie, W.: Attribute-based data sharing scheme revisited in cloud computing. IEEE Trans. Inf. Forensics Secur. 11(8), 1661–1673 (2016)
Yang, Y., Ding, X., Lu, H., Wan, Z., Zhou, J.: Achieving revocable fine-grained cryptographic access control over cloud data. In: Proceedings of the 16th Information Security Conference, ISC 2013 (2013)
Yang, K., Jia, X.: Expressive, efficient, and revocable data access control for multi-authority cloud storage. IEEE Trans. Parallel Distrib. Syst. 25(7), 1735–1744 (2014)
Yang, K., Jia, X., Ren, K., Zhang, B., Xie, R.: DAC-MACS: Effective Data Access Control for Multiauthority Cloud Storage Systems. IEEE Trans. Inf. Forensics Secur. 8(11), 1790–1801 (2013)
Yang, Y., Liu, J.K., Liang, K., Choo, K.-K.R., Zhou, J.: Extended proxy-assisted approach: achieving revocable fine-grained encryption of cloud data. In: Pernul, G., Ryan, P.Y.A., Weippl, E. (eds.) ESORICS 2015. LNCS, vol. 9327, pp. 146–166. Springer, Cham (2015). doi:10.1007/978-3-319-24177-7_8
Yang, Y., Lu, H., Weng, J., Zhang, Y., Sakurai, K.: Fine-grained conditional proxy re-encryption and application. In: Chow, S.S.M., Liu, J.K., Hui, L.C.K., Yiu, S.M. (eds.) ProvSec 2014. LNCS, vol. 8782, pp. 206–222. Springer, Cham (2014). doi:10.1007/978-3-319-12475-9_15
Yu, S., Wang, C., Ren, K., Lou, W.: Achieving secure, scalable, and fine-grained data access control in cloud computing. In: Proceedings of IEEE INFOCOM 2010 (2010)
Acknowledgments
Joseph K. Liu is supported by the Science and Technology Innovation Projects of Shenzhen (GJHZ20160226202520268). Xinyi Huang is supported by the Distinguished Young Scholars Fund of Fujian (2016J06013) and the State Key Laboratory of Cryptology Research Fund.
Author information
Authors and Affiliations
Corresponding author
Editor information
Editors and Affiliations
Appendix: A Review of the Scheme in [32]
Appendix: A Review of the Scheme in [32]
The details of the scheme in [32] are as follows.
-
Setup \((1^{\kappa })\) : On input a security parameter \(1^{\kappa }\), the algorithm:
- –:
-
determines a bilinear map, \(e: G_0\times G_0 \rightarrow G_T\), where \(G_0\) and \(G_T\) are cyclic groups of \(\kappa \)-bit prime order p;
- –:
-
selects g, which is a generator of \(G_0\);
- –:
-
selects a cryptographic hash function, \(H:\{0,1\}^* \rightarrow G_0\);
- –:
-
picks \(\alpha , \beta \in _R Z_p\), and sets \(params = (e, G_0, g, h = g^{\beta }, {\mathcal {G}}_{\alpha } = e(g,g)^{\alpha })\) and \(msk = (\alpha , \beta )\).
-
UKGen(u): On input a user identity u, the algorithm chooses \(x_u \in _R Z_p\), and sets \((pk_u= g^{x_u}, sk_u = x_u)\). It can be seen that \((pk_u,sk_u)\) is a standard ElGamal type key pair. The cloud server also uses this algorithm to generate a key pair, \((pk_{\textsf {CS}} = g^{x_{\textsf {CS}}}, sk_{\textsf {CS}} = x_{\textsf {CS}})\).
-
PxKGen \((msk, pk_{\textsf {CS}}, pk_u, \mathbb {A}_u)\) : On input \(msk = (\alpha , \beta ), pk_{\textsf {CS}} = g^{x_{\textsf {CS}}}, pk_u = g^{x_u}\) and \(\mathbb {A}_u\), the algorithm chooses \(r_1, r_2, r_i \in _R Z_p, \forall i \in \mathbb {A}_u\), and sets
$$\begin{aligned} PxK_u =(k=(pk_{\textsf {CS}}^{r_1}pk_{u}^{\alpha }g^{r_2})^{\frac{1}{\beta }}, k' = g^{r_1}, \forall i\in \mathbb {A}_u: \{k_{i1} =g^{r_2}H(i)^{r_i}, k_{i2}=g^{r_i}\})\nonumber \end{aligned}$$ -
Encrypt \((m,{\mathcal {T}})\) : Taking as input a message, m, and \({\mathcal {T}}\), the algorithm works as follows: Firstly, it selects a polynomial, \(q_n\), for each node, n, (including the leaf nodes) in \({\mathcal {T}}\). These polynomials are chosen in a top-down manner starting from the root node, rt. For each node n, set the degree \(d_n\) of the polynomial \(q_n\) to be \(d_n = t_n-1\), where \(t_n\) is the threshold value of node n. Starting with the root node, rt, the algorithm chooses an \(s\in _R Z_p\), and sets \(q_{rt}(0) = s\). It next selects \(d_{rt}\) other random points to define \(q_{rt}\) completely. For any other node n, it sets \(q_n(0) = q_{\textsf {parent}(n)}(\textsf {index}(n))\), and chooses \(d_n\) other points to define \(q_n\). Let L be the set of leaf nodes in \({\mathcal {T}}\). The algorithm sets the ciphertext, c, as
$$\begin{aligned} c = ({\mathcal {T}}, C=m\cdot {\mathcal {G}}_{\alpha }^s, C'= & {} h^s, C'' = g^s, \nonumber \\ \forall \ell \in L: \{C_{\ell 1}= & {} g^{q_l(0)}, C_{\ell 2} = H(\textsf {att}(\ell ))^{q_l(0)}\}) \nonumber \end{aligned}$$ -
PxDec \((sk_{\textsf {CS}}, PxK_u, c)\) : On input \(sk_{\textsf {CS}} = x_{\textsf {CS}}\), and \(PxK_u = (k, k', \forall i\in \mathbb {A}_u: \{k_{i1}, k_{i2}\})\) associating with a set of attributes, \(\mathbb {A}_u\), and a ciphertext, \(c = ({\mathcal {T}}, C, C', C'', \forall \ell \in L: \{C_{\ell 1}, C_{\ell 2}\})\), the algorithm outputs an intermediate value, v if \({\mathcal {T}}(\mathbb {A}_u)=1\), and \(\bot \) otherwise. Specifically, the algorithm is recursive. We first define an algorithm, DecNd \(_n(PxK_u, c)\), on a node, n, of \({\mathcal {T}}\). If node, n, is a leaf node, we let \(z = \textsf {att}(n)\) and define as follows: \(z \notin \mathbb {A}_u\), DecNd \(_n(PxK_u, c) = \bot \); otherwise DecNd \(_n(PxK_u, c) = F_n\), where
$$\begin{aligned} F_n = \frac{e(k_{z1}, C_{n1})}{e(k_{z2},C_{n2})} = \frac{e(g^{r_2}H(z)^{r_z}, g^{q_n(0)})}{e(g^{r_z}, H(z)^{q_n(0)})} = e(g,g)^{r_2.q_n(0)} \end{aligned}$$(1)We now consider the recursive case when n is a non-leaf node. The algorithm, DecNd \(_n(PxK_u, c)\), then works as follows. For each child node ch of n, it calls DecNd \(_{ch}(PxK_u, c)\), and stores the output as \(F_{ch}\). Let \(S_n\) be an arbitrary \(t_n\)-sized set of child nodes, ch, such that \(F_{ch} \ne \bot \). If such a set does not exist, then the node is not satisfied and \(\textsf {DecNd}_n(PxK_u,c) = F_n =\bot \). Otherwise, we let the Lagrange coefficient, \(\bigtriangleup _{i,S}\) for \(i\in Z_p\), and a set S of elements in \(Z_p\) be \(\bigtriangleup _{i,S}(x) = \prod _{j\in S,j\ne i}\frac{x-j}{i-j}\). We next compute
$$\begin{aligned} F_n= & {} \prod _{ch\in S_n}F_{ch}^{\bigtriangleup _{i,S_n'}(0)}, \text {where}\,\,\, ^{i=\textsf {index}(ch),} _{S_n' = \{\textsf {index}(ch):ch\in S_n\}} \nonumber \\= & {} \prod _{ch\in S_n}(e(g,g)^{r_2.q_{ch}(0)})^{\bigtriangleup _{i,S_n'}(0)} \nonumber \\= & {} \prod _{ch\in S_n}(e(g,g)^{r_2.q_{\text {parent}(ch)}(\text {index}(ch))})^{\bigtriangleup _{i,S_n'}(0)} \nonumber \\= & {} \prod _{ch\in S_n}(e(g,g)^{r_2.q_n(i)})^{\bigtriangleup _{i,S_n'}(0)} \nonumber \\= & {} e(g,g)^{r_2.q_n(0)} \end{aligned}$$(2)In this way, DecNd \(_{rt}(PxK_u, c)\) for the root node rt can be computed if \({\mathcal {T}}_{rt}(\mathbb {A}_u)=1\), where DecNd \(_{rt}(PxK_u, c)=e(g,g)^{r_2.q_{rt}(0)} = e(g,g)^{r_2.s} = F_{rt}\). Next, the proxy decryption algorithm computes
$$\begin{aligned} \frac{e(k, C')}{e(k', C'')^{x_{\textsf {CS}}}F_{rt}} = \frac{e((pk_{\textsf {CS}}^{r_1}pk_u^{\alpha }g^{r_2})^{\frac{1}{\beta }}, h^s)}{e(g^{r_1}, g^s)^{x_{\textsf {CS}}}e(g,g)^{r_2.s}} = e(pk_u, g)^{s.\alpha }. \end{aligned}$$Finally, it sets \(v = (C=m\cdot {\mathcal {G}}_{\alpha }^s, e(pk_u, g)^{s.\alpha })\).
-
UDec \((sk_u, v)\) : On input a user private key, \(sk_u = x_u\), and an intermediate value, \(v = (C=m\cdot {\mathcal {G}}_{\alpha }^s, e(pk_u, g)^{s.\alpha })\), the user decryption algorithm computes \(\frac{m\cdot {\mathcal {G}}_{\alpha }^s}{(e(pk_u, g)^{s.\alpha })^{x_u^{-1}}} = m\).
-
Revoke \((u,{\mathcal {L}}_{PxK})\) : On input a user identity, u, and the Proxy Key list, \({\mathcal {L}}_{PxK}\), the user revoking algorithm deletes the entry corresponding to u from the list – i.e. \({\mathcal {L}}'_{PxK} = {\mathcal {L}}_{PxK}{\setminus }\{u, PxK_u\}\). In a real world application, an interface should be provided to the data owner for the data owner to perform the update in real-time.
Rights and permissions
Copyright information
© 2017 Springer International Publishing AG
About this paper
Cite this paper
Yang, Y., Liu, J., Wei, Z., Huang, X. (2017). Towards Revocable Fine-Grained Encryption of Cloud Data: Reducing Trust upon Cloud. In: Pieprzyk, J., Suriadi, S. (eds) Information Security and Privacy. ACISP 2017. Lecture Notes in Computer Science(), vol 10342. Springer, Cham. https://doi.org/10.1007/978-3-319-60055-0_7
Download citation
DOI: https://doi.org/10.1007/978-3-319-60055-0_7
Published:
Publisher Name: Springer, Cham
Print ISBN: 978-3-319-60054-3
Online ISBN: 978-3-319-60055-0
eBook Packages: Computer ScienceComputer Science (R0)