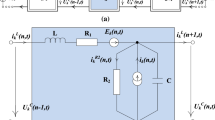
Abstract
This paper develops an Iterative Learning Control (ILC) design applied to an example, active long ladder circuits, of spatially interconnected systems. The design is based on writing the dynamics as those of an equivalent standard differential linear system and then converting to the discrete domain. For this reason, a standard linear systems equivalent model is developed and then discretized. A numerical case study is also given to illustrate the new design.
This is a preview of subscription content, log in via an institution to check access.
Access this chapter
Tax calculation will be finalised at checkout
Purchases are for personal use only
Preview
Unable to display preview. Download preview PDF.
Similar content being viewed by others
References
1. DAndrea, R., Dullerud, G.: Distributed control design for spatially interconnected systems. IEEE Transactions on Automatic Control 48(9) (2003) 1478–1495
2. Alioto, M., Palumbo, G., Poli, M.: Evaluation of energy consumption in RC ladder circuits driven by a ramp input. IEEE Transactions on Very Large Scale Integration (VLSI) Systems 12(10) (2004) 1094–1107
3. Schanbacher, T.: Aspects of positivity in control theory. SIAM Journal on Control and Optimization 27(3) (1989) 457–475
4. Roesser, R.P.: A discrete state-space model for linear image processing. IEEE Transactions on Automatic Control 20(1) (1975) 1–10
5. Fornasini, E., Marchesini, G.: Doubly-indexed dynamical systems: state-space models and structural properties. Mathematical Systems Theory 12 (1978) 59–72
6. Sulikowski, B., Galkowski, K., Kummert, A.: Proportional plus integral control of ladder circuits modeled in the form of two-dimensional (2D) systems. Multidimesional Systems and Signal Processing 26(1) (2015) 267–290 DOI 10.1007/s11045-013-0256-1.
7. Sulikowski, B., Galkowski, K.: Control of discretised sub-class of 2D systems. In: Proceedings of the 35th Chinese Control Conference (CCC), Chengdu, China (2016) 61–66
8. Busłowicz, M., Ruszewski, A.: Computer methods for stability analysis of the Roesser type model of 2D continuous-discrete linear systems. International Journal of Applied Mathematics and Computer Science 22(2) (2012) 401–408
9. Arimoto, S., Kawamura, S., Miyazaki, F.: Bettering operation of robots by learning. Journal of Robotic Systems 1(2) (1984) 123–140
10. Hladowski, L., Galkowski, K., Cai, Z., Rogers, E., Freeman, C.T., Lewin, P.L.: Experimentally supported 2D systems based iterative learning control law design for error convergence and performance. Control Engineering Practice 18(4) (2010) 339–348
11. Paszke, E., Rogers, E., Gałkowski, K., Cai, Z.: Robust finite frequency range iterative learning control design and experimental verification. Control Engineering Practice 21(10) (2013) 1310–1320
12. Sornmo, O., Bernhardsson, B., Kroling, O., Gunnarsson, P., Tenghamn, H.: Frequency-domain iterative learning control of a marine vibrator. Control Engineering Practice 47 (2016) 70–80
13. Rogers, E., Galkowski, K., Owens, D.: Control systems theory and applications for linear repetitive processes. Lecture Notes in Control and Information Sciences, 349. Springer-Verlag, Berlin (2007)
Author information
Authors and Affiliations
Corresponding author
Editor information
Editors and Affiliations
Rights and permissions
Copyright information
© 2017 Springer International Publishing AG
About this paper
Cite this paper
Sulikowski, B., Gałkowski, K., Rogers, E. (2017). Iterative Learning Control for a discretized sub-class of spatially interconnected systems. In: Mitkowski, W., Kacprzyk, J., Oprzędkiewicz, K., Skruch, P. (eds) Trends in Advanced Intelligent Control, Optimization and Automation. KKA 2017. Advances in Intelligent Systems and Computing, vol 577. Springer, Cham. https://doi.org/10.1007/978-3-319-60699-6_72
Download citation
DOI: https://doi.org/10.1007/978-3-319-60699-6_72
Published:
Publisher Name: Springer, Cham
Print ISBN: 978-3-319-60698-9
Online ISBN: 978-3-319-60699-6
eBook Packages: EngineeringEngineering (R0)