Spur-Free and Stable Digital Delta-Sigma Modulator via Using HK-EFM

Abstract

This paper presents a new multi-stage noise-shaping (MASH) digital delta-sigma modulator (DDSM), denoted as HJ-MASH DDSM which can remove spurs in the output spectrum and has long sequence lengths than Jinook structure and HK-MASH in the worst input case by applying HK-EFM in the first stage error feedback modulator (EFM) of the DDSM. In addition, the proposed HJ-MASH DDSM lowers the difficulty of constructing higher order MASH DDSMs compared to HK-MASH DDSM. While the performance and stability are all superior to Jinook structure for all constant inputs, especially for the input which correspond to minimum cycle lengths. The digital delta-sigma modulator applied in fractional-N frequency synthesizers ameliorates the synthesizer’s spectral purity apparently by verification.

1 Introduction

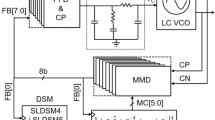
The frequency divider is one of the most significant components of frequency synthesizer, which can support frequency synthesizer to generate multiple high-precision frequency signals. According to divisor, it can be divided into integer divisor and fractional-n divisor. The fractional-n frequency divider can be constructed by using two integer dividers, a divide-by-n divider and a divide-by-(n + 1) divider [1, 2].

The digital delta-sigma modulator (DDSM) is extensively analyzed and used in modern wireless communication subsystems, such as fractional frequency synthesizers, analog-to-digital and digital-to-analog converters, and switched-mode power supplies to acquire an excellent performance and spectral purity. Delta-sigma modulator translate a fine input sequence that should be represented in m bits to a coarse output sequence represented in n bits, where n is significantly less than m. Delta-sigma modulator is a technique for improving the effective resolution of a quantizer by oversampling and noise shaping.

The oversampling ratio OSR is defined as:

$$ OSR = \frac{{f_{s} }}{{2f_{B} }} $$

(1)

where $f_{s}$ is the sampling frequency and $f_{B}$ is the largest frequency component in the signal spectrum. $2f_{B}$ corresponds to the Nyquist frequency. Besides, the low frequency part of the rest of its spectrum is attenuated and its high frequency part is amplified. In that case, the oversampling and the noise shaping property of the DSM can be used together to achieve a high signal-to-quantization-noise ratio using a relatively coarse quantizer [3, 4].

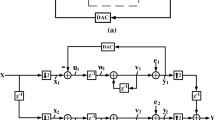
Delta-sigma modulator (DSM) is widely used to select a clock divider in the fractional-N frequency synthesizer. As shown in Fig. 1, the conventional first–order DSM consists of a digital accumulator, a register, a quantizer and feedback loop. Since the DSM is a finite-state machine (FSM), its output sequence is periodic when the input is a constant value. More importantly, the quantization noise sequence is also periodic, and the noise sequence period or the sequence length is strongly dependent on the input value and the DSM structure. If the sequence length is short, the quantization noise power is spread over a small number of tones, resulting in spurs in the noise spectrum.

Fig. 1.

Block diagram of the EFM1

The first-order EFM is widely used in implementing the first-order DSM, since the error feedback modulator (EFM) has a relatively low hardware cost and low power consumption. We show the block diagram of a first order EFM1 that used a multi-bit quantizer. The input to the modulator is a digital word with n bit. When the v[n] is greater than M (2ⁿ), the quantizer overflows and the output signal y[n] (the carry out) will be one. Otherwise, the quantizer does not overflow and y[n] will be zero as follow:

$$ y\left[ n \right] = \left\{ {\begin{array}{*{20}l} {0,} \hfill & {v\left[ n \right] < M} \hfill \\ {1,} \hfill & {v\left[ n \right] < M} \hfill \\ \end{array} } \right. $$

(2)

The rest of this paper is organized as follows. Section 2 summarizes previous works and describes the architecture and performance of HK-MASH and Jinook MASH, respectively. Section 3 presents the proposed MASH structure, and describes the simulation results and comparisons with other works. Concluding remarks are made in Sect. 4 after acknowledgment. Additionally, simulation results are verified by Simulink & MATLAB.

2 Previous MASH Architecture

By contrast with the SQ-DDSM and EFM, both of which use a single quantizer, the multistage noise shaping (MASH) technique allows one to realize high order noise shaping using lower modulators. In MASH DDSM, one can use lower order modulators (with orders as low as 1) in a cascade. If first order stages are available, L stages can be combined to form an L ^th order MASH modulator. A MASH DDSM with 1-bit internal first order modulators is a feedforward structure and is unconditionally stable; this is the principal advantage of the MASH modulator over the SQ-DDSM topology. Furthermore, in a MASH DDSM, the stable input range is equal to the full scale while the stable input range is only a fraction of the full scale in an SQ-DDSM. The MASH DDSM is widely used in commercial fractional-N frequency synthesizer products.

2.1 HK-MASH Architecture

The basic building block of the HK-MASH DDSM [5] is the first order HK-EFM1 shown in Fig. 2, it is very similar to the convention EFM1. The main difference compared to the conventional EFM1 shown in Fig. 1 in that it includes a feedback block denoted as $az^{ - 1}$. Therefore, the cycle lengths of conventional EFMs are maximized by introducing a feedback path from the output of each EFM to its input using a delay block with a particular choice of coefficient a, where a is a small integer that is chose such that $M - a$ is primer.

Fig. 2.

Block diagram of the HK-EFM1

$$ STF\left( z \right) = \frac{1}{M}\frac{1}{{1 - \alpha z^{ - 1} }}\,{\text{and}}\,\,NTF\left( z \right) = \frac{1}{M}\frac{{1 - z^{ - 1} }}{{1 - \alpha z^{ - 1} }} \, $$

(3)

The parameter $\alpha$ is the normalized version $a$ of given by

$$ \alpha = \frac{a}{M} $$

(4)

Figure 3 show a block diagram of an L ^th order MASH DDSM comprising a cascade of n-bit HK-EFM1 blocks and an error cancellation network. As in the conventional MASH structure, the negative of the quantization error from each stage (-ei[n]) is once again fed to the next stage and the output of each stage (yi[n]) is fed to the error cancellation network, which eliminates the intermediate quantization noise terms. The output of the L ^th order HK-MASH DDSM can be expressed in the Z-domain as:

Fig. 3.

Block diagram of an L ^th order HK-MASH DDSM incorporating a cascade of HK-EFM1

$$ Y\left( z \right) = \frac{1}{M}\frac{1}{{1 - \alpha z^{ - 1} }}X\left( z \right) + \frac{1}{M}\frac{{(1 - z^{ - 1} )^{L} }}{{1 - \alpha z^{ - 1} }}E_{L} (z) $$

(5)

By contrast with a conventional modulator ($\alpha = 0$), a pole at $z = \alpha$ is added to both the STF and the NTF. If $\alpha$ is sufficiently small, this pole is very close to the origin in the $z$ plane; equivalently, it is a distant pole which does not significantly affect the overall operation of the modulator. In order to illustrate this point, consider the magnitude response of the multiplying factor $G_{hk} \left( z \right) = \frac{1}{{1 - \alpha z^{ - 1} }}$ which appears in the STF and the NTF. Substituting $z = e^{jw}$ into $G_{hk} \left( z \right)$ and calculating the resulting magnitude yields

$$ 20log_{10} \left( {\left| {G_{hk} \left( {e^{jw} } \right)} \right|} \right) = 20log_{10} (\frac{1}{{\sqrt {1 + \alpha^{2} - 2\alpha { \cos }(w)} }}) $$

(6)

Figure 4 shows (6) for different values of, namely 0, $\frac{1}{{2^{5} }}$, $\frac{3}{{2^{9} }}$, $\frac{3}{{2^{19} }}$. As $\alpha$ decreases, the resulting spectrum approaches that of $\alpha$ = 0. When $\alpha$ = $\frac{3}{{2^{9} }}$, the magnitude of $G_{hk}$ at low frequencies is only 0.05 dB.

Fig. 4.

Magnitude response of the multiplying factor $\frac{1}{{1 - \alpha z^{ - 1} }}$

In our example, we consider a 9-bit HK-MASH DDSM3, a 19-bit HK-MASH-DDSM3 and a 20-bit HK-MASH DDSM3. Therefore, the value of $a$ has been set to 3, 1, 3, respectively, which corresponds to a carry in bit and simplifies the implementation. The output of HK-MASH DDSM3 is given by

$$ Y\left( z \right) = \frac{1}{M}\frac{1}{{1 - \alpha z^{ - 1} }}X\left( z \right) + \frac{1}{M}\frac{{(1 - z^{ - 1} )^{3} }}{{1 - \alpha z^{ - 1} }}E_{3} (z) $$

(7)

The sequence length of the L^th HK-MASH DDSM have been proven mathematically to be equal to $({\text{M}} - {\text{a}})^{\text{L}}$. Therefore, the sequence length of the HK-MASH DDSM3 is $({\text{M}} - {\text{a}})^{3}$.

Figure 5 shows the simulated power spectrum of the HK-MASH DDSM3 when the input is half-scale, once again with zero initial condition and no dither. Note that the spectrum is close to the ideal white noise case, and no individual tones can be seen.

Fig. 5.

Simulated power spectrum for 9-bit, 19-bit, 20-bit HK-MASH DDSM3 (top - down)

2.2 Jinook Structure

The basic building block of the Jinook MASH structure [6, 7] is the first order MEFM1 shown in Fig. 6, it is very similar to the convention EFM1. The main difference compared to the conventional EFM1 shown in Fig. 1 in that it takes two inputs and generates two ouputs to be fed to the next EFM. In the MEFM1, the output is delivered to not only the noise cancellation network but also the subsequent MEFM1. Therefore, the Jinook MASH structure links the EFMs by connecting the output and the quantization error signal of an EFM to the input of the next-stage EFM.

Fig. 6.

Block diagram of the MEFM1

Figure 7 show a block diagram of an L ^th order Jinook MASH DDSM with EFM1 block, MEFM1 blocks and an error cancellation network. The Jinook MASH DDSM totally stands in matching the input value and the output average and that provides long sequence lengths for the full input range. Besides, it’s significant to note that the block of the first stage is a conventional EFM1, therefore, the input of EFM1 is a pure dc signal and not a perturbed one. In the MEFM1, the output and the quantization error signals that are to be connected to the next stage have the same sequence length. Since two periodic inputs can be regarded as one periodic signal, the MEFM1 is functionally equivalent to the traditional EFM, and it generates a periodic output signal.

Fig. 7.

Block diagram of an L ^th order Jinook MASH DDSM

The output of the L ^th Jinook MASH DDSM can be expressed in the Z-domain as:

$$ Y\left( z \right) = \frac{1}{M}X^{'} \left( z \right) + \frac{1}{M}\left( {1 - z^{ - 1} } \right)^{L} E^{'} (z) $$

(8)

$$ X^{'} \left( z \right) = \{ 1 + \frac{1}{M}\left( {1 - z^{ - 1} } \right) + \cdots + \frac{1}{{M^{L - 1} }}\left( {1 - z^{ - 1} } \right)^{L - 1} \} X(z) $$

(9)

$$ E^{'} \left( z \right) = E_{L} \left( z \right) + \frac{1}{M}E_{L - 1} \left( z \right) + \cdots + \frac{1}{{M^{L - 1} }}E_{1} (z) $$

(10)

In our example, we consider a 9-bit Jinook MASH DDSM3, a 19-bit Jinook MASH-DDSM3 and a 20-bit Jinook MASH DDSM3. The output of these Jinook MASH DDSM3 is given by

$$ Y\left( z \right) = \frac{1}{M}\{ 1 + \frac{1}{M}\left( {1 - z^{ - 1} } \right) + \frac{1}{{M^{2} }}\left( {1 - z^{ - 1} } \right)^{2} \} X(z) + \frac{{\left( {1 - z^{ - 1} } \right)^{3} }}{M}\{ E_{3} (z) + \frac{1}{M}E_{2} \left( z \right) + \frac{1}{{M^{2} }}E_{1} \left( z \right)\} $$

(11)

Now, let us derive the sequence length of the Jinook MASH DDSM3. Firstly, the sequence length N ₁ of the first stage is explicitly related to the constant input. The sequence lengths of the second and the third stages of the Jinook MASH DDSM3 is $N_{1} \cdot M$ and $N_{1} \cdot M^{2}$, respectively, if the input signal is constant. Therefore, the sequence length of the L ^th Jinook MASH DDSM is $N_{1} \cdot M^{L - 1}$ if the signal is constant.

Figure 8 shows the simulated power spectrum of the Jinook MASH DDSM3 when the input is half-scale in the left column and the input is only one-tenth of Min the right column, once again with zero initial condition and no dither. Note that the spectrums of the right column are superior to the left ones, because the Jinook MASH DDSM gets the minimum sequence length and the performance of structure is not stable when the input is equal to half-scale in the left column. Due to the unstable performance, it is necessary to advance a new structure which can ameliorate the stability and do not improve the complexity of structure.

Fig. 8.

Simulated power spectrum for 9-bit, 19-bit, 20-bit Jinook MASH DDSM3 (top - down), the input of left subgraph and right subgraph is $\frac{M}{2}$ and $\frac{M}{10}$, respectively

3 Proposed MASH Structure

Although the noise shaping effect of HK-MASH is amazing, it is complicated to construct the hardware implementation of HK-MASH and the input is not exactly equal to the output. Besides, the noise shaping effect of the Jinook structure exhibits instabilities in some input cases and the minimum output sequence length is dependent on the output sequence length of the first-stage EFM cell. In this section, we proposed a new MASH structure shown in Fig. 9 that can totally make a trade-off between complexity and performance. The structure is similar to the Jinook structure but the first-stage EFM cell replaces with HK-EFM, which can effectively increase the sequence length and lower the whole complexity of hardware implementation, so we denote our structure as HJ-MASH.

Fig. 9.

Block diagram of an L ^th order proposed HJ-MASH DDSM

In our example, we consider the 3^rd-order MASH DDSM, The output of the proposed HJ-MASH DDSM3 is given by

$$ Y\left( z \right) = \frac{1}{M}\frac{1}{{1 - \alpha z^{ - 1} }}X^{'} \left( z \right) + p_{1} \left( z \right)E_{1} \left( z \right) + \frac{1}{M}\left( {1 - z^{ - 1} } \right)^{3} E^{'} (Z) $$

(12)

$$ p_{1} \left( z \right) = \frac{{\alpha z^{ - 1} (1 - z^{ - 1} )}}{{M(1 - \alpha z^{ - 1} )}} + \frac{{\alpha z^{ - 1} (1 - z^{ - 1} )^{2} }}{{M^{2} (1 - \alpha z^{ - 1} )}} + \frac{{(1 - z^{ - 1} )^{3} }}{{M^{3} (1 - \alpha z^{ - 1} )}} $$

(13)

$$ X^{'} \left( z \right) = (1 + \frac{{1 - z^{ - 1} }}{M} + \frac{{(1 - z^{ - 1} )^{2} }}{{M^{2} }}) $$

(14)

$$ E^{'} \left( z \right) = E_{3} \left( z \right) + \frac{1}{M}E_{2} (z) $$

(15)

Now, let us derive the sequence length of the proposed HJ-MASH DDSM3. Firstly, the sequence length N ₁ of the first stage is exactly equal to $(M - a)$ for all constant inputs and for all initial condition. The sequence lengths of the second and the third stages of the HJ-MASH DDSM3 is $N_{1} \cdot M$ and $N_{1} \cdot M^{2}$, respectively. Therefore, the sequence length of the L ^th proposed HJ-MASH DDSM is $N_{1} \cdot M^{L - 1}$ if the signal is constant. In that case, the sequence length of the HJ-MASH DDSM3 is exactly equal to $M^{2} (M - a)$, which is higher than the sequence length of HK-MASH DDSM3 and Jinook MASH DDSM3 for most input. Therefore, the sequence length of the L ^th proposed HJ-MASH DDSM is $(M - a) \cdot M^{L - 1}$ if the signal is constant.

Figure 10 shows the simulated power spectrum of the proposed HJ-MASH DDSM3 when the input is half-scale, once again with zero initial condition and no dither. Note that the spectrum is close to the ideal white noise case, and no individual tones can be seen except the first sub-graph. According to Fig. 3, If $\alpha$ is sufficiently small, this pole is very close to the origin in the $z$ plane; equivalently, it is a distant pole which does not significantly affect the overall operation of the modulator.

Fig. 10.

Simulated power spectrum for 9-bit, 19-bit, 20-bit proposed HJ-MASH DDSM3 (top - down)

Figure 11 shows the comparison of simulated power spectrum between the proposed HJ-MASH DDSM3 and the Jinook structure. The input of the first subgraph is half-scale, once again with zero initial condition and no dither. while the input of second subgraph is one-tenth of M. According to this, it can be easily concluded that the performance and stability of proposed HJ-MASH structure are all superior to Jinook structure.

Fig. 11.

Simulated power spectrum for 9-bit, 19-bit proposed HJ-MASH DDSM3 and Jinook DDSM3 (top – down)

4 Conclusion

A new MASH DDSM (denoted as HJ-MASH DDSM) has been presented to remove spurs in the output spectrum. In addition to the spur-free property, when the number of input bits n is large enough, the deviation between input and output resulted from the feedback loop of first-stage EFM can be ignored, and it can be assumed that the input is approximately equal to the output. Meanwhile, the output sequence length of the proposed structure is $M^{L - 1} (M - a)$, the length is higher than Jinook structure and HK-MASH in the worst input case. Besides, the simulation shows that the noise shaping effect of the proposed structure is better than Jinook structure, while almost catch up with HK-MASH, the complexity is decreased and the stability is improved. At the same time, it can be proved that the hardware consumption of the proposed structure is close to the conventional MASH structure, less than HK-MASH [8].

Spur suppression technique are significant to fractional-N frequency synthesizers. Conventional HK-MASH requires extra hardware and has a high complexity to accomplish, and Jinook MASH has a terrible performance while the input is half-scale. The proposed HJ-MASH structure in this paper can perform stable and excellent in any input while just take little hardware overhead as compared with HK-MASH.