Abstract
We consider the problem of developing automated techniques for solving recurrence relations to aid the expected-runtime analysis of programs. The motivation is that several classical textbook algorithms have quite efficient expected-runtime complexity, whereas the corresponding worst-case bounds are either inefficient (e.g., Quick-Sort), or completely ineffective (e.g., Coupon-Collector). Since the main focus of expected-runtime analysis is to obtain efficient bounds, we consider bounds that are either logarithmic, linear or almost-linear (\(\mathcal {O}(\log {n})\), \(\mathcal {O}(n)\), \(\mathcal {O}(n\cdot \log {n})\), respectively, where n represents the input size). Our main contribution is an efficient (simple linear-time algorithm) sound approach for deriving such expected-runtime bounds for the analysis of recurrence relations induced by randomized algorithms. The experimental results show that our approach can efficiently derive asymptotically optimal expected-runtime bounds for recurrences of classical randomized algorithms, including Randomized-Search, Quick-Sort, Quick-Select, Coupon-Collector, where the worst-case bounds are either inefficient (such as linear as compared to logarithmic expected-runtime complexity, or quadratic as compared to linear or almost-linear expected-runtime complexity), or ineffective.
You have full access to this open access chapter, Download conference paper PDF
Similar content being viewed by others

1 Introduction
Static Analysis for Quantitative Bounds. Static analysis of programs aims to reason about programs without running them. The most basic properties for static analysis are qualitative properties, such as safety, termination, liveness, that for every trace of a program gives a Yes or No answer (such as assertion violation or not, termination or not). However, recent interest in analysis of resource-constrained systems, such as embedded systems, as well as for performance analysis, quantitative performance characteristics are necessary. For example, the qualitative problem of termination asks whether a given program always terminates, whereas the quantitative problem asks to obtain precise bounds on the number of steps, and is thus a more challenging problem. Hence the problem of automatically reasoning about resource bounds (such as time complexity bounds) of programs is both of significant theoretical as well as practical interest.
Worst-Case Bounds. The worst-case analysis of programs is the fundamental problem in computer science, which is the basis of algorithms and complexity theory. However, manual proofs of worst-case analysis can be tedious and also require non-trivial mathematical ingenuity, e.g., the book The Art of Computer Programming by Knuth presents a wide range of involved techniques to derive such precise bounds [37]. There has been a considerable research effort for automated analysis of worst-case bounds for programs, see [23, 24, 26, 27] for excellent expositions. For the worst-case analysis there are several techniques, such as worst-case execution time analysis [46], resource analysis using abstract interpretation and type systems [2, 24, 26, 27, 34], ranking functions [7, 8, 15, 17, 41, 42, 44, 47] as well as recurrence relations [2,3,4, 21].
Expected-Runtime Bounds. While several works have focused on deriving worst-case bounds for programs, quite surprisingly little work has been done to derive precise bounds for expected-runtime analysis, with the exception of [20], which focuses on randomization in combinatorial structures (such as trees). This is despite the fact that expected-runtime analysis is an equally important pillar of theoretical computer science, both in terms of theoretical and practical significance. For example, while for real-time systems with hard constraints worst-case analysis is necessary, for real-time systems with soft constraints the more relevant information is the expected-runtime analysis. Below we highlight three key significance of expected-runtime analysis.
-
1.
Simplicity and desired properties: The first key aspect is simplicity: often much simpler algorithms (thus simple and efficient implementations) exist for expected-runtime complexity as compared to worst-case complexity. A classic example is the Selection problem that given a set of n numbers and \(0\le k \le n\), asks to find the k-th largest number (e.g., for median \(k=n/2\)). The classical linear-time algorithm for the problem (see [16, Chap. 9]) is quite involved, and its worst-case analysis to obtain linear time bound is rather complex. In contrast, a much simpler algorithm exists (namely, Quick-Select) that has linear expected-runtime complexity. Moreover, randomized algorithms with expected-runtime complexity enjoy many desired properties, which deterministic algorithms do not have. A basic example is Channel-Conflict Resolution (see Example 7, Sect. 2.4) where the simple randomized algorithm can be implemented in a distributed or concurrent setting, whereas deterministic algorithms are quite cumbersome.
-
2.
Efficiency in practice: Since worst-case analysis concerns with corner cases that rarely arise, many algorithms and implementations have much better expected-runtime complexity, and they perform extremely well in practice. A classic example is the Quick-Sort algorithm, that has quadratic worst-case complexity, but almost linear expected-runtime complexity, and is one of the most efficient sorting algorithms in practice.
-
3.
Worst-case analysis ineffective: In several important cases the worst-case analysis is completely ineffective. For example, consider one of the textbook stochastic process, namely the Coupon-Collector problem, where there are n types of coupons to be collected, and in each round, a coupon type among the n types is obtained uniformly at random. The process stops when all types are collected. The Coupon-Collector process is one of the basic and classical stochastic processes, with numerous applications in network routing, load balancing, etc. (see [39, Chap. 3] for applications of Coupon-Collector problems). For the worst-case analysis, the process might not terminate (worst-case bound infinite), but the expected-runtime analysis shows that the expected termination time is \(\mathcal {O}(n \cdot \log n)\).
Challenges. The expected-runtime analysis brings several new challenges as compared to the worst-case analysis. First, for the worst-case complexity bounds, the most classical characterization for analysis of recurrences is the Master Theorem (cf. [16, Chap. 1]) and Akra-Bazzi’s Theorem [1]. However, the expected-runtime analysis problems give rise to recurrences that are not characterized by these theorems since our recurrences normally involve an unbounded summation resulting from a randomized selection of integers from 1 to n where n is unbounded. Second, techniques like ranking functions (linear or polynomial ranking functions) cannot derive efficient bounds such as \(\mathcal {O}(\log n)\) or \(\mathcal {O}(n \cdot \log n)\). While expected-runtime analysis has been considered for combinatorial structures using generating function [20], we are not aware of any automated technique to handle recurrences arising from randomized algorithms.
Analysis Problem. We consider the algorithmic analysis problem of recurrences arising naturally for randomized recursive programs. Specifically we consider the following:
-
We consider two classes of recurrences: (a) univariate class with one variable (which represents the array length, or the number of input elements, as required in problems such as Quick-Select, Quick-Sort etc.); and (b) separable bivariate class with two variables (where the two independent variables represent the total number of elements and total number of successful cases, respectively, as required in problems such as Coupon-Collector, Channel-Conflict Resolution). The above two classes capture a large class of expected-runtime analysis problems, including all the classical ones mentioned above. Moreover, the main purpose of expected-runtime analysis is to obtain efficient bounds. Hence we focus on the case of logarithmic, linear, and almost-linear bounds (i.e., bounds of form \(\mathcal {O}(\log n)\), \(\mathcal {O}(n)\) and \(\mathcal {O}(n \cdot \log n)\), respectively, where n is the size of the input). Moreover, for randomized algorithms, quadratic bounds or higher are rare.
Thus the main problem we consider is to automatically derive such efficient bounds for randomized univariate and separable bivariate recurrence relations.
Our Contributions. Our main contribution is a sound approach for analysis of recurrences for expected-runtime analysis. The input to our problem is a recurrence relation and the output is either logarithmic, linear, or almost-linear as the asymptotic bound, or fail. The details of our contributions are as follows:
-
1.
Efficient algorithm. We first present a linear-time algorithm for the univariate case, which is based on simple comparison of leading terms of pseudo-polynomials. Second, we present a simple reduction for separable bivariate recurrence analysis to the univariate case. Our efficient (linear-time) algorithm can soundly infer logarithmic, linear, and almost-linear bounds for recurrences of one or two variables.
-
2.
Analysis of classical algorithms. We show that for several classical algorithms, such as Randomized-Search, Quick-Select, Quick-Sort, Coupon-Collector, Channel-Conflict Resolution (see Sects. 2.2 and 2.4 for examples), our sound approach can obtain the asymptotically optimal expected-runtime bounds for the recurrences. In all the cases above, either the worst-case bounds (i) do not exist (e.g., Coupon-Collector), or (ii) are quadratic when the expected-runtime bounds are linear or almost-linear (e.g., Quick-Select, Quick-Sort); or (iii) are linear when the expected-runtime bounds are logarithmic (e.g., Randomized-Search). Thus in cases where the worst-case bounds are either not applicable, or grossly overestimate the expected-runtime bounds, our technique is both efficient (linear-time) and can infer the optimal bounds.
-
3.
Implementation. Finally, we have implemented our approach, and we present experimental results on the classical examples to show that we can efficiently achieve the automated expected-runtime analysis of randomized recurrence relations.
Novelty and Technical Contribution. The key novelty of our approach is an automated method to analyze recurrences arising from randomized recursive programs, which are not covered by Master theorem. Our approach is based on a guess-and-check technique. We show that by over-approximating terms in a recurrence relation through integral and Taylor’s expansion, we can soundly infer logarithmic, linear and almost-linear bounds using simple comparison between leading terms of pseudo-polynomials.
Due to page limit, we omitted some technical details. They can be found in [12].
2 Recurrence Relations
We present our mini specification language for recurrence relations for expected-runtime analysis. The language is designed to capture running time of recursive randomized algorithms which involve (i) only one function call whose expected-runtime complexity is to be determined, (ii) at most two integer parameters, and (iii) involve randomized-selection or divide-and-conquer techniques. We present our language separately for the univariate and bivariate cases. In the sequel, we denote by \(\mathbb {N}\), \(\mathbb {N}_0\), \(\mathbb {Z}\), and \(\mathbb {R}\) the sets of all positive integers, non-negative integers, integers, and real numbers, respectively.
2.1 Univariate Randomized Recurrences
Below we define the notion of univariate randomized recurrence relations. First, we introduce the notion of univariate recurrence expressions. Since we only consider single recursive function call, we use ‘\(\mathrm {T}\)’ to represent the (only) function call. We also use ‘\(\mathfrak {n}\)’ to represent the only parameter in the function declaration.
Univariate Recurrence Expressions. The syntax of univariate recurrence expressions \(\mathfrak {e}\) is generated by the following grammar:
where \(c\in [1,\infty )\) and \(\ln (\centerdot )\) represents the natural logarithm function with base e. Informally, \(\mathrm {T}(\mathfrak {n})\) is the (expected) running time of a recursive randomized program which involves only one recursive routine indicated by \(\mathrm {T}\) and only one parameter indicated by \(\mathfrak {n}\). Then each \(\mathrm {T}(\centerdot )\)-term in the grammar has a direct algorithmic meaning:
-
\(\mathrm {T}\left( \mathfrak {n}-1\right) \) may mean a recursion to a sub-array with length decremented by one;
-
\(\mathrm {T}\left( \left\lfloor \frac{\mathfrak {n}}{2}\right\rfloor \right) \) and \(\mathrm {T}\left( \left\lceil \frac{\mathfrak {n}}{2}\right\rceil \right) \) may mean a recursion related to a divide-and-conquer technique;
-
finally, \(\frac{\sum _{\mathfrak {j}=1}^{\mathfrak {n}-1} \mathrm {T}(\mathfrak {j})}{\mathfrak {n}} \text{ and } \frac{1}{\mathfrak {n}}\cdot \left( \sum _{\mathfrak {j}=\left\lceil \frac{n}{2}\right\rceil }^{\mathfrak {n}-1}\mathrm {T}(\mathfrak {j})+ \sum _{\mathfrak {j}=\left\lfloor \frac{\mathfrak {n}}{2}\right\rfloor }^{\mathfrak {n}-1} \mathrm {T}(\mathfrak {j})\right) \) may mean a recursion related to a randomized selection of an array index.
Substitution. Consider a function \(h:\mathbb {N}\rightarrow \mathbb {R}\) and univariate recurrence expression \({\mathfrak {e}}\). The substitution function, denoted by \(\mathsf {Subst}({\mathfrak {e}},h)\), is the function from \(\mathbb {N}\) into \(\mathbb {R}\) such that the value for n is obtained by evaluation through substituting h for \(\mathrm {T}\) and n for \(\mathfrak {n}\) in \({\mathfrak {e}}\), respectively. Moreover, if \(\mathfrak {e}\) does not involve the appearance of ‘\(\mathrm {T}\)’, then we use the abbreviation \(\mathsf {Subst}({\mathfrak {e}})\) i.e., omit h. For example, (i) if \({\mathfrak {e}}= \mathfrak {n} + \mathrm {T}(\mathfrak {n}-1)\), and \(h: n \mapsto n\cdot \log n\), then \(\mathsf {Subst}({\mathfrak {e}},h)\) is the function \(n \mapsto n+ (n-1)\cdot \log (n-1)\), and (ii) if \({\mathfrak {e}}= 2\cdot \mathfrak {n}\), then \(\mathsf {Subst}({\mathfrak {e}})\) is \(n \mapsto 2n\).
Univariate Recurrence Relation. A univariate recurrence relation \(G=(\mathsf {eq}_1,\mathsf {eq}_2)\) is a pair of equalities as follows:
where \(c\in (0,\infty )\) and \(\mathfrak {e}\) is a univariate recurrence expression. For a univariate recurrence relation G the evaluation sequence \(\mathsf {Eval}(G)\) is as follows: \(\mathsf {Eval}(G)(1)=c\), and for \(n \ge 2\), given \(\mathsf {Eval}(G)(i)\) for \(1\le i < n\), for the value \(\mathsf {Eval}(G)(n)\) we evaluate the expression \(\mathsf {Subst}(\mathfrak {e},\mathsf {Eval}(G))\), since in \(\mathfrak {e}\) the parameter \(\mathfrak {n}\) always decreases and is thus well-defined.
Finite vs Infinite Solution. Note that the above description gives a computational procedure to compute \(\mathsf {Eval}(G)\) for any finite n, in linear time in n through dynamic programming. The interesting question is to algorithmically analyze the infinite behavior. A function \(T_G:\mathbb {N}\rightarrow \mathbb {R}\) is called a solution to G if \(T_G(n)=\mathsf {Eval}(G)(n)\) for all \(n \ge 1\). The function \(T_G\) is unique and explicitly defined as follows: (1) Base Step. \(T_G(1):=c\); and (2) Recursive Step. \(T_G(n):=\mathsf {Subst}(\mathfrak {e},T_G)(n)\) for all \(n\ge 2\). The algorithmic question is to reason about the asymptotic infinite behaviour of \(T_G\).
2.2 Motivating Classical Examples
In this part we present several classical examples of randomized programs whose recurrence relations belong to the class of univariate recurrence relations described in Sect. 2.1. In all cases the base step is \(\mathrm {T}(1)=1\), hence we discuss only the recursive case.
Example 1
\({{ (}\textsc {Randomized}{\text {-}}\textsc {Search}{} { ).}}\) Consider the Sherwood’s Randomized-Search algorithm (cf. [38, Chap. 9]). The algorithm checks whether an integer value d is present within the index range [i, j] (\(0\le i\le j\)) in an integer array ar which is sorted in increasing order and is without duplicate entries. The algorithm outputs either the index for d in ar or \(-1\) meaning that d is not present in the index range [i, j] of ar. The recurrence relation for this example is as follows:
We note that the worst-case complexity for this algorithm is \(\varTheta (n)\). \(\square \)
Example 2
\({{ (}\textsc {Quick}{\text {-}}\textsc {Sort}{} { ).}}\) Consider the Quick-Sort algorithm [16, Chap. 7]. The recurrence relation for this example is:
where \(\mathrm {T}(\mathfrak {n})\) represents the maximal expected execution time where \(\mathfrak {n}\) is the array length and the execution time of pivoting is represented by \(2\cdot \mathfrak {n}\). We note that the worst-case complexity for this algorithm is \(\varTheta (n^2)\). \(\square \)
Example 3
\({ (}\textsc {Quick}{\text {-}}\textsc {Select}{} { ).}\) Consider the Quick-Select algorithm (cf. [16, Chap. 9]). The recurrence relation for this example is
We note that the worst-case complexity for this algorithm is \(\varTheta (n^2)\). \(\square \)
Example 4
\({{ (}\textsc {Diameter}{\text {-}}\textsc {Computation}{} { ).}}\) Consider the Diameter-Computa tion algorithm (cf. [39, Chap. 9]) to compute the diameter of an input finite set S of three-dimensional points. Depending on Eucledian or \(L_1\) metric we obtain two different recurrence relations. For Eucledian we have the following relation:
and for \(L_1\) metric we have the following relation:
We note that the worst-case complexity for this algorithm is as follows: for Euclidean metric it is \(\varTheta (n^2 \cdot \log n)\) and for the \(L_1\) metric it is \(\varTheta (n^2)\). \(\square \)
Example 5
(Sorting with Quick-Select ). Consider a sorting algorithm which selects the median through the Quick-Select algorithm. The recurrence relation is directly obtained as follows:
where \(T^*(\centerdot )\) is an upper bound on the expected running time of Quick-Select (cf. Example 3). We note that the worst-case complexity for this algorithm is \(\varTheta (n^2)\). \(\square \)
2.3 Separable Bivariate Randomized Recurrences
We consider a generalization of the univariate recurrence relations to a class of bivariate recurrence relations called separable bivariate recurrence relations. Similar to the univariate situation, we use ‘\(\mathrm {T}\)’ to represent the (only) function call and ‘\(\mathfrak {n}\)’, ‘\(\mathfrak {m}\)’ to represent namely the two integer parameters.
Separable Bivariate Recurrence Expressions. The syntax of separable bivariate recurrence expressions is illustrated by \(\mathfrak {e},\mathfrak {h}\) and \(\mathfrak {b}\) as follows:
The differences are that (i) we have two independent parameters \(\mathfrak {n},\mathfrak {m}\), (ii) \(\mathfrak {e}\) now represents an expression composed of only \(\mathrm {T}\)-terms, and (iii) \(\mathfrak {h}\) (resp. \(\mathfrak {b}\)) represents arithmetic expressions for \(\mathfrak {n}\) (resp. for \(\mathfrak {m}\)). This class of separable bivariate recurrence expressions (often for brevity bivariate recurrence expressions) stresses a dominant role on \(\mathfrak {m}\) and a minor role on \(\mathfrak {n}\), and is intended to model randomized algorithms where some parameter (to be represented by \(\mathfrak {n}\)) does not change value.
Substitution. The notion of substitution is similar to the univariate case. Consider a function \(h:\mathbb {N}\times \mathbb {N}\rightarrow \mathbb {R}\), and a bivariate recurrence expression \({\mathfrak {e}}\). The substitution function, denoted by \(\mathsf {Subst}({\mathfrak {e}},h)\), is the function from \(\mathbb {N}\times \mathbb {N}\) into \(\mathbb {R}\) such that \(\mathsf {Subst}({\mathfrak {e}},h)(n,m)\) is the real number evaluated through substituting h, n, m for \(\mathrm {T},\mathfrak {n},\mathfrak {m}\), respectively. The substitution for \(\mathfrak {h},\mathfrak {b}\) is defined in a similar way, with the difference that they both induce a univariate function.
Bivariate Recurrence Relations. We consider bivariate recurrence relations \(G=(\mathsf {eq}_1,\mathsf {eq}_2)\), which consists of two equalities of the following form:
where \(c\in (0,\infty )\) and \(\mathfrak {e},\mathfrak {h},\mathfrak {b}\) are from the grammar above.
Solution to Bivariate Recurrence Relations. The evaluation of bivariate recurrence relation is similar to the univariate case. Similar to the univariate case, the unique solution \(T_G:\mathbb {N}\times \mathbb {N}\rightarrow \mathbb {R}\) to a recurrence relation G taking the form (8) is a function defined recursively as follows: (1) Base Step. \(T_G(n,1):=\mathsf {Subst}({\mathfrak {h}})(n)\cdot c\) for all \(n\in \mathbb {N}\); and (2) Recursive Step. \(T_G(n,m):=\mathsf {Subst}({\mathfrak {e}},T_G)(n,m)+\mathsf {Subst}(\mathfrak {h})(n)\cdot \mathsf {Subst}(\mathfrak {b})(m)\) for all \(n\in \mathbb {N}\) and \(m\ge 2\). Again the interesting algorithmic question is to reason about the infinite behaviour of \(T_G\).
2.4 Motivating Classical Examples
In this section we present two classical examples of randomized algorithms where the randomized recurrence relations are bivariate.
Example 6
\({ (}\textsc {Coupon}{\text {-}}\textsc {Collector}{} { ).}\) Consider the Coupon-Collector problem [39, Chap. 3] with n different types of coupons (\(n\in \mathbb {N}\)). The randomized process proceeds in rounds: at each round, a coupon is collected uniformly at random from the coupon types the rounds continue until all the n types of coupons are collected. We model the rounds as a recurrence relation with two variables \(\mathfrak {n},\mathfrak {m}\), where \(\mathfrak {n}\) represents the total number of coupon types and \(\mathfrak {m}\) represents the remaining number of uncollected coupon types. The recurrence relation is as follows:
where \(\mathrm {T}(\mathfrak {n},\mathfrak {m})\) is the expected number of rounds. We note that the worst-case complexity for this process is \(\infty \). \(\square \)
Example 7
(Channel-Conflict Resolution). We consider two network scenarios in which n clients are trying to get access to a network channel. This problem is also called the Resource-Contention Resolution [36, Chap. 13]. In this problem, if more than one client tries to access the channel, then no client can access it, and if exactly one client requests access to the channel, then the request is granted. In the distributed setting, the clients do not share any information. In this scenario, in each round, every client requests an access to the channel with probability \(\frac{1}{n}\). Then for this scenario, we obtain an over-approximating recurrence relation
for the expected rounds until which every client gets at least one access to the channel. In the concurrent setting, the clients share one variable, which is the number of clients which has not yet been granted access. Also in this scenario, once a client gets an access the client does not request for access again. For this scenario, we obtain an over-approximating recurrence relation
We also note that the worst-case complexity for both the scenarios is \(\infty \). \(\square \)
3 Expected-Runtime Analysis
We focus on synthesizing logarithmic, linear, and almost-linear asymptotic bounds for recurrence relations. Our goal is to decide and synthesize asymptotic bounds in the simple form: \(d\cdot \mathfrak {f}+\mathfrak {g}, \mathfrak {f}\in \{\ln {\mathfrak {n}},\mathfrak {n},\mathfrak {n}\cdot \ln {\mathfrak {n}}\}\). Informally, \(\mathfrak {f}\) is the major term for time complexity, d is the coefficient of \(\mathfrak {f}\) to be synthesized, and \(\mathfrak {g}\) is the time complexity for the base case specified in (1) or (8).
Univariate Case: The algorithmic problem in univariate case is as follows:
-
Input: a univariate recurrence relation G taking the form (1) and an expression \(\mathfrak {f}\in \{\ln {\mathfrak {n}},\mathfrak {n},\mathfrak {n}\cdot \ln {\mathfrak {n}}\}\).
-
Output: Decision problem. Output “
 ” if \(T_G \in \mathcal {O}(\mathsf {Subst}(\mathfrak {f}))\), and “
” if \(T_G \in \mathcal {O}(\mathsf {Subst}(\mathfrak {f}))\), and “ ” otherwise.
” otherwise. -
Output: Quantitative problem. A positive real number d such that
$$\begin{aligned} T_G(n) \le d\cdot \mathsf {Subst}(\mathfrak {f})(n)+c \end{aligned}$$(12)for all \(n \ge 1\), or “
 ” otherwise, where c is from (1).
” otherwise, where c is from (1).
Remark 1
First note that while in the problem description we consider the form \(\mathfrak {f}\) part of input for simplicity, since there are only three possibilites we can simply enumerate them, and thus have only the recurrence relation as input. Second, in the algorithmic problem above, w.l.o.g, we consider that every \(\mathfrak {e}\) in (1) or (8) involves at least one \(\mathrm {T}(\centerdot )\)-term and one non-\(\mathrm {T}(\centerdot )\)-term; this is natural since (i) for algorithms with recursion at least one \(\mathrm {T}(\centerdot )\)-term should be present for the recursive call and at least one non-\(\mathrm {T}(\centerdot )\)-term for non-recursive base step. \(\square \)
Bivariate Case: The bivariate-case problem is an extension of the univariate one, and hence the problem definitions are similar, and we present them succinctly below.
-
Input: a bivariate recurrence relation G taking the form (8) and an expression \(\mathfrak {f}\) (similar to the univariate case).
-
Output: Decision problem. Output “
 ” if \(T_G \in \mathcal {O}(\mathsf {Subst}(\mathfrak {f}))\), and “
” if \(T_G \in \mathcal {O}(\mathsf {Subst}(\mathfrak {f}))\), and “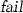 ” otherwise;
” otherwise; -
Output: Quantitative problem. A positive real number d such that \(T_G(n,m) \le d\cdot \mathsf {Subst}(\mathfrak {f})(n,m) +c\cdot \mathsf {Subst}(\mathfrak {h})(n)\) for all \(n,m \ge 1\), or “
 ” otherwise, where \(c,\mathfrak {h}\) are from (8). Note that in the expression above the term \(\mathfrak {b}\) does not appear as it can be captured with \(\mathfrak {f}\) itself.
” otherwise, where \(c,\mathfrak {h}\) are from (8). Note that in the expression above the term \(\mathfrak {b}\) does not appear as it can be captured with \(\mathfrak {f}\) itself.
Recall that in the above algorithmic problems obtaining the finite behaviour of the recurrence relations is easy (through evaluation of the recurrences using dynamic programming), and the interesting aspect is to decide the asymptotic infinite behaviour.
4 The Synthesis Algorithm
In this section, we present our algorithms to synthesize asymptotic bounds for randomized recurrence relations.
Main Idea. The main idea is as follows. Consider as input a recurrence relation taking the form (1) and an univariate recurrence expression \(\mathfrak {f}\in \{\ln {\mathfrak {n}}, \mathfrak {n},\mathfrak {n}\cdot \ln {\mathfrak {n}}\}\) which specifies the desired asymptotic bound. We first define the standard notion of a guess-and-check function which provides a sound approach for asymptotic bound. Based on the guess-and-check function, our algorithm executes the following steps for the univariate case.
-
1.
First, the algorithm sets up a scalar variable d and then constructs the template h to be \(n\mapsto d\cdot \mathsf {Subst}(\mathfrak {f})(n)+c\) for a univariate guess-and-check function.
-
2.
Second, the algorithm computes an over-approximation \(\mathsf {OvAp}(\mathfrak {e}, h)\) of \(\mathsf {Subst}(\mathfrak {e}, h)\) such that the over-approximation \(\mathsf {OvAp}(\mathfrak {e}, h)\) will involve terms from \(\mathfrak {n}^k,\ln ^\ell {\mathfrak {n}}\) (for \(k,\ell \in \mathbb {N}_0\)) only. Note that \(k,\ell \) may be greater than 1, so the above expressions are not necessarily linear (they can be quadratic or cubic for example).
-
3.
Finally, the algorithm synthesizes a value for d such that \(\mathsf {OvAp}(\mathfrak {e},h)(n)\le h(n)\) for all \(n\ge 2\) through truncation of \([2,\infty )\cap \mathbb {N}\) into a finite range and a limit behaviour analysis (towards \(\infty \)).
Our algorithm for bivariate cases is a reduction to the univariate case.
Guess-and-Check Functions. We follow the standard guess-and-check technique to solve simple recurrence relations. Below we first fix a univariate recurrence relation G taking the form (1). By an easy induction on n (starting from the N specified in Definition 1) we obtain Theorem 1.
Definition 1
(Univariate Guess-and-Check Functions). Let G be a univariate recurrence relation taking the form (1). A function \(h:\mathbb {N}\rightarrow \mathbb {R}\) is a guess-and-check function for G if there exists a natural number \(N\in \mathbb {N}\) such that: (1) (Base Condition) \(T_G(n)\le h(n)\) for all \(1\le n\le N\), and (2) (Inductive Argument) \(\mathsf {Subst}(\mathfrak {e},h) (n)\le h(n)\) for all \(n> N\).
Theorem 1
(Guess-and-Check, Univariate Case). If a function \(h:\mathbb {N}\rightarrow \mathbb {R}\) is a guess-and-check function for a univariate recurrence relation G taking the form (1), then \(T_G(n)\le h(n)\) for all \(n\in \mathbb {N}\).
We do not explicitly present the definition for guess-and-check functions in the bivariate case, since we will present a reduction of the analysis of separable bivariate recurrence relations to that of the univariate ones (cf. Sect. 4.2).
Overapproximations for Recurrence Expressions. We now develop tight overapproximations for logarithmic terms. In principle, we use Taylor’s Theorem to approximate logarithmic terms such as \(\ln {(n-1)},\ln {\lfloor \frac{n}{2}\rfloor }\), and integral to approximate summations of logarithmic terms. All the results below are technical and depends on basic calculus.
Proposition 1
For all natural number \(n\ge 2\):
Proposition 2
For all natural number \(n\ge 2\): \(\ln {n}-\frac{1}{n-1}\le \ln {(n-1)}\le \ln {n}-\frac{1}{n}\).
Proposition 3
For all natural number \(n\ge 2\):
-
\(\int _1^n \frac{1}{x}\,\mathrm {d}x-\sum _{j=1}^{n-1} \frac{1}{j}\in \left[ -0.7552,-\frac{1}{6}\right] \);
-
\(\int _1^n \ln {x}\,\mathrm {d}x-\left( \sum _{j=1}^{n-1} \ln {j}\right) - \frac{1}{2}\cdot \int _1^n \frac{1}{x}\,\mathrm {d}x\in \left[ -\frac{1}{12}, 0.2701\right] \);
-
\(\int _1^n x\cdot \ln {x}\,\mathrm {d}x-\left( \sum _{j=1}^{n-1} j\cdot \ln {j}\right) -\frac{1}{2}\cdot \int _1^n \ln {x}\,\mathrm {d}x+\frac{1}{12}\cdot \int _1^n \frac{1}{x}\,\mathrm {d}x-\frac{n-1}{2}\in \left[ -\frac{19}{72},0.1575\right] \).
Note that Proposition 3 is non-trivial since it approximates summation of reciprocal and logarithmic terms up to a constant deviation. For example, one may approximate \(\sum _{j=1}^{n-1} \ln {j}\) directly by \(\int _1^n \ln {x}\,\mathrm {d}x\), but this approximation deviates up to a logarithmic term from Proposition 3. From Proposition 3, we establish a tight approximation for summation of logarithmic or reciprocal terms.
Example 8
Consider the summation \(\sum _{j=\left\lceil \frac{n}{2}\right\rceil }^{n-1}\ln {j}+ \sum _{j=\left\lfloor \frac{n}{2}\right\rfloor }^{n-1} \ln {j}\quad (n\ge 4)\). By Proposition 3, we can over-approximate it as
where \(\varGamma _{\ln {\mathfrak {n}}}(n) := \int _1^n\ln {x}\,\mathrm {d}x-\frac{1}{2}\cdot \int _1^n\frac{1}{x}\,\mathrm {d}x = n\cdot \ln {n}-n-\frac{\ln {n}}{2}+1\). By using Proposition 1, the above expression is roughly \(n\cdot \ln {n}-(1-\ln {2})\cdot n+\frac{1}{2}\cdot \ln {n}+0.6672+\frac{1}{2\cdot n}\). \(\square \)
Remark 2
Although we do approximation for terms related to only almost-linear bounds, Proposition 3 can be extended to logarithmic bounds with higher degree (e.g., \(n^3\ln n\)) since integration of such bounds can be obtained in closed forms. \(\square \)
4.1 Algorithm for Univariate Recurrence Relations
We present our algorithm to synthesize a guess-and-check function in form (12) for univariate recurrence relations. We present our algorithm in two steps. First, we present the decision version, and then we present the quantitative version that synthesizes the associated constant. The two key aspects are over-approximation and use of pseudo-polynomials, and we start with over-approximation.
Definition 2
(Overapproximation). Let \(\mathfrak {f}\in \{\ln {\mathfrak {n}},\mathfrak {n},\mathfrak {n}\cdot \ln {\mathfrak {n}}\}\). Consider a univariate recurrence expression \(\mathfrak {g}\), constants d and c, and the function \(h= d \cdot \mathsf {Subst}(\mathfrak {f}) + c\). We define the over-approximation function, denoted \(\mathsf {OvAp}(\mathfrak {g},h)\), recursively as follows.
-
Base Step A. If \(\mathfrak {g}\) is one of the following: \(c', \mathfrak {n}, \ln {\mathfrak {n}}, \mathfrak {n}\cdot \ln {\mathfrak {n}},\frac{1}{\mathfrak {n}}\), then \(\mathsf {OvAp}(\mathfrak {g},h):=\mathsf {Subst}({\mathfrak {g}})\).
-
Base Step B. If \(\mathfrak {g}\) is a single term which involves \(\mathrm {T}\), then we define \(\mathsf {OvAp}(\mathfrak {g},h)\) from over-approximations Propositions 1–3. In details, \(\mathsf {OvAp}(\mathfrak {g},h)\) is obtained from \(\mathsf {Subst}(\mathfrak {g},h)\) by first over-approximating any summation through Proposition 3, then over-approximating any \(\ln {(\mathfrak {n}-1)}, \left\lfloor \frac{\mathfrak {n}}{2}\right\rfloor , \left\lceil \frac{\mathfrak {n}}{2}\right\rceil , \ln {\left\lfloor \frac{\mathfrak {n}}{2}\right\rfloor }, \ln {\left\lceil \frac{\mathfrak {n}}{2}\right\rceil }\) by Propositions 1 and 2. The details of the important over-approximations are illustrated explicitly in Table 1.
-
Recursive Step. We have two cases: (a) If \(\mathfrak {g}\) is \(\mathfrak {g}_1+\mathfrak {g}_2\), then \(\mathsf {OvAp}(\mathfrak {g},h)\) is \(\mathsf {OvAp}(\mathfrak {g}_1,h)+\mathsf {OvAp}(\mathfrak {g}_2,h)\). (b) If \(\mathfrak {g}\) is \(c'\cdot \mathfrak {g}'\), then \(\mathsf {OvAp}(\mathfrak {g},h)\) is \(c'\cdot \mathsf {OvAp}(\mathfrak {g}',h)\).
Example 9
Consider the recurrence relation for Sherwood’s Randomized-Search (cf. (2)). Choose \(\mathfrak {f}=\ln {\mathfrak {n}}\) and then the template h becomes \(n\mapsto d\cdot \ln {n}+1\). From Example 8, we have that the over-approximation for \(6+\frac{1}{\mathfrak {n}}\cdot \left( \sum _{\mathfrak {j}=\left\lceil \frac{\mathfrak {n}}{2}\right\rceil }^{\mathfrak {n}-1}\mathrm {T}(\mathfrak {j})+ \sum _{\mathfrak {j}=\left\lfloor \frac{\mathfrak {\mathfrak {n}}}{2}\right\rfloor }^{\mathfrak {\mathfrak {n}}-1} \mathrm {T}(\mathfrak {j})\right) \) when \(n\ge 4\) is \(7+ d\cdot \left[ \ln {n}-(1-\ln {2})+\frac{\ln {n}}{2\cdot n}+\frac{0.6672}{n}+\frac{1}{2\cdot n^2}\right] \) \(\Big (\)the second summand comes from an over-approximation of \(\frac{1}{\mathfrak {n}}\cdot \left( \sum _{\mathfrak {j}=\left\lceil \frac{\mathfrak {n}}{2}\right\rceil }^{\mathfrak {n}-1}d\cdot \ln {\mathfrak {j}}+ \sum _{\mathfrak {j}=\left\lfloor \frac{\mathfrak {\mathfrak {n}}}{2}\right\rfloor }^{\mathfrak {\mathfrak {n}}-1} d\cdot \ln {\mathfrak {j}}\right) \Big )\). \(\square \)
Remark 3
Since integrations of the form \(\int x^k\ln ^l x\,\mathrm {d}x\) can be calculated in closed forms (cf. Remark 2), Table 1 can be extended to logarithmic expressions with higher order, e.g., \(\mathfrak {n}^2\ln \mathfrak {n}\). \(\square \)
Pseudo-polynomials. Our next step is to define the notion of (univariate) pseudo-polynomials which extends normal polynomials with logarithm. This notion is crucial to handle inductive arguments in the definition of guess-and-check functions.
Definition 3
(Univariate Pseudo-polynomials). A univariate pseudo-polynomial (w.r.t logarithm) is a function \(p:\mathbb {N}\rightarrow \mathbb {R}\) such that there exist non-negative integers \(k,\ell \in \mathbb {N}_0\) and real numbers \(a_i,b_i\)’s such that for all \(n\in \mathbb {N}\),

W.l.o.g, we consider that in the form (13), it holds that (i) \(a^2_k+b^2_\ell \ne 0\), (ii) either \(a_k\ne 0\) or \(k=0\), and (iii) similarly either \(b_\ell \ne 0\) or \(\ell =0\).
Degree of Pseudo-polynomials. Given a univariate pseudo-polynomial p in the form (13), we define the degree \(\mathrm {deg}(p)\) of p by: \(\mathrm {deg}(p)= k+\frac{1}{2}\) if \(k\ge \ell \text { and }a_k\ne 0\) and \(\ell \) otherwise. Intuitively, if the term with highest degree involves logarithm, then we increase the degree by 1 / 2, else it is the power of the highest degree term.
Leading term \(\overline{p}\). The leading term \(\overline{p}\) of a pseudo-polynomial p in the form (13) is a function \(\overline{p}:\mathbb {N}\rightarrow \mathbb {R}\) defined as follows: \(\overline{p}(n)=a_{k}\cdot n^{k}\cdot \ln {n} \text { if }k\ge \ell \text { and }a_k\ne 0\); and \(b_{\ell }\cdot n^{\ell } \text { otherwise}\); for all \(n\in \mathbb {N}\). Moreover, we let \(C_p\) to be the (only) coefficient of \(\overline{p}\).
With the notion of pseudo-polynomials, the inductive argument of guess-and-check functions can be soundly transformed into an inequality between pseudo-polynomials.
Lemma 1
Let \(\mathfrak {f}\in \{\ln {\mathfrak {n}},\mathfrak {n},\mathfrak {n}\cdot \ln {\mathfrak {n}}\}\) and c be a constant. For all univariate recurrence expressions \(\mathfrak {g}\), there exists pseudo-polynomials p and q such that coefficients (i.e., \(a_i,b_i\)’s in (13)) of q are all non-negative, \(C_q>0\) and the following assertion holds: for all \(d>0\) and for all \(n\ge 2\), with \(h=d\cdot \mathsf {Subst}({\mathfrak {f}})+c\), the inequality \(\mathsf {OvAp}(\mathfrak {g}, h)(n)\le h(n)\) is equivalent to \(d\cdot p(n)\ge q(n)\).
Remark 4
In the above lemma, though we only refer to existence of pseudo-polynomials p and q, they can actually be computed in linear time, because p and q are obtained by simple rearrangements of terms from \(\mathsf {OvAp}(\mathfrak {g}, h)\) and h, respectively.
Example 10
Let us continue with Sherwood’s Randomized-Search. Again choose \(h=d\cdot \ln {\mathfrak {n}}+1\). From Example 9, we obtain that for every \(n\ge 4\), the inequality
resulting from over-approximation and the inductive argument of guess-and-check functions is equivalent to \(d\cdot \left[ (1-\ln {2})\cdot n^2-\frac{n\cdot \ln {n}}{2}-0.6672\cdot n-\frac{1}{2}\right] \ge 6\cdot n^2\). \(\square \)
As is indicated in Definition 1, our aim is to check whether \( \mathsf {OvAp}(\mathfrak {g}, h)(n)\le h(n)\) holds for sufficiently large n. The following proposition provides a sufficient and necessary condition for checking whether \(d\cdot p(n)\ge q(n)\) holds for sufficiently large n.
Proposition 4
Let p, q be pseudo-polynomials such that \(C_q>0\) and all coefficients of q are non-negative. Then there exists a real number \(d>0\) such that \(d\cdot p(n)\ge q(n)\) for sufficiently large n iff \(\mathrm {deg}(p)\ge \mathrm {deg}(q)\) and \(C_p>0\).
Note that by Definition 1 and the special form (12) for univariate guess-and-check functions, a function in form (12) needs only to satisfy the inductive argument in order to be a univariate guess-and-check function: once a value for d is synthesized for a sufficiently large N, one can scale the value so that the base condition is also satisfied. Thus from the sufficiency of Proposition 4, our decision algorithm that checks the existence of some guess-and-check function in form (12) is presented below. Below we fix an input univariate recurrence relation G taking the form (1) and an input expression \(\mathfrak {f}\in \{\ln {\mathfrak {n}},\mathfrak {n},\mathfrak {n}\cdot \ln {\mathfrak {n}}\}\).
Algorithm  : Our algorithm, namely
: Our algorithm, namely  , for the decision problem of the univariate case, has the following steps.
, for the decision problem of the univariate case, has the following steps.
-
1.
Template. The algorithm establishes a scalar variable d and sets up the template \(d\cdot \mathfrak {f}+c\) for a univariate guess-and-check function.
-
2.
Over-approximation. Let h denote \(d \cdot \mathsf {Subst}(\mathfrak {f}) +c\). The algorithm calculates the over-approximation function \(\mathsf {OvAp}(\mathfrak {e},h)\), where \(\mathfrak {e}\) is from (1).
-
3.
Transformation. The algorithm transforms the inequality \(\mathsf {OvAp}(\mathfrak {e},h)(n) \le h(n) \,(n\in \mathbb {N})\) for inductive argument of guess-and-check functions through Lemma 1 equivalently into \(d\cdot p(n)\ge q(n)\,(n\in \mathbb {N})\), where p, q are pseudo-polynomials obtained in linear-time through rearrangement of terms from \(\mathsf {OvAp}(\mathfrak {e},h)\) and h (see Remark 4).
-
4.
Coefficient Checking. The algorithm examines cases on \(C_p\). If \(C_p> 0\) and \(\mathrm {deg}(p) \ge \mathrm {deg}(q)\), then algorithm outputs “
 ” meaning that “there exists a univariate guess-and-check function”; otherwise, the algorithm outputs “
” meaning that “there exists a univariate guess-and-check function”; otherwise, the algorithm outputs “ ”.
”.
Theorem 2
(Soundness for UniDec
). If  outputs “
outputs “ ”, then there exists a univariate guess-and-check function in form (12) for the inputs G and \(\mathfrak {f}\). The algorithm is a linear-time algorithm in the size of the input recurrence relation.
”, then there exists a univariate guess-and-check function in form (12) for the inputs G and \(\mathfrak {f}\). The algorithm is a linear-time algorithm in the size of the input recurrence relation.
Example 11
Consider Sherwood’s Randomized-Search recurrence relation (cf. (2)) and \(\mathfrak {f}=\ln {\mathfrak {n}}\) as the input. As illustrated in Examples 9 and 10, the algorithm asserts that the asymptotic behaviour is \(\mathcal {O}(\ln {n})\). \(\square \)
Remark 5
From the tightness of our over-approximation (up to only constant deviation) and the sufficiency and necessity of Proposition 4, the  algorithm can handle a large class of univariate recurrence relations. Moreover, the algorithm is quite simple and efficient (linear-time). However, we do not know whether our approach is complete. We suspect that there is certain intricate recurrence relations that will make our approach fail.
algorithm can handle a large class of univariate recurrence relations. Moreover, the algorithm is quite simple and efficient (linear-time). However, we do not know whether our approach is complete. We suspect that there is certain intricate recurrence relations that will make our approach fail.
Analysis of Examples of Sect. 2.2. Our algorithm can decide the following optimal bounds for the examples of Sect. 2.2.
-
1.
For Example 1 we obtain an \(\mathcal {O}(\log n)\) bound (recall worst-case bound is \(\varTheta (n)\)).
-
2.
For Example 2 we obtain an \(\mathcal {O}(n\cdot \log n)\) bound (recall worst-case bound is \(\varTheta (n^2)\)).
-
3.
For Example 3 we obtain an \(\mathcal {O}(n)\) bound (recall worst-case bound is \(\varTheta (n^2)\)).
-
4.
For Example 4 we obtain an \(\mathcal {O}(n\cdot \log n)\) (resp. \(\mathcal {O}(n)\)) bound for Euclidean metric (resp. for \(L_1\) metric), whereas the worst-case bound is \(\varTheta (n^2\cdot \log n)\) (resp. \(\varTheta (n^2)\)).
-
5.
For Example 5 we obtain an \(\mathcal {O}(n\cdot \log n)\) bound (recall worst-case bound is \(\varTheta (n^2)\)).
In all cases above, our algorithm decides the asymptotically optimal bounds for the expected-runtime analysis, whereas the worst-case analysis grossly over-estimate the expected-runtime bounds.
Quantitative Bounds. We have already established that our linear-time decision algorithm can establish the asymptotically optimal bounds for the recurrence relations of several classical algorithms. We now take the next step to obtain even explicit quantitative bounds, i.e., to synthesize the associated constants with the asymptotic complexity. To this end, we derive a following proposition which gives explicitly a threshold for “sufficiently large numbers”. We first explicitly constructs a threshold for “sufficiently large numbers”. Then we show in Proposition 5 that \(N_{\epsilon ,p,q}\) is indeed what we need.
Definition 4
(Threshold \(N_{\epsilon ,p,q}\) for Sufficiently Large Numbers). Let p, q be two univariate pseudo-polynomials \(p(n)=\sum _{i=0}^{k} a_i\cdot n^{i}\cdot \ln {n}+\sum _{i=0}^{\ell } b_i\cdot n^{i}\), \(q(n)=\sum _{i=0}^{k'} a'_i\cdot n^{i}\cdot \ln {n}+\sum _{i=0}^{\ell '} b'_i\cdot n^{i}\) such that \(\mathrm {deg}(p)\ge \mathrm {deg}(q)\) and \(C_p,C_q>0\). Then given any \(\epsilon \in (0,1)\), the number \(N_{\epsilon ,p,q}\) is defined as the smallest natural number such that both x, y (defined below) is smaller than \(\epsilon \):
-
\(x=-1+\sum _{i=0}^{k} |a_i|\cdot \frac{N^{i}\cdot \ln {N}}{\overline{p}(N)}+\sum _{i=0}^{\ell } |b_i|\cdot \frac{N^{i}}{\overline{p}(N)}\);
-
\(y=-\mathbf {1}_{\mathrm {deg}(p)=\mathrm {deg}(q)}\cdot \frac{C_q}{C_p}+\sum _{i=0}^{k'} |a'_i|\cdot \frac{N^{i}\cdot \ln {N}}{\overline{p}(N)}+\sum _{i=0}^{\ell '} |b'_i|\cdot \frac{N^{i}}{\overline{p}(N)}\).
where \(\mathbf {1}_{\mathrm {deg}(p)=\mathrm {deg}(q)}\) equals 1 when \({\mathrm {deg}(p)=\mathrm {deg}(q)}\) and 0 otherwise.
Proposition 5
Consider two univariate pseudo-polynomials p, q such that \(\mathrm {deg}(p)\ge \mathrm {deg}(q)\), all coefficients of q are non-negative and \(C_p,C_q>0\). Then given any \(\epsilon \in (0,1)\), \(\frac{q(n)}{p(n)}\le \frac{\mathbf {1}_{\mathrm {deg}(p)=\mathrm {deg}(q)}\cdot \frac{C_q}{C_p}+\epsilon }{1-\epsilon }\) for all \(n\ge N_{\epsilon ,p,q}\) (for \(N_{\epsilon ,p,q}\) of Definition 4).
With Proposition 5, we describe our algorithm  which outputs explicitly a value for d (in (12)) if
which outputs explicitly a value for d (in (12)) if  outputs yes. Below we fix an input univariate recurrence relation G taking the form (1) and an input expression \(\mathfrak {f}\in \{\ln {\mathfrak {n}},\mathfrak {n},\mathfrak {n}\cdot \ln {\mathfrak {n}}\}\). Moreover, the algorithm takes \(\epsilon >0\) as another input, which is basically a parameter to choose the threshold for finite behaviour. For example, smaller \(\epsilon \) leads to large threshold, and vice-versa. Thus we provide a flexible algorithm as the threshold can be varied with the choice of \(\epsilon \).
outputs yes. Below we fix an input univariate recurrence relation G taking the form (1) and an input expression \(\mathfrak {f}\in \{\ln {\mathfrak {n}},\mathfrak {n},\mathfrak {n}\cdot \ln {\mathfrak {n}}\}\). Moreover, the algorithm takes \(\epsilon >0\) as another input, which is basically a parameter to choose the threshold for finite behaviour. For example, smaller \(\epsilon \) leads to large threshold, and vice-versa. Thus we provide a flexible algorithm as the threshold can be varied with the choice of \(\epsilon \).
Algorithm  : Our algorithm for the quantitative problem has the following steps:
: Our algorithm for the quantitative problem has the following steps:
-
1.
Calling
 . The algorithm calls
. The algorithm calls  , and if it returns “
, and if it returns “ ”, then return “
”, then return “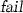 ”, otherwise execute the following steps. Obtain the following inequality \(d\cdot p(n)\ge q(n)\,(n\in \mathbb {N})\) from the transformation step of
”, otherwise execute the following steps. Obtain the following inequality \(d\cdot p(n)\ge q(n)\,(n\in \mathbb {N})\) from the transformation step of  .
. -
2.
Variable Solving. The algorithm calculates \(N_{\epsilon , p,q}\) for a given \(\epsilon \in (0,1)\) by e.g. repeatedly increasing n (see Definition 4) and outputs the value of d as the least number such that the following two conditions hold: (i) for all \(2\le n< N_{\epsilon , p,q}\), we have \(\mathsf {Eval}(G)(n)\le d\cdot \mathsf {Subst}({\mathfrak {f}})(n)+c\) (recall \(\mathsf {Eval}(G)(n)\) can be computed in linear time), and (ii) we have \(d\ge \frac{\mathbf {1}_{\mathrm {deg}(p)=\mathrm {deg}(q)}\cdot \frac{C_q}{C_p}+\epsilon }{1-\epsilon }\).
Theorem 3
(Soundness for UniSynth
). If the algorithm  outputs a real number d, then \(d\cdot \mathsf {Subst}(\mathfrak {f})+c\) is a univariate guess-and-check function for G.
outputs a real number d, then \(d\cdot \mathsf {Subst}(\mathfrak {f})+c\) is a univariate guess-and-check function for G.
Example 12
Consider the recurrence relation for Sherwood’s Randomized-Search (cf. (2)) and \(\mathfrak {f}=\ln {\mathfrak {n}}\). Consider that \(\epsilon :=0.9\). From Examples 9 and 10, the algorithm establishes the inequality \(d\ge \frac{ 6}{(1-\ln {2})-\frac{\ln {n}}{2\cdot n}-\frac{0.6672}{n}-\frac{1}{2\cdot n^2}}\) and finds that \(N_{0.9,p,q}=6\). Then the algorithm finds \(d=204.5335\) through the followings: (a) \(\mathsf {Eval}(G)(2)=7\le d\cdot \ln {2}+1\); (b) \(\mathsf {Eval}(G)(3)=11\le d\cdot \ln {3}+1\); (c) \(\mathsf {Eval}(G)(4)=15\le d\cdot \ln {4}+1\); (d) \(\mathsf {Eval}(G)(5)=17.8\le d\cdot \ln {5}+1\); (e) \(d\ge \frac{\frac{6}{1-\ln {2}}+0.9}{1-0.9}\). Thus, by Theorem 1, the expected running time of the algorithm has an upper bound \(204.5335\cdot \ln {n}+1\). Later in Sect. 5, we show that one can obtain a much better \(d=19.762\) through our algorithms by choosing \(\epsilon :=0.01\), which is quite good since the optimal value lies in [15.129, 19.762] (cf. the first item R.-Sear. in Table 2). \(\square \)
4.2 Algorithm for Bivariate Recurrence Relations
In this part, we present our results for the separable bivariate recurrence relations. The key idea is to use separability to reduce the problem to univariate recurrence relations. There are two key steps which we describe below.
Step 1. The first step is to reduce a separable bivariate recurrence relation to a univariate one.
Definition 5
(From G to \(\mathsf {Uni}(G)\) ). Let G be a separable bivariate recurrence relation taking the form (8). The univariate recurrence relation \(\mathsf {Uni}(G)\) from G is defined by eliminating any occurrence of \(\mathfrak {n}\) and replacing any occurrence of \(\mathfrak {h}\) with 1.
Informally, \(\mathsf {Uni}(G)\) is obtained from G by simply eliminating the roles of \(\mathfrak {h},\mathfrak {n}\). The following example illustrates the situation for Coupon-Collector example.
Example 13
Consider G to be the recurrence relation (9) for Coupon-Collector example. Then \(\mathsf {Uni}(G)\) is as follows: \(\mathrm {T}(\mathfrak {n})=\frac{1}{\mathfrak {n}}+ \mathrm {T}(\mathfrak {n}-1)\) and \(\mathrm {T}(1)=1\). \(\square \)
Step 2. The second step is to establish the relationship between \(T_G\) and \(T_{\mathsf {Uni}(G)}\), which is handled by the following proposition, whose proof is an easy induction on m.
Proposition 6
For any separable bivariate recurrence relation G taking the form (8), the solution \(T_G\) is equal to \((n,m)\mapsto \mathsf {Subst}(\mathfrak {h})(n) \cdot T_{\mathsf {Uni}(G)}(m)\).
Description of the Algorithm. With Proposition 6, the algorithm for separable bivariate recurrence relations is straightforward: simply compute \(\mathsf {Uni}(G)\) for G and then call the algorithms for univariate case presented in Sect. 4.1.
Analysis of Examples in Sect. 2.4. Our algorithm can decide the following optimal bounds for the examples of Sect. 2.4.
-
1.
For Example 6 we obtain an \(\mathcal {O}(n\cdot \log m)\) bound, whereas the worst-case bound is \(\infty \).
-
2.
For Example 7 we obtain an \(\mathcal {O}(n\cdot \log m)\) bound for distributed setting and \(\mathcal {O}(m)\) bound for concurrent setting, whereas the worst-case bounds are both \(\infty \).
Note that for all our examples, \(m \le n\), and thus we obtain \(\mathcal {O}(n\cdot \log n)\) and \(\mathcal {O}(n)\) upper bounds for expected-runtime analysis, which are the asymptotically optimal bounds. In all cases above, the worst-case analysis is completely ineffective as the worst-case bounds are infinite. Moreover, consider Example 7, where the optimal number of rounds is n (i.e., one process every round, which centralized Round-Robin schemes can achieve). The randomized algorithm, with one shared variable, is a decentralized algorithm that achieves O(n) expected number of rounds (i.e., the optimal asymptotic expected-runtime complexity).
5 Experimental Results
We consider the classical examples illustrated in Sects. 2.2 and 2.4. In Table 2 for experimental results we consider the following recurrence relations G: R.-Sear. corresponds to the recurrence relation (2) for Example 1; Q.-Sort corresponds to the recurrence relation (3) for Example 2; Q.-Select corresponds to the recurrence relation (4) for Example 3; Diam. A (resp. Diam. B) corresponds to the recurrence relation (5) (resp. the recurrence relation (6)) for Example 4; Sort-Sel. corresponds to recurrence relation (7) for Example 5, where we use the result from setting \(\epsilon =0.01\) in Q.-Select; Coupon corresponds to the recurrence relation (9) for Example 6; Res. A (resp. Res. B) corresponds to the recurrence relation (10) (resp. the recurrence relation (11)) for Example 7.
In the table, \(\mathfrak {f}\) specifies the input asymptotic bound, \(\epsilon \) and Dec is the input which specifies either we use algorithm  or the synthesis algorithm
or the synthesis algorithm  with the given \(\epsilon \) value, and d gives the value synthesized w.r.t the given \(\epsilon \) (\(\checkmark \) for
with the given \(\epsilon \) value, and d gives the value synthesized w.r.t the given \(\epsilon \) (\(\checkmark \) for  ). We describe \(d_{100}\) below. We need approximation for constants such as e and \(\ln {2}\), and use the interval [2.7182, 2.7183] (resp., [0.6931, 0.6932]) for tight approximation of e (resp., \(\ln {2}\)).
). We describe \(d_{100}\) below. We need approximation for constants such as e and \(\ln {2}\), and use the interval [2.7182, 2.7183] (resp., [0.6931, 0.6932]) for tight approximation of e (resp., \(\ln {2}\)).
The Value \(d_{100}\) . For our synthesis algorithm we obtain the value d. The optimal value of the associated constant with the asymptotic bound, denoted \(d^*\), is defined as follows. For \(z\ge 2\), let \(d_{z}:=\max \left\{ \frac{T_G(n)-c}{\mathsf {Subst}(\mathfrak {f})(n)}\mid 2\le n\le z\right\} \) (c is from (1)). Then the sequence \(d_z\) is increasing in z, and its limit is the optimal constant, i.e., \(d^* =\lim _{z \rightarrow \infty } d_z\). We consider \(d_{100}\) as a lower bound on \(d^*\) to compare against the value of d we synthesize. In other words, \(d_{100}\) is the minimal value such that (12) holds for \(1\le n\le 100\), whereas for \(d^*\) it must hold for all n, and hence \(d^* \ge d_{100}\). Our experimental results show that the d values we synthesize for \(\epsilon =0.01\) is quite close to the optimal value.
We performed our experiments on Intel(R) Core(TM) i7-4510U CPU, 2.00GHz, 8GB RAM. All numbers in Table 2 are over-approximated up to \(10^{-3}\), and the running time of all experiments are less than 0.02 seconds. From Table 2, we can see that optimal d are effectively over-approximated. For example, for Quick-Sort (Eq. (3)) (i.e., Q.-Sort in the table), our algorithm detects \(d=4.051\) and the optimal one lies somewhere in [3.172, 4.051]. The experimental results show that we obtain the results extremely efficiently (less than 1 / 50-th of a second).
6 Related Work
Automated program analysis is a very important problem with a long tradition [45]. The following works consider various approaches for automated worst-case bounds [5, 26, 28,29,30,31,32, 34, 35, 43] for amortized analysis, and the SPEED project [22,23,24] for non-linear bounds using abstract interpretation. All these works focus on the worst-case analysis, and do not consider expected-runtime analysis.
Our main contribution is automated analysis of recurrence relations. Approaches for recurrence relations have also been considered in the literature. Wegbreit [45] considered solving recurrence relations through either simple difference equations or generating functions. Zimmermann and Zimmermann [48] considered solving recurrence relations by transforming them into difference equations. Grobauer [21] considered generating recurrence relations from DML for the worst-case analysis. Flajolet et al. [19] considered allocation problems. Flajolet et al. [20] considered solving recurrence relations for randomization of combinatorial structures (such as trees) through generating functions. The COSTA project [2,3,4] transforms Java bytecode into recurrence relations and solves them through ranking functions. Moreover, The PURRS tool [6] addresses finite linear recurrences (with bounded summation), and some restricted linear infinite recurrence relations (with unbounded summation). Our approach is quite different because we consider analyzing recurrence relations arising from randomized algorithms and expected-runtime analysis by over-approximation of unbounded summations through integrals, whereas previous approaches either consider recurrence relations for worst-case bounds or combinatorial structures, or use generating functions or difference equations to solve the recurrence relations.
For intraprocedural analysis ranking functions have been widely studied [7, 8, 15, 17, 41, 42, 44, 47], which have then been extended to non-recursive probabilistic programs as ranking supermartingales [9,10,11, 13, 14, 18]. However, existing related approaches can not derive optimal asymptotic expected-runtime bounds (such as \(\mathcal {O}(\log n)\), \(\mathcal {O}(n \log n)\)). Proof rules have also been considered for recursive (probabilistic) programs in [25, 33, 40], but these methods cannot be automated and require manual proofs.
7 Conclusion
In this work we considered efficient algorithms for automated analysis of randomized recurrences for logarithmic, linear, and almost-linear bounds. Our work gives rise to a number of interesting questions. First, an interesting theoretical direction of future work would be to consider more general randomized recurrence relations (such as with more than two variables, or interaction between the variables). While the above problem is of theoretical interest, most interesting examples are already captured in our class of randomized recurrence relations as mentioned above. Another interesting practical direction would be automated techniques to derive recurrence relations from randomized recursive programs.
References
Akra, M.A., Bazzi, L.: On the solution of linear recurrence equations. Comp. Opt. Appl. 10(2), 195–210 (1998)
Albert, E., Arenas, P., Genaim, S., Gómez-Zamalloa, M., Puebla, G., Ramírez-Deantes, D.V., Román-Díez, G., Zanardini, D.: Termination and cost analysis with COSTA and its user interfaces. Electr. Notes Theor. Comput. Sci. 258(1), 109–121 (2009)
Albert, E., Arenas, P., Genaim, S., Puebla, G.: Automatic inference of upper bounds for recurrence relations in cost analysis. In: Alpuente, M., Vidal, G. (eds.) SAS 2008. LNCS, vol. 5079, pp. 221–237. Springer, Heidelberg (2008). doi:10.1007/978-3-540-69166-2_15
Albert, E., Arenas, P., Genaim, S., Puebla, G., Zanardini, D.: Cost analysis of Java bytecode. In: Nicola, R. (ed.) ESOP 2007. LNCS, vol. 4421, pp. 157–172. Springer, Heidelberg (2007). doi:10.1007/978-3-540-71316-6_12
Avanzini, M., Lago, U.D., Moser, G.: Analysing the complexity of functional programs: higher-order meets first-order. In: Fisher, K., Reppy, J.H. (eds.) ICFP, pp. 152–164. ACM (2015)
Bagnara, R., Pescetti, A., Zaccagnini, A., Zaffanella, E.: PURRS: towards computer algebra support for fully automatic worst-case complexity analysis. Technical report, University of Parma (2005). https://arxiv.org/abs/cs/0512056
Bournez, O., Garnier, F.: Proving positive almost-sure termination. In: Giesl, J. (ed.) RTA 2005. LNCS, vol. 3467, pp. 323–337. Springer, Heidelberg (2005). doi:10.1007/978-3-540-32033-3_24
Bradley, A.R., Manna, Z., Sipma, H.B.: Linear ranking with reachability. In: Etessami, K., Rajamani, S.K. (eds.) CAV 2005. LNCS, vol. 3576, pp. 491–504. Springer, Heidelberg (2005). doi:10.1007/11513988_48
Chakarov, A., Sankaranarayanan, S.: Probabilistic program analysis with martingales. In: Sharygina, N., Veith, H. (eds.) CAV 2013. LNCS, vol. 8044, pp. 511–526. Springer, Heidelberg (2013). doi:10.1007/978-3-642-39799-8_34
Chatterjee, K., Fu, H.: Termination of nondeterministic recursive probabilistic programs. CoRR abs/1701.02944 (2017). http://arxiv.org/abs/1701.02944
Chatterjee, K., Fu, H., Goharshady, A.K.: Termination analysis of probabilistic programs through Positivstellensatz’s. In: Chaudhuri, S., Farzan, A. (eds.) CAV 2016. LNCS, vol. 9779, pp. 3–22. Springer, Cham (2016). doi:10.1007/978-3-319-41528-4_1
Chatterjee, K., Fu, H., Murhekar, A.: Automated recurrence analysis for almost-linear expected-runtime bounds. CoRR abs/1705.00314 (2017). https://arxiv.org/abs/1705.00314
Chatterjee, K., Fu, H., Novotný, P., Hasheminezhad, R.: Algorithmic analysis of qualitative and quantitative termination problems for affine probabilistic programs. In: Bodík, R., Majumdar, R. (eds.) POPL, pp. 327–342. ACM (2016)
Chatterjee, K., Novotný, P., Žikelić, Đ.: Stochastic invariants for probabilistic termination. In: Castagna, G., Gordon, A.D. (eds.) POPL, pp. 145–160. ACM (2017)
Colón, M.A., Sipma, H.B.: Synthesis of linear ranking functions. In: Margaria, T., Yi, W. (eds.) TACAS 2001. LNCS, vol. 2031, pp. 67–81. Springer, Heidelberg (2001). doi:10.1007/3-540-45319-9_6
Cormen, T.H., Leiserson, C.E., Rivest, R.L., Stein, C.: Introduction to Algorithms, 3rd edn. MIT Press, Cambridge (2009)
Cousot, P.: Proving program invariance and termination by parametric abstraction, Lagrangian relaxation and semidefinite programming. In: Cousot, R. (ed.) VMCAI 2005. LNCS, vol. 3385, pp. 1–24. Springer, Heidelberg (2005). doi:10.1007/978-3-540-30579-8_1
Fioriti, L.M.F., Hermanns, H.: Probabilistic termination: soundness, completeness, and compositionality. In: Rajamani, S.K., Walker, D. (eds.) POPL, pp. 489–501. ACM (2015)
Flajolet, P., Gardy, D., Thimonier, L.: Birthday paradox, coupon collectors, caching algorithms and self-organizing search. Discret. Appl. Math. 39(3), 207–229 (1992)
Flajolet, P., Salvy, B., Zimmermann, P.: Automatic average-case analysis of algorithm. Theor. Comput. Sci. 79(1), 37–109 (1991)
Grobauer, B.: Cost recurrences for DML programs. In: Pierce, B.C. (ed.) ICFP, pp. 253–264. ACM (2001)
Gulavani, B.S., Gulwani, S.: A numerical abstract domain based on expression abstraction and max operator with application in timing analysis. In: Gupta, A., Malik, S. (eds.) CAV 2008. LNCS, vol. 5123, pp. 370–384. Springer, Heidelberg (2008). doi:10.1007/978-3-540-70545-1_35
Gulwani, S.: SPEED: symbolic complexity bound analysis. In: Bouajjani, A., Maler, O. (eds.) CAV 2009. LNCS, vol. 5643, pp. 51–62. Springer, Heidelberg (2009). doi:10.1007/978-3-642-02658-4_7
Gulwani, S., Mehra, K.K., Chilimbi, T.M.: SPEED: precise and efficient static estimation of program computational complexity. In: Shao, Z., Pierce, B.C. (eds.) POPL, pp. 127–139. ACM (2009)
Hesselink, W.H.: Proof rules for recursive procedures. Formal Asp. Comput. 5(6), 554–570 (1993)
Hoffmann, J., Aehlig, K., Hofmann, M.: Multivariate amortized resource analysis. ACM Trans. Program. Lang. Syst. 34(3), 14 (2012)
Hoffmann, J., Aehlig, K., Hofmann, M.: Resource aware ML. In: Madhusudan, P., Seshia, S.A. (eds.) CAV 2012. LNCS, vol. 7358, pp. 781–786. Springer, Heidelberg (2012). doi:10.1007/978-3-642-31424-7_64
Hoffmann, J., Hofmann, M.: Amortized resource analysis with polymorphic recursion and partial big-step operational semantics. In: Ueda, K. (ed.) APLAS 2010. LNCS, vol. 6461, pp. 172–187. Springer, Heidelberg (2010). doi:10.1007/978-3-642-17164-2_13
Hoffmann, J., Hofmann, M.: Amortized resource analysis with polynomial potential. In: Gordon, A.D. (ed.) ESOP 2010. LNCS, vol. 6012, pp. 287–306. Springer, Heidelberg (2010). doi:10.1007/978-3-642-11957-6_16
Hofmann, M., Jost, S.: Static prediction of heap space usage for first-order functional programs. In: Aiken, A., Morrisett, G. (eds.) POPL, pp. 185–197. ACM (2003)
Hofmann, M., Jost, S.: Type-based amortised heap-space analysis. In: Sestoft, P. (ed.) ESOP 2006. LNCS, vol. 3924, pp. 22–37. Springer, Heidelberg (2006). doi:10.1007/11693024_3
Hofmann, M., Rodriguez, D.: Efficient type-checking for amortised heap-space analysis. In: Grädel, E., Kahle, R. (eds.) CSL 2009. LNCS, vol. 5771, pp. 317–331. Springer, Heidelberg (2009). doi:10.1007/978-3-642-04027-6_24
Jones, C.: Probabilistic non-determinism. Ph.D. thesis, The University of Edinburgh (1989)
Jost, S., Hammond, K., Loidl, H., Hofmann, M.: Static determination of quantitative resource usage for higher-order programs. In: Hermenegildo, M.V., Palsberg, J. (eds.) POPL, pp. 223–236. ACM (2010)
Jost, S., Loidl, H.-W., Hammond, K., Scaife, N., Hofmann, M.: “Carbon credits” for resource-bounded computations using amortised analysis. In: Cavalcanti, A., Dams, D.R. (eds.) FM 2009. LNCS, vol. 5850, pp. 354–369. Springer, Heidelberg (2009). doi:10.1007/978-3-642-05089-3_23
Kleinberg, J., Tardos, É.: Algorithm Design. Addison-Wesley, Boston (2004)
Knuth, D.E.: The Art of Computer Programming, vol. I–III. Addison-Wesley, Boston (1973)
McConnell, J.: Analysis of Algorithms - An Active Learning Approach. Jones and Bartlett Publishers, Inc., Burlington (2008)
Motwani, R., Raghavan, P.: Randomized Algorithms. Cambridge University Press, Cambridge (1995)
Olmedo, F., Kaminski, B.L., Katoen, J., Matheja, C.: Reasoning about recursive probabilistic programs. In: Grohe, M., Koskinen, E., Shankar, N. (eds.) LICS, pp. 672–681. ACM (2016)
Podelski, A., Rybalchenko, A.: A complete method for the synthesis of linear ranking functions. In: Steffen, B., Levi, G. (eds.) VMCAI 2004. LNCS, vol. 2937, pp. 239–251. Springer, Heidelberg (2004). doi:10.1007/978-3-540-24622-0_20
Shen, L., Wu, M., Yang, Z., Zeng, Z.: Generating exact nonlinear ranking functions by symbolic-numeric hybrid method. J. Syst. Sci. Complex. 26(2), 291–301 (2013)
Sinn, M., Zuleger, F., Veith, H.: A simple and scalable static analysis for bound analysis and amortized complexity analysis. In: Knoop, J., Zdun, U. (eds.) Software Engineering. LNI, vol. 252, pp. 101–102. GI (2016)
Sohn, K., Gelder, A.V.: Termination detection in logic programs using argument sizes. In: Rosenkrantz, D.J. (ed.) PODS, pp. 216–226. ACM Press (1991)
Wegbreit, B.: Mechanical program analysis. Commun. ACM 18(9), 528–539 (1975)
Wilhelm, R., Engblom, J., Ermedahl, A., Holsti, N., Thesing, S., Whalley, D.B., Bernat, G., Ferdinand, C., Heckmann, R., Mitra, T., Mueller, F., Puaut, I., Puschner, P.P., Staschulat, J., Stenström, P.: The worst-case execution-time problem - overview of methods and survey of tools. ACM Trans. Embedded Comput. Syst. 7(3), 36 (2008)
Yang, L., Zhou, C., Zhan, N., Xia, B.: Recent advances in program verification through computer algebra. Front. Comput. Sci. China 4(1), 1–16 (2010)
Zimmermann, P., Zimmermann, W.: The automatic complexity analysis of divide-and-conquer algorithms. Technical report, HAL Inria (1989). https://hal.inria.fr/inria-00075410/
Acknowledgements
We thank all reviewers for valuable comments. The research is partially supported by Vienna Science and Technology Fund (WWTF) ICT15-003, Austrian Science Fund (FWF) NFN Grant No. S11407-N23 (RiSE/SHiNE), ERC Start grant (279307: Graph Games), the Natural Science Foundation of China (NSFC) under Grant No. 61532019 and the CDZ project CAP (GZ 1023).
Author information
Authors and Affiliations
Corresponding author
Editor information
Editors and Affiliations
Rights and permissions
Copyright information
© 2017 Springer International Publishing AG
About this paper
Cite this paper
Chatterjee, K., Fu, H., Murhekar, A. (2017). Automated Recurrence Analysis for Almost-Linear Expected-Runtime Bounds. In: Majumdar, R., Kunčak, V. (eds) Computer Aided Verification. CAV 2017. Lecture Notes in Computer Science(), vol 10426. Springer, Cham. https://doi.org/10.1007/978-3-319-63387-9_6
Download citation
DOI: https://doi.org/10.1007/978-3-319-63387-9_6
Published:
Publisher Name: Springer, Cham
Print ISBN: 978-3-319-63386-2
Online ISBN: 978-3-319-63387-9
eBook Packages: Computer ScienceComputer Science (R0)





 ” if
” if  ” otherwise.
” otherwise. ” otherwise, where c is from (
” otherwise, where c is from ( ” if
” if 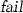 ” otherwise;
” otherwise; ” otherwise, where
” otherwise, where  ” meaning that “there exists a univariate guess-and-check function”; otherwise, the algorithm outputs “
” meaning that “there exists a univariate guess-and-check function”; otherwise, the algorithm outputs “ ”.
”. . The algorithm calls
. The algorithm calls  , and if it returns “
, and if it returns “ ”, then return “
”, then return “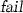 ”, otherwise execute the following steps. Obtain the following inequality
”, otherwise execute the following steps. Obtain the following inequality  .
.