Abstract
We provide the first constructions of identity-based encryption and hierarchical identity-based encryption based on the hardness of the (Computational) Diffie-Hellman Problem (without use of groups with pairings) or Factoring. Our construction achieves the standard notion of identity-based encryption as considered by Boneh and Franklin [CRYPTO 2001]. We bypass known impossibility results using garbled circuits that make a non-black-box use of the underlying cryptographic primitives.
Research supported in part from AFOSR YIP Award, DARPA/ARL SAFEWARE Award W911NF15C0210, AFOSR Award FA9550-15-1-0274, NSF CRII Award 1464397, and research grants by the Okawa Foundation, Visa Inc., and Center for Long-Term Cybersecurity (CLTC, UC Berkeley). The views expressed are those of the author and do not reflect the official policy or position of the funding agencies. Nico Döttling was supported by a postdoc fellowship of the German Academic Exchange Service (DAAD).
You have full access to this open access chapter, Download conference paper PDF
Similar content being viewed by others
1 Introduction
Soon after the invention of public-key encryption [20, 43], Shamir [44] posed the problem of constructing a public-key encryption scheme where encryption can be performed using just the identity of the recipient. In such an identity-based encryption (IBE) scheme there are four algorithms: (1) Setup generates the global public parameters and a master secret key, (2) KeyGen uses the master secret key to generate a secret key for the user with a particular identity, (3) Encrypt allows for encrypting messages corresponding to an identity, and (4) Decrypt can be used to decrypt the generated ciphertext using a secret key for the matching identity.
The ability of IBE to “compress” exponentially many public keys into “small” global public parameters [11, 19] provides a way for simplifying certificate management in e-mail systems. Specifically, Alice can send an encrypted email to Bob at bob@iacr.org by just using the string “bob@iacr.org” and the public parameters generated by a setup authority. In this solution, there is no need for Alice to obtain Bob’s public key. Bob could decrypt the email using a secret key corresponding to “bob@iacr.org” that he can obtain from the setup authority.
The more functional notion of hierarchical IBE (HIBE) [28, 32] additionally allows a user with a secret key for an identity \(\mathsf {id}\) to generate a secret key for any identity \(\mathsf {id}\Vert \mathsf {id}'\). For instance, in the example above, Bob can use the secret key corresponding to identity “bob@iacr.org” to obtain a secret key corresponding to the identity “bob@iacr.org \(\Vert \) 2017”. Bob could then give this key to his secretary who could now decrypt all his emails tagged as being sent during the year 2017, while Bob is on vacation.
The first IBE schemes were realized by Boneh and Franklin [11] and Cocks [19]. Subsequently, significant research effort has been devoted to realizing IBE and HIBE schemes. By now, several constructions of IBE are known based on (i) various assumptions on groups with a bilinear map, e.g. [8, 9, 11, 16, 41, 48], (ii) the quadratic residuocity assumption [12, 19] (in the random oracle model [6]), or (iii) the learning-with-errors (LWE) assumption [3, 17, 27]. On the other hand, HIBE schemes are known based on (i) various assumptions on groups with a bilinear map [8, 10, 25, 28, 32, 35, 45, 47], or (ii) LWE [1, 2, 17].
On the negative side, Boneh et al. [13] show that IBE cannot be realized using trapdoor permutations or CCA-secure public-key encryption in a black-box manner. Furthermore, Papakonstantinou et al. [42] show that black-box use of a group over which DDH is assumed to be hard is insufficient for realizing IBE.
1.1 Our Results
In this work, we show a fully-secure construction of IBE and a selectively secure HIBE based just on the Computational Diffie-Hellman (CDH). In the group of quadratic residues this problem is as hard as the Factoring problem [7, 38, 46]. Therefore, this implies a solution based on the hardness of factoring as well.
Our constructions bypass the known impossibility results [13, 42] by making a non-black-box use of the underlying cryptographic primitives. However, this non-black-box use of cryptographic primitives also makes our scheme inefficient. In Sect. 6, we suggest ideas for reducing the non-black-box of the underlying primitives thereby improving the efficiency of our scheme. Even with these optimizations, our IBE scheme is prohibitive when compared with the IBE schemes based on bilinear maps. We leave open the problem of realizing an efficient IBE scheme from the Diffie-Hellman Assumption.
Subsequent Work. In a followup paper [21] we show how the techniques from this paper can be used to obtain generic constructions of fully-secure IBE and selectively-secure HIBE starting with any selectively-secure IBE scheme.
2 Our Techniques
In this section, we give an intuitive explanation of our construction of IBE from the Decisional Diffie-Hellman (DDH) Assumption. We defer the details on constructing HIBE and obtaining the same results based on Computational Diffie-Hellman to the main body of the paper.
We start by describing a chameleon hash function [34] that supports certain encryption and decryption procedures. We refer to this new primitive as a chameleon encryption scheme.Footnote 1 Subsequently, we describe how chameleon encryption along with garbled circuits can be used to realize IBE.
2.1 Chameleon Encryption
As mentioned above, a chameleon encryption scheme is a chameleon hash function that supports certain encryption and decryption procedures along with. We start by describing the chameleon hash function and then the associated encryption and decryption procedures. Recall that a chameleon hash function is a collision resistant hash function for which the knowledge of a trapdoor enables collision finding.
Our Chameleon Hash. Given a cyclic group \(\mathbb {G}\) of prime order p with a generator g consider the following chameleon hash function:
where \(\mathsf {k}= (g, \{g_{j,0}, g_{j,1}\}_{j\in [n]})\), \(r\in \mathbb {Z}_p\) and \(\mathsf {x}_j\) is the \(j^{th}\) bit of \(\mathsf {x}\in \{0,1\}^n\). It is not very hard to note that this hash function is (i) collision resistant based on the hardness of the discrete-log problem, and (ii) chameleon given the trapdoor information \(\{\mathsf {dlog}_g~g_{j,0},\mathsf {dlog}_g~g_{j,1}\}_{j\in [n]}\)—specifically, given any \(\mathsf {x},r,\mathsf {x}'\) and the trapdoor information we can efficiently compute \(r'\) such that \(\mathsf {H}(\mathsf {k}, \mathsf {x};r)=\mathsf {H}(\mathsf {k}, \mathsf {x}';r')\).
The Associated Encryption—Abstractly. Corresponding to a chameleon hash function, we require encryption and decryption algorithms such that
-
1.
encryption \(\mathsf {Enc}(\mathsf {k},(\mathsf {h},i,b),\mathsf {m})\) on input a key \(\mathsf {k}\), a hash value \(\mathsf {h}\), a location \(i\in [n]\), a bit \(b \in \{0,1\}\), and a message \(\mathsf {m}\in \{0,1\}\) outputs a ciphertext \(\mathsf {ct}\), and
-
2.
decryption \(\mathsf {Dec}(\mathsf {k}, (\mathsf {x}, r), \mathsf {ct})\) on input a ciphertext \(\mathsf {ct}\), \(\mathsf {x}\) and coins \(r\) yields \(\mathsf {m}\) if
$$\mathsf {h}= \mathsf {H}(\mathsf {k},\mathsf {x};r) \text { and } \mathsf {x}_i = b,$$where \((\mathsf {h},i,b)\) are the values used in the generation of the ciphertext \(\mathsf {ct}\).
In other words, the decryptor can use the knowledge of the preimage of \(\mathsf {h}\) as the key to decrypt \(\mathsf {m}\) as long as the \(i^{th}\) bit of the preimage it can supply is equal to the value b chosen at the time of encryption. Our security requirement roughly is that
where \(\mathop {\approx }\limits ^{c}\) denotes computational indistinguishability.Footnote 2
The Associated Encryption—Realization. Corresponding to the chameleon hash defined above our encryption procedure \(\mathsf {Enc}(\mathsf {k}, (\mathsf {h},i,b),\mathsf {m})\) proceeds as follows. Sample a random value \(\rho \xleftarrow {\$}\mathbb {Z}_p\) and output the ciphertext \(\mathsf {ct}\) where \(\mathsf {ct}=(e, c, c', \{c_{j,0},c_{j,1}\}_{j \in [n] \backslash \{ i \}})\) and
It is easy to see that if \(\mathsf {x}_i = b\) then decryption \(\mathsf {Dec}(\mathsf {ct}, (\mathsf {x},r))\) can just output
However, if \(\mathsf {x}_i \ne b\) then the decryptor has access to the value \(g_{i,x_i}^\rho \) but not \(g_{i,b}^\rho \), and this prevents him from learning the message \(\mathsf {m}\). Formalizing this intuition, we can argue security of this scheme based on the DDH assumption.Footnote 3 In a bit more detail, we can use an adversary \(\mathcal {A}\) breaking the security of the chameleon encryption scheme to distinguish DDH tuples \((g,g^{u},g^{v},g^{uv})\) from random tuples \((g,g^{u},g^{v},g^{s})\). Fix (adversarially chosen) \(\mathsf {x}\in \{0,1\} ^n\), index \(i \in [n]\) and a bit \(b \in \{0,1\} \). Given a tuple (g, U, V, T), we can simulate public key \(\mathsf {k}\), hash value \(\mathsf {h}\), coins \(r\) and ciphertext \(\mathsf {ct}\) as follows. Choose uniformly random values \(\alpha _{j,0}, \alpha _{j,1} \xleftarrow {\$}\mathbb {Z}_p\) and set \(g_{j,0} = g^{\alpha _{j,0}}\) and \(g_{j,1} = g^{\alpha _{j,1}}\) for \(j \in [n]\). Now reassign \(g_{i,1 - \mathsf {x}_i}= U\) and set \(\mathsf {k}:=(g,\{ g_{j,0}, g_{j,1} \}_{j \in [n]})\). Choose \(r\xleftarrow {\$}\mathbb {Z}_p\) uniformly at random and set \(\mathsf {h}:=\mathsf {H}(\mathsf {k},\mathsf {x};r)\). Finally prepare a challenge ciphertext \(\mathsf {ct}:=(e,c,c',\{ c_{j,0},c_{j,1} \}_{j \in [n] \backslash \{i\}} )\) by choosing
where \(\mathsf {m}\in \{0,1\} \). Now, if \((g,U,V,T) = (g,g^{u},g^{v},g^{uv})\), then a routine calculation shows that \(\mathsf {k}\), \(\mathsf {h}\), \(r\) and \(\mathsf {ct}\) have the same distribution as in the security experiment, thus \(\mathcal {A}\)’s advantage in guessing \(\mathsf {m}\) remains the same. On the other hand, if T is chosen uniformly at random and independent of g, U, V, then \(\mathcal {A}\)’s advantage to guess \(\mathsf {m}\) given \(\mathsf {k}\), \(\mathsf {h}\), \(r\) and \(\mathsf {ct}\) is obviously 0, which concludes this proof-sketch.
2.2 From Chameleon Encryption to Identity-Based Encryption
The public parameters of an IBE scheme need to encode exponentially many public keys succinctly—one per each identity. Subsequently, corresponding to these public parameters the setup authority should be able to provide the secret key for any of the exponentially many identities. This is in sharp contrast with public-key encryption schemes for which there is only one trapdoor per public key, which if revealed leaves no security. This is the intuition behind the black-box impossibility results for realizing IBE based on trapdoor permutations and CCA secure encryption [13, 42]. At a very high level, we overcome this intuitive barrier by actually allowing for exponentially many public keys which are somehow compressed into small public parameters using our chameleon hash function. We start by describing how these keys are sampled and hashed.
Arrangement of the Keys. We start by describing the arrangement of the exponentially many keys in our IBE scheme for identities of length n bits. First, imagine a fresh encryption decryption key pair for any public-key encryption scheme for each identity in \(\{0,1\}^n\). We will denote this pair for identity \(\mathsf {v}\in \{0,1\}^n\) by \((\mathsf {ek}_\mathsf {v},\mathsf {dk}_\mathsf {v})\). Next, in order to setup the hash values, we sample n hash keys — namely, \(\mathsf {k}_0,\ldots \mathsf {k}_{n-1}\). Now, consider a tree of depth n and for each node \(\mathsf {v}\in \{0,1\}^{\le n-1} \cup \{\epsilon \}\) Footnote 4 the hash value \(\mathsf {h}_\mathsf {v}\) is set as:
where \(r_\mathsf {v}\) for each \(\mathsf {v}\in \{0,1\}^{< n}\cup \{\epsilon \}\) are chosen randomly.
Generating the Tree on Demand. Note that the setup authority cannot generate and hash these exponentially many hash keys at setup time. Instead, it generates them implicitly. More specifically, the setup authority computes each \(\mathsf {h}_\mathsf {v}\) as \(\mathsf {H}(\mathsf {k}_{|\mathsf {v}|},0^\lambda ;\omega _\mathsf {v})\). Then, later on when needed, using the trapdoor \(\mathsf {t}_{|\mathsf {v}|}\) for the hash key \(\mathsf {k}_{|\mathsf {v}|}\) we can obtain coins \(r_\mathsf {v}\) such that the generated value \(\mathsf {h}_\mathsf {v}\) indeed satisfies Eq. 1. Furthermore, in order to maintain consistency (in the tree and across different invocations) the randomness \(\omega _\mathsf {v}\) used for each \(\mathsf {v}\) is chosen using a pseudorandom function. In summary, with this change the entire can be represented succinctly.
What Are the Public Parameters? Note that the root hash value \(\mathsf {h}_\varepsilon \) somehow binds the entire tree of hash values. With this in mind, we sent the public parameters of the scheme to be the n hash keys and the root hash value, i.e.
Secret-Key for a Particular Identity \(\mathsf {id}\) . Given the above tree structure the secret key for some identity \(\mathsf {id}\) simply consists of the hash values along the path from the root to the leaf corresponding to \(\mathsf {id}\) and their siblings along with the decryption key \(\mathsf {dk}_\mathsf {id}\).Footnote 5 Specifically, the secret key \(\mathsf {sk}_{\mathsf {id}}\) for identity \(\mathsf {id}\) consists of \(\left( \{\mathsf {lk}_{\mathsf {v}}\}_{\mathsf {v}\in V}, \mathsf {dk}_\mathsf {id}\right) \) where \(V :=\{\varepsilon , \mathsf {id}[1], \ldots \mathsf {id}[1\ldots n-1]\}\) and
Encryption and Decryption. Before providing details of encryption and decryption, we will briefly discuss how chameleon encryption can be useful in conjunction with garbled circuits.Footnote 6 Chameleon encryption allows an encryptor knowing a key \(\mathsf {k}\) and a hash value \(\mathsf {h}\) to encrypt a set of labels \(\{ \mathsf {lab}_{j,0}, \mathsf {lab}_{j,1} \}_{j}\) such that a decryptor knowing \(\mathsf {x}\) and \(r\) with \(\mathsf {H}(\mathsf {k},\mathsf {x};r) = \mathsf {h}\) can recover \(\{ \mathsf {lab}_{j,\mathsf {x}_j} \}_{j}\). On the other hand, security of chameleon encryption guarantees that the receiver learns nothing about the remaining labels. In summary, using this mechanism, an the generated ciphertexts enable the decryptor to feed \(\mathsf {x}\) into a garbled circuit to be processed further.
To encrypt a message \(\mathsf {m}\) to an identity \(\mathsf {id}\in \{0,1\}^n\), the encryptor will generate a sequence of \(n+1\) garbled circuits \(\{\tilde{P}^0,\ldots \tilde{P}^{n-1},\tilde{T}\}\) such that a decryptor in possession of the identity secret key \(\mathsf {sk}_\mathsf {id}= (\{\mathsf {lk}_{\mathsf {v}}\}_{\mathsf {v}\in V},\mathsf {dk}_\mathsf {id})\) will be able evaluate these garbled circuits one after another. Roughly speaking, circuit \({P}^i\) for any \(i\in \{0\ldots n-1\}\) and \(\mathsf {v}= \mathsf {id}[1\ldots i]\) takes as input a hash value \(\mathsf {h}_{\mathsf {v}}\) and generates chameleon encryptions of the input labels of the next garbled circuit \(\tilde{P}^{i+1}\) using a \(\mathsf {k}_{|\mathsf {v}|}\) hardwired inside it and the hash value \(\mathsf {h}\) given to it as input (in a manner as described above). The last circuit T will just take as input an encryption key \(\mathsf {pk}_\mathsf {id}\) and output an encryption of the plaintext message \(\mathsf {m}\) under \(\mathsf {ek}_\mathsf {id}\). Finally, the encryptor provides input labels for the first garbled circuit \(\tilde{P}^0\) for the input \(\mathsf {h}_{\varepsilon }\) in the ciphertext.
During decryption, for each \(i \in \{0\ldots n-1\}\) and \(\mathsf {v}= \mathsf {id}[1\ldots i]\) the decryptor will use the local key \(\mathsf {lk}_{\mathsf {v}}\) to decrypt the ciphertexts generated by \(\tilde{P}^i\) and obtain the input labels for the garbled circuits \(\tilde{P}^{i+1}\) (or, T if \(i = n-1\)). We will now explain the first iteration of this construction in more detail, all further iterations proceed analogously. The encryptor provides garbled input labels corresponding to input \(\mathsf {h}_\varepsilon \) for the first garbled circuit \(\tilde{P}^0\) in the ciphertext. Thus the decryptor can evaluate \(\tilde{P}^0\) and obtain encryptions of input labels \(\left\{ \mathsf {lab}_{j,0}, \mathsf {lab}_{j,1} \right\} _{j \in [\lambda ]}\) for the circuit \(\tilde{P}^1\), namely:
The garbled circuit has \(\mathsf {id}[1]\) and the input labels \(\left\{ \mathsf {lab}_{j,0}, \mathsf {lab}_{j,1} \right\} _{j \in [\lambda ]}\) hardwired in it. Given these encryptions the decryptor uses \(\mathsf {lk}_\varepsilon = (\mathsf {h}_{\varepsilon },\mathsf {h}_0,\mathsf {h}_1,r_\varepsilon )\) to learn the garbled input labels \(\{\mathsf {lab}_{j,{\mathsf {h}_{\mathsf {id}[1],j}}}\}_{j\in [\lambda ]}\) where \({\mathsf {h}_{\mathsf {id}[1],j}}\) is the \(j^{th}\) bit of \(\mathsf {h}_{\mathsf {id}[1]}\). In other words, the decryptor now possesses input labels for the input \(\mathsf {h}_{\mathsf {id}[1]}\) for the garbled circuit \(\tilde{P}^1\) and can therefore evaluate \(\tilde{P}^1\). Analogous to the previous step, the decryptor uses \(\mathsf {lk}_{\mathsf {id}[1]}\) and \(r_{\mathsf {id}[1]}\) to obtain input labels to \(\tilde{P}^2\) and so on. The decryptor’s ability to provide the local keys \(\mathsf {lk}_{v}\) for \(v \in V\) keeps this process going ultimately revealing an encryption of the message \(\mathsf {m}\) under the encryption key \(\mathsf {pk}_\mathsf {id}\). This final ciphertext can be decrypted using the decryption key \(\mathsf {dk}_\mathsf {id}\). At a high level, our encryption method (and the use of garbled circuits for it) has similarities with garbled RAM schemes [18, 23, 24, 26, 37]. Full details of the construction are provided in Sect. 6.
Proof Sketch. The intuition behind the proof of security which follows by a sequence of hybrid changes is as follows. The first (easy) change is to replace the pseudorandom function used to generate the local keys by a truly random function something that should go undetected against a computationally bounded attacker. Next, via a sequence of hybrids we change the \(n+1\) garbled circuits \(\tilde{P}^0,\ldots \tilde{P}^{n-1}, \tilde{T}\) to their simulated versions one by one. Once these changes are made the simulated circuit \(\tilde{T}\) just outputs an encryption of the message \(\mathsf {m}\) under the encryption key \(\mathsf {pk}_{\mathsf {id}^*}\) corresponding challenge identity \(\mathsf {id}^*\), which hides \(\mathsf {m}\) based on semantic security of the encryption scheme.
The only “tricky” part of the proof is the one that involves changing garbled circuits to their simulated versions. In this intuitive description, we explain how the first garbled circuit \(\tilde{P}^0\) is moved to its simulated version. The argument of the rest of the garbled circuits is analogous. This change involves a sequence of four hybrid changes.
-
1.
First, we change how \(\mathsf {h}_\varepsilon \) is generated. As a quick recap, recall that \(\mathsf {h}_\varepsilon \) is generated as \(\mathsf {H}(\mathsf {k}_0,0^{2\lambda };\omega _\varepsilon )\) and \(r_\varepsilon \) are set to \(\mathsf {H}^{-1}(\mathsf {t}_0, (0^{2\lambda },\omega _\varepsilon ), \mathsf {h}_0\Vert \mathsf {h}_1)\). We instead generate \(\mathsf {h}_\varepsilon \) directly to be equal to the value \(r_\varepsilon \) are set to \(\mathsf {H}(\mathsf {k}_0, \mathsf {h}_0\Vert \mathsf {h}_1, r_\varepsilon )\) using fresh coins \(r_\varepsilon \). The trapdoor collision and uniformity properties of the chameleon encryption scheme ensure that this change does not affect the distribution of the \(\mathsf {h}_\varepsilon \) and \(r_\varepsilon \), up to a negligible error.
-
2.
The second change we make is that the garbled circuit \(\tilde{P}^0\) is not generates in simulated form instead of honestly. Note that at this point the distribution of this garbled circuit depends only on its output which is \(\{\mathsf {Enc}(\mathsf {k}_{\varepsilon }, (\mathsf {h}_{\varepsilon },j,b), \mathsf {lab}_{j,b}) \}_{j \in [\lambda ], b \in \{0,1\}}\) where \(\{\mathsf {lab}_{j,b}\}_{j \in [\lambda ], b \in \{0,1\}}\) are the input labels for the garbled circuit \(\tilde{P}^1\).
-
3.
Observe that at this point the trapdoor \(\mathsf {t}_\varepsilon \) is not being used at all and \(\tilde{P}^0\) is the simulated form. Therefore, based on the security of the chameleon encryption we have that for all \(j \in [\lambda ], \mathsf {Enc}(\mathsf {k}_{\varepsilon }, (\mathsf {h}_{\varepsilon },j,1-\mathsf {h}_{\mathsf {id}[1],j}),\mathsf {lab}_{j,1-\mathsf {h}_{\mathsf {id}[1],j}}) \) hides \(\mathsf {lab}_{j,1-\mathsf {h}_{\mathsf {id}[1],j}}\). Hence, we can change the hardcoded ciphertexts from
$$ \{\mathsf {Enc}(\mathsf {k}_{\varepsilon }, (\mathsf {h}_{\varepsilon },j,b), \mathsf {lab}_{j,b}) \}_{j \in [\lambda ], b\in \{0,1\}} $$to
$$ \{\mathsf {Enc}(\mathsf {k}_{\varepsilon }, (\mathsf {h}_{\varepsilon },j,b), \mathsf {lab}_{j,\mathsf {h}_{\mathsf {id}[1],j}}) \}_{j \in [\lambda ], b\in \{0,1\}} $$ -
4.
Finally, the fourth change we make is that we reverse the first change. In particular, we generate \(\mathsf {h}_\varepsilon \) as is done in the real execution.
As a consequence, at this point only the labels \(\{ \mathsf {lab}_{j,\mathsf {h}_{\mathsf {id}[1],j}}\}_{j \in [\lambda ]}\) are revealed in an information theoretic sense and the same sequence of hybrids can be repeated for the next garbled circuit \(\tilde{P}^1\). The only change in this step is that now both \(\mathsf {h}_0\) and \(\mathsf {h}_1\) will be generated (if needed) by first sampling their children. The full proof of security is provided in Sect. 6.2.
3 Preliminaries
Let \(\lambda \) denote the security parameter. We use the notation [n] to denote the set \(\{1,\ldots ,n\}\). By PPT we mean a probabilistic polynomial time algorithm. For any set S, we use \(x \xleftarrow {\$}S\) to mean that x is sampled uniformly at random from the set S.Footnote 7 Alternatively, for any distribution D we use \(x \xleftarrow {\$}D\) to mean that x is sampled from the distribution D. We use the operator \(:=\) to represent assignment and \(=\) to denote an equality check.
3.1 Computational Problems
Definition 1
(The Diffie-Hellman (DH) Problem). Let \((\mathbb {G},\cdot )\) be a cyclic group of order p with generator g. Let a, b be sampled uniformly at random from \(\mathbb {Z}_p\) (i.e., \(a,b \xleftarrow {\$}\mathbb {Z}_p\)). Given \((g,g^a,g^b)\), the \(\mathsf {DH}(\mathbb {G})\) problem asks to compute \(g^{ab}\).
Definition 2
(The Factoring Problem). Given a Blum integer \(N = pq\) (p and q are large primes with \(p = q = 3 \mod 4\)) the \(\mathsf {FACT}\) problem asks to compute p and q.
3.2 Identity-Based Encryption
Below we provide the definition of identity-based encryption (IBE).
Definition 3
(Identity-Based Encryption (IBE) [11, 44]). An identity-based encryption scheme consists of four PPT algorithms \((\mathsf {Setup}, \mathsf {KeyGen}, \mathsf {Encrypt}, \mathsf {Decrypt})\) defined as follows:
-
\(\mathsf {Setup}(1^\lambda )\): given the security parameter, it outputs a master public key \(\mathsf {mpk}\) and a master secret key \(\mathsf {msk}\).
-
\(\mathsf {KeyGen}(\mathsf {msk},\mathsf {id})\): given the master secret key \(\mathsf {msk}\) and an identity \(\mathsf {id}\in \{0,1\} ^n\), it outputs a decryption key \(\mathsf {sk}_\mathsf {id}\).
-
\(\mathsf {Encrypt}(\mathsf {mpk}, \mathsf {id}, \mathsf {m})\): given the master public key \(\mathsf {mpk}\), an identity \(\mathsf {id}\in \{0,1\} ^n\), and a message \(\mathsf {m}\), it outputs a ciphertext \(\mathsf {ct}\).
-
\(\mathsf {Decrypt}(\mathsf {sk}_\mathsf {id}, \mathsf {ct})\): given a secret key \(\mathsf {sk}_\mathsf {id}\) for identity \(\mathsf {id}\) and a ciphertext \(\mathsf {ct}\), it outputs a string \(\mathsf {m}\).
The following completeness and security properties must be satisfied:
-
Completeness: For all security parameters \(\lambda \), identities \(\mathsf {id}\in \{0,1\} ^n\) and messages \(\mathsf {m}\), the following holds:
$$\begin{aligned} \mathsf {Decrypt}(\mathsf {sk}_\mathsf {id}, \mathsf {Encrypt}(\mathsf {mpk}, \mathsf {id}, \mathsf {m})) = \mathsf {m}\end{aligned}$$where \(\mathsf {sk}_\mathsf {id}\leftarrow \mathsf {KeyGen}(\mathsf {msk},\mathsf {id})\) and \((\mathsf {mpk},\mathsf {msk}) \leftarrow \mathsf {Setup}(1^\lambda )\).
-
Security: For any PPT adversary \(\mathcal {A} = (\mathcal {A}_1,\mathcal {A}_2)\), there exists a negligible function \(\mathsf {negl}(.)\) such that the following holds:
$$\Pr [\text {IND}_{\mathcal {A}}^{\text {IBE}}(1^\lambda ) = 1] \le \dfrac{1}{2} + \mathsf {negl}(\lambda )$$where \(\text {IND}_{\mathcal {A}}^{\text {IBE}}\) is shown in Fig. 1, and for each key query \(\mathsf {id}\) that \(\mathcal {A}\) sends to the \(\mathsf {KeyGen}\) oracle, it must hold that \(\mathsf {id}\ne \mathsf {id}^*\).
Hierarchical Identity-Based Encryption (HIBE). A HIBE scheme is an IBE scheme except that we set \(\mathsf {sk}_\varepsilon :=\mathsf {msk}\) and modify the \(\mathsf {KeyGen}\) algorithm. In particular, \(\mathsf {KeyGen}\) takes \(\mathsf {sk}_\mathsf {id}\) and a string \(\mathsf {id}'\) as input and outputs a secret key \(\mathsf {sk}_{\mathsf {id}\Vert \mathsf {id}'}\). More formally:
-
\(\mathsf {KeyGen}(\mathsf {sk}_\mathsf {id},\mathsf {id}')\): given the secret key \(\mathsf {sk}_\mathsf {id}\) and an identity \(\mathsf {id}' \in \{0,1\} ^*\), it outputs a decryption key \(\mathsf {sk}_{\mathsf {id}\Vert \mathsf {id}'}\).
Correctness condition for HIBE is same as it was from IBE. Additionally, the security property is analogous to \(\text {IND}_{\mathcal {A}}^{\text {IBE}}(1^\lambda )\) except that now we only consider the notion of selective security for HIBE—namely, the adversary \(\mathcal {A}\) is required to announce the challenge identity \(\mathsf {id}^*\) before it has seen the \(\mathsf {mpk}\) and has made any secret key queries. This experiment \(\text {IND}_{\mathcal {A}}^{\text {HIBE}}\) is shown formally in Fig. 2.
3.3 Garbled Circuits
Garbled circuits were first introduced by Yao [49] (see Lindell and Pinkas [36] and Bellare et al. [5] for a detailed proof and further discussion). A circuit garbling scheme is a tuple of PPT algorithms \((\mathsf {GCircuit},\mathsf {Eval})\). Very roughly \(\mathsf {GCircuit}\) is the circuit garbling procedure and \(\mathsf {Eval}\) the corresponding evaluation procedure. More formally:
-
\((\widetilde{\mathsf {C}},\{\mathsf {lab}_{w,b}\}_{w\in \mathsf {inp}(\mathsf {C}), b\in {\{0,1\}}}) \xleftarrow {\$}\mathsf {GCircuit}\left( 1^\lambda , \mathsf {C}\right) \): \(\mathsf {GCircuit}\) takes as input a security parameter \(\lambda \) and a circuit \(\mathsf {C}\). This procedure outputs a garbled circuit \(\widetilde{\mathsf {C}}\) and labels \(\{\mathsf {lab}_{w,b}\}_{w\in \mathsf {inp}(\mathsf {C}), b\in {\{0,1\}}}\) where each \(\mathsf {lab}_{w,b} \in {\{0,1\}}^\lambda \).Footnote 8
-
\(y:=\mathsf {Eval}\left( \widetilde{\mathsf {C}}, \{\mathsf {lab}_{w,x_w}\}_{w\in \mathsf {inp}(\mathsf {C})}\right) \): Given a garbled circuit \(\widetilde{\mathsf {C}}\) and a garbled input represented as a sequence of input labels \(\{ \mathsf {lab}_{w,x_w}\}_{w\in \mathsf {inp}(\mathsf {C})}\), \(\mathsf {Eval}\) outputs an output \(y\).
Correctness. For correctness, we require that for any circuit \(\mathsf {C}\) and input \(x \in {\{0,1\}}^{m}\) (here \(m\) is the input length to \(\mathsf {C}\)) we have that:
where \((\widetilde{\mathsf {C}}, \{\mathsf {lab}_{w,b}\}_{w\in \mathsf {inp}(\mathsf {C}), b\in {\{0,1\}}}) \xleftarrow {\$}\mathsf {GCircuit}\left( 1^\lambda , \mathsf {C}\right) \).
Security. For security, we require that there is a PPT simulator \(\mathsf {Sim}\) such that for any \(\mathsf {C}, x\), we have that
where \((\widetilde{\mathsf {C}}, \{\mathsf {lab}_{w,b}\}_{w\in \mathsf {inp}(\mathsf {C}), b\in {\{0,1\}}}) \xleftarrow {\$}\mathsf {GCircuit}\left( 1^\lambda , \mathsf {C}\right) \).Footnote 9
4 Chameleon Encryption
In this section, we give the definition of a chameleon encryption scheme.
Definition 4
(Chameleon Encryption). A chameleon encryption scheme consists of five PPT algorithms \(\mathsf {Gen}\), \(\mathsf {H}\), \(\mathsf {H}^{-1}\), \(\mathsf {Enc}\), and \(\mathsf {Dec}\) with the following syntax.
-
\(\mathsf {Gen}(1^\lambda ,n)\): Takes the security parameter \(\lambda \) and a message-length n (with \(n = \mathsf {poly}(\lambda )\)) as input and outputs a key \(\mathsf {k}\) and a trapdoor \(\mathsf {t}\).
-
\(\mathsf {H}(\mathsf {k},\mathsf {x};r)\): Takes a key \(\mathsf {k}\), a message \(\mathsf {x}\in \{0,1\} ^n\), and coins \(r\) and outputs a hash value \(\mathsf {h}\), where \(\mathsf {h}\) is \(\lambda \) bits.
-
\(\mathsf {H}^{-1}(\mathsf {t}, (\mathsf {x},r),\mathsf {x}')\): Takes a trapdoor \(\mathsf {t}\), previously used message \(\mathsf {x}\in \{0,1\}^n\) and coins \(r\), and a message \(\mathsf {x}' \in \{0,1\} ^n\) as input and returns \(r'\).
-
\(\mathsf {Enc}(\mathsf {k},(\mathsf {h},i,b),\mathsf {m})\): Takes a key \(\mathsf {k}\), a hash value \(\mathsf {h}\), an index \(i \in [n]\), \(b \in \{0,1\}\), and a message \(\mathsf {m}\in \{0,1\} ^*\) as input and outputs a ciphertext \(\mathsf {ct}\).Footnote 10
-
\(\mathsf {Dec}(\mathsf {k},(\mathsf {x},r),\mathsf {ct})\): Takes a key \(\mathsf {k}\), a message \(\mathsf {x}\), coins \(r\) and a ciphertext \(\mathsf {ct}\), as input and outputs a value \(\mathsf {m}\) (or \(\bot \)).
We require the following propertiesFootnote 11
-
Uniformity: For \(\mathsf {x},\mathsf {x}' \in \{0,1\} ^n\) we have that the two distributions \(\mathsf {H}(\mathsf {k},\mathsf {x};r)\) and \(\mathsf {H}(\mathsf {k},\mathsf {x}';r')\) are statistically close (when \(r,r'\) are chosen uniformly at random).
-
Trapdoor Collisions: For every choice of \(\mathsf {x},\mathsf {x}' \in \{0,1\} ^n\) and \(r\) it holds that if \((\mathsf {k},\mathsf {t}) \xleftarrow {\$}\mathsf {Gen}(1^\lambda ,n)\) and \(r' := \mathsf {H}^{-1}(\mathsf {t},(\mathsf {x},r),\mathsf {x}')\), then it holds that
$$ \mathsf {H}(\mathsf {k},\mathsf {x};r) = \mathsf {H}(\mathsf {k},\mathsf {x}';r'), $$i.e. \(\mathsf {H}(\mathsf {k},\mathsf {x};r)\) and \(\mathsf {H}(\mathsf {k},\mathsf {x}';r')\) generate the same hash \(\mathsf {h}\). Moreover, if \(r\) is chosen uniformly at random, then \(r'\) is also statistically close to uniform.
-
Correctness: For any choice of \(\mathsf {x}\in \{0,1\} ^n\), coins \(r\), index \(i \in [n]\) and message \(\mathsf {m}\) it holds that if \((\mathsf {k},\mathsf {t}) \xleftarrow {\$}\mathsf {Gen}(1^\lambda ,n)\), \(\mathsf {h}:= \mathsf {H}(\mathsf {k}, \mathsf {x};r)\), and \(\mathsf {ct}\xleftarrow {\$}\mathsf {Enc}(\mathsf {k},(\mathsf {h},i,\mathsf {x}_i),\mathsf {m})\) then \(\mathsf {Dec}(\mathsf {k},\mathsf {ct},(\mathsf {x},r)) = \mathsf {m}\).
-
Security: For any PPT adversary \(\mathcal {A} = (\mathcal {A}_1,\mathcal {A}_2)\) there exists a negligible function \(\mathsf {negl}(\cdot )\) such that the following holds:
$$\begin{aligned} \Pr [\text {IND}^{\text {CE}}_{\mathcal {A}}(1^\lambda ) = 1]\le \frac{1}{2} + \mathsf {negl}(\lambda ) \end{aligned}$$where \(\text {IND}^{\text {CE}}_{\mathcal {A}}\) is shown in Fig. 3.
5 Constructions of Chameleon Encryption from CDH
Let \((\mathbb {G},\cdot )\) be a cyclic group of order p (not necessarily prime) with generator g. Let \(\mathsf {Sample}(\mathbb {G})\) be a PPT algorithm such that its output is statistically close to a uniform element in \(\mathbb {Z}_p\), where p (not necessarily prime) is the order of \(\mathbb {G}\).Footnote 12 We will now describe a chameleon encryption scheme assuming that the \(\mathsf {DH}(\mathbb {G})\) problem is hard.
-
\(\mathsf {Gen}(1^\lambda ,n)\): For each \(j \in [n]\), choose uniformly random values \(\alpha _{j,0}, \alpha _{j,1} \xleftarrow {\$}\mathsf {Sample}(\mathbb {G})\) and compute \(g_{j,0} := g^{\alpha _{j,0}}\) and \(g_{j,1} := g^{\alpha _{j,1}}\). Output \((\mathsf {k},\mathsf {t})\) whereFootnote 13
$$\begin{aligned} \mathsf {k}:= \left( g, \begin{pmatrix} g_{1,0}, g_{2,0} \ldots , g_{n,0} \\ g_{1,1}, g_{2,1}, \ldots , g_{n,1}\end{pmatrix}\right) \qquad \mathsf {t}:= \begin{pmatrix} \alpha _{1,0}, \alpha _{2,0} \ldots , \alpha _{n,0} \\ \alpha _{1,1}, \alpha _{2,1}, \ldots , \alpha _{n,1}\end{pmatrix}.\end{aligned}$$(2) -
\(\mathsf {H}(\mathsf {k},\mathsf {x};r)\): Parse \(\mathsf {k}\) as in Eq. 2, sample \(r\xleftarrow {\$}\mathsf {Sample}(\mathbb {G})\), set \(\mathsf {h}:= g^r\cdot \prod _{j\in [n]} g_{j,\mathsf {x}_j}\) and output \(\mathsf {h}\)
-
\(\mathsf {H}^{-1}(\mathsf {t},(\mathsf {x},r),\mathsf {x}')\): Parse \(\mathsf {t}\) as in Eq. 2, compute \(r'\,:=\,r+ \sum _{j\in [n]} ( \alpha _{j,\mathsf {x}_j} - \alpha _{j,\mathsf {x}'_j}) \mod p\). Output \(r'\).
-
\(\mathsf {Enc}(\mathsf {k},(\mathsf {h},i,b),\mathsf {m})\): Parse \(\mathsf {k}\) as in Eq. 2, \(\mathsf {h}\in \mathbb {G}\) and \(\mathsf {m}\in \{0,1\} \). Sample \(\rho \xleftarrow {\$}\mathsf {Sample}(\mathbb {G})\) and proceed as follows:
-
1.
Set \(c\,:=\,g^\rho \) and \(c'\,:=\,\mathsf {h}^\rho \).
-
2.
For every \(j \in [n] \backslash \{ i \}\), set \(c_{j,0}\,:=\,g_{j,0}^\rho \) and \(c_{j,1}\,:=\,g_{j,1}^\rho \).
-
3.
Set \(c_{i,0}\,:=\,\bot \) and \(c_{i,1}\,:=\,\bot \).
-
4.
Set \(e\,:=\,\mathsf {m}\oplus \mathsf {HardCore}(g_{i,b}^\rho )\).Footnote 14
-
5.
Output \(\mathsf {ct}\,:=\,\left( e, c, c', \begin{pmatrix} c_{1,0}, c_{2,0} \ldots , c_{n,0} \\ c_{1,1}, c_{2,1}, \ldots , c_{n,1}\end{pmatrix}\right) \).
-
1.
-
\(\mathsf {Dec}(\mathsf {k},(\mathsf {x},r),\mathsf {ct})\): Parse \(\mathsf {ct}\,:=\,\left( e, c, c', \begin{pmatrix} c_{1,0}, c_{2,0} \ldots , c_{n,0} \\ c_{1,1}, c_{2,1}, \ldots , c_{n,1}\end{pmatrix}\right) \) Output \(e \oplus \mathsf {HardCore}\left( \frac{c'}{ c^r\cdot \prod _{j\in [n] \backslash \{ i \}} c_{j,\mathsf {x}_j} } \right) \).
Multi-bit Encryption. The encryption procedure described above encrypts single bit messages. Longer messages can be encrypted by encrypting individual bits.
Lemma 1
Assuming that \(\mathsf {DH}(\mathbb {G})\) is hard, the construction described above is a chameleon encryption scheme, i.e. it satisfies Definition 4.
Proof
We need to argue the trapdoor collision property, uniformity property, correctness of encryption property and semantic security of the scheme above and we that below.
-
Uniformity: Observe that for all \(\mathsf {k}\) and \(\mathsf {x}\), we have that \(\mathsf {H}(\mathsf {k},\mathsf {x};r) = g^{r}\cdot \prod _{j \in [n]} g_{j,\mathsf {x}_j}\) is statistically close to a uniform element in \(\mathbb {G}\). This is because \(r\) is sampled statistically close to uniform in \(\mathbb {Z}_p\), where p is the order of \(\mathbb {G}\).
-
Trapdoor Collisions: For any choice of \(\mathsf {x}, \mathsf {x}', r, \mathsf {k},\mathsf {t}\) the value \(r'\) is obtained as \(r+ \sum _{j\in [n]} ( \alpha _{j,\mathsf {x}_j} - \alpha _{j,\mathsf {x}'_j}) \mod p\). It is easy to check that \(\mathsf {H}(\mathsf {k},\mathsf {x}';r')\) is equal to \(\mathsf {H}(\mathsf {k},\mathsf {x};r)\).
Moreover, as \(r\) is statistically close to uniform in \(\mathbb {Z}_p\), \(r' :=r+ \sum _{j\in [n]} ( \alpha _{j,\mathsf {x}_j} - \alpha _{j,\mathsf {x}'_j}) \mod p\) is also statistically close to uniform in \(\mathbb {Z}_p\).
-
Correctness: For any choice of \(\mathsf {x}\in \{0,1\} ^n\), coins \(r\), index \(i \in [n]\) and message \(\mathsf {m}\in \{0,1\} \) if \((\mathsf {k},\mathsf {t}) \xleftarrow {\$}\mathsf {Gen}(1^\lambda ,n)\), \(\mathsf {h}:= \mathsf {H}(\mathsf {k}, \mathsf {x};r)\), and \(\mathsf {ct}:=\mathsf {Enc}(\mathsf {k},(\mathsf {h},i,\mathsf {x}_i),\mathsf {m})\) then we have that \(\mathsf {Dec}\left( \mathsf {k},(\mathsf {x},r),\mathsf {ct}\right) = e \oplus \mathsf {HardCore}\left( \frac{c'}{ c^r\cdot \prod _{j\in [n] \backslash \{ i \}} c_{j,\mathsf {x}_j} }\right) \) which evaluates to \(e \oplus \mathsf {HardCore}(g_{i,\mathsf {x}_i}^\rho )\). Finally, this value can be seen to be equal to \(\mathsf {m}\).
-
Security: For the sake of contradiction, let us assume that there exists a PPT adversary \(\mathcal {A} = (\mathcal {A}_1,\mathcal {A}_2)\) and a non-negligible function \(\mu (\cdot )\) such that
$$\begin{aligned} \Pr [\text {IND}^{\text {CE}}_{\mathcal {A}}(1^\lambda ) = 1]\ge \frac{1}{2} + \mu (\lambda ). \end{aligned}$$Now we will provide a PPT reduction \(\mathcal {R}^{\mathcal {A}}\) which on input \(g, U = g^u, V= g^v\) correctly computes the hardcore bit \(\mathsf {HardCore}(g^{uv})\) with probability \(\frac{1}{2} + \nu (\lambda )\) for some non-negligible function \(\nu \). Formally, Reduction \(\mathcal {R}^{\mathcal {A}= (\mathcal {A}_1,\mathcal {A}_2) }(g,U,V)\) proceeds as follows:
-
1.
For each \(j \in [n]\), sample \(\alpha _{j,0}, \alpha _{j,1} \xleftarrow {\$}\mathsf {Sample}(\mathbb {G})\) and set \(g_{j,0} :=g^{\alpha _{j,0}}\) and \(g_{j,1} :=g^{\alpha _{j,1}}.\)
-
2.
Sample \({x} \xleftarrow {\$}\{0,1\}\) and \(i^* \xleftarrow {\$}[n]\) and reassign \(g_{i^*,{x}} :=U\). Finally set
$$\mathsf {k}:=\left( g, \begin{pmatrix} g_{1,0}, g_{2,0} \ldots , g_{n,0} \\ g_{1,1}, g_{2,1}, \ldots , g_{n,1}\end{pmatrix}\right) .$$ -
3.
\((\mathsf {x},r,i) \xleftarrow {\$}\mathcal {A}_1(\mathsf {k})\).
-
4.
If \( i \ne i^*\) or \(\mathsf {x}_i = x\) then skip rest of the steps and output a random bit \(b \xleftarrow {\$}\{0,1\} \).
-
5.
Otherwise, set \(\mathsf {h}:=\mathsf {H}(\mathsf {k},\mathsf {x};r)\) and \(\mathsf {ct}:=\left( e, c, c',\begin{pmatrix} c_{1,0}, c_{2,0} \ldots , c_{n,0} \\ c_{1,1}, c_{2,1}, \ldots , c_{n,1}\end{pmatrix}\right) \) where:
$$\begin{aligned}&c := V&c' := V^{r+ \sum _{j \in [n]} \alpha _{i,\mathsf {x}_i}},\\ \forall j \in [n]\backslash \{i\},\quad&c_{j,0} :=V^{\alpha _{j,0}}&c_{j,1}:=V^{\alpha _{j,1}}, \\&e \xleftarrow {\$}\{0,1\} .&\end{aligned}$$ -
6.
\(b \xleftarrow {\$}\mathcal {A}_2(\mathsf {k},(\mathsf {x},r),\mathsf {ct}).\)
-
7.
Output \(b \oplus e.\)
Let E be the event that the \(i = i^*\) and \(x_i \ne x\). Now observe that the distribution of \(\mathsf {k}\) in Step 3 is statistically close to distribution resulting from \(\mathsf {Gen}\). This implies that (1) the view of the attacker in Step 3 is statistically close to experiment \(\text {IND}_{\mathcal {A}}^{\text {CE}}\), and (2) \(\Pr [E]\) is close to \(\frac{1}{2n}\) up to a negligible additive term. Furthermore, conditioned on the fact that E occurs we have that the view of the attacker in Step 3 is statistically close to experiment \(\text {IND}_{\mathcal {A}}^{\text {CE}}\) where \(\mathsf {ct}\) is an encryption of \(e\oplus \mathsf {HardCore}(g^{uv})\) (where \(U = g^u\) and \(V = g^v\)). Now, if \(\mathcal {A}_2\) in Step 6 correctly predicts \(e \oplus \mathsf {HardCore}(g^{uv})\) then we have that the output of our reduction \(\mathcal {R}\) is a correct prediction of \(\mathsf {HardCore}(g^{uv})\). Thus, we conclude that \(\mathcal {R}\) predicts \(\mathsf {HardCore}(g^{uv})\) correctly with probability at least \(\frac{1}{2} \cdot \left( 1 - \frac{1}{2n} \right) + \frac{1}{2n}\cdot \left( \frac{1}{2} + \mu \right) = \frac{1}{2} + \frac{\mu }{2n}\) up to a negligible additive term.
-
1.
5.1 Instantiations
Instantiating by Prime Order Groups. Our scheme can be directly instantiated in any prime order group \(\mathbb {G}\) where \(\mathsf {DH}(\mathbb {G})\) is assumed to be hard. Candidates are prime order multiplicative subgroups of finite fields [20] and elliptic curve groups [33, 39].
Corollary 1
Under the assumption that \(\mathsf {DH}(\mathbb {G})\) is hard over some group \(\mathbb {G}\), there exists a chameleon encryption scheme.
Instantiating by Composite Order Groups and Reduction to the Factoring Assumption. Consider the group of quadratic residues \(\mathbb {QR}_N\) over a Blum integer \(N = PQ\) (P and Q are large safe primesFootnote 15 with \(P = Q = 3 \mod 4\)). Let g be a random generator of \(\mathbb {G}\) and \(\mathsf {Sample}(\mathbb {G})\) just outputs a uniformly random number from the set \([(N-1)/4]\). Shmuely [46] and McCurley [38] proved that the \(\mathsf {DH}(\mathbb {QR}_N)\) problem is at least as hard as \(\mathsf {FACT}\) (also see [7, 31]).
For this instantiation, we assume that the \(\mathsf {Gen}\) algorithm generates a fresh Blum integer \(N = PQ = (2p + 1)(2q +1)\), includes N in the public key \(\mathsf {k}\) and \(|\mathbb {G}| = |\mathbb {QR}_N| = \phi (N)/4 = pq\) in the trapdoor \(\mathsf {t}\). Notice that only the trapdoor-collision algorithm \(\mathsf {H}^{-1}\) needs to know the group-order \(|\mathbb {G}| = pq\), while all other algorithms use the public sampling algorithm \(\mathsf {Sample}(\mathbb {G})\).
Hence, using the group \(\mathbb {QR}_N\) in the above described construction yields a construction of chameleon encryption based on the \(\mathsf {FACT}\) Assumption.
Corollary 2
Under the assumption that \(\mathsf {FACT}\) is hard there exists a chameleon encryption scheme.
6 Construction of Identity-Based Encryption
In this section, we describe our construction of IBE from chameleon encryption. Let \(\mathsf {PRF}: \{0,1\} ^\lambda \times \{0,1\}^{\le n}\cup \{\varepsilon \}\rightarrow \{0,1\} ^\lambda \) be a pseudorandom function, \((\mathsf {Gen},\mathsf {H},\mathsf {H}^{-1},\mathsf {Enc},\mathsf {Dec})\) be a chameleon encryption scheme and \((\mathsf {G},\mathsf {E},\mathsf {D})\) be any semantically secure public-key encryption scheme.Footnote 16 We let \(\mathsf {id}[i]\) denote the \(i^{th}\)-bit of \(\mathsf {id}\) and let \(\mathsf {id}[1\ldots i]\) denote the first i bits of \(\mathsf {id}\). Note that \(\mathsf {id}[1\ldots 0]\) is the empty string denoted by \(\varepsilon \) of length 0.
\(\mathsf {NodeGen}\) and \(\mathsf {LeafGen}\) Functions. As explained in the introduction, we need an exponential sized tree of hash values. The functions \(\mathsf {NodeGen}\) and \(\mathsf {LeafGen}\) provides efficient access to the hash value corresponding to any node in this (exponential sized) tree. We will use these function repeatedly in our construction. The \(\mathsf {NodeGen}\) function takes as input the hash keys \(\mathsf {k}_0,\ldots \mathsf {k}_{n-1}\) and corresponding trapdoors \(\mathsf {t}_0,\ldots \mathsf {t}_{n-1}\), the PRF seed s, and a node \(\mathsf {v}\in {\{0,1\}}^{\le n-2} \cup \{\varepsilon \}\). On the other hand, the \(\mathsf {LeafGen}\) function takes as input the hash key \(\mathsf {k}_{n-1}\) and corresponding trapdoor \(\mathsf {t}_{n-1}\), the PRF seed s, and a node \(\mathsf {v}\in {\{0,1\}}^{n-1}\). The \(\mathsf {NodeGen}\) and \(\mathsf {LeafGen}\) functions are described in Fig. 4.
Construction. We describe our IBE scheme \((\mathsf {Setup},\mathsf {KeyGen},\mathsf {Encrypt},\mathsf {Decrypt})\).
-
\(\mathsf {Setup}(1^\lambda ,1^n)\): Proceed asFootnote 17 follows:
-
1.
Sample \(s \xleftarrow {\$}\{0,1\} ^\lambda \) (seeds for the pseudorandom function \(\mathsf {PRF}\)).
-
2.
For each \(i \in \{0,\ldots n-1\}\) sample \((\mathsf {k}_i, \mathsf {t}_i) \xleftarrow {\$}\mathsf {Gen}(1^\lambda , 2\lambda )\).
-
3.
Obtain \((\mathsf {h}_{\varepsilon },\mathsf {h}_0,\mathsf {h}_1,r_\varepsilon ) :=\mathsf {NodeGen}((\mathsf {k}_0,\ldots \mathsf {k}_{n-1}), (\mathsf {t}_0,\ldots \mathsf {t}_{n-1},s),\varepsilon )\)
-
4.
Output \((\mathsf {mpk},\mathsf {msk})\) where \(\mathsf {mpk}:=(\mathsf {k}_0,\ldots \mathsf {k}_{n-1},\mathsf {h}_\varepsilon )\) and \(\mathsf {msk}:=(\mathsf {mpk},\mathsf {t}_0, \ldots \mathsf {t}_{n-1},s)\)
-
1.
-
\(\mathsf {KeyGen}(\mathsf {msk}= ((\mathsf {k}_0,\ldots \mathsf {k}_{n-1},\mathsf {h}_\varepsilon ),\mathsf {t}_0,\ldots \mathsf {t}_{n-1},s),\mathsf {id}\in \{0,1\}^{n})\):
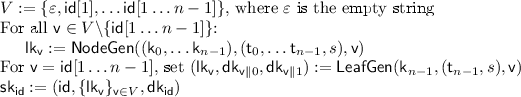
-
\(\mathsf {Encrypt}(\mathsf {mpk}= (\mathsf {k}_0,\ldots \mathsf {k}_{n-1},\mathsf {h}_\varepsilon ),\mathsf {id}\in \{0,1\} ^n,\mathsf {m})\): Before describing the encryption procedure we describe two circuitsFootnote 18 that will be garbled during the encryption process.
-
\(\mathsf {T}[\mathsf {m}](\mathsf {ek})\): Compute and output \(\mathsf {E}(\mathsf {ek}, \mathsf {m})\).
-
\(\mathsf {P}[\beta \in \{0,1\} ,\mathsf {k},\overline{\mathsf {lab}}](\mathsf {h})\): Compute and output \(\{\mathsf {Enc}(\mathsf {k},(\mathsf {h},j+ \beta \cdot \lambda ,b), \mathsf {lab}_{j,b})\}_{j\in [\lambda ], b \in \{0,1\} }\), where \(\overline{\mathsf {lab}}\) is short for \(\{\mathsf {lab}_{j,b}\}_{j \in [\lambda ], b \in \{0,1\} }\).
Encryption proceeds as follows:
-
1.
Compute \(\tilde{T}\) as:
$$\begin{aligned}(\tilde{T}, \overline{\mathsf {lab}}) \xleftarrow {\$}\mathsf {GCircuit}(1^\lambda , \mathsf {T}[\mathsf {m}]). \end{aligned}$$ -
2.
For \(i = n-1,\ldots , 0\) generate \((\tilde{P}^i, \overline{\mathsf {lab}}') \xleftarrow {\$}\mathsf {GCircuit}(1^\lambda , \mathsf {P}[\mathsf {id}[i+1],\mathsf {k}_i,\overline{\mathsf {lab}}])\) and set \(\overline{\mathsf {lab}} :=\overline{\mathsf {lab}}'\).
-
3.
Output \(\mathsf {ct}:=(\{\mathsf {lab}^{}_{j,\mathsf {h}_{\varepsilon ,j}}\}_{j \in [\lambda ]},\{\tilde{P}^0,\ldots , \tilde{P}^{n-1},\tilde{T}\})\) where \(\mathsf {h}_{\varepsilon ,j}\) is the \(j^{th}\) bit of \(\mathsf {h}_\varepsilon \).
-
-
\(\mathsf {Decrypt}(\mathsf {ct}, \mathsf {sk}_\mathsf {id}= (\mathsf {id}, \{\mathsf {lk}_\mathsf {v}\}_{\mathsf {v}\in V}),\mathsf {dk}_\mathsf {id})\): Decryption proceeds as follows:
-
1.
Parse \(\mathsf {ct}\) as \((\{\mathsf {lab}^{}_{j,\mathsf {h}_{\varepsilon ,j}}\}_{j \in [\lambda ]},\{\tilde{P}^0,\ldots , \tilde{P}^{n-1},\tilde{T}\}).\)
-
2.
Parse \(\mathsf {lk}_{\mathsf {v}}\) as \((\mathsf {h}_\mathsf {v}, \mathsf {h}_{\mathsf {v}\Vert 0},\mathsf {h}_{\mathsf {v}\Vert 1}, r_\mathsf {v})\) for each \(\mathsf {v}\in V\backslash \{\mathsf {id}[1\ldots n-1]\}\). (Recall \(V = \{\varepsilon ,\mathsf {id}[1]\ldots \mathsf {id}[1\ldots n-1]\}\).)
-
3.
And for \(\mathsf {v}= \mathsf {id}[1\ldots n-1] \), parse \(\mathsf {lk}_{\mathsf {v}}\) as \((\mathsf {h}_{\mathsf {v}},\mathsf {ek}_{\mathsf {v}\Vert 0},\mathsf {pk}_{\mathsf {v}\Vert 1},r_\mathsf {v}).\)
-
4.
Set \(y :=\mathsf {h}_\varepsilon \).
-
5.
For each \(i\in \{0,\ldots n-1\}\), set \(\mathsf {v}:= \mathsf {id}[1\ldots i]\), and proceed as follows:
-
(a)
\(\{e_{j,b}\}_{j \in [\lambda ], b\in \{0,1\} } :=\mathsf {Eval}(\tilde{P}^i, \{\mathsf {lab}_{j,y_{j}}\}_{j \in [\lambda ]})\).
-
(b)
If \(i = n-1\) then set \(y :=\mathsf {ek}_\mathsf {id}\) and for each \(j \in [\lambda ]\), compute
$$\mathsf {lab}^{}_{j,y_j} :=\mathsf {Dec}(\mathsf {k}_{\mathsf {v}}, e_{j,y_{j}}, (\mathsf {ek}_{\mathsf {v}\Vert 0}\Vert \mathsf {ek}_{\mathsf {v}\Vert 1},r_{\mathsf {v}})).$$ -
(c)
If \(i \ne n-1\) then set \(y :=\mathsf {h}_\mathsf {v}\) and for each \(j \in [\lambda ]\), compute
$$\mathsf {lab}^{}_{j,y_j} :=\mathsf {Dec}(\mathsf {k}_{\mathsf {v}}, e_{j,y_{j}}, (\mathsf {h}_{\mathsf {v}\Vert 0}\Vert \mathsf {h}_{\mathsf {v}\Vert 1},r_{\mathsf {v}})).$$
-
(a)
-
6.
Compute \(f :=\mathsf {Eval}(\tilde{T},\{ \mathsf {lab}_{j,y_{j}}\}_{j \in [\lambda ]}).\)
-
7.
Output \(\mathsf {m}:= \mathsf {Dec}(\mathsf {dk}_\mathsf {id}, f).\)
-
1.
A Note on Efficiency. The most computationally intensive part of the construction is the non-black box use of \(\mathsf {Enc}\) inside garblings of the circuit \(\mathsf {P}\) and \(\mathsf {E}\) inside garbling of the circuit \(\mathsf {T}\). However, we note that not all of the computation corresponding to \(\mathsf {Enc}\) and \(\mathsf {E}\) needs to be performed inside the garbled circuit and it might be possible to push some of it outside of the garbled circuits. In particular, when \(\mathsf {Enc}\) is instantiated with the DDH based chameleon encryption scheme then we can reduce each \(\mathsf {Enc}\) to a single modular exponentiation inside the garbled circuit. Similar optimization can be performed for \(\mathsf {E}\). In short, this reduces the number of non-black-box modular exponentiations to \(2\lambda \) for every circuit \(\mathsf {P}\) and 1 for the circuit \(\mathsf {T}\). Finally, we note that additional improvements in efficiency might be possible by increasing the arity of the tree from 2 to a larger value. This would also reduce the depth of the tree and thereby reduce the number of non-black-box modular exponentiations needed.
6.1 Proof of Correctness
We will first show that our scheme is correct. For any identity \(\mathsf {id}\), let \(V = \{\varepsilon ,\mathsf {id}[1],\ldots \mathsf {id}[1\ldots n-1]\}\). Then the secret key \(\mathsf {sk}_\mathsf {id}\) consists of \((\mathsf {id},\{\mathsf {lk}_\mathsf {v}\}_{\mathsf {v}\in V},\mathsf {dk}_\mathsf {id})\). We will argue that a correctly generated ciphertext on decryption reveals the original message. Note that by construction (and the trapdoor collision property of the chameleon encryption scheme for the first equation below) for all nodes \(\mathsf {v}\in V\backslash \{\mathsf {id}[1\ldots n-1]\}\) we have that:
and additionally for \(\mathsf {v}= \mathsf {id}[1\ldots n-1]\) we have
Next consider a ciphertext \(\mathsf {ct}= (\{\mathsf {lab}^{}_{j,\mathsf {h}_{\varepsilon ,j}}\}_{j \in [\lambda ]},\{\tilde{P}^0,\ldots , \tilde{P}^{n-1},\tilde{T}\})\). We argue correctness as each step of decryption is performed. By correctness of garbled circuits, we have that the evaluation of \(\tilde{P}^0\) yields correctly formed ciphertexts \(e_{j,b}\) which are encryptions of labels of the next garbled circuit \(\tilde{P}^1\). Next, by correctness of \(\mathsf {Dec}\) of the chameleon encryption scheme we have that the decrypting the appropriate ciphertexts yields the correct labels \(\{\mathsf {lab}_{j,\mathsf {h}_{\mathsf {id}[1],j}}\}_{j \in [\lambda ]}\) for the next garbled circuit, namely \(\tilde{P}^{1}\). Following the same argument we can argue that the decryption of the appropriate ciphertexts generated by \(\tilde{P}^1\) yields the correct input labels for \(\tilde{P}^2\). Repeatedly applying this argument allows us to conclude that the last garbled circuit \(\tilde{P}^{n-1}\) outputs labels corresponding to \(\mathsf {ek}_\mathsf {id}\) as input for the circuit \(\mathsf {T}\) which outputs an encryption of \(\mathsf {m}\) under \(\mathsf {ek}_\mathsf {id}\). Finally, using the correctness of the public-key encryption scheme \((\mathsf {G},\mathsf {E},\mathsf {D})\) we have that the recovered message \(\mathsf {m}\) is the same as the one encrypted.
6.2 Proof of Security
We are now ready to prove the security of the IBE construction above. For the sake of contradiction we proceed by assuming that there exists an adversary \(\mathcal {A}\) such that \(\Pr [\text {IND}_{\mathcal {A}}^{\text {IBE}}(1^\lambda ) = 1] \ge \frac{1}{2} + \epsilon \) for a non-negligible \(\epsilon \) (in \(\lambda \)), where \(\text {IND}_{\mathcal {A}}^{\text {IBE}}\) is shown in Fig. 1. Assume further that q is a polynomial upper bound for the running-time of \(\mathcal {A}\), and thus also an upper bound for the number of \(\mathcal {A}\)’s key queries. Security follows by a sequence of hybrids. In our hybrids, changes are made in how the secret key queries of the adversary \(\mathcal {A}\) are answered and how the challenge ciphertext is generated. Furthermore, these changes are intertwined and need to be done carefully. Our proof consist of a sequence of \(n+2\) hybrids \(\mathcal {H}_{-1},\mathcal {H}_0, \mathcal {H}_1,\ldots \mathcal {H}_{n+1}\). We next describe these hybrids.
-
\(\mathcal {H}_{-1}\): This hybrid corresponds to the experiment \(\text {IND}_{\mathcal {A}}^{\text {IBE}}\) as shown in Fig. 1.
-
\(\mathcal {H}_{0}\): In this hybrid, we change how the public parameters are generated and how the adversary’s requests to the \(\mathsf {KeyGen}\) oracle are answered. Specifically, we replace all pseudorandom function calls \(\mathsf {PRF}(s,\cdot )\) with a random function.
The only change from \(\mathcal {H}_{-1}\) to \(\mathcal {H}_0\) is that calls to a pseudorandom are replaced by a random function. Therefore, the indistinguishability between the two hybrids follows directly from the pseudorandomness property of the pseudorandom function.
-
\(\mathcal {H}_\tau \) for \(\tau \in \{0\ldots n\}\): For every \(\tau \), this hybrid is identical to the experiment \(\mathcal {H}_0\) except in how the ciphertext is generated. Recall that the challenge ciphertext consists of a sequence of \(n+1\) garbled circuits. In hybrid \(\mathcal {H}_\tau \), we generate the first \(\tau \) of these garbled circuits using the simulator provided by the garbled circuit construction. The outputs hard-coded in the simulated circuits are set to be consistent with the output that would have resulted from the execution of honestly generated garbled circuits in there unsimulated versions. More formally, for the challenge identity \(\mathsf {id}^*\) the challenge ciphertext is generated as follows (modifications with respect to honest ciphertext generation have been highlighted in red). Even though, the adversary never queries \(\mathsf {sk}_\mathsf {id}\), we can generate it locally. In particular, it contains the values \(\mathsf {lk}_\mathsf {v}=(\mathsf {h}_\mathsf {v}, \mathsf {h}_{\mathsf {v}\Vert 0},\mathsf {h}_{\mathsf {v}\Vert 1},r_\mathsf {v})\) for each \(\mathsf {v}\in \{\varepsilon ,\ldots \mathsf {id}[1\ldots n-2]\}\), \(\mathsf {lk}_\mathsf {v}=(\mathsf {h}_\mathsf {v}, \mathsf {ek}_{\mathsf {v}\Vert 0},\mathsf {ek}_{\mathsf {v}\Vert 1},r_\mathsf {v})\) for each \(\mathsf {v}= \mathsf {id}[1\ldots n-1]\), and \(\mathsf {dk}_{\mathsf {id}^*}\).
-
1.
Compute \(\tilde{T}\) as:
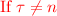 $$\begin{aligned} (\tilde{T}, \overline{\mathsf {lab}}) \xleftarrow {\$}\mathsf {GCircuit}(1^\lambda , \mathsf {T}[\mathsf {m}]) \end{aligned}$$
$$\begin{aligned} (\tilde{T}, \overline{\mathsf {lab}}) \xleftarrow {\$}\mathsf {GCircuit}(1^\lambda , \mathsf {T}[\mathsf {m}]) \end{aligned}$$where \(\overline{\mathsf {lab}} = \{\mathsf {lab}_{j,b}\}_{j \in [\lambda ], b \in \{0,1\}}\).
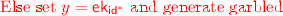



-
2.
For
 generate \((\tilde{P}^i, \overline{\mathsf {lab}}') \xleftarrow {\$}\mathsf {GCircuit}(1^\lambda , \mathsf {P}[\mathsf {id}[i+1],\mathsf {k}_i,\overline{\mathsf {lab}}])\) and set \(\overline{\mathsf {lab}} :=\overline{\mathsf {lab}}'\).
generate \((\tilde{P}^i, \overline{\mathsf {lab}}') \xleftarrow {\$}\mathsf {GCircuit}(1^\lambda , \mathsf {P}[\mathsf {id}[i+1],\mathsf {k}_i,\overline{\mathsf {lab}}])\) and set \(\overline{\mathsf {lab}} :=\overline{\mathsf {lab}}'\). -
3.



-
4.
Output \(\mathsf {ct}:=(\{\mathsf {lab}^{}_{j,\mathsf {h}_{\varepsilon ,j}}\}_{j \in [\lambda ]},\{\tilde{P}^0,\ldots , \tilde{P}^{n-1},\tilde{T}\})\) where \(\mathsf {h}_{\varepsilon ,j}\) is the \(j^{th}\) bit of \(\mathsf {h}_\varepsilon \).
-
1.
The computational indistinguishability between hybrids \(\mathcal {H}_{\tau -1}\) and \(\mathcal {H}_{\tau }\) is based on Lemma 2 which is proved in Sect. 6.3.
Lemma 2
For each \(\tau \in \{1\ldots n\}\) it is the case that  .
.
-
\(\mathcal {H}_{n+1}\): This hybrid is same as \(\mathcal {H}_n\) except that we change the ciphertext \(\mathsf {E}(\mathsf {ek}_{\mathsf {id}^*}, \mathsf {m})\) hardwired in the simulated garbling of the circuit T to be \(\mathsf {E}(\mathsf {ek}_{\mathsf {id}^*}, 0)\). Note that the adversary \(\mathcal {A}\) never queries for \(\mathsf {sk}_{\mathsf {id}^*}\). Therefore, it is never provided the value \(\mathsf {dk}_{\mathsf {id}^*}\). Therefore, we can use an adversary distinguishing between \(\mathcal {H}_{n}\) and \(\mathcal {H}_{n+1}\) to construct an attacker against the semantic security of the public-key encryption scheme \((\mathsf {G},\mathsf {E},\mathsf {D})\). This allows us to conclude that \(\mathcal {H}_{n}\mathop {\approx }\limits ^{c} \mathcal {H}_{n+1}\).
Finally, note that the hybrid \(\mathcal {H}_{n+1}\) is information theoretically independent of the plaintext message \(\mathsf {m}\).
6.3 Proof of Lemma 2
The proof follows by a sequence of sub-hybrids \(\mathcal {H}_{\tau ,0}\) to \(\mathcal {H}_{\tau ,6}\) where \(\mathcal {H}_{\tau ,0}\) is same as \(\mathcal {H}_{{\tau -1}}\) and \(\mathcal {H}_{{\tau },6}\) is same as \(\mathcal {H}_{\tau }\).
-
\(\mathcal {H}_{\tau ,0}\): This hybrid is same as \(\mathcal {H}_{{\tau -1}}\).
-
\(\mathcal {H}_{\tau ,1}\): Skip this hybrid if \(\tau = n\). Otherwise, this hybrid is identical to \(\mathcal {H}_{\tau ,0}\), except that we change how the values \(\mathsf {h}_\mathsf {v}\) and \(r_\mathsf {v}\) for \(\mathsf {v}\in \{0,1\}^{\tau }\) (if needed to answer a \(\mathsf {KeyGen}\) query of the adversary) are generated.
Recall that in hybrid \(\mathcal {H}_{\tau ,0}\), \(\mathsf {h}_\mathsf {v}\) is generated as \(\mathsf {H}(\mathsf {k}_\tau ,0^{2\lambda };\omega _\mathsf {v})\) and then
$$r_\mathsf {v}:={\left\{ \begin{array}{ll} \mathsf {H}^{-1}(\mathsf {k}_\tau ,(0^{2\lambda },\omega _\mathsf {v}), \mathsf {h}_{\mathsf {v}\Vert 0}\Vert \mathsf {h}_{\mathsf {v}\Vert 1} )&{} \text { if } \tau < n-1\\ \mathsf {H}^{-1}(\mathsf {k}_\tau ,(0^{2\lambda },\omega _\mathsf {v}), \mathsf {ek}_{\mathsf {v}\Vert 0}\Vert \mathsf {ek}_{\mathsf {v}\Vert 1} ) &{} \text {otherwise} \end{array}\right. }.$$In this hybrid, we generate \(r_\mathsf {v}\) first as being chosen uniformly. Next,
$$\mathsf {h}_\mathsf {v}:={\left\{ \begin{array}{ll} \mathsf {H}(\mathsf {k}_\tau , \mathsf {h}_{\mathsf {v}\Vert 0}\Vert \mathsf {h}_{\mathsf {v}\Vert 1};r_\mathsf {v})&{} \text { if } \tau < n-1\\ \mathsf {H}(\mathsf {k}_\tau , \mathsf {ek}_{\mathsf {v}\Vert 0}\Vert \mathsf {ek}_{\mathsf {v}\Vert 1};r_\mathsf {v}) &{} \text {otherwise} \end{array}\right. }.$$Statistical indistinguishability of hybrids \(\mathcal {H}_{\tau ,0}\) and \(\mathcal {H}_{\tau ,1}\) follows from the trapdoor collision and uniformity properties of the chameleon encryption scheme.
-
\(\mathcal {H}_{\tau , 2}\): We start with the case when \(\tau < n\). For this case, in this hybrid, we change how the garbled circuit \(\tilde{P}^{\tau }\) is generated. Let \(\mathsf {v}= \mathsf {id}^*[1\ldots \tau ]\) and recall that
$$\mathsf {lk}_{\mathsf {v}} = {\left\{ \begin{array}{ll}(\mathsf {h}_{\mathsf {v}}, \mathsf {ek}_{\mathsf {v}\Vert 0}, \mathsf {h}_{\mathsf {v}\Vert 1}, r_{\mathsf {v}}) &{} \text { if } \tau < n-1 \\ (\mathsf {h}_{\mathsf {v}}, \mathsf {ek}_{\mathsf {v}\Vert 0}, \mathsf {ek}_{\mathsf {v}\Vert 1}, r_{\mathsf {v}}) &{} \text { if } \tau = n-1 \end{array}\right. }.$$In this hybrid, we change the generation process of the garbled circuit \(\tilde{P}^{\tau }\) from
$$(\tilde{P}^{\tau }, \overline{\mathsf {lab}}') \xleftarrow {\$}\mathsf {GCircuit}(1^\lambda , \mathsf {P}[\mathsf {id}[\tau +1],\mathsf {k}_\tau ,\overline{\mathsf {lab}}])$$and setting \(\overline{\mathsf {lab}} :=\overline{\mathsf {lab}}'\) to

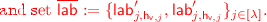 For the case when \(\tau = n\), then we change computation of \(\tilde{T}\) from $$\begin{aligned} (\tilde{T}, \overline{\mathsf {lab}}) \xleftarrow {\$}\mathsf {GCircuit}(1^\lambda , \mathsf {T}[\mathsf {m}]) \end{aligned}$$
For the case when \(\tau = n\), then we change computation of \(\tilde{T}\) from $$\begin{aligned} (\tilde{T}, \overline{\mathsf {lab}}) \xleftarrow {\$}\mathsf {GCircuit}(1^\lambda , \mathsf {T}[\mathsf {m}]) \end{aligned}$$where \(\overline{\mathsf {lab}} = \{\mathsf {lab}_{j,b}\}_{j \in [\lambda ], b \in \{0,1\}}\) to
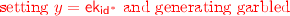
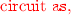
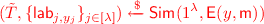
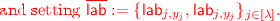 For the case when \(\tau < n\), computational indistinguishability of hybrids \(\mathcal {H}_{\tau ,1}\) and \(\mathcal {H}_{\tau , 2}\) follows by the security of the garbling scheme and the fact that \(\{\mathsf {Enc}(\mathsf {k}_{\mathsf {v}},(\mathsf {h}_{\mathsf {v}},j ,b),\mathsf {lab}_{j,{b}})\}_{j\in [\lambda ], b \in \{0,1\} }\) is exactly the output of the circuit \(\mathsf {P}[\mathsf {id}[\tau +1],\mathsf {k}_\tau ,\overline{\mathsf {lab}}]\) on input \(\mathsf {h}_\mathsf {v}\). On the other hand, for the case when \(\tau = n\), then again indistinguishability of hybrids \(\mathcal {H}_{n,1}\) and \(\mathcal {H}_{n, 2}\) follows by the security of the garbling scheme and the fact that \(\mathsf {E}(\mathsf {ek}_{\mathsf {id}^*},\mathsf {m})\) is the output of the circuit \(\mathsf {T}[\mathsf {m}]\) on input \(\mathsf {ek}_{\mathsf {id}^*}\).
For the case when \(\tau < n\), computational indistinguishability of hybrids \(\mathcal {H}_{\tau ,1}\) and \(\mathcal {H}_{\tau , 2}\) follows by the security of the garbling scheme and the fact that \(\{\mathsf {Enc}(\mathsf {k}_{\mathsf {v}},(\mathsf {h}_{\mathsf {v}},j ,b),\mathsf {lab}_{j,{b}})\}_{j\in [\lambda ], b \in \{0,1\} }\) is exactly the output of the circuit \(\mathsf {P}[\mathsf {id}[\tau +1],\mathsf {k}_\tau ,\overline{\mathsf {lab}}]\) on input \(\mathsf {h}_\mathsf {v}\). On the other hand, for the case when \(\tau = n\), then again indistinguishability of hybrids \(\mathcal {H}_{n,1}\) and \(\mathcal {H}_{n, 2}\) follows by the security of the garbling scheme and the fact that \(\mathsf {E}(\mathsf {ek}_{\mathsf {id}^*},\mathsf {m})\) is the output of the circuit \(\mathsf {T}[\mathsf {m}]\) on input \(\mathsf {ek}_{\mathsf {id}^*}\). -
\(\mathcal {H}_{\tau , 3}\): Skip this hybrid if \(\tau = n\). This hybrid is identical to \(\mathcal {H}_{\tau ,2}\), except that using \(\mathsf {v}:=\mathsf {id}[1\ldots \tau ]\) we change
$$ (\tilde{P}^i, \{\mathsf {lab}_{j,\mathsf {h}_{\mathsf {v},j}}'\}_{j \in [\lambda ]}) :=\mathsf {Sim}(1^\lambda ,\{\mathsf {Enc}(\mathsf {k}_{\mathsf {v}},(\mathsf {h}_{\mathsf {v}},j ,b),\mathsf {lab}_{j,{b}})\}_{j\in [\lambda ], b \in \{0,1\} }) $$to
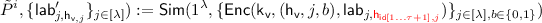
Notice that \(\mathsf {t}_\mathsf {v}\) is not used in this experiment. Therefore computational indistinguishability of hybrids \(\mathcal {H}_{\tau , 2}\) and \(\mathcal {H}_{\tau ,3}\) follows by \(\lambda ^2\) invocations (one invocation for each bit of the \(\lambda \) labels) of the security of the chameleon encryption scheme. We now provide the reduction for one change below.
More formally, we now describe a reduction to the security of the chameleon hash function. Specifically, the challenger provides a hash key \(\mathsf {k}^*\) and the attacker needs to submit \(\mathsf {x}^*,r^*\). Our reduction achieves this by setting \(\mathsf {k}_\tau :=\mathsf {k}^*\). It then submits the \(\mathsf {x}^* :=\mathsf {h}_{\mathsf {v}\Vert 0}\Vert \mathsf {h}_{\mathsf {v}\Vert 1}\) and randomly chosen coins \(r_\mathsf {v}:=r^*\) used in the computation of \(\mathsf {h}_\mathsf {v}:= \mathsf {H}(\mathsf {k}_\tau , \mathsf {x}^*;r^*)\) for the node \(\mathsf {v}\). Now we can use the attackers ability to distinguish the encryptions of the provided labels to break the security of the chameleon encryption scheme.
Remark: We note that the ciphertexts hardwired inside the garbled circuit only provide the labels \(\{\mathsf {lab}_{j,{\mathsf {h}_{\mathsf {id}[1\ldots \tau +1]},j}} \}_{j \in [\lambda ]}\) (in an information theoretical sense).
-
\(\mathcal {H}_{\tau , 4}\): Skip this hybrid if \(\tau = n\). In this hybrid, we undo the change made in going from hybrid \(\mathcal {H}_{\tau , 0}\) to hybrid \(\mathcal {H}_{\tau , 1}\), i.e. we go back to generating all \(\mathsf {h}_\mathsf {v}\) values using \(\mathsf {NodeGen}\) and \(\mathsf {LeafGen}\).
Computational indistinguishability of hybrids \(\mathcal {H}_{\tau ,3}\) and \(\mathcal {H}_{\tau ,4}\) follows from the trapdoor collision and uniformity properties of the chameleon encryption scheme. Observe that the hybrid \(\mathcal {H}_{\tau ,4}\) is the same as hybrid \(\mathcal {H}_{\tau }\).
7 Construction of Hierarchical Identity-Based Encryption
In this section, we describe our construction of HIBE from chameleon encryption. Let \((\mathsf {Gen},\mathsf {H},\mathsf {H}^{-1},\mathsf {Enc},\mathsf {Dec})\) be a chameleon encryption scheme and \((\mathsf {G},\mathsf {E},\mathsf {D})\) be any semantically secure public-key encryption scheme. We let \(\mathsf {id}[i]\) denote the \(i^{th}\)-bit of \(\mathsf {id}\) and \(\mathsf {id}[1\ldots i]\) denote the first i bits of \(\mathsf {id}\) (and \(\mathsf {id}[1\ldots 0] = \varepsilon \)).
Notation for the Pseudorandom Function \(\mathsf {F}\) . Let \(\mathsf {PRG}: \{0,1\}^{\lambda }\rightarrow \{0,1\} ^{3\lambda }\) be a length tripling pseudorandom generator and \(\mathsf {PRG}_0, \mathsf {PRG}_1\) and \(\mathsf {PRG}_2\) be the \(1\ldots \lambda \), \(\lambda +1\ldots 2\lambda \) and \(2\lambda +1\ldots 3\lambda \) bits of the output of \(\mathsf {PRG}\), respectively. Now define a GGM-type [29] pseudo-random function \(\mathsf {F}: \{0,1\} ^\lambda \times \{0,1,2\}^* \rightarrow \{0,1\} ^\lambda \) such that \(\mathsf {F}(s,x) := \mathsf {PRG}_{x_{n}}(\mathsf {PRG}_{x_{n-1}}(\ldots (\mathsf {PRG}_{x_1}(s))\ldots ))\), where \(n = |x|\) and for each \(i \in [n]\) \(x_i\) is the \(i^{th}\) element (from 0, 1 or 2) of string x.Footnote 19
\(\mathsf {NodeGen}\) and \(\mathsf {NodeGen}'\) Functions. As explained in the introduction, we need an exponential sized tree of local-keys. The function \(\mathsf {NodeGen}\) provides efficient access to local-keys corresponding to any node in this (exponential sized) tree. We will use this function repeatedly in our construction. The function takes as input the hash key \(\mathsf {k}_G\) (a key of the chameleon hash function from \(2\ell + 2\lambda \) bits to \(\lambda \) bits, where \(\ell \) is specified later), a node \(\mathsf {v}\in {\{0,1\}}^{*} \cup \{\varepsilon \}\) (\(\varepsilon \) denotes the empty string), and \(s = (s_1,s_2,s_3)\) seeds for the pseudo-random function \(\mathsf {PRF}\). This function is explained in the Fig. 5.
We also define a function \(\mathsf {NodeGen}'\), which is identical to \(\mathsf {NodeGen}\) except that it additionally takes a bit \(\beta \) as input and outputs \(\mathsf {dk}_{\mathsf {v}\Vert \beta }\). More formally, \(\mathsf {NodeGen}'(\mathsf {k}_G,\mathsf {v}, (s_1,s_2,s_3),\beta )\) executes just like \(\mathsf {NodeGen}\) but in Step 8 it outputs \(\mathsf {dk}_{\mathsf {v}\Vert \beta }\).
Construction. We describe our HIBE scheme \((\mathsf {Setup},\mathsf {KeyGen},\mathsf {Encrypt},\mathsf {Decrypt})\).
-
\(\mathsf {Setup}(1^\lambda )\): Proceed as follows:
-
1.
Sample \(s\xleftarrow {\$}\{0,1\} ^\lambda \) (seeds for the pseudorandom function \(\mathsf {PRF}\)).
-
2.
Setup a global hash function \((\mathsf {k}_G, \cdot ) :=\mathsf {Gen}(1^\lambda , 2\ell + 2\lambda )\) Footnote 20 where \(\ell = \ell ' + \lambda \) and \(\ell '\) is the length of \(\mathsf {k}\) generated from \(\mathsf {Gen}(1^\lambda , \lambda )\).
-
3.
Obtain \((\mathsf {k}_{\varepsilon },\mathsf {h}_{\varepsilon }, r_{\varepsilon },\mathsf {h}'_{\varepsilon }, r'_{\varepsilon }, \mathsf {k}_{0}, \mathsf {h}_{0}, \mathsf {k}_{1}, \mathsf {h}_{1}) :=\mathsf {NodeGen}(\mathsf {k}_G,\varepsilon ,s)\)
-
4.
Output \((\mathsf {mpk},\mathsf {msk})\) where \(\mathsf {mpk}:=(\mathsf {k}_G,\mathsf {k}_{\varepsilon },\mathsf {h}_{\varepsilon })\) and \(\mathsf {msk}= \mathsf {sk}_\varepsilon :=(\varepsilon ,\emptyset , s, \bot )\)
-
1.
-
\(\mathsf {KeyGen}(\mathsf {sk}_\mathsf {id}= (\mathsf {id},\{\mathsf {lk}_\mathsf {v}\}_{\mathsf {v}\in V}, s , \mathsf {dk}_\mathsf {id}),\mathsf {id}' \in \{0,1\}^{*})\):Footnote 21
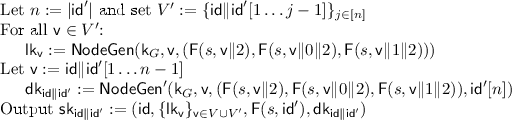
Remark: We note that in our construction the secret key for any identity is unique regardless of many iterations of \(\mathsf {KeyGen}\) operations were performed to obtain it.
-
\(\mathsf {Encrypt}(\mathsf {mpk}= (\mathsf {k}_G,\mathsf {k}_{\varepsilon },\mathsf {h}_{\varepsilon }),\mathsf {id}\in \{0,1\} ^n,\mathsf {m})\): Before describing the encryption procedure we describe four circuits that will be garbled during the encryption process.
-
\(\mathsf {T}[\mathsf {m}](\mathsf {ek})\): Compute and output \(\mathsf {E}(\mathsf {ek}, \mathsf {m})\).
-
\(\mathsf {Q}_{last}[\beta \in \{0,1\} ,\mathsf {k}_G,\overline{\mathsf {tlab}}](\mathsf {h})\): Compute and output \(\{\mathsf {Enc}(\mathsf {k}_G,(\mathsf {h},j+ \beta \cdot \lambda + 2\ell ,b), \mathsf {tlab}_{j,b})\}_{j\in [\lambda ], b \in \{0,1\} }\), where \(\overline{\mathsf {tlab}}\) is short for \(\{\mathsf {tlab}_{j,b}\}_{j\in [\lambda ], b \in \{0,1\} }\).
-
\(\mathsf {Q}[\beta \in \{0,1\} ,\mathsf {k}_G,\overline{\mathsf {plab}}^{}](\mathsf {h})\): Compute and output \(\{\mathsf {Enc}(\mathsf {k}_G,(\mathsf {h},j+ \beta \cdot \ell ,b), \mathsf {plab}_{j,b})\}_{j\in [\ell ], b \in \{0,1\} }\), where \(\overline{\mathsf {plab}}^{}\) is short for \(\{\mathsf {plab}_{j,b}^{}\}_{j\in [\ell ], b \in \{0,1\} }\).
-
\(\mathsf {P}[\overline{\mathsf {qlab}}^{}](\mathsf {k},\mathsf {h})\): Compute and output \(\{\mathsf {Enc}(\mathsf {k},(\mathsf {h},j ,b), \mathsf {qlab}_{j,b})\}_{j\in [\lambda ], b \in \{0,1\} }\), where \(\overline{\mathsf {qlab}}^{}\) is short for \(\{\mathsf {qlab}_{j,b}^{}\}_{j\in [\lambda ], b \in \{0,1\} }\).
Encryption proceeds as follows:
-
1.
Compute \(\tilde{T}\) as:
$$\begin{aligned}(\tilde{T}, \overline{\mathsf {tlab}}) \xleftarrow {\$}\mathsf {GCircuit}(1^\lambda , \mathsf {Q}_{out}[\mathsf {k}_G,\mathsf {m}]) \end{aligned}$$ -
2.
For \(i = n,\ldots , 1\) generate
-
(a)
If \(i = n\) then
$$(\tilde{Q}^n, \overline{\mathsf {qlab}}^{n}) \xleftarrow {\$}\mathsf {GCircuit}(1^\lambda , \mathsf {Q}_{last}[\mathsf {id}[n],\mathsf {k}_G,\overline{\mathsf {tlab}}]),$$else
$$(\tilde{Q}^i, \overline{\mathsf {qlab}}^{i}) \xleftarrow {\$}\mathsf {GCircuit}(1^\lambda , \mathsf {Q}[\mathsf {id}[i],\mathsf {k}_G,\overline{\mathsf {plab}}^{i+1}]).$$ -
(b)
\((\tilde{P}^i, \overline{\mathsf {plab}}^{i}) \xleftarrow {\$}\mathsf {GCircuit}(1^\lambda , \mathsf {P}[\overline{\mathsf {qlab}}^{i}]).\)
-
(a)
-
3.
Set \(x_\varepsilon := \mathsf {k}_\varepsilon \Vert \mathsf {h}_\varepsilon \).
-
4.
Output \(\mathsf {ct}:=(\{\mathsf {plab}^{1}_{j,x_{\varepsilon ,j}}\}_{j \in [\ell ]},\{\tilde{P}^i, \tilde{Q}^i\}_{i \in [n]},\tilde{T})\) where \(x_{\varepsilon ,j}\) is the \(j^{th}\) bit of \(x_\varepsilon \).
-
-
\(\mathsf {Decrypt}(\mathsf {ct}, \mathsf {sk}_\mathsf {id}= (\mathsf {id}, \{\mathsf {lk}_\mathsf {v}\}_{\mathsf {v}\in V}),s,\mathsf {dk}_\mathsf {id})\): Decryption proceeds as follows:
-
1.
Parse \(\mathsf {ct}\) as \((\{\mathsf {plab}^{1}_{j,x_{\varepsilon ,j}}\}_{j \in [\ell ]},\{\tilde{P}^i, \tilde{Q}^i\}_{i \in [n]},\tilde{T})\) where \(x_{\varepsilon } := \mathsf {k}_\varepsilon \Vert \mathsf {h}_\varepsilon \) and \(x_{\varepsilon ,j}\) is its \(j^{th}\) bit.
-
2.
Parse \(\mathsf {lk}_{\mathsf {v}}\) as \((\mathsf {h}_\mathsf {v},r_\mathsf {v}, \mathsf {h}'_\mathsf {v}, r'_\mathsf {v}, \mathsf {k}_{\mathsf {v}\Vert 0}, \mathsf {h}_{\mathsf {v}\Vert 0},\mathsf {k}_{\mathsf {v}\Vert 1}, \mathsf {h}_{\mathsf {v}\Vert 1},\mathsf {ek}_{\mathsf {v}\Vert 0},\mathsf {ek}_{\mathsf {v}\Vert 1})\) for each \(\mathsf {v}\in V\). (Recall \(V = \{\mathsf {id}[1\ldots j-1]\}_{j \in [n]}\).)
-
3.
For each \(i\in [n]\), proceed as follows:
-
(a)
Set \(\mathsf {v}:= \mathsf {id}[1\ldots i-1]\), \(x_\mathsf {v}:= \mathsf {k}_\mathsf {v}\Vert \mathsf {h}_\mathsf {v}\), \(y_\mathsf {v}:= \mathsf {h}_\mathsf {v}'\), and if \(i < n\) then set \( z_{\mathsf {v}} :=\mathsf {k}_{\mathsf {v}\Vert \mathsf {id}[i]}\Vert \mathsf {h}_{\mathsf {v}\Vert \mathsf {id}[i]}\) else set \( z_{\mathsf {v}} :=\mathsf {ek}_\mathsf {id}\).Footnote 22
-
(b)
\(\{e_{j,b}^i\}_{j \in [\lambda ], b\in \{0,1\} } :=\mathsf {Eval}(\tilde{P}^i, \{\mathsf {plab}^i_{j,x_{\mathsf {v},j}}\}_{j \in [\ell ]})\).
-
(c)
For each \(j \in [\lambda ]\), compute \(\mathsf {qlab}^i_{j,y_{\mathsf {v},j}} :=\mathsf {Dec}(\mathsf {k}_{\mathsf {v}}, e_{j,y_{\mathsf {v},j}}^i, (\mathsf {h}_{\mathsf {v}}',r_{\mathsf {v}}))\).
-
(d)
If \(i < n\) then,
$$\begin{aligned}&\{f_{j,b}^i\}_{j \in [\ell ], b\in \{0,1\} } :=\mathsf {Eval}(\tilde{Q}^i, \mathsf {qlab}^i_{j,y_{\mathsf {v},j}})\end{aligned}$$and for each \(j \in [\ell ]\)
$$\begin{aligned}&\mathsf {plab}^{i+1}_{j,z_{\mathsf {v},j}} :=\mathsf {Dec}(\mathsf {k}_{G}, f_{j,z_{\mathsf {v},j}}^i, (\mathsf {k}_{\mathsf {v}\Vert 0}\Vert \mathsf {h}_{\mathsf {v}\Vert 0}\Vert \mathsf {k}_{\mathsf {v}\Vert 1}\Vert \mathsf {h}_{\mathsf {v}\Vert 1}\Vert \mathsf {ek}_{\mathsf {v}\Vert 0}\Vert \mathsf {pk}_{\mathsf {v}\Vert 1},r_{\mathsf {v}}')) \end{aligned}$$ -
(e)
else,
$$\begin{aligned}&\{g_{j,b}\}_{j \in [\lambda ],b\in \{0,1\} } :=\mathsf {Eval}(\tilde{Q}^{n}, \mathsf {qlab}^{n}_{j,y_{\mathsf {v},j}})\end{aligned}$$and for each \(j \in [\lambda ]\)
$$\begin{aligned}&\mathsf {tlab}_{j,z_{\mathsf {v},j}} :=\mathsf {Dec}(\mathsf {k}_{G}, g_{j,z_{\mathsf {v},j}}, (\mathsf {k}_{\mathsf {v}\Vert 0}\Vert \mathsf {h}_{\mathsf {v}\Vert 0}\Vert \mathsf {k}_{\mathsf {v}\Vert 1}\Vert \mathsf {h}_{\mathsf {v}\Vert 1} \Vert \mathsf {pk}_{\mathsf {v}\Vert 0}\Vert \mathsf {pk}_{\mathsf {v}\Vert 1},r_{\mathsf {v}}')). \end{aligned}$$
-
(a)
-
4.
Output \(\mathsf {D}(\mathsf {dk}_\mathsf {id},\mathsf {Eval}(\tilde{T}, \{\mathsf {tlab}_{j,\mathsf {ek}_{\mathsf {id},j}}\}_{j \in [\lambda ]}))\).
-
1.
7.1 Proof of Correctness
For any identity \(\mathsf {id}\), let \(V = \{\mathsf {id}[1\ldots j-1]\}_{j \in [n]}\) be the set of nodes on the root-to-leaf path corresponding to identity \(\mathsf {id}\). Then the secret key \(\mathsf {sk}_\mathsf {id}\) consists of \(\{\mathsf {lk}_\mathsf {v}\}_{\mathsf {v}\in V}\), \(\mathsf {dk}_\mathsf {id}\) and a seed of the pseudorandom function \(\mathsf {F}\). \(\{\mathsf {lk}_\mathsf {v}\}_{\mathsf {v}\in V}\), \(\mathsf {dk}_\mathsf {id}\) and will be used for decryption and s is used for delegating keys. Note that by construction (and the trapdoor collision property of the chameleon encryption scheme for the first equation below) for all nodes \(\mathsf {v}\in V\) we have that:
By correctness of garbled circuits, we have that the evaluation of \(\tilde{P}^1\) yields correctly formed ciphertexts \(f_{j,b}^1\). Next, by correctness of \(\mathsf {Dec}\) of the chameleon encryption scheme we have that the decrypted values \(\mathsf {qlab}_{j,y_{\varepsilon ,j}}^1\) are the correct input labels for the next garbled circuit \(\tilde{Q}^{1}\). Following the same argument we can argue that the decryption of ciphertexts generated by \(\tilde{Q}^1\) yields the correct input labels for \(\tilde{P}^2\). Repeatedly applying this argument allows us to conclude that the last garbled circuit \(\tilde{Q}^{n}\) outputs correct encryptions of input labels of \(\tilde{T}\). The decryption of appropriate ciphertexts among these and the execution of the garbled circuit \(\tilde{T}\) using the obtained labels yields the ciphertext \(\mathsf {E}(\mathsf {ek}_\mathsf {id},\mathsf {m})\) which can be decrypted using the decryption key \(\mathsf {dk}_\mathsf {id}\). Correctness of the last steps depends on the correctness of the public-key encryption scheme.
Next, the correctness of delegation follows from the fact that for every \(\mathsf {id}\) and \(\mathsf {id}'\)
This fact follows directly from the following property of the GGM PRF. Specifically, for every x we have that \(\mathsf {F}(s,\mathsf {id}\Vert x) = \mathsf {F}(\mathsf {F}(s,\mathsf {id}),x).\)
7.2 Proof of Security
We are now ready to prove the selective security of the HIBE construction above. For the sake of contradiction we proceed by assuming that there exists an adversary \(\mathcal {A}\) such that \(\Pr [\text {IND}_{\mathcal {A}}^{\text {HIBE}}(1^\lambda ) = 1] \ge \frac{1}{2} + \epsilon \) for a non-negligible \(\epsilon \) (in \(\lambda \)), where \(\text {IND}_{\mathcal {A}}^{\text {HIBE}}\) is shown in Fig. 2. Assume further that q is a polynomial upper bound for the running-time of \(\mathcal {A}\), and thus also an upper bound for the number of \(\mathcal {A}\)’s key queries. Security follows by a sequence of hybrids. In our hybrids, changes are made in how the secret key queries of the adversary \(\mathcal {A}\) are answered and how the challenge ciphertext is generated. However, unlike the IBE case these changes are not intertwined with each other. In particular, we will make changes to the secret keys first and then the ciphertext. We describe our hybrids next. Our proof consist of a sequence of hybrids \(\mathcal {H}_{-3},\mathcal {H}_{-2}, \mathcal {H}_{-1}, \mathcal {H}_0, \mathcal {H}_1,\ldots \mathcal {H}_{n+2}\). We describe these below. Since we are in the selective the case the adversary declares the challenge identity \(\mathsf {id}^*\) before the public parameters \(\mathsf {mpk}\) are provided to it. Also, we let \(V^*\) be the set \(\{\varepsilon ,\mathsf {id}^*[1]\ldots \mathsf {id}^*[1\ldots n-1]\}\).
-
\(\mathcal {H}_{-3}\): This hybrid corresponds to the experiment \(\text {IND}_{\mathcal {A}}^{\text {HIBE}}\) as shown in Fig. 2.
-
\(\mathcal {H}_{-2}\): In this hybrid, we change how the seed s of generated in Step 1 of \(\mathsf {Setup}\) is used. Specifically, we sample \(s\xleftarrow {\$}\{0,1\} ^\lambda \) and generate
-
1.
For each \(i \in [n],\) let \(a_i :=\mathsf {F}(s,\mathsf {id}^*[1\ldots i-1]\Vert (1-\mathsf {id}^*[i]).\)
-
2.
\(b :=\mathsf {F}(s,\mathsf {id}^*)\).
-
3.
For each \(i \in \{0\ldots n-1\},\) let \(c_i :=\mathsf {F}(s,\mathsf {id}^*[1\ldots i]\Vert 2)\).
Now, through out the execution of the experiment we replace the use of s with the values \((\{a_i\}, b, \{c_i\})\). First, observe that (by standard properties of the GGM pseudorandom function) given these values we can generate \(\mathsf {F}(s,\mathsf {v}\Vert 2)\) for all \(\mathsf {v}\in \{0,1\}^*\cup \{\varepsilon \}\). Also, note that for the execution of the functions \(\mathsf {NodeGen}\) and \(\mathsf {NodeGen}'\) only \(\mathsf {F}(s,\mathsf {v}\Vert 2)\) needs to be generated. Therefore, all executions of \(\mathsf {NodeGen}\) and \(\mathsf {NodeGen}'\) remain unaffected.
Secondly, note that the \(\mathcal {A}\) is only allowed to make \(\mathsf {KeyGen}\) queries for identities \(\mathsf {id}\not \in V^*\cup \{\mathsf {id}^*\}\). Therefore, in order to answer these queries the experiment needs to generate \(\mathsf {F}(s,\mathsf {v})\) for \(\mathsf {v}\notin V^*\cup \{\mathsf {id}^*\}\). Observe that using \((\{a_i\}, b)\) by standard properties of the GGM pseudorandom function the experiment can compute \(\mathsf {F}(s,\mathsf {v})\) for any \(\mathsf {v}\not \in V^*\). Therefore, all of \(\mathcal {A}\)’s \(\mathsf {KeyGen}\) queries can be answered.Footnote 23
The hybrids \(\mathcal {H}_{-3}\) and \(\mathcal {H}_{-2}\) are the same distribution and the only change we have made is syntactic.
-
1.
-
\(\mathcal {H}_{-1}\): In this hybrids, we change how each \(c_i\) is generated. In particular, we sample each \(c_i\) uniformly and independently instead of using \(\mathsf {F}\).
The indistinguishability between hybrids \(\mathcal {H}_{-2}\) and \(\mathcal {H}_{-1}\) follows based on the pseudorandomness of the pseudorandom function \(\mathsf {F}\).
-
\(\mathcal {H}_0\): In this hybrid, we change how \(\mathsf {NodeGen}\) and \(\mathsf {NodeGen}'\) behave when computed with an input \(\mathsf {v}\in V^*\).Footnote 24 For all \(\mathsf {v}\not \in V^*\) the behavior of \(\mathsf {NodeGen}\) and \(\mathsf {NodeGen}'\) remains unchanged. At a high level, the goal is to change the generating of \(\{\mathsf {lk}_\mathsf {v}\}_{\mathsf {v}\in V^*}\) such that the trapdoor values \(\mathsf {t}_{\mathsf {v}\in V^*}\) are unused and so that the encryption key \(\mathsf {ek}_{\mathsf {id}^*}\) is sampled independent of everything else. The execution of \(\mathsf {NodeGen}\) and \(\mathsf {NodeGen}'\) for every \(\mathsf {v}\not \in V^*\) remain unaffected. In particular, at \(\mathsf {Setup}\) time we proceed as follows and fix the values \(\{\mathsf {lk}_{\mathsf {v}}\}_{\mathsf {v}\in V^*}\) and \(\{\mathsf {dk}_{\mathsf {v}\Vert 0},\mathsf {dk}_{\mathsf {v}\Vert 1}\}_{\mathsf {v}\in V^*}\).Footnote 25
-
1.
For every \(\mathsf {v}\in V^*\):
-
(a)
Generate \((\mathsf {k}_{\mathsf {v}},\mathsf {t}_{\mathsf {v}}) \xleftarrow {\$}\mathsf {Gen}(1^\lambda )\).
-
(b)
Generate \((\mathsf {ek}_{\mathsf {v}\Vert 0},\mathsf {dk}_{\mathsf {v}\Vert 0}) \xleftarrow {\$}\mathsf {G}(1^\lambda )\) and \((\mathsf {ek}_{\mathsf {v}\Vert 1},\mathsf {dk}_{\mathsf {v}\Vert 1}) \xleftarrow {\$}\mathsf {G}(1^\lambda )\).
-
(c)
Sample \(r'_{\mathsf {v}}\), \(r_\mathsf {v}\).
-
(a)
-
2.
Let \(S^* :=\{\mathsf {id}^*[1\ldots i-1]\Vert (1-\mathsf {id}^*[i])\}_{i \in [n]}\cup \{\mathsf {id}^*\}\). (Note that \(S^* \cap V^* = \emptyset \).)
-
3.
For all \(\mathsf {v}\in S^*\) set \(\mathsf {k}_{\mathsf {v}},\mathsf {h}_{\mathsf {v}}\) as first two outputs of \(\mathsf {NodeGen}(\mathsf {k}_G,\mathsf {v},(\mathsf {F}(s,\mathsf {v}\Vert 2), \mathsf {F}(s,\mathsf {v}\Vert 0\Vert 2), \mathsf {F}(s,\mathsf {v}\Vert 1\Vert 2))).\)
-
4.
For each \(i \in \{n-1\ldots 0\}\):
-
(a)
Set \(\mathsf {v}:=\mathsf {id}^*[1\ldots i]\)
-
(b)
Generate \(\mathsf {h}'_{\mathsf {v}} :=\mathsf {H}(\mathsf {k}_G,\mathsf {k}_{\mathsf {v}\Vert 0}||\mathsf {h}_{\mathsf {v}\Vert 0}||\mathsf {k}_{\mathsf {v}\Vert 1}||\mathsf {h}_{\mathsf {v}\Vert 1}\Vert \mathsf {ek}_{\mathsf {v}\Vert 0}\Vert \mathsf {ek}_{\mathsf {v}\Vert 1}; r'_{\mathsf {v}})\).
-
(c)
\(\mathsf {h}_\mathsf {v}:=\mathsf {H}(\mathsf {k}_{\mathsf {v}}, \mathsf {h}'_\mathsf {v}; r_{\mathsf {v}})\).
-
(d)
\(\mathsf {lk}_{\mathsf {v}} :=(\mathsf {k}_{\mathsf {v}},\mathsf {h}_{\mathsf {v}}, r_{\mathsf {v}},\mathsf {h}'_{\mathsf {v}}, r'_{\mathsf {v}}, \mathsf {k}_{\mathsf {v}\Vert 0}, \mathsf {h}_{\mathsf {v}\Vert 0}, \mathsf {k}_{\mathsf {v}\Vert 1}, \mathsf {h}_{\mathsf {v}\Vert 1},\mathsf {ek}_{\mathsf {v}\Vert 0},\mathsf {ek}_{\mathsf {v}\Vert 1})\).
-
(a)
-
5.
Output \(\{\mathsf {lk}_{\mathsf {v}}\}_{\mathsf {v}\in V^*}\) and \(\{\mathsf {dk}_{\mathsf {v}\Vert 0},\mathsf {dk}_{\mathsf {v}\Vert 1}\}_{\mathsf {v}\in V^*}\).
Statistical indistinguishability of hybrids \(\mathcal {H}_{\tau ,-1}\) and \(\mathcal {H}_{\tau ,0}\) follows from the trapdoor collision and uniformity properties of the chameleon encryption scheme. Note that in this hybrid the trapdoor \(\mathsf {t}_\mathsf {v}\) for any node \(\mathsf {v}\in V^*\) is no longer being used.
-
1.
-
\(\mathcal {H}_{\tau }\text { for } \tau \in \{1\ldots n\}:\) This hybrid is identical to \(\mathcal {H}_0\) except we change how the ciphertext is generated. Recall that the challenge ciphertext consists of a sequence of \(2n+1\) garbled circuits. In hybrid \(\mathcal {H}_\tau \), we generate the first \(2\tau \) of these garbled circuits (namely, \(\tilde{P}^1,\tilde{Q}^1\ldots \tilde{P}^\tau ,\tilde{Q}^\tau \)) using the simulator provided by the garbled circuit construction. The outputs hard-coded in the simulated circuits are set to be consistent with the output that would have resulted from the execution of honestly generated garbled circuits using keys obtained from invocations of \(\mathsf {NodeGen}\). More formally, for the challenge identity \(\mathsf {id}^*\) the challenge ciphertext is generated as follows (modifications with respect to honest ciphertext generation have been highlighted in red):
-
1.
Compute \(\tilde{T}\) as:
$$\begin{aligned}(\tilde{T}, \overline{\mathsf {tlab}}) \xleftarrow {\$}\mathsf {GCircuit}(1^\lambda , \mathsf {Q}_{out}[\mathsf {k}_G,\mathsf {m}]) \end{aligned}$$ -
2.
For
 generate
generate-
(a)
If \(i = n\) then
$$(\tilde{Q}^n, \overline{\mathsf {qlab}}^{n}) \xleftarrow {\$}\mathsf {GCircuit}(1^\lambda , \mathsf {Q}_{last}[\mathsf {id}[n],\mathsf {k}_G,\overline{\mathsf {tlab}}]),$$else
$$(\tilde{Q}^i, \overline{\mathsf {qlab}}^{i}) \xleftarrow {\$}\mathsf {GCircuit}(1^\lambda , \mathsf {Q}[\mathsf {id}[i],\mathsf {k}_G,\overline{\mathsf {plab}}^{i+1}]).$$ -
(b)
\((\tilde{P}^i, \overline{\mathsf {plab}}^{i}) \xleftarrow {\$}\mathsf {GCircuit}(1^\lambda , \mathsf {P}[\overline{\mathsf {qlab}}^{i}]).\)
-
(a)
-
3.
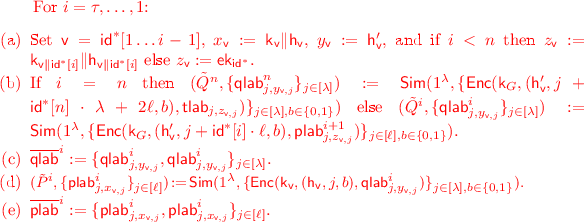
-
4.
Set \(x_\varepsilon := \mathsf {k}_\varepsilon \Vert \mathsf {h}_\varepsilon \).
-
5.
Output \(\mathsf {ct}:=(\{\mathsf {plab}^{1}_{j,x_{\varepsilon ,j}}\}_{j \in [\lambda ]},\{\tilde{P}^i, \tilde{Q}^i\}_{i \in [n]},\tilde{T})\) where \(x_{\varepsilon ,j}\) is the \(j^{th}\) bit of \(x_\varepsilon \).
-
1.
The computational indistinguishability between hybrids \(\mathcal {H}_{\tau -1}\) and \(\mathcal {H}_{\tau }\) is based on Lemma 3 which is proved in Sect. 7.3.
Lemma 3
For each \(\tau \in \{1\ldots n\}\) it is the case that  .
.
-
\(\mathcal {H}_{n+1}\): This hybrid is same as hybrid \(\mathcal {H}_n\) except that we generate the garbled circuit \(\tilde{T}\) to using the garbling simulator. More specifically, instead of generating \(\tilde{T}\) as
$$\begin{aligned}(\tilde{T}, \overline{\mathsf {tlab}}) \xleftarrow {\$}\mathsf {GCircuit}(1^\lambda , \mathsf {Q}_{out}[\mathsf {k}_G,\mathsf {m}]) \end{aligned}$$we set \(y = \mathsf {ek}_{\mathsf {id}^*}\) and generate garbled circuit as,
$$\begin{aligned} (\tilde{T}, \{\mathsf {lab}_{j, y_{j}}\}_{j\in [\lambda ]}) \xleftarrow {\$}\mathsf {Sim}(1^\lambda , \mathsf {E}(y ,\mathsf {m})) \end{aligned}$$and set \(\overline{\mathsf {lab}} :=\{\mathsf {lab}_{j,y_j},\mathsf {lab}_{j,y_j}\}_{j\in [\lambda ]}\).
Computational indistinguishability between hybrids \(\mathcal {H}_{n}\) and \(\mathcal {H}_{n+1}\) follows directly from the security of the gabled circuits.
-
\(\mathcal {H}_{n+2}\): This hybrid is same as \(\mathcal {H}_n\) except that we change the ciphertext \(\mathsf {E}(\mathsf {ek}_{\mathsf {id}^*}, \mathsf {m})\) hardwired in the simulated garbling of the circuit T to be \(\mathsf {E}(\mathsf {ek}_{\mathsf {id}^*}, 0)\).
Note that the adversary \(\mathcal {A}\) never queries for \(\mathsf {sk}_{\mathsf {id}^*}\). Therefore, it is never provided the value \(\mathsf {dk}_{\mathsf {id}^*}\). Therefore, we can use an adversary distinguishing between \(\mathcal {H}_{n+1}\) and \(\mathcal {H}_{n+2}\) to construct an attacker against the semantic security of the public-key encryption scheme \((\mathsf {G},\mathsf {E},\mathsf {D})\). This allows us to conclude that \(\mathcal {H}_{n+1}\mathop {\approx }\limits ^{c} \mathcal {H}_{n+2}\).
Finally, note that the hybrid \(\mathcal {H}_{n+2}\) is information theoretically independent of the plaintext message \(\mathsf {m}\).
7.3 Proof of Lemma 3
The proof follows by a sequence of sub-hybrids \(\mathcal {H}_{\tau ,0}\) to \(\mathcal {H}_{\tau ,4}\) where \(\mathcal {H}_{\tau ,0}\) is same as \(\mathcal {H}_{{\tau -1}}\) and \(\mathcal {H}_{{\tau },4}\) is same as \(\mathcal {H}_{\tau }\).
-
\(\mathcal {H}_{\tau ,0}\): This hybrid is same as \(\mathcal {H}_{{\tau -1}}\).
-
\(\mathcal {H}_{\tau , 1}\): In this hybrid, we change how the garbled circuit \(\tilde{P}^{\tau }\) is generated. Let \(\mathsf {v}= \mathsf {id}^*[1\ldots {\tau -1}]\) and \(\mathsf {lk}_{\mathsf {v}} = (\mathsf {k}_{\mathsf {v}},\mathsf {h}_{\mathsf {v}}, r_{\mathsf {v}},\mathsf {h}'_{\mathsf {v}}, r'_{\mathsf {v}}, \mathsf {k}_{\mathsf {v}\Vert 0}, \mathsf {h}_{\mathsf {v}\Vert 0}, \mathsf {k}_{\mathsf {v}\Vert 1},\mathsf {h}_{\mathsf {v}\Vert 1},\mathsf {ek}_{\mathsf {v}\Vert 0},\mathsf {ek}_{\mathsf {v}\Vert 1})\) and define \(x_{\mathsf {v}} :=\mathsf {k}_{\mathsf {v}}\Vert \mathsf {h}_{\mathsf {v}}\). The change we make is the following. We generate

now as

 Computational indistinguishability of hybrids \(\mathcal {H}_{\tau ,0}\) and \(\mathcal {H}_{\tau , 1}\) follows by the security of the garbling scheme \(\mathsf {GCircuit}\) and the fact that \(\{\mathsf {Enc}(\mathsf {k}_{\mathsf {v}},(\mathsf {h}_{\mathsf {v}},j ,b), \mathsf {qlab}^{\tau }_{j,b})\}_{j\in [\lambda ], b \in \{0,1\} }\) is exactly the output of the circuit \(P[\overline{\mathsf {qlab}}^{\tau }]\) on input \(x_\mathsf {v}\).
Computational indistinguishability of hybrids \(\mathcal {H}_{\tau ,0}\) and \(\mathcal {H}_{\tau , 1}\) follows by the security of the garbling scheme \(\mathsf {GCircuit}\) and the fact that \(\{\mathsf {Enc}(\mathsf {k}_{\mathsf {v}},(\mathsf {h}_{\mathsf {v}},j ,b), \mathsf {qlab}^{\tau }_{j,b})\}_{j\in [\lambda ], b \in \{0,1\} }\) is exactly the output of the circuit \(P[\overline{\mathsf {qlab}}^{\tau }]\) on input \(x_\mathsf {v}\). -
\(\mathcal {H}_{\tau , 2}\): This hybrid is identical to \(\mathcal {H}_{\tau ,2}\), except that for \(\mathsf {v}= \mathsf {id}^*[1\ldots \tau -1]\) we change
$$ \>(\tilde{P}^\tau , \{\mathsf {plab}^{\tau }_{j,x_{\mathsf {v},j}}\}_{j \in [\ell ]}) :=\mathsf {Sim}(1^\lambda ,\{\mathsf {Enc}(\mathsf {k}_{\mathsf {v}},(\mathsf {h}_{\mathsf {v}},j ,b), \mathsf {qlab}^\tau _{j,b})\}_{j\in [\lambda ], b \in \{0,1\} }) $$to
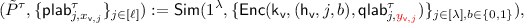
where \(y_{\mathsf {v}} :=\mathsf {h}'_\mathsf {v}\).
Notice that node \(\mathsf {v}\) is generated so that the trapdoor value \(\mathsf {t}_\mathsf {v}\) is not used in the execution of the experiment. Therefore, computational indistinguishability of hybrids \(\mathcal {H}_{\tau , 1}\) and \(\mathcal {H}_{\tau ,2}\) follows by \(\lambda ^2\) invocations (one invocation for each bit of the \(\lambda \) labels) of the security of the chameleon encryption scheme. The reduction is analogous to the reduction proving indistinguishability of hybrids \(\mathcal {H}_{\tau ,2}\) and \(\mathcal {H}_{\tau ,3}\) in the proof of Lemma 2.
Remark: We note that the ciphertexts hardwired inside the garbled circuit only provide the labels \(\{\mathsf {qlab}^\tau _{j,y_{\mathsf {v},j}} \}_{j \in [\lambda ]}\) (in an information theoretical sense).
-
\(\mathcal {H}_{\tau , 3}\) This hybrid is identical to \(\mathcal {H}_{\tau ,2}\), except that for \(\mathsf {v}= \mathsf {id}^*[1\ldots \tau -1]\) we change how \(\tilde{Q}^\tau \) is generated. If \(\tau = n\) then
$$ (\tilde{Q}^n, \overline{\mathsf {qlab}}^{n}) \xleftarrow {\$}\mathsf {GCircuit}(1^\lambda , \mathsf {Q}_{last}[\mathsf {id}^*[n],\mathsf {k}_G,\overline{\mathsf {tlab}}]), $$is changed to
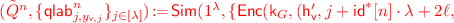

Otherwise, if \(\tau \ne n\) then
$$ (\tilde{Q}^\tau , \overline{\mathsf {qlab}}^{\tau }) \xleftarrow {\$}\mathsf {GCircuit}(1^\lambda , \mathsf {Q}[\mathsf {id}^*[\tau ],\mathsf {k}_G,\overline{\mathsf {plab}}^{\tau +1}])$$is changed to
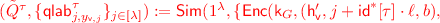

Computational indistinguishability between hybrids \(\mathcal {H}_{\tau , 2}\) and \(\mathcal {H}_{\tau , 3}\) follows by the security of the garbling scheme and the fact that is the output of the circuit \(\mathsf {Q}_{last}[\mathsf {id}^*[n],\mathsf {k}_G,\overline{\mathsf {tlab}}]\) is \(\{\mathsf {Enc}(\mathsf {k}_G,(\mathsf {h}'_{\mathsf {v}},j+ \mathsf {id}^*[n] \cdot \lambda + 2 \ell ,b), \mathsf {tlab}_{j,b})\}_{j\in [\lambda ], b \in \{0,1\} }\) and the output of the circuit \(\mathsf {Q}[\mathsf {id}^*[\tau ],\mathsf {k}_G,\overline{\mathsf {plab}}^{\tau +1}]\) is \(\{\mathsf {Enc}(\mathsf {k}_G,(\mathsf {h}'_{\mathsf {v}},j+ \mathsf {id}^*[\tau ] \cdot \ell ,b), \mathsf {plab}^{\tau +1}_{j,{b}})\}_{j\in [\ell ], b \in \{0,1\} }\).
-
\(\mathcal {H}_{\tau , 4}\): This hybrid is identical to \(\mathcal {H}_{\tau , 4}\), except that we change generation of \(\tilde{Q}^\tau \). Specifically, in the case \(\tau = n\) then we change the generation process of \(\tilde{Q}^n\) from \((\tilde{Q}^n, \{\mathsf {qlab}^{n}_{j,y_{\mathsf {v},j}}\}_{j \in [\lambda ]}) :=\mathsf {Sim}(1^\lambda ,\{\mathsf {Enc}(\mathsf {k}_G,(\mathsf {h}'_{\mathsf {v}},j+ \mathsf {id}^*[n] \cdot \lambda + 2 \ell ,b), \mathsf {tlab}_{j,{b}})\}_{j\in [\lambda ], b \in \{0,1\} })\) to
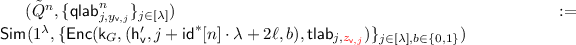 , where \(z_\mathsf {v}:=\mathsf {ek}_{\mathsf {id}^*}\). On the other hand, when \(\tau \ne n\) then it is changed from \((\tilde{Q}^\tau , \{\mathsf {qlab}^{\tau }_{j,y_{\mathsf {v},j}}\}_{j \in [\lambda ]}) :=\mathsf {Sim}(1^\lambda ,\{\mathsf {Enc}(\mathsf {k}_G, (\mathsf {h}'_{\mathsf {v}},j+ \mathsf {id}^*[\tau ] \cdot \ell ,b), \mathsf {plab}^{\tau +1}_{j,{b}})\}_{j\in [\ell ], b \in \{0,1\} })\) to
, where \(z_\mathsf {v}:=\mathsf {ek}_{\mathsf {id}^*}\). On the other hand, when \(\tau \ne n\) then it is changed from \((\tilde{Q}^\tau , \{\mathsf {qlab}^{\tau }_{j,y_{\mathsf {v},j}}\}_{j \in [\lambda ]}) :=\mathsf {Sim}(1^\lambda ,\{\mathsf {Enc}(\mathsf {k}_G, (\mathsf {h}'_{\mathsf {v}},j+ \mathsf {id}^*[\tau ] \cdot \ell ,b), \mathsf {plab}^{\tau +1}_{j,{b}})\}_{j\in [\ell ], b \in \{0,1\} })\) to  where \(z_{\mathsf {v}} :=\mathsf {h}_{\mathsf {v}\Vert \mathsf {id}^*[\tau ]}\Vert \mathsf {k}_{\mathsf {v}\Vert \mathsf {id}^*[\tau ]}\). Notice that since the trapdoor for \(\mathsf {k}_G\) is unavailable (never generated or used), computational indistinguishability of hybrids \(\mathcal {H}_{\tau , 3}\) and \(\mathcal {H}_{\tau , 4}\) follows by \(\lambda ^2\) invocations (one invocation per bit of the \(\lambda \) labels) if \(\tau = n\) and by \(\ell \lambda \) invocations (one invocation per bit of the \(\ell \) labels) otherwise of the security of the chameleon encryption scheme. And the reduction to the security of the chameleon encryption scheme is analogous to the reduction described for indistinguishability between hybrids \(\mathcal {H}_{\tau , 1}\) and \(\mathcal {H}_{\tau , 2}\).
where \(z_{\mathsf {v}} :=\mathsf {h}_{\mathsf {v}\Vert \mathsf {id}^*[\tau ]}\Vert \mathsf {k}_{\mathsf {v}\Vert \mathsf {id}^*[\tau ]}\). Notice that since the trapdoor for \(\mathsf {k}_G\) is unavailable (never generated or used), computational indistinguishability of hybrids \(\mathcal {H}_{\tau , 3}\) and \(\mathcal {H}_{\tau , 4}\) follows by \(\lambda ^2\) invocations (one invocation per bit of the \(\lambda \) labels) if \(\tau = n\) and by \(\ell \lambda \) invocations (one invocation per bit of the \(\ell \) labels) otherwise of the security of the chameleon encryption scheme. And the reduction to the security of the chameleon encryption scheme is analogous to the reduction described for indistinguishability between hybrids \(\mathcal {H}_{\tau , 1}\) and \(\mathcal {H}_{\tau , 2}\).Observe that the hybrid \(\mathcal {H}_{\tau ,4}\) is the same as hybrid \(\mathcal {H}_{\tau }\).
Notes
- 1.
- 2.
- 3.
In Sect. 5, we explain our constructions of chameleon encryption based on the (Computational) Diffie-Hellman Assumption, or the Factoring Assumption.
- 4.
We use \(\epsilon \) to denote the empty string.
- 5.
- 6.
For this part of the intuition, we assume familiarity with garbled circuits.
- 7.
We use this notion only when the sampling can be done by a PPT algorithm and the sampling algorithm is implicit.
- 8.
Typical definitions of garbled circuits do not require the length of each input label to be \(\lambda \) bits long. This additional requirement is crucial in our constructions as we chain garbled circuits. Note that input labels in any garbled circuit construction can always be shrunk to \(\lambda \) bits using a pseudorandom function.
- 9.
In abuse of notation we assume that \(\mathsf {Sim}\) knows the (non-private) circuit C. When C has (private) hardwired inputs, we assume that the labels corresponding to these are included in the garbled circuit \(\tilde{C}\).
- 10.
\(\mathsf {ct}\) is assumed to contain \((\mathsf {h},i,b)\).
- 11.
Typically, Chameleon Hash functions are defined to also have the collision resilience property. This property is implied by the semantic security requirement below. However, we do not need this property directly. Therefore, we do not explicitly define it here.
- 12.
We will later provide instantiations of \(\mathbb {G}\) which are of prime order and composite order. The use of \(\mathsf {Sample}(\mathbb {G})\) procedure is done to unify these two instantiations.
- 13.
We also implicitly include the public and secret parameters for the group \(\mathbb {G}\) in \(\mathsf {k}\) and \(\mathsf {t}\) respectively.
- 14.
We assume that the \(\mathsf {HardCore}(g^{ab})\) is a hardcore bit of \(g^{ab}\) given \(g^a\) and \(g^b\). If a deterministic hard-core bit for the specific function is not known then we can always use the Goldreich-Levin [30] construction. We skip the details of that with the goal of keeping exposition simple.
- 15.
A prime number \(P > 2\) is called safe prime if \((P-1)/2\) is also prime.
- 16.
The algorithm \(\mathsf {G}\) takes as input the security parameter \(1^\lambda \) and generates encryption key and decryption key pair \(\mathsf {ek}\) and \(\mathsf {dk}\) respectively, where the encryption key \(\mathsf {ek}\) is assumed to be \(\lambda \) bits long. The encryption algorithm \(\mathsf {E}(\mathsf {ek},\mathsf {m})\) takes as input an encryption key \(\mathsf {ek}\) and a message \(\mathsf {m}\) and outputs a ciphertext \(\mathsf {ct}\). Finally, the decryption algorithm \(\mathsf {D}(\mathsf {dk},\mathsf {ct})\) takes as input the secret key and the ciphertext and outputs the encrypted message \(\mathsf {m}\).
- 17.
The IBE scheme defined in Sect. 3 does not fix the length of identities that it can be used with. However, in this section we fix the length of identities at setup time and use appropriately changed definitions. Looking ahead, the HIBE construction in Sect. 7 works for identities of arbitrary length.
- 18.
Random coins used by these circuits are hardwired in them. For simplicity, we do not mention them explicitly.
- 19.
\(\mathsf {F}(s,\varepsilon )\) is set to output s.
- 20.
The trapdoor for the global hash function is not needed in the construction or the proof and is therefore dropped.
- 21.
HIBE is often defined to have separate \(\mathsf {KeyGen}\) and \(\mathsf {Delegate}\) algorithms. For simplicity, we describe our scheme with just one \(\mathsf {KeyGen}\) algorithm that enables both the tasks of decryption and delegation. Secret-keys without delegation capabilities can be obtained by dropping the third entry (the PRG seed) from \(\mathsf {sk}_{\mathsf {id}}\).
- 22.
For \(i < n\), \(z_\mathsf {v}\) will become the \(x_\mathsf {v}\) in next iteration.
- 23.
The experiment can provide \(\mathsf {F}(s,\mathsf {id}^*)\) even though it does not appear in any of the \(\mathcal {A}\)’s secret key queries. The reason is that \(\mathsf {F}(s,\mathsf {id}^*)\) allows the capabilities of delegation but not decryption for ciphertexts to identity \(\mathsf {id}^*\).
- 24.
Observe that these are specifically the cases in which one or two of the values \(s_1,s_2\) and \(s_3\) given as input to \(\mathsf {NodeGen}\) and \(\mathsf {NodeGen}'\) depend on the \(\{c_i\}\) values.
- 25.
Note that since the adversary never makes a \(\mathsf {KeyGen}\) query for an identity \(\mathsf {id}\) that is a prefix of \(\mathsf {id}^*\). Therefore, we have that \(\mathsf {dk}_{\mathsf {v}}\) for \(\mathsf {v}\in V^*\cup \{\mathsf {id}^*\}\) will not be provided to \(\mathcal {A}\).
References
Agrawal, S., Boneh, D., Boyen, X.: Efficient lattice (H)IBE in the standard model. In: Gilbert, H. (ed.) EUROCRYPT 2010. LNCS, vol. 6110, pp. 553–572. Springer, Heidelberg (2010). doi:10.1007/978-3-642-13190-5_28
Agrawal, S., Boneh, D., Boyen, X.: Lattice basis delegation in fixed dimension and shorter-ciphertext hierarchical IBE. In: Rabin, T. (ed.) CRYPTO 2010. LNCS, vol. 6223, pp. 98–115. Springer, Heidelberg (2010). doi:10.1007/978-3-642-14623-7_6
Agrawal, S., Boyen, X.: Identity-based encryption from lattices in the standard model. Manuscript (2009)
Ananth, P., Boneh, D., Garg, S., Sahai, A., Zhandry, M.: Differing-inputs obfuscation and applications. Cryptology ePrint Archive, Report 2013/689 (2013). http://eprint.iacr.org/2013/689
Bellare, M., Hoang, V.T., Rogaway, P.: Foundations of garbled circuits. In: Yu, T., Danezis, G., Gligor, V.D. (eds.) ACM CCS 2012, pp. 784–796. ACM Press, Raleigh, 16–18 October 2012
Bellare, M., Rogaway, P., Random oracles are practical: a paradigm for designing efficient protocols. In: Ashby, V. (ed.) ACM CCS 1993, pp. 62–73. ACM Press, Fairfax, 3–5 November 1993
Biham, E., Boneh, D., Reingold, O.: Generalized Diffie-Hellman modulo a composite is not weaker than factoring. Cryptology ePrint Archive, Report 1997/014 (1997). http://eprint.iacr.org/1997/014
Boneh, D., Boyen, X.: Efficient selective-ID secure identity-based encryption without random oracles. In: Cachin, C., Camenisch, J.L. (eds.) EUROCRYPT 2004. LNCS, vol. 3027, pp. 223–238. Springer, Heidelberg (2004). doi:10.1007/978-3-540-24676-3_14
Boneh, D., Boyen, X.: Secure identity based encryption without random oracles. In: Franklin, M. (ed.) CRYPTO 2004. LNCS, vol. 3152, pp. 443–459. Springer, Heidelberg (2004). doi:10.1007/978-3-540-28628-8_27
Boneh, D., Boyen, X., Goh, E.-J.: Hierarchical identity based encryption with constant size ciphertext. In: Cramer, R. (ed.) EUROCRYPT 2005. LNCS, vol. 3494, pp. 440–456. Springer, Heidelberg (2005). doi:10.1007/11426639_26
Boneh, D., Franklin, M.: Identity-based encryption from the weil pairing. In: Kilian, J. (ed.) CRYPTO 2001. LNCS, vol. 2139, pp. 213–229. Springer, Heidelberg (2001). doi:10.1007/3-540-44647-8_13
Boneh, D., Gentry, C., Hamburg, M.: Space-efficient identity based encryption without pairings. In: 48th FOCS, pp. 647–657. IEEE Computer Society Press, Providence, 20–23 October 2007
Boneh, D., Papakonstantinou, P.A., Rackoff, C., Vahlis, Y., Waters, B.: On the impossibility of basing identity based encryption on trapdoor permutations. In: 49th FOCS, pp. 283–292. IEEE Computer Society Press, Philadelphia, 25–28 October 2008
Boyle, E., Chung, K.-M., Pass, R.: On extractability obfuscation. In: Lindell, Y. (ed.) TCC 2014. LNCS, vol. 8349, pp. 52–73. Springer, Heidelberg (2014). doi:10.1007/978-3-642-54242-8_3
Brassard, G., Chaum, D., Crépeau, C.: Minimum disclosure proofs of knowledge. J. Comput. Syst. Sci. 37(2), 156–189 (1988)
Canetti, R., Halevi, S., Katz, J.: A forward-secure public-key encryption scheme. In: Biham, E. (ed.) EUROCRYPT 2003. LNCS, vol. 2656, pp. 255–271. Springer, Heidelberg (2003). doi:10.1007/3-540-39200-9_16
Cash, D., Hofheinz, D., Kiltz, E., Peikert, C.: Bonsai trees, or how to delegate a lattice basis. In: Gilbert, H. (ed.) EUROCRYPT 2010. LNCS, vol. 6110, pp. 523–552. Springer, Heidelberg (2010). doi:10.1007/978-3-642-13190-5_27
Cho, C., Döttling, N., Garg, S., Gupta, D., Miao, P., Polychroniadou, A.: Laconic receiver oblivious transfer and its applications. In: CRYPTO (2017, to appear)
Cocks, C.: An identity based encryption scheme based on quadratic residues. In: Honary, B. (ed.) Cryptography and Coding 2001. LNCS, vol. 2260, pp. 360–363. Springer, Heidelberg (2001). doi:10.1007/3-540-45325-3_32
Diffie, W., Hellman, M.E.: New directions in cryptography. IEEE Trans. Inf. Theory 22(6), 644–654 (1976)
Döttling, N., Garg, S.: From selective IBE to full IBE and selective HIBE. Manuscript (2017)
Garg, S., Gentry, C., Sahai, A., Waters, B.: Witness encryption and its applications. In: Boneh, D., Roughgarden, T., Feigenbaum, J. (eds.) 45th ACM STOC, pp. 467–476. ACM Press, Palo Alto, 1–4 June 2013
Garg, S., Lu, S., Ostrovsky, R.: Black-box garbled RAM. In: Guruswami, V. (ed.) 56th FOCS, pp. 210–229. IEEE Computer Society Press, Berkeley, 17–20 October 2015
Garg, S., Lu, S., Ostrovsky, R., Scafuro, A.: Garbled RAM from one-way functions. In: Servedio, R.A., Rubinfeld, R. (eds.) 47th ACM STOC, pp. 449–458. ACM Press, Portland, 14–17 June 2015
Gentry, C., Halevi, S.: Hierarchical identity based encryption with polynomially many levels. In: Reingold, O. (ed.) TCC 2009. LNCS, vol. 5444, pp. 437–456. Springer, Heidelberg (2009). doi:10.1007/978-3-642-00457-5_26
Gentry, C., Halevi, S., Lu, S., Ostrovsky, R., Raykova, M., Wichs, D.: Garbled RAM revisited. In: Nguyen, P.Q., Oswald, E. (eds.) EUROCRYPT 2014. LNCS, vol. 8441, pp. 405–422. Springer, Heidelberg (2014). doi:10.1007/978-3-642-55220-5_23
Gentry, C., Peikert, C., Vaikuntanathan, V.: Trapdoors for hard lattices and new cryptographic constructions. In: Ladner, R.E., Dwork, C. (eds.) 40th ACM STOC, pp. 197–206. ACM Press, Victoria, 17–20 May 2008
Gentry, C., Silverberg, A.: Hierarchical ID-based cryptography. In: Zheng, Y. (ed.) ASIACRYPT 2002. LNCS, vol. 2501, pp. 548–566. Springer, Heidelberg (2002). doi:10.1007/3-540-36178-2_34
Goldreich, O., Goldwasser, S., Micali, S.: How to construct random functions (extended abstract). In: 25th FOCS, pp. 464–479. IEEE Computer Society Press, Singer Island, 24–26 October 1984
Goldreich, O., Levin, L.A.: A hard-core predicate for all one-way functions. In: 21st ACM STOC, pp. 25–32. ACM Press, Seattle, 15–17 May 1989
Hofheinz, D., Kiltz, E.: The group of signed quadratic residues and applications. In: Halevi, S. (ed.) CRYPTO 2009. LNCS, vol. 5677, pp. 637–653. Springer, Heidelberg (2009). doi:10.1007/978-3-642-03356-8_37
Horwitz, J., Lynn, B.: Toward hierarchical identity-based encryption. In: Knudsen, L.R. (ed.) EUROCRYPT 2002. LNCS, vol. 2332, pp. 466–481. Springer, Heidelberg (2002). doi:10.1007/3-540-46035-7_31
Koblitz, N.: Elliptic curve cryptosystems. Math. Comput. 48(177), 203–209 (1987)
Krawczyk, H., Rabin, T.: Chameleon hashing and signatures. Cryptology ePrint Archive, Report 1998/010 (1998). http://eprint.iacr.org/1998/010
Lewko, A., Waters, B.: New techniques for dual system encryption and fully secure HIBE with short ciphertexts. In: Micciancio, D. (ed.) TCC 2010. LNCS, vol. 5978, pp. 455–479. Springer, Heidelberg (2010). doi:10.1007/978-3-642-11799-2_27
Lindell, Y., Pinkas, B.: A proof of security of Yao’s protocol for two-party computation. J. Cryptol. 22(2), 161–188 (2009)
Lu, S., Ostrovsky, R.: How to garble RAM programs? In: Johansson, T., Nguyen, P.Q. (eds.) EUROCRYPT 2013. LNCS, vol. 7881, pp. 719–734. Springer, Heidelberg (2013). doi:10.1007/978-3-642-38348-9_42
McCurley, K.S.: A key distribution system equivalent to factoring. J. Cryptol. 1(2), 95–105 (1988)
Miller, V.S.: Use of elliptic curves in cryptography. In: Williams, H.C. (ed.) CRYPTO 1985. LNCS, vol. 218, pp. 417–426. Springer, Heidelberg (1986). doi:10.1007/3-540-39799-X_31
Naor, M., Yung, M.: Universal one-way hash functions and their cryptographic applications. In: 21st ACM STOC, pp. 33–43. ACM Press, Seattle, 15–17 May 1989
Okamoto, T., Takashima, K.: Fully secure functional encryption with general relations from the decisional linear assumption. In: Rabin, T. (ed.) CRYPTO 2010. LNCS, vol. 6223, pp. 191–208. Springer, Heidelberg (2010). doi:10.1007/978-3-642-14623-7_11
Papakonstantinou, P.A., Rackoff, C.W., Vahlis, Y.: How powerful are the DDH hard groups? Cryptology ePrint Archive, Report 2012/653 (2012). http://eprint.iacr.org/2012/653
Rivest, R.L., Shamir, A., Adleman, L.M.: A method for obtaining digital signature and public-key cryptosystems. Commun. Assoc. Comput. Mach. 21(2), 120–126 (1978)
Shamir, A.: Identity-based cryptosystems and signature schemes. In: Blakley, G.R., Chaum, D. (eds.) CRYPTO 1984. LNCS, vol. 196, pp. 47–53. Springer, Heidelberg (1985). doi:10.1007/3-540-39568-7_5
Shi, E., Waters, B.: Delegating capabilities in predicate encryption systems. In: Aceto, L., Damgård, I., Goldberg, L.A., Halldórsson, M.M., Ingólfsdóttir, A., Walukiewicz, I. (eds.) ICALP 2008. LNCS, vol. 5126, pp. 560–578. Springer, Heidelberg (2008). doi:10.1007/978-3-540-70583-3_46
Shmuely, Z.: Composite Diffie-hellman public-key generating systems are hard to break. Technical report no. 356, Computer Science Department, Technion, Israel (1985)
Waters, B.: Dual system encryption: realizing fully secure IBE and HIBE under simple assumptions. In: Halevi, S. (ed.) CRYPTO 2009. LNCS, vol. 5677, pp. 619–636. Springer, Heidelberg (2009). doi:10.1007/978-3-642-03356-8_36
Waters, B.: Efficient identity-based encryption without random oracles. In: Cramer, R. (ed.) EUROCRYPT 2005. LNCS, vol. 3494, pp. 114–127. Springer, Heidelberg (2005). doi:10.1007/11426639_7
Yao, A.C.-C.: Protocols for secure computations (extended abstract). In: 23rd FOCS, pp. 160–164. IEEE Computer Society Press, Chicago, 3–5 November 1982
Acknowledgments
We thank the anonymous reviewers of CRYPTO 2017 for their valuable feedback.
Author information
Authors and Affiliations
Corresponding author
Editor information
Editors and Affiliations
Rights and permissions
Copyright information
© 2017 International Association for Cryptologic Research
About this paper
Cite this paper
Döttling, N., Garg, S. (2017). Identity-Based Encryption from the Diffie-Hellman Assumption. In: Katz, J., Shacham, H. (eds) Advances in Cryptology – CRYPTO 2017. CRYPTO 2017. Lecture Notes in Computer Science(), vol 10401. Springer, Cham. https://doi.org/10.1007/978-3-319-63688-7_18
Download citation
DOI: https://doi.org/10.1007/978-3-319-63688-7_18
Published:
Publisher Name: Springer, Cham
Print ISBN: 978-3-319-63687-0
Online ISBN: 978-3-319-63688-7
eBook Packages: Computer ScienceComputer Science (R0)









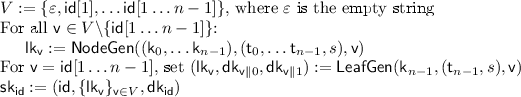
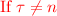
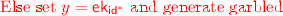



 generate
generate 



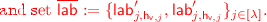 For the case when
For the case when 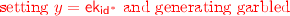
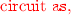
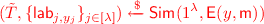
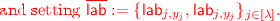 For the case when
For the case when 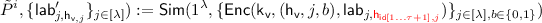
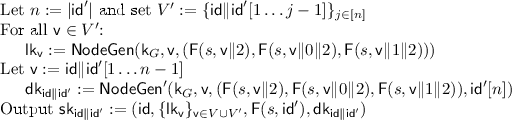

 generate
generate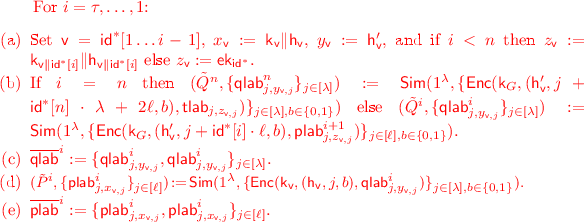


 Computational indistinguishability of hybrids
Computational indistinguishability of hybrids 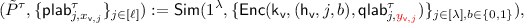
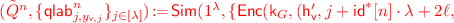

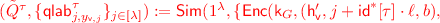

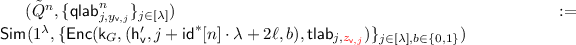 , where
, where  where
where 