Abstract
Predicate encodings (Wee, TCC 2014; Chen, Gay, Wee, EUROCRYPT 2015), are symmetric primitives that can be used for building predicate encryption schemes. We give an algebraic characterization of the notion of privacy from predicate encodings, and explore several of its consequences. Specifically, we propose more efficient predicate encodings for boolean formulae and arithmetic span programs, and generic optimizations of predicate encodings. We define new constructions to build boolean combination of predicate encodings. We formalize the relationship between predicate encodings and pair encodings (Attrapadung, EUROCRYPT 2014), another primitive that can be transformed generically into predicate encryption schemes, and compare our constructions for boolean combinations of pair encodings with existing similar constructions from pair encodings. Finally, we demonstrate that our results carry to tag-based encodings (Kim, Susilo, Guo, and Au, SCN 2016).
You have full access to this open access chapter, Download conference paper PDF
Similar content being viewed by others
Keywords
These keywords were added by machine and not by the authors. This process is experimental and the keywords may be updated as the learning algorithm improves.
1 Introduction
Predicate Encryption (PE) [13, 25] is a form of public-key encryption that supports fine-grained access control for encrypted data. In predicate encryption, everyone can create ciphertexts while keys can only be created by the master key owner. Predicate encryption schemes use predicates to model (potentially complex) access control policies, and attributes are attached to both ciphertexts and secret keys. A predicate encryption scheme for a predicate \(\mathsf {P}\) guarantees that decryption of a ciphertext \(\mathsf{ct}_{x}\) with a secret key \(\mathsf{sk}_{y}\) is allowed if and only if the attribute x associated to the ciphertext \(\mathsf{ct}\) and the attribute y associated to the secret key \(\mathsf{sk}\) verify the predicate \(\mathsf {P}\), i.e. \(\mathsf {P}(x,y)=1\). Predicate encryption schemes exist for several useful predicates, such as Zero Inner Product Encryption (ZIPE), where attributes are vectors \(\varvec{x}\) and \(\varvec{y}\) and the predicate \(\mathsf {P}(\varvec{x},\varvec{y})\) is defined as \(\varvec{x}^{\top }\varvec{y}=0\). Predicate encryption subsumes several previously defined notions of public-key encryption. For example, Identity-Based Encryption (IBE) [34] can be obtained by defining \(\mathsf {P}(x,y)\) as \(x = y\) and Attribute-Based Encryption (ABE) [33] can be obtained similarly. More concretely, for Key-Policy ABE (KP-ABE), the attribute x is a boolean vector, the attribute y is a boolean function, and the predicate \(\mathsf {P}(x,y)\) is defined as \(y(x) = 1\). For Ciphertext-Policy ABE (CP-ABE), the roles of the attributes x and y are swapped.
Modular Approaches for PE. In 2014, two independent works by Wee [37] and Attrapadung [6] proposed generic and unifying frameworks for obtaining efficient fully secure PE schemes for a large class of predicates. Both works use the dual system methodology introduced by Lewko and Waters [27, 36] and define a compiler that takes as input a relatively simple symmetric primitive and produces a fully secure PE construction. Wee introduced so-called predicate encodings, an information-theoretic primitive inspired from linear secret sharing. Attrapadung introduced so-called pair encodings and provided computational and information-theoretic security notions. These approaches greatly simplify the construction and analysis of predicate encryption schemes and share several advantages. First, they provide a good trade-off between expressivity and performance, while the security relies on standard and well studied assumptions. Second, they unify existing constructions into a single framework, i.e., previous PE constructions can be seen as instantiations of these new compilers with certain encodings. Third, building PE schemes by analyzing and building these simpler encodings is much easier than building PE schemes directly. Compared to full security for PE, the encodings must verify much weaker security requirements. The power of pair and predicate encodings is evidenced by the discovery of new constructions and efficiency improvements over existing ones. However, both approaches were designed over composite order bilinear groups. In Chen et al. [15] and Attrapadung [7] respectively extended the predicate encoding and pair encoding compiler to the prime order setting. Next, Agrawal and Chase [1] improved on Attrapadung’s work by relaxing the security requirement on pair encodings and thus, capturing new constructions. In addition, their work also brings both generic approaches closer together, because like in [15], the new compiler relies (in a black-box way) on Dual System Groups (DSG) [16, 17]. Additionally Kim et al. [22] recently introduced a new generic framework for modular design of predicate encryption that improves on the performance of existing compilers. Their core primitive, tag-based encodings, is very similar to predicate encodings.
1.1 Our Contributions
We pursue the study of predicate encodings and establish several general results and new constructions that broaden their scope and improve their efficiency. We also compare predicate encodings to pair and tag-based encodings.
Predicate Encodings. We show that the information-theoretic definition of \(\alpha \)-privacy used in [15, 37] is equivalent to an algebraic statement (furthermore independent of \(\alpha \)) about the existence of solutions for a linear system of equations. Leveraging this result, we prove a representation theorem for predicate encodings: every triple of encoding functions implicitly defines a unique predicate for which it is a valid predicate encoding. Conversely, every predicate \(\mathsf {P}\) that admits a predicate encoding is logically equivalent to the implicit predicate induced by its encoding functions. Moreover, our algebraic definition of privacy simplifies all subsequent results in the paper.
First, we define a generic optimization of predicate encodings that often leads to efficiency improvements and reduce the number of required group elements in keys and ciphertexts. We prove the soundness of the transformations and validate their benefits experimentally on examples from [15, 37]; we successfully apply these simplifications to reduce the size of keys and ciphertexts by up to 50% and to reduce the number of group operations needed in some of the existing encodings.
Second, we define generic methods for combining predicate encodings. We provide encoding transformations for the disjunction, conjunction and negation of predicates, and for the dual predicate.
Tag-Based Encodings. We show that our results on predicate encodings generalize to tag-based encodings. In particular, we give a purely algebraic characterization of the hiding property of tag-based encodings. Moreover, we demonstrate that the hiding property can be strengthened without any loss of generality, by requiring equality rather than statistical closeness of distributions.
Comparison of Encodings. We compare the expressivity of the three core primitives (predicate encodings, pair encodings and tag-based encodings) corresponding to the three different modular frameworks. We provide an embedding that produces an information-theoretical pair encoding from every predicate encoding. Then, we use this encoding to compare our constructions to build boolean combination of predicate encodings with similar constructions for pair encodings that were introduced by [6].
In addition, we provide a transformationFootnote 1 from tag-based encodings into predicate encodings.
New Constructions. We develop several new constructions of predicate encodings and predicate encryption:
-
Combining predicates. We show how to combine our results to build Dual-Policy Attribute-Based Encryption (DP-ABE) [9, 10] in the frameworks of predicate encodings and tag-based encodings (Sect. 6.1). Additionally, we consider the idea of combining arbitrary encodings with a broadcast encryption encoding to achieve direct revocation of keys. The former encoding takes care of revocation, while the latter encodes the desired access structure.
-
Improved predicate encodings. We provide new instances of predicate encodings that improve on best known predicate encodings proposed in [15] and have additional properties (Sect. 6.2).
-
Extra features. Finally, we show how to construct a weakly attribute-hiding predicate encoding for boolean formulas and how to enhance any predicate encoding with support for delegation (Sect. 6.3).
Implementation and Evaluation. We implement a general library for predicate encryption with support for the predicate encoding and pair encoding frameworks. Our library uses the Relic-Toolkit [5] for pairings with a 256-bits Barreto-Naehrig Curve [11]. We use our library for validating our constructions; experimental results are presented in the relevant sections. All the experiments were executed on a 8-core machine with 2.40 GHz Intel Core i7-3630QM CPU and 8 GB of RAM. Our scalability experiments show that predicate encodings can be used for real applications. The code is publicly available and open sourceFootnote 2.
1.2 Prior Work
Predicate encodings have been introduced in [37] and we use a refined version that is defined in [15] as our starting point. Both variants use an information-theoretic definition of the hiding while we show that there is an equivalent algebraic definition. Another related work is [20], initiating a systematic study of the communication complexity of the so-called conditional secret disclosure primitive, which is closely related to predicate encodings.
Other works also optimize existing predicate encryption schemes, for example many works focus on going from composite order constructions to the more efficient prime order ones [7, 15, 26]. In [15] they also propose performance improvements on dual system groups. We believe our optimizations via predicate encodings complement other possible enhancements of predicate encryption.
Boolean combinations of predicates have also been considered in the setting of pair encodings. Attrapadung [9, 10] proposes generic transformations for conjunction and for the dual predicate, but neither for negation nor disjunction. We propose new transformations for conjunction and dual in the framework of predicate encodings and we also deal with negation and disjunction.
The main advantage of DP-ABE is the possibility of considering policies over objective attributes (associated to data) and policies over subjective attributes (associated to user credentials) at the same time. DP-ABE has been considered by Attrapadung in the pair encoding framework [9, 10]. To the best of our knowledge, we are the first to provide DP-ABE in the predicate encoding and tag-based encoding frameworks.
Revocation is a desirable property for PE and ABE schemes that has also been considered by many works in the literature. Revocation allows to invalidate a user’s secret key in such a way that it becomes useless, even if its associated attribute satisfies the policy associated to the ciphertext. Some attempts [32] propose indirect revocation that requires that the master secret owner periodically updates secret keys for non-revoked users. Other attempts achieve direct revocation [8, 23, 30, 31], but either rely on strong assumptions or provide only selectively security. Our construction not only allows to achieve revocation in a fully secure framework, but it allows to add revocation to arbitrary predicate encodings.
Policy hiding is another property of PE, and ABE in particular, that has been broadly studied. In this context, policies associated to ciphertexts are not attached to them and therefore, unauthorized users will only learn the fact that their key does not satisfy the policy, but nothing else. Policy Hiding has been considered in several works [13, 25]. The security of our construction improves on earlier works, thanks to the compiler from [15]. Our observation extends the expressivity of attribute-hiding predicate encryption for ZIPE proposed in [15] to support policy-hiding for boolean formulas.
In [15], the authors introduce the notion of spatial encryption predicate encodings. We generalize this notion and introduce a transformation that makes delegation possible for every predicate encoding.
Several works evaluate the suitability of ABE for different applications. For example, ABE has been used and benchmarked to enforce privacy of Electronic Medical Records (EMR) [3], in a system where healthcare organizations export EMRs to external storage locations. Other examples are Sieve [35] or Streamforce [18], systems that provide enforced access control for user data and stream data in untrusted clouds. In contrast to these works, we are the first to evaluate predicate encryption and ABE based on modern modular approaches such as the predicate encoding and pair encoding frameworks. The resulting schemes also satisfy a stronger security notion (full vs. selective security) compared to the previously mentioned evaluations. We focus on synthetic case studies, while other works analyze more realistic settings and integration of ABE into bigger systems. Combining our methods with these more practical case studies is a very interesting direction for future work.
1.3 Comparison with Agrawal and Chase (EUROCRYPT 2017)
Concurrently and independently, Agrawal and Chase [2] introduce a new security notion, which they call symbolic property, for pair encodings. They adapt previous generic frameworks [1, 7] to define a compiler that takes pair encodings satisfying the symbolic property and produces fully secure predicate encryption schemes under the q-ratio assumption—a new assumption that is implied by some q-type assumptions proposed in [6, 29]. Moreover, they introduce the notion of tivially broken pair encoding and show that any not trivially broken pair encoding must satisfy their symbolic property. Their definitions of symbolic property and trivially broken for pair encodings are closely related to our algebraic characterization of privacy of predicate encodings. However, the two results are incomparable: although pair encodings are more general than predicate encodings (see Sect. 5.1 for a more detailed comparison), their results rely of q-type assumption, whereas our results build on previous frameworks that rely on weaker assumptions (Matrix-DH or k-LIN).
2 Background
In this section, we first introduce some mathematical notation and then define predicate encodings, tag-based encodings and pair encodings the three primitives used in the three different modular frameworks for predicate encryption.
2.1 Notation
For finite sets S, we use \(x \mathop {\leftarrow }\limits ^{\$}S\) to denote that x is uniformly sampled from S. We define [n] as the range \(\{1,\dots ,n\}\) for an arbitrary \(n \in \mathbb {N}\). For a predicate \(\mathsf {P}: \mathcal {X}\times \mathcal {Y}\rightarrow \{0,1\}\), we use \((x,y) \in \mathsf {P}\) as a shorthand for \(\mathsf {P}(x,y) = 1\). We use the same conventions for matrix-representations of linear maps on finite-dimensional spaces. We define vectors \(\varvec{v} \in \mathbb {F}^{n}\) as column matrices and denote the transpose of a matrix A by \(A^{\top }\). We use \(\mathsf{diag}(\varvec{v})\) to denote the diagonal matrix with main diagonal \(\varvec{v}\). We denote the identity matrix of dimension n by \(I_{n}\), a zero vector of length n by \(\varvec{0}_n\) and a zero matrix of m rows and n columns by \({\mathbf {0}}_{m, n}\). Let S be a set of indices and A be a matrix. \(A_S\) denotes the matrix formed from the set of columns of A with indices is in S. We define the colspan of a matrix \(M \in \mathbb {F}^{m\times n}\) as the set of all possible linear combinations columns of M. That is  . We analogously define the rowspan of a matrix. We consider prime order bilinear groups \(\mathcal{G}= (\mathbb {G}_1,\mathbb {G}_2,\mathbb {G}_t, e:\mathbb {G}_1 \times \mathbb {G}_2 \rightarrow \mathbb {G}_t)\) and use \(g_1\), \(g_2\), \(g_t\) to denote their respective generators. The map e satisfies \(e(g_1^a, g_2^b) = g_t^{ab}\) for every \(a,b \in \mathbb {N}\). A bilinear group is said to be symmetric if \(\mathbb {G}_1 = \mathbb {G}_2\), otherwise it is called asymmetric. We abuse of notation and write \(g^{\varvec{v}}\) to denote \((g^{\varvec{v}_1}, \dots , g^{\varvec{v}_n})\) for a group element g and a vector \(\varvec{v} \in \mathbb {Z}_p^{n}\).
. We analogously define the rowspan of a matrix. We consider prime order bilinear groups \(\mathcal{G}= (\mathbb {G}_1,\mathbb {G}_2,\mathbb {G}_t, e:\mathbb {G}_1 \times \mathbb {G}_2 \rightarrow \mathbb {G}_t)\) and use \(g_1\), \(g_2\), \(g_t\) to denote their respective generators. The map e satisfies \(e(g_1^a, g_2^b) = g_t^{ab}\) for every \(a,b \in \mathbb {N}\). A bilinear group is said to be symmetric if \(\mathbb {G}_1 = \mathbb {G}_2\), otherwise it is called asymmetric. We abuse of notation and write \(g^{\varvec{v}}\) to denote \((g^{\varvec{v}_1}, \dots , g^{\varvec{v}_n})\) for a group element g and a vector \(\varvec{v} \in \mathbb {Z}_p^{n}\).
2.2 Predicate Encodings
Predicate encodings are information-theoretic primitives that can be used for building predicate encryption schemes [37]. We adopt the definition from [15], but prefer to use matrix notation.
Definition 1
(Predicate encoding). Let \(\mathsf {P}: \mathcal {X}\times \mathcal {Y}\rightarrow \{0,1\}\) be a binary predicate over finite sets \(\mathcal {X}\) and \(\mathcal {Y}\). Given a prime \(p\in \mathbb {N}\), and \(s,r,w \in \mathbb {N}\), a (s, r, w)-predicate encoding for \(\mathsf {P}\) consists of five deterministic algorithms \((\mathsf {sE},\mathsf {rE},\mathsf {kE},\) \(\mathsf {sD},\mathsf {rD})\): the sender encoding algorithm \(\mathsf {sE}\) maps \(x \in \mathcal {X}\) into a matrix \(\mathsf {sE}_x \in \mathbb {Z}_p^{s\times w}\), the receiver encoding algorithm \(\mathsf {rE}\) maps \(y \in \mathcal {Y}\) into a matrix \(\mathsf {rE}_y \in \mathbb {Z}_p^{r \times w}\), the key encoding algorithm \(\mathsf {kE}\) maps \(y \in \mathcal {Y}\) into a vector \(\mathsf {kE}_y \in \mathbb {Z}_p^{r}\), while the sender and receiver decoding algorithms, respectively \(\mathsf {sD}\) and \(\mathsf {rD}\), map a pair \((x,y) \in \mathcal {X}\times \mathcal {Y}\) into vectors \(\mathsf {sD}_{x,y} \in \mathbb {Z}_p^{s}\) and \(\mathsf {rD}_{x,y} \in \mathbb {Z}_p^{r}\) respectively. We require that the following properties are satisfied:
-
reconstructability: for all \((x,y) \in \mathsf {P}\), \(\mathsf {sD}_{x,y}^{\top } \mathsf {sE}_x = \mathsf {rD}_{x,y}^{\top } \mathsf {rE}_y\) and \(\mathsf {rD}_{x,y}^{\top } \mathsf {kE}_y = 1\);
-
\(\alpha \) -privacy: for all \((x,y) \notin \mathsf {P}, \alpha \in \mathbb {Z}_p\),
$$\begin{aligned} \varvec{w}\mathop {\leftarrow }\limits ^{\$}\mathbb {Z}_p^{w}; \textsf { return } (\mathsf {sE}_x \varvec{w}, \, \mathsf {rE}_y \varvec{w}+ \alpha \cdot \mathsf {kE}_y) \, \, \equiv \, \, \varvec{w}\mathop {\leftarrow }\limits ^{\$}\mathbb {Z}_p^{w}; \textsf { return } (\mathsf {sE}_x \varvec{w}, \, \mathsf {rE}_y \varvec{w}) \end{aligned}$$where \(\equiv \) denotes equality of distributions.
Reconstructability allows to recover \(\alpha \) from \((x,y,\, \mathsf {sE}_x \varvec{w}, \, \mathsf {rE}_y \varvec{w}+ \alpha \cdot \mathsf {kE}_y)\) if \((x,y) \in \mathsf {P}\). Privacy ensures that \(\alpha \) is perfectly hidden for such tuples if \((x,y) \notin \mathsf {P}\).
Example 1
(IBE predicate encoding). Let \(\mathcal {X}=\mathcal {Y}=\mathbb {Z}_p\) and let \(s = r = 1\), \(w = 2\). We define the encoding functions as follows:

The above is a predicate encoding for identity-based encryption, i.e., for the predicate \(\mathsf {P}(x,y) = 1 \text { iff } x = y\). Note that  when \(x = y\), so reconstructability is satisfied. On the other hand, \(\alpha \)-privacy follows from the fact that if \(x \ne y\), \(x\cdot w_1 + w_2\) and \(y \cdot w_1 + w_2\) are pair-wise independent. \(\blacksquare \)
when \(x = y\), so reconstructability is satisfied. On the other hand, \(\alpha \)-privacy follows from the fact that if \(x \ne y\), \(x\cdot w_1 + w_2\) and \(y \cdot w_1 + w_2\) are pair-wise independent. \(\blacksquare \)
Predicate Encryption from Predicate Encodings. We try to provide some intuition on how predicate encodings are compiled to predicate encryption schemes by the compiler from [15]. We consider a simplified compiler (see explanations below). The master keys, ciphertexts and secret keys have the following form:
The encrypted message \(m\in \mathbb {G}_t\) is blinded by a random factor \(e(g_1,g_2)^{\alpha s}\). The so-called reconstruction property of predicate encodings ensures that this blinding factor can be recovered for a pair \((\mathsf{ct}_{x}\),\(\mathsf{sk}_{y})\) if \(\mathsf {P}(x,y) = 1\). More concretely, for all pairs (x, y) such that \(\mathsf {P}(x,y) = 1\), because multiplying by matrices \(\mathsf {sD}_{x,y}\),\(\mathsf {rD}_{x,y}\) is a linear operation, it is possible operate in the exponent and compute
obtaining \(g_{1}^{s\beta }\) and \(g_2^{\alpha + r\beta }\) for \(\beta = \mathsf {sD}_{x,y}^{\top }\mathsf {sE}_x \varvec{w}= \mathsf {rD}_{x,y}^{\top } \mathsf {rE}_y \varvec{w}\) (note that knowing the value of \(\beta \) is not necessary). Now, it is simple to recover \(e(g_1,g_2)^{\alpha s}\) from \(e(g_1^{s},g_2^{\alpha + r \beta })\) and \(e(g_1^{s\beta }, g_2^{r})\). Security is ensured by the \(\alpha \) -privacy property of the encoding together with decisional assumptions about dual system groups. Intuitively, the \(\alpha \)-privacy property states that given certain values derived from the output of the encoding functions for random input, \(\alpha \) remains information-theoretic hidden.
Note that the following is a simplification of their compiler, where we avoid DSG for simplicity. The real scheme produced by their compiler would have twice as many group elements (under SXDH) or three times as many (under DLIN).
2.3 Tag-Based Encodings
Tag-based encodings is a new primitive defined in a very recent work [22] that defines a new generic framework (using prime order groups) for modular design of predicate encryption.
Definition 2
(Tag-based encoding). Let \(\mathsf {P}: \mathcal {X}\times \mathcal {Y}\rightarrow \{0,1\}\) be a binary predicate over finite sets \(\mathcal {X}\) and \(\mathcal {Y}\). Given a prime \(p\in \mathbb {N}\), and \(c,k,h \in \mathbb {N}\), a (c, k, h)-tag-based encoding encoding for \(\mathsf {P}\) consists of two deterministic algorithms \((\mathsf {cE},\mathsf {kE})\): the ciphertext encoding algorithm \(\mathsf {cE}\) maps \(x \in \mathcal {X}\) into a matrix \(\mathsf {cE}_x \in \mathbb {Z}_p^{c\times h}\) and the key encoding algorithm \(\mathsf {kE}\) maps \(y \in \mathcal {Y}\) into a matrix \(\mathsf {kE}_y \in \mathbb {Z}_p^{k \times h}\). We require that the following properties are satisfied:
-
reconstructability: for all \((x,y) \in \mathsf {P}\), there exists an efficient algorithm that on input (x, y) computes vectors \(\varvec{m}_c \in \mathbb {Z}_p^{c}\), \(\varvec{m}_k \in \mathbb {Z}_p^{k}\) such that
$$\begin{aligned} \varvec{m}_c^{\top } \mathsf {cE}_x = \varvec{m}_k^{\top } \mathsf {kE}_y \ne \varvec{0}^{\top }_{h} \end{aligned}$$ -
\(\varvec{h}\) -hiding: for all \((x,y) \notin \mathsf {P}\),
$$\begin{aligned} \varvec{h} \mathop {\leftarrow }\limits ^{\$}\mathbb {Z}_p^{h};\, \textsf { return } (\mathsf {cE}_x \varvec{h},\, \mathsf {kE}_y \varvec{h}) \quad \approx _s\quad \varvec{h}, \varvec{h}' \mathop {\leftarrow }\limits ^{\$}\mathbb {Z}_p^{h};\, \textsf { return } (\mathsf {cE}_x \varvec{h},\, \mathsf {kE}_y \varvec{h}') \end{aligned}$$where \(\approx _s\) denotes negligible statistical distance between distributions.
The compiler proposed in [22] uses similar ideas to the one for predicate encodings. However, it does not rely on dual system groups and can be instantiated with symmetric bilinear maps. The message is blinded and ciphertexts and keys contain a set of group elements that are enough to recover the blinding factor only when the predicate is true. This compiler has the advantage that some elements of ciphertexts and keys are \(\mathbb {Z}_p\) values and not group elements, which reduces the storage size.
2.4 Pair Encodings
Attrapadung [6, 7] proposes an independent modular framework for predicate encryption, based on a primitive called pair encoding. For our purposes, it suffices to consider a more restrictive, information-theoretic, notion of pair encodings.
Definition 3
(Information-theoretic pair encoding). Let \(\mathsf {P}: \mathcal {X}\times \mathcal {Y}\rightarrow \{0,1\}\) be a binary predicate over finite sets \(\mathcal {X}\) and \(\mathcal {Y}\). Given a prime \(p \in \mathbb {N}\), and \(c,k,l,m,n \in \mathbb {N}\), let \(\varvec{h} = (h_1,\dots ,h_n)\), \(\varvec{s} = (s_0, s_1,\dots ,s_{l})\) and \(\varvec{r} = (\alpha , r_1,\dots ,r_{m})\) be sets of variables. An information-theoretic (c, k, n)-pair encoding scheme for \(\mathsf {P}\) consists of three deterministic algorithms \((\mathsf{Enc1},\mathsf{Enc2},\mathsf{Pair})\): the ciphertext encoding algorithm \(\mathsf{Enc1}\) maps a value \(x \in \mathcal {X}\) into a list of polynomials \(\varvec{c}_x \in \mathbb {Z}_p[\varvec{s},\varvec{h}]^{c}\), the key encoding algorithm \(\mathsf{Enc2}\) maps a value \(y \in \mathcal {Y}\) into a list of polynomials \(\varvec{k}_y \in \mathbb {Z}_p[\varvec{r},\varvec{h}]^k\) and the decoding algorithm \(\mathsf{Pair}\) maps a pair \((x,y) \in \mathcal {X}\times \mathcal {Y}\) into a matrix \(E_{x,y} \in \mathbb {Z}_p^{c\times k}\). We require that the following properties are satisfied:
-
polynomial constraints:
-
\(\bullet \) For every \(x \in \mathcal {X}\) and every \(f \in \mathsf{Enc1}(x)\), \(f = f(\varvec{s},\varvec{h})\) only contains monomials of the form \(s_i\) or \(s_ih_j\), \(i \in [0,l]\), \(j \in [n]\).
-
\(\bullet \) For every \(y \in \mathcal {Y}\) and every \(f \in \mathsf{Enc2}(y)\), \(f = f(\varvec{r},\varvec{h})\) only contains monomials of the form \(\alpha \), \(r_i\) or \(r_ih_j\), \(i \in [m]\), \(j \in [n]\).
-
-
reconstructability: for all \((x,y) \in \mathsf {P}\) and all \(\varvec{c}_x \leftarrow \mathsf{Enc1}(x)\), \(\varvec{k}_y \leftarrow \mathsf{Enc2}(y)\), \(E_{x,y} \leftarrow \mathsf{Pair}(x,y)\), the following polynomial equality holds \(\varvec{c}_x^{\top }E_{x,y}\varvec{k}_y = \alpha s_0\).
-
perfect security: for all \((x,y) \notin \mathsf {P}\) and all \(\varvec{c}_x \leftarrow \mathsf{Enc1}(x)\), \(\varvec{k}_y \leftarrow \mathsf{Enc2}(y)\),
$$\begin{aligned} \begin{array}{lll} &{} \varvec{h} \mathop {\leftarrow }\limits ^{\$}\mathbb {Z}_p^{n};\, \varvec{r} \mathop {\leftarrow }\limits ^{\$}(\mathbb {Z}_p^*)^{m};\, \varvec{s} \mathop {\leftarrow }\limits ^{\$}\mathbb {Z}_p^{l+1};\, &{} \textsf { return } (\varvec{c}_x(\varvec{s}, \varvec{h}), \, \varvec{k}_y(0,\varvec{r},\varvec{h})) \quad \equiv \\ &{} \varvec{h} \mathop {\leftarrow }\limits ^{\$}\mathbb {Z}_p^{n};\, \varvec{r} \mathop {\leftarrow }\limits ^{\$}(\mathbb {Z}_p^*)^{m};\, \varvec{s} \mathop {\leftarrow }\limits ^{\$}\mathbb {Z}_p^{l+1}; \alpha \mathop {\leftarrow }\limits ^{\$}\mathbb {Z}_p;\, &{} \textsf { return } (\varvec{c}_x(\varvec{s}, \varvec{h}), \, \varvec{k}_y(\alpha ,\varvec{r},\varvec{h})) \end{array} \end{aligned}$$where \(\equiv \) denotes equality of distributions.
The compiler from pair encodings follows similar ideas to the other compilers. The message is blinded by a random factor and ciphertexts and keys contain all the information necessary to recover this blinded factor, only when the predicate holds. The compiler from pair encodings requires to compute a polynomial number of pairings during decryption, unlike the compilers for predicate encodings and tag-based encodings that needFootnote 3 6 and 8 pairings respectively.
3 Predicate Encodings: Properties and Consequences
In this section, we present a purely algebraic (and independent of \(\alpha \)) characterization of the \(\alpha \)-privacy property. It simplifies both the analysis and the construction of predicate encodings. In particular, we use our characterization to define and prove a new optimization of predicate encodings, i.e., a transformation that makes the encoding functions smaller while preserving the predicate. Additionally, we unify the reconstructability and privacy properties and show that they are mutually exclusive and complementary, i.e., for every \((x,y) \in \mathcal {X}\times \mathcal {Y}\), one and only one of the two conditions holds. This unified treatment facilitates the construction and study of predicate encodings.
3.1 Algebraic Properties of Predicate Encodings
The following theorem captures two essential properties of predicate encodings: first, privacy admits a purely algebraic characterization (furthermore independent of \(\alpha \)) given in terms of existence of solutions of a linear system of equations. Second, reconstructability and privacy, when viewed as properties of a single pair (x, y), negate each other; i.e. a pair (x, y) always satisfies exactly one of the two properties.
Theorem 1
(Algebraic characterization of privacy). Let \(p\in \mathbb {N}\) be a prime, let \(s, r, w \in \mathbb {N}\) and let \(S \in \mathbb {Z}_p^{s \times w}\), \(R \in \mathbb {Z}_p^{r \times w}\), \(\varvec{k} \in \mathbb {Z}_p^{r}\). The following are equivalent:
-
\(\alpha \) -privacy For every \(\alpha \in \mathbb {Z}_p\),
$$\begin{aligned}&\varvec{w}\mathop {\leftarrow }\limits ^{\$}\mathbb {Z}_p^{w}; \textsf { return } (S \varvec{w}, \, R \varvec{w}+ \alpha \cdot \varvec{k}) \quad \equiv \quad&\varvec{w}\mathop {\leftarrow }\limits ^{\$}\mathbb {Z}_p^{w}; \textsf { return } (S \varvec{w}, \, R \varvec{w})&\end{aligned}$$ -
(algebraic) privacy There exists \(\varvec{w}\in \mathbb {Z}_p^{w}\) such that \(S \varvec{w}= \varvec{0}_{s}\) and \(R \varvec{w}= \varvec{k}\)
-
non-reconstructability For every \(\varvec{s} \in \mathbb {Z}_p^{s}\) and \(\varvec{r} \in \mathbb {Z}_p^{r}\), either \(\varvec{s}^{\top }S \ne \varvec{r}^{\top }R\) or \(\varvec{r}^{\top }\varvec{k} \ne 1\).
Proof
We first prove that \(\alpha \)-privacy is equivalent to algebraic privacy. Note that the fact that \(\forall \, \alpha \in \mathbb {Z}_p\),
is equivalent to the existence of a bijection \(\rho _{\alpha }\) such that for all \(\varvec{w}\in \mathbb {Z}_p^{w}\), \(S \varvec{w}= S \cdot \rho _{\alpha }(\varvec{w}) \,\, \wedge \,\, R \varvec{w}+ \alpha \cdot \varvec{k} = R \cdot \rho _{\alpha }(\varvec{w})\). By linearity, it can be rewritten as
Now, the existence of such a bijection is equivalent to the existence of a solution for the following (parametric in \(\alpha \)) linear system on \(\varvec{w}\): \( S \varvec{w}= \varvec{0}_{s} \,\, \wedge \,\, R \varvec{w}= \alpha \cdot \varvec{k} \). To see this, note that if \(\rho _{\alpha }\) is such a bijection, \(\rho _{\alpha }(\varvec{w}_0) - \varvec{w}_0\) is a solution of the system for every \(\varvec{w}_0\in \mathbb {Z}_p^{w}\). On the other hand, if \(\varvec{w}^*\) is a solution of the system, the bijection \(\rho _{\alpha }(\varvec{w}) = \varvec{w}+ \varvec{w}^*\) satisfies the required identities. To conclude, note that the above system has a solution iff the following (independent of \(\alpha \)) does:
Next, we prove the equivalence between algebraic privacy and non-reconstructability. We use the following helping lemma from [12, Claim 2]: for every field \(\mathbb {F}\), let \(A\in \mathbb {F}^{m\times n}\) and \(\varvec{b}\in \mathbb {F}^{n}\) be matrices with coefficients in \(\mathbb {F}\), the following two statements are equivalent:
-
for every \(\varvec{a}\in \mathbb {F}^{m}\), \(\varvec{b}^{\top } \ne \varvec{a}^{\top }A\);
-
there exists \(\varvec{z}\in \mathbb {F}^{n}\) such that \(\varvec{z}^{\top } \varvec{b} = 1\) and \(A \varvec{z} = \varvec{0}_{m}\).
Assume that algebraic privacy does not hold, i.e., for every \(\varvec{w}\in \mathbb {Z}_p^{w}\), either \(S \varvec{w}\ne \varvec{0}_{s}\) or \(R \varvec{w}\ne \varvec{k}\). Equivalently, for every \(\varvec{w}\in \mathbb {Z}_p^{w}\)

which is equivalent (by our helping lemma) to the existence of \((\varvec{z}_1,\varvec{z}_2)\in \mathbb {Z}_p^{s} \times \mathbb {Z}_p^{r}\) such that

That is, there exists \(\varvec{z}_1 \in \mathbb {Z}_p^{s}\), \(\varvec{z}_2 \in \mathbb {Z}_p^{r}\) such that \(\varvec{z}_1^{\top } S = \varvec{z}_2^{\top } R \,\, \wedge \,\, \varvec{z}_2^{\top } \varvec{k} = 1\), which is exactly reconstructability. The proof follows from the fact all the steps are equivalences. \(\square \)
Our next result is a representation theorem. It is based on the notion of partial encoding; informally, a partial encoding consists of the first three algorithms of a predicate encoding; it is not attached to any specific predicate, nor is required to satisfy any property.
Definition 4
(Partial encoding). Let \(\mathcal {X}\) and \(\mathcal {Y}\) be finite sets. Let \(p\in \mathbb {N}\) be a prime and \(s,r,w\in \mathbb {N}\). A (s, r, w)-partial encoding is given by three deterministic algorithms \((\mathsf {sE},\mathsf {rE},\mathsf {kE})\): \(\mathsf {sE}\) maps \(x \in \mathcal {X}\) into a matrix \(\mathsf {sE}_x \in \mathbb {Z}_p^{s \times w}\), and \(\mathsf {rE}\), \(\mathsf {kE}\) map \(y \in \mathcal {Y}\) into a matrix \(\mathsf {rE}_y \in \mathbb {Z}_p^{r \times w}\) and a vector \(\mathsf {kE}_y \in \mathbb {Z}_p^{r}\) respectively.
The representation theorem shows that there exists an embedding from partial encodings to predicate encodings, and that every predicate encoding lies the image of the embedding.
Theorem 2
(Representation theorem). Let \(\mathcal {X}\) and \(\mathcal {Y}\) be finite sets. Let \(p\in \mathbb {N}\) be a prime and \(s,r,w\in \mathbb {N}\). Every (s, r, w)-partial encoding \((\mathsf {sE}, \mathsf {rE}, \mathsf {kE})\) for \(\mathcal {X}\) and \(\mathcal {Y}\) induces a predicate encoding \((\mathsf {sE}, \mathsf {rE}, \mathsf {kE}, \mathsf {sD}, \mathsf {rD})\) for the following predicate (henceforth coined implicit predicate):
Moreover, if \((\mathsf {sE}, \mathsf {rE}, \mathsf {kE}, \mathsf {sD}, \mathsf {rD})\) is a predicate encoding for \(\mathsf {P}\), then for every \((x,y) \in \mathcal {X}\times \mathcal {Y}\), \(\mathsf {P}(x,y) \Leftrightarrow {{\mathrm{\mathsf {Pred}}}}(x,y)\).
Example 2
(Implicit predicate of IBE predicate encoding). If we consider the following partial encoding functions corresponding to the encoding presented in Example 1:

our Theorem 2 guarantees that it is a valid predicate encoding for the implicit predicate:
A simple analysis shows that the above predicate is equivalent to \(x=y\). \(\blacksquare \)
A consequence of Theorem 2 is that a predicate \(\mathsf {P}\) over \(\mathcal {X}\) and \(\mathcal {Y}\) can be instantiated by a (s, r, w)-predicate encoding iff there exist \(\mathcal {X}\)-indexed and \(\mathcal {Y}\)-indexed matrices \(S_x \in \mathbb {Z}_p^{s\times w}\) and \(R_y \in \mathbb {Z}_p^{r\times w}\) and \(\mathcal {Y}\)-indexed vectors \(\varvec{k}_y \in \mathbb {Z}_p^{r}\) such that:

That is helpful to analyze the expressivity of predicate encodings of certain size.
Example 3
Let \(\mathcal {X}\) and \(\mathcal {Y}\) be finite sets, let \(n \in \mathbb {N}\), we will characterize all the predicates that can be achieved from a (1, 1, n)-partial encoding, say \((\mathsf {sE}, \mathsf {rE}, \mathsf {kE})\). Note that for every pair (x, y), \(\mathsf {sE}_x\) and \(\mathsf {rE}_y\) are vectors of length n, while \(\mathsf {kE}_y\) is a single element. Say,
for certain functions \(f_i : \mathcal {X}\rightarrow \mathbb {Z}_p\), \(g_i, h : \mathcal {Y}\rightarrow \mathbb {Z}_p\) for every \(i \in [n]\). Theorem 2 guarantees that the above is a valid predicate encoding for the predicate
It can be shown that the predicate \(\mathsf {P}((x_1,x_2), y) = 1 \text { iff } (x_1 = y) \, \vee \, (x_2 = y)\) cannot be captured by (1, 1, n)-predicate encodings, while on the contrary, the predicate \(\mathsf {P}((x_1,x_2), y) = 1 \text { iff } (x_1 = y) \, \wedge \, (x_2 = y)\) could be instantiated. \(\blacksquare \)
3.2 Optimizing Predicate Encodings
In this section, we show that the efficiency of predicate encodings can be improved by pre- and post-processing. Specifically, we show that an (s, r, w)-encoding \((\mathsf {sE},\mathsf {rE},\mathsf {kE},\mathsf {sD},\mathsf {rD})\) for a predicate \(\mathsf {P}\) can be transformed into a \((s',r',w')\)-encoding \((\mathsf {sE}',\mathsf {rE}',\mathsf {kE}',\mathsf {sD}',\mathsf {rD}')\) for the same predicate, by applying a linear transformation to the matrices induced by \(\mathsf {sE},\mathsf {rE},\mathsf {kE}\).
More precisely, if we define \(\mathsf {sE}'_x = A\mathsf {sE}_x\), \(\mathsf {rE}'_y = B\mathsf {rE}_y\) and \(\mathsf {kE}'_y = B\mathsf {kE}_y\) for two matrices A and B, the privacy of the encoding will be preserved, but reconstructability may be destroyed. On the contrary, when we consider the partial encoding \(\mathsf {sE}'_x = \mathsf {sE}_xC\), \(\mathsf {rE}'_y = \mathsf {rE}_yC\) and \(\mathsf {kE}'_y = \mathsf {kE}_y\) for a matrix C, reconstructability is automatically guaranteed, but privacy could not hold (for the same predicate). Intuitively, this occurs because reconstructability depends on the rowspan of the matrices \(\mathsf {sE}_x, \mathsf {rE}_y\), while privacy depends on their colspan. Our following theorem imposes conditions on these matrices A, B and C so that the resulting predicate encoding is equivalent to the original one.
Theorem 3
Let \(\mathcal {X}\) and \(\mathcal {Y}\) be finite sets. Let \(p\in \mathbb {N}\) be a prime, \(s, r, w, s',\) \(r', w' \in \mathbb {N}\), and let \((\mathsf {sE},\mathsf {rE},\mathsf {kE},\mathsf {sD},\mathsf {rD})\) be a (s, r, w)-predicate encoding for \(\mathsf {P}: \mathcal {X}\times \mathcal {Y}\rightarrow \{0,1\}\). Let \(\mathsf{A}\) be a function that maps every element \(x \in \mathcal {X}\) into a matrix \(\mathsf{A}_x \in \mathbb {Z}_p^{s'\times s}\), \(\mathsf{B}\) be a function that maps \(y \in \mathcal {Y}\) into a matrix \(\mathsf{B}_y \in \mathbb {Z}_p^{r' \times r}\) and let \(\mathsf{C}\in \mathbb {Z}_p^{w \times w'}\) be a matrix. There exists a \((s',r',w')\)-partial encoding \((\mathsf {sE}',\mathsf {rE}',\mathsf {kE}',\mathsf {sD}',\mathsf {rD}')\) for \(\mathsf {P}\), where
provided the following conditions hold:
-
For all \((x,y) \in \mathsf {P}\),
 and
and 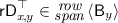 ;
; -
For all \((x,y) \notin \mathsf {P}\), there exists
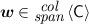 s.t. \(\mathsf {sE}_x\varvec{w}= \varvec{0}_{s}\) and \(\mathsf {rE}_y \varvec{w}= \mathsf {kE}_y\).
s.t. \(\mathsf {sE}_x\varvec{w}= \varvec{0}_{s}\) and \(\mathsf {rE}_y \varvec{w}= \mathsf {kE}_y\).
This transformation is useful to make predicate encodings simpler and more efficient in different manners. For instance, it can be used to make the matrices corresponding to encoding and decoding functions become sparser. That is, if we consider \(\mathsf{A}\) and \(\mathsf{B}\) as functions that apply matrix Gaussian elimination Footnote 4 to the matrices associated to \(\mathsf {sE}\) and \(\mathsf {rE},\mathsf {kE}\), many entries from these matrices will be zero. Hence, fewer group operations will be performed during encryption and key generation, improving the performance. Moreover, the transformation can be used to reduce the size of \(\mathsf{mpk}\), \(\mathsf{ct}_{x}\) and \(\mathsf{sk}_{y}\). If \(w'<w\), the number of elements in \(\mathsf{mpk}\) will decrease. This will also improve the performance of encryption and key generation (both depend directly on \(\mathsf{mpk}\)). Additionally, if \(s'<s\) or \(r'<r\), the number of elements in \(\mathsf{ct}_{x}\) and \(\mathsf{sk}_{y}\) will also decrease respectively.
Note that a simplification from the right (multiplying by \(\mathsf{C}\)) changes the structure of the encoding and may open the possibility of left-simplifications that were not available before and vice versa. Example 4 illustrates this idea. We optimize a predicate encoding that corresponds to the result of applying our negation transformation (from next section, Theorem 6) to the predicate encoding from Example 1.
Example 4
Let \(\mathcal {X}= \mathcal {Y}= \mathbb {Z}_p\) and consider the (2, 3, 4)-predicate encoding \((\mathsf {sE},\mathsf {rE},\mathsf {kE},\mathsf {sD},\mathsf {rD})\) for \(\mathsf {P}(x,y) = 1 \text { iff } x \ne y\), defined as


Note that for every pair \((x,y) \notin \mathsf {P}\), i.e. \(x = y\), the single solution of the system \(\mathsf {sE}_x\varvec{w}= \varvec{0}_2 \, \wedge \, \mathsf {rE}_y\varvec{w}= \mathsf {kE}_y\) is  , thus the matrix
, thus the matrix

satisfies the conditions of Theorem 3. Therefore, the (2, 3, 2)-partial encoding \((\mathsf {sE}', \mathsf {rE}', \mathsf {kE}')\), where

induces a predicate encoding for the same predicate. The previous simplification, opens the possibility of applying again the theorem, with matrices \(\mathsf{A}_x\) and \(\mathsf{B}_y\), obtaining a (1, 2, 2)-predicate encoding for \(\mathsf {P}(x,y) = 1 \text { iff } x \ne y\). Concretely,

\(\blacksquare \)
The above simplifications can be successfully applied to actual predicate encodings proposed in [15]. In Sect. 6.2 we propose improved predicate encodings for monotonic boolean formulas and arithmetic span programs.
3.3 Combining Predicates
Using the new characterization of predicate encodings from the previous section, we define transformations to combine predicate encodings into new predicate encodings for more complex predicates. In particular, we define predicate encoding transformations for disjunction, conjunction, negation and the dual predicate. These combinations are useful to create new schemes that inherit different properties from the more basic building blocks. In Sect. 6, we propose several constructions that rely on these transformations.
Disjunction. We present a method to build a predicate encoding for the disjunction of \(\mathsf {P}_1\) and \(\mathsf {P}_2\) from predicate encodings for \(\mathsf {P}_1\) and \(\mathsf {P}_2\). Observe that the predicate encryption scheme obtained from the resulting predicate encoding is more efficient than the predicate encryption scheme obtained by compiling the predicate encodings of \(\mathsf {P}_1\) and \(\mathsf {P}_2\) separately, and then applying a generic transformation that builds predicate encryption schemes for a disjunction from predicate encryption schemes of its disjuncts.
Theorem 4
(Disjunction of predicate encodings). For every \((s_1,r_1,w_1)\)-predicate encoding \(({\mathsf {sE}}^{1}, {\mathsf {rE}}^{1}, {\mathsf {kE}}^{1}, {\mathsf {sD}}^{1}, {\mathsf {rD}}^{1})\) for \(\mathsf {P}_1:\mathcal {X}_1 \times \mathcal {Y}_1 \rightarrow \{0,1\}\) and every \((s_2,r_2,w_2)\)-predicate encoding \(({\mathsf {sE}}^{2}, {\mathsf {rE}}^{2}, {\mathsf {kE}}^{2}, {\mathsf {sD}}^{2}, {\mathsf {rD}}^{2})\) for \(\mathsf {P}_2:\mathcal {X}_2 \times \mathcal {Y}_2 \rightarrow \{0,1\}\), there exists a \((s_1+s_2,r_1+r_2,w_1+w_2)\)-predicate encoding \((\mathsf {sE},\mathsf {rE},\mathsf {kE},\mathsf {sD},\mathsf {rD})\) for the predicate \(\mathsf {P}: ({\mathcal {X}}_{1}, {\mathcal {X}}_{2}) \times ({\mathcal {Y}}_{1}, {\mathcal {Y}}_{2}) \rightarrow \{0,1\}\) such that:
Concretely,


Note that it is possible to obtain sharing between attributes, e.g., if \({\mathcal {X}}_{1}= {\mathcal {X}}_{2}\) and the sender uses only the subset \(\{ (x,x) \mid x \in {\mathcal {X}}_{1}\}\) of \({\mathcal {X}}_{1}\times {\mathcal {X}}_{2}\), the predicate becomes \(\mathsf {P}(x,({y}_{1},{y}_{2})) = 1 \text { iff } \mathsf {P}_1(x,{y}_{1}) \vee \mathsf {P}_2(x,{y}_{2})\).
Conjunction. In contrast to disjunction, the naive solution that just concatenates secret keys fails. Given keys for attribute pairs \((y_1,y_2)\) and \((y_1',y_2')\), it would be possible to recombine the components and obtain a key for \((y_1,y_2')\) leading to collusion attacks. Our predicate encoding transformation deals with this problem by “tying” the two components together with additional randomness.
Theorem 5
(Conjunction of predicate encodings). For every \((s_1,r_1,w_1)\)-predicate encoding \(({\mathsf {sE}}^{1}, {\mathsf {rE}}^{1}, {\mathsf {kE}}^{1}, {\mathsf {sD}}^{1}, {\mathsf {rD}}^{1})\) for \(\mathsf {P}_1:\mathcal {X}_1 \times \mathcal {Y}_1 \rightarrow \{0,1\}\) and every \((s_2,r_2,w_2)\)-predicate encoding \(({\mathsf {sE}}^{2}, {\mathsf {rE}}^{2}, {\mathsf {kE}}^{2}, {\mathsf {sD}}^{2}, {\mathsf {rD}}^{2})\) for \(\mathsf {P}_2:\mathcal {X}_2 \times \mathcal {Y}_2 \rightarrow \{0,1\}\), there exists a \((s_1+s_2, \,r_1+r_2, \,w_1+w_2+1)\)-predicate encoding \((\mathsf {sE},\mathsf {rE},\mathsf {kE},\mathsf {sD},\mathsf {rD})\) for the predicate \(\mathsf {P}: ({\mathcal {X}}_{1}, {\mathcal {X}}_{2}) \times ({\mathcal {Y}}_{1}, {\mathcal {Y}}_{2}) \rightarrow \{0,1\}\) such that:
Concretely,

Note that it is possible to combine Theorems 4 and 5 to create a predicate encoding for \(\mathsf {P}_1\bowtie \mathsf {P}_2\), where the placeholder \(\bowtie \in \{\vee , \wedge \}\) can be part of keys or ciphertexts.
Negation. To obtain a functionally complete set of boolean predicate encoding transformers, we now define a transformation for negation. Our transformation unifies negated predicates like Non-zero Inner Product Encryption (NIPE) and Zero Inner Product Encryption (ZIPE). In Sect. 6.2 we use this transformation to build optimized predicate encodings. The technique works for predicate encodings where the negation transformation yields a predicate encoding that can be further simplified (using our method from Sect. 3.2).
Theorem 6
(Negation of predicate encodings). For every (s, r, w)-predicate encoding \((\mathsf {sE}, \mathsf {rE}, \mathsf {kE}, \mathsf {sD},\mathsf {rD})\) for \(\mathsf {P}:\mathcal {X}\times \mathcal {Y}\rightarrow \{0,1\}\) there exists a \((w,w+1,s+w+r)\)-predicate encoding \((\mathsf {sE}',\mathsf {rE}',\mathsf {kE}',\mathsf {sD}',\mathsf {rD}')\) for the predicate \(\mathsf {P}': \mathcal {X}\times \mathcal {Y}\rightarrow \{0,1\}\) such that \(\mathsf {P}'(x,y) \Leftrightarrow \lnot \mathsf {P}(x,y)\). Concretely,


where for a pair \((x,y) \in \mathcal {X}\times \mathcal {Y}\) such that \(\mathsf {P}(x,y) = 0\), \(\varvec{w}_{x,y}\) is defined as the witness for algebraic privacy, i.e., a vector such that
Note that such a vector always exists when \(\mathsf {P}(x,y) = 0\). Moreover, \(\mathsf {sD}\) and \(\mathsf {rD}\) do not need to be defined when \(\mathsf {P}'(x,y)\) is not 1, that is, when \(\mathsf {P}(x,y)\) is not 0.
A similar construction has been considered in a posterior work [4] to this work. Specifically, they show how to transform a conditional disclosure of secrets (CDS) for f into a CDS for \(\bar{f}\) (the complement of f).
Dual. In the literature, the notions of KP-ABE and CP-ABE are considered separately. In fact, many works are only valid for one of the two versions of Attribute Based Encryption. Our transformation unifies the notion of KP-ABE and CP-ABE in the framework of predicate encodings. In this context they should not be considered separately, because our transformation provides a Ciphertext-Policy predicate encoding from any Key-Policy predicate encoding and vice versa.
Theorem 7
(Dual predicate encoding). For every (s, r, w)-predicate encoding \((\mathsf {sE}, \mathsf {rE}, \mathsf {kE}, \mathsf {sD},\mathsf {rD})\) for \(\mathsf {P}:\mathcal {X}\times \mathcal {Y}\rightarrow \{0,1\}\) there exists a \((r,s+1,w+1)\)-predicate encoding \((\mathsf {sE}',\mathsf {rE}',\mathsf {kE}',\mathsf {sD}',\mathsf {rD}')\) for the predicate \(\mathsf {P}': \mathcal {Y}\times \mathcal {X}\rightarrow \{0,1\}\) such that \(\mathsf {P}'(y,x) \Leftrightarrow \mathsf {P}(x,y)\). Concretely,
4 Tag-Based Encodings
We show that our techniques for predicate encodings can be extended to the framework of tag-based encodings. In particular, we show a similar result to our Theorem 1, which establishes that \(\varvec{h}\)-hiding and reconstructability are mutually exclusive and complementary.
Theorem 8
Let \(p \in \mathbb {N}\) be a prime, let \(k,c,h\in \mathbb {N}\) and let \(C \in \mathbb {Z}_p^{c\times h}\), \(K \in \mathbb {Z}_p^{k\times h}\). The following are equivalent:
-
\(\varvec{h}\) -hiding: \(\varvec{h} \mathop {\leftarrow }\limits ^{\$}\mathbb {Z}_p^{h};\, \textsf { return } (C \varvec{h},\, K \varvec{h}) \,\, \equiv \,\, \varvec{h}, \varvec{h}' \mathop {\leftarrow }\limits ^{\$}\mathbb {Z}_p^{h};\, \textsf { return } (C \varvec{h},\, K \varvec{h}')\)
-
non-reconstructability For every \(\varvec{m}_c \in \mathbb {Z}_p^{c}\) and very \(\varvec{m}_k \in \mathbb {Z}_p^{k}\), either \(\varvec{m}_c^{\top } C \ne \varvec{m}_k^{\top } K\) or \(\varvec{m}_c^{\top } C = \varvec{0}^{\top }_{h}\).
where \(\equiv \) denotes equality of distributions.
A consequence of Theorem 8 is that every valid tag-based encoding is perfectly hiding, or equivalently, there cannot exist a tag-based encoding where the two distributions from \(\varvec{h}\)-hiding are negligibly close but not identical.
Thanks to the above theorem, it is possible to define disjunction and conjunction transformations for tag-based encodings along the lines of predicate encodings. We were not able to design a negation transformation for tag-based encodings and leave it for future work. On the other hand, the dual transformation is straightforward in this framework, as mentioned in [22], because the encoding primitives are completely symmetric.
Expressivity of Tag-Based Encodings vs Predicate Encodings. We propose a transformation that produces valid predicate encodings from valid tag-based encodings for the same predicate.
Theorem 9
Given a (c, 1, h)-tag-based encoding \((\mathsf {cE},\mathsf {kE})\) for \(\mathsf {P}: \mathcal {X}\times \mathcal {Y}\rightarrow \{0,1\}\), the (c, 1, h)-partial predicate encoding \((\mathsf {sE}',\mathsf {rE}',\mathsf {kE}')\) defined as \(\mathsf {sE}'_x = \mathsf {cE}_x\), \(\mathsf {rE}'_y = \mathsf {kE}_y\), \(\mathsf {kE}'_y = \left( \begin{array}{c} 1 \end{array} \right) \), induces a predicate encoding for \(\mathsf {P}\).
Note that because of the symmetry of tag-based encodings, Theorem 9 can be also applied to (1, k, h)-tag-based encodings. All the tag-based encodings proposed in [22] (except one) have either \(c = 1\) or \(k = 1\), so the above theorem can be applied to them.
5 Pair Encodings
In this section we provide an embedding that transforms every predicate encoding into an information-theoretic pair encoding. Consequently, we can see predicate encodings as a subclass of pair encodings. This opens the possibility of reusing the conjunction and dual transformation proposed by Attrapadung [9, 10] for pair encodings, to create combinations of predicate encodings via our embedding. We show that this alternative method is fundamentally different from our direct conjunction and dual transformations on predicate encodings, where our combinations produce more efficient encodings.
5.1 Embedding Predicate Encodings into Pair Encodings
In this section we provide an embedding that produces a valid information-theoretic pair encoding from every valid predicate encoding (see Definitions 1 and 3 for predicate encodings and pair encodings respectively).
Definition 5
(Embedding to Pair Encodings). Given a (s, r, w)-predicate encoding \(pe = (\mathsf {sE},\mathsf {rE},\mathsf {kE},\mathsf {sD},\mathsf {rD})\), we define the embedding \(\mathsf{Emb}(pe) = (\mathsf{Enc1}_{pe},\) \( \mathsf{Enc2}_{pe} ,\mathsf{Pair}_{pe})\) as follows:
-
\(\mathsf{Enc1}_{pe}(x) = (c_0, \varvec{c})\), where \(c_0(s_0,\varvec{h}) = s_0, \,\varvec{c}(s_0,\varvec{h}) = s_0\cdot \mathsf {sE}_{x}\varvec{h}\)
-
\(\mathsf{Enc2}_{pe}(y) = (k_0, \varvec{k})\), where \(k_0(\alpha ,r_1,\varvec{h}) = r_1, \, \varvec{k}(\alpha ,r_1,\varvec{h}) = \alpha \cdot \mathsf {kE}_{y} + r_1\cdot \mathsf {rE}_{y}\varvec{h}\)
-
\(\mathsf{Pair}_{pe}(x,y) = \)

All variables \(\varvec{s} = (s_0)\) and \(\varvec{r} = (r_1)\) appear in the clear in the \(\mathsf{Enc1}\) and \(\mathsf{Enc2}\) polynomials respectively. This simplifies the pair encoding’s information-theoretical security notion into one equivalent to the privacy of the predicate encoding (see proof of Theorem 10).
Theorem 10
(Correctness of the embedding). If \(pe = (\mathsf {sE},\mathsf {rE},\mathsf {kE},\mathsf {sD},\mathsf {rD})\) is a valid (s, r, w)-predicate encoding for \(\mathsf {P}\), then \(\mathsf{Emb}(pe)\) is a valid information theoretic \((s+1,\, r+1,\,w)\)-pair encoding for \(\mathsf {P}\).
Our embedding shows that every predicate encoding can be transformed into a perfectly secure pair encoding. In fact, after applying the compiler from [1] to the embedding of a predicate encoding, we get the same predicate encryption scheme that the one provided by the compiler from [15].
We conclude that predicate encodings can be transformed into a very special class of pair encodings: encodings that allow decryption with 2 pairings and have only one element of randomness in both, ciphertexts and secret keys (what makes them very efficient).
5.2 Comparison Between Encoding Transformations
Attrapadung proposed generic transformations of pair encodings [9, 10]. In particular, he proposed the conjunction and dual transformations. In this section we compare these transformations with the ones proposed in this work. For this, we compare the conjunction of two pair encodings, (embedded from predicate encodings) with the embedding of the conjunction of a \((s_1,r_1,w_1)\)-predicate encoding \(pe^{1} = ({\mathsf {sD}}^{1},{\mathsf {rE}}^{1},{\mathsf {kE}}^{1},{\mathsf {sD}}^{1},{\mathsf {rD}}^{1})\) and a \((s_2,r_2,w_2)\)-predicate encoding \(pe^{2} = ({\mathsf {sD}}^{2},{\mathsf {rE}}^{2},{\mathsf {kE}}^{2},{\mathsf {sD}}^{2},{\mathsf {rD}}^{2})\), i.e.,
where \(\wedge _{pred}\) and \(\wedge _{pair}\) are the conjunction of predicate encodings and pair encodings respectively. Note that \(\wedge _{pred}\) corresponds to the transformation from our Theorem 5. On the other hand, for \(\wedge _{pair}\) we use the conjunction proposed in [10].
where \(\varvec{h} = (h_0, \varvec{h}_1, \varvec{h}_2)\) and

where \(\varvec{h} = (\varvec{h}_1, \varvec{h}_2)\) and

The resulting pair encodings are different. The first one (result of our conjunction) does not introduce new random variables and does not increase the number of pairings for decryption. On the other hand, the second conjunction adds new random variables to key generation and increases the number of pairings needed during decryption. This overhead will be amplified if nested conjunctions are used. We include a detailed comparison between the dual transformations in the full version of this paper.
6 Constructions
We provide new instances of predicate encodings to achieve predicate encryption schemes with new properties or better performance.
6.1 Combining Predicates
Dual-Policy ABE. Dual-Policy Attribute Based Encryption [9, 10] has already been considered in the pair encodings framework. It combines KP-ABE and CP-ABE into a single construction that simultaneously allows two access control mechanisms. The main advantage is the possibility of considering policies over objective attributes (associated to data) and policies over subjective attributes (associated to user credentials) at the same time.
Our combinations of predicate encodings allow us to create predicate encryption constructions for Dual-Policy ABE in the framework of pair encodings and tag-based encodings. In particular, given an arbitrary predicate encoding for \(\mathsf {P}: \mathcal {X}\times \mathcal {Y}\rightarrow \{0,1\}\), applying Theorems 7 and 5 we get an encoding for DP-ABE, i.e., for the predicate \(\mathsf {P}^{\star } : (\mathcal {X}\times \mathcal {Y}) \times (\mathcal {Y}\times \mathcal {X}) \rightarrow \{0,1\}\) defined as
Revocation. Another application of our combinations is predicate encryption with revocation, by combining a boolean formula predicate encoding with a broadcast encryption predicate encoding. The former is used to encode the actual policy of the scheme, while the latter takes care of revocation.
Broadcast encryption has been considered in the literature to approach revocation [19, 23, 30]. In broadcast encryption, a broadcasting authority encrypts a message in such a way that only authorized users will be able to decrypt it. This can be expressed with the predicate \( \mathsf {P}(\varvec{x},i) = 1 \text { if and only if } \varvec{x}_i = 1\), where \(\varvec{x} \in \mathcal {X}= \{0,1\}^{n}\) and \(i \in \mathcal {Y}= [n]\). A drawback is that the number of users in the system, n, is polynomial size. Figure 1 shows the performance of predicate encryption built from a predicate encoding that combines boolean formulas with broadcast encryption. The system supports thousands of users in reasonable time.
6.2 Improved Predicate Encodings
In this section we propose new predicate encodings that are more efficient than some of the encodings proposed previously in [15]. Our encodings are built by applying Theorem 6 to obtain negated encodings and observing that, in some cases, Theorem 3 can be applied to simplify the negated version into a more efficient encoding than the original one. The predicate associated to this new encoding is negated, but if inputs are also negated, the predicate will be equivalent. Figure 2 illustrates this idea. On the left, there is a boolean formula CP-ABE for 4 attributes \(\{a,b,c,d\}\). On the right side, secret keys and policies are modified so that the negated version is equivalent. The attribute universe is formed by the negated attributes, secret keys are formed by all negated attributes do not appear in the original key as normal attributes, policies are negated and expressed in NNF (Negation Normal Form).
Boolean Formulas. In [15], the authors propose two predicate encoding (KP and CP versions) for monotonic boolean formulas. The predicate they consider is a particular case of a Linear Secret Sharing scheme [24]. Let \(\mathcal {X}=\{0,1\}^{n}, \mathcal {Y}=\mathbb {Z}_p^{n\times k}\) for some \(n,k \in \mathbb {N}\),

where \(M_{\varvec{x}}\) denotes the matrix M filtered by \(\varvec{x}\), i.e., \(M_{\varvec{x}}\) includes the i-th row of M iff \(\varvec{x}_i = 1\).
It has been shown [28] that for everyFootnote 5 monotonic boolean formula f with attributes from \(\mathcal {X}\) there exists a matrix \(M \in \mathcal {Y}\) such that for every \(\varvec{x} \in \mathcal {X}\), \(f(\varvec{x}) \Leftrightarrow \mathsf {P}(\varvec{x},M)\). The key-policy predicate encoding from [15] is the following,

where \(M_{\{1\}}\) denotes the first column of matrix M, \(M_{\{2,\dots ,k\}}\) represents the rest of the matrix. We do not include explicit decryption functions \(\mathsf {sD}\) and \(\mathsf {rD}\), but they can be computed efficiently by Gaussian elimination.
In the above encoding, the number of elements in secret keys and ciphertexts is always maximal, it equals the number of (possibly duplicated) attributes, even for small policies. Furthermore, the maximum number of and-gates in a policy must be fixed a priori (because it is related the number of columns in the matrix).
We propose the following improved predicate encoding for (negated) key-policy monotonic boolean formulas, which is an equivalent predicate if instantiated with negated inputs. Let \(\mathcal {X}= \{0,1\}^{n}\) and \(\mathcal {Y}= \mathbb {Z}_p^{n \times k}\),

In our encoding, the number of columns has been reduced up to halfFootnote 6. Furthermore, the size of secret keys is proportional to the complexity of policies. In particular, it is equal to the number of and-gates in the policy (or equivalently, the number of or-gates in the non-negated version). Note that our improvement also works in the ciphertext-policy case.
In Fig. 3 we present a comparison between our improved encoding for key-policy monotonic boolean formulas and the original one. To this end, we generate random boolean formulas for different sizes, starting from a random set of leaf nodes and combining them with boolean operators \(\vee \) and \(\wedge \). Our tables report on the average time for each algorithm. Our encoding needs 50% less time than the original algorithms for setup, encryption and key generation. For decryption the performance is similar. All the analyzed schemes were instantiated with the same compiler, therefore all achieve the same level of security (under SXDH assumption). In terms of secret key size, our encoding is smaller in general (in the worst case, when all the gates in the policy are or-gates, key sizes are equal).
Arithmetic Span Programs. Chen et al. proposed in [15] a predicate encoding for Arithmetic Span Programs (ASP). That is, an encoding for the predicate \(\mathsf {P}\) defined as follows. Let \(\mathcal {X}= \mathbb {Z}_p^{n}\), \(\mathcal {Y}= \mathbb {Z}_p^{n \times k} \times \mathbb {Z}_p^{n \times k}\), for some \(n,k \in \mathbb {N}\); for every \(\varvec{x} \in \mathcal {X}\) and every \((Y,Z) \in \mathcal {Y}\),

In [21], Ishai and Wee show how to relate Arithmetic Span Programs computations of polynomial functions over a finite field \(\mathbb {F}\), i.e., functions \(f:\mathbb {F}^{n} \rightarrow \mathbb {F}\) that only use addition and multiplication over the field. Therefore, the above predicate can be seen as \(f(\varvec{x}) = 0\), where f is the polynomial function induced by (Y, Z). Let \(\mathcal {X}= \mathbb {Z}_p^n\), \(\mathcal {Y}= \mathbb {Z}_p^{n \times k} \times \mathbb {Z}_p^{n \times k}\), the original predicate encoding for arithmetic span programs proposed in [15] is the following:

We present a more efficient encoding for (negatedFootnote 7) arithmetic span programs:

Figure 4 shows the performance of our new encoding for KP-ABE for Arithmetic Span Programs compared to the original encoding from [15]. As we expected, our encoding needs 66% of the time required for the original encoding for setup, encryption and key generation. Additionally, secret key size is halved with our encoding.
6.3 Extra Features
In this section we consider new theoretical results that can be proved thanks to our algebraic characterization of \(\alpha \)-privacy and can be used to produce new predicate encodings enhanced with extra properties.
Attribute-Hiding for Boolean Formulas. Chen et al. proposed an extension of the compiler in [15] to build weakly attribute-hiding predicate encryption schemes [13, 25]. In a weakly attribute-hiding scheme, the ciphertext attribute x remains secret for unauthorized users, that only learn the fact that their secret keys are not valid. This additional compiler needs to be instantiated with predicate encodings satisfying additional properties. The following is a definition from [15].
Definition 6
(Attribute-Hiding Encodings). A (s, r, w)-predicate encoding, \((\mathsf {sE}, \mathsf {rE}, \mathsf {kE}, \mathsf {sD}, \mathsf {rD})\) for \(\mathsf {P}: \mathcal {X}\times \mathcal {Y}\rightarrow \{0,1\}\) is attribute-hiding if it verifies the additional requirements:
-
x -oblivious reconstruction: \(\mathsf {sD}_{x,y}\) and \(\mathsf {rD}_{x,y}\) are independent of x.
-
attribute-hiding: for all \((x,y) \notin \mathsf {P}\),
$$\begin{aligned} \varvec{w}\mathop {\leftarrow }\limits ^{\$}\mathbb {Z}_p^{w};\, \textsf {return } (\mathsf {sE}_x \varvec{w},\, \mathsf {rE}_y \varvec{w}) \quad \equiv \quad \varvec{s} \mathop {\leftarrow }\limits ^{\$}\mathbb {Z}_p^{s}; \varvec{r} \mathop {\leftarrow }\limits ^{\$}\mathbb {Z}_p^{r};\, \textsf {return } (\varvec{s}, \, \varvec{r}) \end{aligned}$$where \(\equiv \) denotes equality of distributions.
The following theorem relates the second property with our alternative definition of predicate encodings:
Theorem 11
(Algebraic characterization of attribute-hiding). Let \(p\in \mathbb {N}\) be a prime, let \(s, r, w \in \mathbb {N}\) and let \(S \in \mathbb {Z}_p^{s \times w}\), \(R \in \mathbb {Z}_p^{r \times w}\), \(\varvec{k} \in \mathbb {Z}_p^{r}\). The following are equivalent:
-
\(\varvec{w}\mathop {\leftarrow }\limits ^{\$}\mathbb {Z}_p^{w};\, \textsf {return } (S \varvec{w},\, R \varvec{w}) \,\, \equiv \,\, \varvec{s} \mathop {\leftarrow }\limits ^{\$}\mathbb {Z}_p^{s};\, \varvec{r} \mathop {\leftarrow }\limits ^{\$}\mathbb {Z}_p^{r};\, \textsf {return } (\varvec{s}, \, \varvec{r})\)
-
\(\mathrm{rank}{\left( \begin{array}{c} S \\ R \end{array} \right) } = s + r\)
Note that for every (s, r, w)-predicate encoding \((\mathsf {sE}, \mathsf {rE}, \mathsf {kE}, \mathsf {sD}, \mathsf {rD})\) that is attribute-hiding, there exists an equivalent (s, 1, w)-predicate encoding. This is because \(\mathsf {rD}\) is independent from x and thus, we can apply our optimization Theorem 3 with matrices \(\mathsf{B}_y = \mathsf {rD}_{x,y}^{\top } \in \mathbb {Z}_p^{1 \times w}\), \(\mathsf{A}_x = I_{s}\), \(\mathsf{C}= I_{w}\). Therefore, the class of predicates that can be built from attribute-hiding encodings is included in the class of predicates achieved from (s, 1, w)-predicate encodings.
Further, note that our disjunction and conjunction combinations for predicate encodings (Theorems 4 and 5 respectively) preserve the notion of attribute-hidingFootnote 8. Exploiting this fact, we propose a Policy-Hiding ABE scheme for non-monotonic boolean formulas expressed in DNF (Disjunctive Normal Form). The inner product can be used to encode conjunctions [25]. More concretely, let \(\varvec{y} \in \{0,1\}^{n} \subseteq \mathbb {Z}_p^{n}\). We establish that the i-th attribute \(a_i\) appears in a secret key for \(\varvec{y}\) iff \(\varvec{y}_i=1\). Let \(S,\bar{S} \subseteq \{a_i\}_{i=1}^{n}\) be sets such that \(S\cap \bar{S} = \emptyset \),Footnote 9

Note that the ZIPE predicate encoding from [15, Appendix A.1] can be modified into an attribute-hiding encoding for the predicate \(\mathsf {P}((\varvec{x},\gamma ),\varvec{y}) = 1 \text { iff } \varvec{x}^{\top }\varvec{y} = \gamma \).
Therefore, with a disjunction of k predicate encodings like the former we can encode boolean formulas that have at most k disjuncts. Note that the resulting encoding is attribute-hiding but it is not x-oblivious. However, without the knowledge of the policy x, one can guess for the disjunct his secret key satisfies (if any). In this way, a valid key will be enough to decrypt after at most k decryption tries (one for every disjunct).
Delegation. Delegation of keys is a desirable property for every predicate encryption scheme. Roughly, it allows the owner of a secret key to weaken his key creating a new one that is less powerful than the original one. This property can be used to achieve forward secrecy (see [14] for an application to ABE that supports delegation), where past sessions are protected from the compromise of future secret keys. More formally, we say that a predicate \(\mathsf {P}: \mathcal {X}\times \mathcal {Y}\rightarrow \{0,1\}\) supports delegation if there is a partial ordering \(\preceq \) on \(\mathcal {Y}\) such that for every \(x\in \mathcal {X}\), if \(\mathsf {P}(x,y) = 1\) and \((y\preceq y')\), then \(\mathsf {P}(x,y') = 1\).
Delegation has been considered in [15] as the property of some predicate encodings. We propose a generic method to convert any predicate encoding into one supporting delegation.
Theorem 12
(Delegation). For every (s, r, w)-predicate encoding \((\mathsf {sE}, \mathsf {rE}\), \(\mathsf {kE},\) \(\mathsf {sD},\) \(\mathsf {rD})\) for \(\mathsf {P}:\mathcal {X}\times \mathcal {Y}\rightarrow \{0,1\}\), for every \(k \in \mathbb {N}\), \((\mathsf {sE}',\mathsf {rE}',\mathsf {kE}',\mathsf {sD}',\mathsf {rD}')\) defined below is a valid \((s, r+k, w+k)\)-predicate encoding for \(\mathsf {P}\).

The additional set of not-null rows in \(\mathsf {rE}'_y\) can be used to weaken the linear span of \(\mathsf {rE}_y\), what directly modifies the predicate. In particular, this method works really well for monotonic boolean formulas (see Fig. 5 for an example).
Notes
- 1.
This transformation has side conditions, thus it is not universal, but all existing tag-based encodings (except one) satisfy these side conditions.
- 2.
Source code at https://github.com/miguel-ambrona/abe-relic.
- 3.
Decryption in the framework of predicate encodings needs 4 pairings under SXDH assumption or 6 under DLIN, in the framework of tag-based encodings decryption requires 8 pairings and the assumption is DLIN.
- 4.
Note that if matrices \(\mathsf{A}_x\), \(\mathsf{B}_y\) or \(\mathsf{C}\) are invertible, they always satisfy their respective requirements.
- 5.
Where every attribute appears at most once and the number of and-gates is lower than k (one could overcome the one-use restriction by considering duplicated attributes).
- 6.
Being half when the bound on the number of and-gates is maximal.
- 7.
In [21] there is a modification of their algorithm that produces matrices (Y, Z) such that the predicate associated is \(f(\varvec{x}) \ne 0\) (the double negation will cancel out).
- 8.
Conjunction also preserves x-oblivious reconstruction, while disjunction does not.
- 9.
This equivalence holds when \(|S| < p\), but in practice p is a large prime.
- 10.
Note that \(\alpha \mathop {\leftarrow }\limits ^{\$}\mathbb {Z}_p\), \(r_1 \mathop {\leftarrow }\limits ^{\$}\mathbb {Z}_p^*\) and therefore, \(\alpha /r_1\) distributes uniformly over \(\mathbb {Z}_p\), so we can apply the \(\alpha \)-privacy property from the predicate encoding.
References
Agrawal, S., Chase, M.: A study of pair encodings: predicate encryption in prime order groups. In: Kushilevitz, E., Malkin, T. (eds.) TCC 2016. LNCS, vol. 9563, pp. 259–288. Springer, Heidelberg (2016). doi:10.1007/978-3-662-49099-0_10
Agrawal, S., Chase, M.: Simplifying design and analysis of complex predicate encryption schemes. Cryptology ePrint Archive, Report 2017/233 (2017). EUROCRYPT (2017)
Akinyele, J.A., Lehmann, C.U., Green, M.D., Pagano, M.W., Peterson, Z.N.J., Rubin, A.D.: Self-protecting electronic medical records using attribute-based encryption. Cryptology ePrint Archive, Report 2010/565 (2010). http://eprint.iacr.org/2010/565
Applebaum, B., Arkis, B., Raykov, P., Vasudevan, P.N.: Conditional disclosure of secrets: amplification, closure, amortization, lower-bounds, and separations. In: Electronic Colloquium on Computational Complexity (ECCC), vol. 24, p. 38 (2017)
Aranha, D.F., Gouvêa, C.P.L.: RELIC is an Efficient LIbrary for Cryptography. https://github.com/relic-toolkit/relic
Attrapadung, N.: Dual system encryption via doubly selective security: framework, fully secure functional encryption for regular languages, and more. In: Nguyen, P.Q., Oswald, E. (eds.) EUROCRYPT 2014. LNCS, vol. 8441, pp. 557–577. Springer, Heidelberg (2014). doi:10.1007/978-3-642-55220-5_31
Attrapadung, N.: Dual system encryption framework in prime-order groups. Cryptology ePrint Archive, Report 2015/390 (2015). http://eprint.iacr.org/2015/390
Attrapadung, N., Imai, H.: Conjunctive broadcast and attribute-based encryption. In: Shacham, H., Waters, B. (eds.) Pairing 2009. LNCS, vol. 5671, pp. 248–265. Springer, Heidelberg (2009). doi:10.1007/978-3-642-03298-1_16
Attrapadung, N., Imai, H.: Dual-policy attribute based encryption. In: Abdalla, M., Pointcheval, D., Fouque, P.-A., Vergnaud, D. (eds.) ACNS 2009. LNCS, vol. 5536, pp. 168–185. Springer, Heidelberg (2009). doi:10.1007/978-3-642-01957-9_11
Attrapadung, N., Yamada, S.: Duality in ABE: converting attribute based encryption for dual predicate and dual policy via computational encodings. Cryptology ePrint Archive, Report 2015/157 (2015). http://eprint.iacr.org/2015/157
Barreto, P.S.L.M., Naehrig, M.: Pairing-friendly elliptic curves of prime order. Cryptology ePrint Archive, Report 2005/133 (2005). http://eprint.iacr.org/2005/133
Beimel, A.: Secret-sharing schemes: a survey. In: Chee, Y.M., Guo, Z., Ling, S., Shao, F., Tang, Y., Wang, H., Xing, C. (eds.) IWCC 2011. LNCS, vol. 6639, pp. 11–46. Springer, Heidelberg (2011). doi:10.1007/978-3-642-20901-7_2
Boneh, D., Waters, B.: Conjunctive, subset, and range queries on encrypted data. In: Vadhan, S.P. (ed.) TCC 2007. LNCS, vol. 4392, pp. 535–554. Springer, Heidelberg (2007). doi:10.1007/978-3-540-70936-7_29
Canetti, R., Halevi, S., Katz, J.: A forward-secure public-key encryption scheme. J. Cryptol. 20(3), 265–294 (2007)
Chen, J., Gay, R., Wee, H.: Improved dual system ABE in prime-order groups via predicate encodings. In: Oswald, E., Fischlin, M. (eds.) EUROCRYPT 2015. LNCS, vol. 9057, pp. 595–624. Springer, Heidelberg (2015). doi:10.1007/978-3-662-46803-6_20
Chen, J., Wee, H.: Fully, (almost) tightly secure IBE and dual system groups. In: Canetti, R., Garay, J.A. (eds.) CRYPTO 2013. LNCS, vol. 8043, pp. 435–460. Springer, Heidelberg (2013). doi:10.1007/978-3-642-40084-1_25
Chen, J., Wee, H.: Dual system groups and its applications – compact hibe and more. Cryptology ePrint Archive, Report 2014/265 (2014). http://eprint.iacr.org/2014/265
Dinh, T.T.A., Datta, A.: Streamforce: outsourcing access control enforcement for stream data to the clouds. In: Fourth ACM Conference on Data and Application Security and Privacy, CODASPY 2014, San Antonio, TX, USA, 03–05 March 2014, pp. 13–24 (2014)
Garg, S., Kumarasubramanian, A., Sahai, A., Waters, B.: Building efficient fully collusion-resilient traitor tracing and revocation schemes. In: Al-Shaer, E., Keromytis, A.D., Shmatikov, V. (eds.) ACM CCS 10, pp. 121–130. ACM Press, October 2010
Gay, R., Kerenidis, I., Wee, H.: Communication complexity of conditional disclosure of secrets and attribute-based encryption. In: Gennaro, R., Robshaw, M. (eds.) CRYPTO 2015. LNCS, vol. 9216, pp. 485–502. Springer, Heidelberg (2015). doi:10.1007/978-3-662-48000-7_24
Ishai, Y., Wee, H.: Partial garbling schemes and their applications. In: Esparza, J., Fraigniaud, P., Husfeldt, T., Koutsoupias, E. (eds.) ICALP 2014. LNCS, vol. 8572, pp. 650–662. Springer, Heidelberg (2014). doi:10.1007/978-3-662-43948-7_54
Guo, F., Kim, J., Susilo, W., Au, M.H.: A tag based encoding: an efficient encoding for predicate encoding in prime order groups. Cryptology ePrint Archive, Report 2016/655 (2016). http://eprint.iacr.org/2016/655
Junod, P., Karlov, A.: An efficient public-key attribute-based broadcast encryption scheme allowing arbitrary access policies. In: Proceedings of the Tenth Annual ACM Workshop on Digital Rights Management, DRM 2010, pp. 13–24. ACM, New York (2010)
Karchmer, M., Wigderson, A.: On span programs. In: Proceedings of the 8th IEEE Structure in Complexity Theory, pp. 102–111. IEEE Computer Society Press (1993)
Katz, J., Sahai, A., Waters, B.: Predicate encryption supporting disjunctions, polynomial equations, and inner products. In: Smart, N. (ed.) EUROCRYPT 2008. LNCS, vol. 4965, pp. 146–162. Springer, Heidelberg (2008). doi:10.1007/978-3-540-78967-3_9
Lewko, A.B.: Tools for simulating features of composite order bilinear groups in the prime order setting. In: Pointcheval, D., Johansson, T. (eds.) EUROCRYPT 2012. LNCS, vol. 7237, pp. 318–335. Springer, Heidelberg (2012). doi:10.1007/978-3-642-29011-4_20
Lewko, A.B., Waters, B.: New techniques for dual system encryption and fully secure HIBE with short ciphertexts. In: Micciancio, D. (ed.) TCC 2010. LNCS, vol. 5978, pp. 455–479. Springer, Heidelberg (2010). doi:10.1007/978-3-642-11799-2_27
Lewko, A.B., Waters, B.: Decentralizing attribute-based encryption. In: Paterson, K.G. (ed.) EUROCRYPT 2011. LNCS, vol. 6632, pp. 568–588. Springer, Heidelberg (2011). doi:10.1007/978-3-642-20465-4_31
Lewko, A.B., Waters, B.: New proof methods for attribute-based encryption: achieving full security through selective techniques. In: Safavi-Naini, R., Canetti, R. (eds.) CRYPTO 2012. LNCS, vol. 7417, pp. 180–198. Springer, Heidelberg (2012). doi:10.1007/978-3-642-32009-5_12
Liu, Z., Wong, D.S.: Practical ciphertext-policy attribute-based encryption: traitor tracing, revocation, and large universe. In: Malkin, T., Kolesnikov, V., Lewko, A.B., Polychronakis, M. (eds.) ACNS 2015. LNCS, vol. 9092, pp. 127–146. Springer, Cham (2015). doi:10.1007/978-3-319-28166-7_7
Lubicz, D., Sirvent, T.: Attribute-based broadcast encryption scheme made efficient. In: Vaudenay, S. (ed.) AFRICACRYPT 2008. LNCS, vol. 5023, pp. 325–342. Springer, Heidelberg (2008). doi:10.1007/978-3-540-68164-9_22
Sahai, A., Seyalioglu, H., Waters, B.: Dynamic credentials and ciphertext delegation for attribute-based encryption. In: Safavi-Naini, R., Canetti, R. (eds.) CRYPTO 2012. LNCS, vol. 7417, pp. 199–217. Springer, Heidelberg (2012). doi:10.1007/978-3-642-32009-5_13
Sahai, A., Waters, B.: Fuzzy identity-based encryption. In: Cramer, R. (ed.) EUROCRYPT 2005. LNCS, vol. 3494, pp. 457–473. Springer, Heidelberg (2005). doi:10.1007/11426639_27
Shamir, A.: Identity-based cryptosystems and signature schemes. In: Blakley, G.R., Chaum, D. (eds.) CRYPTO 1984. LNCS, vol. 196, pp. 47–53. Springer, Heidelberg (1985). doi:10.1007/3-540-39568-7_5
Wang, F., Mickens, J., Zeldovich, N., Vaikuntanathan, V.: Sieve: cryptographically enforced access control for user data in untrusted clouds. In: 13th USENIX Symposium on Networked Systems Design and Implementation (NSDI 16), pp. 611–626, Santa Clara, CA. USENIX Association, March 2016
Waters, B.: Dual system encryption: realizing fully secure IBE and HIBE under simple assumptions. In: Halevi, S. (ed.) CRYPTO 2009. LNCS, vol. 5677, pp. 619–636. Springer, Heidelberg (2009). doi:10.1007/978-3-642-03356-8_36
Wee, H.: Dual system encryption via predicate encodings. In: Lindell, Y. (ed.) TCC 2014. LNCS, vol. 8349, pp. 616–637. Springer, Heidelberg (2014). doi:10.1007/978-3-642-54242-8_26
Acknowledgements
The work presented here was supported by projects S2013/ICE-2731 N-GREENS Software-CM, ONR Grants N000141210914 and N000141512750.
Author information
Authors and Affiliations
Corresponding author
Editor information
Editors and Affiliations
A Proofs from Main Body
A Proofs from Main Body
Proof
(Of Theorem 2 ). The proof follows from Theorem 1 and the observation that reconstructability of predicate encodings is equivalent to \({{\mathrm{\mathsf {Pred}}}}\), while privacy of predicate encodings is equivalent to \(\lnot {{\mathrm{\mathsf {Pred}}}}\). \(\square \)
Proof
(Of Theorem 3 ). To see correctness of the new encoding, note that for all \((x,y)\in \mathsf {P}\), since

there exist \({\mathsf {sD}'}_{x,y}^{\top }\) and \({\mathsf {rD}'}_{x,y}^{\top }\) such that
Therefore,
To see privacy, note that for every \((x,y) \notin \mathsf {P}\), there exists  such that \(\mathsf {sE}_x\varvec{w}= \varvec{0}_{s} \, \wedge \, \mathsf {rE}_y \varvec{w}= \mathsf {kE}_y\). Therefore, there also exists \(\varvec{w}' \in \mathbb {Z}_p^{w'}\) such that \(\varvec{w}= \mathsf{C}\varvec{w}'\). Note that,
such that \(\mathsf {sE}_x\varvec{w}= \varvec{0}_{s} \, \wedge \, \mathsf {rE}_y \varvec{w}= \mathsf {kE}_y\). Therefore, there also exists \(\varvec{w}' \in \mathbb {Z}_p^{w'}\) such that \(\varvec{w}= \mathsf{C}\varvec{w}'\). Note that,
so algebraic privacy is satisfied. \(\square \)
Proof
(Of Theorem 4 ). Reconstructability can be seen by a simple check based on the reconstructability of the original encodings.
To see privacy, note that \(\mathsf {P}_1({x}_{1},{y}_{1}) \, \vee \, \mathsf {P}_2({x}_{2},{y}_{2}) = 0\) implies \(\mathsf {P}_1({x}_{1},{y}_{1}) = 0\) and \(\mathsf {P}_2({x}_{2},{y}_{2}) = 0\) implies. Let \(\varvec{w}_1\) and \(\varvec{w}_2\) be witnesses of privacy of predicate encodings 1 and 2 respectively. It is easy to check that \(\varvec{w}^{\top } = \left( \begin{array}{cc} \varvec{w}_1^{\top }&\,\, \varvec{w}_2^{\top } \end{array} \right) \) is a witness of privacy of the transformed encoding. \(\square \)
Proof
(Of Theorem 5
). A simple check shows reconstructability. To see privacy, \(\mathsf {P}_1({x}_{1},{y}_{1}) \, \wedge \, \mathsf {P}_2({x}_{2},{y}_{2}) = 0\) implies \(\mathsf {P}_1({x}_{1},{y}_{1}) = 0\) or \(\mathsf {P}_2({x}_{2},{y}_{2}) = 0\). If the first holds, let \(\varvec{w}_1\) be a witness of privacy of the first encoding. Then,  is a witness of the algebraic privacy of the transformed encoding. If the second holds, let \(\varvec{w}_2\) be a witness of privacy of the second encoding. A valid witness now is \(\varvec{w}^{\top } = \left( \begin{array}{ccc} \varvec{0}_{w_2}^{\top }&\,\, 2\varvec{w}_2^{\top }&\,\, 1 \end{array} \right) \). \(\square \)
is a witness of the algebraic privacy of the transformed encoding. If the second holds, let \(\varvec{w}_2\) be a witness of privacy of the second encoding. A valid witness now is \(\varvec{w}^{\top } = \left( \begin{array}{ccc} \varvec{0}_{w_2}^{\top }&\,\, 2\varvec{w}_2^{\top }&\,\, 1 \end{array} \right) \). \(\square \)
Proof
(Of Theorem 6
). It is not difficult to check reconstructability. Privacy holds because when \(\mathsf {P}(x,y) = 1\), we can define  which can be checked to be a witness of the algebraic privacy of the transformed predicate encoding. \(\square \)
which can be checked to be a witness of the algebraic privacy of the transformed predicate encoding. \(\square \)
Proof
(Of Theorem 7
). A simple check is enough to verify reconstructability. For privacy, note that when \(\mathsf {P}'(y,x) = 0\), we have \(\mathsf {P}(x,y) = 0\). Let \(\varvec{w}\) be a witness of the algebraic privacy of the original encoding. Now,  is a witness of the dual predicate encoding. \(\square \)
is a witness of the dual predicate encoding. \(\square \)
Proof
(Of Theorem 8 ). The proof follows directly from the following lemma and the observation that (i) is equivalent to \(\varvec{h}\)-hiding, while (iii) is non-reconstructability (take \(A = C\) and \(B = K\)). \(\square \)
Lemma 1
Let \(A \in \mathbb {Z}_p^{m\times n}\) and \(B \in \mathbb {Z}_p^{l\times n}\) be matrices. Let \(C \in \mathbb {Z}_p^{(m+l) \times n}\) be the concatenation of A and B by rows. The following three statements are equivalent:
-
(i)
\(\forall \varvec{a} \in \mathbb {Z}_p^{m}, \forall \varvec{b} \in \mathbb {Z}_p^{l}\), \(\displaystyle \mathop {\Pr }\limits _{\varvec{x} \mathop {\leftarrow }\limits ^{\$}\mathbb {Z}_p^{n}}\left[ A\varvec{x} = \varvec{a} \, | \, B\varvec{x} = \varvec{b}\right] = \mathop {\Pr }\limits _{\varvec{x} \mathop {\leftarrow }\limits ^{\$}\mathbb {Z}_p^{n}}\left[ A \varvec{x} = \varvec{a} \right] \)
-
(ii)
\(\mathrm{rank}(C) = \mathrm{rank}(A) + \mathrm{rank}(B)\)
-
(iii)
\(\forall \varvec{a} \in \mathbb {Z}_p^{m}, \forall \varvec{b} \in \mathbb {Z}_p^{l},\quad \varvec{a}^{\top }A \ne \varvec{b}^{\top }B \,\, \vee \,\, \varvec{a}^{\top }A = \varvec{0}^{\top }_{n}\)
Proof
(Of the Lemma). Note that (i) holds for every \(\varvec{a}\in \mathbb {Z}_p^{m}, \varvec{b}\in \mathbb {Z}_p^{l}\) such that \(A\varvec{x} = \varvec{a}\) or \(B\varvec{x} = \varvec{b}\) have no solution. Let \(\varvec{a}\in \mathbb {Z}_p^{m}, \varvec{b}\in \mathbb {Z}_p^{l}\) be such that the systems \(A\varvec{x} = \varvec{a}\) and \(B\varvec{x} = \varvec{b}\) have individually at least one solution (note that such \(\varvec{a}\) and \(\varvec{b}\) always exist). We define the sets \(\varOmega _{A} = \{ \varvec{x} \in \mathbb {Z}_p^{n} : A\varvec{x} = \varvec{a} \}\), \(\varOmega _{B} = \{ \varvec{x} \in \mathbb {Z}_p^{n} : B\varvec{x} = \varvec{b} \}\), \(\varOmega _{AB} = \{ \varvec{x} \in \mathbb {Z}_p^{n} : A\varvec{x} = \varvec{a} \ \wedge \ B\varvec{x} = \varvec{b} \}\). By the Rouché-Capelli Theorem,
Note that (i) can be expressed as \( \frac{\left| \varOmega _{AB}\right| }{p^{n}} = \frac{\left| \varOmega _{A}\right| }{p^{n}}\cdot \frac{\left| \varOmega _{B}\right| }{p^{n}} \) which is equivalent to the equation \(p^{n}\cdot \left| \varOmega _{AB}\right| = \left| \varOmega _{A}\right| \cdot \left| \varOmega _{B}\right| \), and therefore, \( p^{n} \cdot p^{n-\mathrm{rank}(C)} = p^{n-\mathrm{rank}(A)}\cdot p^{n-\mathrm{rank}(B)} \) if and only if \(\mathrm{rank}(C) = \mathrm{rank}(A) + \mathrm{rank}(B)\) which is \(\textit{(ii)}\).
Now, note that \(\mathrm{rank}(C) = \mathrm{rank}(A) + \mathrm{rank}(B)\) if and only if there is not a non-zero linear combination of rows of A that can be expressed as a linear combination of rows of B, which is equivalent to statement (iii). \(\square \)
Proof
(Of Theorem 9 ). According to our Theorem 2, the partial encoding \((\mathsf {sE}',\) \(\mathsf {rE}',\mathsf {kE}')\) induces a predicate encoding for the predicate \({{\mathrm{\mathsf {Pred}}}}(x,y) = 1 \text { iff } \exists \varvec{s} \in \mathbb {Z}_p^{c}, r \in \mathbb {Z}_p^{1}\) s.t. \(\varvec{s}^{\top }\mathsf {sE}'_x = r\cdot \mathsf {rE}'_y\) and \(r\cdot \mathsf {kE}'_y = 1\), or equivalently, \(\exists \varvec{s} \in \mathbb {Z}_p^{c} \text { s.t. } \varvec{s}^{\top }\mathsf {cE}_x = \mathsf {kE}_y\), which is equivalent to the reconstructability of the tag-based encoding \((\mathsf {cE},\mathsf {kE})\). According to Theorem 8 it is also equivalent to the predicate \(\mathsf {P}\). \(\square \)
Proof
(Of Theorem 10 ). Verifying correctness of the pair encoding is a simple check. For perfect security we need to check that, when \((x,y) \notin \mathsf {P}\), the following two distributions are identical:
Since both distributions provide \(s_0\) and \(r_1\) in the clear, the above checking is equivalent to the following:
but those distributions are identical due to the \(\alpha \)-privacy of the predicate encodingFootnote 10. \(\square \)
Proof
(Of Theorem 11 ). Given \((\varvec{s},\varvec{r})\in \mathbb {Z}_p^{s} \times \mathbb {Z}_p^{r}\), we define \(\varOmega _{\varvec{s},\varvec{r}} = \{ \varvec{w}\in \mathbb {Z}_p^{w} : S \varvec{w}= \varvec{s} \ \wedge \ R \varvec{w}= \varvec{r} \}\). The condition on the second bullet holds iff \(w-s-r \ge 0\) and the cardinality of \(\varOmega _{\varvec{s},\varvec{r}}\) is \(p^{w-s-r}\). Additionally, \(|\varOmega _{\varvec{s},\varvec{r}}|\) is independent from \(\varvec{r}\) and \(\varvec{s}\) iff the two distributions from the first bullet are identical. \(\square \)
Proof
(Of Theorem 12 ). Correctness can be easily checked. For privacy, let \((x,y) \notin \mathsf {P}\) and let \(\varvec{w}\in \mathbb {Z}_p^{w}\) be such that \(\mathsf {sE}_x \varvec{w}= \varvec{0}_{s}\) and \(\mathsf {rE}_y \varvec{w}= \mathsf {kE}_y\). Note that \(\varvec{w}'^{\top } = \left( \begin{array}{cc} \varvec{w}^{\top }&\,\, \varvec{0}_{k}^{\top } \end{array} \right) \) is a witness of privacy for \((\mathsf {sE}',\mathsf {rE}',\mathsf {kE}',\mathsf {sD}',\mathsf {rD}')\). \(\square \)
Rights and permissions
Copyright information
© 2017 International Association for Cryptologic Research
About this paper
Cite this paper
Ambrona, M., Barthe, G., Schmidt, B. (2017). Generic Transformations of Predicate Encodings: Constructions and Applications. In: Katz, J., Shacham, H. (eds) Advances in Cryptology – CRYPTO 2017. CRYPTO 2017. Lecture Notes in Computer Science(), vol 10401. Springer, Cham. https://doi.org/10.1007/978-3-319-63688-7_2
Download citation
DOI: https://doi.org/10.1007/978-3-319-63688-7_2
Published:
Publisher Name: Springer, Cham
Print ISBN: 978-3-319-63687-0
Online ISBN: 978-3-319-63688-7
eBook Packages: Computer ScienceComputer Science (R0)





 and
and 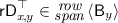 ;
;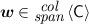 s.t.
s.t. 





