Abstract
The pseudorandom-function oracle-Diffie–Hellman (PRF-ODH) assumption has been introduced recently to analyze a variety of DH-based key exchange protocols, including TLS 1.2 and the TLS 1.3 candidates, as well as the extended access control (EAC) protocol. Remarkably, the assumption comes in different flavors in these settings and none of them has been scrutinized comprehensively yet. In this paper here we therefore present a systematic study of the different PRF-ODH variants in the literature. In particular, we analyze their strengths relative to each other, carving out that the variants form a hierarchy. We further investigate the boundaries between instantiating the assumptions in the standard model and the random oracle model. While we show that even the strongest variant is achievable in the random oracle model under the strong Diffie–Hellman assumption, we provide a negative result showing that it is implausible to instantiate even the weaker variants in the standard model via algebraic black-box reductions to common cryptographic problems.
You have full access to this open access chapter, Download conference paper PDF
Similar content being viewed by others
1 Introduction
Proposing new cryptographic assumptions is a valid strategy to analyze or design protocols which escape a formal treatment so far. Yet, the analysis of the protocol, usually carried out via a reduction to the new assumption, is only the first step. Only the evaluation of the new assumption completes the analysis and yields a meaningful security claim.
1.1 The \(\mathsf {PRF}\textsf {-}\mathsf {ODH}\) Assumption
In the context of key exchange protocols, a new assumption, called the pseudorandom-function oracle-Diffie–Hellman (\(\mathsf {PRF}\textsf {-}\mathsf {ODH}\)) assumption has recently been put forward by Jager et al. [23] for the analysis of TLS 1.2. It is a variant of the oracle-Diffie–Hellman assumption introduced by Abdalla et al. [1] in the context of the encryption scheme DHIES. The \(\mathsf {PRF}\textsf {-}\mathsf {ODH}\) assumption basically says that the function value \(\mathsf {PRF}(g^{uv},x^\star )\) for a DH key \(g^{uv}\) looks random, even if given \(g^u\) and \(g^v\) and if seeing related values \(\mathsf {PRF}(S^u,x)\) and/or \(\mathsf {PRF}(T^v,x)\) for chosen values S, T, and x.
The \(\mathsf {PRF}\textsf {-}\mathsf {ODH}\) appears to be a natural assumption for any DH-based key exchange protocol, aiming at security against man-in-the-middle attacks (see Fig. 1). In DH-based protocols both parties, the client and the server, exchange values \(g^u,g^v\) and locally compute the session key by applying a key derivation (or pseudorandom) function to the key \(g^{uv}\) and usually some parts of the transcript. The man-in-the-middle adversary can now try to attack the server’s session key \(\mathsf {PRF}(g^{uv},\dots )\) by submitting a modified value S instead of \(g^v\) to the client, yielding a related key \(\mathsf {PRF}(S^u,\dots )\) on the client’s side. The \(\mathsf {PRF}\textsf {-}\mathsf {ODH}\) assumption guarantees now that the server’s key is still fresh.
Note that simple authentication of transmissions does not provide a remedy against the above problem. The adversary could act under a different, corrupt server identity towards the client, and only re-use the Diffie–Hellman data, authenticated under the corrupt server’s key. Then the Diffie–Hellman keys in the executions would still be non-trivially related. This happens especially if keys are used in multiple sessions. Another problem is that some protocols may derive keys early, before applying signatures, e.g., such as for handshake encryption as well as in the post-handshake authentication mechanism in TLS 1.3 [36].
It therefore comes as no surprise that the \(\mathsf {PRF}\textsf {-}\mathsf {ODH}\) assumption has been used in different protocols for the security analysis, including the analysis of the TLS 1.2 [13] ephemeral and static Diffie–Hellman handshake modes [8, 23, 29], the TLS 1.3 [36] Diffie–Hellman-based and resumption handshake candidates [14,15,16] as well as 0-RTT handshake candidates [18], and a 0-RTT extension of the extended access control (EAC) protocol [10], for the original EAC protocol listed, for example, in Document 9303 of the International Civil Aviation Organization [22]. Notably, these scientific works use different versions of the \(\mathsf {PRF}\textsf {-}\mathsf {ODH}\) assumption, due to the different usages of the key shares \(g^u\), \(g^v\). These key shares can be ephemeral (for a single session), semi-static (for a small number of sessions), or static (for multiple sessions). Therefore, the man-in-the middle adversary may ask to see no related key for either key share, a single related key, or multiple related keys. For instance, while Jager et al. [23] required only security against a single query for one of the two key shares, Krawczyk et al. [29] modify the original \(\mathsf {PRF}\textsf {-}\mathsf {ODH}\) assumption because they require security against multiple oracle queries against this key share. In [18] an extra query to the other key share has been added, and [10] require multiple queries to both key shares.
1.2 Evaluating the \(\mathsf {PRF}\textsf {-}\mathsf {ODH}\) Assumptions
Consequently, and to capture all of the above assumptions simultaneously, we generally speak of the \(\mathsf {\mathsf {l}\mathsf {r}{}PRF}\textsf {-}\mathsf {ODH}\) assumption, allowing the adversary no (\(\mathsf {l},\mathsf {r}=\mathsf {n}\)), a single (\(\mathsf {l},\mathsf {r}=\mathsf {s}\)), or multiple (\(\mathsf {l},\mathsf {r}=\mathsf {m}\)) related key queries, for the “left” key \(g^u\) or the “right” key \(g^v\). Such queries are handled by oracles \(\mathsf {ODH}_u\) and \(\mathsf {ODH}_v\), returning the corresponding pseudorandom function value. This results in nine variants, for each combination \(\mathsf {l},\mathsf {r}\in \{\mathsf {n},\mathsf {s},\mathsf {m}\}\). We also discuss some more fine-grained distinctions, e.g., if the adversary learns both keys \(g^u\), \(g^v\) before choosing the input \(x^\star \) for the challenge value \(\mathsf {PRF}(g^{uv},x^\star )\), or if \(x^\star \) can only depend on \(g^u\).
To evaluate the strengths of the different types of \(\mathsf {\mathsf {l}\mathsf {r}{}PRF}\textsf {-}\mathsf {ODH}\) assumptions one can ask how the variants relate to each other. Another important aspect is the question whether, and if so, to which (well investigated) Diffie–Hellman problem it possibly relates to, e.g., the computational Diffie–Hellman (\(\mathsf {CDH}\)), the decisional Diffie–Hellman (\(\mathsf {DDH}\)), the strong Diffie–Hellman (\(\mathsf {StDH}\)), or the even more general Gap-Diffie–Hellman (\(\mathsf {GapDH}\)) problem. While the answer to this question may rely on the random oracle model, the final issue would be to check if (any version of) the assumption can be instantiated in the standard model.
Especially the question whether the \(\mathsf {PRF}\textsf {-}\mathsf {ODH}\) assumption (or which variant) can be instantiated in the standard model is of utmost interest. Some of the aforementioned works refer to the(ir) \(\mathsf {PRF}\textsf {-}\mathsf {ODH}\) assumption as a standard-model assumption, since there is no immediate reference to a random oracle. This would not only apply to the schemes analyzed with respect to the \(\mathsf {PRF}\textsf {-}\mathsf {ODH}\) assumption, but potentially also to other works where the Gap-DH or related assumptions in the random oracle have been used for the analysis, yet where the \(\mathsf {PRF}\textsf {-}\mathsf {ODH}\) assumption is a promising alternative for carrying out a proof. Examples include the QUIC protocol [17, 32] and OPTLS [30] which forms the base for TLS 1.3.
1.3 Our Results
Figure 2 gives an overview over our results. We explain the details next.
Relations between the different \(\mathsf {PRF}\textsf {-}\mathsf {ODH}\) variants (in solid-line rounded rectangles) from Definition 1 and other assumptions (in dotted-line rounded rectangles). Solid arrows indicate the trivial implications between \(\mathsf {PRF}\textsf {-}\mathsf {ODH}\) variants, dashed arrows indicate implications we establish. Struck-out, densely dotted arrows indicate separations in the standard model via the indicated function \(\mathsf {F}_n \in \mathcal {F}\) (cf. Definition 5). Struck-out, sparsely dotted arrows indicated separations in the random-oracle model. The dashed horizontal line demarcates the boundary below which our impossibility result for standard-model algebraic black-box reductions from Sect. 5 holds. Numbers in parentheses indicate the respective propositions and theorems.
Instantiations. Our first contribution is to discuss instantiation possibilities of the \(\mathsf {PRF}\textsf {-}\mathsf {ODH}\) variants. We stress that some of these results mainly confirm the expectation: the \(\mathsf {nnPRF}\textsf {-}\mathsf {ODH}\) assumption where no oracle queries are allowed can be based upon the decisional Diffie–Hellman assumption \(\mathsf {DDH}\), and the one-sided assumptions \(\mathsf {mnPRF}\textsf {-}\mathsf {ODH}\) and \(\mathsf {nmPRF}\textsf {-}\mathsf {ODH}\) where the adversary has (multiple) access to either oracle \(\mathsf {ODH}_u\) or \(\mathsf {ODH}_v\) can be based on the strong Diffie–Hellman assumption in the random oracle model. The strong DH assumption (\(\mathsf {StDH}\)) demands that the adversary solves the computational problem of computing \(g^{uv}\) from \(g^u,g^v\), but having access to a decisional oracle \(\mathsf {DDH}(g^u,\cdot ,\cdot )\) checking for DH tuples. Such checks are necessary to provide consistency when simulating the random oracle through lazy sampling, i.e., in the case that random values are only sampled on their first explicit usage. The proofs for \(\mathsf {mnPRF}\textsf {-}\mathsf {ODH}\) and \(\mathsf {nmPRF}\textsf {-}\mathsf {ODH}\) appear already implicitly in previous work about key exchange, e.g., [12, 17, 26, 30,31,32, 37], but where the reduction to the \(\mathsf {StDH}\) problem in the random oracle model has been carried out by dragging along all the steps of the key exchange protocols.
Our final instantiation result for the strongest notion \(\mathsf {mmPRF}\textsf {-}\mathsf {ODH}\) holds in the random oracle model under the strong DH (\(\mathsf {StDH}\)) assumption. Surprisingly, the proof is less straightforward than one would expect, since the availability of both oracles \(\mathsf {ODH}_u\) and \(\mathsf {ODH}_v\) imposes the need for further consistency checks between cross-over calls for the two oracles in the simulation. We show that such consistency checks can indeed be implemented assuming \(\mathsf {StDH}\), but causing a square-root loss in the security reduction to \(\mathsf {StDH}\). This loss is due to the fact that in an intermediate step we go through the square-DH problem \(\mathsf {SqDH}\) (given \(g,g^v\) compute \(g^{v^2}\)) to which \(\mathsf {CDH}\) reduces by making two calls to the square-DH problem adversary (see, e.g., [24]), effectively squaring the success probability.
The instantiations are shown through the boxes with dotted surrounding lines in Fig. 2. We also discuss briefly the relationship to related-key security for pseudorandom functions, where the adversary can ask to see values for transformed keys \(\phi (K)\). While similar in spirit at first glance, it seems to us that the notions differ in technical details which makes it hard to relate them.
Relations. The instantiation results give a sort of general method to achieve any \(\mathsf {PRF}\textsf {-}\mathsf {ODH}\) notion, leaving open the possibility that one notion may be actually easier to achieve. This is even more relevant in light of the fact that previous works used different notions. In order to support a better comparison between the various notions we relate them in terms of strength of the assumption. Some of these relationships, especially implications, are easy to establish. For example, since the adversary in the \(\mathsf {mmPRF}\textsf {-}\mathsf {ODH}\) game can always forgo using its \(\mathsf {ODH}_v\) oracle, this immediately implies \(\mathsf {mnPRF}\textsf {-}\mathsf {ODH}\) security. All implications are marked by solid arrows in Fig. 2.
As for separations we are able to rule out a number of implications unconditionally. By this we mean that we only make the minimal assumption that a secure instantiation exists, and then build one still satisfying this notion but not the stronger one. These separations are displayed in Fig. 2 through dotted arrows.
We are also able to separate further notions conditionally, using random oracles and a plausible number-theoretic assumption. Namely, under these assumptions, the notion of \(\mathsf {snPRF}\textsf {-}\mathsf {ODH}\) (with a single call to \(\mathsf {ODH}_u\)) is strictly stronger than the \(\mathsf {nmPRF}\textsf {-}\mathsf {ODH}\) notion where the adversary can ask the \(\mathsf {ODH}_v\) oracle multiple times but does not get access to the \(\mathsf {ODH}_u\) oracle. With a similar strategy we can also separate \(\mathsf {mnPRF}\textsf {-}\mathsf {ODH}\) with multiple \(\mathsf {ODH}_u\) queries from \(\mathsf {smPRF}\textsf {-}\mathsf {ODH}\), where the adversary can now make one extra call to \(\mathsf {ODH}_u\) on top of the \(\mathsf {ODH}_v\) queries.
The conditional separations are not symmetric in the sense that they apply to the other oracle as well. The reason is that these results exploit that the adversary receives \(g^u\) before \(g^v\), such that the converse does not simply follow. Besides these opposite cases there are also some other cases where we could not provide a separation, e.g., from \(\mathsf {mmPRF}\textsf {-}\mathsf {ODH}\) to \(\mathsf {msPRF}\textsf {-}\mathsf {ODH}\). We give more insights within.
Impossibility Result. The third important contribution is our impossibility result. We show that proving security of even the mild \(\mathsf {snPRF}\textsf {-}\mathsf {ODH}\) or \(\mathsf {nsPRF}\textsf {-}\mathsf {ODH}\) notions based on general cryptographic problems is hard. Besides the common assumption that the reduction uses the adversary only as a black box, we also assume that the reduction is algebraic. This means that whenever the reduction passes a group element A to the outside, it knows a representation \((\alpha _1,\alpha _2,\dots )\) such that \(A=\prod g_i^{\alpha _i}\) for the reduction’s input values \(g_1,g_2,\dots \). This notion of algebraic reductions has been used in other separation works before, e.g., [9, 20, 35]. Unlike generic reductions, algebraic reductions can take advantage of the representation of group elements.
In detail, we then show via a meta-reduction technique [9, 21, 35], that one cannot prove security of the \(\mathsf {snPRF}\textsf {-}\mathsf {ODH}\) or \(\mathsf {nsPRF}\textsf {-}\mathsf {ODH}\) assumption via algebraic black-box reductions to a class of cryptographic problems. The problems we rule out are quite general, saying that the adversary receives some input, can interact multiple times with a challenger in an arbitrary way, and should then provide a solution. We remark that we also need to augment this problem by a Diffie–Hellman problem in order to give a reference point for the algebraicity of the reduction. Our result also requires that the decisional square-DH problem is hard, i.e., that \(g,g^v,g^{v^2}\) is indistinguishable from \(g,g^v,g^z\) for random v, z.Footnote 1
In a sense, our negative result, displayed by the dashed horizontal line on top in Fig. 2, is optimal in terms of the relation of \(\mathsf {PRF}\textsf {-}\mathsf {ODH}\) assumptions, as it rules out exactly the notions “one above” the \(\mathsf {nnPRF}\textsf {-}\mathsf {ODH}\) notion with a standard model instantiation. We still note that the restrictions on the reduction, and the additional assumption, may allow to bypass our result. This also means that our implications and separations between the different notions, established earlier, are not moot.
Implications for Practical Key Derivation Functions. Since the \(\mathsf {PRF}\textsf {-}\mathsf {ODH}\) assumptions have been used in connection with applied protocols like TLS, we finally address the question which security guarantees we get for practical key derivation functions used in such protocols. We are especially interested in \(\mathsf {HMAC}\) [25] on which the key derivation function \(\mathsf {HKDF}\) [27, 28] is based upon. Our instantiation results in the random oracle so far treat the key derivation function as a monolithic random oracle, whereas key derivation functions like \(\mathsf {HMAC}\) have an iterative structure. At the same time, our impossibility result tells us that giving a standard-model proof for \(\mathsf {HMAC}\), based on say collision-resistance of the compression function, may be elusive. We thus make the assumption that the compression function is a random oracle.
We show that \(\mathsf {HMAC}\) provides the strong notion of \(\mathsf {mmPRF}\textsf {-}\mathsf {ODH}\) security, assuming \(\mathsf {StDH}\) and that the compression function is a random oracle. We note that Coron et al. [11] show that a variant of \(\mathsf {HMAC}\) is indifferentiable from a random oracle, and Krawczyk [27] briefly remarks that the result would carry over to the actual \(\mathsf {HMAC}\) construction. However, in \(\mathsf {HKDF}\) the \(\mathsf {HMAC}\) function is applied in a special mode in which the key part is hashed first, and it is therefore unclear if our result for the monolithic random oracle immediately applies. But based on the techniques used in the instantiation part we can give a direct proof of the security of (the general mode of) \(\mathsf {HMAC}\).
2 PRF-ODH Definition
Different variants of the new PRF oracle-Diffie–Hellman (\(\mathsf {PRF}\textsf {-}\mathsf {ODH}\)) assumption have been introduced and used in the literature in the context of key exchange protocols. In this section we first provide a generic \(\mathsf {PRF}\textsf {-}\mathsf {ODH}\) assumption definition capturing all different flavors and discuss its relation to previous occurrences [10, 15, 16, 18, 23, 29].
Definition 1
(Generic \(\mathsf {PRF}\textsf {-}\mathsf {ODH}\) assumption). Let \(\mathbb {G}\) be a cyclic group of order q with generator g. Let \(\mathsf {PRF}:\mathbb {G}\times \{0,1\}^* \rightarrow \{0,1\}^\lambda \) be a pseudorandom function that takes a key \(K \in \mathbb {G}\) and a label \(x \in \{0,1\}^*\) as input and outputs a value \(y \in \{0,1\}^\lambda \), i.e., \(y \leftarrow \mathsf {PRF}(K, x)\).
We define a generic security notion \(\mathsf {\mathsf {l}\mathsf {r}{}PRF}\textsf {-}\mathsf {ODH}\) which is parameterized by \(\mathsf {l}, \mathsf {r}\in \{\mathsf {n}, \mathsf {s}, \mathsf {m}\}\) indicating how often the adversary is allowed to query a certain “left” resp. “right” oracle (\(\mathsf {ODH}_u\) resp. \(\mathsf {ODH}_v\)) where \(\mathsf {n}\) indicates that no query is allowed, \(\mathsf {s}\) that a single query is allowed, and \(\mathsf {m}\) that multiple (polynomially many) queries are allowed to the respective side. Consider the following security game \(\mathsf {Game}_{\mathsf {PRF},\mathcal {A}}^{\mathsf {\mathsf {l}\mathsf {r}{}PRF}\textsf {-}\mathsf {ODH}}\) between a challenger \(\mathcal {C}\) and a probabilistic polynomial-time (PPT) adversary \(\mathcal {A}\).
-
1.
The challenger \(\mathcal {C}\) samples
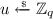 and provides \(\mathbb {G},g,\) and \(g^u\) to the adversary \(\mathcal {A}\).
and provides \(\mathbb {G},g,\) and \(g^u\) to the adversary \(\mathcal {A}\). -
2.
If \(\mathsf {l}= \mathsf {m}\), \(\mathcal {A}\) can issue arbitrarily many queries to the following oracle \(\mathsf {ODH}_u\).
- \(\mathsf {ODH}_u\) oracle. :
-
On a query of the form (S, x), the challenger first checks if \(S \notin \mathbb {G}\) and returns \(\bot \) if this is the case. Otherwise, it computes \(y \leftarrow \mathsf {PRF}(S^u, x)\) and returns y.
-
3.
Eventually, \(\mathcal {A}\) issues a challenge query \(x^\star \). On this query, \(\mathcal {C}\) samples
 and a bit
and a bit  uniformly at random. It then computes \(y^\star _0 = \mathsf {PRF}(g^{uv},x^\star )\) and samples
uniformly at random. It then computes \(y^\star _0 = \mathsf {PRF}(g^{uv},x^\star )\) and samples 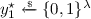 uniformly random. The challenger returns \((g^v, y^\star _b)\) to \(\mathcal {A}\).
uniformly random. The challenger returns \((g^v, y^\star _b)\) to \(\mathcal {A}\). -
4.
Next, \(\mathcal {A}\) may issue (arbitrarily interleaved) queries to the following oracles \(\mathsf {ODH}_u\) and \(\mathsf {ODH}_v\) (depending on \(\mathsf {l}\) and \(\mathsf {r}\)).
- \(\mathsf {ODH}_u\) oracle. :
-
The adversary \(\mathcal {A}\) may ask no (\(\mathsf {l}= \mathsf {n}\)), a single (\(\mathsf {l}= \mathsf {s}\)), or arbitrarily many (\(\mathsf {l}= \mathsf {m}\)) queries to this oracle. On a query of the form (S, x), the challenger first checks if \(S \notin \mathbb {G}\) or \((S, x) = (g^v, x^\star )\) and returns \(\bot \) if this is the case. Otherwise, it computes \(y \leftarrow \mathsf {PRF}(S^u, x)\) and returns y.
- \(\mathsf {ODH}_v\) oracle. :
-
The adversary \(\mathcal {A}\) may ask no (\(\mathsf {r}= \mathsf {n}\)), a single (\(\mathsf {r}= \mathsf {s}\)), or arbitrarily many (\(\mathsf {r}= \mathsf {m}\)) queries to this oracle. On a query of the form (T, x), the challenger first checks if \(T \notin \mathbb {G}\) or \((T, x) = (g^u, x^\star )\) and returns \(\bot \) if this is the case. Otherwise, it computes \(y \leftarrow \mathsf {PRF}(T^v, x)\) and returns y.
-
5.
At some point, \(\mathcal {A}\) stops and outputs a guess \(b^\prime \in \{0,1\}\).
We say that the adversary wins the \(\mathsf {\mathsf {l}\mathsf {r}{}PRF}\textsf {-}\mathsf {ODH}\) game if \(b^\prime = b\) and define the advantage function
and, assuming a sequence of groups in dependency of the security parameter, we say that a pseudorandom function \(\mathsf {PRF}\) with keys from \((\mathbb {G}_\lambda )_\lambda \) provides \(\mathsf {\mathsf {l}\mathsf {r}{}PRF}\textsf {-}\mathsf {ODH}\) security (for \(\mathsf {l}, \mathsf {r}\in \{\mathsf {n},\mathsf {s},\mathsf {m}\}\)) if for any \(\mathcal {A}\) the advantage \(\mathsf {Adv}_{\mathsf {PRF},\mathcal {A}}^{\mathsf {\mathsf {l}\mathsf {r}{}PRF}\textsf {-}\mathsf {ODH}}(\lambda )\) is negligible in the security parameter \(\lambda \).
In the following, if clear from the context, we will omit the group \(\mathbb {G}\) and sometimes its generator g as explicit inputs to the adversary.
Relations to Previous \(\mathsf {PRF}\textsf {-}\mathsf {ODH}\) Assumptions. The above generic and parameterized \(\mathsf {\mathsf {l}\mathsf {r}{}PRF}\textsf {-}\mathsf {ODH}\) definition captures different variants of the PRF-ODH assumption present in the literature. The \(\mathsf {PRF}\textsf {-}\mathsf {ODH}\) formulation put forward by Jager et al. [23] is captured by ours in case the parameters are set to \(\mathsf {l}= \mathsf {s}\) and \(\mathsf {r}= \mathsf {n}\) meaning that only the “left” oracle (querying the DH share \(g^u\)) can be queried once. Note that Step 2 is only required if \(\mathsf {l}= \mathsf {m}\), capturing that Jager et al. first request their challenge before issuing an oracle query. The same variant, \(\mathsf {snPRF}\textsf {-}\mathsf {ODH}\), was also used by Dowling et al. [16]. Krawczyk et al. [29] modified the \(\mathsf {PRF}\textsf {-}\mathsf {ODH}\) formulation of Jager et al. since they require security against multiple (“left”) oracle queries against the DH key share. Thus, their variant is captured by ours through setting the parameters to \(\mathsf {l}= \mathsf {m}\) and \(\mathsf {r}= \mathsf {n}\), and thus making use of Step 2. Recent works further introduced an additional query to the other DH key share, due to the fact that the keys are static or semi-static, respectively. In more detail, Fischlin and Günther [18] require an extra single (“right”) oracle query while still requesting polynomial many queries to the “left” oracle. This is captured by our definition through setting the parameters to \(\mathsf {l}= \mathsf {m}\) and \(\mathsf {r}= \mathsf {s}\). Lastly, Brendel and Fischlin [10] require to query both key shares multiple times, which our definition captures as well by choosing the parameters as \(\mathsf {l}= \mathsf {m}\) and \(\mathsf {r}= \mathsf {m}\).
Design Options. The above generic definition can be refined further, e.g., by enabling the challenger to provide the value \(g^v\) to the adversary at the outset in Step 1. This variant was used in the analysis of earlier TLS 1.3 draft handshakes by Dowling et al. [15]. Such change would be accompanied by giving the adversary in Step 2 also access to the \(\mathsf {ODH}_v\) oracle in case \(\mathsf {r}= \mathsf {m}\). Another reasonable change could encompass enabling the adversary in multi-query variants (i.e., \(\mathsf {l}= \mathsf {m}\) or \(\mathsf {r}= \mathsf {m}\)) to also issue multiple challenge queries in Step 3, for the same value \(g^v\) or even freshly chosen values \(g^{v_i}\) in each call. However, one can show via a standard hybrid argument that both notions (i.e., single challenge query and multiple challenge query) are polynomially equivalent.
In this work, we focus on the common structure of previously studied \(\mathsf {PRF}\textsf {-}\mathsf {ODH}\) notions [10, 16, 18, 23, 29] which are captured by our generic definition above. Additionally, in Sect. 4 we briefly discuss the impact of such changes regarding the analysis of the relations between the different variants of the assumption.
3 Instantiating the PRF-ODH Assumption
We next turn to the question how to instantiate the \(\mathsf {PRF}\textsf {-}\mathsf {ODH}\) assumption. Concretely, we provide instantiations of the two notions that mark both ends of the strength spectrum of the PRF-ODH variants. First, we show that the weakest PRF-ODH variant, \(\mathsf {nnPRF}\textsf {-}\mathsf {ODH}\), can be instantiated in the standard model under well-established assumptions, namely the Decisional Diffie–Hellman (\(\mathsf {DDH}\)) assumption and (ordinary) PRF security in a group \(\mathbb {G}\). Second, we establish that, in the (programmable) random oracle model, both the strongest one-sided PRF-ODH variants, \(\mathsf {mnPRF}\textsf {-}\mathsf {ODH}\) and \(\mathsf {nmPRF}\textsf {-}\mathsf {ODH}\), as well as the most general \(\mathsf {mmPRF}\textsf {-}\mathsf {ODH}\) assumption can be instantiated from the strong Diffie–Hellman assumption (\(\mathsf {StDH}\)). We define all these number-theoretic assumptions when discussing the security notions. Furthermore, we discuss the relation of the PRF-ODH notion to that of PRF security under related-key attacks.
3.1 Standard-Model Instantiation of \(\mathsf {nnPRF}\textsf {-}\mathsf {ODH}\)
We begin with instantiating the \(\mathsf {nnPRF}\textsf {-}\mathsf {ODH}\) assumption in the standard model. For this we speak of a function \(\mathsf {F}:\mathbb {G}\times \{0,1\}^* \rightarrow \{0,1\}^\lambda \) to be \(\mathsf {PRF}_\mathbb {G}\)-secure if no efficient adversary which, upon querying x, gets to see either the function value \(\mathsf {F}(K,x)\) for a then chosen random key  , or a random value, can distinguish the two cases. As in the other games before, the choice of answering genuinely or randomly is made at random, and we let \(\mathsf {Adv}_{\mathsf {F},\mathcal {A}}^{\mathsf {PRF}_\mathbb {G}}\) denote the advantage of algorithm \(\mathcal {A}\). Here, we normalize again the advantage by subtracting the guessing probability of \(\tfrac{1}{2}\) and multiplying the result by a factor of 2. Note that the difference to the \(\mathsf {nnPRF}\textsf {-}\mathsf {ODH}\) assumption is that the adversary does not get to see a pair \(g^u,g^v\) from which the key is generated.
, or a random value, can distinguish the two cases. As in the other games before, the choice of answering genuinely or randomly is made at random, and we let \(\mathsf {Adv}_{\mathsf {F},\mathcal {A}}^{\mathsf {PRF}_\mathbb {G}}\) denote the advantage of algorithm \(\mathcal {A}\). Here, we normalize again the advantage by subtracting the guessing probability of \(\tfrac{1}{2}\) and multiplying the result by a factor of 2. Note that the difference to the \(\mathsf {nnPRF}\textsf {-}\mathsf {ODH}\) assumption is that the adversary does not get to see a pair \(g^u,g^v\) from which the key is generated.
The underlying DDH assumption says that one cannot efficiently distinguish tuples \((g,g^u,g^v,g^{uv})\) from tuples \((g,g^u,g^v,g^z)\) for random \(u,v,z\in \mathbb {Z}_q\). More formally, for an adversary \(\mathcal {B}\) we define \(\mathsf {Adv}_{\mathbb {G},\mathcal {B}}^{\mathsf {DDH}}\) to be the probability of \(\mathcal {B}\) predicting a random bit b, when given \(g,g^u,g^v,g^{uv}\) for \(b=0\) and \(g,g^u,g^v,g^z\) for \(b=1\), with the usual normalization as above. Alternatively, one may define \(\mathsf {Adv}_{\mathbb {G},\mathcal {B}}^{\mathsf {DDH}}\) to be the advantage in the \(\mathsf {nnPRF}\textsf {-}\mathsf {ODH}\) game for the function \(\mathsf {F}(K,x)=K\).
Theorem 2
( \(\mathsf {DDH}+ \mathsf {PRF}_{\mathbb {G}} \implies \mathsf {nnPRF}\textsf {-}\mathsf {ODH}\) ). If a function \(\mathsf {F}:\mathbb {G}\times \{0,1\}^* \rightarrow \{0,1\}^\lambda \) is \(\mathsf {PRF}_\mathbb {G}\)-secure and the \(\mathsf {DDH}\) assumption holds in \(\mathbb {G}\), then \(\mathsf {F}\) is also \(\mathsf {nnPRF}\textsf {-}\mathsf {ODH}\)-secure. More precisely, for any efficient adversary \(\mathcal {A}\) against the \(\mathsf {nnPRF}\textsf {-}\mathsf {ODH}\) security of \(\mathsf {F}\), there exist efficient algorithms \(\mathcal {B}_1\) and \(\mathcal {B}_2\) such that
We note that the factor 2 is the common loss due to the game-hopping technique, when switching from indistinguishability for two fixed games to choosing one of the games at random. The proof appears in the full version of this paper.
3.2 Random-Oracle Instantiation of \(\mathsf {mnPRF}\textsf {-}\mathsf {ODH}\) and \(\mathsf {nmPRF}\textsf {-}\mathsf {ODH}\)
Abdalla et al. [1] proved that the oracle DH assumption \(\mathsf {ODH}\) is implied by the strong Diffie–Hellman assumption in the random oracle model. Here, we show that our strongest one-sided PRF-ODH variants, \(\mathsf {mnPRF}\textsf {-}\mathsf {ODH}\) and \(\mathsf {nmPRF}\textsf {-}\mathsf {ODH}\), can be instantiated under the strong Diffie–Hellman assumption \(\mathsf {StDH}\). The assumption says that, given \(g,g^u,g^v\) and access to a decisional DH oracle for fixed value \(g^u\), i.e., \(\mathsf {DDH}(g^u,\cdot ,\cdot )\), it is infeasible to compute \(g^{uv}\). Observe that this assumption is implied by the \(\mathsf {GapDH}\) assumption, where the adversary can choose the first group element freely, too. Let \(\mathsf {Adv}_{\mathbb {G},\mathcal {B}}^{\mathsf {StDH}}\) denote the probability of algorithm \(\mathcal {B}^{\mathsf {DDH}(g^u,\cdot ,\cdot )}(g,g^u,g^v)\) outputting \(g^{uv}\).
Theorem 3
In the random oracle model, \(\mathsf {StDH}\) implies \(\mathsf {mnPRF}\textsf {-}\mathsf {ODH}\) security and \(\mathsf {nmPRF}\textsf {-}\mathsf {ODH}\) security of \(\mathsf {F}(K,x)=\mathsf {RO}(K,x)\) for random oracle \(\mathsf {RO}\). More precisely, for any efficient adversary \(\mathcal {A}\) against the \(\mathsf {mnPRF}\textsf {-}\mathsf {ODH}\) or \(\mathsf {nmPRF}\textsf {-}\mathsf {ODH}\) security of \(\mathsf {F}\), there exists an efficient algorithms \(\mathcal {B}\) such that
The proof appears in the full version. It follows previous proofs in the context of key exchange protocols. The crucial aspect here is that one programs the random oracle for \(\mathsf {ODH}_u\) queries (S, x) by returning random values. This implicitly defines the random oracle value for (unknown) key \(S^u\) and x, but such that one later needs to check for consistency if the adversary makes a random oracle query about key \(K=S^u\) and x and one simulates the answer. This verification can be performed via the oracle \(\mathsf {DDH}(g^u,\cdot ,\cdot )\) by checking if \(\mathsf {DDH}(g^u,S,K)=1\) for any previous \(\mathsf {ODH}_u\) query (S, x). Vice versa, one also needs to check for \(\mathsf {ODH}_u\) queries (S, x) if the random oracle value for \((S^u,x)\) has already been set. This can be done again via the \(\mathsf {DDH}(g^u,\cdot ,\cdot )\) oracle.
If a consistent simulation is enforced then the only possibility for the adversary to distinguish a real or random challenge \(y^\star \) is to ask the random oracle about the DH key \(K=g^{uv}\) at some point. This is again easy to detect by checking if \(\mathsf {DDH}(g^u,g^v,K)=1\) for any such query K, in which case we solve the \(\mathsf {StDH}\) problem.
3.3 Random-Oracle Instantiation of \(\mathsf {mmPRF}\textsf {-}\mathsf {ODH}\)
We next look at the case that the adversary can make queries to both oracles, \(\mathsf {ODH}_u\) and \(\mathsf {ODH}_v\). Interestingly, this does not follow straightforwardly from the \(\mathsf {StDH}\) assumption as above. The reason is that, there, we have used the \(\mathsf {DDH}\)-oracle with fixed element \(g^u\) to check for consistency of \(\mathsf {ODH}_u\) queries with random oracle queries. In the most general \(\mathsf {mmPRF}\textsf {-}\mathsf {ODH}\) case, however, we would also need to check consistency across \(\mathsf {ODH}_u\) and \(\mathsf {ODH}_v\) queries. In particular, a simulator would need to be able to check for queries (S, x) to \(\mathsf {ODH}_u\) and (T, x) to \(\mathsf {ODH}_v\) if they result in the same key \(S^u=K=T^v\), but the simulator is given only \(S,T,g,g^u\), and \(g^v\). Such a test cannot be immediately performed with the \(\mathsf {DDH}(g^u,\cdot ,\cdot )\) oracle as in the \(\mathsf {StDH}\) case, and not even with the more liberal \(\mathsf {DDH}(\cdot ,\cdot ,\cdot )\) oracle as in the \(\mathsf {GapDH}\) case.
Suppose that we take the \(\mathsf {StDH}\) problem and augment it by another oracle which allows to check for “claws” S, T with \(S^u=T^v\). Call this the claw-verifying oracle \(\mathsf {Claw}\) and the problem the \(\mathsf {Claw\mathsf {StDH}}\) problem. For pairing-friendly groups \(\mathbb {G}\) we get this oracle for free via the bilinear map e as \(\mathsf {Claw}(S,T)=[e(g^u,S)=e(g^v,T)?]\). Next, we show that for general groups the claw-verifying oracle can be implemented in the \(\mathsf {StDH}\) game, too, but at the cost of a loose security reduction to \(\mathsf {StDH}\).
The idea of representing the oracle \(\mathsf {Claw}\) is as follows. Suppose that, in addition to \(g,g^u\) and \(g^v\) we would also receive the value \(g^{u/v}\) (where we assume here and in the following that \(v\ne 0\), since the case \(v=0\) is trivial to deal with). Then we can run the check for claws via the stronger \(\mathsf {DDH}\) oracle by calling \(\mathsf {DDH}(g^{u/v},S,T)\), checking that \(S^{u/v}=T\) and therefore \(S^u=T^v\). The question remains if the computational problem of computing \(g^{uv}\) given \(g^{u/v}\) (in the presence of a \(\mathsf {DDH}\) oracle) becomes significantly easier, and if we can relax the requirement to a \(\mathsf {DDH}(g^u,\cdot ,\cdot )\) oracle. Switching to the square DH problem in an intermediate step, we show that this is not the case, although the intermediate step causes a loose security relationship.
Assume that we have an algorithm \(\mathcal {A}\) which (given oracle access to \(\mathsf {DDH}(g^u,\cdot ,\cdot )\), \(\mathsf {DDH}(g^v,\cdot ,\cdot )\), and the claw-verifying oracle \(\mathsf {Claw}\)) on input \((g,g^u,g^v)\) is able to compute \(g^{uv}\). Then we show that we can use this algorithm to build an algorithm \(\mathcal {B}\) for the square-DH problem (given \(g,g^v\) compute \(g^{v^2}\)) relative to a \(\mathsf {DDH}(g^v,\cdot ,\cdot )\) oracle. For this, algorithm \(\mathcal {B}\) for input \(g,g^v\) picks  and sets \(g^u=(g^v)^r\). With this choice, \(g^{u/v}=g^r\) can be easily computed with the knowledge of r, allowing to implement the claw-verifying oracle for free. Similarly, we have \(\mathsf {DDH}(g^u,\cdot ,\cdot )=\mathsf {DDH}(g^v,(\cdot )^{r},\cdot )\), giving us the “mirrored” oracle for free. Algorithm \(\mathcal {B}\) now runs \(\mathcal {A}\) on input \((g,g^u,g^v)\) and answers all oracle requests of \(\mathcal {A}\) during the computation with the help of its \(\mathsf {DDH}(g^v,\cdot ,\cdot )\) oracle. Suppose that the adversary \(\mathcal {A}\) eventually outputs K. Then, \(\mathcal {B}\) returns \(K^{1/r}\) which equals \(g^{v^2}\) for a correct answer \(K=g^{uv}=g^{rv^2}\) of \(\mathcal {A}\).
and sets \(g^u=(g^v)^r\). With this choice, \(g^{u/v}=g^r\) can be easily computed with the knowledge of r, allowing to implement the claw-verifying oracle for free. Similarly, we have \(\mathsf {DDH}(g^u,\cdot ,\cdot )=\mathsf {DDH}(g^v,(\cdot )^{r},\cdot )\), giving us the “mirrored” oracle for free. Algorithm \(\mathcal {B}\) now runs \(\mathcal {A}\) on input \((g,g^u,g^v)\) and answers all oracle requests of \(\mathcal {A}\) during the computation with the help of its \(\mathsf {DDH}(g^v,\cdot ,\cdot )\) oracle. Suppose that the adversary \(\mathcal {A}\) eventually outputs K. Then, \(\mathcal {B}\) returns \(K^{1/r}\) which equals \(g^{v^2}\) for a correct answer \(K=g^{uv}=g^{rv^2}\) of \(\mathcal {A}\).
Next, we show that from a solver for the square-DH problem (with \(\mathsf {DDH}(g^v,\cdot ,\cdot )\) oracle) we can build a solver for the \(\mathsf {StDH}\) problem. Going from the square-DH problem to the \(\mathsf {CDH}\) problem is already known. Interestingly, though, the common strategies in the literature [2, 19, 33] require three calls to the square-DH solver, basically to compute the square \(g^{(u+v)^2}=g^{u^2+2uv+v^2}\) and then to divide out \(g^{u^2}\) and \(g^{v^2}\). Fortunately, two calls are sufficient, see for example [24], yielding a tighter security bound.
So suppose we have a square-DH algorithm (with oracle \(\mathsf {DDH}(g^v,\cdot ,\cdot )\)) then we call this algorithm once on \(g,g^{u+v}\) and once on \(g,g^{r(u-v)}\) for randomizer  . Since both inputs are random and independent, we get two valid answers \(g^{u^2+2uv+v^2}\) and \(g^{r^2(u^2-2uv+v^2)}\) with the product of the square-DH algorithm’s success probability. Note that these two executions at most double the number of oracle queries to the \(\mathsf {DDH}\) oracle. Dividing out the exponent \(r^2\) from the second term by raising it to the power \(1/r^2\), and then dividing the two group elements we obtain \(g^{4uv}\) from which we can easily compute \(g^{uv}\).
. Since both inputs are random and independent, we get two valid answers \(g^{u^2+2uv+v^2}\) and \(g^{r^2(u^2-2uv+v^2)}\) with the product of the square-DH algorithm’s success probability. Note that these two executions at most double the number of oracle queries to the \(\mathsf {DDH}\) oracle. Dividing out the exponent \(r^2\) from the second term by raising it to the power \(1/r^2\), and then dividing the two group elements we obtain \(g^{4uv}\) from which we can easily compute \(g^{uv}\).
Overall, we can show that solving the problem in presence of the decisional oracles for \(g^u\) and \(g^v\), and an additional claw-verifying oracle, is implied by the \(\mathsf {StDH}\) assumption, albeit with a security loss. More precisely, for any efficient adversary \(\mathcal {A}\) against \(\mathsf {Claw\mathsf {StDH}}\) we get an efficient adversary \(\mathcal {B}\) (making at most twice as many calls to its \(\mathsf {StDH}\) oracle as \(\mathcal {A}\)) such that
We can now give our security proof for \(\mathsf {mmPRF}\textsf {-}\mathsf {ODH}\), implying also security of \(\mathsf {msPRF}\textsf {-}\mathsf {ODH}\) and \(\mathsf {smPRF}\textsf {-}\mathsf {ODH}\), of course:
Theorem 4
In the random oracle model, \(\mathsf {Claw\mathsf {StDH}}\) (resp. \(\mathsf {StDH}\)) implies \(\mathsf {mmPRF}\textsf {-}\mathsf {ODH}\) security of \(\mathsf {F}(K,x)=\mathsf {RO}(K,x)\) for random oracle \(\mathsf {RO}\). More precisely, for any efficient adversary \(\mathcal {A}\) against the \(\mathsf {mmPRF}\textsf {-}\mathsf {ODH}\) security of \(\mathsf {F}\), there exist efficient algorithms \(\mathcal {B}_1,\mathcal {B}_2\) such that
The proof is almost identical to the one for \(\mathsf {mnPRF}\textsf {-}\mathsf {ODH}\), only that we here simulate the other oracle \(\mathsf {ODH}_v\) as the oracle \(\mathsf {ODH}_u\), and for each query to either of the oracles also check via the help of \(\mathsf {Claw}\) consistency between \(\mathsf {ODH}_u\) and \(\mathsf {ODH}_v\) evaluations. This provides a sound simulation of the random oracle. It follows as before that the adversary \(\mathcal {A}\) can only distinguish genuine \(y^\star \) from random ones if it queries the random oracle about \(g^{uv}\) (in the sound simulation), in which case \(\mathcal {B}_1\) finds this value in the list of queries.
3.4 On the Relation Between PRF-ODH and Security Against Related-Key Attacks
The PRF-ODH assumption demands the output of a PRF to be indistinguishable from random even when given access to PRF evaluations under a related (group-element) key, sharing (at least) one exponent of the challenge key. On a high level, this setting resembles the concept of related-key attack (RKA) security for pseudorandom functions as introduced by Bellare and Kohno [4]. This raises the question if the PRF-ODH assumption can be instantiated from RKA-secure PRFs (or vice versa).
Related-key attack security of a PRF \(f :\mathcal {K} \times \mathcal {D} \rightarrow \mathcal {R}\) with respect to a set \(\varPhi \) of related-key-deriving (RKD) functions is defined as the indistinguishability of two oracles \(F_{(\cdot ,K)}(\cdot )\) and \(G_{(\cdot ,K)}(\cdot )\) for a randomly chosen key  . The distinguishing adversary \(\mathcal {A}\) may query the oracles on inputs \((\phi , x) \in \varPhi \times \mathcal {D}\) on which the oracles respond as \(F_{(\phi ,K)}(x) := f(\phi (K),x)\) and \(G_{(\phi ,K)}(x) := g(\phi (K), x)\) for a function g drawn uniformly at random from the set \(\mathcal {FF}(\mathcal {K}, \mathcal {D}, \mathcal {R})\) of all functions \(\mathcal {K} \times \mathcal {D} \rightarrow \mathcal {R}\). Formally, the advantage of \(\mathcal {A}\) against the RKA-PRF security of f with respect to set \(\varPhi \) is defined as
. The distinguishing adversary \(\mathcal {A}\) may query the oracles on inputs \((\phi , x) \in \varPhi \times \mathcal {D}\) on which the oracles respond as \(F_{(\phi ,K)}(x) := f(\phi (K),x)\) and \(G_{(\phi ,K)}(x) := g(\phi (K), x)\) for a function g drawn uniformly at random from the set \(\mathcal {FF}(\mathcal {K}, \mathcal {D}, \mathcal {R})\) of all functions \(\mathcal {K} \times \mathcal {D} \rightarrow \mathcal {R}\). Formally, the advantage of \(\mathcal {A}\) against the RKA-PRF security of f with respect to set \(\varPhi \) is defined as

Intuitively, one should now be able to relate \(\mathsf {RKA}\textsf {-}\mathsf {PRF}\) security to \(\mathsf {PRF}\textsf {-}\mathsf {ODH}\) security by considering two correlated sets of RKD functions corresponding to the PRF-ODH oracles \(\mathsf {ODH}_u\) and \(\mathsf {ODH}_v\) with respect to a group \(\mathbb {G}\) with generator g and two exponents \(u,v \in \mathbb {Z}_q\):
Insurmountable hurdles however seem to remain when trying to relate PRF-ODH notions and RKA-PRF security (for according sets \(\varPhi \)) via implications. In the one direction, the adversary in the PRF-ODH setting is provided with the DH shares \(g^u\) and \(g^v\) forming the (challenge) PRF key while such side information on the key is not given in the RKA-PRF setting. Hence, in a reduction of PRF-ODH security to some RKA-PRF notion, even for an appropriate RKD function set a simulation always lacks means to provide the PRF-ODH adversary with these shares. In the other direction, the RKA-PRF challenge can be issued on any related key \(\phi (K)\) for an admissible RKD function \(\phi \) while the PRF-ODH challenge is, for the case of the real PRF response, always computed on the key \(g^{uv}\). A reduction would hence need to map the RKA-PRF challenge for an arbitrary, related key onto the fixed PRF-ODH challenge key.
Though on a high level capturing a relatively similar idea, the relation between PRF-ODH and RKA-PRF security hence remains an open question.
4 PRF-ODH Relations
In this section we study the relations of different \(\mathsf {PRF}\textsf {-}\mathsf {ODH}\) variants spanned by our generic Definition 1. The relationships are also illustrated in Fig. 2.
Let us start with observing the trivial implications (indicated by solid arrows in Fig. 2) which are induced by restricting the adversary’s capabilities in our definition. That is, by restricting the access to one of the oracles \(\mathsf {ODH}_u\) and \(\mathsf {ODH}_v\) (from multiple queries to a single query or from a single query to no query) for a notion from Definition 1, we obtain a trivially weaker variant. The more interesting question is which of these implications are strict, i.e., for which of two \(\mathsf {PRF}\textsf {-}\mathsf {ODH}\) variant pairs one notion is strictly stronger than the other. For a majority of these cases we can give separations which only require the assumption that the underlying primitive exists at all, for some separations we rely on the random oracle model (and a plausible number-theoretic assumption).
4.1 Separations in the Standard Model
For our standard model separations we introduce the following family of functions \(\mathcal {F}\).
Definition 5
(Separating function family \(\mathcal {F}\) ). Let \(\mathsf {G}:\mathbb {G}\times \{0,1\}^* \rightarrow \{0,1\}^\lambda \). We define the family of functions \(\mathcal {F}= \{\mathsf {F}_n\}_{n \in \mathbb {N}}\) with \(\mathsf {F}_n :\mathbb {G}\times \{0,1\}^* \rightarrow \{0,1\}^\lambda \) as follows:
As a warm-up, let us first consider the (in)security of functions \(\mathsf {F}_n \in \mathcal {F}\) in the standard PRF setting. It is easy to see that no function \(\mathsf {F}_n \in \mathcal {F}\) can satisfy the (regular) security notion for pseudorandom functions: for any function \(\mathsf {F}_n\), querying the PRF oracle on \(x_0 = 0\), ..., \(x_n = n\) yields responses \(y_0\), ..., \(y_n\) for which the combined XOR value \(y = y_0 \oplus \dots \oplus y_n\), in case the oracle computes the real function \(\mathsf {F}_n\), is always 0 whereas otherwise it is 0 only with probability \(2^{-\lambda }\). However, in a restricted setting where the PRF adversary \(\mathcal {A}\) is allowed to query the oracle only a limited number of times (at most n queries for function \(\mathsf {F}_n\)), we can indeed establish the following, restricted PRF security for functions \(\mathsf {F}_n \in \mathcal {F}\).
Proposition 6
( \(\mathcal {F}\) is restricted-PRF-secure). If \(\mathsf {G}\) is an (ordinary) secure pseudorandom function, then each \(\mathsf {F}_n \in \mathcal {F}\) from Definition 5 is an n-restricted secure pseudorandom function in the sense that it provides PRF security against any adversary that is allowed to query the PRF oracle at most n times.
Proof
(informal). Fix a function \(\mathsf {F}_n \in \mathcal {F}\). First, we replace \(\mathsf {G}\) in the definition of \(\mathsf {F}_n\) by a truly random function \(\mathsf {G}'\). The introduced advantage difference for adversary \(\mathcal {A}\) by this step can be bounded by the advantage of an adversary \(\mathcal {B}\) against the PRF security of \(\mathsf {G}\), simulating the (restricted) PRF game for \(\mathcal {A}\) using its own PRF oracle for \(\mathsf {G}\).
After this change, the output values of \(\mathsf {F}_n\) on inputs \(x > 1\) are independent random values and the output on \(x = 0\) is the XOR of the outputs on \(x = 1,\dots ,n\). In contrast, for a truly random function, the outputs on all inputs (incl. \(x = 0\)) are independent and random. However, any adversary \(\mathcal {A}\) that is allowed to query the PRF oracle on at most n inputs cannot distinguish these two cases, bounding its success probability at this point by 0. \(\square \)
Let us now turn to the more involved \(\mathsf {PRF}\textsf {-}\mathsf {ODH}\) setting. Equipped with the function family \(\mathcal {F}\), we can establish separations between various \(\mathsf {PRF}\textsf {-}\mathsf {ODH}\) variants, as illustrated in Fig. 2. The key insight for these separations is similar to the one in the standard PRF setting: an adversary with a limited number of n queries (including the challenge query in the \(\mathsf {PRF}\textsf {-}\mathsf {ODH}\) setting) cannot distinguish (a challenge under) \(\mathsf {F}_n\) from (a challenge under) a truly random function. As subsequent propositions establish, this allows us to separate the notion \(\mathsf {nnPRF}\textsf {-}\mathsf {ODH}\) (with only one challenge query) from \(\mathsf {snPRF}\textsf {-}\mathsf {ODH}\) and \(\mathsf {nsPRF}\textsf {-}\mathsf {ODH}\) (with two queries, the challenge and one to an \(\mathsf {ODH}\) oracle) via function \(\mathsf {F}_1\). Furthermore, the notions \(\mathsf {snPRF}\textsf {-}\mathsf {ODH}\) and \(\mathsf {nsPRF}\textsf {-}\mathsf {ODH}\) (with two queries) are separated from \(\mathsf {mnPRF}\textsf {-}\mathsf {ODH}\), \(\mathsf {ssPRF}\textsf {-}\mathsf {ODH}\), and \(\mathsf {nmPRF}\textsf {-}\mathsf {ODH}\) (with three or polynomially many queries) via \(\mathsf {F}_2\). Finally, we establish that the notion \(\mathsf {ssPRF}\textsf {-}\mathsf {ODH}\) (three queries) can be separated from \(\mathsf {mnPRF}\textsf {-}\mathsf {ODH}\) and \(\mathsf {nmPRF}\textsf {-}\mathsf {ODH}\) (multiple queries) using function \(\mathsf {F}_3\). Note that functions \(\mathsf {F}_n \in \mathcal {F}\) cannot provide a separation between two notions that both allow polynomially many queries (e.g., \(\mathsf {mnPRF}\textsf {-}\mathsf {ODH}\) and \(\mathsf {msPRF}\textsf {-}\mathsf {ODH}\)). To keep the propositions compact, the given separations constitute the minimal spanning set; recall that if a notion A implies another notion B, separating a notion C from B also separates C from A.
We begin with separating \(\mathsf {nnPRF}\textsf {-}\mathsf {ODH}\) from \(\mathsf {snPRF}\textsf {-}\mathsf {ODH}\) and \(\mathsf {nsPRF}\textsf {-}\mathsf {ODH}\) security.
Proposition 7
(
 ). If \(\mathsf {G}\) from Definition 5 is \(\mathsf {nnPRF}\textsf {-}\mathsf {ODH}\)-secure, then \(\mathsf {F}_1 \in \mathcal {F}\) is \(\mathsf {nnPRF}\textsf {-}\mathsf {ODH}\)-secure, but neither \(\mathsf {snPRF}\textsf {-}\mathsf {ODH}\)- nor \(\mathsf {snPRF}\textsf {-}\mathsf {ODH}\)-secure. More precisely, for any efficient adversary \(\mathcal {A}\) against the \(\mathsf {nnPRF}\textsf {-}\mathsf {ODH}\) security of \(\mathsf {F}_1\), there exists an efficient algorithm \(\mathcal {B}\) such that
). If \(\mathsf {G}\) from Definition 5 is \(\mathsf {nnPRF}\textsf {-}\mathsf {ODH}\)-secure, then \(\mathsf {F}_1 \in \mathcal {F}\) is \(\mathsf {nnPRF}\textsf {-}\mathsf {ODH}\)-secure, but neither \(\mathsf {snPRF}\textsf {-}\mathsf {ODH}\)- nor \(\mathsf {snPRF}\textsf {-}\mathsf {ODH}\)-secure. More precisely, for any efficient adversary \(\mathcal {A}\) against the \(\mathsf {nnPRF}\textsf {-}\mathsf {ODH}\) security of \(\mathsf {F}_1\), there exists an efficient algorithm \(\mathcal {B}\) such that
but there exist algorithms \(\mathcal {A}_1\), \(\mathcal {A}_2\) with non-negligible advantage \(\mathsf {Adv}_{\mathsf {F}_1,\mathcal {A}_1}^{\mathsf {snPRF}\textsf {-}\mathsf {ODH}} = \mathsf {Adv}_{\mathsf {F}_1,\mathcal {A}_2}^{\mathsf {nsPRF}\textsf {-}\mathsf {ODH}} = 1 - 2^{-\lambda }\).
Proof
First, observe the following \(\mathsf {snPRF}\textsf {-}\mathsf {ODH}\)-adversary \(\mathcal {A}_1\) and \(\mathsf {nsPRF}\textsf {-}\mathsf {ODH}\)-adversary \(\mathcal {A}_2\) are successful (except with negligible probability). Both first challenge \(\mathsf {F}_1\) on \(x^\star = 0\) (obtaining as \(y^\star \) either \(y^\star _0 = \mathsf {G}(g^{uv}, 1)\) or  ), then query \((g^v, 1)\) resp. \((g^u, 1)\) to their \(\mathsf {ODH}_u\) resp. \(\mathsf {ODH}_v\) oracle, obtaining a value \(y = \mathsf {G}(g^{uv}, 1)\). They distinguish the challenge by outputting 0 if \(y^\star = y\) and 1 otherwise and win except if coincidentally \(y^\star _1 = y\), which happens with probability \(2^{-\lambda }\).
), then query \((g^v, 1)\) resp. \((g^u, 1)\) to their \(\mathsf {ODH}_u\) resp. \(\mathsf {ODH}_v\) oracle, obtaining a value \(y = \mathsf {G}(g^{uv}, 1)\). They distinguish the challenge by outputting 0 if \(y^\star = y\) and 1 otherwise and win except if coincidentally \(y^\star _1 = y\), which happens with probability \(2^{-\lambda }\).
To see that \(\mathsf {F}_1\) is \(\mathsf {nnPRF}\textsf {-}\mathsf {ODH}\)-secure if \(\mathsf {G}\) is, consider an algorithm \(\mathcal {B}\) that simply relays its obtained value \(g^u\) to \(\mathcal {A}\) and the challenge query of \(\mathcal {A}\) to its challenger unmodified if \(x^\star \ne 0\), but for \(x^\star = 0\) asks its challenge query on 1. Forwarding the response and outputting the same bit \(b'\) as \(\mathcal {A}\) outputs, \(\mathcal {B}\) provides a correct simulation for \(\mathcal {A}\) and, moreover, wins if \(\mathcal {A}\) does. \(\square \)
We continue with three further separations:
-
\(\mathsf {snPRF}\textsf {-}\mathsf {ODH}\) from \(\mathsf {mnPRF}\textsf {-}\mathsf {ODH}\), \(\mathsf {ssPRF}\textsf {-}\mathsf {ODH}\), and \(\mathsf {nmPRF}\textsf {-}\mathsf {ODH}\);
-
\(\mathsf {nsPRF}\textsf {-}\mathsf {ODH}\) from \(\mathsf {mnPRF}\textsf {-}\mathsf {ODH}\), \(\mathsf {ssPRF}\textsf {-}\mathsf {ODH}\), and \(\mathsf {nmPRF}\textsf {-}\mathsf {ODH}\); and
-
\(\mathsf {ssPRF}\textsf {-}\mathsf {ODH}\) from \(\mathsf {mnPRF}\textsf {-}\mathsf {ODH}\) and \(\mathsf {nmPRF}\textsf {-}\mathsf {ODH}\).
Due to space restrictions, we only state the respective propositions and defer the proofs to the full version. Note that the proofs follow the same underlying idea as the one of Proposition 7, namely that an adversary being allowed to query a PRF oracle only n times cannot distinguish \(\mathsf {F}_n\) from a truly random function (given the internal function \(\mathsf {G}\) satisfies pseudorandomness properties we specify).
Proposition 8
(
 ). If \(\mathsf {G}\) from Definition 5 is \(\mathsf {mnPRF}\textsf {-}\mathsf {ODH}\)-secure, then \(\mathsf {F}_2 \in \mathcal {F}\) is \(\mathsf {snPRF}\textsf {-}\mathsf {ODH}\)-secure, but neither \(\mathsf {mnPRF}\textsf {-}\mathsf {ODH}\)-, nor \(\mathsf {ssPRF}\textsf {-}\mathsf {ODH}\)-, nor \(\mathsf {nmPRF}\textsf {-}\mathsf {ODH}\)-secure. More precisely, for any efficient adversary \(\mathcal {A}\) against the \(\mathsf {snPRF}\textsf {-}\mathsf {ODH}\) security of \(\mathsf {F}_2\), there exist efficient algorithms \(\mathcal {B}_1\), ..., \(\mathcal {B}_4\) such that
). If \(\mathsf {G}\) from Definition 5 is \(\mathsf {mnPRF}\textsf {-}\mathsf {ODH}\)-secure, then \(\mathsf {F}_2 \in \mathcal {F}\) is \(\mathsf {snPRF}\textsf {-}\mathsf {ODH}\)-secure, but neither \(\mathsf {mnPRF}\textsf {-}\mathsf {ODH}\)-, nor \(\mathsf {ssPRF}\textsf {-}\mathsf {ODH}\)-, nor \(\mathsf {nmPRF}\textsf {-}\mathsf {ODH}\)-secure. More precisely, for any efficient adversary \(\mathcal {A}\) against the \(\mathsf {snPRF}\textsf {-}\mathsf {ODH}\) security of \(\mathsf {F}_2\), there exist efficient algorithms \(\mathcal {B}_1\), ..., \(\mathcal {B}_4\) such that
but there exist algorithms \(\mathcal {A}_1\), ..., \(\mathcal {A}_3\) with non-negligible advantage \(\mathsf {Adv}_{\mathsf {F}_2,\mathcal {A}_1}^{\mathsf {mnPRF}\textsf {-}\mathsf {ODH}} = \mathsf {Adv}_{\mathsf {F}_2,\mathcal {A}_2}^{\mathsf {ssPRF}\textsf {-}\mathsf {ODH}} = \mathsf {Adv}_{\mathsf {F}_2,\mathcal {A}_3}^{\mathsf {nmPRF}\textsf {-}\mathsf {ODH}} = 1 - 2^{-\lambda }\).
Proposition 9
(
 ). If \(\mathsf {G}\) from Definition 5 is \(\mathsf {nmPRF}\textsf {-}\mathsf {ODH}\)-secure, then \(\mathsf {F}_2 \in \mathcal {F}\) is \(\mathsf {nsPRF}\textsf {-}\mathsf {ODH}\)-secure, but neither \(\mathsf {mnPRF}\textsf {-}\mathsf {ODH}\)-, nor \(\mathsf {ssPRF}\textsf {-}\mathsf {ODH}\)-, nor \(\mathsf {nmPRF}\textsf {-}\mathsf {ODH}\)-secure. More precisely, for any efficient adversary \(\mathcal {A}\) against the \(\mathsf {nsPRF}\textsf {-}\mathsf {ODH}\) security of \(\mathsf {F}_2\), there exist efficient algorithms \(\mathcal {B}_1\), ..., \(\mathcal {B}_4\) such that
). If \(\mathsf {G}\) from Definition 5 is \(\mathsf {nmPRF}\textsf {-}\mathsf {ODH}\)-secure, then \(\mathsf {F}_2 \in \mathcal {F}\) is \(\mathsf {nsPRF}\textsf {-}\mathsf {ODH}\)-secure, but neither \(\mathsf {mnPRF}\textsf {-}\mathsf {ODH}\)-, nor \(\mathsf {ssPRF}\textsf {-}\mathsf {ODH}\)-, nor \(\mathsf {nmPRF}\textsf {-}\mathsf {ODH}\)-secure. More precisely, for any efficient adversary \(\mathcal {A}\) against the \(\mathsf {nsPRF}\textsf {-}\mathsf {ODH}\) security of \(\mathsf {F}_2\), there exist efficient algorithms \(\mathcal {B}_1\), ..., \(\mathcal {B}_4\) such that
but there exist algorithms \(\mathcal {A}_1\), ..., \(\mathcal {A}_3\) with non-negligible advantage \(\mathsf {Adv}_{\mathsf {F}_2,\mathcal {A}_1}^{\mathsf {mnPRF}\textsf {-}\mathsf {ODH}} = \mathsf {Adv}_{\mathsf {F}_2,\mathcal {A}_2}^{\mathsf {ssPRF}\textsf {-}\mathsf {ODH}} = \mathsf {Adv}_{\mathsf {F}_2,\mathcal {A}_3}^{\mathsf {nmPRF}\textsf {-}\mathsf {ODH}} = 1 - 2^{-\lambda }\).
Proposition 10
(
 ). If \(\mathsf {G}\) from Definition 5 is \(\mathsf {msPRF}\textsf {-}\mathsf {ODH}\)-secure, then \(\mathsf {F}_3 \in \mathcal {F}\) is \(\mathsf {ssPRF}\textsf {-}\mathsf {ODH}\)-secure, but neither \(\mathsf {mnPRF}\textsf {-}\mathsf {ODH}\)- nor \(\mathsf {nmPRF}\textsf {-}\mathsf {ODH}\)-secure. More precisely, for any efficient adversary \(\mathcal {A}\) against the \(\mathsf {ssPRF}\textsf {-}\mathsf {ODH}\) security of \(\mathsf {F}_3\), there exist efficient algorithms \(\mathcal {B}_1\), ..., \(\mathcal {B}_5\) such that
). If \(\mathsf {G}\) from Definition 5 is \(\mathsf {msPRF}\textsf {-}\mathsf {ODH}\)-secure, then \(\mathsf {F}_3 \in \mathcal {F}\) is \(\mathsf {ssPRF}\textsf {-}\mathsf {ODH}\)-secure, but neither \(\mathsf {mnPRF}\textsf {-}\mathsf {ODH}\)- nor \(\mathsf {nmPRF}\textsf {-}\mathsf {ODH}\)-secure. More precisely, for any efficient adversary \(\mathcal {A}\) against the \(\mathsf {ssPRF}\textsf {-}\mathsf {ODH}\) security of \(\mathsf {F}_3\), there exist efficient algorithms \(\mathcal {B}_1\), ..., \(\mathcal {B}_5\) such that
but there exist algorithms \(\mathcal {A}_1\), \(\mathcal {A}_2\) with non-negligible advantage \(\mathsf {Adv}_{\mathsf {F}_3,\mathcal {A}_1}^{\mathsf {mnPRF}\textsf {-}\mathsf {ODH}} = \mathsf {Adv}_{\mathsf {F}_3,\mathcal {A}_2}^{\mathsf {nmPRF}\textsf {-}\mathsf {ODH}} = 1 - 2^{-\lambda }\).
4.2 Separations in the Random Oracle Model
In the following we use the following problem of computing non-trivial v-th roots in \(\mathbb {G}\) for implicitly given v. That is, consider an algorithm \(\mathcal {A}\) which outputs some group element \(x\in \mathbb {G}\) with \(x\ne 1\) (and some state information), then receives \(g^v\) for random  , and finally outputs y given \(g^v\) and the state information, such that \(y^v=x\). Denote by \(\mathsf {Adv}_{\mathbb {G},\mathcal {A}}^{\mathsf {iiDH}}\) the probability that \(\mathcal {A}\) succeeds in this interactive inversion DH problem.
, and finally outputs y given \(g^v\) and the state information, such that \(y^v=x\). Denote by \(\mathsf {Adv}_{\mathbb {G},\mathcal {A}}^{\mathsf {iiDH}}\) the probability that \(\mathcal {A}\) succeeds in this interactive inversion DH problem.
Note that the problem would be trivial if \(x=1\) was allowed (in which case \(y=1\) would provide a solution), or if x can be chosen after having seen \(g^v\) (in which case \(x=g^v\) and \(y=g\) would trivially work). Excluding these trivial cases, in terms of generic or algebraic hardness the problem is equivalent to the CDH problem. Namely, assume \(\mathcal {A}\) “knows” \(\alpha \in \mathbb {Z}_q\) such that \(x=g^\alpha \). Since x is chosen before seeing \(g^v\) the adversary can only compute it as a power of g and, in addition, \(x\ne 1\) implies \(\alpha \ne 0\). Therefore, for any valid solution y the value \(y^{1/\alpha }\) would be a v-th root of g, because \((y^{1/\alpha })^v=x^{1/\alpha }=g\). This problem of computing \(g^{1/v}\) from \(g,g^v\), however, is known as the inversion-DH (iDH) problem; it is equivalent to the CDH problem with a loose reduction [2].
For our separation result we still need a slightly stronger version here where, in the second phase, the adversary also gets access to a decision oracle which, on input two group elements \(A,B\in \mathbb {G}\) outputs 1 if and only if \(A^v=B\). We call this the strong interactive-inversion DH problem and denote it by \(\mathsf {siiDH}\). Note that for example for a pairing-based group such an oracle is given for free, while computing a v-th root of g (or, equivalently, solving the DH problem may still be hard).
Proposition 11
(
 ). In the random oracle model, and assuming \(\mathsf {StDH}\) and \(\mathsf {siiDH}\), there exists a function \(\mathsf {F}^\mathsf {RO}\) which is \(\mathsf {nmPRF}\textsf {-}\mathsf {ODH}\)-secure but not \(\mathsf {snPRF}\textsf {-}\mathsf {ODH}\)-secure. More precisely, for any efficient adversary \(\mathcal {A}^\mathsf {RO}\) against the \(\mathsf {nmPRF}\textsf {-}\mathsf {ODH}\) security of \(\mathsf {F}^\mathsf {RO}\), there exist efficient algorithms \(\mathcal {B}_1,\mathcal {B}_2\), such that
). In the random oracle model, and assuming \(\mathsf {StDH}\) and \(\mathsf {siiDH}\), there exists a function \(\mathsf {F}^\mathsf {RO}\) which is \(\mathsf {nmPRF}\textsf {-}\mathsf {ODH}\)-secure but not \(\mathsf {snPRF}\textsf {-}\mathsf {ODH}\)-secure. More precisely, for any efficient adversary \(\mathcal {A}^\mathsf {RO}\) against the \(\mathsf {nmPRF}\textsf {-}\mathsf {ODH}\) security of \(\mathsf {F}^\mathsf {RO}\), there exist efficient algorithms \(\mathcal {B}_1,\mathcal {B}_2\), such that
for the at most h queries to the random oracle, but there exists an algorithm \(\mathcal {A}^\mathsf {RO}\) with non-negligible advantage \(\mathsf {Adv}_{\mathsf {F}^\mathsf {RO},\mathcal {A}}^{\mathsf {snPRF}\textsf {-}\mathsf {ODH}} \ge 1 - 2^{-\lambda +1}\).
The idea is to use the following function:
For this function it is easy for an adversary to check for the challenge value \(x^\star =(g^u,0^\lambda )\) if the reply \(y^\star \) is real or random, by making an \(\mathsf {ODH}_u\) query about \((g^{v+1},(g^u,y^\star ))\). With high probability this will trigger the exceptional case of \(\mathsf {F}^\mathsf {RO}\) for \(\mathsf {RO}(g^{u(v+1)}g^{-u},g^u,0^\lambda )=y^\star \) if and only if \(y^\star \) is the correct function value. On the other hand, any adversary with oracle access to \(\mathsf {ODH}_v\) only, will not be able to take advantage of this special evaluation mode for the key \(g^{uv}\) and challenge value \(x^\star =(x,y)\), since this would mean that such a query (T, x) to the \(\mathsf {ODH}_v\) oracle implies that \(x=(Tg^{-u})^v\), i.e., that the adversary can compute a v-th root of x, which is chosen before learning the value \(g^v\). This, however, would contradict the \(\mathsf {siiDH}\) assumption. Moreover, the adversary will not ask the random oracle about the key \(g^{uv}\) either, or else we get a contradiction to the \(\mathsf {StDH}\) assumption (with a loose reduction). But then the challenge value still looks perfectly random to the adversary. The complete proof following this idea appears in the full version.
The idea can now be transferred to the case that we still allow one oracle query to \(\mathsf {ODH}_u\), basically by “secret sharing” the reply in the exceptional case among two queries:
Proposition 12
(
 ). In the random oracle model, and assuming \(\mathsf {StDH}\) and \(\mathsf {siiDH}\), there exists a function \(\mathsf {F}^\mathsf {RO}\) which is \(\mathsf {smPRF}\textsf {-}\mathsf {ODH}\)-secure but not \(\mathsf {mnPRF}\textsf {-}\mathsf {ODH}\)-secure. More precisely, for any efficient adversary \(\mathcal {A}^\mathsf {RO}\) against the \(\mathsf {smPRF}\textsf {-}\mathsf {ODH}\) security of \(\mathsf {F}^\mathsf {RO}\), there exist efficient algorithms \(\mathcal {B}_1,\mathcal {B}_2\), such that
). In the random oracle model, and assuming \(\mathsf {StDH}\) and \(\mathsf {siiDH}\), there exists a function \(\mathsf {F}^\mathsf {RO}\) which is \(\mathsf {smPRF}\textsf {-}\mathsf {ODH}\)-secure but not \(\mathsf {mnPRF}\textsf {-}\mathsf {ODH}\)-secure. More precisely, for any efficient adversary \(\mathcal {A}^\mathsf {RO}\) against the \(\mathsf {smPRF}\textsf {-}\mathsf {ODH}\) security of \(\mathsf {F}^\mathsf {RO}\), there exist efficient algorithms \(\mathcal {B}_1,\mathcal {B}_2\), such that
for the at most h queries to the random oracle, but there exists an algorithm \(\mathcal {A}^\mathsf {RO}\) with non-negligible advantage \(\mathsf {Adv}_{\mathsf {F}^\mathsf {RO},\mathcal {A}^\mathsf {RO}}^{\mathsf {mnPRF}\textsf {-}\mathsf {ODH}} \ge 1 - 2^{-\lambda +1}\).
In fact, in the negative result for \(\mathsf {mnPRF}\textsf {-}\mathsf {ODH}\) the adversary only needs to ask two queries to the \(\mathsf {ODH}_u\) oracle after receiving the challenge query. Since the function is still secure for a single \(\mathsf {ODH}_u\) query, this is optimal in this regard.
The proof appears in the full version.
4.3 Discussion
Let us close this section with some remarks about the separations.
Remark 13
Our separating function family (cf. Definition 5) establishes quite a number of separations, but cannot be used in order to separate the remaining variants. This is due to the fact that our function family cannot separate between notions that both allow polynomial many queries as for example \(\mathsf {nmPRF}\textsf {-}\mathsf {ODH}\) and \(\mathsf {smPRF}\textsf {-}\mathsf {ODH}\). Thus, we have turned to the random oracle model to establish further separations. Using this model is alleviated by the result about the implausibility of instantiating the \(\mathsf {PRF}\textsf {-}\mathsf {ODH}\) assumption in the standard model.
In the random oracle model we have shown that it is crucial if the adversary has access to the \(\mathsf {ODH}_u\) oracle or not (or how many times). This uses some asymmetry in the two oracles, namely, that \(g^u\) is given before the challenge query, and \(g^v\) only after. Our separations take advantage of this difference, visualized via the interactive-inversion DH problem which is only hard if \(x^\star \) is chosen before receiving \(g^v\).
It is currently open if the other notions are separable. Beyond the asymmetry that \(g^u\) is already available before the challenge, it is unclear how to “encode” other distinctive information into the input to the “memoryless” \(\mathsf {PRF}\) which one oracle can exploit but the other one cannot.
Remark 14
In case our generic \(\mathsf {PRF}\textsf {-}\mathsf {ODH}\) assumption (cf. Definition 1) would provide the adversary additionally with the share \(g^v\) in the initialization phase (cf. step 1) then Fig. 2 would symmetrically “collapse” along the vertical axis in the middle. In other words, this would result in equivalences of the notions \(\mathsf {snPRF}\textsf {-}\mathsf {ODH}\) and \(\mathsf {nsPRF}\textsf {-}\mathsf {ODH}\), \(\mathsf {mnPRF}\textsf {-}\mathsf {ODH}\) and \(\mathsf {nmPRF}\textsf {-}\mathsf {ODH}\), as well as \(\mathsf {msPRF}\textsf {-}\mathsf {ODH}\) and \(\mathsf {smPRF}\textsf {-}\mathsf {ODH}\). Note that this is not a contradiction to our separation results among those notions, as they only work if (and exploit that) \(g^v\) is not given in advance.
5 On the Impossibility of Instantiating \(\mathsf {PRF}\textsf {-}\mathsf {ODH}\) in the Standard Model
In this section we show that there is no algebraic black-box reduction \(\mathcal {R}\) which reduces the \(\mathsf {snPRF}\textsf {-}\mathsf {ODH}\) assumption (and analogously the \(\mathsf {nsPRF}\textsf {-}\mathsf {ODH}\) assumption) to a class of hard cryptographic problems, called DDH-augmented abstract problems. With these problems one captures reductions to the DDH problem or to some general, abstract problem like collision resistance of hash functions.
5.1 Overview
The idea is to use the meta-reduction technique. Assume that we have an algebraic reduction \(\mathcal {R}\) from the \(\mathsf {snPRF}\textsf {-}\mathsf {ODH}\) assumption which turns any black-box adversary into a solver for a DDH-augmented problem. Then we in particular consider an inefficient adversary \(\mathcal {A}_\infty \) which successfully breaks the \(\mathsf {snPRF}\textsf {-}\mathsf {ODH}\) assumption with constant probability. The reduction, with black-box access to \(\mathcal {A}_\infty \), must then solve the DDH-augmented problem. For this it can then either not take any advantage of the infinite power of \(\mathcal {A}_\infty \)—in which case we can already break the DDH-augmented problem—or it tries to elicit some useful information from \(\mathcal {A}_\infty \). In the latter case we build our meta-reduction by simulating \(\mathcal {A}_\infty \) efficiently. This is accomplished by exploiting the algebraic property of the reduction and “peeking” at the internals of the reduction’s group element choices. Our meta-reduction will then solve the decisional square-DH problem, saying that \((g,g^a,g^{a^2})\) is indistinguishable from \((g,g^a,g^b)\) from random a, b.
Our impossibility result works for pseudorandom functions \(\mathsf {PRF}\), which take as input arbitrary bit strings and maps them to \(\lambda \) bits. We stick with this convention here, but remark that our negative result also holds if the input length is 1 only, and the output length is super-logarithmic in \(\lambda \). Similarly, we assume that \(\mathsf {PRF}\) is a \(\mathsf {nnPRF}\textsf {-}\mathsf {ODH}\), although it suffices for our negative result that the function \(\mathsf {PRF}\) for a random group element (and some fixed input, say 1) is pseudorandom, i.e., that \(\mathsf {PRF}(X,1)\) is indistinguishable from random for a uniformly chosen group element  (without giving any “Diffie–Hellman decomposition” of X).
(without giving any “Diffie–Hellman decomposition” of X).
Theorem 15
Assume that there is an efficient algebraic black-box reduction \(\mathcal {R}\) from the \(\mathsf {snPRF}\textsf {-}\mathsf {ODH}\) (or \(\mathsf {nsPRF}\textsf {-}\mathsf {ODH}\)) assumption to a DDH-augmented problem. Then either the DDH-augmented problem is not hard, or the decisional square-DH problem is not hard.
If one assumes vice versa that both the underlying augmented-DDH problem and decisional square-DH problem are hard, then this means that there cannot be a reduction as in the theorem to show security of the \(\mathsf {nsPRF}\textsf {-}\mathsf {ODH}\) or \(\mathsf {snPRF}\textsf {-}\mathsf {ODH}\) assumption.
5.2 DDH-augmented Cryptographic Problems
DDH-augmented problems are cryptographic problems in which the adversary either solves a DDH problem or some abstract (and independent) problem in which it receives some instance \(\mathsf {inst}\), can make oracle queries about this instance, and then generates a potential solution \(\mathsf {sol}\). The adversary can decide on the fly which of the two problems to solve. In terms of our setting here we build a reduction against such DDH-augmented problems, capturing for example the case that one aims to show security of the \(\mathsf {PRF}\textsf {-}\mathsf {ODH}\) assumption by assembling a scheme out of several primitives, including the DDH assumption, and giving reductions to each of them.
We next define cryptographic problems in a general way, where it is convenient to use the threshold of \(\tfrac{1}{2}\) for decisional games to measure the adversary’s advantage. We note that we can “lift” common computational games where the threshold is the constant 0 by outputting 1 if the adversary succeeds or if an independent coin flip lands on 1. Formally, a cryptographic problem consists of three probabilistic polynomial-time algorithms \(\mathsf {P}=(\mathsf {P}.\mathsf {Gen},\mathsf {P}.\mathsf {Ch},\mathsf {P}.\mathsf {Vf})\) such that for any probabilistic polynomial-time algorithm \(\mathcal {A}\) we have

is negligible.
A DDH-augmented cryptographic problem \(\mathsf {P}^{\text {DDH}}\) for some group \(\mathbb {G}\) (or, more precisely, for some sequence of groups) based on a problem \(\mathsf {P}\), consists of the following algorithms:
-
\(\mathsf {P}.\mathsf {Gen}^{\text {DDH}}(1^\lambda )\) runs
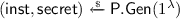 , picks
, picks  and
and 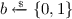 , and outputs \(\mathsf {inst}^\text {DDH}=(g^x,g^y,g^{xy+bz},\mathsf {inst})\) and \(\mathsf {secret}^\text {DDH}=(b,\mathsf {secret})\).
, and outputs \(\mathsf {inst}^\text {DDH}=(g^x,g^y,g^{xy+bz},\mathsf {inst})\) and \(\mathsf {secret}^\text {DDH}=(b,\mathsf {secret})\). -
\(\mathsf {P}.\mathsf {Ch}^\text {DDH}(\mathsf {secret}^\text {DDH},\cdot )\) runs \(\mathsf {P}.\mathsf {Ch}(\mathsf {secret},\cdot )\).
-
\(\mathsf {P}.\mathsf {Vf}^\text {DDH}(\mathsf {secret}^\text {DDH},\mathsf {sol}^\text {DDH})\) checks if \(\mathsf {sol}^\text {DDH}=(``\textsf {DDH}",b')\) and, if so, outputs 1 if and only if \(b=b'\) for bit b in \(\mathsf {secret}^\text {DDH}\). If \(\mathsf {sol}^\text {DDH}=(``\mathsf {P}",\mathsf {sol})\) then the algorithm here outputs \(\mathsf {P}.\mathsf {Vf}(\mathsf {secret},\mathsf {sol})\). In any other case it returns 0.
5.3 Algebraic Reductions for the \(\mathsf {snPRF}\textsf {-}\mathsf {ODH}\) Assumption
Algebraic reductions have been considered in [9] and abstractly defined in [35]. The idea is that the reduction can only perform group operations in the pre-defined way, e.g., by multiplying given elements. As a consequence, whenever the reduction on input group elements \(g_1,g_2,\dots \) generates a group element \(A\in \mathbb {G}\) one can output a representation \((\alpha _1,\alpha _2,\dots )\) such that \(A=\prod g_i^{\alpha _i}\). In [35] this is formalized by assuming the existence of an algorithm which, when receiving the reduction’s input and random tape, can output the representation in addition to A.
In order to simplify the presentation here, we simply assume that the reduction, when forwarding some group element to the adversary, outputs the representation itself. The base elements \(g_1,g_2,\dots \) for the representation are those which the reduction has received so far, as part of the DDH-part of the input or from the interaction with the adversary. The representation is hidden from the adversary in the simulation, of course, but our meta-reduction may exploit this information.
We consider (algebraic) reductions \(\mathcal {R}\) which use the adversary \(\mathcal {A}\) in a black-box way. The reduction may invoke multiple copies of the adversary, possibly rewinding copies. We use the common technique of derandomizing our (unbounded) adversary in question by assuming that it internally calls a truly random function on the communication so far, when it needs to generate some randomness. Note that the truly random function is an integral part of the adversary, and that we view the adversary being picked randomly from all adversaries with such an embedded function. Since the reduction is supposed to work for all successful adversaries, it must also work for such randomly chosen adversaries.
It is now convenient to enumerate the adversary’s instances which the reduction invokes as \(\mathcal {A}_{i}\) for \(i=1,2,\dots \). Since our adversary in question is deterministic we can assume that the reduction “abandons” a copy \(\mathcal {A}_i\) forever, if it starts the next copy \(\mathcal {A}_{i+1}\). This is without loss of generality because the reduction can re-run a fresh copy to the state where it has left the previous instance. This also means that the reduction can effectively re-set executions with the adversary.
The reduction receives as input a triple \((g^x,g^y,g^z)\) and some instance \(\mathsf {inst}\) and should decide if \(g^z=g^{xy}\) or \(g^z\) is random, or provide a solution \(\mathsf {sol}\) to \(\mathsf {inst}\) with the help of oracle \(\mathsf {P}.\mathsf {Ch}\). We stress that the reduction is algebraic with respect the DDH-part of the DDH-augmented problem. In particular, encasing a \(\mathsf {PRF}\textsf {-}\mathsf {ODH}\)-like assumption into the general \(\mathsf {P}\) problem and providing a trivial reduction to the problem itself is not admissible. The group elements (and their representations) handed to the adversary in the reduction are determined by the DDH-part of the input. Finally, we note that we only need that, if \(\mathcal {R}\) interacts with an adversary against \(\mathsf {snPRF}\textsf {-}\mathsf {ODH}\) with advantage \(1-2^{-\lambda }\), then \(\mathcal {R}\) solves the DDH-augmented problem with a non-negligible advantage.
5.4 Outline of Steps
Our negative result proceeds in three main steps:
-
1.
We first define an all-powerful adversary \(\mathcal {A}_\infty \) which breaks the \(\mathsf {snPRF}\textsf {-}\mathsf {ODH}\) assumption by using its infinite power. This adversary will, besides receiving the challenge at point \(x^\star =0\), ask the \(\mathsf {ODH}_u\) oracle to get the value at (S, 1) for random \(S=g^s\), where the random value s is generated via the integral random function. It then uses its power to compute the Diffie–Hellman key \(g^{uv}\), verifies the answer of oracle \(\mathsf {ODH}_u\) with the help of s, and only if this one is valid, gives the correct answer concerning the challenge query. In any other case, the adversary aborts.
-
2.
We then show that the algebraic reduction \(\mathcal {R}\), potentially spawning many black-box copies of our adversary \(\mathcal {A}_\infty \), must answer correctly to the \(\mathsf {ODH}_u\) query in one copy and use the input values \(g^x,g^y,g^z\) non-trivially, or else we can already break the underlying DDH-augmented problem efficiently.
-
3.
Next we show that, if the reduction answers correctly and non-trivially in one of the copies, then we can—using the algebraic nature of the reduction—replace the adversary \(\mathcal {A}_\infty \) by an efficient algorithm, the meta-reduction \(\mathcal {M}\), and either break the decisional square-DH assumption or refute the pseudorandomness of \(\mathsf {PRF}\) for a fresh random group element.
The decisional square-DH assumption says that it is infeasible to distinguish \((g,g^a,g^{a^2})\) from \((g,g^a,g^b)\) for random a, b. It implies the DDH assumption, but is only known to be equivalent to classical DH problem in the computational case [2]. More formally, we will use the following variation: \((g,g^a,g^{a^2},g^{a^2b},g^b,g^{ab})\) is indistinguishable from \((g,g^a,g^{a^2},g^{a^2b},g^b,g^c)\) for random a, b, c.
We briefly argue that the above decision problem follows from the decisional square-DH assumption. The latter assumption implies that we can replace \(g^{a^2}\) and \(g^{a^2b}\) in these tuples by group elements \(g^{d},g^{db}\) for random d, using knowledge of b to compute the other elements. Then, by the DDH assumption, we can replace \(g^{ab}\) in such tuples by a random group element \(g^c\), using knowledge of d to compute the other group elements \(g^d,g^{bd}\). In the last step we can re-substitute \(g^{d},g^{db}\) again by \(g^{a^2}\) and \(g^{a^2b}\), using knowledge of b and c to create the other group elements.
5.5 Defining the All-Powerful Adversary
Let us define our adversary \(\mathcal {A}_\infty \) (with an internal random function \(f:\{0,1\}^*\rightarrow \mathbb {Z}_q\)) against \(\mathsf {snPRF}\textsf {-}\mathsf {ODH}\) formally:
-
1.
Adversary \(\mathcal {A}_\infty \) receives \(g,g^u\) as input.
-
2.
It then asks the challenge oracle about \(x^\star =0\) to receive \(y^\star \) and \(g^v\). We call this the challenge step.
-
3.
It computes \(s=f(g^u,g^v,y^\star )\) and \(S=g^s\) and asks the \(\mathsf {ODH}_u\) oracle about (S, 1) to get some \(y_t\). We call this the test step.
-
4.
It computes \(S^u=(g^u)^s\) and, using its unbounded computational power, also \(g^{uv}\).
-
5.
If \(y_t\ne \mathsf {PRF}(S^u,1)\) then \(\mathcal {A}_\infty \) aborts.
-
6.
Else, \(\mathcal {A}_\infty \) outputs 0 if and only if \(y^\star =\mathsf {PRF}(g^{uv},0)\), and 1 otherwise.
Note that the probability that \(\mathcal {A}_\infty \) outputs the correct answer in an actual attack is \(1-2^{-\lambda }\) and thus optimal; the small error of \(2^{-\lambda }\) is due to the case that the random \(y^\star \) may accidentally hit the value of the \(\mathsf {PRF}\) function.
5.6 Reductions Without Help
Ideally we would now first like to conclude that any reduction which does not provide a correct answer for the test step in any of the copies, never exploits the adversary’s unlimited power and would thus essentially need to immediately succeed, without the help of \(\mathcal {A}_\infty \). We can indeed make this argument formal, simulating \(\mathcal {A}_\infty \) efficiently by using lazy sampling techniques for the generation of s and always aborting in Step 5 if reaching this point. However, we need something slightly stronger here.
Assume that the reduction provides some \(g^u\) in one of the copies for which it knows the discrete logarithm u, i.e., it is not a non-trivial combination of the input values \(g^x,g^y,g^z\) for unknown logarithms. Then the reduction can of course answer the adversary’s test query (S, 1) successfully by computing \(S^u\) and \(\mathsf {PRF}(S^u,1)\). Yet, in such executions it can also compute the reply to the challenge query itself, even if it does not know the discrete logarithm of \(g^v\). In this sense the reduction cannot gain any knowledge about its DDH input, and we also dismiss such cases as useless.
Formally, we call the j-th run of one of the adversary’s copies useless if either the instance aborts in (or before) Step 5, or if the representation of the adversary’s input \(g^u\) in this copy in the given group elements \(g,g^x,g^y,g^z\) and the challenge query values \(S_1,S_2,\dots ,S_{j-1}\) so far, i.e.,
satisfies \(x\alpha +y\beta +z\gamma =0\bmod {q}\). Note that the reduction may form \(g^u\) with respect to all externally provided group elements, including the \(S_i\)’s, such that we also need to account for those elements. We will, however, always set all of them to \(S_i=g^{s_i}\) for some known \(s_i\), such that we are only interested in the question if combination of the DDH input values \(g^x,g^y,g^z\) vanishes.
Let \(\mathsf {useless}_j\) be the event that the j-th instance is useless in the above sense. For such a useless copy we can efficiently simulate adversary \(\mathcal {A}_\infty \), because it either aborts early enough, or the algebraic reduction outputs some \(g^u\) with its representation from which we can compute the discrete logarithm \(u=\delta +\sum _{i<j}s_i\sigma _i\bmod {q}\) and thus execute the decision and test steps of \(\mathcal {A}_\infty \). Let \(\mathsf {useless}\) be the event that all executions of \(\mathcal {A}_\infty \) of the reduction are useless. We next argue that, if the event \(\mathsf {useless}\) happens with overwhelming probability, then we can solve the DDH-augmented problem immediately.
The claim holds as we can emulate the all-powerful adversary \(\mathcal {A}_\infty \) easily, if the reduction essentially always forgoes to run the adversary till the very end or uses only trivial values \(g^u\). Let \((g^x,g^y,g^z,\mathsf {inst})\) be our input and pass this to the reduction. We simply emulate all the copies of the adversary efficiently by:
-
using lazy sampling to emulate the random function f,
-
for each invocation check at the beginning that \((g^x)^\alpha (g^y)^\beta (g^z)^\gamma =1\) for the representation received with the input \(g^u\) for that instance, in which case we can use the discrete logarithm \(u=\delta +\sum _{i<j} s_i\sigma _i\bmod {q}\) to run this copy of \(\mathcal {A}_\infty \), and
-
else always abort after having received y in Step 3.
Denote this way of simulating each copy by adversary \(\mathcal {A}_\text {ppt}\) (even though, technically, the copies share state for the lazy sampling technique and should be thus considered as one big simulated adversary). Then

The latter probability for event \(\overline{\mathsf {useless}}\) is negligible by assumption. We therefore get an efficient algorithm \(\mathcal {R}^{\mathcal {A}_\text {ppt}}\) which breaks the DDH-augmented problem with non-negligible advantage.
5.7 Our Meta-reduction
We may from now on thus assume that  is non-negligible. This implies that the reduction answers at least in one copy of \(\mathcal {A}_\infty \) of the at most polynomial number \(q(\lambda )\) in the test queries in Step 3 with the correct value \(y_t\) for some non-trivial input \(g^u\), with non-negligible probability. Our meta-reduction will try to guess the first execution k where this happens and to “inject” its input \(g^a,g^{a^2},g^{a^2b},g^b,g^c\) into that execution in a useful way. More precisely, it will insert these values into \(g^x,g^y,g^z\) and \(S_k\) such that the expected key K for evaluating \(\mathsf {PRF}\) for the test query equals a function of \(g^{ab}\) if \(g^c=g^{ab}\), but is random if \(g^c\) is random. In the latter case predicting y is infeasible for the reduction, though, because the \(\mathsf {PRF}\) is evaluated on a fresh and random key. This allows to distinguish the two cases.
is non-negligible. This implies that the reduction answers at least in one copy of \(\mathcal {A}_\infty \) of the at most polynomial number \(q(\lambda )\) in the test queries in Step 3 with the correct value \(y_t\) for some non-trivial input \(g^u\), with non-negligible probability. Our meta-reduction will try to guess the first execution k where this happens and to “inject” its input \(g^a,g^{a^2},g^{a^2b},g^b,g^c\) into that execution in a useful way. More precisely, it will insert these values into \(g^x,g^y,g^z\) and \(S_k\) such that the expected key K for evaluating \(\mathsf {PRF}\) for the test query equals a function of \(g^{ab}\) if \(g^c=g^{ab}\), but is random if \(g^c\) is random. In the latter case predicting y is infeasible for the reduction, though, because the \(\mathsf {PRF}\) is evaluated on a fresh and random key. This allows to distinguish the two cases.
The meta-reduction’s injection strategy captures two possible choices of the reduction concerning the equation \(x\alpha +y\beta +z\gamma \ne 0\bmod {q}\) in the (hopefully correctly guessed) k-th execution. One is for the case that \(x\alpha +y\beta \ne 0\bmod {q}\), the other one is for the case that \(x\alpha +y\beta =0\bmod {q}\) and thus \(z\gamma \ne 0\bmod {q}\) according to the assumption \(x\alpha +y\beta +z\gamma \ne 0\bmod {q}\). The meta-reduction will try to predict (via a random bit e) which case will happen and inject the values differently for the cases. This is necessary since the \(g^z\)-value, if it is not random, should contain the DH value of the other two elements.
Our meta-reduction \(\mathcal {M}\) works as follows:
-
1.
The meta-reduction receives \(g^a,g^{a^2},g^{a^2b},g^b,g^c\) as input and should decide if \(g^c=g^{ab}\). If \(a=0\) then we can decide easily, such that we assume that \(a\ne 0\) from now on.
-
2.
The meta-reduction picks an index
 for the polynomial bound \(q(\lambda )\) of adversarial copies the reduction \(\mathcal {R}\) runs with \(\mathcal {A}_\infty \). It also picks
for the polynomial bound \(q(\lambda )\) of adversarial copies the reduction \(\mathcal {R}\) runs with \(\mathcal {A}_\infty \). It also picks 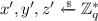 ,
, 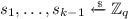 ,
,  , and samples
, and samples  .
. -
3.
For the first injection strategy, \(e=0\), it sets
$$\begin{aligned} g^x=(g^a)^{x'}, \, g^y=(g^a)^{y'},\, g^z=(g^{a^2})^{x'y'}\text { for } d=0= \text { resp. } g^z=(g^{a^2})^{z'} \text { for } d=1. \end{aligned}$$For the other injection strategy, \(e=1\), it sets
$$\begin{aligned} g^x=(g^a)^{x'}, \quad g^y=g^{y'},\quad g^z=(g^{a})^{x'y'}\text { for } d=0 \text { resp. }g^z=g^{az'} \text { for } d=1. \end{aligned}$$ -
4.
It invokes the reduction \(\mathcal {R}\) on input \(g^x,g^y,g^z\) as well as \(\mathsf {inst}\).
-
5.
The meta-reduction simulates the interactions of \(\mathcal {R}\) with \(\mathsf {P}.\mathsf {Ch}\) and \(\mathcal {A}_\infty \) as follows:
-
Each oracle query to \(\mathsf {P}.\mathsf {Ch}\) is answered by running the original algorithm \(\mathsf {P}.\mathsf {Ch}\) for \(\mathsf {secret}\).
-
Use lazy sampling to emulate the random function f.
-
For each of the first \(j<k\) invocations of \(\mathcal {A}_\infty \) check at the beginning that \((g^x)^{\alpha _j}(g^y)^{\beta _j}(g^z)^{\gamma _j}=1\) for the representation received with the input \(g^{u_j}\) for that instance, in which case \(\mathcal {M}\) can use the discrete logarithm \(u_j=\delta _j+\sum _{i<j} s_i\sigma _i\bmod {q}\) to efficiently run this copy of \(\mathcal {A}_\infty \), using \(S_j=g^{s_j}\) for the test query.
-
Otherwise, if \((g^x)^{\alpha _j}(g^y)^{\beta _j}(g^z)^{\gamma _j}\ne 1\), for the j-th invocation of an adversarial copy of \(\mathcal {A}_\infty \) for \(j<k\), up to Step 3, efficiently simulate \(\mathcal {A}_\infty \) using \(S_j=g^{s_{j}}\) for the test query, and immediately abort after this step.
-
-
6.
For the k-th invocation simulate \(\mathcal {A}_\infty \) by using \(S_k=g^b\). If \(\mathcal {M}\) receives a reply \(y_t\) from \(\mathcal {R}\), do the following. Let \(g^{u_k}\) be the input value of this adversary’s copy. Since the reduction is algebraic it has also output values \(\alpha _k,\beta _k,\gamma _k,\delta _k\), \(\sigma _1,\dots ,\sigma _{k-1}\in \mathbb {Z}_q\) such that
$$\begin{aligned} g^{u_k}=(g^x)^{\alpha _k} (g^y)^{\beta _k} (g^z)^{\gamma _k} g^{\delta _k} \cdot \prod _{i<k} S_i^{\sigma _i}. \end{aligned}$$Note that all the base elements, up to this point, only depend on \(g,g^{a}\) (and \(g^{a^2}\) in case of strategy \(e=0\)) of \(\mathcal {M}\)’s inputs \(g^a,g^{a^2},g^{a^2b},g^b,g^c\), because \(g^{u_k}\) is output before seeing \(S_k=g^b\).Footnote 2
-
7.
If strategy \(e=0\) is used and we have \(a(x'\alpha _k+y'\beta _k)\ne 0\bmod {q}\) (which can be checked for \(a\ne 0\) by consulting the known values \(x',\alpha _k,y',\beta _k\)), then the meta-reduction decides as follows. From the value \(g^{a^2b}\) it can compute \(g^{bz\gamma _k}=(g^{a^2b})^{x'y'\gamma _k}\) resp. \((g^{a^2b})^{z'\gamma }\) for both cases \(d\in \{0,1\}\) and can then set
$$\begin{aligned} K =(g^c)^{x'\alpha _k+y'\beta _k} g^{bz\gamma _k} (g^b)^{\delta _k+\sum _{i<k}s_i\sigma _i}. \end{aligned}$$It immediately outputs 0 if \(y_t=\mathsf {PRF}(K,1)\), else it continues.
-
8.
If strategy \(e=1\) is used and we have \(ax'\alpha _k+y'\beta _k=0\bmod {q}\) (which can be checked by verifying that \((g^a)^{x'\alpha _k}g^{y'\beta _k}=1\)), then the meta-reduction computes the key as
$$ K = {\left\{ \begin{array}{ll}(g^c)^{x'y'\gamma _k} (g^b)^{\delta _k+\sum _{i<k}s_i\sigma _i} &{} \text { for d=0 and }\\ (g^c)^{z'\gamma _k} (g^b)^{\delta _k+\sum _{i<k}s_i\sigma _i} &{} \text { for d=1} \end{array}\right. } $$and immediately outputs 0 if \(y_t=\mathsf {PRF}(K,1)\); else it continues.
-
9.
In any other case, if the reduction aborts prematurely or if the insertion strategy has been false, i.e., the choice of e does not match the condition on \(x'\alpha _k+y'\beta _k\ne 0\bmod {q}\), then output a random bit.
5.8 Analysis
For the analysis assume for the moment that our meta-reduction has actually chosen the index k of the first correct and non-trivial answer \(y_t\), i.e., where \(x\alpha _k+y\beta _k+z\gamma _k\ne 0\bmod {q}\). Additionally, assume that \((x\alpha _k+y\beta _k)\ne 0\bmod {q}\). Then \(e=0\) with probability at least \(\tfrac{1}{2}\). This holds since the reduction remains perfectly oblivious about the choice of e, because all values in the interaction have the same distributions in both cases for e. Then the actual key for answering the test query is
This implies that the meta-reduction’s input \(g^c\) yields the same key K if \(g^c=g^{ab}\) and hence equality for the \(\mathsf {PRF}\) value. Yet, it yields a random value if \(g^c\) is random (since the exponent \(x'\alpha _k+y'\beta _k\) does not vanish). In the latter case, since the value \(g^c\) is at no point used in the simulation before the reduction outputs \(y_t\), the probability that \(y_t\) predicts \(\mathsf {PRF}(K,1)\) for the fresh random key, is negligible. This final step in the argument can be formalized straightforwardly.
Assume next that, besides the correct prediction of index k, we have \(e=1\) and \(ax'\alpha _k+y'\beta _k=0\bmod {q}\). Then, since \(ax'\alpha _k+y'\beta _k+z\gamma _k\ne 0\bmod {q}\), we must have that \(z\gamma _k\ne 0\bmod {q}\) and therefore also \(x'y'\gamma _k\ne 0\bmod {q}\) for \(d=0\) resp. \(z'\gamma _k\ne 0\bmod {q}\) for \(d=1\). The same argument as in the previous case applies now. Namely, for \(g^c=g^{ab}\) the meta-reduction computes the expected key, whereas for random \(g^c\) the contribution to the computed value K is for a non-zero exponent, such that equality for the \(\mathsf {PRF}\) value only holds with negligible probability.
Putting the pieces together, for \(g^c=g^{ab}\) our algorithm correctly outputs 0 if the reduction uses the adversary’s help (with non-negligible probability  ), if the prediction k is correct (with non-negligible probability \(\tfrac{1}{q(\lambda )}\)), and if the insertion strategy is correct (with probability at least \(\tfrac{1}{2}\)). Let
), if the prediction k is correct (with non-negligible probability \(\tfrac{1}{q(\lambda )}\)), and if the insertion strategy is correct (with probability at least \(\tfrac{1}{2}\)). Let

denote the non-negligible probability that the meta-reduction outputs 0 early. It also outputs 0 with probability \(\tfrac{1}{2}\) in any other case, such that the probability of outputting 0 for \(g^c=g^{ab}\) is at least
In case that \(g^c\) is random, our meta-reduction only outputs 0 if the \(\mathsf {PRF}\) value matches \(y_t\) for the random key K, or if the final randomly chosen bit equals 0. The probability of this happening is only negligibly larger than \(\tfrac{1}{2}\). This conversely means that the meta-reduction correctly outputs 1 in this case with probability at least \(\tfrac{1}{2}- \text {negl} \!\!\left( \lambda \right) \) for some negligible function \( \text {negl} \!\!\left( \lambda \right) \).
Overall, the probability of distinguishing the cases is at least
which is non-negligibly larger than \(\tfrac{1}{2}\) for non-negligible \(\epsilon (\lambda )\).
6 PRF-ODH Security of HMAC
In this section we briefly discuss the \(\mathsf {PRF}\textsf {-}\mathsf {ODH}\) security of \(\mathsf {HMAC}\) [25], augmenting previous results on the PRF security of \(\mathsf {HMAC}\) [5, 11, 27]. We show that \(\mathsf {HMAC}(K,X)\) as well as its dual-PRF [3] usage \(\mathsf {HMAC}(X,K)\), as encountered in TLS 1.3, are \(\mathsf {mmPRF}\textsf {-}\mathsf {ODH}\) secure, which is our strongest notion of \(\mathsf {PRF}\textsf {-}\mathsf {ODH}\) security. For a complete treatment see the full version.
Recall that \(\mathsf {HMAC}\) is usually based on a Merkle-Damgård hash function H, using a compression function \(h:\{0,1\}^c \times \{0,1\}^b \rightarrow \{0,1\}^c\). The function \(\mathsf {HMAC}\) is then defined as
for key \(K \in \{0,1\}^b\) and label X, \(\mathsf {HMAC}\), where \(\mathsf {opad}\) and \(\mathsf {ipad}\) are fixed (distinct) constants in \(\{0,1\}^b\). In terms of the iterated compression function we have
Keys which are shorter than b bits are padded first, and longer keys K are first hashed down to \(H(K) \in \{0,1\}^c\) and then padded.
In the full version we show the following security property of \(\mathsf {HMAC}\), independently of whether the key \(K\in \mathbb {G}\) is longer or shorter than the block length b:
Theorem 16
Assume that the underlying compression function \(h:\{0,1\}^c \times \{0,1\}^b \rightarrow \{0,1\}^c\) of \(\mathsf {HMAC}\) is a random oracle. Then \(\mathsf {HMAC}\) is \(\mathsf {mmPRF}\textsf {-}\mathsf {ODH}\)-secure under the \(\mathsf {StDH}\) assumption. More precisely, for any efficient adversary \(\mathcal {A}\) against the \(\mathsf {mmPRF}\textsf {-}\mathsf {ODH}\) security of \(\mathsf {HMAC}\), there exists an efficient algorithm \(\mathcal {B}\) such that
where q with the respective index denotes the maximal number of the according oracle queries, and \(\ell _{\mathsf {ODH}}\) the maximal number of oracle calls to h in each evaluation of any \(\mathsf {ODH}\) oracle call.
As mentioned earlier, one specific use case of the \(\mathsf {PRF}\textsf {-}\mathsf {ODH}\) assumption arises in the setting of TLS 1.3. Here, the \(\mathsf {HKDF}\) scheme [27, 28] is adapted for key derivation. In particular, the function \(\mathsf {HKDF}\mathsf {.Extract}\) is used to derive an internal key \(K'\) as
where an adversarially known value X is used as the \(\mathsf {HMAC}\) key while the secret randomness source in the form of a \(\mathsf {DH}\) shared secret \(K=g^{uv}\) is used as the label. At a first glance, this swapping of inputs may seem odd. However, the specified purpose of \(\mathsf {HKDF}\mathsf {.Extract}\) is to extract uniform randomness from its second component.
One way to prove that \(K'\) is indeed a random key (as long as \(g^{uv}\) is not revealed to the adversary) is to model \(\mathsf {HKDF}\mathsf {.Extract}(X, \cdot )\) as a random oracle. An alternative approach is pursued in [15, 16, 18] where the authors prove the statement under the assumption that \(\mathsf {HKDF}\mathsf {.Extract}( XTS , IKM ) = \mathsf {HMAC}( XTS , IKM )\) is \(\mathsf {PRF}\textsf {-}\mathsf {ODH}\) secure when understood as a PRF keyed with \( IKM \in \mathbb {G}\) (i.e., when the key is the second input). In this light, it is beneficial to show that \(\mathsf {HMAC}(X,K)\) remains \(\mathsf {PRF}\textsf {-}\mathsf {ODH}\) secure for key \(K \in \mathbb {G}\) and \(X \in \{0,1\}^\star \).Footnote 3 Fortunately, our general treatment of \(\mathsf {HMAC}(K,X)\) in Theorem 16 with arbitrarily long keys allows us to conclude the analogous result for \(\mathsf {HMAC}(X,K)\) with swapped key and label. This is formally stated in the full version.
In recent developments initiated by the NIST hash function competition it has been established that sponge-based constructions can be used to build cryptographic hash functions. We are confident that the proof of Theorem 16 can be adapted to achieve the same result for \(\mathsf {HMAC}\) if the underlying cryptographic hash function H is replaced by a sponge-based construction such as \(\mathsf {SHA\text {-}3}\) with the random permutation \(\pi \) modeled as a random oracle.Footnote 4 This proof can also be established along the lines of Bertoni et al. [7] who provide results showing that the sponge construction is indifferentiable from a random oracle when being used with a random transformation or a random permutation.
7 Conclusion
To the best of our knowledge, this is the first systematic study of the relations between different variants of the \(\mathsf {PRF}\textsf {-}\mathsf {ODH}\) assumption which is prominently being used in the realm of analyzing major real-world key exchange protocols. We provide a generic definition of the \(\mathsf {PRF}\textsf {-}\mathsf {ODH}\) assumption subsuming those different variants and show separations between most of the variants. Our results give strong indications that instantiating the \(\mathsf {PRF}\textsf {-}\mathsf {ODH}\) assumption without relying on the random oracle methodology is a challenging task, even though it can be formalized in the standard model. In particular, we show that it is implausible to instantiate the assumption in the standard model via algebraic black-box reductions to DDH-augmented problems.
Despite our negative result, we emphasize that using the \(\mathsf {PRF}\textsf {-}\mathsf {ODH}\) assumption still provides some advantage over the \(\mathsf {StDH}\) assumption in the random oracle model. Namely, it supports a modular approach to proving key exchange protocols to be secure, shifting the heavy machinery of random-oracle reductions to \(\mathsf {StDH}\) in the context of complex key exchange protocols to a much simpler assumption. As the \(\mathsf {PRF}\textsf {-}\mathsf {ODH}\) naturally appears in such protocols and enables simpler proofs, it is still worthwhile to use the assumption directly.
Notes
- 1.
While the computational version of the square-DH problem is known to be equivalent to the \(\mathsf {CDH}\) problem, it is unclear if the decisional version follows from \(\mathsf {DDH}\).
- 2.
The same is true for \(g^{v_k}\) generated in the challenge query before, such that the result applies to the \(\mathsf {nsPRF}\textsf {-}\mathsf {ODH}\) assumption accordingly.
- 3.
Though formally defined for arbitrary length, recall that the minimal recommended length is c bits.
- 4.
References
Abdalla, M., Bellare, M., Rogaway, P.: The oracle Diffie-Hellman assumptions and an analysis of DHIES. In: Naccache, D. (ed.) CT-RSA 2001. LNCS, vol. 2020, pp. 143–158. Springer, Heidelberg (2001). doi:10.1007/3-540-45353-9_12
Bao, F., Deng, R.H., Zhu, H.F.: Variations of Diffie-Hellman problem. In: Qing, S., Gollmann, D., Zhou, J. (eds.) ICICS 2003. LNCS, vol. 2836, pp. 301–312. Springer, Heidelberg (2003). doi:10.1007/978-3-540-39927-8_28
Bellare, M.: New proofs for NMAC and HMAC: security without collision-resistance. In: Dwork, C. (ed.) CRYPTO 2006. LNCS, vol. 4117, pp. 602–619. Springer, Heidelberg (2006). doi:10.1007/11818175_36
Bellare, M., Kohno, T.: A theoretical treatment of related-key attacks: RKA-PRPs, RKA-PRFs, and applications. In: Biham, E. (ed.) EUROCRYPT 2003. LNCS, vol. 2656, pp. 491–506. Springer, Heidelberg (2003). doi:10.1007/3-540-39200-9_31
Bellare, M., Lysyanskaya, A.: Symmetric and dual PRFs from standard assumptions: a generic validation of an HMAC assumption. Cryptology ePrint Archive, Report 2015/1198 (2015). http://eprint.iacr.org/2015/1198
Bertoni, G., Daemen, J., Peeters, M., Assche, G.V.: The Keccak SHA-3 submission. Submission to NIST (Round 3) (2011). http://keccak.noekeon.org/Keccak-submission-3.pdf
Bertoni, G., Daemen, J., Peeters, M., Assche, G.: On the indifferentiability of the sponge construction. In: Smart, N. (ed.) EUROCRYPT 2008. LNCS, vol. 4965, pp. 181–197. Springer, Heidelberg (2008). doi:10.1007/978-3-540-78967-3_11
Bhargavan, K., Fournet, C., Kohlweiss, M., Pironti, A., Strub, P.-Y., Zanella-Béguelin, S.: Proving the TLS handshake secure (as it is). In: Garay, J.A., Gennaro, R. (eds.) CRYPTO 2014. LNCS, vol. 8617, pp. 235–255. Springer, Heidelberg (2014). doi:10.1007/978-3-662-44381-1_14
Boneh, D., Venkatesan, R.: Breaking RSA may not be equivalent to factoring. In: Nyberg, K. (ed.) EUROCRYPT 1998. LNCS, vol. 1403, pp. 59–71. Springer, Heidelberg (1998). doi:10.1007/BFb0054117
Brendel, J., Fischlin, M.: Zero round-trip time for the extended access control protocol. Cryptology ePrint Archive, Report 2017/060 (2017). http://eprint.iacr.org/2017/060
Coron, J.-S., Dodis, Y., Malinaud, C., Puniya, P.: Merkle-Damgård revisited: how to construct a hash function. In: Shoup, V. (ed.) CRYPTO 2005. LNCS, vol. 3621, pp. 430–448. Springer, Heidelberg (2005). doi:10.1007/11535218_26
Dagdelen, Ö., Fischlin, M.: Security analysis of the extended access control protocol for machine readable travel documents. In: Burmester, M., Tsudik, G., Magliveras, S., Ilić, I. (eds.) ISC 2010. LNCS, vol. 6531, pp. 54–68. Springer, Heidelberg (2011). doi:10.1007/978-3-642-18178-8_6
Dierks, T., Rescorla, E.: The transport layer security (TLS) protocol version 1.2. RFC 5246 (proposed standard), August 2008. http://www.ietf.org/rfc/rfc5246.txt. Updated by RFCs 5746, 5878, 6176, 7465, 7507, 7568, 7627, 7685, 7905, 7919
Dowling, B., Fischlin, M., Günther, F., Stebila, D.: A cryptographic analysis of the TLS 1.3 handshake protocol candidates. In: Ray, I., Li, N., Kruegel: C. (eds.) ACM CCS 2015, pp. 1197–1210. ACM Press, October 2015
Dowling, B., Fischlin, M., Günther, F., Stebila, D.: A cryptographic analysis of the TLS 1.3 handshake protocol candidates. Cryptology ePrint Archive, Report 2015/914 (2015). http://eprint.iacr.org/2015/914
Dowling, B., Fischlin, M., Günther, F., Stebila, D.: A cryptographic analysis of the TLS 1.3 draft-10 full and pre-shared key handshake protocol. Cryptology ePrint Archive, Report 2016/081 (2016). http://eprint.iacr.org/2016/081
Fischlin, M., Günther, F.: Multi-stage key exchange and the case of Google’s QUIC protocol. In: Ahn, G.J., Yung, M., Li, N. (eds.) ACM CCS 2014, pp. 1193–1204. ACM Press, November 2014
Fischlin, M., Günther, F.: Replay attacks on zero round-trip time: the case of the TLS 1.3 handshake candidates. In: 2017 IEEE European Symposium on Security and Privacy. IEEE, April 2017
Galbraith, S.D.: Mathematics of Public Key Cryptography. Cambridge University Press, Cambridge (2012)
Garg, S., Bhaskar, R., Lokam, S.V.: Improved bounds on security reductions for discrete log based signatures. In: Wagner, D. (ed.) CRYPTO 2008. LNCS, vol. 5157, pp. 93–107. Springer, Heidelberg (2008). doi:10.1007/978-3-540-85174-5_6
Goldwasser, S., Micali, S., Rivest, R.L.: A digital signature scheme secure against adaptive chosen-message attacks. SIAM J. Comput. 17(2), 281–308 (1988)
International Civil Aviation Organization (ICAO): Machine Readable Travel Documents, Part 11, Security Mechanisms for MRTDs, 7th edn. Doc 9303 (2015)
Jager, T., Kohlar, F., Schäge, S., Schwenk, J.: On the security of TLS-DHE in the standard model. In: Safavi-Naini, R., Canetti, R. (eds.) CRYPTO 2012. LNCS, vol. 7417, pp. 273–293. Springer, Heidelberg (2012). doi:10.1007/978-3-642-32009-5_17
Kiltz, E.: A tool box of cryptographic functions related to the Diffie-Hellman function. In: Rangan, C.P., Ding, C. (eds.) INDOCRYPT 2001. LNCS, vol. 2247, pp. 339–349. Springer, Heidelberg (2001). doi:10.1007/3-540-45311-3_32
Krawczyk, H., Bellare, M., Canetti, R.: HMAC: keyed-hashing for message authentication. RFC 2104 (Informational), February 1997. http://www.ietf.org/rfc/rfc2104.txt. Updated by RFC 6151
Krawczyk, H.: HMQV: a high-performance secure Diffie-Hellman protocol. In: Shoup, V. (ed.) CRYPTO 2005. LNCS, vol. 3621, pp. 546–566. Springer, Heidelberg (2005). doi:10.1007/11535218_33
Krawczyk, H.: Cryptographic extraction and key derivation: the HKDF scheme. In: Rabin, T. (ed.) CRYPTO 2010. LNCS, vol. 6223, pp. 631–648. Springer, Heidelberg (2010). doi:10.1007/978-3-642-14623-7_34
Krawczyk, H., Eronen, P.: HMAC-based extract-and-expand key derivation function (HKDF). RFC 5869 (Informational), May 2010. https://rfc-editor.org/rfc/rfc5869.txt
Krawczyk, H., Paterson, K.G., Wee, H.: On the security of the TLS protocol: a systematic analysis. In: Canetti, R., Garay, J.A. (eds.) CRYPTO 2013. LNCS, vol. 8042, pp. 429–448. Springer, Heidelberg (2013). doi:10.1007/978-3-642-40041-4_24
Krawczyk, H., Wee, H.: The OPTLS protocol and TLS 1.3. In: 2016 IEEE European Symposium on Security and Privacy, pp. 81–96. IEEE, March 2016
Li, X., Xu, J., Zhang, Z., Feng, D., Hu, H.: Multiple handshakes security of TLS 1.3 candidates. In: IEEE Symposium on Security and Privacy, SP 2016, San Jose, CA, USA, 22–26 May 2016, pp. 486–505. IEEE Computer Society (2016)
Lychev, R., Jero, S., Boldyreva, A., Nita-Rotaru, C.: How secure and quick is QUIC? Provable security and performance analyses. In: 2015 IEEE Symposium on Security and Privacy, pp. 214–231. IEEE Computer Society Press, May 2015
Maurer, U.M., Wolf, S.: Diffie-Hellman oracles. In: Koblitz, N. (ed.) CRYPTO 1996. LNCS, vol. 1109, pp. 268–282. Springer, Heidelberg (1996). doi:10.1007/3-540-68697-5_21
NIST: Federal Information Processing Standard 202, SHA-3 Standard: Permutation-based hash and extendable-output functions, August 2015. http://dx.doi.org/10.6028/NIST.FIPS.202
Paillier, P., Vergnaud, D.: Discrete-log-based signatures may not be equivalent to discrete log. In: Roy, B. (ed.) ASIACRYPT 2005. LNCS, vol. 3788, pp. 1–20. Springer, Heidelberg (2005). doi:10.1007/11593447_1
Rescorla, E.: The transport layer security (TLS) protocol version 1.3 - draft-ietf-tls-tls13-20, April 2017. https://tools.ietf.org/html/draft-ietf-tls-tls13-20
Ustaoglu, B.: Obtaining a secure and efficient key agreement protocol from (H)MQV and NAXOS. Des. Codes Cryptography 46(3), 329–342 (2008)
Acknowledgments
We thank the anonymous reviewers for valuable comments. This work has been co-funded by the DFG as part of project S4 within the CRC 1119 CROSSING and as part of project D.2 within the RTG 2050 “Privacy and Trust for Mobile Users”.
Author information
Authors and Affiliations
Corresponding author
Editor information
Editors and Affiliations
Rights and permissions
Copyright information
© 2017 International Association for Cryptologic Research
About this paper
Cite this paper
Brendel, J., Fischlin, M., Günther, F., Janson, C. (2017). PRF-ODH: Relations, Instantiations, and Impossibility Results. In: Katz, J., Shacham, H. (eds) Advances in Cryptology – CRYPTO 2017. CRYPTO 2017. Lecture Notes in Computer Science(), vol 10403. Springer, Cham. https://doi.org/10.1007/978-3-319-63697-9_22
Download citation
DOI: https://doi.org/10.1007/978-3-319-63697-9_22
Published:
Publisher Name: Springer, Cham
Print ISBN: 978-3-319-63696-2
Online ISBN: 978-3-319-63697-9
eBook Packages: Computer ScienceComputer Science (R0)







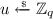 and provides
and provides  and a bit
and a bit  uniformly at random. It then computes
uniformly at random. It then computes 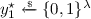 uniformly random. The challenger returns
uniformly random. The challenger returns 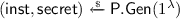 , picks
, picks  and
and 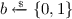 , and outputs
, and outputs  for the polynomial bound
for the polynomial bound 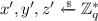 ,
, 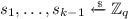 ,
,  , and samples
, and samples  .
.