Abstract
In 1982, Yao introduced a technique of “circuit garbling” that became a central building block in cryptography. The question of garbling general random-access memory (RAM) programs was introduced by Lu and Ostrovsky in 2013. The most recent results of Garg, Lu, and Ostrovsky (FOCS 2015) achieve a garbled RAM with black-box use of any one-way functions and poly-log overhead of data and program garbling in all the relevant parameters, including program run-time. The advantage of Garbled RAM is that large data can be garbled first, and act as persistent garbled storage (e.g. in the cloud) and later programs can be garbled and sent to be executed on this garbled database in a non-interactive manner.
One of the main advantages of cloud computing is not only that it has large storage but also that it has a large number of parallel processors. Despite multiple successful efforts on parallelizing (interactive) Oblivious RAM, the non-interactive garbling of parallel programs remained open until very recently. Specifically, Boyle, Chung and Pass in their TCC 2016-A [4] have shown how to garble PRAM programs with poly-logarithmic (parallel) overhead assuming non-black-box use of identity-based encryption (IBE). The question of whether the IBE assumption, and in particular, the non-black-box use of such a strong assumption is needed. In this paper, we resolve this question and show how to garble parallel programs, with black-box use of only one-way functions and with only poly-log overhead in the (parallel) running time. Our result works for any number of parallel processors.
S. Lu – This material is based upon work supported in part by the DARPA Brandeis program.
R. Ostrovsky – Research supported in part by NSF grant 1619348, DARPA, US-Israel BSF grant 2012366, OKAWA Foundation Research Award, IBM Faculty Research Award, Xerox Faculty Research Award, B. John Garrick Foundation Award, Teradata Research Award, and Lockheed-Martin Corporation Research Award. Work done in part while consulting for Stealth Software Technologies, Inc. The views expressed are those of the authors and do not reflect position of the Department of Defense or the U.S. Government.
You have full access to this open access chapter, Download conference paper PDF
Similar content being viewed by others
Keywords
1 Introduction
Yao [23] introduced a technique that allows one to “garble” a circuit into an equivalent “garbled circuit” that can be executed (once) by someone else without understanding internal circuit values during evaluation. A drawback of circuit representation (for garbling general-purpose programs) is that one can not decouple garbling encrypted data on which the program operates from the program code and inputs. Thus, to run Random Access Machine (RAM) program, one has to unroll all possible execution paths and memory usage when converting programs into circuits. For programs with multiple “if-then-else” branches, loops, etc. this often leads to an exponential blow-up, especially when operating on data which is much larger than program running time. A classic example is for a binary search over n elements, the run time of RAM program is logarithmic in n but the garbled circuit is exponentially larger as it has n size since it must touch all data items.
An alternative approach to program garbling (that does not suffer from this exponential blowup that the trivial circuit unrolling approach has) was initiated by Lu and Ostrovsky in 2013 [20], where they developed an approach that allows to separately encrypt data and separately convert a program into a garbled program without converting it into circuits first and without expanding it to be proportional to the size of data. In the Lu-Ostrovsky approach, the program garbled size and the run time is proportional to the original program run-time (times poly-log terms). The original paper required a complicated circular-security assumption but in sequence of follow-up works [11, 13, 14] the assumption was improved to a black-box use any one-way function with poly-logarithmic overhead in all parameters.
Circuits have another benefit that general RAM programs do not have. Specifically, the circuit model is inherently parallelizable - all gates at the same circuit level can be executed in parallel given sufficiently many processors. In the 1980s and 1990s a parallel model of computation was developed for general programs that can take advantage of multiple processors. Specifically, a Parallel Random Access Memory (PRAM), can take advantage of m processors, executing all of them in parallel with m parallel reads/writes. Indeed, this model was used in various Oblivious RAM papers such as in the works of Boyle, Chung, and Pass [4], as well as Chen, Lin, and Tessaro [8] in TCC 2016-A. In fact, [4] demonstrates the feasibility of garbled parallel RAM under the existince of Identity-based Encryption. However, constructing it from one-way functions remains open, and furthermore, to construct it in a black-box manner. The question that we ask in this paper is this:

The reason this is a hard problem to answer is that now one has to garble memory in such a way that multiple garbled processor threads can read in parallel multiple garbled memory locations, which leads to complicated (garbled) interactions, and remained an elusive goal for these technical reasons. The importance of achieving such a goal in a black-box manner from minimal assumptions is motivated by the fact that almost all garbled circuit constructions are built in a black-box manner. Only the recent work of GLO [11], and the works of Garg et al. [10] and Miao [21] satisfies this for garbled RAM.
In this paper we show that our desired goal is possible to achieve. Specifically, we show a result that is tight both in terms of cryptographic assumptions and the overhead achieved (up to polylog factors): we show that any PRAM program with persistent memory can be compiled into parallel Garbled PRAM program (Parallel-GRAM) based on only a black-box use of one-way functions and with poly-log (parallel) overhead. We remark that the techniques that we develop to achieve our result significantly depart from the works of [4, 11].
1.1 Problem Statement
Suppose a user has a large database D that it wants to encrypt and store in a cloud as some garbled \(\tilde{D}\). Later, the user wants to encrypt several PRAM programs \(\Pi _1,\Pi _2,\ldots \) where \(\Pi _i\) is a parallel program that requires m processors and updates \(\tilde{D}\). Indeed, the user wants to garble each \(\Pi _i\) and ask the cloud to execute the garbled \(\tilde{\Pi }\) program against \(\tilde{D}\) using m processors. The programs may update/modify that encrypted database. We require correctness in that all garbled programs output the same output as the original PRAM program (when operated on persistent, up-to-date D.) At the same time, we require privacy which means that nothing but each program’s running time and the output are revealed. Specifically, we require a simulator that can simulate the parallel program execution for each program, given only its run time and its output. The simulator must be able to simulate each output without knowing any future outputs. We measure the parallel efficiency in terms of garbled program size, garbled data size, and garbled running time.
1.2 Comparison with Previous Work
In the interactive setting, a problem of securely evaluating programs (as opposed to circuits) was started in the works on Oblivious RAM by Goldreich and Ostrovsky [16, 17, 22]. The work of non-interactive evaluation of RAM programs were initiated in the Garbled RAM work of Lu and Ostrovsky [20]. This work showed how to garble memory and program so that programs could be non-interactively and privately evaluated on persistent memory. Subsequent works on GRAM [11, 13, 14] improved the security assumptions, with the latest one demonstrating a fully black-box GRAM from one-way functions.
Parallel RAM. The first work on parallel Garbled RAM was initiated in the papers of Boyle, Chung and Pass [4] and Chen, Lin, and Tessaro [8] where they study it in the context of building an Oblivious Parallel RAM. Boyle et al. [4] show how to construct garbled PRAM assuming non-black-box use of identity-based encryption. That is, they use the actual code of identity-based encryption in order to implement their PRAM garbled protocol. In contrast, we achieve black-box use of one-way functions only, and while maintaining poly-logarithmic (parallel) overhead (matching classical result of Yao for circuits) for PRAM computations. One of the main reasons of why Yao’s result is so influential is that it used one-way function in a black-box way. Black-box use of a one-way function is also critical because in addition to its theoretical interest, the black-box property allows implementers to use their favored instantiation of the cryptographic primitive: this could include proprietary implementations or hardware-based ones (such as hardware support for AES).
Succinct Garbled RAM. In a highly related sequence of works, researchers have also worked in the setting where the garbled programs are also succinct or reusable, so that the size of the garbled programs were independent of the running time. Following the TCC 2013 Rump Session talk of Lu and Ostrovsky, Gentry et al. [15] first presented a scheme based on a stronger notion of differing inputs obfuscation. At STOC 2015, works due to Koppula et al. [19], Canetti et al. [7], and Bitansky et al. [3], each using different machinery in clever ways, made progress toward the problem of succinct garbling using indistinguishability obfuscation. Recently, Chen et al. [9] and Canetti-Holmgren [6] achieve succinct garbled RAM from similar constructions, and the former discusses how to garble PRAM succinctly as well.
Adaptive vs Selective Security. Adaptive security has also become a recent topic of interest. Namely, the security of GRAM schemes where the adversary can adaptively choose inputs based on the garbling itself. Such schemes have recently been achieved for garbled circuits under one-way functions [18]. Adaptive garbled RAM has also been discovered recently, in the works of Canetti et al. [5] and Ananth et al. [1].
1.3 Our Results
In this paper, we provide the first construction of a fully black-box garbled PRAM, i.e. both the construction and the security reduction make only black-box use of any one-way function.
Main Theorem (Informal). Assuming only the existence of one-way functions, there exists a black-box garbled PRAM scheme, where the size of the garbled database is \(\tilde{O}(|D|)\), the size of the garbled parallel program is \(\tilde{O}(T\cdot m)\) where m is the number of processors needed and T is its (parallel) run time and its evaluation time is \(\tilde{O}(T)\) where T is the parallel running time of program \(\Pi \). Here \(\tilde{O}(\cdot )\) ignores \(\textsf {poly}(\log T, \log |D|, \log m, \kappa )\) factors where \(\kappa \) is the security parameter.
1.4 Overview of New Ideas for Our Construction
There are several technical difficulties that must be overcome in order to construct a parallelized GRAM using only black-box access to a one-way function. One attempt is to take the existing black-box construction of [11] and to apply all m processors in order to evaluate their garbling algorithms. However, the problem is that due to the way those circuits are packed into a node: a circuit will not learn how far a child has gone until the predecessor circuit is evaluated. So there must be some sophisticated coordination as the tree is being traversed or else parallelism will not help beyond faster evaluation of individual circuits inside the memory tree. Furthermore, circuits in the tree only accommodates a single CPU key per circuit. To take full advantage of parallelism, we have the ability to evaluate wider circuits that hold more CPU keys. However, we do not know apriori where these CPUs will read, so we must carefully balance the width of the circuit so that it is wide enough to hold all potential CPU keys that gets passed through it, yet not be too large as to impact the overhead. Indeed, the challenge is that the overhead of the storage size cannot depend linearly on the number of processors. We summarize the two main techniques used in our construction that greatly differentiates our new construction from all existing Garbled RAM constructions.
Garbled Label Routing. As there are now m CPUs that are evaluating per step, the garbled CPU labels that pass through our garbled memory tree must be passed along the tree so that each label reaches its according destination. At the leaf level, we want there to be no collisions between the locations so that each reach leaf emits exactly one data element encoded with one CPU’s garbled labels. Looking ahead, in the concrete OPRAM scheme we will compile our solution with that of Boyle, Chung, and Pass [4], which guarantees collision-freeness and uniform access pattern. While this resolves the problem at the leaves, we must still be careful as the paths of all the CPUs will still merge at points in the tree that are only known at run-time. We employ a hybrid technique of using both parallel evaluation of wide circuits, and at some point we switch and evaluate, in parallel, a sequence of thin circuits to achieve this.
Level-dependent Circuit Width. In order to account for the multiple CPU labels being passed in at the root, we widen the circuits. Obviously, if we widen each circuit by a factor of m then this expands the garbled memory size by a prohibitively large factor of m. We do not know until run-time the number of nodes that will be visited at each level, with the exception of the root and leaves, and thus we must balance the sizes of the circuits to be not too large yet not too small. If we assume that the accesses are uniform, then we can expect the number of CPU keys a garbled memory circuit needs to hold is roughly halved at each level. Because of this, we draw inspiration from techniques derived from occupancy and concentration bounds and partition the garbled memory tree into two portions at a dividing boundary level b. This level b will be chosen so that levels above b, i.e. levels closer to the root, will have nodes which we assume will always be visited. However, we also want that the “occupancy” of CPU circuits at level b be sufficiently low that we can jump into the sequential hybrid mentioned above.
The combination of these techniques carefully joined together allows us to cut the overall garbled evaluation time and memory size so that the overhead is still poly-log.
1.5 Roadmap
In Sect. 2 we provide preliminaries and notation for our paper. We then give the full construction of our black-box garbled parallel RAM in Sect. 3. In Sect. 4 we prove that the overhead is polylogarithmic as claimed, and also provide a proof of correctness. We prove a weaker notion of security of our construction in Appendix A, show the transformation from the weaker version to full security in Appendix B and provide the full security proof in Sect. 5.
2 Preliminaries
2.1 Notation
We follow the notation of [4, 11]. Let [n] denote the set \(\{0,\ldots , n-1\}\). For any bitstring L, we use \(L_i\) to denote the \(i^{th}\) bit of L where \(i \in [|x|]\) with the \(0^{th}\) bit being the highest order bit. We let \(L_{0\ldots j-1}\) denote the j high order bits of L. We use shorthand for referring to sets of inputs and input labels of a circuit: if \(\textsf {lab}=\{\textsf {lab}^{i,b}\}_{i\in |x|, b\in {\{0,1\}}}\) describes the labels for input wires of a garbled circuit, then we let \(\textsf {lab}_x\) denote the labels corresponding to setting the input to x, i.e. the subset of labels \(\{\textsf {lab}^{i,x_i}\}_{i\in |x|}\). We write \({\overline{x}}\) to denote that x is a vector of elements, with x[i] being the i-th element. As we will see, half of our construction relies on the same types of circuits used in [11] and we follow their scheme of partitioning circuit inputs into separate logical colors.
2.2 PRAM: Parallel RAM Programs
We follow the definitions of [4, 11]. A m parallel random-access machine is collection of m processors \(\textsf {CPU}_1,\ldots , \textsf {CPU}_{m}\), having local memory of size \(\log N\) which operate synchronously in parallel and can make concurrent access to a shared external memory of size \(N\).
A PRAM program \(\Pi \), on input \(N, m\) and input \({\overline{x}}\), provides instructions to the CPUs that can access to the shared memory. Each processor can be thought of as a circuit that evaluates \(C^\Pi _{\textsf {CPU}[i]}(\textsf {state},\textsf {data}) = (\textsf {state}',{\textsf {R/W}},L,z)\). These circuit steps execute until a halt state is reached, upon which all CPUs collectively output \({\overline{y}}\).
This circuit takes as input the current CPU state \(\textsf {state}\) and a block \(\text {``data''}\). Looking ahead this block will be read from the memory location that was requested for in the previous CPU step. The CPU step outputs an updated state \(\textsf {state}'\), a read or write bit \({\textsf {R/W}}\), the next location to read/write \(L \in [N]\), and a block z to write into the location (\(z=\bot \) when reading). The sequence of locations and read/write values collectively form what is known as the access pattern, namely \(\textsf {MemAccess}= \{ (L^{\tau }, {\textsf {R/W}}^\tau , z^\tau , \textsf {data}^\tau ) : \tau = 1,\ldots ,t \}\), and we can consider the weak access pattern \(\textsf {MemAccess}2 = \{L^{\tau } : \tau = 1,\ldots ,t \}\) of just the memory locations accessed.
We work in the CRCW – concurrent read, concurrent write – model, though as we shall see, we can reduce this to a model where there are no read/write collisions. The (parallel) time complexity of a PRAM program \(\Pi \) is the maximum number of time steps taken by any processors to evaluate \(\Pi \).
As mentioned above, the program gets a “short” input \({\overline{x}}\), can be thought of the initial state of the CPUs for the program. We use the notation \(\Pi ^D({\overline{x}})\) to denote the execution of program \(\Pi \) with initial memory contents D and input \({\overline{x}}\). We also consider the case where several different parallel programs are executed sequentially and the memory persists between executions.
Example Program Execution Via CPU Steps. The computation \(\Pi ^D({\overline{x}})\) starts with the initial state set as \(\textsf {state}_0 = {\overline{x}}\) and initial read location \({\overline{L}}={\overline{0}}\) as a dummy read operation. In each step \(\tau \in \{0,\ldots T-1\}\), the computation proceeds by reading memory locations \({\overline{L^{\tau }}}\), that is by setting \({\overline{\textsf {data}^{{\textsf {read}},\tau }}} := (D[L^{\tau }[0]],\ldots ,D[L^{\tau }[m-1]])\) if \(\tau \in \{1,\ldots T-1\}\) and as \({\overline{0}}\) if \(\tau =0\). Next it executes the CPU-Step Circuit \(C^\Pi _{\textsf {CPU}[i]}(\textsf {state}^{\tau }[i], \textsf {data}^{{\textsf {read}},\tau }[i]) \rightarrow (\textsf {state}^{\tau +1}[i], L^{\tau +1}[i],\) \(\textsf {data}^{\mathsf{write},\tau +1}[i])\). Finally we write to the locations \({\overline{L^{\tau }}}\) by setting \(D[L^{\tau }[i]] := \textsf {data}^{\mathsf{write},\tau +1}[i]\). If \(\tau = T-1\) then we output the state of each CPU as the output value.
2.3 Garbled Circuits
We give a review on Garbled Circuits, primarily following the verbiage and notation of [11]. Garbled circuits were first introduced by Yao [23]. A circuit garbling scheme is a tuple of PPT algorithms \((\textsf {GCircuit},\textsf {Eval})\). Very roughly \(\textsf {GCircuit}\) is the circuit garbling procedure and \(\textsf {Eval}\) the corresponding evaluation procedure. Looking ahead, each individual wire w of the circuit will be associated with two labels, namely \(\textsf {lab}^w_0, \textsf {lab}^w_1\). Finally, since one can apply a generic transformation (see, e.g. [2]) to blind the output, we allow output wires to also have arbitrary labels associated with them. We also require that there exists a well-formedness test for labels which we call \(\textsf {Test}\), which can trivially be instantiated, for example, by enforcing that labels must begin with a sufficiently long string of zeroes.
-
\(\left( \tilde{C}\right) \leftarrow \textsf {GCircuit}\left( 1^\kappa , C, \{(w,b, \textsf {lab}^{w}_b)\}_{w \in \textsf {inp}(C), b\in {\{0,1\}}}\right) \): \(\textsf {GCircuit}\) takes as input a security parameter \(\kappa \), a circuit C, and a set of labels \(\textsf {lab}^{w}_b\) for all the input wires \(w \in \textsf {inp}(C)\) and \(b \in {\{0,1\}}\). This procedure outputs a garbled circuit \(\tilde{C}\).
-
It can be efficiently tested if a set of labels is meant for a garbled circuit.
-
\(y = \textsf {Eval}(\tilde{C}, \{(w, \textsf {lab}^{w}_{x_w})\}_{w \in \textsf {inp}(C)})\): Given a garbled circuit \(\tilde{C}\) and a garbled input represented as a sequence of input labels \(\{(w, \textsf {lab}^{w}_{x_w})\}_{w \in \textsf {inp}(C)}\), \(\textsf {Eval}\) outputs an output y in the clear.
Correctness. For correctness, we require that for any circuit C and input \(x \in {\{0,1\}}^{n}\) (here \(n\) is the input length to C) we have that:
where \(\left( \tilde{C}\right) \leftarrow \textsf {GCircuit}\left( 1^\kappa , C, \{(w,b, \textsf {lab}^{w}_b)\}_{w \in \textsf {inp}(C), b\in {\{0,1\}}}\right) \).
Security. For security, we require that there is a PPT simulator \(\textsf {CircSim}\) such that for any C, x, and uniformly random labels \(\left( \{(w, b, \textsf {lab}^{w}_b)\}_{w \in \textsf {inp}(C), b\in {\{0,1\}}}\right) \), we have that:
where \(\left( \tilde{C}\right) \leftarrow \textsf {GCircuit}\left( 1^\kappa , C, \{(w ,\textsf {lab}^{w}_b)\}_{w \in \textsf {out}(C), b\in {\{0,1\}}}\right) \) and \(y = C(x)\).
2.4 Oblivious PRAM
For the sake of simplicity, we let the CPU activation pattern, i.e. the processors active at each step, simply be that each processor is awake at each step and we only are concerned with the location access pattern \(\textsf {MemAccess}2\).
Definition 1
An Oblivious Parallel RAM (OPRAM) compiler \(\mathcal {O}\), is a PPT algorithm that on input \(m,N\in \mathbb {N}\) and a deterministic m-processors PRAM program \(\Pi \) with memory size \(N\), outputs an m-processor program \(\Pi '\) with memory size \(\textsf {mem}(m, N)\cdot N\) such that for any input x, the parallel running time of \(\Pi '(m, N, x)\) is bounded by \(\textsf {com}(m, N)\cdot T\), where \(T\) is the parallel runtime of \(\Pi (m, N, x)\), where \(\textsf {mem}(\cdot , \cdot ), \textsf {com}(\cdot , \cdot )\) denotes the memory and complexity overhead respectively, and there exists a negligible function \(\nu \) such that the following properties hold:
-
Correctness: For any \(m, N\in \mathbb {N}\), and any string \(x\in {\{0,1\}}^{*}\), with probability at least \(1-\nu (N)\), it holds that \(\Pi (m, N, x) = \Pi '(m,N,x)\).
-
Obliviousness: For any two PRAM programs \(\Pi _1, \Pi _2\), any \(m, N\in \mathbb {N}\), any two inputs \(x_1, x_2 \in {\{0,1\}}^{*}\) if \(|\Pi _1(m, N, x_1)|\) = \(|\Pi _2(m, N, x_2)|\) then \(\textsf {MemAccess}2_1\) is \(\nu \)-close to \(\textsf {MemAccess}2_2\), where \(\textsf {MemAccess}2\) is the induced access pattern.
Definition 2
[Collision-Free]. An OPRAM compiler \(\mathcal {O}\) is said to be collision free if given \(m, N\in \mathbb {N}\), and a deterministic PRAM program \(\Pi \) with memory size \(N\), the program \(\Pi '\) output by \(\mathcal {O}\) has the property that no two processors ever access the same data address in the same timestep.
Remark. The concrete OPRAM compiler of Boyle et al. [4] will satisfy the above properties and also makes use of a convenient shorthand for inter-CPU messages. In their construction, CPUs can “virtually” communicate and coordinate with one another (e.g. so they don’t access the same location) via a fixed-topology network and special memory locations. We remark that this can be emulated as a network of circuits, and will use this fact later.
2.5 Garbled Parallel RAM
We now define the extension of garbled RAM to parallel RAM programs. This primarily follows the definition of previous garbled RAM schemes, but in the parallel setting, and we refer the reader to [11, 13, 14] for additional details. As with many previous schemes, we have persistent memory in the sense that memory data D is garbled once and then many different garbled programs can be executed sequentially with the memory changes persisting from one execution to the next. We define full security and reintroduce the weaker notion of Unprotected Memory Access 2 (UMA2) in the parallel setting (c.f. [11]).
Definition 3
A (UMA2) secure garbled m-parallel RAM scheme consists of four procedures \((\textsf {GData},\) \(\textsf {GProg},\) \(\textsf {GInput},\) \(\textsf {GEval})\) with the following syntax:
-
\((\tilde{D}, {s}) \leftarrow \textsf {GData}(1^\kappa , D)\): Given a security parameter \(1^\kappa \) and memory \(D \in {\{0,1\}}^N\) as input \(\textsf {GData}\) outputs the garbled memory \(\tilde{D}\).
-
\((\tilde{\Pi },s^{in}) \leftarrow \textsf {GProg}(1^\kappa , 1^{\log N}, 1^t, \Pi , s, {t_{old}})\): Takes the description of a parallel RAM program \(\Pi \) with memory-size \(N\) as input. It also requires a key s and current time \({t_{old}}\). It then outputs a garbled program \(\tilde{\Pi }\) and an input-garbling-key \(s^{in}\).
-
\(\tilde{x}\leftarrow \textsf {GInput}(1^\kappa \), \(\overline{x}\),\(s^{in}\)): Takes as input \(\overline{x}\) where \(x[i] \in {\{0,1\}}^n\) for \(i=0,\ldots ,m-1\) and an input-garbling-key \(s^{in}\), outputs a garbled-input \(\tilde{x}\).
-
\(\overline{y} = \textsf {GEval}^{\tilde{D}}(\tilde{\Pi }, \tilde{x})\): Takes a garbled program \(\tilde{\Pi }\), garbled input \(\tilde{x}\) and garbled memory data \(\tilde{D}\) and outputs a vector of values \(y[0],\ldots ,y[m-1]\). We model \(\textsf {GEval}\) itself as a parallel RAM program with m processors that can read and write to arbitrary locations of its memory initially containing \(\tilde{D}\).
Efficiency. We require the parallel run-time of \(\textsf {GProg}\) and \(\textsf {GEval}\) to be \(t\cdot \textsf {poly}(\log N, \log t,\log m, \kappa )\), and the size of the garbled program \(\tilde{\Pi }\) to be \(m \cdot t\cdot \textsf {poly}(\log N, \log t,\log m, \kappa )\). Moreover, we require that the parallel run-time of \(\textsf {GData}\) should be \(N\cdot \textsf {poly}(\log N, \log t,\log m, \kappa )\), which also serves as an upper bound on the size of \(\tilde{D}\). Finally the parallel running time of \(\textsf {GInput}\) is required to be \(n\cdot \textsf {poly}(\kappa )\).
Correctness. For correctness, we require that for any program \(\Pi \), initial memory data \(D \in {\{0,1\}}^N\) and input \(\overline{x}\) we have that:
where \((\tilde{D}, s) \leftarrow \textsf {GData}(1^\kappa , D)\), \((\tilde{\Pi },s^{in}) \leftarrow \textsf {GProg}(1^\kappa , 1^{\log N}, 1^t, \Pi ,s,{t_{old}})\), \(\tilde{x}\leftarrow \textsf {GInput}(1^\kappa , \overline{x},s^{in})\).
Security with Unprotected Memory Access 2 (Full vs UMA2). For full or UMA2-security, we require that there exists a PPT simulator \(\textsf {Sim}\) such that for any program \(\Pi \), initial memory data \(D \in {\{0,1\}}^N\) and input vector \(\overline{x}\), which induces access pattern \(\textsf {MemAccess}2\) we have that:
where \((\tilde{D}, {s}) \leftarrow \textsf {GData}(1^\kappa , D)\), \((\tilde{\Pi },s^{in}) \leftarrow \textsf {GProg}(1^\kappa , 1^{\log N}, 1^t, \Pi ,s,{t_{old}})\) and \(\tilde{x}\leftarrow \textsf {GInput}(1^\kappa , \overline{x},s^{in})\), and \(\overline{y} = \Pi ^D(\overline{x})\). For full security, the simulator \(\textsf {Sim}\) does not get \(\textsf {MemAccess}2\) as input.
Security for multiple programs on persistent memory. In the case where there are multiple PRAM programs being executed in sequence, we consider the garbled memory being initially garbled and then garbled programs can then be ran on the persistent memory in sequence. That is to say, \((\tilde{D}, {s}) \leftarrow \textsf {GData}(1^\kappa , D)\) is used to generate an initial garbled memory, then given programs \(\Pi _1,\ldots ,\Pi _u\), with running times \(t_1,\ldots ,t_u\) we produce garbled programs produced by \((\tilde{\Pi }_i,s^{in}_i) \leftarrow \textsf {GProg}(1^\kappa , 1^{\log N}, 1^{t_i}, \Pi , s, \sum _{j<i}{t_j})\), where the last parameter governs the sequential ordering as a program can only start running at its given time. Given inputs \((\overline{x}_1,\ldots ,\overline{x}_u\) we can produce garbled inputs \(\tilde{x}_i \leftarrow \textsf {GInput}(1^\kappa , \overline{x}_i,s^{in}_i)\). Finally, we have outputs evaluated by running the programs on the persistent memory \(\overline{y}_i = \textsf {GEval}^{\tilde{D}_{i-1}}(\tilde{\Pi }_i, \tilde{x}_i)\), where \(\tilde{D}_i\) is the updated persistent memory after step i. If each program induces some memory access pattern \(\textsf {MemAccess}2_i\), then
Similarly, for full security, the simulator \(\textsf {Sim}\) does not get \(\textsf {MemAccess}2\) as input.
3 Construction of Black-Box Parallel GRAM
3.1 Overview
We first summarize our construction at a high level. An obvious first point to consider is to ask where the difficulty arises when attempting to parallelize the construction of Garg, Lu, and Ostrovsky (GLO) [11]. There are two main issues that go beyond that considered by GLO: first, there must be coordination amongst the CPUs so that if different CPUs want access to the same location, they don’t collide, and second, the control flow is highly sequential, allowing only one CPU key to be passed down the tree per “step”. In order to resolve these issues, we build up a series of steps that transform a PRAM program into an Oblivious PRAM program that satisfies nice properties, and then show how to modify the structure of the garbled memory in order to accommodate parallel accesses.
In a similar vein to previous GRAM constructions, we want to transform a PRAM program first into an Oblivious PRAM program where the memory access patterns are distributed uniformly. However, a uniform distribution of m elements would result in collisions with non-negligible probability. As such, we want an Oblivious PRAM construction where the CPUs can utilize a “virtual” inter-CPU communication to achieve collision-freeness. Looking ahead, in the concrete OPRAM scheme we are using of Boyle, Chung, and Pass (BCP) [4], this property is already satisfied, and we use this in Sect. 5 to achieve full security.
A challenge that remains is to parallelize the garbled memory so that each garbled time step can process m garbled processors in parallel assuming the evaluator has m processors. In order to pass control from one CPU step to the next, we have two distinct phases: one where the CPUs are reading from memory, and another is when the CPUs are communicating amongst themselves to pass messages and coordinating. Because the latter computation can be done with an apriori fixed network of \(\textsf {polylog}(m,N)\) size, we can treat it as a small network of circuits that talk to only a few other CPUs that we can then garble (recall that in order for one CPU to talk to another when garbled, it must have the appropriate input labels hardwired, so we require low locality which is satisfied by these networks). The main technical challenge is therefore being able to read from memory in parallel.
In order to address this challenge, we first consider a solution where we widen each circuit by a factor of m so that m garbled CPU labels (or keys as we will call them) can fit into a circuit at once. This first attempt falls short for several reasons. It expands the garbled memory size by a factor of m, and although keys can be passed down the tree, there is still the issue of how fast these circuits are consumed and how it would affect the analysis of the GLO construction.
To get around the size issue, we employ a specifically calibrated size halving technique: because the m accesses are a random m subset of the \(N\) memory locations, it is expected that half the CPUs want to read to the left, and the other half to the right. Thus, as we move down the tree, the number of CPU keys a garbled memory circuit needs to hold can be roughly halved at each level. Bounding the speed of consumption is a more complex issue. A counting argument can be used to show that at level i, the probability that a particular node will be visited is \(1-\left( {\begin{array}{c}N-N/2^i\\ m\end{array}}\right) /\left( {\begin{array}{c}N\\ m\end{array}}\right) \). As \(N/2^i\) and m may vary from constant to logarithmic to polynomial in \(N\), standard asymptotic bounds might not apply, or would result in a complicated bound. Because of this, we draw inspiration from techniques derived from occupancy and concentration bounds and partition the garbled memory tree into two portions at a dividing boundary level b. This level b will be chosen so that levels above b, i.e. levels closer to the root, will have nodes which we assume will always be visited. However, we also want that at level b, the probability that within a single parallel step more than \(B=\log ^4(N)\) CPUs will all visit a single node is negligible.
It follows then that above level b, for each time step, one garbled circuit at each node at each level will be consumed. Below level b, the tree will fall back to the GLO setting with one major change: level \(b+1\) will be the new “virtual” root of the GLO tree. We must ensure that b is sufficiently small so that this does not negatively impact the overall number of circuits. The boundary nodes at level b will output B garbled queries for each child (which includes the location and CPU keys), which will then be processed one at a time at level \(b+1\). Indeed, each subtree below the nodes at level b will induce a sequence of at most B reads, where each read is performed as in GLO, all of them sequential, but different subtrees will be processed in parallel. This allows us to cut the overall garbled evaluation time down so that the parallel overhead is still poly-log. After the formal construction is given in this section, we provide a full cost analysis of this in Sect. 4, along with the proof of correctness. This construction will then be sufficient to achieve UMA2-security and se will prove in Appendix A, and as mentioned above, we show full security in Sect. 5. We now state our goal/main theorem and spend the rest of the paper providing the formal construction and proof.
Theorem (Main Theorem). Assuming the existence of one-way functions, there exists a fully black-box secure garbled PRAM scheme for arbitrary m-processor PRAM programs. The size of the garbled database is \(\tilde{O}(|D|)\) , size of the garbled input is \(\tilde{O}(|x|)\) and the size of the garbled program is \(\tilde{O}(m T)\) and its m-parallel evaluation time is \(\tilde{O}(T)\) where T is the m-parallel running time of program P. Here \(\tilde{O}(\cdot )\) ignores \(\textsf {poly}(\log T, \log |D|, \log m, \kappa )\) factors where \(\kappa \) is the security parameter.
3.2 Data Garbling: \((\tilde{D}, {s}) \leftarrow \textsf {GData}(1^\kappa , D)\)
We start by providing an informal description of the data garbling procedure, which turns out to be the most involved part of the construction. The formal description of \(\textsf {GData}\) is provided in Fig. 5. Before looking at the garbling algorithm, we consider several sub-circuits. Our garbled memory consists of four types of circuits and an additional table (inherited from the GLO scheme) to keep track of previously output garbled labels. As described in the overview, there will be “wide” circuits near the root that contains main CPU keys, a boundary layer at level b (to be determined later) of boundary nodes that transition wide circuits into thin circuits that are identical to those in the GLO construction. We describe the functionality of the new circuits and review the operations of the GLO style circuits.
Conceptually, the memory can be thought of as a tree of nodes, and each node contains a sequence of garbled circuits. For the circuits, which we call \(\textsf {C}^\textsf {wide}\), above level b, their configuration is straightforward: for every time step, there will be one circuit at every node corresponding to that time step. Below level b, the circuits are configured as in GLO, via \(\textsf {C}^\textsf {node}\) and \(\textsf {C}^\textsf {leaf}\) with the difference being that there will be a fixed multiplicative factor of more circuits per node to account for the parallel reads. At level b, the circuits \(\textsf {C}^\textsf {edge}\) will serve as a transition on the edge between wide and thin circuits as we describe below.
The behavior of the circuits are as follows. \(\textsf {C}^\textsf {wide}\) takes as input a parallel CPU query which consists of a tuple \((\overline{{\textsf {R/W}}},\overline{L},\overline{z},\overline{{\textsf {cpuDKey}}})\). This is interpreted as a vector of indicators to read or write, the location to read or write to, the data to write, and the key of the next CPU step for the CPU that initiated this query. On the k-th circuit of this form at a given node, the circuit has hardwired within it keys for precisely the k-th left and right child (as opposed to a window of child keys focused around k/2 as in the GLO circuit configuration). This circuit routes the queries to the left or right child depending on the location L and passes the (garbled) query down appropriately to exactly one left and one right child. The formal description is provided in Fig. 1.
\(\textsf {C}^\textsf {edge}\) operates similarly and routes the query, but now must interface with the thin circuits below that only accept a single CPU key as input. As such, it will take as input a vector of queries and outputs labels for multiple left and right children circuits. Looking ahead, the precise number of children circuits this will execute will be determined by our analysis, but will be known and fixed in advance for \(\textsf {GData}\). The formal description is provided in Fig. 2.
Formal description of the nonleaf, thin memory circuit with key passing. This is identical to the node circuit in [11].
Finally, the remaining \(\textsf {C}^\textsf {node}\) and \(\textsf {C}^\textsf {leaf}\) behave as they did in the GLO scheme. Their formal descriptions are provided in Figs. 3 and 4. As a quick review, circuits within a node process the query L and activates either a left or a right child circuit (not both, unlike the circuits above). As such, it must also pass on information from one circuit to the subsequent on in the node, providing it information on whether it went left or right, and provides keys to an appropriate window of left and right child circuits. Finally, at the leaf level, the leaf processes the query by either outputting the stored data encoded under the appropriate CPU key, or writes data to its successor leaf circuit. This information passing is stored in a table as in the GLO scheme.
3.3 Program Garbling: \((\tilde{\Pi },s^{in}) \leftarrow \textsf {GProg}(1^\kappa , 1^{\log N}, 1^t, \Pi , {s}, {t_{old}})\)
As we assumed, the program \(\Pi \) is a collision-free OPRAM program. We conceptually identify three distinct steps that are used to compute a parallel CPU step: the main CPU step itself (where each processor takes an input and state, and produces a new state and read/write request), and two types of inter-CPU communication steps that routes the appropriate read/write values before and after memory is accessed. We compile them together as a single large circuit which we describe in Fig. 6.
Then each of the t parallel CPU steps are then garbled in sequence as with previous GRAM constructions. We provide the formal garbling of the steps in Fig. 7.
3.4 Input Garbling: \(\overline{\tilde{x}} \leftarrow \textsf {GInput}(1^\kappa , \overline{x},s^{in})\)
Input garbling is straightforward: the inputs are treated as selection bits for the m-vector of labels. We give a formal description of \(\textsf {GProg}\) in Fig. 8.
3.5 Garbled Evaluation: \(y \leftarrow \textsf {GEval}^{\tilde{D}}(\tilde{\Pi }, \tilde{x})\)
The  procedure gets as input the garbled program \(\tilde{\Pi }\) which we write as \(\left( {t_{old}},\{\tilde{C}^{\tau }\}_{\tau \in \{{t_{old}},\ldots ,{t_{old}}+t-1\}}, {\textsf {cpuDKey}}\right) \), the garbled input \(\tilde{x}= \overline{{\textsf {cpuSKey}}}\) and random access into the garbled database
procedure gets as input the garbled program \(\tilde{\Pi }\) which we write as \(\left( {t_{old}},\{\tilde{C}^{\tau }\}_{\tau \in \{{t_{old}},\ldots ,{t_{old}}+t-1\}}, {\textsf {cpuDKey}}\right) \), the garbled input \(\tilde{x}= \overline{{\textsf {cpuSKey}}}\) and random access into the garbled database  as well as m parallel processors. In order to evaluate a garbled time step \(\tau \), it evaluates every garbled circuit where \(i=0\ldots b, j\in [2^i],k=\tau \) using parallelism to evaluate the wide circuits, then it switches into evaluating \(B({\frac{1}{2}}+\delta )+\kappa \) sequential queries of each of the subtrees below level b as in GLO. Looking ahead, we will see that \(2^b \approx m\) and so we can evaluate the different subtrees in parallel. A formal description of \(\textsf {GEval}\) is provided in Fig. 9.
as well as m parallel processors. In order to evaluate a garbled time step \(\tau \), it evaluates every garbled circuit where \(i=0\ldots b, j\in [2^i],k=\tau \) using parallelism to evaluate the wide circuits, then it switches into evaluating \(B({\frac{1}{2}}+\delta )+\kappa \) sequential queries of each of the subtrees below level b as in GLO. Looking ahead, we will see that \(2^b \approx m\) and so we can evaluate the different subtrees in parallel. A formal description of \(\textsf {GEval}\) is provided in Fig. 9.
4 Cost and Correctness Analysis
4.1 Overall Cost
In this section, we analyze the cost and correctness of the algorithms above, before delving into the security proof. We work with \(d=\log N\), \(b=\log (m)/\log (4/3)\), \(\epsilon =\frac{1}{\log N}\),\(\gamma =\log ^3N\), and \(B=\log ^4N\). First, we observe from the GLO construction, that \(|C^\textsf {node}|\) and \(|C^\textsf {leaf}|\) are both \(\textsf {poly}(\log N, \log t,\log m, \kappa )\), and that the CPU step (with the fixed network of inter-CPU communication) is \(m\cdot \textsf {poly}(\log N, \log t,\log m, \kappa )\).
It remains to analyze the size of \(|C^\textsf {wide}|\) and \(|C^\textsf {edge}|\). Depending on the level in which these circuits appear, they may be of different sizes. Note, if we let \(W_0=m\) and \(W_i = \lfloor ({\frac{1}{2}}+ \delta ) W_{i-1}\rfloor + \kappa \), then \(|C^\textsf {wide}|\) at level i is of size \((W_i+2W_{i+1}) \cdot \textsf {poly}(\log N, \log t,\log m, \kappa )\). We also note \(|C^\textsf {edge}|\) has size at most \(3B\cdot \textsf {poly}(\log N, \log t,\log m, \kappa )= \textsf {poly}(\log N, \log t,\log m, \kappa )\).
We calculate the cost of the individual algorithms.
Cost of GData . The cost of the algorithm \(\textsf {GData}(1^\kappa ,D)\) is dominated by the cost of garbling each circuit (the table generation is clearly \(O(N)\cdot \textsf {poly}(\log N, \log t,\log m, \kappa )\)). We give a straightforward bound of \(K_{b+1+i} \le \left( {\frac{1}{2}}+\epsilon \right) ^{i} ( BN/m + i\kappa )\) and \(W_i \le \left( {\frac{1}{2}}+\epsilon \right) ^i ( m + i\gamma )\).
We must be careful in calculating the cost of the wide circuits, as they cannot be garbled in \(\textsf {poly}(\log N, \log t,\log m, \kappa )\) time, seeing as how their size depends on m. Thus we require a more careful bound, and the cost of garblings of \(C^\textsf {node}\) (ignoring \(\textsf {poly}(\log N, \log t,\log m, \kappa )\) factors) is given as
Plugging in the values for \(d,b,\epsilon ,\gamma ,B\), we obtain \(N\cdot \textsf {poly}(\log N, \log t,\log m, \kappa )\).
Cost of GProg
. The algorithm \(\textsf {GProg}(1^\kappa , 1^{\log N}, 1^t, P, {s}, {t_{old}})\) computes t values for \(\overline{{\textsf {cpuSKey}}}\)s,\(\overline{{\textsf {cpuDKey}}}\)s, and  s. It also garbles t \(C^\textsf {step}\) circuits and outputs them, along with a single \(\overline{{\textsf {cpuSKey}}}\). Since each individual operation is \(m \cdot \textsf {poly}(\log N, \log t,\log m, \kappa )\), the overall space cost is \(\textsf {poly}(\log N, \log t,\log m, \kappa )\cdot t \cdot m\), though despite the larger space, it can be calculated in m-parallel time \(\textsf {poly}(\log N, \log t,\log m, \kappa )\cdot t\).
s. It also garbles t \(C^\textsf {step}\) circuits and outputs them, along with a single \(\overline{{\textsf {cpuSKey}}}\). Since each individual operation is \(m \cdot \textsf {poly}(\log N, \log t,\log m, \kappa )\), the overall space cost is \(\textsf {poly}(\log N, \log t,\log m, \kappa )\cdot t \cdot m\), though despite the larger space, it can be calculated in m-parallel time \(\textsf {poly}(\log N, \log t,\log m, \kappa )\cdot t\).
Cost of GInput . The algorithm \(\textsf {GInput}(1^\kappa , \overline{x},s^{in})\) selects labels of the state key based on the state as input. As such, the space cost is \(\textsf {poly}(\log N, \log t,\log m, \kappa )\cdot m\), and again can be prepared in time \(\textsf {poly}(\log N, \log t,\log m, \kappa )\).
Cost of GEval . For the sake of calculating the cost of \(\textsf {GEval}\), we assume that it does not abort with an error (which, looking ahead, will only occur with negligible probability). At each CPU step, one circuit is evaluated per node above and including level b. At some particular level \(i<b\) the circuit is wide and contains \(O(W_i)\) gates (but shallow, and hence can be parallelized). From our analysis above, we know that \(\sum _{i=0}^{b} 2^i W_i \le \sum _{i=0}^{b} (1+2\epsilon )^i(m+b\gamma ) \le e^{2b\epsilon } (m+b\gamma )\), and can be evaluated in \(\textsf {poly}(\log N, \log t,\log m, \kappa )\) time given m parallel processors. For the remainder of the tree, we can think of virtually spawning \(2^{b+1}\) processes where each process sequentially performs B queries against the subtrees. The query time below level b is calculated from GLO of having amortized \(\textsf {poly}(\log N, \log t,\log m, \kappa )\) cost, and therefore incurs \(2^{b+1} \cdot B \cdot \textsf {poly}(\log N, \log t,\log m, \kappa )\) cost. However, \(2^{b+1} \le m\) and therefore can be parallelized down to \(\textsf {poly}(\log N, \log t,\log m, \kappa )\) overhead.
4.2 Correctness
The arrangement of the circuits below level b follows that of the GLO scheme, and by their analysis, the errors overflow errors \(\texttt {OVERCONSUMPTION-ERROR-I}\) and \(\texttt {OVERCONSUMPTION-ERROR-II}\) do not occur except with a negligible probability. Therefore, for correctness, we must show that \(\texttt {KEY-OVERFLOW-ERROR}\) never occurs except with negligible probability, both at \(C^\textsf {wide}\) and \(C^\textsf {edge}\).
Claim
\(\texttt {KEY-OVERFLOW-ERROR}\) with probability negligible in \(N\).
Proof
The only two ways this error is thrown is if a wide circuit of a parent of level i attempts to place more than \(W_i\) CPU keys into a child node at level i, or an edge circuit fails the bound \(w\le B\). We show that this cannot happen with very high probability. In order to do so, we first put a lower bound on \(W_i\) and then show that the probability that a particular query will cause a node at level i to have more than \(W_i\) CPU keys is negligible. We have that
Our goal is to bound the probability that if we pick m random leaves that more than \(W_i\) paths from the root to those leaves go through a particular node at level i. Of course, the m random leaves are chosen to be uniformly distinct values, but we can bound this by performing an easier analysis where m are chosen uniformly at random with repetition.
We let X be a variable that indicates the number of paths that take a particular node at level i. We can treat X as a sum of m independent trials, and thus expect \(\mu =\frac{m}{2^i}\) hits on average. We set \(\delta = 2\epsilon + \frac{\gamma }{\mu }\). Then by the strong form of the Chernoff bound, we have:
Since \(\epsilon \gamma =\frac{\log ^3N}{\log N}\), this is negligible in \(N\).
Finally, need to show that \(W_b\le B\) so that \(C^\textsf {edge}\) does not cause the error. Here, we use the upper bound for \(W_b\), and assume \(\log N>4\). We calculate:
\(\square \)
5 Main Theorem
We complete the proof of our main theorem in this section, where we combine our UMA2-secure GPRAM scheme with statistical OPRAM. First, we state a theorem from [4]:
Theorem 4
(Theorem from [4]). There exists an activation-preserving and collision-free OPRAM compiler with polylogarithmic worst-case computational overhead and \(\omega (1)\) memory overhead.
We make the additional observation that the scheme also produces a uniformly random access pattern that always chooses m random memory locations to read from at each step, hence a program compiled under this theorem satisfies the assumption of our UMA2-security theorem. We make the following remark:
Remark on Circuit Replenishing As with many previous garbled RAM schemes such as [11, 13, 14], the garbled memory eventually becomes consumed and will needed to be refreshed as they are being consumed across multiple programs. Our garbled memory is created for \(N/m\) timesteps and for the sake of brevity we refer the reader to [12] for the details of applying such a technique.
Then, by combining Theorem 4 with Theorem 6 and Lemma 7, we obtain our main theorem.
Theorem 5
(Main Theorem). Assuming the existence of one-way functions, there exists a fully black-box secure garbled PRAM scheme for arbitrary m-processor PRAM programs. The size of the garbled database is \(\tilde{O}(|D|)\), size of the garbled input is \(\tilde{O}(|x|)\) and the size of the garbled program is \(\tilde{O}(m T)\) and its m-parallel evaluation time is \(\tilde{O}(T)\) where T is the m-parallel running time of program P. Here \(\tilde{O}(\cdot )\) ignores \(\textsf {poly}(\log T, \log |D|, \log m, \kappa )\) factors where \(\kappa \) is the security parameter.
References
Ananth, P., Chen, Y.-C., Chung, K.-M., Lin, H., Lin, W.-K.: Delegating RAM computations with adaptive soundness and privacy. In: Hirt, M., Smith, A. (eds.) TCC 2016. LNCS, vol. 9986, pp. 3–30. Springer, Heidelberg (2016). doi:10.1007/978-3-662-53644-5_1
Applebaum, B., Ishai, Y., Kushilevitz, E.: From secrecy to soundness: efficient verification via secure computation. In: Abramsky, S., Gavoille, C., Kirchner, C., Meyer auf der Heide, F., Spirakis, P.G. (eds.) ICALP 2010. LNCS, vol. 6198, pp. 152–163. Springer, Heidelberg (2010). doi:10.1007/978-3-642-14165-2_14
Bitansky, N., Garg, S., Lin, H., Pass, R., Telang, S.: Succinct randomized encodings and their applications. In: Servedio, R.A., Rubinfeld, R. (eds.) 47th Annual ACM Symposium on Theory of Computing, Portland, OR, USA, June 14–17, 2015, pp. 439–448. ACM Press (2015)
Boyle, E., Chung, K.-M., Pass, R.: Oblivious parallel RAM and applications. In: Kushilevitz, E., Malkin, T. (eds.) TCC 2016. LNCS, vol. 9563, pp. 175–204. Springer, Heidelberg (2016). doi:10.1007/978-3-662-49099-0_7
Canetti, R., Chen, Y., Holmgren, J., Raykova, M.: Adaptive succinct garbled RAM or: how to delegate your database. In: Hirt, M., Smith, A. (eds.) TCC 2016. LNCS, vol. 9986, pp. 61–90. Springer, Heidelberg (2016). doi:10.1007/978-3-662-53644-5_3
Canetti, R., Holmgren, J.: Fully succinct garbled RAM. In: Sudan, M. (ed.) ITCS 2016: 7th Innovations in Theoretical Computer Science, Cambridge, MA, USA, January 14–16, 2016, pp. 169–178. Association for Computing Machinery (2016)
Canetti, R., Holmgren, J., Jain, A., Vaikuntanathan, V.: Succinct garbling and indistinguishability obfuscation for RAM programs. In: Servedio, R.A., Rubinfeld, R. (eds.) 47th Annual ACM Symposium on Theory of Computing, Portland, OR, USA, June 14–17, 2015, pp. 429–437. ACM Press (2015)
Chen, B., Lin, H., Tessaro, S.: Oblivious parallel RAM: improved efficiency and generic constructions. In: Kushilevitz, E., Malkin, T. (eds.) TCC 2016. LNCS, vol. 9563, pp. 205–234. Springer, Heidelberg (2016). doi:10.1007/978-3-662-49099-0_8
Chen, Y.-C., Chow, S.S.M., Chung, K.-M., Lai, R.W.F., Lin, W.-K., Zhou, H.-S.: Cryptography for parallel RAM from indistinguishability obfuscation. In: Sudan, M. (ed.) ITCS 2016: 7th Innovations in Theoretical Computer Science, Cambridge, MA, USA, January 14–16, 2016, pp. 179–190. Association for Computing Machinery (2016)
Garg, S., Gupta, D., Miao, P., Pandey, O.: Secure multiparty RAM computation in constant rounds. In: Hirt, M., Smith, A. (eds.) TCC 2016. LNCS, vol. 9985, pp. 491–520. Springer, Heidelberg (2016). doi:10.1007/978-3-662-53641-4_19
Garg, S., Lu, S., Ostrovsky, R.: Black-box garbled RAM. In: Guruswami, V. (ed.) 56th Annual Symposium on Foundations of Computer Science, Berkeley, CA, USA, October 17–20, 2015, pp. 210–229. IEEE Computer Society Press (2015)
Garg, S., Lu, S., Ostrovsky, R.: Black-box garbled RAM. Cryptology ePrint Archive, Report 2015/307 (2015). http://eprint.iacr.org/2015/307
Garg, S., Lu, S., Ostrovsky, R., Scafuro, A.: Garbled RAM from one-way functions. In: Servedio, R.A., Rubinfeld, R. (ed.) 47th Annual ACM Symposium on Theory of Computing, Portland, OR, USA, June 14–17, 2015, pp. 449–458. ACM Press (2015)
Gentry, C., Halevi, S., Lu, S., Ostrovsky, R., Raykova, M., Wichs, D.: Garbled RAM revisited. In: Nguyen, P.Q., Oswald, E. (eds.) EUROCRYPT 2014. LNCS, vol. 8441, pp. 405–422. Springer, Heidelberg (2014). doi:10.1007/978-3-642-55220-5_23
Gentry, C., Halevi, S., Raykova, M., Wichs, D.: Outsourcing private RAM computation. In: 55th Annual Symposium on Foundations of Computer Science, Philadelphia, PA, USA, October 18–21, 2014, pp. 404–413. IEEE Computer Society Press (2014)
Goldreich, O.: Towards a theory of software protection and simulation by oblivious RAMs. In: Aho, A. (ed.) 19th Annual ACM Symposium on Theory of Computing, New York City, NY, USA, May 25–27, 1987, pp. 182–194. ACM Press (1987)
Goldreich, O., Ostrovsky, R.: Software protection and simulation on oblivious RAMs. J. ACM 43(3), 431–473 (1996)
Hemenway, B., Jafargholi, Z., Ostrovsky, R., Scafuro, A., Wichs, D.: Adaptively secure garbled circuits from one-way functions. In: Robshaw, M., Katz, J. (eds.) CRYPTO 2016. LNCS, vol. 9816, pp. 149–178. Springer, Heidelberg (2016). doi:10.1007/978-3-662-53015-3_6
Koppula, V., Lewko, A.B., Waters, B.: Indistinguishability obfuscation for turing machines with unbounded memory. In: Servedio, R.A., Rubinfeld, R. (ed.) 47th Annual ACM Symposium on Theory of Computing, Portland, OR, USA, June 14–17, 2015, pp. 419–428. ACM Press (2015)
Lu, S., Ostrovsky, R.: How to Garble RAM programs? In: Johansson, T., Nguyen, P.Q. (eds.) EUROCRYPT 2013. LNCS, vol. 7881, pp. 719–734. Springer, Heidelberg (2013). doi:10.1007/978-3-642-38348-9_42
Miao, P.: Cut-and-choose for garbled RAM. Cryptology ePrint Archive, Report 2016/907 (2016). http://eprint.iacr.org/2016/907
Ostrovsky, R.: Efficient computation on oblivious RAMs. In: 22nd Annual ACM Symposium on Theory of Computing, Baltimore, MD, USA, May 14–16, 1990, pp. 514–523. ACM Press (1990)
Yao, A.C.-C.: Protocols for secure computations (extended abstract). In: 23rd Annual Symposium on Foundations of Computer Science, Chicago, Illinois, November 3–5, 1982, pp. 160–164. IEEE Computer Society Press (1982)
Acknowledgments
We thank Alessandra Scafuro for helpful discussions. We thank the anonymous reviewers for their useful comments.
Author information
Authors and Affiliations
Corresponding authors
Editor information
Editors and Affiliations
Appendices
A UMA2-security Proof
In this section we state and prove our main technical contribution on fully black-box garbled parallel RAM that leads to our full theorem. Below, we provide our main technical theorem:
Theorem 6
(UMA2-security). Let F be a PRF and \((\textsf {GCircuit},\textsf {Eval},\textsf {CircSim})\) be a circuit garbling scheme, both of which can be built from any one-way function in black-box manner. Then our construction \((\textsf {GData},\) \(\textsf {GProg},\) \(\textsf {GInput},\) \(\textsf {GEval})\) is a UMA2-secure garbled PRAM scheme for m-processor uniform parallel access programs running in total time \(T<N/m\) making only black-box access to the underlying OWF.
Proof.
Informally, at a high level, we can describe our proof as follows. We know that below level b, the circuits can all be properly simulated due to the fact they are constructed identically to that of GLO (except there are simply more circuits). On the other hand, circuits above this level have no complex parent-to-child wiring, i.e. for each time step, every parent contains exactly the keys for its two children at that time step and not any other time step. Furthermore, circuits within a node above level b do not communicate to each other. Thus, simulating these circuits are straightforward: at time step \({t_{old}}\), simulate the root circuit \(\tilde{C}^{0,0,\tau }\) then simulate the next level down \(\tilde{C}^{1,0,\tau }\) and \(\tilde{C}^{1,1,\tau }\) and so forth.
The formal analysis is as follows. Since we are proving UMA2-security, we know ahead of time the number of time steps, the access locations, and hence the exact circuits that will be executed and in which order. Of course, we are evaluating circuits in parallel, but as we shall see, whenever we need to resolve the ordering of two circuits are being executed in parallel, we will already be working in a hybrid in which they are independent of one another, and hence we can arbitrarily assign an order (lexicographically). Let \(\textsf {CircSim}\) be the garbled circuit simulator, and let U be the total number of circuits that will be evaluated in the real execution. We show how to construct a simulator \(\textsf {Sim}\) and then give a series of hybrids \(\hat{H}^0,H^0,\ldots ,H^U,\hat{H}^U\) such that the first hybrid outputs the \((\tilde{D},\tilde{\Pi },\tilde{x})\) of the is the real execution and the last hybrid is the output of \(\textsf {Sim}\), which we will define. The construction will have a similar structure of previous garbling hybrid schemes, and for the circuits below level b we use the same analysis as in [11], but still the proof will require new analysis for circuits above level b. \(H^0\) is the real execution with the PRF F replaced with a uniform random function (where previously evaluated values are tabulated). Since the PRF key is not used in evaluation, we immediately obtain \(\hat{H}^0\mathop {\approx }\limits ^{{\tiny {\mathrm {comp}}}}H^0\).
Consider the sequence of circuits that would have been evaluated given \(\textsf {MemAccess}\). This sequence is entirely deterministic and therefore we let \(S_1,\ldots ,\) \(S_U\) be this sequence of circuits, e.g. \(S_1=\tilde{C}^0 \text {(the first parallel CPU step circuit)},\) \( S_2=\tilde{C}^{0,0,0} \text {(the first root circuit)},\ldots \). \(H^u\) simulates the first u of these circuits, and generates all other circuits as in the real execution.
Hybrid Definition: \((\tilde{D},\tilde{\Pi },\tilde{x}) \leftarrow H^u\)
The hybrid \(H^u\) proceeds as follows: For each circuit not in \(S_1,\ldots ,S_u\), generate it as you would in the real execution (note that \(\textsf {GData}\) can generate circuits using only, and for each circuit \(S_u,\ldots ,S_1\) (in that order) we simulate the circuit using \(\textsf {CircSim}\) by giving it as output what it would have generated in the real execution or what was provided as the simulated input labels. Note that this may use information about the database D and the inputs \(\overline{x}\), and our goal is to show that at the very end, \(\textsf {Sim}\) will not need this information.
We now show \(H^{u-1}\mathop {\approx }\limits ^{{\tiny {\mathrm {comp}}}}H^u\). Either \(S_u\) is a circuit in the tree, in which case let i be its level, or else \(S_u\) is a CPU step circuit. We now analyze the possible cases:
-
1.
\(i=0:\) In a root node, the only circuit that holds its
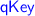 is the previous step node, which would have already been simulated, so the output of \(\textsf {CircSim}\) is indistinguishable from a real garbling.
is the previous step node, which would have already been simulated, so the output of \(\textsf {CircSim}\) is indistinguishable from a real garbling. -
2.
\(0<i\le b:\) In a wide or edge node, the only circuit that holds its
 is the parent circuit from the same time step. Since this was previously evaluated and simulated, we can again simulate this circuit with \(\textsf {CircSim}\).
is the parent circuit from the same time step. Since this was previously evaluated and simulated, we can again simulate this circuit with \(\textsf {CircSim}\). -
3.
\(i=b+1:\) In the level below the edge node, the circuits are arranged as in the root of the GLO construction. However, the
 and
and 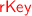 inputs for these circuits now can either come from the parent (edge circuit) or a predecessor thin circuit in the same level. These can be handled in batches of B, sequentially, because every node still has a distinct parent that holds its
inputs for these circuits now can either come from the parent (edge circuit) or a predecessor thin circuit in the same level. These can be handled in batches of B, sequentially, because every node still has a distinct parent that holds its  (that will never be passed on to subsequent parents, as edge circuits do not pass information from one to the next), as well as its immediate predecessor which will already have been simulated. Thus, again we can invoke \(\textsf {CircSim}\).
(that will never be passed on to subsequent parents, as edge circuits do not pass information from one to the next), as well as its immediate predecessor which will already have been simulated. Thus, again we can invoke \(\textsf {CircSim}\). -
4.
\(i>b+1:\) Finally, these nodes all behave as in the GLO construction, and it similarly follows by the analysis of their construction, these nodes can all also be simulated.
In the final case, if \(S_u\) is a CPU step circuit, then only the CPU circuit of the previous time step has its \(\overline{{\textsf {cpuSKey}}}\). On the other hand, its \(\overline{{\textsf {cpuDKey}}}\) originated from the previous CPU step, but was passed down the entire tree. Due to the way we order the circuits, we ensure that all parallel steps have been completed before this circuit is evaluated, and this ensures that any circuit that passed a \({\textsf {cpuDKey}}\) as a value have already been simulated in an earlier hybrid. Thus, any distinguisher of \(H^{u-1}\) and \(H^u\) can again be used to distinguish between the output of \(\textsf {CircSim}\) and a real garbling.
After the course of evaluation, there will be of course unevaluated circuits in the final hybrid \(\hat{H}^U\). As with [11], we use the same circuit encryption technique (see Appendix B in [12] for a formal proof) and encrypt these circuits so that partial inputs of a garbled circuit reveal nothing about the circuit.
Therefore, our simulator  can output the distribution \(\hat{H}^U\) without access to D or \(\overline{x}\). We see this as follows: the simulator, given \(\textsf {MemAccess}\) can determine the sequence \(S_1,\ldots ,S_U\). The simulator starts by first replacing all circuits that won’t be evaluated by replacing them with encryptions of zero. It then simulates the \(S_u\) in reverse order, starting with simulating \(S_U\) using the output \(\overline{y}\), and then working backwards simulates further ones ensuring that their output is set to the appropriate inputs.
can output the distribution \(\hat{H}^U\) without access to D or \(\overline{x}\). We see this as follows: the simulator, given \(\textsf {MemAccess}\) can determine the sequence \(S_1,\ldots ,S_U\). The simulator starts by first replacing all circuits that won’t be evaluated by replacing them with encryptions of zero. It then simulates the \(S_u\) in reverse order, starting with simulating \(S_U\) using the output \(\overline{y}\), and then working backwards simulates further ones ensuring that their output is set to the appropriate inputs.
\(\square \)
B UMA2 to Full Security
In this section, we describe how to achieve multi-program full security from UMA2 security by applying a Oblivious PRAM scheme. We mention that this transformation is an adaptation of the UMA2-to-full transformation of the GLO solution into PRAM setting. As such, we will paraphrase much of the proof found in [12] though in the context of parallel programs.
Lemma 7
Assume there exists a UMA2-secure Garbled PRAM scheme for programs with uniform memory access, and a statistically secure ORAM scheme with uniform memory access that protects the access pattern but not necessarily the contents of memory. Then there exists a fully secure Garbled Parallel RAM scheme.
Proof
We note that although we consider uniform memory access, we do not require the memory access to be strictly uniform, c.f. [12] for a discussion on leveled uniformity. Thus, we focus on the simpler case of uniform access and the proof extends to the current setting of statistical Oblivious PRAM. We show the existence of such a GPRAM scheme by explicitly constructing the new GPRAM scheme in a black-box manner as follows. Let \((\textsf {GData},\) \(\textsf {GProg},\) \(\textsf {GInput},\) \(\textsf {GEval})\) be a UMA2-secure GPRAM and let \((\textsf {OData},\textsf {OProg})\) be an Oblivious PRAM scheme. We construct a new GPRAM scheme \((\widehat{\textsf {GData}},\) \(\widehat{\textsf {GProg}},\) \(\widehat{\textsf {GInput}},\) \(\widehat{\textsf {GEval}})\) as follows:
-
\(\widehat{\textsf {GData}}(1^\kappa ,D)\): Execute \((D^*) \leftarrow \textsf {OData}(1^\kappa ,D)\) then \((\tilde{D}, {s}) \leftarrow \textsf {GData}(1^\kappa ,D^*)\). Output \(\widehat{D}=\tilde{D}\) and \(\widehat{{s}}={s}\). Note that \(\textsf {OData}\) does not require a key as it is a statistical scheme.
-
\(\widehat{\textsf {GProg}}(1^\kappa , 1^{\log N}, 1^t, \Pi , \widehat{{s}}, {t_{old}})\): Execute \({\Pi }^*\leftarrow \textsf {OProg}(1^\kappa ,1^{\log N},1^t,\Pi )\) followed by \((\tilde{\Pi }, s^{in}) \leftarrow \textsf {GProg}(1^\kappa , 1^{\log N'}, 1^{t'},{\Pi }^*,\widehat{{s}}, {t_{old}}')\), where the primed variables are the growth in size due to the Oblivious PRAM transformation. Output \(\widehat{\Pi }=\tilde{\Pi }\), \(\widehat{s^{in}}=s^{in}\).
-
\(\widehat{\textsf {GInput}}(1^\kappa , \overline{x},\widehat{s^{in}})\): Note that \(\overline{x}\) is a valid (parallel) input for the oblivious program \({\Pi }^*\). Execute \(\tilde{x}\leftarrow \textsf {GInput}(1^\kappa , \overline{x},\widehat{s^{in}})\), and output \(\widehat{x}=\tilde{x}\).
-
\(\widehat{\textsf {GEval}}^{\widehat{D}}(\widehat{\Pi },\widehat{x})\): Execute \(\overline{y} \leftarrow \textsf {GEval}^{\widehat{D}}(\widehat{\Pi },\widehat{x})\) and output \(\overline{y}\).
We now prove that \((\widehat{\textsf {GData}},\) \(\widehat{\textsf {GProg}},\) \(\widehat{\textsf {GInput}},\) \(\widehat{\textsf {GEval}})\) is a fully secure Garbled PRAM scheme. Suppose \(\Pi _1, \ldots ,\Pi _u\) are a sequence of programs with running times \(t_1,\ldots ,t_u\), and let \(T_j=\sum _{i<j}t_i\) denote the sum of the running times of the first \(j-1\) programs. Let \(D \in {\{0,1\}}^N\) be any initial memory data, let \(\overline{x}_1,\ldots ,\overline{x}_u\) be inputs and \((\overline{y}_1,\ldots , \overline{y}_u) \) be the outputs of the sequential execution of the programs on D. Let \((\widehat{D}_0,\widehat{{s}}) \leftarrow \widehat{\textsf {GData}}(1^\kappa , D)\), and for \(i=1\ldots u\): \((\widehat{\Pi }_i,\widehat{s^{in}_i}) \leftarrow \widehat{\textsf {GProg}}(1^\kappa , 1^{\log N}, 1^{t_i}, \Pi _i, \widehat{{s}}, T_i)\), \(\widehat{x}_i \leftarrow \widehat{\textsf {GInput}}(1^\kappa , \overline{x}_i,\widehat{s^{in}_i})\). Finally, we consider the sequential execution of the garbled programs for \(i=1\ldots u\): \(\overline{y}'_i \leftarrow \widehat{\textsf {GEval}}^{\widehat{D}_{i-1}}(\widehat{\Pi }_i,\widehat{x}_i)\) which updates the garbled database to \(\widehat{D}_i\).
Correctness. We argue that
This follows directly from our underlying evaluation algorithms: \(\widehat{\textsf {GEval}}\) executes the underlying GPRAM scheme for evaluation, the correctness of the underlying scheme guarantees that \((\overline{y}'_1,\ldots ,\overline{y}'_u)=({\Pi }^*_1(\overline{x}_1),\ldots ,{\Pi }^*_u(\overline{x}_u))^{D^*}\). Then by the correctness of the underlying OPRAM scheme, \(({\Pi }^*_1(\overline{x}_1),\ldots ,{\Pi }^*_u(\overline{x}_u))^{D^*}= (\Pi _1(x_1),\ldots ,\Pi _u(x_u))^D=(\overline{y}_1,\ldots ,\overline{y}_u)\).
Security. For any programs \({\Pi _1,\ldots ,\Pi _u}\), database D, and inputs \({\overline{x}_1,\ldots ,\overline{x}_u}\), let
We show how to construct a simulator \(\textsf {Sim}\) such that for all \(D,\{\Pi _i,\overline{x}_i\}\), we have that \(\textsc {Real}^{D,\{\Pi _i,\overline{x}_i\}} \mathop {\approx }\limits ^{{\tiny {\mathrm {comp}}}}\textsf {Sim}(1^\kappa , 1^N, \{1^{t_i}, \overline{y}_i\})\). We let \(\textsf {OSim}\) be the Oblivious PRAM simulator, and \(\textsf {USim}\) be the simulator for the UMA2-secure GPRAM scheme. We describe \(\textsf {Sim}\) as follows.
-
1.
Compute \((N',\textsf {MemAccess}) \leftarrow \textsf {OSim}(1^\kappa , 1^N, \{1^{t_i}, \overline{y}_i\}_{i=1}^u)\). We note that we run a multi-program OPRAM simulator which then statistically simulates \(\textsf {MemAccess}\) across all programs though not \(D^*\) (only its size).
-
2.
Compute \((\tilde{D}, \{\tilde{\Pi }_i,\tilde{x}_i\}_{i=1}^u) \leftarrow \textsf {USim}(1^\kappa , 1^{N'}, \{1^{t'_i}, \overline{y}_i\}_{i=1}^u,\textsf {MemAccess})\), where as before, the primed variables are the expanded ones resulting from applying OPRAM.
-
3.
Output \((\widehat{D}_0, {\widehat{\Pi }_i, \widehat{x}_i}_{i=1}^u)=(\tilde{D}, \{\tilde{\Pi }_i,\tilde{x}_i\}_{i=1}^u)\).
We show that the simulated output is computationally indistinguishable from the real distribution. For any \(D,\{\Pi _i,\overline{x}_i\}\), we define a series of hybrid distributions \(\mathbf {Hyb}_0,\mathbf {Hyb}_1,\mathbf {Hyb}_2\) with \(\mathbf {Hyb}_0\) being the real distribution, \(\mathbf {Hyb}_2\) being the simulated distribution, and argue that for \(j=0,1\) we have \(\mathbf {Hyb}_j \mathop {\approx }\limits ^{{\tiny {\mathrm {comp}}}}\mathbf {Hyb}_{j+1}\).
-
\(\mathbf {Hyb}_0\): This is the real distribution \(\textsc {Real}^{D,\Pi _i,\overline{x}_i\}}\).
-
\(\mathbf {Hyb}_1\): Use the correctly generated \((D^*)\) from \(\widehat{\textsf {GData}}\) and \({\Pi }^*_i\) from \(\widehat{\textsf {GProg}}\) and execute
 and a sequence of memory accesses \(\textsf {MemAccess}\). Run \((\tilde{D}, \{\tilde{\Pi }_i,\tilde{x}_i\}_{i=1}^u) \leftarrow \textsf {USim}(1^\kappa , 1^{N'}, \{1^{t'_i}, \overline{y}_i\}_{i=1}^u, \textsf {MemAccess})\) and output \((\widehat{D}_0, {\widehat{\Pi }_i, \widehat{x}_i}_{i=1}^u)=(\tilde{D}, \{\tilde{\Pi }_i,\tilde{x}_i\}_{i=1}^u)\).
and a sequence of memory accesses \(\textsf {MemAccess}\). Run \((\tilde{D}, \{\tilde{\Pi }_i,\tilde{x}_i\}_{i=1}^u) \leftarrow \textsf {USim}(1^\kappa , 1^{N'}, \{1^{t'_i}, \overline{y}_i\}_{i=1}^u, \textsf {MemAccess})\) and output \((\widehat{D}_0, {\widehat{\Pi }_i, \widehat{x}_i}_{i=1}^u)=(\tilde{D}, \{\tilde{\Pi }_i,\tilde{x}_i\}_{i=1}^u)\). -
\(\mathbf {Hyb}_2\): This is the simulated distribution \(\textsf {Sim}(1^\kappa , 1^N, \{1^{t_i}, \overline{y}_i\}_{i=1}^u)\).
We now demonstrate indistiguishability.
\(\mathbf {Hyb}_0\mathop {\approx }\limits ^{{\tiny {\mathrm {comp}}}}\mathbf {Hyb}_1:\) Let \(\mathcal {A}\) be a PPT distinguisher between these two hybrids for some \(D,\{\Pi _i,\overline{x}_i\}\). By way of contradiction, we demonstrate an algorithm \(\mathcal {B}\) that breaks the UMA2-security of the underlying GPRAM scheme. First, \(\mathcal {B}\) runs \( (D^*) \leftarrow \textsf {OData}(1^\kappa ,D) , {\Pi }^*_i \leftarrow \textsf {OProg}(1^\kappa ,1^{\log N},1^{t_i},\Pi _i)\) and declares \(D^*,\{{\Pi }^*_i,\overline{x}_i)\}\) as the challenge database, programs and inputs for the UMA2-security GRAM game. The UMA2-security challenger then outputs \((\tilde{D}', \{\tilde{\Pi }'_i,\tilde{x}'_i\})\) and \(\mathcal {B}\) must output a guess whether it is real or simulated. \(\mathcal {B}\) sets \((\widehat{D}', \{\widehat{\Pi }'_i,\widehat{x}'_i\}l) = (\tilde{D}', \{\tilde{\Pi }'_i,\tilde{x}'_i\}_{i=1}^u)\) and internally invokes this as the challenge to \(\mathcal {A}\). \(\mathcal {B}\) then outputs the same guess as \(\mathcal {A}\).
Observe that if the UMA2-challenger outputs real values, then \((\widehat{D}', \{\widehat{\Pi }'_i,\widehat{x}'_i\})\) is distributed identically as if it were generated from \(\mathbf {Hyb}_0\), and if the UMA challenger outputs simulated values, then \((\widehat{D}', \{\widehat{\Pi }'_i,\widehat{x}'_i\}_{i=1}^u)\) is distributed identically as if it were generated from \(\mathbf {Hyb}_1\). Therefore, \(\mathcal {A}\) distinguishes with the same probability as \(\mathcal {B}\), which is negligible by the UMA2-security of the underlying GPRAM scheme.
\(\mathbf {Hyb}_1\mathop {\approx }\limits ^{{\tiny {\mathrm {comp}}}}\mathbf {Hyb}_2:\)Let \(\mathcal {A}\) be a PPT distinguisher between these two hybrids for some \(D,\{\Pi _i,\overline{x}_i\}\). Again, by way of contradiction, \(\mathcal {B}\) that breaks the security of the underlying OPRAM scheme that proceeds as follows. First, \(\mathcal {B}\) announces \(D,\{\Pi _i,\overline{x}_i\}\) as the challenge database, programs, and inputs for the OPRAM security game. The OPRAM challenger then outputs a challenge memory access pattern for the programs \((\textsf {MemAccess}')\) which can be real or simulated. Then, \(\mathcal {B}\) computes \((y_1,\ldots ,y_u)=(\Pi _1(\overline{x}_1),\ldots ,\Pi _u(\overline{x}_u))^D\) and runs the UMA2-simulator \((\tilde{D}', \{\tilde{\Pi }'_i,\tilde{x}'_i\}_{i=1}^u) \leftarrow \textsf {USim}(1^\kappa , 1^{N'}, \{1^{t'_i}, \overline{y}_i\}, \textsf {MemAccess}')\). Next, \(\mathcal {B}\) sets \((\widehat{D}', \{\widehat{\Pi }'_i,\widehat{x}'_i\}_{i=1}^u)=(\tilde{D}', \{\tilde{\Pi }'_i,\tilde{x}'_i\}_{i=1}^u)\) and passes this to \(\mathcal {A}\). \(\mathcal {B}\) then outputs the same guess as \(\mathcal {A}\).
Observe that if the OPRAM challenger outputs the real values, then the tuple \((\widehat{D}', \{\widehat{\Pi }'_i,\widehat{x}'_i\})\) is distributed identically as if it were generated from \(\mathbf {Hyb}_1\), and alternatively, if the OPRAM challenger outputs simulated values, then \((\widehat{D}', \{\widehat{\Pi }'_i,\widehat{x}'_i\})\) is distributed identically as if it were generated from \(\mathbf {Hyb}_2\). Therefore, \(\mathcal {A}\) distinguishes with the same probability as \(\mathcal {B}\), which is negligible by the security of the underlying OPRAM scheme. \(\square \)
Rights and permissions
Copyright information
© 2017 International Association for Cryptologic Research
About this paper
Cite this paper
Lu, S., Ostrovsky, R. (2017). Black-Box Parallel Garbled RAM. In: Katz, J., Shacham, H. (eds) Advances in Cryptology – CRYPTO 2017. CRYPTO 2017. Lecture Notes in Computer Science(), vol 10402. Springer, Cham. https://doi.org/10.1007/978-3-319-63715-0_3
Download citation
DOI: https://doi.org/10.1007/978-3-319-63715-0_3
Published:
Publisher Name: Springer, Cham
Print ISBN: 978-3-319-63714-3
Online ISBN: 978-3-319-63715-0
eBook Packages: Computer ScienceComputer Science (R0)









 in [
in [




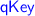 is the previous step node, which would have already been simulated, so the output of
is the previous step node, which would have already been simulated, so the output of  is the parent circuit from the same time step. Since this was previously evaluated and simulated, we can again simulate this circuit with
is the parent circuit from the same time step. Since this was previously evaluated and simulated, we can again simulate this circuit with  and
and 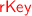 inputs for these circuits now can either come from the parent (edge circuit) or a predecessor thin circuit in the same level. These can be handled in batches of B, sequentially, because every node still has a distinct parent that holds its
inputs for these circuits now can either come from the parent (edge circuit) or a predecessor thin circuit in the same level. These can be handled in batches of B, sequentially, because every node still has a distinct parent that holds its  (that will never be passed on to subsequent parents, as edge circuits do not pass information from one to the next), as well as its immediate predecessor which will already have been simulated. Thus, again we can invoke
(that will never be passed on to subsequent parents, as edge circuits do not pass information from one to the next), as well as its immediate predecessor which will already have been simulated. Thus, again we can invoke  and a sequence of memory accesses
and a sequence of memory accesses 