Abstract
Heterogeneous systems are nowadays a common choice in the path to Exascale. Through the use of accelerators they offer outstanding energy efficiency. The programming of these devices employs the host-device model, which is suboptimal as CPU remains idle during kernel executions, but still consumes energy. Making the CPU contribute computing effort might improve the performance and energy consumption of the system. This paper analyses the advantages of this approach and sets the limits of when its beneficial. The claims are supported by a set of models that determine how to share a single data-parallel task between the CPU and the accelerator for optimum performance, energy consumption or efficiency. Interestingly, the models show that optimising performance does not always mean optimum energy or efficiency as well. The paper experimentally validates the models, which represent an invaluable tool for programmers when faced with the dilemma of whether to distribute their workload in these systems.
You have full access to this open access chapter, Download conference paper PDF
Similar content being viewed by others
1 Introduction
There is an ever growing interest on heterogeneous systems in the HPC community, by integrating GPUs, as they increase the computing power and improve the energy efficiency of these large systems [10]. The programming of these is based mainly in frameworks or APIs like CUDA and OpenCL, designed around the Host-Device programming model. Which relies on offloading data-parallel sections to the accelerator while the CPU remains idle. During the latter, despite not contributing computational effort to the system, the devices still draw a significant amount of power, known as static power consumption [5]. This leads to think that a load-balanced co-execution might be necessary to improve the efficiency of the system. However, with the above frameworks, co-execution is possible but far from trivial, and neither is determining the optimal load balance.
Despite the difficulties, co-execution can give benefits in terms of performance and energy efficiency. If the task is successfully balanced among the devices, the computing power of the heterogeneous system is the sum of that of the devices, consequently improving the performance. Regarding energy consumption, without co-execution idle devices still require energy to operate, called static energy, consequently reducing the energy efficiency of the heterogeneous system as a whole. Given the execution of a data-parallel task, Fig. 1.a shows the power consumed by the system when only the GPU is used. The CPU consumes power even though it is only waiting for the GPU. Figure 1.b shows that the collaboration of the CPU improves performance, as the computation is finished faster, but might also improve the total energy consumption.
This paper studies, from an analytical point of view, whether co-execution of a single massively data-parallel kernel in a heterogeneous system with two devices is beneficial. And how load balancing affects each of the proposed metrics: the performance, the energy consumption or the energy efficiency, and if they can be optimised simultaneously. This allows programmers decide beforehand on the suitability of co-execution in their applications, thus reducing the programming effort.
The main contributions of this paper are:
-
To aid the programmer to take an early decision on whether it is worth dividing the workload of a single kernel among the devices of a heterogeneous system.
-
Obtaining a series of models that allow determining the workload sharing proportion that optimises the performance, energy consumption or efficiency.
-
Conducting an experimental study that proves the validity of the proposed models. The values given by the models match those of the experiments.
Some proposals can be found in the literature, that allow the CPU and the accelerator to share the execution of data-parallel sections [2, 3, 6,7,8,9, 12, 15]. These focus on sharing the workload among the devices to maximise performance. Some of these include both static [7, 8] and dynamic [2, 3, 6, 9, 15] load balancing algorithms. In general, these allow optimising only the performance of the systems, ignoring their energy consumption, which is one of the most important challenges of computers nowadays. There are other approaches to the problem of optimising the performance of single kernels co-executed on several devices [16]. But, to the extent of the authors’ knowledge, this paper is the first that proposes an analytical model that can be used to take an a priori decision on the suitability of co-execution, taking energy into account.
The rest of this paper is organized as follows. Section 2 describes the proposed load balancing models. Section 3 explains the experimental methodology, while Sect. 4 evaluates the proposals. Finally in Sect. 5, the most important conclusions are presented.
2 Load Balancing Model
To sustain the claims of this paper, it is necessary to obtain a series of models and algorithms that allow determining an optimal share of the load among the computing devices. A definition of a set of concepts and parameters is necessary, as they characterize both the parallel application and the devices of the system.
-
Work-item: in OpenCL is the unit of concurrent execution. This paper assumes that each one represents the same amount of compute load.
-
Total Workload ( W ): is the number of work-items needed to solve a problem. It is determined by some input parameters of the application.
-
Device Workload ( \(W_C, W_G\) ): is the number of work-items assigned to each device: \(W_C\) for the CPU and \(W_G\) for the GPU.
-
Processing speeds of devices ( \(S_C, S_G\) ): are the number of work-items that each device can execute per time unit, taking into account the communication times.
-
Processing speed of the system ( \(S_T\) ): is the sum of the speeds of all the devices in the system.
$$\begin{aligned} S_T = S_C+S_G \end{aligned}$$ -
Device execution time ( \(T_C, T_G\) ): is the time required by a device to complete its assigned workload.
$$\begin{aligned} T_C = \frac{W_C}{S_C} \qquad T_G = \frac{W_G}{S_G} \end{aligned}$$ -
Total execution time ( T ): is the time required by the whole system to execute the application, determined by the last device to finish its task.
$$\begin{aligned} T = max\{T_C, T_G\} \end{aligned}$$ -
Workload partition ( \(\alpha \) ): dictates the proportion of the total workload that is given to the CPU. Then, the proportion for the GPU is \(1-\alpha \).
$$\begin{aligned} W_C = \alpha W \qquad W_G = (1 - \alpha ) W \end{aligned}$$
Based on the above, the total execution time (T) is obtained from the workload of each device and their processing speed:
It is also necessary to model the energetic behaviour of the system, by considering the specifications of the devices.
-
Static power ( \(P_C^S, P_G^S\) ): is consumed by each device while idle. This is unavoidable and will be consumed throughout the execution of the application.
-
Dynamic power ( \(P_C^D, P_G^D\) ): is consumed when the devices are computing.
-
Device energy ( \(E_C, E_G\) ): is consumed by each device during the execution.
-
Total energy ( E ): is the drawn by the heterogeneous system while executing the application. And it is the sum of the energy of each device.
The total consumed energy is the addition of the static (first term in Eq. 2) and dynamic (second term in Eq. 2) energies. The static energy is consumed by both devices throughout the execution of the task. Thus is obtained by multiplying the static power of the devices \(P_C^S\), \(P_G^S\) by the total execution time T (Eq. 1). The dynamic energy is consumed only when the device is computing. The dynamic energy of the CPU is \(P^D_C T_C\) and \(P^D_G T_G\) for the GPU.
2.1 Optimal Performance Load Balancing
Attending strictly to performance, an ideal load balancing algorithm causes both devices to take the same time \(T_{opt}\) to conclude their assigned workload. Because none of them incur in idle time waiting for the other to finish.
The question remains as to which that work distribution is, or what \(\alpha \) satisfies the above equation. Intuitively, it will depend on the speeds of the devices. In Expression 1, it was shown that the execution times of each device are determined by the workload assigned to them, as well as their processing speed.
Both times are linear with \(\alpha \), so they each define a segment in the range \((0 \le \alpha \le 1)\). \(T_C\) has positive slope and its maximum value is reached at \(\alpha = 1\). While \(T_G\) has its maximum value at \(\alpha = 0\) and negative slope. Then, where both segments cross, both devices are taking the same time to execute, and therefore the optimal \(\alpha _{opt}\) share is found.
Finally, it is also possible to determine the gain (or speedup) of the optimal execution compared to running on each of the devices alone.
2.2 Optimal Energy Load Balancing
The value of \(\alpha _{opt}\) determined by Expression 3 tells how to share the workload between both devices to obtain the best performance. Now it is interesting to know if this sharing also gives the best energy consumption.
Regarding the total energy of the system (Expression 2), note that it uses the maximum function. To analyse this, also note that \(\alpha _{opt}\) is the turning point where the CPU finishes earlier than the GPU, and where the maximum is going to change its result. Then the total energy of the system can be expressed in a piece-wise manner with two linear segments joined at \(\alpha _{opt}\). This expression is not differentiable but it is continuous. In order to determine local minima, three cases have to be analysed.
-
1.
Both segments have positive slope, so \(\alpha = 0\) will give the minimum energy.
-
2.
Both segments have negative slope. Then the minimum is found at \(\alpha = 1\).
-
3.
The slope of the left segment is negative and the right is positive. Then the minimum occurs at \( \alpha _{opt} = \frac{S_C}{S_C+S_G} \).
The problem is now finding when each of the cases occur. For this, each segment has to be analysed separately.
Left Side. In the range of \(( 0< \alpha < \alpha _{opt})\) the CPU is being underused. Its workload is not enough to keep it busy and has to wait for the overworked GPU to finish. Therefore the execution time is dictated by the GPU, and the energy of the whole system is:
To find when the segment has a negative slope, it is differentiated with respect to \(\alpha \) and compared to 0:
Right Side. In the range \((\alpha _{opt}< \alpha < 1)\) the opposite situation occurs. The CPU is overloaded, taking longer to complete its workload than the GPU. Then the execution time is determined by the CPU, and the system energy is:
As before the slope of the segment is found differentiating, only this time it is desired to find when the slope is positive.
Satisfying both Expressions (4 and 5) means that the third case occurs, where the minimum energy is found at \(\alpha _{opt} = \frac{S_C}{S_C+S_G}\). Combining these leads to:
This indicates that the ratio between the speeds of the devices must lie within a given range in order for the sharing to make sense from an energy perspective. The energy consumed in this case can be expressed as:
Should the above condition not be satisfied, then it is advisable to use only one of the devices. If \(\frac{S_G}{S_C} < \frac{P_G^D}{P_C^S + P_G^S + P_C^D} \), then the minimum appears at \(\alpha = 0\). Meaning that using the CPU is pointless, as no matter how small the portion of work, it is going to waste energy. The consumption in this case is:
When the condition is not satisfied on the other side: \(\frac{S_G}{S_C} > \frac{P_C^S + P_G^S + P_G^D}{P_C^D}\), the minimum is found at \(\alpha = 1\). Then it is the CPU that must be used exclusively. As assigning the smallest workload to the GPU is going to be detrimental to the energy consumption of the system.
2.3 Optimal Energy Efficiency Load Balancing
Finally, this section analyses the advantage of co-execution when considering the energy efficiency. The metric used to evaluate the efficiency is the Energy-Delay Product (EDP), of the product of the consumed energy and the execution time of the application. The starting point is then combining the expressions of time and energy (1 and 2) of the system.
Again, since both expressions include the maximum function they have to be analysed in pieces. This time, both pieces will be quadratic functions of \(\alpha \), that may have local extrema at any point in the curve. Therefore it is necessary to equate the differential to 0 and solve for \(\alpha \).
Left Side. If (\( 0< \alpha < \frac{S_C}{S_T})\) the expressions for time and energy are multiplied obtaining the EDP. Differentiating on \(\alpha \) and solving the differential equated to 0 leads to an extreme point at \(\alpha _{left}\).
Right Side. Now the range (\( \frac{S_C}{S_T}< \alpha < 1)\) is considered. Again, combining the time and energy expressions for this interval gives the EDP, which is differentiated and equated to 0 to locate the extremum at \(\alpha _{right}\).
The analysis of both sides shows that determining the minimum EDP is less obvious than in previous analysis. There are five possible \(\alpha \) values. The first three are, \(\alpha =0\), \(\alpha _{opt}\) and \(\alpha =1\). But due to the quadratic nature of both parts of the EDP expression, it is possible to find a local minimum in each of them. As was shown above, these can occur in \(\alpha _{left}\) and \(\alpha _{right}\). However, these minima are only relevant if they lie within the appropriate ranges \(0< \alpha _{left} < \frac{S_C}{S_T}\) and \(\frac{S_C}{S_T}< \alpha _{right} < 1\). To find the optimum workload share, the energy efficiency is evaluated at the relevant points, and the best is chosen. Again, if the optimal \(\alpha \) is not 0 or 1, it means that it is advisable to use co-execution.
3 Methodology
To validate the above models, a set of experiments has been carried out on two different machines. The first machine used for experimentation is composed of two 2.0 GHz Intel Xeon E5-2620 CPUs with six cores each and a Kepler GPU. Thanks to the QPI connection the CPUs are treated as a single device. Therefore, throughout the remainder of this document, any reference to the CPU of this system includes both processors. The GPU is a NVIDIA K20m with 13 stream multiprocessors, 2496 cores. The experiments for this system have been performed with the maximum and minimum frequencies supported by the GPU: 324 and 758 MHz. Henceforth referenced as Kepler 324 and Kepler 758. Increasing the frequency naturally escalates the power consumption and reduces the execution times, all having an impact in the energy efficiency of the system. At the lowest frequency, the computing speed of GPU is comparable to that of the CPU, thus making the system less heterogeneous.
The second system includes one 3.60 GHz Intel i3-4160 CPU with two cores and a NVIDIA GTX950 with 6 Stream Multiprocessors and 768 cores. Any reference to this system will be labeled as GTX950.
The experiments have been carried out with a static algorithm. This means that the work assigned to each device is determined at the beginning of the execution, allowing full control of how the workload is assigned to each device. Six benchmarks have been used, four of which are part of the AMD APP SDK [1] (MatMul, NBody, Binomial, Mandelbrot) and two are in-house developments. One performs a bidimensional Taylor approximation for a set of points and the other calculates the Gaussian blur of an image. Each application has been run using a problem size big enough to justify its distribution among the available devices. For MatMul 12800 by 12800 matrices were used. For NBody 51200 elements were considered for simulation. Binomial uses 20480000 options. Mandelbrot generates a 20480 by 20480 pixel image. Taylor calculates the approximation for a mesh of 1000 by 1000 points. Finally, Gaussian performs the blur on a 8000 by 8000 pixel image using an 81 by 81 pixel filter.
The performance has been measured as the time required to complete the kernel execution, including data distribution, kernel launch overhead and result collection. From these times the values for the computational speeds \(S_C\) and \(S_G\) were calculated. Additionally, the consumed energy must be measured. A measurement application, named Sauna was developed to, periodically monitor the different compute devices and gather their power consumption [13]. This takes advantage of the Running Average Power Limit (RAPL) registers [14] in Intel CPUS and the NVIDIA Management Library (NVML) [11] for the GPUs. The sampling rate used for the measurements was 33 Hz. To obtain the energy efficiency of the system, the time and energy measurements must be multiplied, giving the EDP [4].
4 Experimental Evaluation
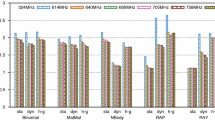
This section presents the results of the experiments performed to validate the models proposed in Sect. 2. Due to the similar behaviour of MatMul and Gaussian to that of NBody and Binomial, only the results of the latter are presented. The four applications executed on the three systems lead to twelve different scenarios. Table 1 shows the parameters of the models, extracted from test executions, where the performance is shown normalised to \(S_C\). Figures 2, 3 and 4 all have a similar structure, they show the execution time, consumed energy and EDP of the different benchmarks and the three systems: Kepler 324, Kepler 758 and GTX950. Note that this last system is referred to the right axis. The horizontal axis sweeps \(\alpha \) from 0, where all the work is done by the GPU, through 1, where only the CPU is used.
Regarding execution time, the first observation that can be made is that all benchmarks present a minimum time value that depends on the ratio of the computing speeds of the devices (See Fig. 2). The exact values of \(\alpha \) where the execution time is minimum are listed in Table 1, together with the measured optimal \(\alpha \). It is noteworhty that the model accurately predicts the results. The small discrepancies between the model and experiments are due to the interval with which \(\alpha \) was swept.
In the case of the GTX950, with Taylor and Mandelbrot, a larger error is observed. The explanation is a combination of two factors. For these benchmarks, the device speed ratio \(\frac{S_G}{S_C}\) is less than 1, meaning that the CPU is more productive than the GPU. On the other hand, when the GPU concludes its workload, it rises an interrupt that the CPU must handle immediately. And taking into account that this machine has only two cores, one of them will be devoted entirely to attending the GPU interruption. The observed error is then explained because the CPU suffers an overhead that was not included in the model. This lowers the effective speed of the CPU and the observed value of \(\alpha _{opt}\), as the GPU has more time to do extra work. This has been experimentally confirmed, running the benchmarks in one core, leaving the other free to attend the GPU.
Regarding the energy, the model gives three possibilities for the optimum \(\alpha \) depending on whether the device speed ratio \(\frac{S_G}{S_C}\) falls within a particular range or not (Expression 6). Figure 3 shows examples of the three behaviours and confirm the predictions of the model.
With Binomial and NBody, the minimum energy is consumed with \(\alpha =0\). This is because the speed ratio falls on the left side of the range, and consequently both segments in the energy graph have positive slope. In practical terms this means that although from a pure performance point of view the CPU contributes, from an energy perspective using it becomes wasteful. On the Mandelbrot and Taylor benchmarks, and both Kepler 324 and Kepler 758, the ratio lies within the range. Meaning that the points of optimum energy consumption and maximum performance coincide in the same \(\alpha _{opt}\). However, on the GTX950, the ratio falls to the right, indicating that both segments will have negative slope and the minimum energy will be found at \(\alpha =1\). That is, the GPU is wasting energy. These results show that co-execution is only worth pursuing in four of the twelve analysed cases, two of them benefit of using the CPU alone, while in the rest using only the GPU is the most advisable solution.
Finally, regarding the energy efficiency of the system, the model presented in Sect. 2 declares five points susceptible of being the optimal workload share. Namely \(\alpha =0\), \(\alpha _{opt}\), \(\alpha =1\), \(\alpha _{left}\) and \(\alpha _{right}\). For the tested benchmarks and systems, \(\alpha _{left}\) and \(\alpha _{right}\) always lie outside their valid ranges, except for \(\alpha _{left}\) for Binomial on Kepler 324. Studying these points, it was determined that the minimum EDP would occur at the \(\alpha \) values specified in Table 2. This also presents the corresponding experimental \(\alpha \), extracted from the results shown in Fig. 4.
It can be said that the model for energy efficiency always predicted the correct \(\alpha \) value that minimises the EDP. A second observation reveals that these points coincide with either the \(\alpha \) that maximises performance or the one that minimises energy. However, the model states that this might not always be the case as local minimums could be found. In fact, there are many cases, those with \(\alpha = 0\) or \(\alpha = 1\) in Table 2, where it is better using only one device to optimise EDP, even when this does not give the optimum performance.
5 Conclusion
This paper analyses the advantages of co-execution and load balancing in heterogeneous systems when considering three different metrics: performance, energy consumption and energy efficiency. Through the proposal of a set of analytical models, it allows determining if co-execution is beneficial in terms of the three metrics. Since co-execution represents a large programming effort, the use of these models allow the programmer to predict if such an approach is worth.
From a performance perspective, the model shows that there is always an advantage in co-execution. It also predicts the gain of this solution. In practical terms, if the gain is very small it might not be noticeable due to diverse overheads in the load balancing algorithm. On contrast, when considering energy consumption or efficiency, the model clearly shows that there are cases in which it is not advisable to use co-execution. Through experimental evaluation, the paper shows that the models accurately predict the observed results. The proposed models consider an ideal load balancing algorithm, this means that provided that the used algorithm is good enough, the predictions of the models will be met, regardless of it being static or dynamic.
In the future, it is intended to extend the models to systems with more than two devices, and consider irregular applications. Also, the experimentation will be extended to cover other kinds of accelerator devices.
References
AMD Accelerated Parallel Processing (APP) Software Development Kit (SDK) V3. http://developer.amd.com/tools-and-sdks/opencl-zone/amd-accelerated-parallel-processing-app-sdk/. Accessed November 2016
Binotto, A., Pereira, C., Fellner, D.: Towards dynamic reconfigurable load-balancing for hybrid desktop platforms. In: Proceedings of IPDPS, pp. 1–4. IEEE Computer Society, April 2010
Boyer, M., Skadron, K., Che, S., Jayasena, N.: Load balancing in a changing world: dealing with heterogeneity and performance variability. In: Proceedings of the ACM International Conference on Computing Frontiers, pp. 21:1–21:10 (2013)
Castillo, E., Camarero, C., Borrego, A., Bosque, J.L.: Financial applications on multi-CPU and multi-GPU architectures. J. Supercomput. 71(2), 729–739 (2015)
Hong, S., Kim, H.: An integrated GPU power and performance model. SIGARCH Comput. Archit. News 38(3), 280–289 (2010)
Kaleem, R., Barik, R., Shpeisman, T., Lewis, B.T., Hu, C., Pingali, K.: Adaptive heterogeneous scheduling for integrated GPUs. In: Proceedings of PACT. ACM (2014)
de la Lama, C.S., Toharia, P., Bosque, J.L., Robles, O.D.: Static multi-device load balancing for OpenCL. In: Proceedings of ISPA, pp. 675–682. IEEE Computer Society (2012)
Lee, J., Samadi, M., Park, Y., Mahlke, S.: Transparent CPU-GPU collaboration for data-parallel kernels on heterogeneous systems. In: Proceedings of PACT, pp. 245–256. IEEE Press, Piscataway (2013)
Ma, K., Li, X., Chen, W., Zhang, C., Wang, X.: GreenGPU: a holistic approach to energy efficiency in GPU-CPU heterogeneous architectures. In: 41st International Conference on Parallel Processing, ICPP (2012)
Mittal, S., Vetter, J.S.: A survey of methods for analyzing and improving GPU energy efficiency. ACM Comput. Surv. 47(2), 19:1–19:23 (2014)
NVIDIA: NVIDIA Management Library (NVML). https://developer.nvidia.com/nvidia-management-library-nvml. Accessed April 2016
Pérez, B., Bosque, J.L., Beivide, R.: Simplifying programming and load balancing of data parallel applications on heterogeneous systems. In: Proceedings of the 9th Workshop on General Purpose Processing using GPU, pp. 42–51 (2016)
Pérez, B., Stafford, E., Bosque, J.L., Beivide, R.: Energy efficiency of load balancing for data-parallel applications in heterogeneous systems. J. Supercomput. 73(1), 330–342 (2017)
Rotem, E., Naveh, A., Rajwan, D., Ananthakrishnan, A., Weissmann, E.: Power management architecture of the 2nd generation Intel Core microarchitecture, formerly codenamed Sandy Bridge. In: IEEE International Symposium on High-Performance Chips (2011)
Wang, G., Ren, X.: Power-efficient work distribution method for CPU-GPU heterogeneous system. In: International Symposium on Parallel and Distributed Processing with Applications, pp. 122–129, September 2010
Zhang, F., Zhai, J., He, B., Zhang, S., Chen, W.: Understanding co-running behaviors on integrated CPU/GPU architectures. IEEE Trans. Parallel Distrib. Syst. 28(3), 905–918 (2017)
Acknowledgments
This work has been supported by the University of Cantabria (CVE-2014-18166), the Spanish Science and Technology Commission (TIN2016-76635-C2-2-R), the European Research Council (G.A. No 321253) and the European HiPEAC Network of Excellence. The Mont-Blanc project has received funding from the European Unions Horizon 2020 research and innovation programme under grant agreement No 671697.
Author information
Authors and Affiliations
Corresponding authors
Editor information
Editors and Affiliations
Rights and permissions
Copyright information
© 2017 Springer International Publishing AG
About this paper
Cite this paper
Stafford, E., Pérez, B., Bosque, J.L., Beivide, R., Valero, M. (2017). To Distribute or Not to Distribute: The Question of Load Balancing for Performance or Energy. In: Rivera, F., Pena, T., Cabaleiro, J. (eds) Euro-Par 2017: Parallel Processing. Euro-Par 2017. Lecture Notes in Computer Science(), vol 10417. Springer, Cham. https://doi.org/10.1007/978-3-319-64203-1_51
Download citation
DOI: https://doi.org/10.1007/978-3-319-64203-1_51
Published:
Publisher Name: Springer, Cham
Print ISBN: 978-3-319-64202-4
Online ISBN: 978-3-319-64203-1
eBook Packages: Computer ScienceComputer Science (R0)