A Generic yet Efficient Method for Secure Inner Product

Abstract

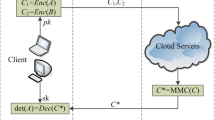
Secure inner product, namely the computation of inner product whose terms are all in encrypted form, is the central technique for various privacy-preserving applications. In this paper, we propose a generic yet efficient method to compute secure inner products of vectors (or matrices) using matrix trace properties. Indeed, our method not only applies to both LWE-based and ring-LWE-based homomorphic encryption schemes, but also is more efficient compared to previously known methods.

A Formal Correctness of the Protocol in Sect. 5

Proof. For $m \in \mathcal {R}=\mathbb {Z}[x]/(x^n+1)$, it is easily to check that F(m) satisfies:

Since $x^n=-1$ and $F^{-1}$ is inverse map, i.e., $F^{-1}(F(m))=m$, we have results:

• (r1)
• (r2)
• (r3)

Accordingly,

$$ \begin{array}{l} \langle \overline{m}, \overline{m'} \rangle = m\cdot m'^{(t)} \mod x = F^{-1}(F(m) \cdot F(m')^T) \mod x = \mathsf{Tr}(F(m) \cdot F(m')^T)/n \end{array} $$

According to (a1)–(a4) and (r1)–(r3), the algorithms $\mathsf{InnerP}_M$ and $\mathsf{DecIP}_M$ over $\mathbb {Z}_q^{n \times n}$ for the coefficient circulante matrices of elements of ring $\mathcal {R}_q$ can be represented back to that for ring element over $\mathcal {R}_q$ by running $F^{-1}$. Therefore,

where $S^*$ $=$ $SS^{(t)}$, $S_M^*=F(S) F(S)^T, \tilde{S_M}=F(S)^T\in \mathbb {Z}_q^{n \times n}$, and $\xi _M=\langle F(c_2), F(d_2) \rangle _F$ $\in \mathbb {Z}_q$. Therefore,

$$ \begin{array}{l} \langle \overline{m}, \overline{m'} \rangle =IP \mod p. \end{array} $$

The proof is completed.