Abstract
In this paper, we present a histopathology image classification method with supervised intra-embedding of Fisher vectors. Recently in general computer vision, Fisher encoding combined with convolutional neural network (ConvNet) has become popular as a highly discriminative feature descriptor. However, Fisher vectors have two intrinsic problems that could limit their performance: high dimensionality and bursty visual elements. To address these problems, we design a novel supervised intra-embedding algorithm with a multilayer neural network model to transform the ConvNet-based Fisher vectors into a more discriminative feature representation. We apply this feature encoding method on two public datasets, including the BreaKHis image dataset of benign and malignant breast tumors, and IICBU 2008 lymphoma dataset of three malignant lymphoma subtypes. The results demonstrate that our supervised intra-embedding method helps to enhance the ConvNet-based Fisher vectors effectively, and our classification results largely outperform the state-of-the-art approaches on these datasets.
You have full access to this open access chapter, Download conference paper PDF
Similar content being viewed by others
1 Introduction
Diagnosis of cancers usually relies on the visual analysis of tissue samples under the microscope. The morphological features in histopathology images provide the important clue to differentiate benign and malignant tumors or identify different cancer subtypes. To encode the morphological features for automated classification, handcrafted [2, 6] and learning-based [3] feature descriptors have been designed over the years. The most recent trend in this area is the use of convolutional neural network (ConvNet). For example, pretrained or customized ConvNet models have been applied to classify lymphoma images [5] and breast cancer images [11]. Other related applications include cell detection and segmentation [13, 14]. Such ConvNet approaches often demonstrate improved performance over the more traditional techniques based on handcrafted features.
Recently in the general imaging domain, a feature descriptor that integrates ConvNet with Fisher encoding has been proposed [4]. With this method, the patch-level features of an image are first extracted using a ConvNet model, then these patch features are encoded into a Fisher vector (FV) [7] as the image-level feature descriptor. This CFV (short for ConvNet-based FV) descriptor provides significantly higher classification performance than using only the ConvNet model for texture classification and object categorization [4]. FV descriptors have also been adopted into biomedical imaging applications for histopathology image classification [3, 10] and HEp-2 cell classification [15]. In these studies, the FV descriptors are generated by Fisher encoding of various types of patch-level features (other than the ConvNet model), and consistently high classification performance is reported.
There are however two issues that could affect the discriminative power of FV descriptors. First, FV descriptors are high dimensional. An FV descriptor is constructed by pooling the difference vectors between the patch features and a number of Gaussian centers, and the resultant CFV descriptor can be 64K dimensional or higher. With a limited number of training images, such high dimensionality could cause overfitting and decrease the classification performance on test data. Second, FV descriptors can have bursty visual elements. This means that there can be some artificially large elements in the FV descriptor due to large repetitive patterns in the image, and such large elements would lower the contribution from the other important elements and thus affect the representativeness of the descriptor. For the first issue, dimensionality reduction with principal component analysis (PCA) and large margin distance metric learning have been experimented [9, 10]. To overcome the second issue, the intra-normalization technique [1] is often applied to perform L2 normalization within each block (corresponding to one Gaussian component) of the FV descriptor.
In this study, we design a supervised intra-embedding method to address these two issues. We borrow the block-based normalization idea from intra-normalization, but instead of simple L2 normalization within each block, a discriminative dimension reduction algorithm based on multilayer neural network is designed to embed each block of the CFV descriptor to a lower dimensional feature space. Also, the block-wise elements are integrated with further neural network layers and a hinge loss layer to optimize the discriminative power of whole descriptor collectively rather than just the individual blocks. We conduct experimental evaluation on two public histopathology image datasets, including the BreaKHis dataset for classifying benign and malignant breast tumors [12], and IICBU 2008 lymphoma dataset for classifying three malignant lymphoma subtypes [8]. We obtain improved performance over the existing approaches, and demonstrate that the proposed supervised intra-embedding method can effectively enhance the discriminative power of the CFV descriptors.
2 Methods
2.1 Fisher Vector
Fisher vector [7] is a type of feature encoding technique that aggregates the patch-level features into an image-level descriptor. With FV encoding, a Gaussian mixture model (GMM) is constructed from the patch features. Then the mean first and second order difference vectors between each Gaussian center and all patch features are computed weighted by soft assignments. Assume that the patch-level feature is of dimension H. The first and second order difference vectors would also each have a dimension H. The final FV descriptor is a concatenation of all these difference vectors corresponding to all K Gaussian components, hence the total dimension of the FV descriptor is 2KH.
The patch-level features can be extracted in different ways. In this study, we adopt the ConvNet-based method [4]. Specifically, an image is first rescaled to multiple sizes with scale factors of \(2^s,s=-3,-2.5,\ldots ,1.5\). For each rescaled image, the VGG-VD ConvNet model with 19 layers pretrained on ImageNet is applied and the last convolutional layer produces a set of patch features with \(H=512\) dimensions. Then these patch features from all rescaled images are pooled together to generate the CFV descriptor of this image. Note that from our empirical results, the effectiveness of the ImageNet-pretrained model demonstrates that although the natural images in ImageNet seem quite different from histopathology images, the intrinsic feature details could be highly similar.
We generate the GMM model with \(K=64\) components. We find that a smaller K (e.g. 32) reduces the effectiveness of the descriptor, while a larger K (e.g. 128) increases the computational cost without notable performance improvement. The CFV descriptor is thus \(2\times 64\times 512=65535\) dimensional.
2.2 Supervised Intra-embedding
To reduce the dimensionality and bursty effect of CFV descriptors, we design a supervised intra-embedding method. Formally, we denote the CFV descriptor as f. The objective of the supervised intra-embedding method is to transform f to a lower dimension, and the transformed descriptor g is expected to provide good classification performance. For this, we design a multilayer neural network model, with locally connected layers for local transformation of descriptor blocks and a hinge loss layer for global optimization of the entire descriptor.
The overall network structure is illustrated in Fig. 1. The input layer is the CFV descriptor of 2KH dimensions. The second layer is a locally connected layer, which is formed by 2K filters with each filter of \(D_1\) neurons. One filter is fully connected to a descriptor block of \(H=512\) elements in the input layer (one descriptor block corresponds to one first or second order difference vector of 512 dimensions) and generates \(D_1\) outputs:
where \(W_2(i)\in \mathbb {R}^{D_1\times H}\) and \(b_2(i)\in \mathbb {R}^{D_1}\) are the weights and bias of the ith filter, \(f_1(i)\in \mathbb {R}^{H}\) denotes the ith block in the input layer, and \(f_2(i)\in \mathbb {R}^{D_1}\) is the ith output at this locally connected layer. The output of this layer is a concatenation of outputs from all filters, and is thus of \(2KD_1\) dimensions. Note that since \(D_1<H\), this layer reduces the dimensionality of the input descriptor.
The rational of designing a locally connected layer is that a CFV descriptor can be considered as having 2K blocks each of H dimensions and corresponding to a first or second order difference vector. The localized filters can help to achieve different ways of transformation in different blocks. This provides more locally adaptive processing compared to the convolutional and fully connected layers in ConvNet, in which a filter is applied to the entire input. On the other hand, such local filters also increase the number of learning parameters significantly and could cause overfitting. To reduce the number of filter parameters, we make every four consecutive filters share the same weights and bias, so there are altogether 2K/4 unique filters.
The third layer is an intra-normalization layer, in which each output \(f_2(i)\) from the previous layer is L2 normalized. In this way, the different blocks would contribute with equal weights in the transformed descriptor. Together with the locally connected layer, such local transformation provides a supervised learning-based approach to overcome the bursty visual elements. The fourth layer is a ReLU layer, and the ReLU activation is applied to the entire \(2KD_1\)-dimensional output of the third layer. Next, layers two to four are repeated as layers five to seven in the network structure, to provide another level of transformation. Assume that the individual local filters at the fourth layer have \(D_2\) neurons. The output \(f_7\) at the seventh layer has then \(2KD_2\) dimensions, and this is the final transformed descriptor g to be used in classification.
For the last layer, we design a hinge loss layer to impose the optimization objective of the supervised intra-embedding. Typically FV descriptors (original or dimension reduced) are classified using a linear-kernel support vector machine (SVM) to produce good classification results [4, 10]. Therefore, to align the optimization objective in our multilayer neural network with the SVM classification objective, we choose to use an SVM formulation in the loss layer. Specifically, assume that the dataset contains L image classes. We construct a one-versus-all multi-class linear-kernel classification model to compute the hinge loss. Denote the weight vector as \(w_l\in \mathbb {R}^{2KD_2}\) for each class \(l\in \{1,\ldots ,L\}\). The overall loss value based on N input CFV descriptors (for training) is computed as:
where n is the index of the input descriptor, \(f_7^n\) is the corresponding output at the seventh layer, \(\lambda _l^n=1\) if the nth input belongs to class l and \(\lambda _l^n=-1\) otherwise, and C is the regularization parameter. Minimizing this loss value \(\varepsilon \) at the last layer mimics the margin maximization in an SVM classifier. The hinge loss layer thus effectively integrates the local transformations and local filters would influence each other during the optimization.
During training, a dropout layer with a rate of 0.2 is added before the loss layer to provide some regularization. Also, to initialize the filter weights, we first train the filters individually with one block of descriptors as the input layer. The transformed descriptor g at the seventh layer has \(2KD_2\) dimensions, and is classified using the linear-kernel SVM to obtain the image label. The key parameters \(D_1\) and \(D_2\) are set to 64, hence the resultant feature dimension is \(2\times 64\times 64=8192\). The regularization parameter C is set to 0.1.
3 Results
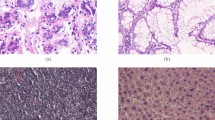
We use two public datasets in our experimental study. (1) The BreaKHis dataset contains 7909 hematoxylin and eosin (H&E) stained microscopy images. The images are collected at four magnification factors from 82 patients with breast tumors. Each image has \(700\times 460\) pixels, and among the images, 2480 are benign and 5429 are malignant. The task is to classify the images into benign or malignant cases at both image-level and patient-level, and for the individual magnification factors. (2) The IICBU 2008 malignant lymphoma dataset contains 374 H&E stained microscopy images captured using brightfield microscopy. Each image is of \(1388\times 1040\) pixels and there is a large degree of staining variation among the images. The dataset contains 113 chronic lymphocytic leukemia (CLL), 139 follicular lymphoma (FL), and 133 mantle cell lymphoma (MCL) cases. The task is to classify these three subtypes of malignant lymphoma. Figure 2 shows example images from the two datasets.
For training and testing, the BreaKHis dataset releases five splits for cross validation and each split contains 70% of images as training data and 30% as testing data. Images of the same patient are partitioned into either the training or testing set only. We use the same five splits in our study. For the IICBU dataset, we perform four-fold cross validation, with 3/4 of data for training and 1/4 for testing in each split. For the supervised intra-embedding, 50 epochs are trained on the BreaKHis dataset and 100 epochs are trained on the IICBU dataset.
We compared our results with the state-of-the-art approaches reported on these datasets, including [11, 12] on the BreaKHis dataset: [12] with a set of customized features, and [11] with a domain-specific ConvNet model; and [5, 10] on the IICBU dataset: [10] with SIFT-based FV descriptor and distance metric-based dimensionality reduction, and [5] with a combination of handcrafted and ConvNet features. In addition, we also experimented with the more standard way of using VGG-VD, which is to use the 4096-dimensional output from the last fully connected layer as the feature descriptor. Classifying the CFV descriptor without supervised intra-embedding is also evaluated. We also compared with the more standard techniques to address the issues with FV descriptor: PCA for dimensionality reduction, and intra-normalization for bursty visual element.
For the BreaKHis dataset, the state-of-the-art [11] shows that random sampling of 1000 patches of \(64\times 64\) pixels provided the best overall result and max pooling of four different ConvNet models produced further enhancement. We thus include the results from these two techniques ([11] rand, and [11] max) in the comparison, as shown in Table 1. The patient-level classification is derived by majority voting of the image-level results. The original approach [12] reported the patient-level results only. Our method achieved consistently better performance than [11, 12] except for the image-level classification of images with \(40\times \) magnification. It can be seen that while the random sampling approach [11] produced the best image-level classification for the \(40\times \) magnification, its patient-level results of all magnification factors were all lower than the those of the max pooling approach [11] and our method. Overall, the results illustrate that using CFV feature representation with supervised intra-embedding can outperform the handcrafted features [12] and ConvNet models [11] that are specifically designed for the particular histopathology dataset.
Table 2 shows the result comparison on the IICBU dataset. It can be seen that our method achieved the best result. CFV outperforms [10], indicating the advantage of using ConvNet-based patch features rather than SIFT in FV encoding, even when discriminative dimension reduction is also included in [10]. In addition, similar to our method, [5] also involves an ImageNet-pretrained ConvNet model but with additional steps for segmentation, handcrafted feature extraction, and ensemble classification. The advantage of our method over [5] illustrates the benefit of FV encoding and multilayer neural network-based dimensionality reduction. Also, compared to [5], our method is less complicated without the need to segment the cellular objects.
On both datasets, it can be seen that our method outperformed the approach with CFV descriptor only, demonstrating the benefit of supervised intra-embedding. When comparing CFV with VGG-VD (the 4096-dimensional descriptor), the advantage of using FV encoding of ConvNet-based patch features is evident. In addition, it can be seen that PCA and intra-normalization generally improved the results compared to using the original CFV descriptor. This indicates that it is beneficial to reduce the feature dimension and bursty effect of the CFV descriptor, and in general, intra-normalization has a greater effect on the classification performance than PCA. Our method provided larger improvement over CFV compared to PCA and intra-normalization. This shows that our learning-based transformation could provide a more effective approach to address the two issues with CFV.
4 Conclusions
A histopathology image classification method is presented in this paper. We encode the image content with ConvNet-based FV descriptor. To further improve the discriminative power of the descriptor, we design a supervised intra-embedding method to transform the descriptor to a lower dimension and reduce the bursty effect. Our results on the BreaKHis breast tumor and IICBU 2008 lymphoma datasets show that our method provides consistent improvement over the state of the art on these datasets. For future study, we will investigate extending our method to conduct tile-based classification for whole-slide images.
References
Arandjelovic, R., Zisserman, A.: All about VLAD. In: CVPR, pp. 1578–1585 (2013)
Barker, J., et al.: Automated classification of brain tumor type in whole-slide digital pathology images using local representative tiles. Med. Image Anal. 30(1), 60–71 (2016)
BenTaieb, A., Li-Chang, H., Huntsman, D., Hamarneh, G.: Automatic diagnosis of ovarian carcinomas via sparse multiresolution tissue representation. In: Navab, N., Hornegger, J., Wells, W.M., Frangi, A.F. (eds.) MICCAI 2015. LNCS, vol. 9349, pp. 629–636. Springer, Cham (2015). doi:10.1007/978-3-319-24553-9_77
Cimpoi, M., et al.: Deep filter banks for texture recognition, description, and segmentation. Int. J. Compt. Vis. 118(1), 65–94 (2016)
Codella, N., et al.: Lymphoma diagnosis in histopathology using a multi-stage visual learning approach. In: SPIE, p. 97910H (2016)
Kandemir, M., Zhang, C., Hamprecht, F.A.: Empowering multiple instance histopathology cancer diagnosis by cell graphs. In: Golland, P., Hata, N., Barillot, C., Hornegger, J., Howe, R. (eds.) MICCAI 2014. LNCS, vol. 8674, pp. 228–235. Springer, Cham (2014). doi:10.1007/978-3-319-10470-6_29
Perronnin, F., Sánchez, J., Mensink, T.: Improving the Fisher kernel for large-scale image classification. In: Daniilidis, K., Maragos, P., Paragios, N. (eds.) ECCV 2010. LNCS, vol. 6314, pp. 143–156. Springer, Heidelberg (2010). doi:10.1007/978-3-642-15561-1_11
Shamir, L., et al.: IICBU 2008: a proposed benchmark suite for biological image analysis. Med. Biol. Eng. Comput. 46(9), 943–947 (2008)
Simonyan, K., et al.: Fisher vector faces in the wild. In: BMVC, pp. 1–12 (2013)
Song, Y., Li, Q., Huang, H., Feng, D., Chen, M., Cai, W.: Histopathology image categorization with discriminative dimension reduction of Fisher vectors. In: Hua, G., Jégou, H. (eds.) ECCV 2016. LNCS, vol. 9913, pp. 306–317. Springer, Cham (2016). doi:10.1007/978-3-319-46604-0_22
Spanhol, F., et al.: Breast cancer histopathological image classification using convolutional neural networks. In: IJCNN, pp. 1–8 (2016)
Spanhol, F., et al.: A dataset for breast cancer histopathological image classification. IEEE Trans. Biomed. Eng 63(7), 1455–1462 (2016)
Wang, J., MacKenzie, J.D., Ramachandran, R., Chen, D.Z.: Neutrophils identification by deep learning and voronoi diagram of clusters. In: Navab, N., Hornegger, J., Wells, W.M., Frangi, A.F. (eds.) MICCAI 2015. LNCS, vol. 9351, pp. 226–233. Springer, Cham (2015). doi:10.1007/978-3-319-24574-4_27
Xing, F., et al.: An automatic learning-based framework for robust nucleus segmentation. IEEE Trans. Med. Imag. 35(2), 550–566 (2016)
Xu, X., Lin, F., Ng, C., Leong, K.P.: Adaptive co-occurrence differential texton space for HEp-2 cells classification. In: Navab, N., Hornegger, J., Wells, W.M., Frangi, A.F. (eds.) MICCAI 2015. LNCS, vol. 9351, pp. 260–267. Springer, Cham (2015). doi:10.1007/978-3-319-24574-4_31
Author information
Authors and Affiliations
Corresponding author
Editor information
Editors and Affiliations
Rights and permissions
Copyright information
© 2017 Springer International Publishing AG
About this paper
Cite this paper
Song, Y., Chang, H., Huang, H., Cai, W. (2017). Supervised Intra-embedding of Fisher Vectors for Histopathology Image Classification. In: Descoteaux, M., Maier-Hein, L., Franz, A., Jannin, P., Collins, D., Duchesne, S. (eds) Medical Image Computing and Computer Assisted Intervention − MICCAI 2017. MICCAI 2017. Lecture Notes in Computer Science(), vol 10435. Springer, Cham. https://doi.org/10.1007/978-3-319-66179-7_12
Download citation
DOI: https://doi.org/10.1007/978-3-319-66179-7_12
Published:
Publisher Name: Springer, Cham
Print ISBN: 978-3-319-66178-0
Online ISBN: 978-3-319-66179-7
eBook Packages: Computer ScienceComputer Science (R0)