Keywords

1 Introduction

Lens-free imaging (LFI) is a technique based on the principle of digital holography, in which a coherent light source (e.g., a laser) is used to illuminate the object specimen. As light passes through the specimen it is diffracted by the specimen, and the resulting diffraction pattern is recorded by an image sensor. Once the diffraction pattern has been recorded, an image of the specimen is reconstructed by post-processing the diffraction pattern using a mathematical model of the diffraction process [4].

Holographic LFI has several advantages over conventional microscopy. First, because there are no lenses in the imaging system, its overall cost and physical size can be greatly reduced compared to traditional microscopes. Second, LFI allows much wider fields of view to be imaged than a conventional microscope with equal magnification. Third, because the image of the specimen is generated through post-processing the recorded diffraction pattern, there is no need for an operator to manually focus the system as the focal depth can be adjusted automatically through post-processing [4].

In principle, if one could record the exact, complex-valued diffraction pattern of an object illuminated with a coherent light source, then reconstructing an image of the specimen would be straight-forward by simply computing the back-propagation of the recorded wave-front to the plane of the object using an appropriate diffraction model. However, imaging sensors are typically only capable of recording the (squared) magnitude of the diffraction pattern but not the phase. This presents a significant challenge for applying LFI in practice, and images reconstructed with conventional approaches typically contain significant artifacts (commonly referred to as twin-image artifacts) [3, 4]. Additionally, the problem can be further complicated if the specimen contains objects at multiple focal depths, as the diffraction patterns from out-of-focus objects will corrupt the reconstructed images at a particular focal depth, which traditional LFI image reconstruction approaches typically do not consider.

This paper addresses both of these issues by proposing a method to efficiently reconstruct images of a specimen over potentially multiple focal depths from a single recorded diffraction pattern while simultaneously estimating the phase information missing from the diffraction pattern. Using this technique results in significantly improved image quality over traditional image reconstruction techniques, allows for a 3D volume of the specimen to be reconstructed simultaneously, and provides a robust means of finding focal depths that contain objects, eliminating the need to manually tune focal depth.

2 Basics of Holographic Imaging

Holographic imaging is a technique based on optical diffraction. A full review of diffraction theory is beyond the scope of this work, but a commonly used approximation that is very accurate for the typical distances used in holography is to model the diffraction process as a 2D convolution [4]. In particular, the propagation of an optical wavefront \(X_0\) at a plane located at a distance z from the image plane produces the wavefront \(X_z = T(z) *X_0\), where T(z) is a transfer function that models the diffraction of light over a distance z and \(*\) denotes a 2D convolution. Various choices can be made for T(z) depending on the particular approximations one chooses in the model of the diffraction process (e.g., Fresnel, Huygens, far-field) [4]. In this paper we use the wide-angular spectrum (WAS) approximation, which defines the transfer function in the Fourier domain as

$$\begin{aligned} \mathcal {F}(T(z))[k_x,k_y]= \exp \left( iz \sqrt{k^2-k_x^2-k_y^2}\right) , \end{aligned}$$
(1)

where \(k = 2 \pi /\bar{\lambda }\) is the wavenumber for light with wavelength \(\bar{\lambda }\) and (\(k_x\),\(k_y\)) denote the spatial frequencies in the horizontal and vertical directions, respectively. Note that T(z) has several easily verified properties: (1) \(T(z_1) *T(z_2) = T(z_1+z_2)\), (2) \(T(0) *X = X\), (3) \(T(-z) = \overline{T(z)}\), where \(\overline{T(z)}\) denotes the complex conjugate of T(z), and (4) the linear operator \(\mathcal {T}_z(X) \equiv T(z) *X\) is unitary.

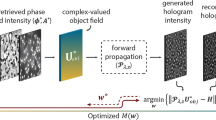
Using the WAS approximation to model light diffraction, if one is given a diffraction pattern, \(H \in \mathbb {R}^{m \times n}\), recorded from an image sensor, then one can try to find a corresponding image of a specimen, \(X \in \mathbb {C}^{m \times n}\), at a given focal depth, \(z \in \mathbb {R}\), such that \(H = T(z) *X\). A simple way to reconstruct an estimate of X is to solve the least-squares problem

$$\begin{aligned} \min _{X} \tfrac{1}{2}\Vert H-T(z) *X\Vert _F^2. \end{aligned}$$
(2)

Notice that from the properties of T(z) listed above and the fact that the Frobenius norm is invariant to unitary operations we have that the optimal solution to the above problem can be easily computed in closed form as \(X^* = T(-z) *H\). However, recall that image sensors are only capable of recording the magnitude of the diffraction pattern but not the phase (i.e., H is real valued in practice when in actuality it should be complex valued). This limitation results in the twin-image artifact in the reconstructed image, which is typically characterized by wave-like artifacts emanating from the object. The left column of Fig. 1 shows an example image of human blood reconstructed using this approach;Footnote 1 note the large amount of artifacts present in the background of the reconstructed image.

One way to address this issue is to modify the problem in (2) to account for the fact that because the phase is unknown one should only be concerned with matching the magnitude of the estimated hologram. This leads to the least-squares problem

$$\begin{aligned} \min _X \tfrac{1}{2}\Vert H - |T(z) *X| \Vert _F^2. \end{aligned}$$
(3)

Note that this problem can be equivalently expressed as

$$\begin{aligned} \min _{X,W} \tfrac{1}{2} \Vert H \odot W - T(z) *X \Vert _F^2 \text { s.t. }|W| = \varvec{1}, \end{aligned}$$
(4)

where \(\odot \) is the element-wise product of the matrix entries and \(|W| = \varvec{1}\) denotes that the magnitudes of the entries of \(W \in \mathbb {C}^{m \times n}\) should be equal to 1. The equivalence between (3) and (4) is seen by noting that the optimal solution for W in (4) for any value of X is given by \(W^*[i,j] = \exp (i \ \sphericalangle (T(z) *X)[i,j])\). Substituting this value for \(W^*\) into (4) gives (3).

While the modification of (2) into forms (3) and (4) has accounted for the fact that the phase information is missing from the recorded hologram, H, note that since T(z) is a unitary operator, for any choice of W one can generate a reconstructed image X such that \(H \odot W = T(z) *X\). In other words, the estimated phase, W, is totally arbitrary in this model, so additional modeling assumptions are needed to find meaningful solutions.

Due to the significant practical challenges discussed above, many techniques have been proposed to mitigate the effects of the twin-image artifact. Additionally, due to the fact that the diffraction hologram contains sufficient information to potentially reconstruct 3D reconstructions of objects, several techniques have been proposed to estimate a 3D volume of an object specimen. However, many existing approaches either rely on acquiring multiple holograms under various illumination conditions, which complicates the hardware requirements, or they have not achieved sufficient performance when using a single recorded hologram to be widely used in practice [3, 4]. For example, the authors of [2] explore an iterative reconstruction process that attempts to estimate the portion of the reconstructed image that corresponds to the twin-image artifact versus the portion of the reconstructed image corresponding to the true object. Using this estimate, a masking operation is performed in an attempt to estimate the phase of the hologram by removing the influence of the artifact; however, the method only results in relatively modest improvements in image quality when applied to real data [2].

Most closely related to our work, several prior studies have also explored the use of an assumption of sparsity on the reconstructed image (i.e., most pixels do not contains objects and are at the background intensity) as a means to improve holographic image reconstruction. The authors of [1] consider a sparse reconstruction model that promotes sparsity in the reconstructed image similar to what we propose. However, the primary difference from our work is that the authors of [1] use a model which is purely in the real domain and do not attempt to estimate the missing phase information. This approach is only suitable if the imaged objects are sufficiently small and separated in space to ensure that their holograms do not significantly interact. As we show in experiments, recovering the phase of the hologram dramatically improves the quality of the image reconstruction.

In very recent work, the authors of [6] propose a model similar to (3) with an added \(\ell _0\) pseudo-norm regularization on X (a count of the number of non-zero elements in X), and attempt to solve a problem of the form

$$\begin{aligned} \min _X \Vert X\Vert _0 \text { s.t. }\Vert H-|T(z)*X|\Vert \le \epsilon . \end{aligned}$$
(5)

This formulation presents significant practical challenges due to the fact that problems penalized by the \(\ell _0\) pseudo-norm are typically NP-hard, so one must resort to approximate solutions. As such, the algorithm proposed in [6] requires one to greedily update an estimate of the pixels that contain an object and solve a non-convex least-squares regression problem at each iteration. For large images that are sparse but still contain a significant number of objects, the computational costs of this approach are very significant, and additionally, the variable updates cannot be solved to completion at any given iteration due to the non-convexity of the sub-problems. In other recent work, sparsity has been proposed in a reconstruction framework that combines information from multiple holograms recorded at different focal depths to reconstruct an image [5]. While this method produces high-quality reconstructions, in addition to requiring that multiple holograms be recorded at different focal depths, this method is also very computationally intensive, needing approximately 28 min to reconstruct a single image [5].

The main contribution of this work is a method to reconstruct images from recorded holograms based on sparsity which (1) provides an estimate of the missing phase information, (2) only requires a single recorded hologram (greatly simplifying hardware design), and (3) allows for reconstructions over full 3D volumes and robustly finds the focal depth of objects in the specimen. Further, our method is highly efficient and reconstructs large images in under a second, and experimental results demonstrate significantly improved image quality over existing methods based on single hologram reconstructions. In Sect. 3 we present our model for reconstructing single images, and then in Sect. 4 we extend our model to reconstructions over 3D volumes.

3 Sparse Phase Recovery

Due to the fact that the LFI reconstruction problem in (4) is underdetermined, additional assumptions are needed to find meaningful solutions. A natural and rather general assumption in many applications is that the reconstructed image, X, be sparse, an assumption that is justified whenever the objects in the specimen occupy only a portion of the pixels in the field of view with many of the pixels being equal to the background intensity. Note that there are many ways to measure the sparsity of a signal, but here we use the \(\ell _1\) norm as it has the desirable property of encouraging sparse solutions while still being a convex function and conducive to efficient optimization. Additionally, typical measures of sparseness require that most of the entries be identically 0, while here if a pixel doesn’t contain an object the value of the pixel will be equal to the background intensity of the illumination light. As a result, we account for the non-zero background by adding an additional term \(\mu \in \mathbb {C}\) to the model to capture (planar) illumination. This results in the final model that we propose in this work,

$$\begin{aligned} \min _{X,W,\mu } \tfrac{1}{2} \Vert H \odot W - \mu \varvec{1} - T(z) *X \Vert _F^2 + \lambda \Vert X\Vert _1 \text { s.t. }|W| = \varvec{1}. \end{aligned}$$
(6)

While our model given in (6) has many theoretical justifications based on the nature of the LFI reconstruction problem, unfortunately, the optimization problem is non-convex due to the constraint that \(|W| = \varvec{1}\). Nevertheless, despite this challenge, here we describe an algorithm based on alternating minimization that allows for efficient, closed-form updates to all of the variables which displays strong empirical convergence using trivial initializations. In particular, one has the following closed-form updates for our variables,

$$\begin{aligned} {\mathop {\hbox {arg min}}\limits _{W}} \, (6)&= \exp ( i \ \sphericalangle (\mu \varvec{1} + T(z) *X)) \end{aligned}$$
(7)
$$\begin{aligned} {\mathop {\hbox {arg min}}\limits _{\mu }} \, (6)&= \tfrac{1}{mn} \langle H \odot W - T(z) *X, \varvec{1} \rangle \end{aligned}$$
(8)
$$\begin{aligned} {\mathop {\hbox {arg min}}\limits _{X}} \, (6)&= SFT_\lambda \{T(-z) *(\!H \odot W ) - \mu \exp (-izk) \varvec{1} \} \end{aligned}$$
(9)

where \(SFT_\lambda \{\cdot \}\) denotes the complex soft-thresholding operator, given by

$$\begin{aligned} SFT_\lambda \{Z\}[i,j] = {\left\{ \begin{array}{ll} Z[i,j] \frac{|Z[i,j]|-\lambda }{|Z[i,j]|} &{} |Z[i,j]| > \lambda \\ 0 &{} |Z[i,j]| \le \lambda . \end{array}\right. } \end{aligned}$$
(10)

Note that the update for X comes from the unitary invariance of the Frobenius norm, the properties of T(z) described above, the fact that \(\mathcal {F}(T(z))[0,0]= \exp (izk)\), and the standard proximal operator of the \(\ell _1\) norm.

Fig. 1.
figure 1

Example image reconstructions of a whole blood sample using different reconstruction algorithms. Left Panel: Reconstructed images using the basic reconstruction (Left Column), sparse reconstruction without phase estimation (Middle Column), and the full model (Right Column) shown with the full grayscale range of the reconstruction (Top Row) and with the grayscale range clipped with a maximum of 2 to better visualize the clarity of the background (Bottom Row). Top Right Panel: Linescan plots of the 3 reconstruction methods over the colored lines indicated in the left panel. The pink region highlights a large area of the image background. Bottom Right Panel: Zoomed in crops of a cluster of cells for the 3 methods.

Full size image

From this, it is possible to efficiently reconstruct images from the recorded diffraction patterns using the alternating sequence of updates to the variables described by Eqs. (7)–(9), and full details are provided in Algorithm 1 in the supplement. We note that we observe very strong convergence within approximately just 10–15 iterations of the algorithm from trivially initializing with \(X = \varvec{0}\), \(\mu =0\), and \(W=\varvec{1}\). Due to the fact that the main computational burden of the cyclical updates lies in computing Fourier transforms (for the convolution) and element-wise operations, the computation is significantly accelerated by performing the calculation on a graphical processing unit (GPU), and images with \(2048 \times 4096\) pixels can be reconstructed in approximately 0.7 s on a Nvidia K80 GPU using 15 iterations of the algorithm. Figure 1(Left) shows an image of human blood reconstructed using a basic reconstruction method which does not estimate phase nor use a sparse prior on X (i.e., \(\lambda =0\) and W fixed at \(W=\varvec{1}\)), a reconstruction that uses a sparse prior but does not estimate the missing phase information (by keeping W fixed at \(W=\varvec{1}\) as in [1]), and finally the proposed method (Full Model). Note that the basic reconstruction has significant artifacts. Adding the sparse prior on X attenuates the artifacts somewhat, but the artifacts are still clearly visible with a clipped grayscale range (bottom row). Finally, in our full model the artifacts have been completely eliminated (the small particles that remain are predominately platelets in the blood), and the contrast of the red blood cells in the image has been increased significantly (see the linescan in the top right panel). A value of \(\lambda =1\) was used for both models involving sparsity.

4 Multi-depth Reconstructions

To this point, the discussion has largely pertained to reconstructing an image at a single focal depth. However, one of the main advantages of holographic imaging over conventional microscopy is the potential to reconstruct an entire 3D volume of the specimen versus just a single image at one focal depth. One possibility is to reconstruct multiple images independently using the algorithm described in Sect. 3 while varying the focal depth. Unfortunately, if the specimen contains objects at multiple focal depths, the diffraction patterns from out-of-focus objects will corrupt the reconstruction at any given focal depth. Additionally, even in the case where only one image at a single focal depth is needed, it is still necessary to determine the correct focal depth, which can be tedious to do manually. To address these issues, we extend the model in Sect. 3 to reconstruct 3D volumes of a specimen. In particular, we extend the single focal depth model in (6), from reconstructing a single image, \(X \in \mathbb {C}^{m \times n}\), to now reconstruct a sequence of images, \({X_j}_{j=1}^D\), where each \(X_j \in \mathbb {C}^{m \times n}\) image corresponds to an image at a specified depth \(\varvec{z}[j]\). More formally, if we are given a vector of desired reconstruction depths \(\varvec{z} \in \mathbb {R}^D\), then we seek to solve the model,

$$\begin{aligned} \min _{ \{X_j\}_{j=1}^D,W,\mu } \tfrac{1}{2} \Vert H \odot W - \mu \varvec{1} - \sum _{j=1}^D T(\varvec{z}[j]) *X_j \Vert _F^2 + \lambda \sum _{j=1}^D \Vert X_j\Vert _1 \text { s.t. }|W| = \varvec{1}. \end{aligned}$$
(11)
Fig. 2.
figure 2

Left: Example crops of the 3D reconstruction at different depths. The displayed depth ranges from [800, 980] microns increasing from left-to-right, top-to-bottom. Right: Magnitude of the reconstructed 3D volume over focal depth, as measured by the \(\ell _1\) norms of the reconstructed images, \(\Vert X_j\Vert _1\), for 101 evenly spaced focal depths over the range [650, 1150] microns. The red-line depicts the focal depth obtained by manually focusing the image.

Full size image

This model is essentially the same as the model for reconstructing an image at a single focal depth used in (6) but extended to a discretized 3D volume. Unfortunately, due to multiple focal-depths it is no longer possible to derive a closed form update for all of X (although one can still derive a closed form update for an image at a particular depth, \(X_j\)). Instead we use a hybrid algorithm that uses alternating minimization to update the W and \(\mu \) variables and proximal gradient descent steps to update X [7]. The detailed steps of the algorithm are described in Algorithm 2 of the supplement, and Fig. 2 shows the magnitudes of the reconstructed \(X_j\) images as a function of the specified focal depth for 101 uniformly spaced focal depths over the range [650, 1150] microns along with example crops of the 3D reconstruction at different depthsFootnote 2. Note that the image depth with the largest magnitude corresponds to the focal depth found by manually focusing the depth of reconstruction, demonstrating how reconstructing images over a 3D volume with the proposed method robustly and automatically recovers the focal depth of objects within the specimen.

5 Conclusions

We have presented a method based on sparse regularization for reconstructing holographic lens-free images and recovering the missing phase information from a single recorded hologram. Our method converges quickly to a robust solution in a computationally efficient manner, significantly improves reconstruction quality over existing methods, is capable of reconstructing images over a 3D volume, and provides a robust means to find the focal depth of objects within the specimen volume, eliminating the need to manually tune focal depth.