Abstract
This paper introduces a parametric level-set method for tomographic reconstruction of partially discrete images. Such images consist of a continuously varying background and an anomaly with a constant (known) grey-value. We express the geometry of the anomaly using a level-set function, which we represent using radial basis functions. We pose the reconstruction problem as a bi-level optimization problem in terms of the background and coefficients for the level-set function. To constrain the background reconstruction, we impose smoothness through Tikhonov regularization. The bi-level optimization problem is solved in an alternating fashion; in each iteration we first reconstruct the background and consequently update the level-set function. We test our method on numerical phantoms and show that we can successfully reconstruct the geometry of the anomaly, even from limited data. On these phantoms, our method outperforms Total Variation reconstruction, DART and P-DART.
You have full access to this open access chapter, Download conference paper PDF
Similar content being viewed by others
Keywords
1 Introduction
The need to reconstruct (quantitative) images of an object from tomographic measurements appears in many applications. At the heart of many of these applications is a projection model based on the Radon transform. Characterizing the object under investigation by a function \(u(\mathbf {x})\) with \(\mathbf {x}\in \mathcal {D}=[0,1]^2\), tomographic measurements are modeled as
where \(s_i \in [0,1]\) denotes the shift, \(\theta _i\in [0,2\pi )\) denotes the angle and \(\mathbf {n}(\theta ) = (\cos \theta ,\sin \theta )\). The goal is to retrieve u from a number, m, of such measurements for various shifts and directions.
If the shifts and angles are regularly and densely sampled, the transform can be inverted directly by Filtered back-projection or Fourier reconstruction [9]. A common approach for dealing with non-regularly sampled or missing data, is algebraic reconstruction. Here, we express u in terms of a basis
where b are piece-wise polynomial basis functions and \(\{\mathbf {x}_j\}_{j=1}^n\) is a regular (pixel) grid. This leads to a set of m linear equations in n unknowns
with \(w_{ij} = \int _{\mathcal {D}}\, b(\mathbf {x} - \mathbf {x}_j)\delta (s_i - \mathbf {n}(\theta _i)\cdot \mathbf {x})\,\mathrm {d}\mathbf {x}\). Due to noise in the data or errors in the projection model the system of equations is typically inconsistent, so a solution may not exist. Furthermore, there may be many solutions that fit the observations equally well when the system is underdetermined. A standard approach to mitigate these issues is to formulate a regularized least-squares problem
where R is the regularization operator with parameter \(\lambda \) balancing the data-misfit and regularity of the solution. Such a formulation is popular mainly because very efficient algorithms exist for solving it. Depending on the choice of R, however, this formulation forces the solution to have certain properties which may not reflect the truth. For example, setting R to be the discrete Laplace operator will produce a smooth reconstruction, whereas setting R to be the identity matrix forces the individual coefficients \(u_i\) to be small. In many applications such quadratic regularization terms do not reflect the characteristics of the object we are reconstructing. For example, if we expect u to be piecewise constant, we could use a Total Variation regularization term \(\Vert R\mathbf {u}\Vert _1\) where R is a discrete gradient operator [13]. Recently, a lot of progress has been made in developing efficient algorithms for solving such non-smooth optimization problems [6]. If the object under investigation is known to consist of only two distinct materials, the regularization can be formulated in terms of a non-convex constraint \(\mathbf {u} \in \{u_0, u_1\}^n\). The latter leads to a combinatorial optimization problem, solutions to which can be approximated using heuristic algorithms [3].
In this paper, we consider tomographic reconstruction of partially discrete objects that consist of a region of constant density embedded in a continuously varying background. In this case, neither the quadratic, Total Variation nor non-convex constraints by themselves are suitable. We therefore propose the following parametrization
The inverse problem now consists of finding \(u_0(\mathbf {x})\), \(u_1\) and the set \(\varOmega \). We can subsequently apply suitable regularization to \(u_0\) separately. To formulate a tractable optimization algorithm, we represent the set \(\varOmega \) using a level-set function \(\phi (\mathbf {x})\) as follows:
In the following sections, we assume knowledge of \(u_1\) and discuss how to formulate a variational problem to reconstruct \(\varOmega \) and \(u_0\) based on a parametric level-set representation of \(\varOmega \).
The outline of the paper is as follows. In Sect. 2 we discuss the parametric level-set method and propose some practical heuristics for choosing various parameters that occur in the formulation. A joint background-anomaly reconstruction algorithm for partially discrete tomography is discussed in Sect. 3. The results on a few moderately complicated numerical phantoms are presented in Sect. 4. We provide some concluding remarks in Sect. 5.
2 Level-Set Methods
In terms of the level-set function, we can express u as
where h is the Heaviside function.
Level-set methods have received much attention in geometric inverse problems, interface tracking, segmentation and shape optimization. In the classical level-set method, introduced by Sethian and Osher [11], the level-set is evolved according to the Hamilton-Jacobi equation
where \(\phi (\mathbf {x},t)\) now denotes the level-set function as a time-dependent quantity for representing the shape and v denotes the normal velocity at the boundary of the shape. In the inverse-problems setting, the velocity v is often derived from the gradient of the cost function with respect to the model parameter [5, 7]. There are various numerical issues associated with the numerical solution of level-set equation, e.g. reinitialization of the level-set. We refer the interested reader to a seminal paper in level-set methods [11] and its application to computational tomography [10].
Instead of taking this classical level-set approach, we employ a parametric level-set approach, first introduced by Aghasi et al. [1]. In this method, the level-set function is parametrized using radial basis functions (RBF)
where \(\varPsi (\cdot )\) is a radial basis function, \(\{\alpha _j\}_{j=1}^{n'} \) and \(\{\varvec{\chi }_j\}_{j=1}^{n'}\) are the amplitudes and nodes respectively, and the parameters \(\{\beta _j\}_{j=1}^{n'}\) control the widths. Introducing the kernel matrix \(A(\varvec{\chi }, \varvec{\beta })\) with elements
we can now express \(\mathbf {u}\) on the computational grid \(\{\mathbf {x}_i\}_{i=1}^{n}\) as
where h is applied element-wise to the vector \(A(\varvec{\chi }, \varvec{\beta }) \varvec{\alpha }\) and \(\odot \) denotes the element-wise (Hadamard) product. By choosing the parameters \((\varvec{\chi }, \varvec{\beta }, \varvec{\alpha })\) appropriately we can represent any (smooth) shape. To simplify matters and make the resulting optimization problem more tractable, we consider a fixed regular grid \(\{\varvec{\chi }_j\}_{j=1}^{n'}\) and a fixed width \(\beta _j \equiv \beta \). In the following we choose \(\beta \) in accordance with the grid spacing \(\varDelta \chi \) as \(\beta = 1/(\eta \varDelta \chi )\), where \(\eta \) corresponds to the width of the RBF in grid points.
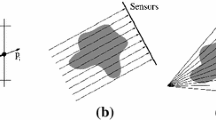
Example. To illustrate the representation of a shape using finitely many radial basis functions, we consider the green shape shown in Fig. 1(a). Starting from an initial guess (Fig. 1(a), red) we obtain the coefficients \(\varvec{\alpha }\) by solving a non-linear least-squares problem \(\min _{\varvec{\alpha }} \Vert h(A\varvec{\alpha }) - \mathbf {y}\Vert _2^2\), where \(\mathbf {y}\in \{0,1\}^n\) indicates the true shape. This leads to the representation shown in Fig. 1(b). With \({n'} = 196\) RBFs, it is possible to reconstruct a smooth shape discretized on a grid with \(n = 256 \times 256\) pixels.
Any (sufficiently) smooth level-set can be reconstructed from radial basis functions. (a) The shape to be reconstructed is denoted in green. The initial shape (dash-dotted line) is generated by some positive RBF coefficients (denoted by red pluses) near the center and negative coefficients elsewhere (denoted by blue dots). Also shown is the corresponding initial level-set function. The reconstructed shape denoted with a dash-dotted line, the sign of the RBF-coefficients as well as the corresponding level-set function are shown in (b). (Color figure online)
Finally, the discretized reconstruction problem for determining the shape is now formulated as
where \(h_{\epsilon }\) is a smooth approximation of the Heaviside function. The gradient and Gauss-Newton Hessian of \({f(\varvec{\alpha })}\) are given by
where the diagonal matrix and residual vectors are given by
Using a Gauss-Newton method, the level-set parameters are updated as
where \(\mu _k\) is a stepsize chosen to satisfy the weak Wolfe conditions [15] and \(\varvec{\alpha }^{(0)}\) is a given initial estimate of the shape. The weak Wolfe conditions consist of sufficient decrease and curvature conditions and ensure global convergence to a local minimum.
From Eq. (4), it can be observed that the ability to update the level-set parameters depends on two main factors: (1) The difference between \(\mathbf {u}_0\) and \(u_1\), and (2) the derivative of the Heaviside function. Hence, the support and smoothness of \(h'_{\epsilon }\) plays a crucial role in the sensitivity. More details on the choice of \(h_{\epsilon }\) are discussed in Sect. 2.1.
Example. We demonstrate the parametric level-set method on a (binary) discrete tomography problem. We consider the model described in Fig. 2(a). For a full-angle case (\(0 \le \theta \le \pi \)) with a large number of samples, Fig. 2(c) shows that it is possible to accurately reconstruct a complex shape. The model is reconstructed by iteratively updating \(\varvec{\alpha }\) using Eq. (5).
Parametric level-set method for Discrete tomography problem. (a) True model (\(n = 256 \times 256\)) (b) RBF grid (\(n' = 27 \times 27\)) with initial level-set denoted by green line, positive and negative RBFs are denoted by red pluses and blue dots respectively (c) Final level-set denoted by the green line, and the corresponding positive and negative RBFs (d) Initial level-set function (e) level-set function after 10 iterations (f) final level-set function after 25 iterations. (Color figure online)
2.1 Approximation to Heaviside Function
The update of the level-set function depends crucially on the choice of the Heaviside function. In Eq. (4) we see that \(h'_{\epsilon }\) acts as a windowing function that controls which part of the level-set function is updated. The windowing function should achieve the following: (i) limit the update to a small region around the boundary of the shape; (ii) have a uniform amplitude in the boundary region; and (iii) guarantee a minimum width of the boundary region. Failure to meet these requirements may result in poor updates for the level-set parameter \(\varvec{\alpha }\) and premature break-down of the algorithm.
Requirement \((i )\) is easily fulfilled as any smooth approximation of the Heaviside will have a rapidly decaying derivative. To satisfy the second requirement we construct the Heaviside function by smoothing the piece-wise linear function \({\textstyle \frac{1}{2}} + {\textstyle \frac{x}{2\epsilon }}\) for \(|x| \le \epsilon \). This approximation is shown in Fig. 3 alongside two common smooth approximations of the Heaviside. We now discuss how we can satisfy the third requirement, starting with a formal definition of the width of the level-set boundary layer as shown in Fig. 3(c).
Definition 1
In accordance with the compact approximation of the Heaviside function with width \(\epsilon \), we define the minimum width of the level-set boundary layer as \(\varDelta = \min _{\mathbf {x}_0,\mathbf {x}_1} \Vert \mathbf {x}_0 - \mathbf {x}_1 \Vert _2\) such that \(\phi (\mathbf {x}_0) = 0\) and \(|\phi (\mathbf {x}_1)| = \epsilon \).
Lemma 1
For any smooth and compact approximation of the Heaviside function with finite width \(\epsilon \), the width of the level-set boundary layer, \(\varDelta \), satisfies
Proof
A Taylor series expansion of \(\phi (\mathbf {x})\) around \(\mathbf {x}_0\) for which \(\phi (\mathbf {x}_0) = 0\), we get
with \(\varvec{\xi } = t \mathbf {x}_0 + (1-t)\mathbf {x}\) for some \(t\in [0,1]\). This leads to
Choosing \(\mathbf {x} = \mathbf {x}_1\) with \(|\phi (\mathbf {x}_1)| = \epsilon \), we have \(\Vert \mathbf {x}_1 - \mathbf {x}_0\Vert _2 \ge \epsilon /\Vert \nabla \phi \Vert _{\infty }\). Since this holds for all \(\mathbf {x}_0, \mathbf {x}_1\) we obtain the desired result. \(\square \)
To ensure a minimum width of the boundary layer, Lemma 1 suggest to choose \(\epsilon \) proportional to \(\Vert \nabla \phi \Vert _{\infty }\). For computational simplicity, we approximate this using upper and lower bounds [8] and set:
where \(\kappa \) controls the width of level-set boundary in terms of the underlying computational grid. A small value of \(\kappa \) leads to the narrow boundary while big value leads a wide boundary.
New formulation for approximating the Heaviside function. The Heaviside functions (a) and corresponding Dirac-Delta functions (b) with \(\epsilon = 1\). Global approximation is constructed from inverse tangent function (\(\tfrac{1}{2}(1 + \tfrac{2}{\pi }\arctan (\pi \tfrac{x}{\epsilon }))\)), while compact one is composed of linear and sinusoid functions. (c) level-set boundary (orange region) around zero level-set denoted by blue line, n represents the normal direction at \(\mathbf {x}_0\). (Color figure online)
3 Joint Reconstruction Algorithm
Reconstructing both the shape and the background parameter can be cast as a bi-level optimization problem
where L is of form \([L_x^T \quad L_y^T]^T\) where \(L_x\) and \(L_y\) is the second-order finite-difference operators in the x and y direction, respectively. This optimization problem is separable; it is quadratic in \(\mathbf {u}_0\) and non-linear in \(\varvec{\alpha }\). In order to exploit the fact that the problem has a closed-form solution in \(\mathbf {u}_0\) for each \(\varvec{\alpha }\), we introduce a reduced objective
The gradient and Hessian of this reduced objective are given by
where \(\overline{\mathbf {u}}_0 = \mathop {\mathrm {argmin}}\nolimits _{\mathbf {u}_0} f(\varvec{\alpha },\mathbf {u}_0)\) [2].
Using a modified Gauss-Newton algorithm to find a minimizer of \(\overline{f}\), it leads to the following alternating algorithm
where the expressions for the gradient and Gauss-Newton Hessian are given by (4). Convergence of this alternating approach to a local minimum of (7) is guaranteed as long as the step-length satisfies the strong Wolfe conditions [15].
The reconstruction algorithm based on this iterative scheme is presented in Algorithm 1. We use the LSQR method in step 3, with a pre-defined maximum number of iterations (typically 200) and a tolerance value. A trust-region method is applied to compute \(\varvec{\alpha }^{(k+1)}\) in step 4 restricting the conjugate gradient to only 10 iterations. We perform a total of \(K=50\) iterations to reconstruct the model.

4 Numerical Experiments
The numerical experiments are performed on 4 phantoms shown in Fig. 4. We scale the phantoms such that \(u_1 = 1\). For the first two phantoms, the background varies from 0 to 0.5, while for the next two, it varies from 0 to 0.8. In order to avoid the inverse crime, we use two different discretization schemes for Eq. (1) (namely, line kernel [4] for data generation, and Joseph kernel [4] for forward modeling). We use ASTRA toolbox to compute the forward and backward projections [4]. First, we show the results on the full-view data and later we compare various methods on a limited-angle case.
For the parametric level-set method, we use Wendland compactly supported radial basis functions [8]. The RBF nodes are placed on a 5 times coarser grid than the model grid, with an extension of two points outside the model grid to avoid boundary effects. To constrain the initial level-set boundary to 4 grid-points, the Heaviside width parameter \(\kappa \) is set to be 0.01.
The level-set parameter \(\varvec{\alpha }\) is optimized using the fminunc package (trust-region algorithm) in Matlab. A total of 50 iterations are performed for predicting the \(\varvec{\alpha }\), while 200 iterations are performed for predicting \(\mathbf {u}_0(x)\) using LSQR at each step.
4.1 Regularization Parameter Selection
The reconstruction with the proposed algorithm is influenced by the regularization parameter \(\lambda \) (cf. (7)). In general, there are various strategies to choose this parameter, e.g., [14]. As our problem formulation is non-linear, many of these strategies do not apply. Instead we analyze the influence of the regularization parameter numerically as follows.
Variation of residuals with regularization parameter for Tikhonov. Appropriate region for choosing \(\lambda \) exists between \(3.79 \times 10^5\) and \(6.95 \times 10^6\). (a) behavior of DR and MR over \(\lambda \) for model A with noisy limited-angle data. (b), (c), (d), (e) show reconstructions for various \(\lambda \) values.
We define two measures (in the least-squares sense) to quantify the residuals: the data residual (DR), which determines the fit between the true data and reconstructed data, and the model residual (MR), which determines the fit between reconstructed model and true model. Finally, we use the Jaccard index (JI), defined as a similarity coefficient between two sets, to capture the error in the reconstructed shape. In practice, one can only use the data residual to select the regularization parameter \(\lambda \). It is evident from Fig. 5 that there exists a sufficiently large region of \(\lambda \) for which the reconstructions are equally good. Moreover, this region is easily identifiable from the data residual plot for various \(\lambda \) values.
4.2 Full-View Test
For the full-view case, the projection data is generated on a \(256 \times 256\) grid with 256 detectors and 180 equidistant projections (\(0 \le \theta \le \pi \)). The Gaussian noise of 10 dB Signal-to-Noise ratio (SNR) is added to the data. The results on phantoms A, B, C and D with the full-view data are shown in Fig. 6. The geometry of the anomalies in all of these reconstructed models are very close to the ground truth, as is indicated by the Jaccard index shown above the figures. The background, though, has been smoothened out with the Tikhonov regularization.
4.3 Limited-Angle Test
In this case, we generate synthetic data using only 5 projections, namely, \(\theta = \{ 0, \pi /6, \pi /3, \pi /2, 2\pi /3 \}\). We add Gaussian noise of 10 dB SNR to the synthetic data. To check the performance of the proposed method, we compare it to Total Variation method [4], DART [3] and its modified version for partially discrete tomography, P-DART [12]. For Total Variation, we determine the shape from the final reconstruction via a simple segmentation step (thresholding). A total of 200 iterations were performed with the Total Variation method and the regularization parameter determined such that it optimally reconstructs the shape. In DART, the background is modeled using 20 discrete grey-values for model A and B, while 30 discrete grey-values for model C and D. True model has been segmented per mentioned grey-values to generate data for DART. 40 DART iterations were performed in each case. For P-DART, a total of 150 iterations were performed.
Reconstructions with noisy limited data. The first column shows the true models, while the last 4 columns show the reconstructions with various methods. Red dotted line shows the contour of the segmented model in Total Variation method. Different measures are also shown below each reconstructed model. (Color figure online)
The results on limited-angle data are presented in Fig. 7. The proposed method is able to capture most of the fine details (evident from the Jaccard Index) in the phantoms even with the very limited data with moderate noise. The P-DART method achieves the least amount of data residual in all the cases, but fails to capture the complete geometry of the anomaly. The Total variation method gives surprisingly good reconstructions of the shape. However, we obtained these results by selecting the best over a large range of regularization parameters. The level-set method consistently gives the best reconstruction of the shape.
5 Conclusions and Discussion
We discussed a parametric level-set method for partially discrete tomography. We model such objects as a constant-valued shape embedded in a continuously varying background. The shape is represented using a level-set function, which in turn is represented using radial basis functions. The reconstruction problem is posed as a bi-level optimization problem for the background and level-set parameters. This reconstruction problem can be efficiently solved using a variable projection approach, where the shape is iteratively updated. Each iteration requires a full reconstruction of the background. The algorithm includes some practical heuristics for choosing various parameters that are introduced as part of the parametric level-set method. Numerical experiments on a few numerical phantoms show that the proposed approach can outperform other popular methods for (partially) discrete tomography in terms of the reconstruction error. As the proposed algorithm requires repeated full reconstructions, it is currently an order of magnitude slower than the other methods. Future research is directed at making the method more efficient.
References
Aghasi, A., Kilmer, M., Miller, E.L.: Parametric level set methods for inverse problems. SIAM J. Imaging Sci. 4(2), 618–650 (2011)
Aravkin, A.Y., Van Leeuwen, T.: Estimating nuisance parameters in inverse problems. Inverse Prob. 28(11), 115016 (2012)
Batenburg, K.J., Sijbers, J.: Dart: a practical reconstruction algorithm for discrete tomography. IEEE Trans. Image Process. 20(9), 2542–2553 (2011)
Bleichrodt, F., van Leeuwen, T., Palenstijn, W.J., van Aarle, W., Sijbers, J., Batenburg, K.J.: Easy implementation of advanced tomography algorithms using the astra toolbox with spot operators. Numer. Algorithms 71(3), 673–697 (2016)
Burger, M.: A level set method for inverse problems. Inverse Prob. 17(5), 1327 (2001)
Chambolle, A., Pock, T.: A first-order primal-dual algorithm for convex problems with applications to imaging. J. Math. Imaging Vis. 40(1), 120–145 (2011)
Dorn, O., Lesselier, D.: Level set methods for inverse scattering. Inverse Prob. 22(4), R67 (2006)
Kadu, A., Van Leeuwen, T., Mulder, W.A.: Salt reconstruction in full waveform inversion with a parametric level-set method. IEEE Trans. Comput. Imaging 3(2), 305–315 (2016)
Kak, A.C., Slaney, M.: Principles of Computerized Tomographic Imaging. SIAM, Philadelphia (2001)
Klann, E., Ramlau, R., Ring, W.: A mumford-shah level-set approach for the inversion and segmentation of SPECT/CT data. Inverse Probl. Imaging 5(1), 137–166 (2011)
Osher, S., Fedkiw, R.: Level Set Methods and Dynamic Implicit Surfaces, vol. 153. Springer, New York (2006). doi:10.1007/b98879
Roelandts, T., Batenburg, K., Biermans, E., Kübel, C., Bals, S., Sijbers, J.: Accurate segmentation of dense nanoparticles by partially discrete electron tomography. Ultramicroscopy 114, 96–105 (2012)
Sidky, E.Y., Pan, X.: Image reconstruction in circular cone-beam computed tomography by constrained, total-variation minimization. Phys. Med. Biol. 53(17), 4777 (2008)
Thompson, A.M., Brown, J.C., Kay, J.W., Titterington, D.M.: A study of methods of choosing the smoothing parameter in image restoration by regularization. IEEE Trans. Pattern Anal. Mach. Intell. 13(4), 326–339 (1991)
Wright, S., Nocedal, J.: Numerical Optimization. Springer Series in Operations Research and Financial Engineering. Springer, New York (1999). doi:10.1007/b98874
Acknowledgments
This work is part of the Industrial Partnership Programme (IPP) ‘Computational sciences for energy research’ of the Foundation for Fundamental Research on Matter (FOM), which is part of the Netherlands Organisation for Scientific Research (NWO). This research programme is co-financed by Shell Global Solutions International B.V. The second and third authors are financially supported by the NWO as part of research programmes 613.009.032 and 639.073.506 respectively.
Author information
Authors and Affiliations
Corresponding author
Editor information
Editors and Affiliations
Rights and permissions
Copyright information
© 2017 Springer International Publishing AG
About this paper
Cite this paper
Kadu, A., van Leeuwen, T., Batenburg, K.J. (2017). A Parametric Level-Set Method for Partially Discrete Tomography. In: Kropatsch, W., Artner, N., Janusch, I. (eds) Discrete Geometry for Computer Imagery. DGCI 2017. Lecture Notes in Computer Science(), vol 10502. Springer, Cham. https://doi.org/10.1007/978-3-319-66272-5_11
Download citation
DOI: https://doi.org/10.1007/978-3-319-66272-5_11
Published:
Publisher Name: Springer, Cham
Print ISBN: 978-3-319-66271-8
Online ISBN: 978-3-319-66272-5
eBook Packages: Computer ScienceComputer Science (R0)