Euclidean and Geodesic Distance Profiles

Abstract

This paper presents a boundary-based, topological shape descriptor: the distance profile. It is inspired by the LBP (= local binary pattern) scale space – a topological shape descriptor computed by a filtration with concentric circles around a reference point. For rigid objects, the distance profile is computed by the Euclidean distance of each boundary pixel to a reference point. A geodesic distance profile is proposed for articulated or deformable shapes: the distance is measured by a combination of the Euclidean distance of each boundary pixel to the nearest pixel of the shape’s medial axis and the geodesic distance along the shape’s medial axis to the reference point. In contrast to the LBP scale space, it is invariant to deformations and articulations and the persistence of the extrema in the profiles allows pruning of spurious branches (i.e. robustness against noise on the boundary). The distance profiles are applicable to any shape, but the geodesic distance profile is especially well-suited for articulated or deformable objects (e.g.applications in biology).

1 Introduction

Shape is a widely used feature to describe and distinguish objects for a variety of computer vision tasks such as image retrieval, object classification and recognition, segmentation or tracking. A shape descriptor should be invariant to transformations, distortions and occlusions of the shape. Furthermore, it is desirable for a shape descriptor to be independent of the application and to be low in computational complexity (especially for online image retrieval).

Zhang et al. [21] divide shape descriptors into two classes: region-based and boundary-based (contour-based) approaches. Each class can be further divided into structural and global approaches. Structural approaches describe shapes by segments while global approaches describe shapes as a whole.

The distance profiles presented in this paper are boundary-based descriptors for 2D shapes without holes. They allow a global description of the shape, but are also able to divide the shape into segments based on intervals of topological persistence (see Sects. 2.2 and 3.2). Two distance profiles are presented: (I) Euclidean distance profile ($DP$) and (II) geodesic distance profile ($DP^*$).

These profiles are based on the idea of the LBP scale space [11] (see Sect. 2), which describes a shape based on a filtration process from a chosen reference point. This filtration yields a translation- and rotation-invariant topological description of the shape.

In comparison to the LBP scale space, the distance profiles (Euclidean and geodesic) in this paper speed up the computation of the descriptor and are in addition invariant against scaling, articulation and deformation (in case of $DP^*$). Furthermore, they allow the pruning of spurious branches based on persistence.

1.1 State of the Art

The proposed distance profiles are mostly related to topological shape descriptors, shape signatures and spectral descriptors.

Verri et al. [20] use topological persistence for shape description in the form of size functions, which represent the persistence of the connected components. Carlsson et al. [4] propose persistence barcodes for shape description and classification. Barcodes visualize the lifetime for which features persist. For shape retrieval, shapes may be compared based on their persistence diagram using the matching distance as presented by Cerri et al. [5]. Another topological shape representation are Reeb graphs [1]. The simplest way to obtain a Reeb graph of a 2D or 3D shape is to use a height function as Morse function. In the same way persistence diagrams or barcodes can be determined using a filtration (see Sect. 2.2) based on a height function. Topological shape representations in general depend on the filtration. Height functions for example are not invariant to rotations and therefore lack in representational power.

Distance profiles are also related to shape signatures, which are one dimensional functions derived from the shape’s boundary. There are different kinds of shape signatures [7, 19, 21]: centroidal profile, complex coordinates, centroid distance, tangent angle, cumulative angle, curvature, area and chord-length. Shape signatures are sensitive to noise on the boundary. Small changes in the boundary may cause large errors when matching the shapes (e.g. image retrieval). Considering the persistence of extrema, it is possible to filter out noise (i.e. spurious branches of the medial axis) and make distance profiles invariant to noise on the boundary.

Spectral descriptors, such as Fourier descriptors (FD) [6, 9, 22] and wavelet descriptors (WD) [18], are another kind of boundary-based shape descriptors, which are usually derived from a spectral transform on a shape signature. They overcome the problem of noisy boundaries by analyzing shapes in the spectral domain. Spectral descriptors are derived from spectral transforms on one dimensional shape signatures.

1.2 Overview of the Paper

Sect. 2 recalls the LBP scale space and its persistence. Section 3 presents the proposed distance profiles and their local extrema. Furthermore, Sect. 3 explains how persistence is defined on the distance profiles. First experiments on the distance profiles of discrete shapes are presented in Sect. 4. Conclusions are given in Sect. 5.

2 Recall: LBP Scale Space

Originally, LBPs were introduced for texture classification in 1996 [14]. A LBP describes the local texture around a pixel $p=(x,y)$ by a bit pattern $BP$. This bit pattern, results from a comparison of the grayvalue of the center pixel g(p) and the grayvalues $g(q_i)$ along a circle sub-sampled with P points $q_i, i=1,\ldots ,P$:

$$\begin{aligned} BP (q_i)= {\left\{ \begin{array}{ll} 1 &{} \text {if } g(p)-g(q_i) \ge 0\\ 0, &{} \text {otherwise} \end{array}\right. } \end{aligned}$$

(1)

Two parameters determine the computation of a LBP: r defines the radius of the circular neighborhood around p, and $P=| BP |$ fixes the number of sampling points along the circle, i.e. the number of bits $BP =(s_1, s_2, \ldots , s_P)$ [15].

Fig. 1.

(a) Increasing radius r shifts intersections along the boundary B (blue arrows). (b) LBP scale space in the continuous case – critical points marked. (Color figure online)

2.1 Describing Local Topology with LBPs

LBPs can be employed to describe the local topology of a binary image region around a reference point p. Based on the bit pattern LBP types can be defined by counting the number of transitions from 0 to 1 and vice versa. A transition equals an intersection $b_i$ of the boundary B with the LBP circle of radius r at position p: $B \cap c(p,r)$. Following topological types can be derived from LBPs:

 

(local) maximum: :

no transition, bit pattern contains only 0 s and $g(p)=1$;

(local) minimum: :

no transition, bit pattern contains only 1 s and $g(p)=0$;

plateau: :

no transition, bit pattern contains only 1 s and $g(p)=1$;

slope: :

two transitions (compare uniform patterns [15]);

saddle point: :

four or more transitions [10].

 

2.2 LBP Based Persistence

The persistence of a feature (e.g. LBP type) – its lifetime, is measured by the filtration of a space, which is “a nested sequence of subspaces that begins with the empty and ends with the complete space” [8, p. 5].

Filtration Based on LBPs: One possibility to perform a filtration using LBPs is by varying the radius r of the LBP computation for a fixed reference point p and a boundary B [11]. Varying r corresponds to a movement along B (blue arrows in Fig. 1a). This filtration process changes the intersection points of the circle c with the boundary B, i.e. the bit patterns BP (number of transitions) and thus influences the topological LBP types.

The persistence of an LBP type is measured by these 2n intersection points, which divide the shape in $n+1$ regions and the boundary in 2n segments (persistence diagram: “birth” for each region/segment). By increasing r the intersection points move along B. Once two intersection points coincide the LBP type changes (persistence diagram: “death” of the respective segment/region).

2.3 LBP Scale Space

The LBP scale space was proposed as shape descriptor in [11]. From a chosen reference point p inside a shape, a filtration based on LBPs is performed. The filtration may start with a radius $r=0$, which is increased according to a predefined sampling scheme (for discrete case: r increased by 1 covers all integer radii). For the shape descriptor, the number of transitions observed for each of the LBP radii is stored, i.e. the changes in the local topology. Figure 1b illustrates the LBP scale space for sampling at critical points.

Besides applications in classification or recognition, the LBP scale space enables the reconstruction of a shape when extended by polar coordinates [11].

3 Distance Profiles

The brute force computation (see Fig. 1) of the LBP scale space starts with a small circle for which the intersections with the shape’s boundary are computed. Then the radius of the LBP circle is increased and the computation of the intersections is done again. This process is repeated until the shape is completely inside the LBP circle and no more intersections can be observed for a connected shape. Such an implementation of the LBP scale space is computationally expensive. Hence, this paper proposes an alternative and more efficient way to compute the LBP scale space based on the definition of distance profiles.

Fig. 2.

LBP scale space computation using the (a) Euclidean distance profile DP and (b) geodesic distance profile $DP^*$. (Color figure online)

First, the distances d of all points $b_i$ along the shape’s boundary B to the reference point p are computed:

$$\begin{aligned} \text{ DP }(b_i,p) = || b_i - p ||,\ b_i, p \in \mathfrak {R}^2 \end{aligned}$$

(2)

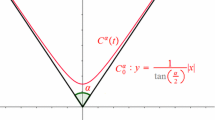
We call $DP : B \mapsto \mathfrak {R}^+$ the Euclidean distance profile for each $b_i\in B$ (see Eq. (2) and Fig. 2a). The LBP scale space [11] corresponds to this Euclidean distance profile $DP$. By changing the metric and using the medial axis of the shape S, a geodesic distance profile $DP ^*: B \mapsto \mathfrak {R}^+$ can be defined in two parts: (I) the distance of a point $b_i \in B$ to the closest point $a_l$ of the shape’s medial axis $MA (S)$ plus (II) the geodesic distance along this axis from $a_l$ to the reference point p:

$$\begin{aligned} \text{ DP }^*(b_i,p) = ||b_i-a_l||+ \text {arclength}(a_l,p), p \in MA (S) \end{aligned}$$

(3)

A visualization of the geodesic distance profile $DP^*$ is given in Fig. 2b.

Note that a connected medial axis $MA$ is essential for this approach. Therefore, we assume that a connected medial axis can be derived for a given binary shape and do not focus on the computation of the $MA$ itself. Furthermore, the input of the proposed method is currently limited to binary shapes without holes.

3.1 Local Extrema Along a Distance Profile

Let $DT : S \subset \mathfrak {R}^2 \mapsto \mathfrak {R}^+$ denote the Euclidean distance transform [16] of the shape. It assigns to each point $p \in S$ inside the shape the radius of the largest inscribed circle with radius $DT (p)$, which touches the shape’s boundary B at a boundary point $b_i: ||p - b_i|| = DT (p)$. Let p be the LBP scale space center.

Lemma 1

If the reference point $p\in S$ is inside the shape S, then there is at least one local minimum along the distance profile.

Since $p \in S, DT (p)$ is the radius of a circle touching B. Increasing the (maximal) circle at p would cross the boundary assigning larger distance values to neighbors of $b_i$. Hence, the touching point is a local minimum of $DP$.

For the geodesic distance profile $DP ^*$ we consider the medial axis $MA \subset S$: every circle with center on the $MA$ touches the shape’s boundary B at two or more points.

Leyton’s curvature-symmetry duality relates each local curvature maximum with an end point $a_e \in MA$ [12]. Such a maximum in curvature also produces a maximum in both distance profiles for reference points p along the $MA$-branch of $a_e$. This is generally the case if p is located inside the shape farther away from the curvature maximum than the radius of the osculating circle.

The maximally inscribed circle at a branching point of MA touches the boundary of the shape in at least as many points as there are branches. If the branching point is taken as the reference point for the distance profile, it shows a local minimum at each of these touching points. Maximal circles touch the shape’s boundary in two points, if their centers are located at $MA$ of the shape, but not at an end or at a branching point of the $MA$.

The extrema of the distance profiles may be used for shape description and representation. At these extrema the topology changes: a connected component either starts or ends at the distance associated with the local extremum for this distance profile. The LBP scale space [11] similarly describes a shape based on a sequence of changes in the topology of the shape through a filtration for a certain LBP center. The Euclidean distance profile DP and the LBP scale space representations are identical, but the computation of the DP is more efficient. In contrast, the geodesic distance profile $DP^*$ provides a similar representation based on a different metric, which is more robust against articulations and deformations.

The number of maxima in a distance profile is determined by the number of end points of $MA$ (i.e. the number of positive local curvature maxima), whereas the number of minima must be equal to the number of maxima along B since a minimum has to be located between every pair of maxima. This is the smallest number of extrema for a shape and it depends exclusively on the number of $MA$-branches.

Consequently, spurious branches of $MA$ generate extra extrema, which can be removed by the concept of persistence (see Sect. 3.2). The Euclidean $DP$ may contain more extrema than the geodesic $DP ^*$ due to bent branches.

3.2 Persistence Defined on the Distance Profile

As in classical persistence [8], we consider the lifetime of connected components generated by thresholding the distance profile. The corresponding space is the boundary B of the shape S and the sub-level sets of the profile function give the filtration. This corresponds to the choice of a particular radius in the LBP scale space. The transitions from 0 to 1 and vice versa in the LBP code for a certain radius correspond to the transition between the different connected components.

Fig. 3.

A spurious branch generates non-persistent extrema. $MA$ in yellow. (Color figure online)

The extrema $E=(b_1, b_2, \ldots , b_{2M}), b_i \in B$ derived from $DP$ are alternating (i.e. maximum – minimum – maximum – ...), where M is the number of maxima. The persistence P of each of the extrema $b_j$, $j=1 \dots 2M$, is defined by the smallest difference to the adjacent two extrema:

$$\begin{aligned} \small P(b_j) = \min \{ |DP(b_{j-1},p) - DP(b_j,p)|, |DP(b_{j+1},p) - DP(b_j,p)| \}. \end{aligned}$$

(4)

If an extremum is close to an adjacent extremum, then this difference is small and a small modification of the threshold used for filtration would suffice to change the intersections between an LBP circle and the shape’s boundary.

Figure 3 shows part of an elongated true branch (in direction x) and a typical spurious branch generated by a small bump (circle with small radius $r'$) along the boundary of the actual branch. The bump itself (centered at position $x_2$) is a local maximum of the distance profile (we denote by $b_i$ the boundary point corresponding to the axis point $x_i$)

$$\begin{aligned} DP^*(b_2)= & {} x_2+r_2=(x_1+r')+(r_1+2 r')=(x_1+r_1)+ 3 r'\\= & {} DP^*(b_1)+3 r' > DP^*(b_1) \nonumber \end{aligned}$$

(5)

while the return to the main branch at $x_3$ is a local minimum with distance

$$\begin{aligned} DP^*(b_3)= & {} x_3+r_3=(x_1+2 r')+r_1=(x_1+r_1)+ 2 r'\\= & {} DP^*(b_1)+2 r'< DP^*(b_2) \nonumber \end{aligned}$$

(6)

$b_2$ is clearly a local maximum and $b_3$ a local minimum since $DP^*(b(x))>DP^*(b_3)$ for $x> x_3$ and the width of the branch is constant, but the geodesic distance to the reference point increases.

The difference between the two extrema $b_2$ and $b_3$ (their persistence) is related to the size of the bump, e.g. $r'$, but independent of the width of the main branch. As in many pruning strategies for the $MA$, branches with a long axis are considered reliable while short branches often occur due to noise. Large differences between local minima and maxima of the distance profile also indicate long distances along the axis and thus long branches. A highly persistent reference point (LBP center) should induce a small number of extrema of the distance profile and favor the center of the diameter of the $MA$ as primary locus.

4 Experiments

The $DP$ and the $DP^*$ defined in the continuous case in Sect. 3 have been implemented for a practical evaluation in the discrete case. Morphological thinning has been used as a pre-processing step to obtain a connected skeleton. The two distance profiles together with persistence applied to $DP^*$ have been evaluated in experiments on binary shapes of the Kimi99 [17] and the Myth [2, 3] dataset.

Fig. 4.

Binary input shape and obtained distances for DP and $DP^*$, reference point = white square, blue indicates small distances, red large distances. (Color figure online)

For the $DP$ the Euclidean distance from every pixel along a shape’s boundary to a fixed reference point on the skeleton of the shape is calculated. The $DP^*$ is computed as the geodesic distance along the skeleton from the reference point to every skeleton pixel plus the medial axis radius (computed using a distance transformation) at each skeleton position. Figure 4 shows a binary input shape, the skeleton of the shape, as well as the $DP$ and the $DP^*$.

Extrema of the distance profiles are determined as local minima and maxima in the ordered sequence of distances. For the $DP$, this sequence is the sequence of distances observed when tracing a shape’s boundary in either clockwise or counter-clockwise direction. In the case of the $DP^*$, the ordered sequence of distances is retrieved by tracing the skeleton clockwise or counter-clockwise. Note that due to this difference in the computation the length of the sequences of distances of the two distance profiles may vary.

Figures 5a and b show the extrema marked along $DP$ and $DP^*$ for the binary hand shape shown in Fig. 4a. The $DP$ shows a higher number of extrema, as it is prone to noise due to small variations along the boundary. Additional extrema in the $DP$ can also be caused by the deformation of a shape through bending. This deformation however does not affect the extrema of $DP^*$. Note that no filtering based on persistence has been done for Fig. 5a and b.

Fig. 5.

Distance profiles (a) DP and (b) $DP^*$ and (c) persistence (threshold $=$ 5) applied to $DP^*$: $DP^*_{pers}$ for the hand shape. indicate maxima, indicate minima. (Color figure online)

These observations have further been evaluated on all shapes of the Kimia99 dataset. In total 4824 extrema were found along DP for the 99 shapes and 2162 extrema in total along $DP^*$. The minimum difference in the number of extrema per shape on the Kimia99 dataset between DP and $DP^*$ is 0, however the maximum difference is 96. In average $DP^*$ produces 27.8 less extrema than DP for every shape in the Kimia99 dataset.

Table 1. Shapes in the Kimia99 dataset clustered according to the difference in number of extrema in the distance profiles $\varDelta = |DP-DP^*|$.

Fig. 6.

Geodesic distance profiles under application of persistence (threshold$~=~$8 for the three shapes shown in the left column respectively. indicate maxima, indicate minima. (Color figure online)

This difference in number of extrema of the two distance profiles $\varDelta = |DP-DP^*|$ has further been used to cluster the shapes in the Kimia99 dataset and to identify common features among shapes within a cluster. The dataset was partitioned into four cluster with $\varDelta = [0,10]$, $\varDelta = [11,30]$, $\varDelta = [31,50]$ or $\varDelta = [51,96]$. Table 1 shows the number of shapes in each of these intervals. Since the Kimia99 dataset is meant for shape classification and retrieval experiments, the images of the dataset are mainly grouped into classes. The dataset consists of 6 major classes of shapes with minimum 7 and maximum 11 images per class. The remaining 40 images are either single shapes or shape classes with only two or three images per class. Interestingly, the shapes within one of these major classes of the Kimia99 dataset are with a high percentage (73% or more) also in the same cluster regarding $\varDelta$. Table 1 shows a shape for each cluster, representing the class of the Kimia99 dataset with the highest number of images in the respective cluster. Furthermore, the recall, the percentage of images of each such class in the cluster to the total number of images in the class, is given in the last row of Table 1 (recall of class).

The persistence defined on the distance profile $DP^*$ (see Sect. 3.2) has been subject to further experiments. If persistence is applied to the distance profile $DP^*$ ($DP^*_{pers}$) with a very small distance threshold of 5, it further reduces the total number of extrema for all shapes in the Kimia99 dataset to 1174 $DP^*_{pers}$ (compared to 2162 for $DP^*$ and 4824 for DP). In average the number of extrema in $DP^*$ is already reduced by 54% for this small threshold in $DP^*_{pers}$. Figure 5c shows $DP^*_{pers}$ for the hand shape introduced in Fig. 4a.

The robustness of the geodesic distance profile with persistence based pruning $DP^*_{pers}$ to articulated deformations is demonstrated on three shapes of the Myth dataset. The three shapes together with their respective distance profiles $DP^*_{pers}$ are shown in Fig. 6. While legs and tail of the horse move from Fig. 6a to c and the horse is angling its torso upwards from Fig. 6c to e, the respective distance profiles given in the Figs. 6b, d and f show high similarity for all three shapes.

5 Conclusion and Future Work

This paper presented the Euclidean and geodesic distance profiles, which are consistent with Leyton’s shape evolution as expressed in his process-grammar [13]. The distance profiles are shape descriptors based on the ideas of the LBP scale space. Both profiles are invariant against translation, rotation and scaling. The geodesic distance profile is also invariant against articulations and deformations. Local extrema along the distance profiles can be filtered with their persistence to prune spurious branches of the $MA$. Hence, the filtered distance profiles are robust against noise on the boundary. First experiments on the computation of the profiles result in the expected alternating sequence of local minima and maxima.