Abstract
We present the first internal calculi for Lewis’ conditional logics characterized by uniformity and reflexivity, including non-standard internal hypersequent calculi for a number of extensions of the logic \(\mathbb {V}\mathbb {T}\mathbb {U}\). These calculi allow for syntactic proofs of cut elimination and known connections to \(\mathsf {S5}\). We then introduce standard internal hypersequent calculi for all these logics, in which sequents are enriched by additional structures to encode plausibility formulas as well as diamond formulas. These calculi provide both a decision procedure for the respective logics and constructive countermodel extraction from a failed proof search attempt.
Supported by the Project TICAMORE ANR-16-CE91-0002-01, by the EU under Marie Skłodowska-Curie Grant Agreement No. [660047], and by the project “ExceptionOWL”, Università di Torino and Compagnia di San Paolo, call 2014 “Excellent (young) PI”.
Access this chapter
Tax calculation will be finalised at checkout
Purchases are for personal use only
Similar content being viewed by others
Notes
- 1.
Using this notation we thus have: \(x \Vdash A\preccurlyeq B \) iff for all
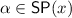 . \( \alpha \Vdash ^{\forall } \lnot B \) or \( \alpha \Vdash ^{\exists } A \).
. \( \alpha \Vdash ^{\forall } \lnot B \) or \( \alpha \Vdash ^{\exists } A \). - 2.
Observe that \( \mathbb {V}\mathbb {T}\mathbb {A}\)+weak centering collapses to S5, since in any model over a set of worlds W it must be for all \(w\in W\),
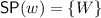 . Furthermore, \( \mathbb {V}\mathbb {T}\mathbb {A}\) + centering collapses to Classical Logic, as in any model the set of worlds must be a singleton \(\{w\}\) and
. Furthermore, \( \mathbb {V}\mathbb {T}\mathbb {A}\) + centering collapses to Classical Logic, as in any model the set of worlds must be a singleton \(\{w\}\) and 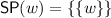 , so that \(A\preccurlyeq B\) is equivalent to the material implication \(B \rightarrow A\). See also Proposition 16 below..
, so that \(A\preccurlyeq B\) is equivalent to the material implication \(B \rightarrow A\). See also Proposition 16 below..
References
Alenda, R., Olivetti, N.: Preferential semantics for the logic of comparative similarity over triangular and metric models. In: Cerro, L.F., Herzig, A., Mengin, J. (eds.) JELIA 2012. LNCS (LNAI), vol. 7519, pp. 1–13. Springer, Heidelberg (2012). doi:10.1007/978-3-642-33353-8_1
Avron, A.: The method of hypersequents in the proof theory of propositional non-classical logics. In: Hodges, W., Hyland, M., Steinhorn, C., Truss, J. (eds.) Logic: From Foundations to Applications. Clarendon Press, New York (1996)
Burgess, J.P.: Quick completeness proofs for some logics of conditionals. Notre Dame J. Formal Log. 22, 76–84 (1981)
Chellas, B.F.: Basic conditional logics. J. Philos. Log. 4, 133–153 (1975)
Friedman, N., Halpern, J.Y.: On the complexity of conditional logics. In: Doyle, J., Sandewall, E., Torasso, P. (eds.) KR 1994, pp. 202–213. Morgan Kaufmann (1994)
Giordano, L., Gliozzi, V., Olivetti, N., Schwind, C.: Tableau calculus for preference-based conditional logics: PCL and its extensions. ACM TOCL 10(3), 21:1–21:50 (2009)
Girlando, M., Lellmann, B., Olivetti, N., Pozzato, G.L.: Standard sequent calculi for Lewis’ logics of counterfactuals. In: Michael, L., Kakas, A. (eds.) JELIA 2016. LNCS, vol. 10021, pp. 272–287. Springer, Cham (2016). doi:10.1007/978-3-319-48758-8_18
Grahne, G.: Updates and counterfactuals. J. Log. Comput. 8(1), 87–117 (1998)
Kraus, S., Lehmann, D., Magidor, M.: Nonmonotonic reasoning, preferential models and cumulative logics. Artif. Intell. 44(1–2), 167–207 (1990)
Kuznets, R., Lellmann, B.: Grafting hypersequents onto nested sequents. Log. J. IGPL 24, 375–423 (2016)
Lellmann, B.: Hypersequent rules with restricted contexts for propositional modal logics. Theoret. Comput. Sci. 656, 76–105 (2016)
Lellmann, B., Pattinson, D.: Sequent systems for Lewis’ conditional logics. In: Cerro, L.F., Herzig, A., Mengin, J. (eds.) JELIA 2012. LNCS, vol. 7519, pp. 320–332. Springer, Heidelberg (2012). doi:10.1007/978-3-642-33353-8_25
Lewis, D.: Counterfactuals. Blackwell, London (1973)
Nute, D.: Topics in Conditional Logic. Reidel, Dordrecht (1980)
Olivetti, N., Pozzato, G.L.: A standard internal calculus for Lewis’ counterfactual logics. In: Nivelle, H. (ed.) TABLEAUX 2015. LNCS, vol. 9323, pp. 270–286. Springer, Cham (2015). doi:10.1007/978-3-319-24312-2_19
Restall, G.: Proofnets for S5: sequents and circuits for modal logic. In: Logic Colloquium 2005. Lecture Notes in Logic, vol. 28, pp. 151–172. Cambridge University Press (2007)
Sheremet, M., Tishkovsky, D., Wolter, F., Zakharyaschev, M.: A logic for concepts and similarity. J. Log. Comput. 17(3), 415–452 (2007)
Stalnaker, R.: A theory of conditionals. In: Rescher, N. (ed.) Studies in Logical Theory, pp. 98–112. Blackwell (1968)
Author information
Authors and Affiliations
Corresponding author
Editor information
Editors and Affiliations
Rights and permissions
Copyright information
© 2017 Springer International Publishing AG
About this paper
Cite this paper
Girlando, M., Lellmann, B., Olivetti, N., Pozzato, G.L. (2017). Hypersequent Calculi for Lewis’ Conditional Logics with Uniformity and Reflexivity. In: Schmidt, R., Nalon, C. (eds) Automated Reasoning with Analytic Tableaux and Related Methods. TABLEAUX 2017. Lecture Notes in Computer Science(), vol 10501. Springer, Cham. https://doi.org/10.1007/978-3-319-66902-1_8
Download citation
DOI: https://doi.org/10.1007/978-3-319-66902-1_8
Published:
Publisher Name: Springer, Cham
Print ISBN: 978-3-319-66901-4
Online ISBN: 978-3-319-66902-1
eBook Packages: Computer ScienceComputer Science (R0)





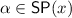 .
. 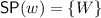 . Furthermore,
. Furthermore, 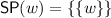 , so that
, so that