Abstract
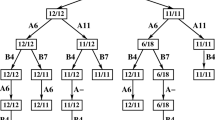
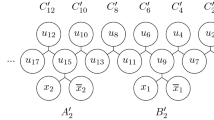
We discuss a game theoretic variant of the subset sum problem, in which two players compete for a common resource represented by a knapsack. Each player owns a private set of items, players pack items alternately, and each player either wants to maximize the total weight of his own items packed into the knapsack or to minimize the total weight of the items of the other player.
We show that finding the best packing strategy against a hostile or a selfish adversary is PSPACE-complete, and that against these adversaries the optimal reachable item weight for a player cannot be approximated within any constant factor (unless P=NP). The game becomes easier when the adversary is short-sighted and plays greedily: finding the best packing strategy against a greedy adversary is NP-complete in the weak sense. This variant forms one of the rare examples of pseudo-polynomially solvable problems that have a PTAS, but do not allow an FPTAS.
Access this chapter
Tax calculation will be finalised at checkout
Purchases are for personal use only
Similar content being viewed by others
References
Caprara, A., Carvalho, M., Lodi, A., Woeginger, G.J.: A complexity and approximability study of the bilevel knapsack problem. SIAM J. Optim. 24, 823–838 (2014)
Darmann, A., Nicosia, G., Pferschy, U., Schauer, J.: The subset sum game. Euro. J. Oper. Res. 233, 539–549 (2014)
Garey, M.R., Johnson, D.S.: Computers and Intractability: A Guide to the Theory of NP-Completeness. Freeman, San Francisco (1979)
Schaefer, T.J.: On the complexity of some two-person perfect-information games. J. Comput. Syst. Sci. 16, 185–225 (1978)
Woeginger, G.J.: When does a dynamic programming formulation guarantee the existence of a fully polynomial time approximation scheme (FPTAS)? INFORMS J. Comput. 12, 57–75 (2000)
Author information
Authors and Affiliations
Corresponding author
Editor information
Editors and Affiliations
Rights and permissions
Copyright information
© 2017 Springer International Publishing AG
About this paper
Cite this paper
Pieterse, A., Woeginger, G.J. (2017). The Subset Sum Game Revisited. In: Rothe, J. (eds) Algorithmic Decision Theory. ADT 2017. Lecture Notes in Computer Science(), vol 10576. Springer, Cham. https://doi.org/10.1007/978-3-319-67504-6_16
Download citation
DOI: https://doi.org/10.1007/978-3-319-67504-6_16
Published:
Publisher Name: Springer, Cham
Print ISBN: 978-3-319-67503-9
Online ISBN: 978-3-319-67504-6
eBook Packages: Computer ScienceComputer Science (R0)