Optimal Control of Multi-strain Epidemic Processes in Complex Networks

Abstract

The emergence of new diseases, such as HIV/AIDS, SARS, and Ebola, represent serious problems for the public health and medical science research to address. Despite the rapid development of vaccines and drugs, one challenge in disease control is the fact that one pathogen sometimes generates many strains with different spreading features. Hence it is of critical importance to investigate multi-strain epidemic dynamics and its associated epidemic control strategies. In this paper, we investigate two controlled multi-strain epidemic models for heterogeneous populations over a large complex network and obtain the structure of optimal control policies for both models. Numerical examples are used to corroborate the analytical results.

1 Introduction

Infectious diseases remain a serious medical burden all around the world with 15 million deaths per year estimated to be directly related to infectious diseases. The emergence of new diseases such as HIV/AIDS, the severe acute respiratory syndrome (SARS) and, most recently, the rise of Ebola, represent a few examples of the serious problems that the public health and medical science research need to address.

While for centuries mankind seemed helpless against these sudden epidemics, in recent time, our ability to control future epidemic outbreaks has been facilitated by the advances in modern science. The cures for a number of dangerous pathogens are available and can be developed and manufactured faster than ever before thanks to the genetic revolution new drugs to prevent and reduce the health consequences of new epidemics. The vaccine against new influenza A (H1N1) has been developed rapidly to be available only a few months after the beginning of the epidemic.

However, one challenge in disease control is the fact that one pathogen sometimes generates many strains with different spreading features, and hence a detailed investigation of multi-strain epidemic dynamics has great relevance [1,2,3]. For example, the human immunodeficiency virus (HIV) (which causes acquired immune deficiency syndrome (AIDS)) has many genetic varieties and can be divided into several distinct strains, such as strain HIV-1 and strain HIV-2 [4]. On the other hand, one pathogen is always incorporated with other pathogens [5]. The influenza A (H1N1) virus has the potential to develop into the first influenza pandemic of the twenty-first century [6], and it is accompanied by seasonal influenza [7].

In this paper, we establish a control-theoretic model to design disease control strategies through quarantine and immunization to mitigate the impact of epidemics on our society. Disease transmission in epidemics can be represented by dynamics on a graph where vertices denote individuals and an edge connecting a pair of vertices indicates an interaction between individuals. Due to a large population of people involved in the process of disease transmission, random graph models such as the small-world networks in [8] or scale-free networks in [9] are convenient to capture the heterogeneous patterns in the large-scale complex network.

We investigate two controlled multi-strain epidemic models for heterogeneous populations over a large complex network. One is the Susceptible-Infected-Recovered (SIR) epidemic process. The control is to quarantine a fraction of the infected nodes. Another model is the Susceptible-Infected-Susceptible (SIS) epidemic process. The control in this model is to provide treatment to the infected individuals, while treated individuals can become susceptible again to the infection of the disease.

The paper is organized as follows. Section 2 presents the controlled SIR mathematical model. Section 3, using Pontryagin’s minimum principle, defines the structure optimal control policies. Section 4 presents the optimal control problem for controlled SIS model. Section 5 focuses on the analysis of the optimal control of SIS model. Numerical examples will be presented in Sect. 6. Section 7 concludes the paper and presents future research directions.

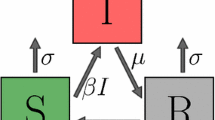
2 SIR Model for Two-Strain Viruses

Denote by $S_k(t), R_k(t)$ the population densities of the Susceptible and Recovered nodes with degree k at time t. We consider two strains of viruses co-exist in the network. $I^1_k(t), I^2_k(t)$ are the population densities of the Infected nodes of degree k at time t. We assume that the total population is constant in the network for all t, i.e., $S_k(t)+ I^1_k(t)+ I^2_k(t)+ R_k(t)=1$. We have extended the simple SIR model introduced by [10] to describe the situation with two virus types over a complex network.

$$\begin{aligned} \begin{array}{l} \frac{dS_k}{dt}=-\delta _1 S_kI^1_k\varTheta _1-\delta _2 S_kI^2_k\varTheta _2;\\ \frac{dI^1_k}{dt}=(\delta _1 S_k\varTheta _1-\sigma _1 -u^1_k)I^1_k;\\ \frac{dI^2_k}{dt}=(\delta _2 S_k \varTheta _2-\sigma _2 -u^2_k) I^2_k;\\ \frac{dR_k}{dt}=(\sigma _1+u^1_k) I^1_k+(\sigma _2+u^2_k )I^2_k,\\ \end{array} \end{aligned}$$

(1)

where $\delta _i$ are infection rates for virus $V_i$, $i=1,2$, and $\sigma _i$ are recovered rates.

At the beginning of epidemic process $t=0$, most of nodes in the network belong to the susceptible subgroup, and small subgroup in total population is infected; and the remaining nodes are in the recovered subgroup. Hence initial states are $0<S_k(0)< 1$, $0<I^1_k(0)< 1$, $0<I^2_k(0)< 1$, $R_k(0)=1-S_k(0)-I^1_k(0)-I^2_k(0)$. $\varTheta _i(t)$ can be written in general (see [11, 12]) as

$$\begin{aligned} \varTheta _i(t)=\sum \limits _{k'}\frac{\tau (k')P(k'|k)I^j_{k'}}{k'}, \ i=1,2, \end{aligned}$$

(2)

where $\tau (k)$ denotes the infectivity of a node with degree k. $P(k'|k)$ describes the probability of a node with degree k pointing to a node with degree $k'$, and $P(k'|k)=\frac{k' P(k')}{k'}$, where $\langle k\rangle =\sum \limits _{k'}k P(k)$. For scale-free node distribution $P(k)=C^{-1}k^{-2-\gamma },\ 0<\gamma \le 1$, where $C=\zeta (2+\gamma )$ is Riemann’s zeta function, which provides an appropriate normalization constant for sufficiently large networks.

The control parameters which can be used to protect the network from the propagation of the virus with k links are defined as $u_k=(u^1_k, u^2_k)$. Here, $u^i_k$ are the fractions of the infected nodes which are quarantined in the population. The rates $\sigma _i$ are the coefficients of “self-recovery", which can be interpreted as the activity of stationary antivirus software or firewalls.

The objective function: We minimize the overall cost in time interval [0, T]. At any given t, the following costs $f_1(I^1_k(t)), f_2(I^2_k(t))$ are treatment costs; $g(R_k(t))$ is utility of having $R_k(t)$ fraction of nodes recovered at time t; $h_1(u^1_k(t)), h_2(u^2_k(t))$ are costs for using antivirus patches or quarantine that help to reduce epidemic spreading, $k_{I^1_k}$, $k_{I^2_k}$, $k_{R}$ represent the cost and benefit for the infected and the recovered in the end of the epidemic, respectively. Here, functions $f_i(t)$ are non-decreasing and twice-differentiable, convex functions, with $f_i(0)=0$, $f_i(I^i_k)>0$ for $I^i_k >0,i=1,2$; $g(R_k(t))$ is non-decreasing and differentiable, and $g(0)=0$; $h_i(u^i_k(t))$ is a twice-differentiable and increasing function in $u^i_k(t)$ such that $h_i(0)=0$, $h_i(u^i_k)>0,\ i=1,2$ when $u^i_k>0$.

The aggregated system cost is given by

$$\begin{aligned} J=&\int \limits _0^T f_1(I^1_k(t))+f_2(I^2_k(t))-g(R_k(t))+h_1(u^1_k(t)) \nonumber \\&+\, h_2(u^2_k(t))dt+k_{I^1_k}I^1_k(T)+k_{I^2_k}I^2_k(T)-k_{R_k}R_k(T) \end{aligned}$$

(3)

and the optimal control problem is to minimize the cost, i.e., $\min _{\{u^1_k, u^2_k\}} J$. To simplify the analysis, we consider the case where $k_{I^1_k}=k_{I^2_k}=k_{R_k}=0$.

Treatment or isolation can be considered as the control parameters that can reduce the fraction of infected nodes in network. We define $u_k=(u^1_k, u^2_k)$ as control variables with $0\le u^1_k(t)\le 1$, $0\le u^2_k(t)\le 1,\ \text{ for } \text{ all }\ t$.

3 Optimal Control of SIR Model

We use Pontryagin’s minimum principle [13] to find the optimal solution $u_k(t)=(u^1_k(t), u^2_k(t))$ to the problem described above. Define the associated Hamiltonian H and adjoint functions $\lambda _{S_k}$, $\lambda _{I^1_k}$, $\lambda _{I^2_k}$, $\lambda _{R_k}$ as follows:

$$\begin{aligned} \begin{array}{ll} H=&{} f_1(I^1_k(t))+f_2(I^2_k(t))-g(R_k(t))+h_1(u^1_k(t))\\ &{}+\,h_2(u^2_k(t))+(\lambda _{I^1_k}(t)-\lambda _{S_k}(t))\delta _1 S_k(t)I^1_k(t)\varTheta _1(t)\\ &{} + \, (\lambda _{I^2_k}(t)-\lambda _{S_k}(t))\delta _2 S_k(t)I^2_k(t)\varTheta _2(t)\\ &{}+\, (\lambda _{R_k}(t)-\lambda _{I^1_k}(t))\sigma _1I^1_k(t)+ (\lambda _{R_k}(t)-\lambda _{I^2_k}(t))\sigma _2I^2_k(t)\\ &{}-\,(\lambda _{I^1_k}(t)-\lambda _{R_k}(t))I^1_k(t) u^1_k-(\lambda _{I^2_k}(t)-\lambda _{R_k}(t))I^2_k(t) u^2_k(t). \end{array} \end{aligned}$$

(4)

Here, we have used the condition $R=1-S_k-I^1_k-I^2_k$. We construct the associated adjoint system as follows:

$$\begin{aligned} \begin{array}{ll} \dot{\lambda }_S(t) =-\frac{\partial H}{\partial S}=&{} -(\lambda _{I^1_k}-\lambda _{S_k}) \delta _1 I^1_k\varTheta _1 - (\lambda _{I^2_k}-\lambda _{S_k})\delta _2 I^2_k\varTheta _2;\\ \dot{\lambda }_{I^1_k}(t) =-\frac{\partial H}{\partial I^1_k}=&{} -f_1'(I^1_k)+ (\lambda _{S_k}-\lambda _{I^1_k})\delta _1 S_k \varTheta _1 \\ &{} -\,(\lambda _{R_k}- \lambda _{I^1_k})\sigma _1+(\lambda _{I^1_k}-\lambda _{R_k})u^1_k;\\ \dot{\lambda }_{I^2_k}(t) =-\frac{\partial H}{\partial I^2_k}=&{} -f_2'(I^2_k)+(\lambda _{S_k}-\lambda _{I^2_k}) \delta _2 S_k \varTheta _2 \\ &{}-\, (\lambda _{R_k}- \lambda _{I^2_k}) \sigma _1+(\lambda _{I^2_k}-\lambda _{R_k})u^2_k; \\ \dot{\lambda }_{R_k}(t)=-\frac{\partial H}{\partial R_k}=&{}g'(R_k);\\ \end{array} \end{aligned}$$

(5)

with the transversality conditions given by

$$\begin{aligned} \lambda _{I^1_k}(T)=0,\ \lambda _{I^2_k}(T)=0,\ \lambda _{S_k}(T)=0,\ \lambda _{R_k}(T)=0. \end{aligned}$$

(6)

According to Pontryagin’s minimum principle [13], there exist continuous and piecewise continuously differentiable co-state functions $\lambda _i$ that at every point $t\in [0, T]$ where $u^1_k$ and $u^2_k$ is continuous, satisfying (5) and (6). In addition, we have

$$\begin{aligned} (u^1_k, u^2_k)\in \text {arg} \min \limits _{\underline{u^1_k}, \underline{u^2_k}\in [0,1]} H(\overline{\lambda }, (S_k, I^1_k, I^2_k, R_k), (\underline{u^1_k}, \underline{u^2_k})), \end{aligned}$$

(7)

where $\overline{\lambda }=(\lambda _{S_k},\lambda _{I^1_k},\lambda _{I^2_k},\lambda _{R_k})$.

4 Structure of Optimal Control

Based on previous research, e.g., [13,14,15], in this section, we show that an optimal control $u_k(t)=(u^1_k(t), u^2_k(t))$ has the structure summarized in Proposition 1.

Proposition 1

The following statements hold for the optimal control problem described in Sect. 2:

• If $h_i(\cdot )$ are concave, then there exist time moment $t_1$ $(0<t_1<T)$ such that:

  $$ u^i_k(t)=\left\{ \begin{array}{l}1,\ \text{ for }\ \ \phi ^i_k<h_i(1),\ \ 0<t<t_1;\\ 0,\ \text{ for }\ \ \phi ^i_k>h_i(1),\ \ t_1<t<T.\end{array}\right. $$

• If $h_i(\cdot )$ are strictly convex, then exists $t_0,\ t_1$ $(0<t_0<t_1<T)$:

  $$ u^i_k(t)= \left\{ \begin{array}{ll}0, \ \ \ \ \ \ \ \ \ \ \ \ \ \phi ^i_k\le h'_i(0),\ i=1,2, &{} t\in (t_1;T];\\ h'^{-1}(\phi ^i_k), \ \ \ \ h'_i(0)<\phi ^i_k\le h'_i(1),\ i=1,2, &{} t\in (t_0;t_1];\\ 1,\ \ \ \ \ \ \ \ \ \ \ \ \ h'_i(1)<\phi ^i_k,\ i=1,2, &{} t\in [0;t_1].\\ \end{array}\right. $$

Lemma 1

Functions $\phi ^i_k, \ i=1,2$ are decreasing functions of t, for all $t\in [0, T].$

Lemma 2

For all $0 \le t\le T$, we have $(\lambda _{I^1_k}-\lambda _{S_k})>0$, $(\lambda _{I^2_k}-\lambda _{S_k})>0$, $(\lambda _{R_k}-\lambda _{I^1_k})>0$.

The construction of optimal controls for the structured population follows the Pontryagin’s minimum principle [13] and similar approaches used in [14], [15].

5 SIS Model with Two Virus Strains

A set of nodes N is divided into two subgroups: the Susceptible (S), the Infected (I). We suppose that two different viruses with different strains circulate in the network at time t. Let $S_k(t)$, $I^1_k(t)$, $I^2_k(t)$ be the densities of the susceptible and infected nodes with degree k at time t. $\lambda _i=\displaystyle \frac{\delta _i}{\sigma _i}$, where $\delta _i$ is infection rate and infected nodes are cured and become again susceptible with rate $\sigma _i$, $i=1,2$.

$$\begin{aligned} \begin{array}{ll} \displaystyle {\frac{dS_k}{dt}}=&{}-\lambda _1 k S_k(t) \varTheta _1-\lambda _2 k S_k(t) \varTheta _2\\ &{} +u^1_k I^1_k(t)+u^2_kI^2_k(t)+I^1_k(t)+I^2_k(t);\\ \displaystyle {\frac{dI^1_k}{dt}}=&{}\lambda _1 k S_k(t) \varTheta _1- I^1_k(t) -u^1_k(t) I^1_k(t);\\ \displaystyle {\frac{dI^2_k}{dt}}=&{}\lambda _2 k S_k(t) \varTheta _2 -I^2_k(t) -u^2_k(t) I^2_k(t).\\ \end{array} \end{aligned}$$

(8)

Objective function. We will minimize the overall cost in time interval [0, T]. At any given t, the following costs exist in the system: $f_i(I^i_{k}(t))$ are infected costs; $h_i(u^i_k(t))$ are costs for medical measures (i.e. quarantining) that help reduce the epidemic spreading. Here, the functions $f_i(I^i_{k}(t))$ are non-decreasing, twice-differentiable, and convex with $f_i(0)=0$, $f_i(I^i_{k}(t))>0$ for $I^i_k >0$, $g(S_k(t))$ non-decreasing and differentiable function, describing the benefits of using control, where $S_k(t)=1-I^1_k(t)-I^1_k(t)$ and $g(0)=0$; $h_i(u^i_k(t))$ are twice-differentiable and increasing function in $u^i_k(t)$ such that $h_i(0)=0$, $h_i(u^i_k)>0$ when $u^i_k>0$ with feasible controls $u^i_k\in [0,1]$.

The aggregated system cost is given by

$$\begin{aligned} J=&\int \limits _0^T f_1(I^1_{k}(t))+f_2(I^2_{k}(t))+h_1(u^1_k(t))\nonumber \\&+\, h_2(u^2_k(t))-g(S_k(t))dt. \end{aligned}$$

(9)

and the optimal control problem is to minimize the cost, i.e., $\min _{u^1_k, u^2_k\in [0,1]} J$. System (8) describes the propagation of two different strains of viruses in the network. The propagation of the viruses is controlled by parameters $u^i_k,\,i=1,2$. Here, $u^i_k$ are antivirus policies.

We use Pontryagin’s minimum principle to find the optimal control $u_k(t)=(u^1_k(t),u^2_k(t))$ which yields the minimum solution to the functional (9) for the problem described above. Consider the Hamiltonian:

$$\begin{aligned} \begin{array}{ll} H=&{}-l_0 (f_1(I^1_{k}(t))+f_2(I^2_{k}(t))+h_1(u^1_k(t))+h_2(u^2_k(t))\\ &{}-g(S_k(t)))+l_1(t)(-\lambda _1(t) k S_k(t) \varTheta _1(t)\\ &{}-\lambda _2(t) k S_k(t) \varTheta _2(t)+u^1_k(t) I^1_k(t)+u^2_k(t) I^2_k(t)+I^1_k(t) \\ &{}+ I^2_k(t))+l_2(t)(\lambda _1 k S(t) \varTheta _1(t)-I^1_k(t) -u^1_k(t) I^1_k(t))\\ &{}+l_3(t)(\lambda _2(t) k S_k(t) \varTheta _2(t) - I^2_k(t) -u^2_k(t) I^2_k(t)). \end{array} \end{aligned}$$

(10)

where $l_0=1$. The adjoint systems are

$$\begin{aligned} \begin{array}{l} \dot{l}_1(t) =-\frac{\partial H}{\partial S_k}=-g'(S_k)-l_1(-\lambda _1\varTheta _1I^1_k-l_2\lambda _2\varTheta _2I^2_k)- l_2\lambda _1\varTheta _1I^1_k-l_3 \lambda _2\varTheta _2I^2_k;\\ \dot{l}_2(t) =-\frac{\partial H}{\partial I^1_k}= f'_1(I^1_k)-l_1(-\lambda _1\varTheta _1S_k+u^1_k+1)- l_2(\lambda _1S_k\varTheta _1-1-u^1_k);\\ \dot{l}_3(t) =-\frac{\partial H}{\partial I^2_k}= f'_2(I^2_k)-l_1(-\lambda _2S_k\varTheta _2+u^2_k+1)- l_3(\lambda _2S_k\varTheta _2-1-u^2_k),\\ \end{array} \end{aligned}$$

(11)

with the transversality condition:

$$\begin{aligned} l_i(T)=0. \end{aligned}$$

(12)

Consider next derivatives:

$$\begin{aligned} \begin{array}{l} \displaystyle \frac{\partial H}{\partial u^1_k}=h'_1(u^1_k)+(l_1-l_2)I^1_k;\ \ \ \displaystyle \frac{\partial H}{\partial u^2_k}=h'_2(u^2_k)+(l_1-l_3)I^2_k. \end{array} \end{aligned}$$

(13)

According to Pontryagin’s minimum principle, there exist continuous and piecewise continuously differentiable co-state functions $l_i$ that at every point $t\in [0, T]$ where $u_k$ is continuous, satisfy (11) and (12). In addition, we have $l(t)=(l_0(t),l_1(t),l_2(t),l_3(t))$

$$\begin{aligned} u^i_k\in \text{ arg } \max \limits _{\underline{u^i_k} \in [0,1]} H(l, (S_k, I^1_k, I^2_k), \underline{u^i_k}). \end{aligned}$$

(14)

Since $h_i(u^i_k)$ is non-increasing function, then $h'_i(u^i_k)\ge 0$, $I^i_k\ge 0$ as a fraction of infected nodes, then condition (13) is satisfied only if $\psi ^i_k>0$, where

$$\begin{aligned} \psi ^1_k=(l_1-l_2)I^1_k;\ \ \psi ^2_k=(l_1-l_3)I^2_k. \end{aligned}$$

(15)

is defined as the switching function.

Then, to establish the optimal vaccination policy, we formulate the next proposition.

Proposition 2

The optimal vaccination policy has following structure: If $h(\cdot )$ are concave, then exists time moment $0<t_1<T$ such that:

$$\begin{aligned} u^i_k(t)=\left\{ \begin{array}{l} 0 ,\ \ \ \text{ if }\ \ \psi ^i_k<h_i(1),\ \ t\in (t_1;T];\\ 1 ,\ \ \ \text{ if }\ \ \psi ^i_k>h_i(1),\ \ t\in [0;t_1]. \end{array}\right. \end{aligned}$$

(16)

If $h(\cdot )$ is strictly convex, then exists $t_0, t_1$ $(0<t_0<t_1<T)$ such that:

$$\begin{aligned} u^i_k(t)=\left\{ \begin{array}{lll} 0\ ,&{}\qquad \text{ if }\ \psi ^i_k\le \frac{\partial h_i(0)}{\partial u^i_k},&{}\quad t\in (t_1;T]; \\ h'^{-1}(\psi ^i_k)\ ,&{}\qquad \text{ if }\ \frac{\partial h_i(0)}{\partial u^i_k}<\psi ^i_k\le \frac{\partial h_i(1)}{\partial u^i_k},&{}\quad t\in (t_0;t_1];\\ 1\ ,&{}\qquad \text{ if }\ \psi ^i_k>\frac{\partial h_i(1)}{\partial u^i_k},&{}\quad t\in [0;t_0]. \end{array}\right. \end{aligned}$$

(17)

Lemma 3

Functions $\dot{\psi }_i\le 0$ are decreasing over the time interval [0, T).

Lemma 4

Function $(l_1-l_2)\le 0$ and $(l_1-l_3)\le 0$ over the time interval [0, T).

To prove the proposition 2, we follow the same techniques as in [13,14,15].

6 Numerical Simulation

In this section, we present numerical simulations which are used to corroborate the results of main propositions. We depict optimal policies for SIR and SIS models for different cases if cost functions $h_i(u^i_k)$ are strictly convex and concave.

Fig. 1.

The example of scale-free network for $N=20$. Group $S=5$ (blue dots), group $I=3$, (yellow dots), group $R=12$, (red dots). (Color figure online)

Here we take a piecewise linear infectivity,

$$\begin{aligned} \begin{array}{l} \tau (k)=\min (\alpha k, A), \end{array} \end{aligned}$$

(18)

where $\alpha$ and A are positive constants, $0<\alpha \le 1$. We set the infectivity parameter $\alpha =0.02$, then for $k\in [1,10]$ the infectivity rises and from $k> 10$ the individuals have the same infectivity equals to $A=0.2$. To generate a network with scale-free exponent 3 we use the preferential attachment algorithm of Barabási and Albert (parameter $\gamma =1$) [11, 16]. The example of scale-free network for $\gamma =1,\ N=20,\ \langle k\rangle =13.9,$ maximum degree $k =19$ is presented in Fig. 1 [17] (Figs. 2 and 3).

Fig. 2.

Experiment I. SIR model without applying of control (degree $k=10$). Initial states are $I^1_k(0)= 0.2$, $I^2_k(0)= 0.3$, the maximum values are $I_{1max}=0.26$, $I_{2max}=0.67$. Epidemic peaks are reached at $T=20$. Average connectivity $\langle k\rangle =13.9$.

Fig. 3.

Experiment I. SIR multi-strain controlled model (degree $k=10$). Cost functions $h_i(\cdot )$ are strictly convex. Average connectivity $\langle k\rangle =13.9$.

Experiment I. We use the following values for SIR model:initial fractions of susceptible, infected and recovered nodes are $S(0)= 0.5$, $I^1(0)=0.2$, $I^2(0)=0.3$ and $R(0)=0$; infection rates are $\delta _1=0.3$ and $\delta _2=0.4$; recovered rates are $\sigma _1=0.003$ and $\sigma _2=0.001$; epidemic duration is $T=20$ and costs function $f_{I^1_k}=8I^1_k$, $f_{I^2_k}=10I^2_k$, $g(R_k)=0.1R_k$; $h_i(u^i_k)$ are convex functions $h_1(u^1_k)= 0.4(u^1_k)^2$ and $h_2(u^2_k)=0.5(u^2_k)^2$. The optimal control policy is shown in Fig. 4.

Experiment II. Numerical simulations for SIS multi-strain model use the following values: initial fractions of susceptible and infected nodes are $S(0)= 0.7$, $I^1(0)=0.1$, $I^2(0)=0.2$; infection rates are $\delta _1=0.3$ and $\delta _2=0.4$; recovered rates are $\sigma _1=0.003$ and $\sigma _2=0.001$; epidemic duration is $T=20$ and costs function $f_{I^1_k}=8I^1_k$, $f_{I^2_k}=10I^2_k$, $g(R_k)=0.1R_k$; $h_i(u^i_k)$ are strictly convex functions $h_1(u^1_k)=0.4(u^1_k)^2$ and $h_2(u^2_k)=0.5(u^2_k)^2$ (Figs. 5, 6 and 7).

Fig. 4.

Experiment I: Optimal control in SIR model, costs functions $h_i(u^i_k)$ are strictly convex. Switching points are $t_1=1.4$ and $t_2=1.8$.

Fig. 5.

Experiment I: Comparison of the aggregated costs of SIR model: the cost of controlled case is $J=36.39$, the cost of uncontrolled case is $J=701.3$.

Fig. 6.

Experiment II: SIS multi-strain model without control (degree $k=10$). Initial states are $I^1_k(0)= 0.1$, $I^2_k(0)= 0.2$, the maximum values are $I_{1max}=0.12$, $I_{2max}=0.73$. Epidemic peaks are reached at $T=20$. Average connectivity $\langle k\rangle =13.9$.

Fig. 7.

Experiment II: SIS multi-strain controlled model (degree $k=10$). Cost functions $h_i(\cdot )$ are strictly convex. The average connectivity is $\langle k\rangle =13.9$.

For both experiments, we have that the shape of control curves is the same for each k and we have used the same class of functionals for SIR and SIS dynamic systems.

7 Conclusion

This paper has investigated the optimal control of two epidemic models of two co-existing virus strains for heterogeneous populations over a large complex network. We have obtained the structure of the optimal controller in the form of a threshold policy for a specific class of cost functions. Numerical examples have been used to corroborate the results. We would further explore the stability properties of the epidemic process under the optimal control.