Abstract
We introduce \(\mathcal{DLR}^+\), an extension of the n-ary propositionally closed description logic \(\mathcal{DLR}\) to deal with attribute-labelled tuples (generalising the positional notation), projections of relations, and global and local objectification of relations, able to express inclusion, functional, key, and external uniqueness dependencies. The logic is equipped with both TBox and ABox axioms. We show how a simple syntactic restriction on the appearance of projections sharing common attributes in a \(\mathcal{DLR}^+\) knowledge base makes reasoning in the language decidable with the same computational complexity as \(\mathcal{DLR}\). The obtained \(\mathcal{DLR}^{\pm }\) n-ary description logic is able to encode more thoroughly conceptual data models such as EER, UML, and ORM.
You have full access to this open access chapter, Download conference paper PDF
Similar content being viewed by others
1 Introduction
We introduce the description logic (DL) \(\mathcal{DLR}^+\) extending the n-ary DL \(\mathcal{DLR}\) [6], in order to capture database oriented constraints. While \(\mathcal{DLR}\) is a rather expressive logic, tailored for conceptual modelling and ontology design, generalising many aspects of classical description logics and OWL, it lacks a number of expressive means relevant for database applications that can be added without increasing the complexity of reasoning—when used in a carefully controlled way. The added expressivity is motivated by the increasing use of description logics as an abstract conceptual layer (an ontology) over relational databases. For example, the \(\mathcal{DLR}\) family of description logics is used to formalise and perform reasoning in the ORM conceptual modelling language for database design (adopted by Microsoft in Visual Studio) [8, 15].
We remind that a \(\mathcal{DLR}\) knowledge base, as defined in [6], can express axioms with (i) propositional combinations of concepts and (compatible) n-ary relations – as opposed to just binary roles as in classical description logics and OWL, (ii) concepts as unary projections of n-ary relations – generalising the existential operator over binary roles in classical description logics and OWL, and (iii) relations with a selected typed component.
As an example of \(\mathcal{DLR}\), in a knowledge base where \(\mathtt{Pilot}\) and \(\mathtt{RacingCar}\) are concepts and \(\mathtt{DrivesCar}\), \(\mathtt{DrivesMotorbike}\), \(\mathtt{DrivesVehicle}\) are binary relations, the following statements:

assert that a pilot drives a racing car and that driving a car or a motorbike implies driving a vehicle.
The language we propose here, \(\mathcal{DLR}^+\), extends \(\mathcal{DLR}\) in the following ways.
-
While \(\mathcal{DLR}\) instances of n-ary relations are n-tuples of objects—whose components are identified by their position in the tuple—instances of relations in \(\mathcal{DLR}^+\) are attribute-labelled tuples of objects, i.e., tuples where each component is identified by an attribute and not by its position in the tuple (see, e.g., [11]). For example, the relation \(\mathtt{Employee}\) may have the signature:
$$\mathtt{Employee}(\mathtt{firstname}, \mathtt{lastname}, \mathtt{dept}, \mathtt{deptAddr}),$$and an instance of \(\mathtt{Employee}\) could be the tuple:
$$\langle \mathtt{firstname:John, lastname:Doe, dept: Purchase, deptAddr: London}\rangle .$$ -
Attributes can be renamed, for example to recover the positional attributes:

-
Relation projections allow to form new relations by projecting a given relation on some of its attributes. For example, if \(\mathtt{Person}\) is a relation with signature \(\mathtt{Person}(\mathtt{name},\mathtt{surname})\), it could be related to \(\mathtt{Employee}\) as follows::

-
The objectification of a relation (also known as reification) is a concept whose instances are unique object identifiers of the tuples instantiating the relation. Those identifiers could be unique only within an objectified relation (local objectification), or they could be uniquely identifying tuples independently on the relation they are instance of (global objectification). For example, the concept \(\mathtt{EmployeeC}\) could be the global objectification of the relation \(\mathtt{Employee}\), assuming that there is a global 1-to-1 correspondence between pairs of values of the attributes \(\mathtt{firstname,lastname}\) and \(\mathtt{EmployeeC}\) instances:

Consider the relations with the following signatures:
$$\mathtt{DrivesCar(name, surname, car)}, \quad \mathtt{OwnsCar (name, surname, car)},$$and assume that anybody driving a car also owns it:
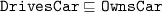 . The locally objectified events of driving and owning, defined as
. The locally objectified events of driving and owning, defined as 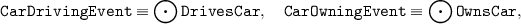
do not imply that a car driving event by a person is the owning event by the same person and the same car:
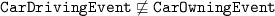 . Indeed, they are even disjoint:
. Indeed, they are even disjoint:  .
.
It turns out that \(\mathcal{DLR}^+\) is an expressive description logic able to assert relevant constraints typical of relational databases. In Sect. 3 we will consider inclusion dependencies, functional and key dependencies, external uniqueness and identification axioms. For example, \(\mathcal{DLR}^+\) can express the fact that the attributes \(\mathtt{firstname,lastname}\) play the role of a multi-attribute key for the relation \(\mathtt{Employee}\):

and that the attribute \(\mathtt{deptAddr}\) functionally depends on the attribute \(\mathtt{dept}\) within the relation \(\mathtt{Employee}\):

While \(\mathcal{DLR}^+\) turns out to be undecidable, we show how a simple syntactic condition on the appearance of projections sharing common attributes in a knowledge base makes the language decidable. The result of this restriction is a new language called \(\mathcal{DLR}^{\pm }\). We prove that \(\mathcal{DLR}^{\pm }\), while preserving most of the \(\mathcal{DLR}^+\) expressivity, has a reasoning problem whose complexity does not increase w.r.t. the computational complexity of the basic \(\mathcal{DLR}\) language.
We also present in Sect. 6 the implementation of an API for the reasoning services in \(\mathcal{DLR}^{\pm }\).
2 The Description Logic \(\mathcal{DLR}^+\)
We start by introducing the syntax of \(\mathcal{DLR}^+\). A \(\mathcal{DLR}^+\) signature is a tuple \(\mathcal {L}=(\mathcal {C},\mathcal {R},\mathcal {O},\mathcal {U},\tau )\) where \(\mathcal {C}\), \(\mathcal {R}\), \(\mathcal {O}\) and \(\mathcal {U}\) are finite, mutually disjoint sets of concept names, relation names, individual names, and attributes, respectively, and \(\tau \) is a relation signature function, associating a set of attributes to each relation name  , with \(n\geqslant 2\).
, with \(n\geqslant 2\).
The syntax of concepts C, relations R, formulas \(\varphi \), and attribute renaming axioms \(\vartheta \) is given in Fig. 1, where  ,
,  ,
,  ,
,  , q is a positive integer and \(2\leqslant k < \textsc {arity}(R)\). The arity of a relation R is the number of the attributes in its signature; i.e., \(\textsc {arity}(R)=\left| \tau (R)\right| \), with the relation signature function \(\tau \) extended to complex relations as in Fig. 2. Note that it is possible that the same attribute appears in the signature of different relations.
, q is a positive integer and \(2\leqslant k < \textsc {arity}(R)\). The arity of a relation R is the number of the attributes in its signature; i.e., \(\textsc {arity}(R)=\left| \tau (R)\right| \), with the relation signature function \(\tau \) extended to complex relations as in Fig. 2. Note that it is possible that the same attribute appears in the signature of different relations.
As mentioned in the introduction, the \(\mathcal{DLR}^+\) constructors added to \(\mathcal{DLR}\) are the local and global objectification ( and
and  , respectively); relation projections with the possibility to count the projected tuples (\(\pi ^{\lesseqgtr q}[U_1,\ldots ,U_k] R\)), and renaming axioms over attributes (
, respectively); relation projections with the possibility to count the projected tuples (\(\pi ^{\lesseqgtr q}[U_1,\ldots ,U_k] R\)), and renaming axioms over attributes ( ). Note that local objectification (
). Note that local objectification ( ) can be applied to relation names, while global objectification (
) can be applied to relation names, while global objectification ( ) can be applied to arbitrary relation expressions. We use the standard abbreviations:
) can be applied to arbitrary relation expressions. We use the standard abbreviations:

A \(\mathcal{DLR}^+\) TBox \(\mathcal {T}\) is a finite set of concept inclusion axioms of the form  and relation inclusion axioms of the form
and relation inclusion axioms of the form  . We use
. We use  as a shortcut for the two axioms
as a shortcut for the two axioms  and \(X_2\sqsubseteq X_1\). A \(\mathcal{DLR}^+\) ABox \(\mathcal {A}\) is a finite set of concept instance axioms of the form \(C\!N(o)\), relation instance axioms of the form \(R\!N(U_1\!:\!o_1,\ldots ,U_n\!:\!o_n)\), and same/distinct individual axioms of the form \(o_1 = o_2\) and \(o_1 \ne o_2\), with
and \(X_2\sqsubseteq X_1\). A \(\mathcal{DLR}^+\) ABox \(\mathcal {A}\) is a finite set of concept instance axioms of the form \(C\!N(o)\), relation instance axioms of the form \(R\!N(U_1\!:\!o_1,\ldots ,U_n\!:\!o_n)\), and same/distinct individual axioms of the form \(o_1 = o_2\) and \(o_1 \ne o_2\), with  . Restricting ABox axioms to concept and relation names only does not affect the expressivity of \(\mathcal{DLR}^+\) due to the availability of unrestricted TBox axioms. A \(\mathcal{DLR}^+\) renaming schema \(\mathfrak {R}\) is a finite set of renaming axioms of the form
. Restricting ABox axioms to concept and relation names only does not affect the expressivity of \(\mathcal{DLR}^+\) due to the availability of unrestricted TBox axioms. A \(\mathcal{DLR}^+\) renaming schema \(\mathfrak {R}\) is a finite set of renaming axioms of the form  . We use the shortcut
. We use the shortcut  to group many renaming axioms with the meaning that
to group many renaming axioms with the meaning that  for all \(i=1,\ldots , n\). A \(\mathcal{DLR}^+\) knowledge base (KB) \(\mathcal {KB}=(\mathcal {T} \!,\mathcal {A},\mathfrak {R})\) is composed by a TBox \(\mathcal {T}\), an ABox \(\mathcal {A}\), and a renaming schema \(\mathfrak {R}\).
for all \(i=1,\ldots , n\). A \(\mathcal{DLR}^+\) knowledge base (KB) \(\mathcal {KB}=(\mathcal {T} \!,\mathcal {A},\mathfrak {R})\) is composed by a TBox \(\mathcal {T}\), an ABox \(\mathcal {A}\), and a renaming schema \(\mathfrak {R}\).
The renaming operator  is an equivalence relation over the attributes \(\mathcal {U}\),
is an equivalence relation over the attributes \(\mathcal {U}\),  . The partitioning of \(\mathcal {U}\) into equivalence classes induced by a renaming schema is meant to represent the alternative ways to name attributes in the knowledge base. A unique canonical representative for each equivalence class is chosen to replace all the attributes in the class throughout the knowledge base. From now on we assume that a knowledge base is consistently rewritten by substituting each attribute with its canonical representative. After this rewriting, the renaming schema does not play any role in the knowledge base. We allow only arity-preserving renaming schemas, i.e., there is no equivalence class containing two attributes from the same relation signature.
. The partitioning of \(\mathcal {U}\) into equivalence classes induced by a renaming schema is meant to represent the alternative ways to name attributes in the knowledge base. A unique canonical representative for each equivalence class is chosen to replace all the attributes in the class throughout the knowledge base. From now on we assume that a knowledge base is consistently rewritten by substituting each attribute with its canonical representative. After this rewriting, the renaming schema does not play any role in the knowledge base. We allow only arity-preserving renaming schemas, i.e., there is no equivalence class containing two attributes from the same relation signature.
As shown in the introduction, the renaming schema is useful to reconcile the named attribute perspective and the positional perspective on relations. It is also important to enforce union compatibility among relations involved in relation inclusion axioms, and among relations involved in  - and
- and  -set expressions. Two relations are union compatible (w.r.t. a renaming schema) if they have the same signature (up to the attribute renaming induced by the renaming schema). Indeed, as it will be clear from the semantics, a relation inclusion axiom involving non union compatible relations would always be false, and a
-set expressions. Two relations are union compatible (w.r.t. a renaming schema) if they have the same signature (up to the attribute renaming induced by the renaming schema). Indeed, as it will be clear from the semantics, a relation inclusion axiom involving non union compatible relations would always be false, and a  - and
- and  -set expression involving non union compatible relations would always be empty.
-set expression involving non union compatible relations would always be empty.
The semantics of \(\mathcal{DLR}^+\) uses the notion of labelled tuples over a countable potentially infinite domain \(\varDelta \). Given a set of labels  an \(\mathcal {X}\)
-labelled tuple over \(\varDelta \) (or tuple for short) is a total function \(t :\mathcal {X} \rightarrow \varDelta \). For
an \(\mathcal {X}\)
-labelled tuple over \(\varDelta \) (or tuple for short) is a total function \(t :\mathcal {X} \rightarrow \varDelta \). For  , we write t[U] to refer to the domain element
, we write t[U] to refer to the domain element  labelled by U. Given
labelled by U. Given  , the expression \({\langle U_1:d_1,\ldots ,U_n:d_n\rangle }\) stands for the tuple t defined on the set of labels \(\{U_1,\ldots ,U_n\}\) such that \({t[U_i]=d_i}\), for \({1\leqslant 1\leqslant n}\). The projection of the tuple t over the attributes \({U_1,\ldots ,U_k}\) is the function t restricted to be undefined for the labels not in \({U_1,\ldots ,U_k}\), and it is denoted by \({t[U_1,\ldots ,U_k]}\). The relation signature function \(\tau \) is extended to labelled tuples to obtain the set of labels on which a tuple is defined. \(T_\varDelta (\mathcal {X})\) denotes the set of all \(\mathcal {X}\)-labelled tuples over \(\varDelta \), for
, the expression \({\langle U_1:d_1,\ldots ,U_n:d_n\rangle }\) stands for the tuple t defined on the set of labels \(\{U_1,\ldots ,U_n\}\) such that \({t[U_i]=d_i}\), for \({1\leqslant 1\leqslant n}\). The projection of the tuple t over the attributes \({U_1,\ldots ,U_k}\) is the function t restricted to be undefined for the labels not in \({U_1,\ldots ,U_k}\), and it is denoted by \({t[U_1,\ldots ,U_k]}\). The relation signature function \(\tau \) is extended to labelled tuples to obtain the set of labels on which a tuple is defined. \(T_\varDelta (\mathcal {X})\) denotes the set of all \(\mathcal {X}\)-labelled tuples over \(\varDelta \), for  , and we overload this notation by denoting with \(T_\varDelta (\mathcal {U})\) the set of all possible tuples with labels within the whole set of attributes \(\mathcal {U} \).
, and we overload this notation by denoting with \(T_\varDelta (\mathcal {U})\) the set of all possible tuples with labels within the whole set of attributes \(\mathcal {U} \).
A \(\mathcal{DLR}^+\) interpretation is a tuple \(\mathcal {I} = (\varDelta , \cdot ^\mathcal {I}, \imath , L)\) consisting of a nonempty countable potentially infinite domain \(\varDelta \) specific to \(\mathcal {I} \), an interpretation function \(\cdot ^\mathcal {I} \), a global objectification function \(\imath \), and a family L containing one local objectification function \(\ell _{R\!N_i}\) for each named relation  . The global objectification function is an injective function, \({\imath :T_{\varDelta }(\mathcal {U}) \rightarrow \varDelta }\), associating a unique global identifier to each tuple. The local objectification functions, \({\ell _{R\!N_i}:T_{\varDelta }(\mathcal {U}) \rightarrow \varDelta }\), are associated to each relation name in the signature, and as the global objectification function they are injective: they associate an identifier—which is guaranteed to be unique only within the interpretation of a relation name—to each tuple.
. The global objectification function is an injective function, \({\imath :T_{\varDelta }(\mathcal {U}) \rightarrow \varDelta }\), associating a unique global identifier to each tuple. The local objectification functions, \({\ell _{R\!N_i}:T_{\varDelta }(\mathcal {U}) \rightarrow \varDelta }\), are associated to each relation name in the signature, and as the global objectification function they are injective: they associate an identifier—which is guaranteed to be unique only within the interpretation of a relation name—to each tuple.
The interpretation function \(\cdot ^\mathcal {I} \) assigns a domain element to each individual,  , a set of domain elements to each concept name,
, a set of domain elements to each concept name,  , and a set of \(\tau (R\!N)\)-labelled tuples over \(\varDelta \) to each relation name \(R\!N\),
, and a set of \(\tau (R\!N)\)-labelled tuples over \(\varDelta \) to each relation name \(R\!N\),  . Note that the unique name assumption is not enforced. The interpretation function \(\cdot ^\mathcal {I} \) is unambiguously extended over concept and relation expressions as specified in Fig. 3. Notice that the construct \(\pi ^{\lesseqgtr q}[U_1,\ldots ,U_k] R\) is interpreted as a classical projection over a relation, thus including only tuples belonging to the relation.
. Note that the unique name assumption is not enforced. The interpretation function \(\cdot ^\mathcal {I} \) is unambiguously extended over concept and relation expressions as specified in Fig. 3. Notice that the construct \(\pi ^{\lesseqgtr q}[U_1,\ldots ,U_k] R\) is interpreted as a classical projection over a relation, thus including only tuples belonging to the relation.
The interpretation \(\mathcal {I} \) satisfies the concept inclusion axiom  if
if  , and the relation inclusion axiom
, and the relation inclusion axiom  if
if  . It satisfies the concept instance axiom \(C\!N(o)\) if
. It satisfies the concept instance axiom \(C\!N(o)\) if  , the relation instance axiom \(R\!N(U_1\!:\!o_1,\ldots ,U_n\!:\!o_n)\) if
, the relation instance axiom \(R\!N(U_1\!:\!o_1,\ldots ,U_n\!:\!o_n)\) if  , and the axioms \(o_1 = o_2\) and \(o_1 \ne o_2\) if \(o_1^{\mathcal {I}} = o_2^{\mathcal {I}} \), and \(o_1^{\mathcal {I}} \ne o_2^{\mathcal {I}} \), respectively. \(\mathcal {I}\) is a model of the knowledge base \((\mathcal {T}\!,\mathcal {A},\mathfrak {R})\) if it satisfies all the axioms in the TBox \(\mathcal {T}\) and in the ABox \(\mathcal {A}\), once the knowledge base has been rewritten according to the renaming schema.
, and the axioms \(o_1 = o_2\) and \(o_1 \ne o_2\) if \(o_1^{\mathcal {I}} = o_2^{\mathcal {I}} \), and \(o_1^{\mathcal {I}} \ne o_2^{\mathcal {I}} \), respectively. \(\mathcal {I}\) is a model of the knowledge base \((\mathcal {T}\!,\mathcal {A},\mathfrak {R})\) if it satisfies all the axioms in the TBox \(\mathcal {T}\) and in the ABox \(\mathcal {A}\), once the knowledge base has been rewritten according to the renaming schema.
Example 1
Consider the relation names \(R_1, R_2\) with \(\tau (R_1) = \{W_1,W_2,W_3,W_4\}\), \(\tau (R_2) = \{V_1,V_2,V_3,V_4,V_5\}\), and a knowledge base with the renaming axiom  and a TBox \(\mathcal {T} _\mathsf{exa}\):
and a TBox \(\mathcal {T} _\mathsf{exa}\):



The axiom (1) expresses that \(W_1,W_2\) form a multi-attribute key for \(R_1\); (2) introduces a functional dependency in the relation \(R_2\) where the attribute \(V_5\) is functionally dependent from attributes \(V_3, V_4\), and (3) states an inclusion between two projections of the relation names \(R_1, R_2\) based on the renaming schema axiom. \(\square \)
KB satisfiability refers to the problem of deciding the existence of a model of a given knowledge base; concept satisfiability (resp. relation satisfiability) is the problem of deciding whether there is a model of the knowledge base with a non-empty interpretation of a given concept (resp. relation). A knowledge base entails (or logically implies) an axiom if all models of the knowledge base are also models of the axiom. For instance, it is easy to see that the TBox in Example 1 entails that \(V_3,V_4\) are a key for \(R_2\):

and that axiom (2) is redundant in \(\mathcal {T} _\mathsf{exa}\). The decision problems in \(\mathcal{DLR}^+\) can be all reduced to KB satisfiability.
Lemma 2
In \(\mathcal{DLR}^+\), concept and relation satisfiability and entailment are reducible to KB satisfiability.
3 Expressiveness of \(\mathcal{DLR}^+\)
\(\mathcal{DLR}^+\) is an expressive description logic able to assert relevant constraints in the context of relational databases, such as inclusion dependencies (namely inclusion axioms among arbitrary projections of relations), equijoins, functional dependency axioms, key and foreign key axioms, external uniqueness axioms, identification axioms, and path functional dependencies.
An equijoin among two relations with disjoint signatures is the set of all combinations of tuples in the relations that are equal on their selected attribute names. Let \(R_1,R_2\) be relations with signatures \(\tau (R_1)=\{U,U_1,\ldots ,U_{n_1}\}\) and \(\tau (R_2)=\{V,V_1,\ldots ,V_{n_2}\}\); their equijoin over U and V is the relation  with signature
with signature  , which is expressed by the \(\mathcal{DLR}^+\) axioms:
, which is expressed by the \(\mathcal{DLR}^+\) axioms:

A functional dependency axiom \((R:U_1\ldots U_j \rightarrow U)\) (also called internal uniqueness axiom [9]) states that the values of the attributes \(U_1\ldots U_j\) uniquely determine the value of the attribute U in the relation R. Formally, the interpretation \(\mathcal {I} \) satisfies this functional dependency axiom if, for all tuples  , \(s[U_1] = t[U_1], \ldots , s[U_j] = t[U_j]\) imply \(s[U] = t[U]\). Functional dependencies can be expressed in \(\mathcal{DLR}^+\), assuming that
, \(s[U_1] = t[U_1], \ldots , s[U_j] = t[U_j]\) imply \(s[U] = t[U]\). Functional dependencies can be expressed in \(\mathcal{DLR}^+\), assuming that  , with the axiom:
, with the axiom:

A special case of a functional dependency are key axioms \((R:U_1\ldots U_j \rightarrow R)\), which state that the values of the key attributes \(U_1\ldots U_j\) of a relation R uniquely identify tuples in R. A key axiom can be expressed in \(\mathcal{DLR}^+\), assuming that  , with the axiom:
, with the axiom:

A foreign key is the obvious result of an inclusion dependency together with a key constraint involving the foreign key attributes.
The external uniqueness axiom \(([U^1]R_1\downarrow \ldots \downarrow [U^h]R_h)\) states that the join R of the relations \(R_1,\ldots ,R_h\) via the attributes \(U^1,\ldots ,U^h\) has the joined attribute functionally dependent on all the others [9]. This can be expressed in \(\mathcal{DLR}^+\) with the axioms:

where \(\tau (R_i)=\{U^i,U^i_1,\ldots , U^i_{n_i}\}, 1\le i\le h\), and R is a new relation name with \(\tau (R)=\{U^1,U^1_{1},\ldots , U^1_{n_1},\ldots ,U^h_{1},\ldots , U^h_{n_h}\}\).
Identification axioms as defined in \(\mathcal {DLR}_\textit{ifd}\) [4] (an extension of \(\mathcal{DLR}\) with functional dependencies and identification axioms) are a variant of external uniqueness axioms, constraining only the elements of a concept C; they can be expressed in \(\mathcal{DLR}^+\) with the axiom:
Path functional dependencies—as defined in the description logics family \(\mathcal {CFD}\) [16]—can be expressed in \(\mathcal{DLR}^+\) as identification axioms involving joined sequences of functional binary relations. \(\mathcal{DLR}^+\) also captures the tree-based identification constraints ( tid ) introduced in [5] to express functional dependencies in \(\textit{DL-Lite}_{\textit{RDFS,tid}}\).
The rich set of constructors in \(\mathcal{DLR}^+\) allows us to extend the known mappings in description logics of popular conceptual database models, and to provide the foundations for their reasoning tasks. The EER mapping as introduced in [1] can be extended to deal with multi-attribute keys (by using identification axioms) and named roles in relations; the ORM mapping as introduced in [8, 15] can be extended to deal with arbitrary subset and exclusive relation constructs (by using inclusions among global objectifications of projections of relations), arbitrary internal and external uniqueness constraints, arbitrary frequency constraints (by using projections), local objectification, named roles in relations, and fact type readings (by using renaming axioms); the UML mapping as introduced in [3] can be fixed to deal properly with association classes (by using local objectification) and named roles in associations.
Aside from conceptual modelling, \(\mathcal{DLR}^+\) could be studied in relation to other tasks relevant for database scenarios, such as query answering [6], constraint checking with respect to a partially closed world (i.e., with DBoxes [13]), inconsistent database repairing, etc. In this paper, we focus just on the basic consistency and entailment reasoning tasks.
4 The \(\mathcal{DLR}^{\pm }\) Fragment of \(\mathcal{DLR}^+\)
Since a \(\mathcal{DLR}^+\) knowledge base can express inclusions and functional dependencies, the entailment problem is undecidable [7]. Thus, in this section we present \(\mathcal{DLR}^{\pm }\), a decidable syntactic fragment of \(\mathcal{DLR}^+\) limiting the coexistence of relation projections in a knowledge base.
Given a \(\mathcal{DLR}^+\) knowledge base \(\mathcal {KB} = (\mathcal {T}\!,\mathcal {A},\mathfrak {R})\), we define the projection signature of \(\mathcal {KB}\) as the set \(\mathscr {T}\) containing the signatures \(\tau (R\!N)\) of all relations  , the singleton sets associated with each attribute name
, the singleton sets associated with each attribute name  , and the relation signatures that appear explicitly in projection constructs in some axiom from \(\mathcal {T}\), together with their implicit occurrences due to the renaming schema. Formally, \(\mathscr {T}\) is the smallest set such that (i)
, and the relation signatures that appear explicitly in projection constructs in some axiom from \(\mathcal {T}\), together with their implicit occurrences due to the renaming schema. Formally, \(\mathscr {T}\) is the smallest set such that (i)  for all
for all  ; (ii)
; (ii)  for all
for all  ; and (iii)
; and (iii)  for all \(\pi ^{\lesseqgtr q}[V_1,\ldots ,V_k] R\) appearing as sub-formulas in \(\mathcal {T} \) and
for all \(\pi ^{\lesseqgtr q}[V_1,\ldots ,V_k] R\) appearing as sub-formulas in \(\mathcal {T} \) and  for \(1\!\leqslant \!i\!\leqslant \!k\).
for \(1\!\leqslant \!i\!\leqslant \!k\).
The projection signature graph of \(\mathcal {KB}\) is the directed acyclic graph corresponding to the Hasse diagram of \(\mathscr {T}\) ordered by the proper subset relation  , whose sinks are the attribute singletons \(\{U\}\). We call this graph
, whose sinks are the attribute singletons \(\{U\}\). We call this graph  . Given a set of attributes
. Given a set of attributes  , the projection signature graph dominated by \(\tau \), denoted as \(\mathscr {T}_\tau \), is the sub-graph of
, the projection signature graph dominated by \(\tau \), denoted as \(\mathscr {T}_\tau \), is the sub-graph of  with \(\tau \) as root and containing all the nodes reachable from \(\tau \). Given two sets of attributes
with \(\tau \) as root and containing all the nodes reachable from \(\tau \). Given two sets of attributes  , \(\textsc {path}_{\mathscr {T}}(\tau _1,\tau _2) \) denotes the set of paths in
, \(\textsc {path}_{\mathscr {T}}(\tau _1,\tau _2) \) denotes the set of paths in  between \(\tau _1\) and \(\tau _2\). Note that, \(\textsc {path}_{\mathscr {T}}(\tau _1,\tau _2) =\varnothing \) both when a path does not exist and when
between \(\tau _1\) and \(\tau _2\). Note that, \(\textsc {path}_{\mathscr {T}}(\tau _1,\tau _2) =\varnothing \) both when a path does not exist and when  . The notation \(\textsc {child}_{\mathscr {T}}(\tau _1,\tau _2) \) means that \({\tau _2}\) is a child (i.e., a direct descendant) of \({\tau _1}\) in
. The notation \(\textsc {child}_{\mathscr {T}}(\tau _1,\tau _2) \) means that \({\tau _2}\) is a child (i.e., a direct descendant) of \({\tau _1}\) in  . We now introduce \(\mathcal{DLR}^{\pm }\) as follows.
. We now introduce \(\mathcal{DLR}^{\pm }\) as follows.
Definition 3
A \(\mathcal{DLR}^{\pm }\) knowledge base is a \(\mathcal{DLR}^+\) knowledge base that satisfies the following syntactic conditions:
-
1.
the projection signature graph
 is a multitree: i.e., for every node
is a multitree: i.e., for every node  , the graph \(\mathscr {T}_\tau \) is a tree; and
, the graph \(\mathscr {T}_\tau \) is a tree; and -
2.
for every projection construct \(\pi ^{\lesseqgtr q}[U_1,\ldots ,U_k] R\) and every concept expression of the form
 appearing in \(\mathcal {T}\), if \(q>1\) then the length of the path \(\textsc {path}_{\mathscr {T}}(\tau (R),\{U_1,\ldots ,U_k\}) \) is 1.
appearing in \(\mathcal {T}\), if \(q>1\) then the length of the path \(\textsc {path}_{\mathscr {T}}(\tau (R),\{U_1,\ldots ,U_k\}) \) is 1.
The first condition in \(\mathcal{DLR}^{\pm }\) restrict \(\mathcal{DLR}^+\) in the way that multiple projections of relations may appear in a knowledge base: intuitively, there cannot be different projections sharing a common attribute. Moreover, observe that in \(\mathcal{DLR}^{\pm }\) \(\textsc {path}_{\mathscr {T}}\) is necessarily functional, due to the multitree restriction. By relaxing the first condition the language becomes undecidable, as we mentioned at the beginning of this Section. The second condition is also necessary to prove decidability of \(\mathcal{DLR}^{\pm }\); however, we do not know whether this condition could be relaxed while preserving decidability.
The projection signature graph of Example 1.
Figure 4 shows that the projection signature graph of the knowledge base from Example 1 is indeed a multitree. Note that in the figure we have collapsed equivalent attributes in a unique equivalence class, according to the renaming schema. Furthermore, since all its projection constructs have \(q=1\), this knowledge base belongs to \(\mathcal{DLR}^{\pm }\).
\(\mathcal{DLR}\) is included in \(\mathcal{DLR}^{\pm }\), since the projection signature graph of any \(\mathcal{DLR}\) knowledge base is always a degenerate multitree with maximum depth equal to 1. Not all the database constraints as introduced in Sect. 3 can be directly expressed in \(\mathcal{DLR}^{\pm }\). While functional dependency and key axioms can be expressed directly in \(\mathcal{DLR}^{\pm }\), equijoins, external uniqueness axioms, and identification axioms introduce projections of a relation which share common attributes, thus violating the multitree restriction. For example, the axioms for capturing an equijoin between two relations, \(R_1, R_2\) would generate a projection signature graph with the signatures of \(R_1, R_2\) as projections of the signature of the join relation R sharing the attribute on which the join is performed, thus violating condition 1.
However, in \(\mathcal{DLR}^{\pm }\) it is still possible to reason over both external uniqueness and identification axioms by encoding them into a set of saturated ABoxes (as originally proposed in [4]) and check whether there is a saturation that satisfies the constraints. Therefore, we can conclude that \(\mathcal {DLR}_\textit{ifd}\) extended with unary functional dependencies is included in \(\mathcal{DLR}^{\pm }\), provided that projections of relations in the knowledge base form a multitree projection signature graph. Since (unary) functional dependencies are expressed via the inclusions of projections of relations, by constraining the projection signature graph to be a multitree, the possibility to build combinations of functional dependencies as the ones in [4] leading to undecidability is ruled out.
Note that the non-conflicting keys sufficient condition guaranteeing the decidability of inclusion dependencies and keys of [12] is in conflict with our more restrictive requirement: indeed [12] allow for overlapping projections, but the considered datalog language is not comparable to \(\mathcal{DLR}^+\). In general, description logic based languages, such as \(\mathcal{DLR}^+\), and datalog based languages, such as the language proposed in [12], are incomparable in terms of expressiveness, due to the inability of description logics to distinguish non-tree models in the TBox. Note that, unlike the typical restrictions of datalog-like languages, there is no problem in stating arbitrary cyclic dependencies in relation inclusion axioms involving projections on the left and right hand sides.
Concerning the ability of \(\mathcal{DLR}^{\pm }\) to capture conceptual data models, only the mapping of ORM schemas is affected by the \(\mathcal{DLR}^{\pm }\) restrictions: \(\mathcal{DLR}^{\pm }\) is able to correctly express an ORM schema if the projections involved in the schema satisfy the \(\mathcal{DLR}^{\pm }\) multitree restriction.
5 Mapping \(\mathcal{DLR}^{\pm }\) to \(\mathcal{ALCQI}\)
This section shows constructively the main technical result of this paper, i.e., that reasoning in \(\mathcal{DLR}^{\pm }\) is an ExpTime-complete problem. The lower bound is clear by observing that \(\mathcal{DLR}\) is a sublanguage of \(\mathcal{DLR}^{\pm }\). More challenging is the upper bound obtained by providing a mapping from \(\mathcal{DLR}^{\pm }\) knowledge bases to \(\mathcal{ALCQI}\) knowledge bases—a propositionally complete description logic with qualified number restrictions  , and inverse roles \(R^-\) (see [2] for more details). We adapt and extend the mapping presented for \(\mathcal{DLR}\) in [6], with the modifications proposed by [10] to deal with ABoxes without the unique name assumption.
, and inverse roles \(R^-\) (see [2] for more details). We adapt and extend the mapping presented for \(\mathcal{DLR}\) in [6], with the modifications proposed by [10] to deal with ABoxes without the unique name assumption.
We recall that the renaming schema \(\mathfrak {R}\) does not play any role since we assumed that a \(\mathcal{DLR}^{\pm }\) knowledge base is rewritten by choosing a single canonical representative for each equivalence class of attributes induced by \(\mathfrak {R}\). Thus, we consider \(\mathcal{DLR}^{\pm }\) knowledge bases as pairs of TBox and ABox axioms.
We first introduce a mapping function \(\cdot ^\dag \) from \(\mathcal{DLR}^{\pm }\) concepts and relations to \(\mathcal{ALCQI}\) concepts. The function \(\cdot ^\dag \) maps each concept name \(C\!N\) and each relation name \(R\!N\) appearing in the \(\mathcal{DLR}^{\pm }\) KB to the \(\mathcal{ALCQI}\) concept names \(C\!N\) and \(A_{R\!N}\), respectively. The latter can be informally understood as the “global” reification of \(R\!N\). For each relation name \(R\!N\), the \(\mathcal{ALCQI}\) signature also includes a concept name \(A_{R\!N}^{l}\) and a role name \(Q_{R\!N}\) to capture local objectification. The mapping \(\cdot ^\dag \) is extended to concept and relation expressions as illustrated in Fig. 5, where the notation \(\exists ^{{\scriptscriptstyle \geqslant 1,}{\scriptscriptstyle \lesseqgtr } q} R\mathpunct {\text{. }}C\) is a shortcut for the conjunction  .
.
The mapping crucially uses the projection signature graph to map projections and selections, by accessing paths in the projection signature graph  associated to the \(\mathcal{DLR}^{\pm }\) KB. If there is a path \(\textsc {path}_{\mathscr {T}}(\tau ,\tau ') = \tau ,\tau _1,\ldots ,\tau _n, \tau '\) from \({\tau }\) to \({\tau '}\) in \(\mathscr {T}\), then the \(\mathcal{ALCQI}\) signature contains role names \(Q_{\tau '}, Q_{\tau _i}\), for \(i=1,\ldots ,n\), and the following role chain expression is generated by the mapping:
associated to the \(\mathcal{DLR}^{\pm }\) KB. If there is a path \(\textsc {path}_{\mathscr {T}}(\tau ,\tau ') = \tau ,\tau _1,\ldots ,\tau _n, \tau '\) from \({\tau }\) to \({\tau '}\) in \(\mathscr {T}\), then the \(\mathcal{ALCQI}\) signature contains role names \(Q_{\tau '}, Q_{\tau _i}\), for \(i=1,\ldots ,n\), and the following role chain expression is generated by the mapping:
In particular, the mapping uses the following notation: the inverse role chain \((R_1\circ \ldots \circ R_n)^-\), for \(R_i\) a role name, stands for the chain \(R_n^-\circ \ldots \circ R_1^-\), with \(R_i^-\) an inverse role, the expression  stands for the \(\mathcal{ALCQI}\) concept expression
stands for the \(\mathcal{ALCQI}\) concept expression  and \(\forall R_1\circ \ldots \circ R_n\mathpunct {\text{. }}C\) for the \(\mathcal{ALCQI}\) concept expression \(\forall R_1\mathpunct {\text{. }}\ldots \mathpunct {\text{. }}\forall R_n\mathpunct {\text{. }}{C}\). Thus, since \(\mathcal{DLR}^{\pm }\) restricts to \(q=1\) the cardinalities on any path of length strictly greater than 1 (see condition 2 in Definition 3), the above notation shows that we remain within the \(\mathcal{ALCQI}\) syntax when the mapping applies to cardinalities. If, e.g., we need to map the \(\mathcal{DLR}^{\pm }\) cardinality constraint \(\exists ^{{\scriptscriptstyle \lesseqgtr } q} [U_i]R\) with \(q>1\), then, to stay within the \(\mathcal{ALCQI}\) syntax, \(U_i\) must not be mentioned in any other projection in such a way that \(|\textsc {path}_{\mathscr {T}}(\tau (R),\{U_i\}) |=1\). Finally, notice that the mapping introduces a concept name \(A_{R\!N}^{\tau _i}\) for each projected signature \(\tau _i\) in the projection signature graph dominated by \(\tau (R\!N)\), i.e.,
and \(\forall R_1\circ \ldots \circ R_n\mathpunct {\text{. }}C\) for the \(\mathcal{ALCQI}\) concept expression \(\forall R_1\mathpunct {\text{. }}\ldots \mathpunct {\text{. }}\forall R_n\mathpunct {\text{. }}{C}\). Thus, since \(\mathcal{DLR}^{\pm }\) restricts to \(q=1\) the cardinalities on any path of length strictly greater than 1 (see condition 2 in Definition 3), the above notation shows that we remain within the \(\mathcal{ALCQI}\) syntax when the mapping applies to cardinalities. If, e.g., we need to map the \(\mathcal{DLR}^{\pm }\) cardinality constraint \(\exists ^{{\scriptscriptstyle \lesseqgtr } q} [U_i]R\) with \(q>1\), then, to stay within the \(\mathcal{ALCQI}\) syntax, \(U_i\) must not be mentioned in any other projection in such a way that \(|\textsc {path}_{\mathscr {T}}(\tau (R),\{U_i\}) |=1\). Finally, notice that the mapping introduces a concept name \(A_{R\!N}^{\tau _i}\) for each projected signature \(\tau _i\) in the projection signature graph dominated by \(\tau (R\!N)\), i.e.,  , informally to capture the global reifications of the various projections of \(R\!N\) in the given KB. We also use the shortcut \(A_{R\!N}\) which stands for \(A_{R\!N}^{\tau (R\!N)}\).
, informally to capture the global reifications of the various projections of \(R\!N\) in the given KB. We also use the shortcut \(A_{R\!N}\) which stands for \(A_{R\!N}^{\tau (R\!N)}\).
Intuitively, each node in the projection signature graph associated to a \(\mathcal{DLR}^{\pm }\) KB denotes a relation projection and the mapping reifies each of these projections. The target \(\mathcal{ALCQI}\) signature resulting from mapping the \(\mathcal{DLR}^{\pm }\) KB of Example 1 is partially presented in Fig. 6, together with the projection signature graph (showed in Fig. 4). Each node of the graph is labelled with the corresponding global reification concept (\(A_{R_i}^{\tau _j}\)), for each  and each projected signature \(\tau _j\) in the projection signature graph dominated by \(\tau (R_i)\), while the edges are labelled by the roles (\(Q_{\tau _i}\)) needed for the reification.
and each projected signature \(\tau _j\) in the projection signature graph dominated by \(\tau (R_i)\), while the edges are labelled by the roles (\(Q_{\tau _i}\)) needed for the reification.
To better clarify the need for the path function in the mapping, notice that each \(\mathcal{DLR}^{\pm }\) relation is reified according to the decomposition dictated by the projection signature graph it dominates. Thus, to access, e.g., an attribute \(U_j\) of a \(\mathcal{DLR}^{\pm }\) relation \({R_i}\) it is necessary to follow the path through the projections that use the attribute. Such a path, from the node denoting the whole signature of the relation, \({\tau (R_i)}\), to the node denoting the attribute \(U_j\) is returned by the \(\textsc {path}_{\mathscr {T}}(\tau (R_i),U_j) \) function. For example, considering the example in Fig. 6, to access the attribute \(W_1\) of the relation \(R_2\) in the expression \((\sigma _{W_1 : C} R_2)\), the mapping of the path \(\textsc {path}_{\mathscr {T}}(\tau (R_2),\{W_1\}) ^\dag \) is equal to the role chain \(Q_{\{W_1,W_2,W_3\}}\circ Q_{\{W_1,W_2\}}\circ Q_{\{W_1\}}\), so that  Similar considerations can be done when mapping cardinalities over relation projections.
Similar considerations can be done when mapping cardinalities over relation projections.
Figures 7 and 8 present in details the mapping of a \(\mathcal{DLR}^{\pm }\) KB into a KB in \(\mathcal{ALCQI}\). Let \(\mathcal {KB} = (\mathcal {T}, \mathcal {A})\) be a \(\mathcal{DLR}^{\pm }\) KB with signature \((\mathcal {C},\mathcal {R},\mathcal {O},\mathcal {U},\tau )\). The mapping \(\gamma (\mathcal {KB})\) is assumed to be unsatisfiable (i.e., it contains the axiom  ) if the ABox contains the relation assertion \(R\!N(t)\) with \(\tau (R\!N)\ne \tau (t)\), for some relation
) if the ABox contains the relation assertion \(R\!N(t)\) with \(\tau (R\!N)\ne \tau (t)\), for some relation  and some tuple t. Otherwise, \(\gamma (\mathcal {KB}) = (\gamma (\mathcal {T}),\gamma (\mathcal {A}))\) defines the mapped \(\mathcal{ALCQI}\) KB.
and some tuple t. Otherwise, \(\gamma (\mathcal {KB}) = (\gamma (\mathcal {T}),\gamma (\mathcal {A}))\) defines the mapped \(\mathcal{ALCQI}\) KB.
Intuitively, \(\gamma _\textit{dsj}\) ensures that relations with different signatures are disjoint, thus, e.g., enforcing the union compatibility. The axioms in \(\gamma _{\textit{rel}}\) introduce classical reification axioms for each relation and its relevant projections. The axioms in \(\gamma _{\textit{lobj}}\) make sure that each local objectification differs from the global one while each role \(Q_{R\!N}\) defines a bijection.
To translate the ABox, we first map each individual  in the \(\mathcal{DLR}^{\pm }\) ABox \(\mathcal {A}\) to an \(\mathcal{ALCQI}\) individual o. Each tuple in relation instance axioms occurring in \(\mathcal {A}\) is mapped via an injective function \(\xi \) to a distinct individual. That is, \(\xi : T_\mathcal {O} (\mathcal {U})\rightarrow \mathcal {O}_\mathcal{ALCQI} \), with
in the \(\mathcal{DLR}^{\pm }\) ABox \(\mathcal {A}\) to an \(\mathcal{ALCQI}\) individual o. Each tuple in relation instance axioms occurring in \(\mathcal {A}\) is mapped via an injective function \(\xi \) to a distinct individual. That is, \(\xi : T_\mathcal {O} (\mathcal {U})\rightarrow \mathcal {O}_\mathcal{ALCQI} \), with  being the set of individual names in \(\gamma (\mathcal {KB})\), \(\mathcal {O} \cap \mathcal {O} ^t = \varnothing \) and
being the set of individual names in \(\gamma (\mathcal {KB})\), \(\mathcal {O} \cap \mathcal {O} ^t = \varnothing \) and

Following [10], the mapping \(\gamma (\mathcal {A})\) in Fig. 8 introduces a new concept name \(Q_o\) for each individual  and a new concept name \(Q_t\) for each relation instance t occurring in \(\mathcal {A}\), with each \(Q_t\) restricted as follows:
and a new concept name \(Q_t\) for each relation instance t occurring in \(\mathcal {A}\), with each \(Q_t\) restricted as follows:

Intuitively, (6) and (7) reify each relation instance axiom occurring in \(\mathcal {A}\) using the projection signature of the involved tuple itself. The Formulas (8) and (9) together with the axioms for concepts \(Q_t\) guarantee that there is exactly one \(\mathcal{ALCQI}\) individual reifying a given tuple in a relation instance axiom. Clearly, the size of \(\gamma (\mathcal {KB})\) is polynomial in the size of \(\mathcal {KB} \) under the same coding of the numerical parameters.
We are now able to state our main technical result.
Theorem 4
A \(\mathcal{DLR}^{\pm }\) knowledge base \(\mathcal {KB} \) is satisfiable iff the \(\mathcal{ALCQI}\) knowledge base \(\gamma (\mathcal {KB})\) is satisfiable.
As a direct consequence of this theorem and the fact that \(\mathcal{DLR}\) is a sublanguage of \(\mathcal{DLR}^{\pm }\), we obtain the following corollary.
Corollary 5
Reasoning in \(\mathcal{DLR}^{\pm }\) is ExpTime-complete.
6 Implementation of a \(\mathcal{DLR}^{\pm }\) API
We have implemented the framework discussed in this paper. DLRtoOWL is a Java library fully implementing \(\mathcal{DLR}^{\pm }\) reasoning services. The library is based on the tool ANTLR4 to parse serialised input, and on OWLAPI4 for the OWL2 encoding, and it includes the OWL reasoner JFact. DLRtoOWL provides a Java \(\mathcal{DLR}\) API package to allow developers to create, manipulate, serialise, and reason with \(\mathcal{DLR}^{\pm }\) knowledge bases in their Java-based application, extending in a compatible way the standard OWL API with the \(\mathcal{DLR}^{\pm }\) tell and ask services.
During the development of this new library we strongly focused on performance. Since the OWL encoding is only possible if we have already built the \(\mathcal{ALCQI}\) projection signature multitree, in principle the program should perform two parsing rounds: one to create the multitree and the other one to generate the OWL mapping. We faced this issue using dynamic programming: during the first (and only) parsing round we store in a data structure each axiom that we want to translate in OWL and, after building the multitree, by the dynamic programming technique we build on-the-fly a Java class which generates the required axioms.
We have used the \(\mathcal{DLR}^{\pm }\) API within a plugin for general ontology reasoning for conceptual design tools based on languages such as EER, UML (with OCL), and ORM (with derivation rules) [14]. This plugin supports the detection of inconsistencies, redundancies, complete derivations of the strictest implicit constructs and unexpected behaviours. Reasoning helps the modeller to detect relevant formal properties of the ontology that may be undetected during the modelling phase, which give rise to design quality degradation and/or increased development times and costs. The system is still at an early stage of completion, but it has been proved to be highly effective and efficient: indeed, it computes derivations in real time in the background while the ontology is being designed.
7 Conclusions
We have introduced the very expressive \(\mathcal{DLR}^+\) description logic, which extends \(\mathcal{DLR}\) with database oriented constraints. \(\mathcal{DLR}^+\) is expressive enough to cover directly and more thoroughly the EER, UML, and ORM conceptual data models, among others. Although reasoning in \(\mathcal{DLR}^+\) is undecidable, we show that a simple syntactic constraint on KBs restores decidability. In fact, the resulting logic \(\mathcal{DLR}^{\pm }\) has the same complexity (ExpTime-complete) as the basic \(\mathcal{DLR}\) language. In other words, handling database constraints does not increase the complexity of reasoning in the logic. To enhance the use and adoption of \(\mathcal{DLR}^{\pm }\), we have developed an API that fully implements reasoning for this language, and maps input knowledge bases into OWL. Using a standard OWL reasoner, we are able to provide a variety of \(\mathcal{DLR}^{\pm }\) reasoning services.
We plan to investigate the problem of query answering under \(\mathcal{DLR}^{\pm }\) ontologies and to check whether the complexity for this problem can be lifted from known results in \(\mathcal{DLR}\) to \(\mathcal{DLR}^{\pm }\).
References
Artale, A., Calvanese, D., Kontchakov, R., Ryzhikov, V., Zakharyaschev, M.: Reasoning over extended ER models. In: Parent, C., Schewe, K.-D., Storey, V.C., Thalheim, B. (eds.) ER 2007. LNCS, vol. 4801, pp. 277–292. Springer, Heidelberg (2007). doi:10.1007/978-3-540-75563-0_20
Baader, F., Calvanese, D., McGuinness, D., Nardi, D., Patel-Schneider, P.F. (eds.): The Description Logic Handbook: Theory Implementation and Applications. Cambridge University Press, New York (2003)
Berardi, D., Calvanese, D., De Giacomo, G.: Reasoning on UML class diagrams. Artif. Intell. 168(1–2), 70–118 (2005)
Calvanese, D., De Giacomo, G., Lenzerini, M.: Identification constraints and functional dependencies in description logics. In: Proceedings of the Seventeenth International Joint Conference on Artificial Intelligence, IJCAI 2001, pp. 155–160. Morgan Kaufmann (2001)
Calvanese, D., Fischl, W., Pichler, R., Sallinger, E., Simkus, M.: Capturing relational schemas and functional dependencies in RDFS. In: Proceedings of the 28th AAAI Conference on Artificial Intelligence (AAAI), pp. 1003–1011. AAAI Press (2014)
Calvanese, D., Giacomo, G.D., Lenzerini, M.: Conjunctive query containment and answering under description logic constraints. ACM Trans. Comput. Logic 9(3), 22:1–22:31 (2008)
Chandra, A.K., Vardi, M.Y.: The implication problem for functional and inclusion dependencies is undecidable. SIAM J. Comput. 14(3), 671–677 (1985)
Franconi, E., Mosca, A., Solomakhin, D.: ORM2: formalisation and encoding in OWL2. In: International Workshop on Fact-Oriented Modeling (ORM 2012), pp. 368–378 (2012)
Halpin, T., Morgan, T.: Information Modeling and Relational Databases, 2nd edn. Morgan Kaufmann, San Francisco (2008)
Horrocks, I., Sattler, U., Tessaris, S., Tobies, S.: How to decide query containment under constraints using a description logic. In: Parigot, M., Voronkov, A. (eds.) LPAR 2000. LNAI, vol. 1955, pp. 326–343. Springer, Heidelberg (2000). doi:10.1007/3-540-44404-1_21
Kanellakis, P.C.: Elements of relational database theory. In: Meyer, A., Nivat, M., Paterson, M., Perrin, D., van Leeuwen, J. (eds.) The Handbook of Theoretical Computer Science, vol. B, Chap. 17, pp. 1075–1144. North Holland (1990)
Lukasiewicz, T., Cali, A., Gottlob, G.: A general datalog-based framework for tractable query answering over ontologies. Web Semant. Sci. Serv. Agents World Wide Web 14, 57–83 (2012)
Patel-Schneider, P.F., Franconi, E.: Ontology constraints in incomplete and complete data. In: Cudré-Mauroux, P., et al. (eds.) ISWC 2012. LNCS, vol. 7649, pp. 444–459. Springer, Heidelberg (2012). doi:10.1007/978-3-642-35176-1_28
Sportelli, F.: NORMA: A software for intelligent conceptual modeling. In: Proceedings of the Joint Ontology Workshops 2016 (JOWO-2016) (2016). http://ceurws.org/Vol-1660/demo-paper3.pdf
Sportelli, F., Franconi, E.: Formalisation of ORM derivation rules and their mapping into OWL. In: Debruyne, C., Panetto, H., Meersman, R., Dillon, T., Kühn, E., O’Sullivan, D., Ardagna, C.A. (eds.) OTM 2016. LNCS, vol. 10033, pp. 827–843. Springer, Heidelberg (2016)
Toman, D., Weddell, G.E.: Applications and extensions of PTIME description logics with functional constraints. In: Proceedings of the 21st International Joint Conference on Artificial Intelligence, IJCAI 2009, pp. 948–954 (2009)
Author information
Authors and Affiliations
Corresponding author
Editor information
Editors and Affiliations
Rights and permissions
Copyright information
© 2017 Springer International Publishing AG
About this paper
Cite this paper
Artale, A., Franconi, E., Peñaloza, R., Sportelli, F. (2017). A Decidable Very Expressive Description Logic for Databases. In: d'Amato, C., et al. The Semantic Web – ISWC 2017. ISWC 2017. Lecture Notes in Computer Science(), vol 10587. Springer, Cham. https://doi.org/10.1007/978-3-319-68288-4_3
Download citation
DOI: https://doi.org/10.1007/978-3-319-68288-4_3
Published:
Publisher Name: Springer, Cham
Print ISBN: 978-3-319-68287-7
Online ISBN: 978-3-319-68288-4
eBook Packages: Computer ScienceComputer Science (R0)








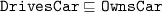 . The locally objectified events of driving and owning, defined as
. The locally objectified events of driving and owning, defined as 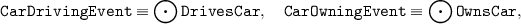
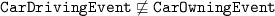 . Indeed, they are even disjoint:
. Indeed, they are even disjoint:  .
.


 is a multitree: i.e., for every node
is a multitree: i.e., for every node  , the graph
, the graph  appearing in
appearing in 



