Self-oscillations of a Vocal Apparatus: A Port-Hamiltonian Formulation

Abstract

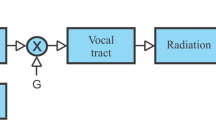
Port Hamiltonian systems (PHS) are open passive systems that fulfil a power balance: they correspond to dynamical systems composed of energy-storing elements, energy-dissipating elements and external ports, endowed with a geometric structure (called Dirac structure) that encodes conservative interconnections. This paper presents a minimal PHS model of the full vocal apparatus. Elementary components are: (a) an ideal subglottal pressure supply, (b) a glottal flow in a mobile channel, (c) vocal-folds, (d) an acoustic resonator reduced to a single mode. Particular attention is paid to the energetic consistency of each component, to passivity and to the conservative interconnection. Simulations are presented. They show the ability of the model to produce a variety of regimes, including self-sustained oscillations. Typical healthy or pathological configuration laryngeal configurations are explored.

A Dynamics of the glottal flow

The dynamics for the mean velocities can also be derived from the volume integration of the Euler equation (4). Using the gradient theorem, it comes that

$$\begin{aligned} m(h)\dot{v}_0 = L h(t) \left( P_{tot}^- - P_{tot}^+\right) \quad \text { and }\quad m(h)\ddot{y}_m = F_r^p - F_l^p. \end{aligned}$$

(8)

The energy balance for the glottal flow writes down as:

$$\begin{aligned} \dot{\varepsilon }(t) + \int _{S^-\cup S^+} \left( p+\frac{1}{2}\rho |v|^2\right) \left( v\cdot n\right) + \int _{S_l\cup S_r} p\left( v\cdot n\right) =0 \end{aligned}$$

(9)

where n is the outgoing normal. As the normal velocity is uniform on the walls, the last term of the energy balance reduces to

$$\begin{aligned} \int _{S_l\cup S_r} p\left( v\cdot n\right) =-\dot{y}_r\int _{S_r} p + \dot{y}_l\int _{S_l} p =\dot{y}_m\left( F_l^p-F_r^p\right) +\frac{\dot{h}}{2}\left( F_r^p+F_l^p\right) . \end{aligned}$$

(10)

The same applies on $S^-\cup S^+$ where $v\cdot n = \pm v_x(x=\pm \ell )$ does not depend on y:

$$\begin{aligned} \int _{S^-\cup S^+} p_{tot}\left( v\cdot n\right)&= v_x(\ell )\int _{S^+} p_{tot} - v_x(-\ell )\int _{S^-} p_{tot}\nonumber \\&= L v_0\left( P_{tot}^+ - P_{tot}^-\right) - L \ell \frac{\dot{h}}{h}\left( P_{tot}^+ + P_{tot}^-\right) . \end{aligned}$$

(11)

Thus, $\displaystyle \dot{\varepsilon } = \dot{y}_m\left( F_r^p-F_l^p\right) -\frac{\dot{h}}{2}\left( F_r^p+F_l^p\right) + L h(t) v_0\left( P_{tot}^- - P_{tot}^+\right) + L \ell \dot{h} \left( P_{tot}^- + P_{tot}^+\right)$. In the meanwhile, the kinetic energy in Eq. (6) can be derived against time: $\displaystyle \dot{\varepsilon } = m(h)\left( v_0\dot{v}_0 + \dot{y}_m\ddot{y}_m\right) + m_3(h)\dot{h}\ddot{h} +\frac{\partial H}{\partial h}\dot{h}$. The identification of the contribution of the mean axial and transverse velocities (see Eq. (8)) leads to the dynamics of the glottal channel expansion rate :

$$\begin{aligned} m_3\ddot{h} = L \ell \left( P_{tot}^- + P_{tot}^+\right) - \frac{F_r^p + F_l^p}{2} -\frac{\partial H}{\partial h}. \end{aligned}$$

(12)