Abstract
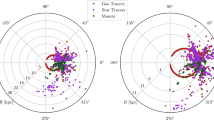
We present a new regression method called geodesic least squares (GLS), which is particularly robust against data and model uncertainty. It is based on minimization of the Rao geodesic distance on a probabilistic manifold. We apply GLS to Tully-Fisher scaling of the total baryonic mass vs. the rotation velocity in disk galaxies and we show the excellent robustness properties of GLS for estimating the coefficients and the tightness of the scaling.
This is a preview of subscription content, log in via an institution to check access.
Access this chapter
Tax calculation will be finalised at checkout
Purchases are for personal use only
Similar content being viewed by others
References
Verdoolaege, G.: A new robust regression method based on minimization of geodesic distances on a probabilistic manifold: Application to power laws. Entropy 17(7), 4602–4626 (2015)
Verdoolaege, G., Noterdaeme, J.-M.: Robust scaling in fusion science: case study for the L-H power threshold. Nucl. Fusion 55(11), 113019, (19 pp.) (2015)
Verdoolaege, G., Shabbir, A., Hornung, G.: Robust analysis of trends in noisy tokamak confinement data using geodesic least squares regression. Rev. Sci. Instrum. 87(11), 11D422, (3 pp.) (2016)
Fletcher, P.T.: Geodesic regression and the theory of least squares on riemannian manifolds. Int. J. Comput. Vis. 105(2), 171–185 (2013)
Pak, R.J.: Minimum hellinger distance estimation in simple regression models; distribution and efficiency. Stat. Probab. Lett. 26(3), 263–269 (1996)
Burbea, J., Rao, C.R.: Entropy differential metric, distance and divergence measures in probability spaces: a unified approach. J. Multivar. Anal. 12(4), 575–596 (1982)
Gill, P.E., Murray, W., Wright, M.H.: Numerical Linear Algebra and Optimization, vol. 1. Addison Wesley, Boston (1991)
Rao, C.R.: Differential metrics in probability spaces. In: Differential Geometry in Statistical Inference. Institute of Mathematical Statistics, Hayward, CA (1987)
McGaugh, S.S.: The baryonic Tully-Fisher relation of gas-rich galaxies as a test of \(\Lambda \)CDM and MOND. Astron. J. 143(2), 40, (15 pp.) (2012)
Author information
Authors and Affiliations
Corresponding author
Editor information
Editors and Affiliations
Rights and permissions
Copyright information
© 2017 Springer International Publishing AG
About this paper
Cite this paper
Verdoolaege, G. (2017). Geodesic Least Squares Regression on the Gaussian Manifold with an Application in Astrophysics. In: Nielsen, F., Barbaresco, F. (eds) Geometric Science of Information. GSI 2017. Lecture Notes in Computer Science(), vol 10589. Springer, Cham. https://doi.org/10.1007/978-3-319-68445-1_72
Download citation
DOI: https://doi.org/10.1007/978-3-319-68445-1_72
Published:
Publisher Name: Springer, Cham
Print ISBN: 978-3-319-68444-4
Online ISBN: 978-3-319-68445-1
eBook Packages: Computer ScienceComputer Science (R0)