Abstract
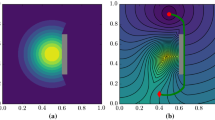
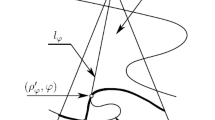
We consider a two player game, where a first player has to install a surveillance system within an admissible region. The second player needs to enter the monitored area, visit a target region, and then leave the area, while minimizing his overall probability of detection. Both players know the target region, and the second player knows the surveillance installation details. Optimal trajectories for the second player are computed using a recently developed variant of the fast marching algorithm, which takes into account curvature constraints modeling the second player vehicle maneuverability. The surveillance system optimization leverages a reverse-mode semi-automatic differentiation procedure, estimating the gradient of the value function related to the sensor location in time \({\mathcal O}(N \ln N)\).
This work has been supported by the 662107-SWARMs-ECSEL-2014-1 European project.
Access this chapter
Tax calculation will be finalised at checkout
Purchases are for personal use only
Similar content being viewed by others
References
Barbaresco, F., Monnier, B.: Minimal geodesics bundles by active contours: radar application for computation of most threathening trajectories areas & corridors. In: 10th European Signal Processing Conference, Tampere, pp. 1–4 (2000)
Barbaresco, F.: Computation of most threatening radar trajectories areas and corridors based on fast-marching & Level Sets. In: IEEE Symposium on Computational Intelligence for Security and Defense Applications (CISDA), Paris, pp. 51–58 (2011)
Bardi, M., Capuzzo-Dolcetta, I.: Optimal Control and Viscosity Solutions of Hamilton-Jacobi-Bellman Equations. Bikhauser, Bosto (1997)
Bekkers, E.J., Duits, R., Mashtakov, A., Sanguinetti, G.R.: Data-driven sub-riemannian geodesics in SE(2). In: Aujol, J.-F., Nikolova, M., Papadakis, N. (eds.) SSVM 2015. LNCS, vol. 9087, pp. 613–625. Springer, Cham (2015). doi:10.1007/978-3-319-18461-6_49
Benmansour, F., Carlier, G., Peyré, G., Santambrogio, F.: Derivatives with respect to metrics and applications: subgradient marching algorithm. Numer. Math. 116(3), 357–381 (2010)
Benmansour, F., Cohen, L.: Tubular structure segmentation based on minimal path method and anisotropic enhancement. Int. J. Comput. Vis. 92(2), 192–210 (2011)
Chen, D., Mirebeau, J.-M., Cohen, L.D.: A new finsler minimal path model with curvature penalization for image segmentation and closed contour detection. In: Proceedings of CVPR 2016, Las Vegas, USA (2016)
Dubins, L.E.: On curves of minimal length with a constraint on average curvature, and with prescribed initial and terminal positions and tangents. Amer. J. Math. 79, 497–516 (1957)
Duits, R., Meesters, S.P.L., Mirebeau, J.-M., Portegies, J.M.: Optimal Paths for Variants of the 2D and 3D Reeds-Shepp. Car with Applications in Image Analysis (Preprint available on arXiv)
Griewank, A., Walther, A.: Evaluating Derivatives: Principles and Techniques of Algorithmic Differentiation. Society for Industrial and Applied Mathematics, Philadelphia (2008)
Mirebeau, J.-M.: Anisotropic Fast-Marching on cartesian grids using Lattice Basis Reduction. SIAM J. Numer. Anal. 52(4), 1573–1599 (2014)
Mirebeau, J.-M.: Anisotropic fast-marching on cartesian grids using Voronois first reduction of quadratic forms (preprint available on HAL)
Mirebeau, J.-M.: Fast Marching methods for Curvature Penalized Shortest Paths (preprint available on HAL)
Rouy, E., Tourin, A.: A viscosity solutions approach to shape-from-shading. SIAM J. Numer. Anal. 29(3), 867–884 (1992)
Sethian, J., Vladimirsky, A.: Ordered upwind methods for static Hamilton-Jacobi equations. Proc. Natl. Acad. Sci. 98(20), 11069–11074 (2001)
Schürmann, A.: Computational geometry of positive definite quadratic forms, University Lecture Series (2009)
Strode, C.; Optimising multistatic sensor locations using path planning and game theory. In: IEEE Symposium on Computational Intelligence for Security and Defense Applications (CISDA), Paris, pp. 9–16 (2011)
Author information
Authors and Affiliations
Corresponding author
Editor information
Editors and Affiliations
Rights and permissions
Copyright information
© 2017 Springer International Publishing AG
About this paper
Cite this paper
Mirebeau, JM., Dreo, J. (2017). Automatic Differentiation of Non-holonomic Fast Marching for Computing Most Threatening Trajectories Under Sensors Surveillance. In: Nielsen, F., Barbaresco, F. (eds) Geometric Science of Information. GSI 2017. Lecture Notes in Computer Science(), vol 10589. Springer, Cham. https://doi.org/10.1007/978-3-319-68445-1_91
Download citation
DOI: https://doi.org/10.1007/978-3-319-68445-1_91
Published:
Publisher Name: Springer, Cham
Print ISBN: 978-3-319-68444-4
Online ISBN: 978-3-319-68445-1
eBook Packages: Computer ScienceComputer Science (R0)