Skip to main content
Springer Nature Link
Log in

A Nonlinear Solution to Closed Queueing Networks for Bike Sharing Systems with Markovian Arrival Processes and Under an Irreducible Path Graph

  • Conference paper
  • First Online:
Queueing Theory and Network Applications (QTNA 2017)

Part of the book series: Lecture Notes in Computer Science ((LNTCS,volume 10591))

Included in the following conference series:

Abstract

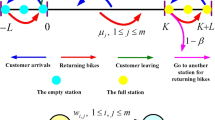
As a favorite urban public transport mode, the bike sharing system is a large-scale and complicated system, and there exists a key requirement that a user and a bike should be matched sufficiently in time. Such matched behavior makes analysis of the bike sharing systems more difficult and challenging. To design a better bike sharing system, it is a key to analyze and compute the probabilities of the problematic (i.e., full or empty) stations. In fact, such a computation is established for some fairly complex stochastic systems. To do this, this paper considers a more general large-scale bike sharing system from two important views: (a) Bikes move in an irreducible path graph, which is related to geographical structure of the bike sharing system; and (b) Markovian arrival processes (MAPs) are applied to describe the non-Poisson and burst behavior of bike-user (abbreviated as user) arrivals, while the burstiness demonstrates that the user arrivals are time-inhomogeneous and space-heterogeneous in practice. For such a complicated bike sharing system, this paper establishes a multiclass closed queueing network by means of some virtual ideas, for example, bikes are abstracted as virtual customers; stations and roads are regarded as virtual nodes. Thus user arrivals are related to service times at station nodes; and users riding bikes on roads are viewed as service times at road nodes. Further, to deal with this multiclass closed queueing network, we provide a detailed observation practically on physical behavior of the bike sharing system in order to establish the routing matrix, which gives a nonlinear solution to compute the relative arrival rates in terms of the product-form solution to the steady-state probabilities of joint queue lengths at the virtual nodes. Based on this, we can compute the steady-state probability of problematic stations, and also deal with other interesting performance measures of the bike sharing system. We hope that the methodology and results of this paper can be applicable in the study of more general bike sharing systems through multiclass closed queueing networks.

This is a preview of subscription content, log in via an institution to check access.

Access this chapter

Log in via an institution

Subscribe and save

Springer+ Basic
$34.99 /Month
  • Get 10 units per month
  • Download Article/Chapter or eBook
  • 1 Unit = 1 Article or 1 Chapter
  • Cancel anytime
Subscribe now

Buy Now

Chapter
USD 29.95
Price excludes VAT (USA)
  • Available as PDF
  • Read on any device
  • Instant download
  • Own it forever

Tax calculation will be finalised at checkout

Purchases are for personal use only

Institutional subscriptions

Similar content being viewed by others

References

  1. Adelman, D.: Price-directed control of a closed logistics queueing network. Oper. Res. 55, 1022–1038 (2007)

    Article  MathSciNet  MATH  Google Scholar 

  2. Baskett, F., Chandy, K.M., Muntz, R.R., Palacios, F.G.: Open, Closed, and Mixed Networks of Queues with Different Classes of Customers. J. ACM 22, 248–260 (1975)

    Article  MathSciNet  MATH  Google Scholar 

  3. Bolch, G., Greiner, S., de Meer, H., Trivedi, K.S.: Queueing Networks and Markov Chains: Modeling and Performance Evaluation with Computer Science Applications. Wiley, New York (2006)

    Book  MATH  Google Scholar 

  4. Bruell, S.C., Balbo, G.: Computational Algorithms for Closed Queueing Networks. Elsevier Science Ltd., Oxford (1980)

    MATH  Google Scholar 

  5. Chakravarthy, S.R.: The batch markovian arrival process: a review and future work. Adv. Probab. Theory Stochast. Process. 1, 21–49 (2001)

    Google Scholar 

  6. DeMaio, P.: Bike-sharing: history, impacts, models of provision, and future. J. Public Transp. 12, 41–56 (2009)

    Article  Google Scholar 

  7. Fishman, E., Washington, S., Haworth, N.: Bike share: a synthesis of the literature. Transp. Rev. 33, 148–165 (2013)

    Article  Google Scholar 

  8. Fricker, C., Gast, N., Mohamed, A.: Mean field analysis for inhomogeneous bike-sharing systems. In: DMTC Proceedings of AQ, AofA 2012, pp. 365–376 (2012)

    Google Scholar 

  9. Fricker, C., Gast, N.: Incentives and redistribution in homogeneous bike-sharing systems with stations of finite capacity. Euro. J. Transp. Logistics 5, 261–291 (2013)

    Article  Google Scholar 

  10. Fricker, C., Tibi, D.: Equivalence of ensembles for large vehicle-sharing models. Annal. Appl. Probab. 27, 883–916 (2017)

    Article  MathSciNet  MATH  Google Scholar 

  11. George, D.K., Xia, C.H.: Fleet-sizing and service availability for a vehicle rental system via closed queueing networks. Eur. J. Oper. Res. 211, 198–207 (2011)

    Article  MathSciNet  MATH  Google Scholar 

  12. Henderson, W., Pearce, C.E.M., Taylor, P.G., van Dijk, N.M.: Closed queueing networks with batch services. Queueing Syst. 6, 59–70 (1990)

    Article  MathSciNet  MATH  Google Scholar 

  13. Kelly, F.P.: Reversibility and Stochastic Networks. Wiley, New York (1979)

    MATH  Google Scholar 

  14. Kelly, F.P.: Reversibility and Stochastic Networks. Cambridge University Press, Cambridge (2001)

    MATH  Google Scholar 

  15. Kelly, F.P., Pollett, P.K.: Sojourn times in closed queueing networks. Adv. Appl. Probab. 15, 638–656 (1983)

    Article  MathSciNet  MATH  Google Scholar 

  16. Labadi, K., Benarbia, T., Barbot, J.P., Hamaci, S., Omari, A.: Stochastic petri net modeling, simulation and analysis of public bicycle sharing systems. IEEE Trans. Autom. Sci. Eng. 12, 1380–1395 (2015)

    Article  Google Scholar 

  17. Leurent, F.: Modelling a Vehicle-Sharing Station as a Dual Waiting System: Stochastic Framework and Stationary Analysis. HAL Id: hal-00757228, pp. 1–19 (2012)

    Google Scholar 

  18. Li, Q.L.: Constructive Computation in Stochastic Models with Applications: The RG-factorizations. Springer, Heidelberg (2010). https://doi.org/10.1007/978-3-642-11492-2

    Book  MATH  Google Scholar 

  19. Li, Q.L., Fan, R.N.: Bike-Sharing Systems under Markovian Environment. arXiv preprint arXiv:1610.01302, pp. 1–44 (2016)

  20. Li, Q.L., Fan, R.N., Ma, J.Y.: A unified framework for analyzing closed queueing networks in bike sharing systems. In: Dudin, A., Gortsev, A., Nazarov, A., Yakupov, R. (eds.) ITMM 2016. CCIS, vol. 638, pp. 177–191. Springer, Cham (2016). https://doi.org/10.1007/978-3-319-44615-8_16

    Chapter  Google Scholar 

  21. Li, Q.L., Chen, C., Fan, R.N., Xu, L., Ma, J.Y.: queueing analysis of a large-scale bike sharing system through mean-field theory. arXiv preprint arXiv:1603.09560, pp. 1–51 (2016)

  22. Lucantoni, D.M.: New results on the single server queue with a batch markovian arrival process. Stoch. Models 7, 1–46 (1991)

    Article  MathSciNet  MATH  Google Scholar 

  23. Meddin, R., DeMaio, P.: The bike-sharing world map (2012). http://www.metrobike.net

  24. Neuts, M.F.: Structured Stochastic Matrices of M/G/1 Type and Their Applications. Marcel Decker Inc., New York (1989)

    MATH  Google Scholar 

  25. Neuts, M.F.: Matrix-analytic methods in the theory of queues. In: Dhashalow, J. (ed.) Advances in Queueing, pp. 265–292. CRC Press, Boca Raton (1995)

    Google Scholar 

  26. Onvural, R.O.: Survey of closed queueing networks with blocking. ACM Comput. Surv. 22, 83–121 (1990)

    Article  Google Scholar 

  27. Ramaswami, V.: The N/G/1 queue and its detailed analysis. Adv. Appl. Probab. 12, 222–261 (1980)

    Article  MathSciNet  MATH  Google Scholar 

  28. Raviv, T., Kolka, O.: Optimal inventory management of a bikesharing station. IIE Trans. 45, 1077–1093 (2013)

    Article  Google Scholar 

  29. Raviv, T., Tzur, M., Forma, I.A.: Static repositioning in a bike-sharing system: models and solution approaches. EURO J. Transp. Logistics 2, 187–229 (2013)

    Article  Google Scholar 

  30. Reiser, M., Kobayashi, H.: Queuing networks with multiple closed chains: theory and computational algorithms. IBM J. Res. Dev. 19, 283–294 (1975)

    Article  MathSciNet  MATH  Google Scholar 

  31. Reiser, M.: Mean-value analysis and convolution method for queue-dependent servers in closed queueing networks. Perform. Eval. 1, 7–18 (1981)

    Article  MathSciNet  MATH  Google Scholar 

  32. Schuijbroek, J., Hampshire, R., van Hoeve, W.J.: Inventory rebalancing and vehicle routing in bike-sharing systems. Technical report 2013–2, Tepper School of Business, Carnegie Mellon University, pp. 1–27 (2013)

    Google Scholar 

  33. Seneta, E.: Non-Negative Matrices and Markov Chains. Springer, New York (2006). https://doi.org/10.1007/0-387-32792-4

    MATH  Google Scholar 

  34. Serfozo, R.: Introduction to Stochastic Networks. Springer, New York (1999). https://doi.org/10.1007/978-1-4612-1482-3

    Book  MATH  Google Scholar 

  35. Shu, J., Chou, M.C., Liu, Q., Teo, C.P., Wang, I.L.: Models for effective deployment and redistribution of bicycles within public bicycle-sharing systems. Oper. Res. 61, 1346–1359 (2013)

    Article  MathSciNet  MATH  Google Scholar 

  36. Waserhole, A., Jost, V.: Vehicle sharing system pricing regulation: transit optimization of intractable queuing network. HAL Id: hal-00751744, pp. 1–20 (2012)

    Google Scholar 

  37. Waserhole, A., Jost, V.: Vehicle sharing system pricing regulation: a fluid approximation. HAL Id: hal-00727041, pp. 1–35 (2013)

    Google Scholar 

  38. Waserhole, A., Jost, V., Brauner, N.: Pricing techniques for self regulation in vehicle sharing systems. Electron. Notes Discrete Math. 41, 149–156 (2013)

    Article  Google Scholar 

  39. Waserhole, A., Jost, V.: Pricing in Vehicle Sharing Systems: Optimization in Queuing Networks with Product Forms. EURO J. Transp. Logistics 5, 293–320 (2016)

    Article  Google Scholar 

Download references

Acknowledgements

This work was supported in part by the National Natural Science Foundation of China under grant Nos. 71671158 and 71471160; and by the Natural Science Foundation of Hebei province under grant No. G2017203277.

Author information

Authors and Affiliations

  1. School of Economics and Management Sciences, Yanshan University, Qinhuangdao, 066004, China

    Quan-Lin Li, Rui-Na Fan & Zhi-Yong Qian

Authors
  1. Quan-Lin Li
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Rui-Na Fan
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. Zhi-Yong Qian
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Rui-Na Fan .

Editor information

Editors and Affiliations

  1. Konan University, Kobe, Japan

    Wuyi Yue

  2. Yanshan University, Qinhuangdao, China

    Quan-Lin Li

  3. Yanshan University, Qinhuangdao, China

    Shunfu Jin

  4. Yanshan University, Qinhuangdao, China

    Zhanyou Ma

Rights and permissions

Reprints and permissions

Copyright information

© 2017 Springer International Publishing AG

About this paper

Check for updates. Verify currency and authenticity via CrossMark

Cite this paper

Li, QL., Fan, RN., Qian, ZY. (2017). A Nonlinear Solution to Closed Queueing Networks for Bike Sharing Systems with Markovian Arrival Processes and Under an Irreducible Path Graph. In: Yue, W., Li, QL., Jin, S., Ma, Z. (eds) Queueing Theory and Network Applications. QTNA 2017. Lecture Notes in Computer Science(), vol 10591. Springer, Cham. https://doi.org/10.1007/978-3-319-68520-5_8

Download citation

  • DOI: https://doi.org/10.1007/978-3-319-68520-5_8

  • Published:

  • Publisher Name: Springer, Cham

  • Print ISBN: 978-3-319-68519-9

  • Online ISBN: 978-3-319-68520-5

  • eBook Packages: Computer ScienceComputer Science (R0)

Publish with us

Policies and ethics