Abstract
Matches between images are represented by partial permutations, which constitute the so-called Symmetric Inverse Semigroup. Synchronization of these matches is tantamount to joining them in multi-view correspondences while enforcing loop-closure constraints.
This paper proposes a novel solution for partial permutation synchronization based on a spectral decomposition. Experiments on both synthetic and real data shows that our technique returns accurate results in the presence of erroneous and missing matches, whereas a previous solution [12] gives accurate results only for total permutations.
You have full access to this open access chapter, Download conference paper PDF
Similar content being viewed by others
Keywords
1 Introduction
Consider a network of nodes where each node is characterized by an unknown state. Suppose that pairs of nodes can measure the ratio (or difference) between their states. The goal of synchronization [14] is to infer the unknown states from the pairwise measures. Typically, states are represented by elements of a group \(\varSigma \). Solving a synchronization problem can be seen as upgrading from relative (pairwise) information, which involves two nodes at a time, onto absolute (global) information, which involves all the nodes simultaneously. In practice, a solution is found by minimizing a suitable cost function which evaluates the consistency between the unknown states and the pairwise measures.
Several instances of synchronization have been studied in the literature, which correspond to different instantiations of \(\varSigma \) [2,3,4, 6,7,8,9, 13, 14, 17]. In particular, \(\varSigma ={\mathcal {S}}_d\) gives rise to permutation synchronization [12], where each state is an unknown permutation (i.e. reordering) of d objects. Permutation synchronization finds application in multi-image matching [5, 18], where a set of matches between pairs of images is computed through standard techniques (e.g. SIFT [11]), and the goal is to combine them in a global way so as to reduce the number of false matches and complete the matches with new ones retrieved indirectly via loop closure.
The authors of [12] derive an approximate solution based on a spectral decomposition, which is then projected onto \({\mathcal {S}}_d\). This method can effectively handle false matches, but it can not deal with missing matches (i.e. partial permutations), as confirmed by the experiments.
To overcome this drawback, we propose a novel method that extends [12] to the synchronization of partial permutations.
The paper is organized as follows. In Sect. 2 the concept of synchronization is formally defined, and it is shown that, if \(\varSigma \) admits a matrix representation, a solution can be obtained via spectral decomposition. In Sect. 3 the multi-view matching problem is introduced, and it is expressed as a synchronization problem. Section 4 reviews the spectral solution proposed in [12] for permutation synchronization, while Sect. 5 is devoted to explain our solution to partial permutation synchronization. Section 6 presents experiments on both synthetic and real data, and Sect. 7 draws the conclusion.
2 Synchronization
The goal of synchronization is to estimate elements of a group given a (redundant) set of measures of their ratios (or differences). Formally, let \(\varSigma \) be a group and let \(*\) denote its operation. Suppose that a set of measures \(z_{ij} \in \varSigma \) is known for some index pairs \((i,j) \subseteq \{1,\dots ,n \} \times \{ 1,\dots ,n \}\). The synchronization problem can be formulated as the problem of recovering \(x_i \in \varSigma \) for \(i=1,\dots ,n\) such that the following consistency constraint is satisfied
It is understood that the solution is defined up to a global (right) product with any group element, i.e., if \(x_i \in \varSigma \) satisfies (1) then also \( x_i*y\) satisfies (1) for any (fixed) \(y \in \varSigma \).
If the input measures are corrupted by noise, then the consistency constraint (1) will not be satisfied exactly, thus the goal is to recover the unknown elements \(x_i \in \varSigma \) such that a consistency error is minimized, which measures the violation of the consistency constraint, as shown in Fig. 1. If we assume that \(\varSigma \) is equipped with a metric function \(\delta : \varSigma \times \varSigma \rightarrow \mathbb {R}^{+}\), the consistency error can be defined as
Definition 1
An inverse semigroup \((\varSigma ,*)\) is a semigroup in which for all \(s \in \varSigma \) there exists an element \(t \in \varSigma \) such that \(s=s*t*s\) and \(t=t*s*t\). In this case, we write \(t = s^{-1}\) and call t the inverse of s. If \(\varSigma \) has an identity element \(1_{\varSigma }\) (i.e. it is a monoid), then it is called an inverse monoid.
Inverses in an inverse semigroup have many of the same properties as inverses in a group, e.g., \((a*b)^{-1} = b^{-1}*a^{-1}\) for all \(a,b \in \varSigma \).
We observe that the notion of synchronization can be extended to the case where \(\varSigma \) is an inverse monoid. In this case Eq. (1) still makes sense, with the provision that \(x_j^{-1}\) now denotes the inverse of \(x_j\) in the semigroup. Note that \(x_j^{-1}*x_j\) and \(x_j * x_j^{-1}\) are not necessarily equal to the identity. The solution to the synchronization problem in an inverse monoid is defined up to a global (right) product with any element \(y \in \varSigma \) such that \(y * y^{-1}=1_{\varSigma }=y^{-1}*y\).
2.1 Matrix Formulation
If \(\varSigma \) admits a matrix representation, i.e. \(\varSigma \) can be embedded in \(\mathbb {R}^{d \times d}\), then the synchronization problem can be expressed as an eigenvalue decomposition, resulting in an efficient and simple solution. Specifically, the unknown states are derived from the leading eigenvectors of a matrix constructed from the pairwise measures.
Suppose, e.g., that \(\varSigma \) is the orthogonal group of dimension d, i.e. \(\varSigma = O(d)\), which admits a matrix representation through orthogonal \(d \times d\) real matrices, where the group operation reduces to matrix multiplication, the inverse becomes matrix transposition and \(1_{\varSigma } = I_d\) (the \(d \times d\) identity matrix). Let \(X_i \in \mathbb {R}^{d \times d}\) and \(Z_{ij} \in \mathbb {R}^{d \times d}\) denote the matrix representations of \(x_{i} \in \varSigma \) and \(z_{ij} \in \varSigma \), respectively. Using this notation, Eq. (1) rewrites \(Z_{ij} = X_i X_j ^{\scriptscriptstyle \mathsf {T}}\).
Let us collect the unknown group elements and all the measures in two matrices \(X \in \mathbb R^{dn \times d}\) and \(Z \in \mathbb R^{dn \times dn}\) respectively, which are composed of \(d \times d\) blocks, namely
Thus the consistency constraint can be expressed in a compact matrix form as
Proposition 1
[14]. The columns of X are d (orthogonal) eigenvectors of Z corresponding to the eigenvalue n.
Proof
Since \(X^{{\scriptscriptstyle \mathsf {T}}} X = n I_d \) it follows that \(Z X = X X^{{\scriptscriptstyle \mathsf {T}}} X = n X \), which means that the columns of X are d eigenvectors of Z corresponding to the eigenvalue n.
Note that, since \(\text {rank}(Z) = d\) all the other eigenvalues are zero, so n is also the largest eigenvalue of Z. In the presence of noise, the eigenvectors of Z corresponding to the d largest eigenvalues can be seen as an estimate of X. Note that closure is not guaranteed, thus such solution must be projected onto \(\varSigma = O(d)\), e.g., via singular value decomposition.
This procedure was introduced in [14] for \( \varSigma = SO(2)\), extended in [1, 15] to \( \varSigma = SO(3)\), and further generalized in [2, 4] to \(\varSigma = SE(d).\) The same formulation appeared in [12] for \(\varSigma = {\mathcal {S}}_d\), which is a subgroup of O(d).
3 Problem Formulation
Consider a set of n nodes. A set of \(k_i\) objects out of d is attached to node i (we say that the node “sees” these \(k_i\) objects) in a random order, i.e., each node has its own local labeling of the objects with integers in the range \(\{1,\dots ,d\}\).
For example, with reference to Fig. 2, the same object is referred to as n. 5, e.g., in node A and as n. 3 in node B. Pairs of nodes can match these objects, establishing which objects are the same in the two nodes, despite the different naming. For example, a match means that the two nodes agree that “my object n. 5 is your object n. 3”. The goal is to infer a global labeling of the objects, such that the same object receives the same label in all the nodes.
A more concrete problem statement can be given in terms of feature matching, where nodes are images and objects are features. A set of matches between pairs of images is given, and the goal is to combine them in a multi-view matching, such that each feature has a unique label in all the images.
Each matching is a bijection between (different) subsets of objects, which is also known as partial permutation (if the subsets are improper then the permutation is total). Total and partial permutations admit a matrix representation through permutation and partial permutation matrices, respectively.
Definition 2
A matrix P is said to be a permutation matrix if exactly one entry in each row and column is equal to 1 and all other entries are 0. A matrix P is said to be a partial permutation matrix if it has at most one nonzero entry in each row and column, and these nonzero entries are all 1.
Specifically, the partial permutation matrix P representing the matching between node B and node A is constructed as follows: \([P]_{h,k}=1\) if object k in node B is matched with object h in node A; \([P]_{h,k}=0\) otherwise. If row \([P]_{h,\cdot }\) is a row of zeros, then object h in node A does not have a matching object in node B. If column \([P]_{\cdot ,k}\) is a column of zeros, then object k in node B does not have a matching object in node A.
The set of all \(d \times d\) permutation matrices forms a group with respect to matrix multiplication, where the inverse is matrix transposition, which is called the symmetric group \({\mathcal {S}}_d\). The set of all \(d \times d\) partial permutation matrices forms an inverse monoid with respect to the same operation, where the inverse is again matrix transposition, which is called the symmetric inverse semigroup \({\mathcal {I}}_d\).
Let \(P_{ij} \in {\mathcal {I}}_d\) denote the partial permutation representing the matching between node j and node i, and let \(P_i \in {\mathcal {I}}_d\) (resp. \(P_j \in {\mathcal {I}}_d\)) denote the unknown partial permutation that reveals the true identity of the objects in node i (resp. j). The matrix \(P_{ij}\) is called the relative permutation of the pair (i, j), and the matrix \(P_i\) (resp. \(P_j\)) is called the absolute permutation of node i (resp. j). It can be easily verified that
Thus the problem of finding the global labeling can be modeled as finding n absolute permutations, assuming that a set of relative permutations is known, where the link between relative and absolute permutations is given by Eq. (5).
If permutations were total, Eq. 5 would be recognized as the consistency constraint of a synchronization problem over \({\mathcal {S}}_d\) [12], and this will be reviewed in Sect. 4. However, in all practical settings, permutations are partial, thus in Sect. 5 we address the synchronization problem over the inverse monoid \({\mathcal {I}}_d\), as the main contribution of this paper.
4 Permutation Synchronization
Let us describe the synchronization problem over \(\varSigma = {\mathcal {S}}_d\) [12]. Since \({\mathcal {S}}_d\) is a subgroup of O(d), permutation synchronization can be addressed as explained in Sect. 2.1. Specifically, as done in Eq. (3), all the absolute/relative permutations are collected in two matrices \(X \in \mathbb {R}^{dn \times d}\) and \(Z \in \mathbb {R}^{dn \times dn}\) respectively, namely
where \(P_{ii} = P_i P_i ^{\scriptscriptstyle \mathsf {T}}= I_d\). Thus the consistency constraint becomes \(Z = X X^{{\scriptscriptstyle \mathsf {T}}}\) with Z of rank d, and the columns of X are d (orthogonal) eigenvectors of Z corresponding to the eigenvalue n, as stated by Proposition 1. In the presence of noise, the eigenvectors of Z corresponding to the d largest eigenvalues are computed.
We now explain the link between this spectral solution and the consistency error of the synchronization problem. Let us consider the following metric \( \delta (P,Q) = d - \text {trace} (P^{{\scriptscriptstyle \mathsf {T}}}Q) = d -\sum _{r,s=1}^d [P]_{r,s} [Q]_{r,s} \), which simply counts the number of objects differently assigned by permutations P and Q. Thus Eq. (2) rewrites
and hence the synchronization problem over \({\mathcal {S}}_d\) becomes equivalent to the following maximization problem
Solving (8) is computationally difficult since the feasible set is non-convex. A tractable approach consists in relaxing the constraints and considering the following optimization problem
which is a generalized Rayleigh problem, whose solution is given by the d leading eigenvectors of Z.
Since Problem (9) is a relaxed version of Problem (8), the solution U formed by eigenvectors is not guaranteed to be composed of permutation matrices. Thus each \(d \times d\) block in U is projected onto \({\mathcal {S}}_d\) via the Kuhn-Munkres algorithm [10]. As long as U is relatively close to the ground-truth X, this procedure works well, as confirmed by the experiments.
5 Partial Permutation Synchronization
Consider now the synchronization problem over \(\varSigma = {\mathcal {I}}_d\). Despite the group structure is missing, we show that a spectral solution can be derived in an analogous way, which can be seen as the extension of [12] to the case of partial permutations.
We define two block-matrices X and Z containing absolute and relative permutations respectively – as done in (6) – so that the consistency constraint becomes \(Z=X X^{{\scriptscriptstyle \mathsf {T}}}\) with Z of rank d. Note that here \(P_i \in {\mathcal {I}}_d\), thus the \(d \times d\) (diagonal) matrix \(P_{ii} = P_i P_i^{{\scriptscriptstyle \mathsf {T}}} \) is not equal, in general, to the identity, unless \(P_i \in {\mathcal {S}}_d\). Indeed, the (k, k)-entry in \(P_{ii}\) is equal to 1 if node i sees object k, and it is equal to 0 otherwise. When all the objects seen by node i are different from those seen by node j we have \( P_i P_j^{\scriptscriptstyle \mathsf {T}}=0\), resulting in a zero block in Z.
Proposition 2
The columns of X are d (orthogonal) eigenvectors of Z and the corresponding eigenvalues are given by the diagonal of \(V := \sum _{i=1}^n P_i^{{\scriptscriptstyle \mathsf {T}}} P_i\).
Proof
Define the \(d \times d \) diagonal matrix \(V:= X^{{\scriptscriptstyle \mathsf {T}}} X = \sum _{i=1}^n P_i^{{\scriptscriptstyle \mathsf {T}}} P_i\). Then \( Z X = X X^{{\scriptscriptstyle \mathsf {T}}} X = X V\) which is a spectral decomposition, i.e. the columns of X are d eigenvectors of Z and the corresponding eigenvalues are on the diagonal of V.
Although \({\mathcal {I}}_d\) is not a group, we have obtained an eigenvalue decomposition problem where the non-zero (and hence leading) eigenvalues are d integers contained in the diagonal of V. Specifically, the k-th eigenvalue counts how many nodes see object k. In the case of total permutations all the nodes see all the objects, thus \(V = n I_d \) and all the eigenvalues are equal, hence we get Proposition 1.
In the presence of noise, the eigenvectors of Z corresponding to the d largest eigenvalues, which are collected in a \(nd \times d\) matrix U, solve Problem (9) as in the case of total permutations.
Note that the reverse of Proposition 2 is not true, i.e., the matrix U is not necessarily equal (up to scale) to X. Indeed, a set of eigenvectors is uniquely determined (up to scale) only if the corresponding eigenvalues are distinct. However, when eigenvalues are repeated, the corresponding eigenvectors span a linear subspace, and hence any (orthogonal) basis for such a space is a solution. Note that all the eigenvalues are integer numbers lower or equal to n. Thus, when the number of objects is larger than the number of nodes (i.e., \(d>n\)) – which is likely to happen in practice – the eigenvalues are indeed repeated, therefore U is not uniquely determined.
So we have to face the problem of how to select, among the infinitely many Us, the one that resembles X, a matrix composed of partial permutations. Projecting each \(d \times d\) block of U onto \({\mathcal {I}}_d\) does not solve the problem, as confirmed by the experiments. A key observation is reported in the following proposition, suggesting that such a problem can be solved via clustering techniques.
Proposition 3
Let U be the \(nd \times d\) matrix composed by the d leading eigenvectors of Z; then U has \(d+1\) different rows (in the absence of noise).
Proof
Let \(\lambda _1, \lambda _2, \dots , \lambda _{\ell }\) denote all the distinct eigenvalues of Z (with \(\ell \le d\)), and let \(m_1, m_2, \dots , m_{\ell }\) be their multiplicities such that \(\sum _{k=1}^{\ell }m_k = d\). Let \(U_{\lambda _k}\) denote the \(m_k\) columns of U corresponding to the eigenvalue \(\lambda _k\), and let \(X_{\lambda _k}\) be the corresponding columns of X. Up to a permutation of the columns, we have
Since \(U_{\lambda _k}\) and \(X_{\lambda _k}\) are (orthogonal) eigenvectors corresponding to the same eigenvalue, there exists an orthogonal matrix \(Q_k \in \mathbb {R}^{m_k \times m_k}\) representing a change of basis in the eigenspace of \(\lambda _k\), such that \(U_{\lambda _k} = X_{\lambda _k} Q_k\). In matrix form this rewrites
where \(\text {blkdiag}(Q_1, Q_2, \dots , Q_{\ell })\) produces a \(d \times d\) block-diagonal matrix with blocks \(Q_1, Q_2, \dots , Q_{\ell }\) along the diagonal. Note that the rows of X are the rows of \(I_d\) plus the zero row. Since Q is invertible (hence injective), \(U = X Q \) has only \(d+1\) different rows as well.
In the presence of noise, we can cluster the rows of U with k-means into \(d+1\) clusters, and then assign the centroid which is closest to zero to the zero row, and arbitrarily assign each of the other d centroids to a row of \(I_d\). Recall that the solution to partial permutation synchronization is defined up to a global total permutation.
Note that, if we assign each row of U to the centroid of the corresponding cluster, then we may not obtain partial permutation matrices. Indeed, since there are no constraints in the clustering phase, it may happen that different rows of a \(d \times d\) block in U are assigned to the same cluster, resulting in more than one entry per column equal to 1. For this reason, for each \(d \times d\) block in U we compute a partial permutation matrix that best maps such block into the set of centroids via the Kuhn-Munkres algorithm [10], and such permutation is output as the sought solution.
Remark 1
As observed (e.g.) in [5], the multi-view matching problem can be seen as a graph clustering problem, where each cluster corresponds to one object (feature) out of d. The underlying graph is constructed as follows: each vertex represents a feature in an image, and edges encode the matches. Note that the matrix Z defined in (6) coincides with the adjacency matrix of such a graph. Our procedure first constructs a \(dn \times d\) matrix U from the d leading eigenvectors of Z, and then applies k-means to the rows of U. This coincides with solving the multi-view matching problem via spectral clustering applied to the adjacency matrix, rather than to the Laplacian matrix as customary.
6 Experiments
The proposed method – henceforth dubbed PartialSynch – was implemented in Matlab and compared to the solution of [12] (which will be referred to as TotalSynch Footnote 1), considering both simulated and real data.
In the synthetic experiments, performances have been measured in terms of precision (number of correct matches returned divided by the number of matches returned) and recall (number of correct matches returned divided by the number of correct matches that should have been returned). In order to provide a single figure of merit we computed the F-score (twice the product of precision and recall divided by their sum), which is a measure of accuracy and reaches its best value at 1. In the real experiments the number of matches that should have been returned is not known, hence only the precision could be computed.
For the synthetic case, a fixed number of \(d= 20\) objects was chosen, while the number of nodes varied from \(n=10\) to \(n=50\). The observation ratio, i.e., the probability that an object is seen in a node, decreased from 1 (that corresponds to total permutations) to 0.2. After generating ground-truth absolute permutations, pairwise matches were computed from Eq. (5). Then random errors were added to relative permutations by switching two matches, removing true matches or adding false ones. The input error rate, i.e., the ratio of mismatches, varied from 0 to 0.8. For each configuration the test was run 20 times and the mean F-score was computed. In order to evaluate a solution, the total permutation that best aligns the estimated absolute permutations onto ground-truth ones was computed with the Kuhn-Munkres algorithm.
Results are reported in Fig. 3, which shows the F-score for the two methods as a function of number of nodes, observation ratio and input error rate. In the case of total permutations (observation ratio = 1) both techniques perform well. Our method (PartialSynch) correctly recovers the absolute permutations even when not all the objects are seen in every node, and in the presence of high contamination. On the contrary, TotalSynch cannot deal with partial permutations, indeed its performances degrade quickly as the observation ratio decreases. In general, the accuracy increases with the number of nodes.
In the experiments with real data, the problem of feature matching across multiple images was considered. The Herz-Jesu-P8 and Fountain-P11 datasets [16] were chosen, which contain 8 and 11 images respectively. A set of features was detected with SIFT [11] in each image. Among them a subset was manually selected by looking at the tracks, with the aim of knowing the total number of objects (equal to \(d=30\)). Subsequently, correspondences between each image pair (i, j) were established using nearest neighbor and ratio test as in [11] and refined using RANSAC. The resulting relative permutations \(P_{ij}\) were given as input to the considered methods.
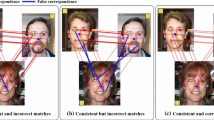
When evaluating the output, matches were considered correct if they lie within a given distance threshold (set equal to 0.01 times the image diagonal) from the corresponding epipolar lines, computed from the available ground-truth camera matrices. The precision achieved by the two methods on these sets is reported in Table 1, which confirm the outcome of the experiments on simulated data. For illustration purposes, Fig. 4 shows the results for some sample images.
7 Conclusion
In this paper we proposed a novel solution for partial permutation synchronization based on a spectral decomposition, that can be applied to multi-image matching. The method was evaluated through synthetic and real experiments, showing that it handles both false and missing matches, whereas [12] gives accurate results only for total permutations.
Notes
- 1.
The code is available at http://pages.cs.wisc.edu/~pachauri/perm-sync/.
References
Arie-Nachimson, M., Kovalsky, S.Z., Kemelmacher-Shlizerman, I., Singer, A., Basri, R.: Global motion estimation from point matches. In: Proceedings of the Joint 3DIM/3DPVT Conference: 3D Imaging, Modeling, Processing, Visualization and Transmission (2012)
Arrigoni, F., Rossi, B., Fusiello, A.: Spectral synchronization of multiple views in SE(3). SIAM J. Imaging Sci. 9(4), 1963–1990 (2016)
Arrigoni, F., Fusiello, A., Rossi, B.: Camera motion from group synchronization. In: Proceedings of the International Conference on 3D Vision (3DV). IEEE (2016)
Bernard, F., Thunberg, J., Gemmar, P., Hertel, F., Husch, A., Goncalves, J.: A solution for multi-alignment by transformation synchronisation. In: Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition (2015)
Chen, Y., Guibas, L., Huang, Q.: Near-optimal joint object matching via convex relaxation. In: Proceedings of the International Conference on Machine Learning, pp. 100–108 (2014)
Cucuringu, M.: Synchronization over \(Z_2\) and community detection in signed multiplex networks with constraints. J. Complex Netw. 3(3), 469–506 (2015)
Giridhar, A., Kumar, P.: Distributed clock synchronization over wireless networks: algorithms and analysis. In: Proceedings of the IEEE Conference on Decision and Control, pp. 4915–4920 (2006)
Govindu, V.M.: Lie-algebraic averaging for globally consistent motion estimation. In: Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, pp. 684–691 (2004)
Hartley, R., Trumpf, J., Dai, Y., Li, H.: Rotation averaging. Int. J. Comput. Vis. 103(3), 267–305 (2013)
Kuhn, H.W.: The Hungarian method for the assignment problem. Naval Res. Logist. Q. 2(2), 83–97 (1955)
Lowe, D.G.: Distinctive image features from scale-invariant keypoints. Int. J. Comput. Vis. 60(2), 91–110 (2004)
Pachauri, D., Kondor, R., Singh, V.: Solving the multi-way matching problem by permutation synchronization. In: Advances in Neural Information Processing Systems, vol. 26, pp. 1860–1868 (2013)
Schroeder, P., Bartoli, A., Georgel, P., Navab, N.: Closed-form solutions to multiple-view homography estimation. In: 2011 IEEE Workshop on Applications of Computer Vision (WACV), pp. 650–657, January 2011
Singer, A.: Angular synchronization by eigenvectors and semidefinite programming. Appl. Comput. Harmon. Anal. 30(1), 20–36 (2011)
Singer, A., Shkolnisky, Y.: Three-dimensional structure determination from common lines in cryo-EM by eigenvectors and semidefinite programming. SIAM J. Imaging Sci. 4(2), 543–572 (2011)
Strecha, C., von Hansen, W., Gool, L.J.V., Fua, P., Thoennessen, U.: On benchmarking camera calibration and multi-view stereo for high resolution imagery. In: Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition (2008)
Wang, L., Singer, A.: Exact and stable recovery of rotations for robust synchronization. Inf. Inference: J. IMA 2(2), 145–193 (2013)
Zhou, X., Zhu, M., Daniilidis, K.: Multi-image matching via fast alternating minimization. In: Proceedings of the International Conference on Computer Vision, pp. 4032–4040 (2015)
Author information
Authors and Affiliations
Corresponding author
Editor information
Editors and Affiliations
Rights and permissions
Copyright information
© 2017 Springer International Publishing AG
About this paper
Cite this paper
Arrigoni, F., Maset, E., Fusiello, A. (2017). Synchronization in the Symmetric Inverse Semigroup. In: Battiato, S., Gallo, G., Schettini, R., Stanco, F. (eds) Image Analysis and Processing - ICIAP 2017 . ICIAP 2017. Lecture Notes in Computer Science(), vol 10485. Springer, Cham. https://doi.org/10.1007/978-3-319-68548-9_7
Download citation
DOI: https://doi.org/10.1007/978-3-319-68548-9_7
Published:
Publisher Name: Springer, Cham
Print ISBN: 978-3-319-68547-2
Online ISBN: 978-3-319-68548-9
eBook Packages: Computer ScienceComputer Science (R0)