Abstract
Leveraging on recent advances in robust matrix decomposition, we revisit Lambertian photometric stereo as a robust low-rank matrix recovery problem with both missing and corrupted entries, tailoring Grasta and R-GoDec to normal surface estimation. A method to automatically detect shadows is proposed. The performance of different robust matrix completion techniques are analyzed on the challenging DiLiGenT datasets.
You have full access to this open access chapter, Download conference paper PDF
Similar content being viewed by others
Keywords
1 Introduction
Robust matrix decomposition and completion has been an active research topic in recent years, and many methods exploiting low rank and sparsity constraints have sprouted out in several fields of applications, such as pattern recognition, machine learning, and signal processing just to name a few. In this work, we explore the performances of these techniques on calibrated Lambertian photometric stereo [9], i.e. the problem of estimating the surface normals of an object by observing several intensity images captured by a fixed camera under different known lighting conditions. In particular, we offer an overview on robust matrix decomposition methods tailored to photometric stereo – using for the fist time Grasta and R-GoDec for this scope – and a quantitative experimental evaluation on the recently proposed DiLiGenT dataset. A simple yet effective shadow detection method is also presented.
Notation: Matrix will be indicated in sans serif font \(\mathsf {A}=[a^i_j]\), the i-th row of \(\mathsf {A}\) is denoted by \(\mathsf {A}^i\), while the j-th column of \(\mathsf {A}\) is indicated by \(\mathsf {A}_j\).
2 The Geometry of Single-Light Images
Let \(I\in \mathbb {R}^p\) be an image composed by p pixels stacked by column. Following [3], under Lambertian assumption the proprieties of interest of an object Y can be encoded in matrix form as \( \text {diag}(R)\mathsf {N}^\top \in \mathbb {R}^{p\times 3}\), where \(R=(\rho _1,\ldots ,\rho _p)^\top \) is the vector of pixels albedos, and \(\mathsf {N}=[\mathsf {N}_1,\ldots , \mathsf {N}_p] \in \mathbb {R}^{3\times p}\) collects the unitary normals of the object. Thus the image of Y illuminated by a distant point-light source \(L\in \mathbb {R}^3\), is given by:
Varying L, one obtains the so-called illumination space of Y defined as \(\mathcal {L}=\{I : I=\text {diag}(R)\mathsf {N}L :L\in \mathbb {R}^3\} \subset \mathbb {R}^p\). Clearly \(\dim (\mathcal {L})=\text {rank}(\mathsf {N}^\top L)\le 3 \), therefore, if the normals span \(\mathbb {R}^3\), the dimension of \(\mathcal {L}\) is 3.
Belhumeur and Kriegman also observe that \(\mathcal {L}\) intersect at mostFootnote 1 \(p(p-1)+2\) orthants of \(\mathbb {R}^p\). Let \(\mathcal {L}_0 = \mathcal {L}\cap \mathbb {R}^{p}_+\), where \(\mathbb {R}^{p}_+=\{x\in \mathbb {R}^p :x_i>0\, \forall i \}\), and \(\mathcal {L}_i\) be the intersection of \(\mathcal {L}\) with the other orthants. By construction, \(\mathcal {L}_i\) are convex cones, and correspond to different shading configuration of pixels. As instance, \(\mathcal {L}_0\) corresponds to images having all the pixels illuminated by a lighting source. The space of all possible images of Y is obtained by adding to \(\mathcal {L}_0\) the images where not all the pixels are simultaneously illuminated, i.e. the projection of the cones \(\mathcal {L}_i\), \(i\ne 0\), on the boundary of \(\mathbb {R}^p_+\) via the map \(P:I\mapsto \max (I,0)\). Therefore, the space of all the images of a convex Lambertian object, varying the direction of a single light source is given by the union of at most \(p(p-1)+2\) convex cones.
Experimentally, it was demonstrated that this union of cones is “flat” and can be approximated by a linear subspace of dimension 3.
3 Robust Matrix Completion and Decomposition
The linear property of light superposition inspired the use of matrix completion and robust decomposition techniques to tackle the photometric stereo problem [10, 11]. Given f images of the same object organized as a \(p\times f\) matrix \(\mathsf {X}=[I_1,\ldots , I_f]\), with images stacked as columns, the main intuition is to recover the illumination space as a low-rank matrix \(\mathsf {A}\) that models the diffusive Lambertian observations, and to handle the non-Lambertian measurements as outliers. In particular, shadows, i.e. pixels outside \(\mathcal {L}_0\), are treated as missing entries, whereas a sparse error matrix \(\mathsf {S}\) accounts for the corruptions produced by strong specularities (highlights).
More formally, the image formation model can be rephrased as
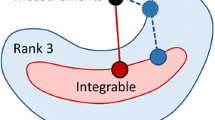
where \(\mathsf {A}= \text {diag}(R) \mathsf {N}^\top \mathsf {L}\) is low rank, \(\mathsf {L}=[\mathsf {L}_1,\ldots , \mathsf {L}_f]\) collects the known light source vectors, \(\varOmega = \{(i,j) :\text { where } \mathsf {N}^\top \mathsf {L}\text { is nonzero}\}\) is the set of observed entries, \(P_\varOmega \) indicates a linear projection of matrices defined component-wise as \([P_\varOmega (\mathsf {A})]^i_j= \mathsf {A}^i_j\) if \((i,j)\in \varOmega \) and 0 otherwise, and \(\mathsf {S}\) is the matrix of sparse error. A graphical representation of this model is depicted in Fig. 1, where the operator \(P_\varOmega \) – which is the matrix counterpart of the projection P onto the positive orthant – is represented in an equivalent fashion as the Hadamard (element-wise) product between \(\mathsf {A}\) and a matrix \(\mathsf {V}\) defined component-wise as
In this way, photometric stereo becomes the problem of recovering a low-rank matrix with both missing entries – the shadows – and corrupted entries corresponding the unmodelled phenomena (e.g., non Lambertian). The rank of \(\mathsf {A}\) may vary according to the image formation model adopted, and for Lambertian photometric stereo \(\text {rank}(\mathsf {A})=3\). Once the low rank matrix have been recovered, in the calibrated scenario, the normals can be easily estimated in closed form by normalizing the row of \(\mathsf {L}^{+} \mathsf {A}\), where \(\mathsf {L}^{+}\) denotes the pseudo-inverse of \(\mathsf {L}\).
Decomposition into low-rank and sparse matrices has been developed in different formulation problems, hereinafter, we briefly review some of them that can be profitably adopted to tackle the Problem (3), namely: Robust Principal Component Analysis and L1-ALM (that have already been tailored to photometric stereo problem), together with Grasta and R-GoDec that we are going to apply to this scenario for the first time.
Robust Principal Component Analysis (RPCA) decomposes \(\mathsf {X}\) into a low rank and sparse terms, without being given rank\((\mathsf {A})\). The cost function is:
Unfortunately this problem turns to be intractable, therefore, instead of directly minimizing the discontinuous rank function and the \(\ell _0\) norm, the above objective function is relaxed to its convex surrogate; the rank of \(\mathsf {A}\) is replaced with the nuclear norm \(\Vert \mathsf {A}\Vert _*\) – i.e. the sum of the singular values of \(\mathsf {A}\) – and the \(\ell _0\) norm is substituted for the \(\ell _1\) norm:
Several technique can be used to minimize Eq. (6); in [10], e.g., an adaptation of the augmented Lagrange multiplier method is used.
L1-ALM [11] proposes to find a solution to Problem (3) by enforcing exactly the low rank constraint \(\text {rank}(\mathsf {A})=r\), and leverages on the factorization of the matrix \(\mathsf {A}= \mathsf {H}\mathsf {K}\) as the product of a \(p\times r\) matrix \(\mathsf {H}\) and a \(r\times f\) matrix \(\mathsf {K}\). As the factorization is defined up to an invertible matrix, in order to shrink the solution space, the matrix \(\mathsf {H}\) is enforced to be column-orthogonal, i.e. \(\mathsf {H}^\top \mathsf {H}=\mathsf {I}_r\), where \(\mathsf {I}_r\) denotes the \(r\times r\) identity matrix. The objective L1-ALM tries to minimize is
where \(P_\varOmega (\mathsf {X}-\mathsf {H}\mathsf {K})\) is the \(\ell _1\) norm of the sparse error matrix \(\mathsf {S}= \mathsf {X}- P_\varOmega (\mathsf {A}) \) and \( \Vert \mathsf {K} \Vert _*= \Vert \mathsf {H}\mathsf {K} \Vert _*= \Vert \mathsf {A} \Vert _*\) is a trace-norm regularization term, which, due to the orthogonality of \(\mathsf {H}\), is equivalent to the nuclear norm of \(\mathsf {A}\). This optimization problem is resolved via inexact augmented Lagrange multiplier and Gauss-Seidel iterations.
Grassmannian Robust Adaptive Subspace Tracking Algorithm (Grasta) [5] is an online robust subspace tracking algorithm, that works in the presence of corrupted and missing data. Given a sequence of incomplete vectors \(\{v_1,\ldots , v_t\}\) that lie on a r-dimensional subspace, Grasta estimates this subspace, by minimizing the \(\ell _1\) error between the recovered subspace and the observed partial vector. This formulation can be casted to the problem of Eq. (3) as
where, similarly to Eq. (7), \(\mathsf {A}\) is expressed as the product of two factors \( \mathsf {H},\mathsf {K}\), the first being an element of the Grassmanian Manifold G(r, p). The problem is iteratively solved for \(\mathsf {H}\) and \(\mathsf {K}\) separately: fixed \(\mathsf {H}\), \(\mathsf {K}\) is update via ADMM, whereas, when \(\mathsf {K}\) is fixed, \(\mathsf {H}\) is updated performing incremental gradient descent on the Grassmanian manifold. Even if the partial measurements of the matrix \(\mathsf {X}\) are required to be exactly fixed, nevertheless, in practice, it was demonstrated that the algorithm is robust to small non sparse additive noise.
Robust Go Decomposition (R-GoDec) [2] proposes a robust approximate matrix completion and decomposition technique that improves GoDec [12]. An additional sparse term \(\mathsf {S}'\) that has support on \(\varOmega ^{C}\) – the complementary of \(\varOmega \) – is introduced to account for missing entries. In addition small sparse noise \(\mathsf {E}\) is explicitly introduced in the decomposition:
The corresponding minimization problem is
such that rank\((\mathsf {A})\le r\), \(\mathsf {S}\) is sparse and \(\mathsf {S}'\) has support in \(\varOmega ^{C}\). This problem is solved using a block-coordinate minimization scheme. At first, the rank-r projection of the incomplete matrix given in input is computed through Bilateral Random Projection – faster than SVD – and assigned to \(\mathsf {A}\). Then, the two sparse terms \(\mathsf {S}\) and \(\mathsf {S}'\) are updated separately. The outlier term \(\mathsf {S}\) is computed via soft-thresholding operator, and \(\mathsf {S}'\) is updated as \(-P_{\varOmega ^C}(\mathsf {A})\).
4 Detecting Shadows
This section is aimed at estimating the set \(\varOmega ^C\) of shadowed pixels, in order to treat them as missing data and to reduce their influence in the low-rank matrix recovery. For this purpose, it becomes necessary to reason about the visibility of light source with respect to each image pixel in order to recognize which lights shine on which points and to discard the pixels in shadow.
To this end, a commonly employed solution is intensity-based thresholding: Pixels whose intensity lies below a certain threshold are considered in shadow. While this heuristic in some cases is enough to recover the light-visibility information, in general, the intensity of individual pixels depends on the variations of the unknown albedo of the object, thus, the brightness alone turns to be an unreliable cue.
In order to overcome this pitfall, other techniques have been proposed. For example, [4] adopts a graph cuts based method to estimate light visibility in a Markov Random Field formulation, where a per-pixels error, based on photometric stereo, is balanced by a smoothness constraints on shadows, aimed at promoting spatial coherence. Sunkavalli et al. in [8] avoid to enforce spatial coherence on shadows and present a method that works both in the calibrated and uncalibrated scenario leveraging on subspace clustering. Pixels sharing the same visibility configuration lie on linear subspaces, termed visibility subspaces, that are extracted using Sequential Ransac. Once these subspaces are recovered and the object surface is segmented accordingly, the set of lights that shine on each region are identified analysing the magnitude of the subspace lighting obtained via SVD.
The visibility information can be encoded in the \(n\times f\) visibility matrix \(\mathsf {V}\) defined as in Eq. (4). Each row of \(\mathsf {V}\) can be seen as the indicator function of the subset of lights visible by each pixel.
In our calibrated scenario, we want to recover \(\mathsf {V}\) given the intensity matrix \(\mathsf {X}\) and the lighting directions \(\mathsf {L}\). To this end, assuming that there are at leas \(f\ge 4\) images, we propose a simple approach based on Lmeds [6].
The main idea is to approximate at first the space of the possible visibility configuration by randomly sampling triplets \(\omega \) of lights. Fixed a pixel i, a tentative normal vector is estimated via least square regression for every lighting triplets. Hence, the normal \(\widehat{\mathsf {N}}_i\) which minimise the median of squared residuals is retained as a solution. By scrutinising the residual vector \(I^i - \max (0, \widehat{\mathsf {N}}_i^\top \mathsf {L})\), a binary weighting vector \(w_i\) is defined setting its j-th entry equals 1, if the j-th error is smaller of \(2.5\hat{\sigma }\), and 0 otherwise, where \(\hat{\sigma }\) is a robust estimate of the variance of the per pixels residuals defined by:
At the end, the normal estimate \(\widehat{N}_i\) is refined using iteratively reweighted least squares (IRLS) on the set of lights \(\{\mathsf {L}_j:w_i^j=1\}\).
The matrix \(\mathsf {W}=[w_1,\ldots , w_p]^\top \), composed by the weight-vectors arranged by row, could be used as a proxy for the visibility matrix, however here we take light directions into account, and we obtain a visibility matrix \(\widehat{\mathsf {V}}\) setting:
5 Evaluation the DiLiGenT Dataset
The methods presented in the previous section are here challenged on the Directional Lightings, objects of General reflectance, and ground Truth shapes datasets (DiLiGenT) [7], a recently proposed benchmark of ten objects shown in Fig. 2.
This collection offers a great variety in terms of materials, appearances, geometries and type of deviations from the Lambertian model – from sparse specular spikes to broad specular lobes. This miscellany of non-diffusive phenomena can be captured analyzing the behavior of the index
with respect to \(\tau \) which represents the smallest number such that the fraction of information discarded by the corresponding rank approximation is less than a threshold \(\tau \): the last three objects are the ones that deviates more from the rank-3 Lambertian approximation.
Visibility Mask. Sample results attained by this method on the DiLiGenT dataset are shown in Fig. 3, where it can be appreciated that \(\widehat{\mathsf {V}}\) well approximates the ground truth visibility – computed as in Eq. 4 using the ground truth normals. As a reference, we also compare the Lmeds approach with the one based on visibility subspace [8]. Some differences can be pointed out. First, the extraction of visibility subspaces requires two parameters, namely the inlier threshold of Ransac and a threshold on the magnitude of light. The inlier threshold is not always an educated guess, as the subspace estimation may be strained by the presence of highlighted pixels whose intensity profiles follow a different distribution with respect to shadowed points. Lmeds, on the contrary, is parameter-free and avoids this difficulties.
Second, Lmeds estimates the visibility configuration locally per pixels, visibility subspace, on the other hand, are estimated globally and pixels that lie in the intersections of multiple subspaces are not properly handled. Third, the random sampling performed to extract the visibility subspace acts on pixels, therefore the dimension of possible samples is \(\left( {\begin{array}{c}p\\ 3\end{array}}\right) \), which, as usually \(p> f\) is higher than the upper bound on the number of samples of Lmeds \(\left( {\begin{array}{c}f\\ 3\end{array}}\right) \). Finally, Lmeds procedure can be parallelized in a straightforward way.
The visibility masks estimated by Lmeds are fed to the matrix completion algorithms to reduce the influence of shadowed pixels on the low rank estimation step.
Normal Estimation. We randomly chose 9 different lighting configurations for each dataset, and we compare the estimated normals with the ground truth ones, averaging the results on 10 trials per dataset. The rank was fixed to 3 for Grasta and R-GoDec, and the regualarization parameter to \(\lambda = 1/\sqrt{p}\), whereas for L1-ALM we used \(\lambda = 10^{-3}\) as suggested in the authors implementation [1]. The performances of the matrix factorization methods are recorded in Table 1 where the mean, the median and the standard deviation of angular errors were reported for each method. As a reference we also detailed the errors attained by Least Square and Lmeds. When the accuracy of a method is worse than Least Square, we colored the corresponding cell with gray. Other colors are used to highlights the best results achieving the minimum error.
Grasta performed well on those datasets that manifest a clear diffusive component corrupted by local and sparse non-Lamberitan effects, whereas it worsened the results of Least Square estimation with respect to the last three sequences.
On the contrary RPCA achieved less accurate results on the first sequences and performed better on those challenging datasets characterized by board specularity and complex BRDF (pot2, goblet,cow and harvest have a metal appearance). R-GoDec behavior is similar to Grasta as can be sensed, looking at Fig. 4 – where the mean angular error is plotted for each sequence of the dataset.
Sample results of attained normals are shown in Fig. 5. One can also note that Lmeds always improved the performance of LS.
Regularization Parameter. We recall that \(\lambda \) is a weighting parameter that is used by L1-ALM, R-GoDec and RPCA to balance between the low-rank and the sparsity terms. In all the above experiments, this parameter was fixed. However, with better choice, it is possible to correct larger amount of outliers, enhancing the performance of the algorithms. Here we demonstrated the effect of \(\lambda \) on L1-ALM, R-GoDec and RPCA with respect to different number of input images we performed normal estimation on 4, 6, 12, 18, 24, 30, 36 randomly drawn images using \(C \frac{1}{\sqrt{p}}\) with \(C\in \{0.05,0.1,0.2,0.4,0.8,1, 1.2,1.4,1.6\}\). The corresponding mean angular errors are shown in Fig. 6, where it can be appreciated that L1-ALM and R-Godec benefit of the prior knowledge of rank being less sensitive to the number of images and the choice of \(\lambda \). The minimum mean angular error per each datasets are reported in Table 2, where, for completeness, we also added the performance of Grasta varying only the number of images (\(\lambda \) is not required).
Distribution of Light Directions. In this experiment, we studied the effects of the distribution of light sources. We considered three different light configurations depicted in Fig. 7b: (A) 9 lights are randomly selected; (B) we choose a central light and the reaming 8 are those maximizing their distance from it; (C) we select 9 neighboring light sources. We run all the methods on the ball dataset, which is the only convex object and therefore results are less affected by the actual light orientations.
The summary of the experiment is that Grasta and R-GoDec preferred random and spread distribution, whereas RPCA and L1-ALM take advantage of the redundancy provided by the dense configuration.
6 Conclusion
In this work, we tackle the problem of photometric stereo leveraging on robust matrix factorization techniques. We showed that the proposed shadow estimation based on Lmeds is able to produce accurate results, that, in turn, can be profitably fed to matrix completion algorithms. Experiments on a challenging datasets demonstrate that, if the object of interest is mostly Lambertian with strong and sparse non diffusive phenomena, it is advisable to adopt matrix approximation method with fixed rank. In this situation Grasta, followed by R-GoDec, performs better than L1-ALM. On the other side, if one is interested in recovering the normals of a surface that does not exhibit a strong diffusive behavior, all the methods suffer of low precision, but RPCA attains the more accurate results.
Notes
- 1.
More precisely, \(\mathcal {L}\) intersects \(\nu (\nu -1)+2\) orthants, where \(\nu \) is the number of distinct normal in B.
References
https://sites.google.com/site/yinqiangzheng/home/RegL1-ALM.zip?attredirects=0
Arrigoni, F., Magri, L., Rossi, B., Fragneto, P., Fusiello, A.: Robust absolute rotation estimation via low-rank and sparse matrix decomposition. In: 2014 2nd International Conference on 3D Vision (3DV), vol. 1, pp. 491–498. IEEE (2014)
Belhumeur, P.N., Kriegman, D.J.: What is the set of images of an object under all possible illumination conditions? Int. J. Comput. Vis. 28(3), 245–260 (1998)
Chandraker, M., Agarwal, S., Kriegman, D.: ShadowCuts: photometric stereo with shadows. In: IEEE Conference on Computer Vision and Pattern Recognition CVPR 2007, pp. 1–8. IEEE (2007)
He, J., Balzano, L., Szlam, A.: Incremental gradient on the grassmannian for online foreground and background separation in subsampled video. In: 2012 IEEE Conference on Computer Vision and Pattern Recognition (CVPR), pp. 1568–1575. IEEE (2012)
Leroy, A.M., Rousseeuw, P.J.: Robust Regression and Outlier Detection. Wiley Series in Probability and Mathematical Statistics. Wiley, New York (1987)
Shi, B., Wu, Z., Mo, Z., Duan, D., Yeung, S.K., Tan, P.: A benchmark dataset and evaluation for non-Lambertian and uncalibrated photometric stereo. In: The IEEE Conference on Computer Vision and Pattern Recognition (CVPR), June 2016
Sunkavalli, K., Zickler, T., Pfister, H.: Visibility subspaces: uncalibrated photometric stereo with shadows. In: Daniilidis, K., Maragos, P., Paragios, N. (eds.) ECCV 2010 Part II. LNCS, vol. 6312, pp. 251–264. Springer, Heidelberg (2010). doi:10.1007/978-3-642-15552-9_19
Woodham, R.J.: Photometric method for determining surface orientation from multiple images. Opt. Eng. 19(1), 191139 (1980). http://dx.doi.org/10.1117/12.7972479
Wu, L., Ganesh, A., Shi, B., Matsushita, Y., Wang, Y., Ma, Y.: Robust photometric stereo via low-rank matrix completion and recovery. In: Kimmel, R., Klette, R., Sugimoto, A. (eds.) ACCV 2010 Part III. LNCS, vol. 6494, pp. 703–717. Springer, Heidelberg (2011). doi:10.1007/978-3-642-19318-7_55
Zheng, Y., Liu, G., Sugimoto, S., Yan, S., Okutomi, M.: Practical low-rank matrix approximation under robust L1-norm. In: 2012 IEEE Conference on Computer Vision and Pattern Recognition (CVPR), pp. 1410–1417. IEEE (2012)
Zhou, T., Tao, D.: GoDec: randomized low-rank & sparse matrix decomposition in noisy case. In: Getoor, L., Scheffer, T. (eds.) Proceedings of the 28th International Conference on Machine Learning (ICML 2011), NY, USA, pp. 33–40. ACM, New York, June 2011
Author information
Authors and Affiliations
Corresponding author
Editor information
Editors and Affiliations
Rights and permissions
Copyright information
© 2017 Springer International Publishing AG
About this paper
Cite this paper
Magri, L., Toldo, R., Castellani, U., Fusiello, A. (2017). A Matrix Decomposition Perspective on Calibrated Photometric Stereo. In: Battiato, S., Gallo, G., Schettini, R., Stanco, F. (eds) Image Analysis and Processing - ICIAP 2017 . ICIAP 2017. Lecture Notes in Computer Science(), vol 10484. Springer, Cham. https://doi.org/10.1007/978-3-319-68560-1_45
Download citation
DOI: https://doi.org/10.1007/978-3-319-68560-1_45
Published:
Publisher Name: Springer, Cham
Print ISBN: 978-3-319-68559-5
Online ISBN: 978-3-319-68560-1
eBook Packages: Computer ScienceComputer Science (R0)