Abstract
In general, the ‘small sample (n)-large feature ( )’ problem of bioinformatics, image analysis, high throughput molecular screening, astronomy, and other high dimensional applications makes the features highly collinear. In this context, the paper presents a new feature extraction algorithm to address this ‘large
)’ problem of bioinformatics, image analysis, high throughput molecular screening, astronomy, and other high dimensional applications makes the features highly collinear. In this context, the paper presents a new feature extraction algorithm to address this ‘large  small n’ issue associated with multimodal data sets. The proposed algorithm judiciously integrates the concept of both regularization and shrinkage with canonical correlation analysis to extract important features. To deal with the singularity problem, the proposed method increases the diagonal elements of covariance matrices by using regularization parameters, while the off-diagonal elements are decreased by shrinkage coefficients. The concept of hypercuboid equivalence partition matrix of rough hypercuboid approach is used to compute both significance and relevance measures of a feature. The importance of the proposed algorithm over other existing methods is established extensively on real life multimodal omics data set.
small n’ issue associated with multimodal data sets. The proposed algorithm judiciously integrates the concept of both regularization and shrinkage with canonical correlation analysis to extract important features. To deal with the singularity problem, the proposed method increases the diagonal elements of covariance matrices by using regularization parameters, while the off-diagonal elements are decreased by shrinkage coefficients. The concept of hypercuboid equivalence partition matrix of rough hypercuboid approach is used to compute both significance and relevance measures of a feature. The importance of the proposed algorithm over other existing methods is established extensively on real life multimodal omics data set.
This work is partially supported by the Department of Electronics and Information Technology, Government of India PhD-MLA/4(90)/2015-16).
You have full access to this open access chapter, Download conference paper PDF
Similar content being viewed by others
1 Introduction
Unimodal based pattern recognition and analysis systems usually provide low level of performance due to the noisy nature and drastic variation of the acquired signals, which lead to inaccurate and insufficient pattern representation of the perception of interest. On the other hand, multimodal data contains more information, which is expected to provide potentially more discriminatory and complete description of the intrinsic characteristics of the pattern, which leads to improve system performance than single modality only [5].
Canonical correlation analysis (CCA) [4] finds the best linear transformation to achieve the maximum correlation between two multidimensional data sets. The modern technology has enabled more directions on data streams, which ensues in very high dimensional feature spaces ( ), while the number of training samples (n) is usually limited. When the number of samples (n) is very less than the number of features (
), while the number of training samples (n) is usually limited. When the number of samples (n) is very less than the number of features ( ), the features in both data sets tend to be highly collinear, which leads to ill-conditioned of the covariance matrices of the data sets. In effect, their inverses are no longer reliable, resulting in an invalid computation of CCA. There are two ways to overcome this problem. The first possible approach is regularized CCA (RCCA) [11], where the diagonal elements of covariance matrices are increased using a grid search optimization. However, the off-diagonal elements of these matrices remain constant. The another method of regularization algorithm is based on the optimal estimate of the correlation matrices and is known as fast RCCA (FRCCA) [1]. In FRCCA, shrinkage coefficients [10] are estimated to invert the covariance matrices. These shrinkage coefficients reduce the values of off-diagonal elements of covariance matrices, while the values of diagonal elements remain same. However, CCA, RCCA and FRCCA all are unsupervised in nature and fail to take complete advantage of available class label information [1, 2]. To incorporate the class information, some supervised versions of RCCA have been proposed, termed as supervised RCCA (SRCCA) [2]. It includes available class label information to select maximally correlated features using grid search optimization.
), the features in both data sets tend to be highly collinear, which leads to ill-conditioned of the covariance matrices of the data sets. In effect, their inverses are no longer reliable, resulting in an invalid computation of CCA. There are two ways to overcome this problem. The first possible approach is regularized CCA (RCCA) [11], where the diagonal elements of covariance matrices are increased using a grid search optimization. However, the off-diagonal elements of these matrices remain constant. The another method of regularization algorithm is based on the optimal estimate of the correlation matrices and is known as fast RCCA (FRCCA) [1]. In FRCCA, shrinkage coefficients [10] are estimated to invert the covariance matrices. These shrinkage coefficients reduce the values of off-diagonal elements of covariance matrices, while the values of diagonal elements remain same. However, CCA, RCCA and FRCCA all are unsupervised in nature and fail to take complete advantage of available class label information [1, 2]. To incorporate the class information, some supervised versions of RCCA have been proposed, termed as supervised RCCA (SRCCA) [2]. It includes available class label information to select maximally correlated features using grid search optimization.
One of the main problems in omics data analysis is uncertainty. Rough set theory [9] is an effective paradigm to deal with uncertainty, vagueness, and incompleteness. It provides a mathematical framework to capture uncertainties associated with the data [9]. In this context, a feature extraction algorithm, termed as CuRSaR [7], has been introduced. It judiciously integrates the merits of SRCCA and rough sets, to extract maximally correlated features from two multidimensional data sets. In [8], another method, named as FaRoC, has been proposed to generate canonical variables sequentially using rough hypercuboid based maximum relevance-maximum significance criterion. However, all these existing methods fail to produce the optimal set of features.
In general, RCCA increases the diagonal elements, whereas FRCCA decreases the off-diagonal elements to deal with the singularity issue of covariance matrices. So, it is expected to give better results if both can be done concurrently. In this regard, the paper presents a new feature extraction algorithm, which integrates the advantages of both RCCA and FRCCA to handle the ill-conditioned of the covariance matrices. The effectiveness of the proposed method, along with a comparison with other methods, is demonstrated on several real life data sets.
2 Basics of Canonical Correlation Analysis
Canonical correlation analysis (CCA) [4] obtains a linear relationship between two multidimensional variables. The objective of CCA is to extract latent features from two data sets  and
and  . Here
. Here  and
and  are the number of features of
are the number of features of  and
and  , respectively, whereas n is the number of samples. CCA obtains two directional basis vectors
, respectively, whereas n is the number of samples. CCA obtains two directional basis vectors  and
and  such that, the correlation between
such that, the correlation between  and
and  is maximum. The correlation coefficient \(\rho \) is given as
is maximum. The correlation coefficient \(\rho \) is given as

where  and
and  are covariance matrices of
are covariance matrices of  and
and  , respectively, while
, respectively, while  is the cross-covariance matrix of
is the cross-covariance matrix of  and
and  . The basis vectors
. The basis vectors  and
and  are the eigenvectors of matrices
are the eigenvectors of matrices  and
and  , respectively, with eigenvalue \(\rho \), where
, respectively, with eigenvalue \(\rho \), where

If the number of features  and
and  of
of  and
and  , respectively, is larger than n, the covariance matrices
, respectively, is larger than n, the covariance matrices  and
and  are ill-conditioned, which make the computation of CCA invalid. That means, the inverses of
are ill-conditioned, which make the computation of CCA invalid. That means, the inverses of  and
and  do not make any sense [3]. To overcome this problem, RCCA [11] increases the diagonal elements of
do not make any sense [3]. To overcome this problem, RCCA [11] increases the diagonal elements of  and
and  by adding small positive quantities,
by adding small positive quantities,  and
and  , which are known as regularization parameters. The optimal parameter set of
, which are known as regularization parameters. The optimal parameter set of  and
and  is selected for which the Pearson’s correlation is maximum. On the other hand, FRCCA [1] decreases the off-diagonal elements of
is selected for which the Pearson’s correlation is maximum. On the other hand, FRCCA [1] decreases the off-diagonal elements of  and
and  by subtracting the shrinkage parameters
by subtracting the shrinkage parameters  and
and  . To find the minimum mean squared error estimator of cross-covariance matrix
. To find the minimum mean squared error estimator of cross-covariance matrix  , the shrinkage parameter
, the shrinkage parameter  is used.
is used.
3 Proposed Method
This section presents a new feature extraction algorithm, integrating judiciously the advantages of both RCCA and FRCCA to take care of the singularity problem of covariance matrices. The proposed method also incorporates the available class label information to make it supervised. It extracts new features from two multidimensional data sets by maximizing their relevance with respect to class label and significance with respect to already-extracted features. Prior to describing the proposed method for multimodal data analysis, some important analytical formulations are reported next.
To deal with this singularity problem, the proposed method integrates the advantages of both RCCA and FRCCA. Here, regularization parameters  and
and  are varied within a range
are varied within a range  , with common differences,
, with common differences,  and
and  for
for  and
and  , respectively. To address this singularity issue, the covariance and cross-covariance matrices can be formulated as
, respectively. To address this singularity issue, the covariance and cross-covariance matrices can be formulated as


where  . Similarly,
. Similarly,  can be computed
can be computed  . The parameters
. The parameters  and
and  denote the number of possible values of
denote the number of possible values of  and
and  , respectively. The best estimator of the shrinkage parameters
, respectively. The best estimator of the shrinkage parameters  and
and  , which minimize the risk function of the mean squared error, can be calculated as [1]
, which minimize the risk function of the mean squared error, can be calculated as [1]

where  ,
,  and
and  are the unbiased empirical variance of
are the unbiased empirical variance of  ,
,  and
and  , respectively. Let us assume that
, respectively. Let us assume that  and
and  be the diagonal matrices, where diagonal elements are the eigenvalues of
be the diagonal matrices, where diagonal elements are the eigenvalues of  and
and  , respectively and the corresponding orthonormal eigenvectors are in the columns of
, respectively and the corresponding orthonormal eigenvectors are in the columns of  and
and  , respectively. If
, respectively. If  and
and  are varied within a range with arithmetic progression, then following two relations can be established, based on the theoretical analysis, reported in [8],
are varied within a range with arithmetic progression, then following two relations can be established, based on the theoretical analysis, reported in [8],

As non-zero eigenvalues of  are same as non-zero eigenvalues of
are same as non-zero eigenvalues of  , one of the matrices is enough to compute the eigenvector of
, one of the matrices is enough to compute the eigenvector of  or
or  [7], which are the basis vectors
[7], which are the basis vectors  and
and  , respectively.
, respectively.
To compute both the relevance and significance of an extracted feature, the hypercuboid equivalence partition matrix of rough hypercuboid approach [6] is used. The regularization parameters are optimized through computing the relevance and significance measures [7]. Hence, the problem of extracting a relevant and significant feature set \(\mathbb {S}\) from all possible combinations of regularization parameters  and
and  is equivalent to maximize the average relevance of all extracted features as well as to maximize the average significance among them. To solve this problem, the following greedy algorithm is used.
is equivalent to maximize the average relevance of all extracted features as well as to maximize the average significance among them. To solve this problem, the following greedy algorithm is used.
-
1.
Compute two covariance matrices
 and
and  , of
, of  and
and  , respectively.
, respectively. -
2.
Compute the cross-covariance matrix
 , of
, of  and
and  .
. -
3.
Determine the values of
 and
and  using (4).
using (4). -
4.
Compute
 ,
,  and
and  using (3).
using (3). -
5.
Calculate eigenvalues
 and
and  of
of  and
and  , respectively, along with corresponding eigenvectors
, respectively, along with corresponding eigenvectors  and
and  .
. -
6.
Repeat the following six steps for all
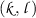 -th regularization parameters of
-th regularization parameters of  and
and  , where
, where  and
and  .
.-
(i)
Initialize
 .
. -
(ii)
Compute
 using (5).
using (5). -
(iii)
Calculate all
 basis vectors
basis vectors  and
and  , which are the eigenvectors of
, which are the eigenvectors of  and
and 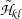 , respectively, where
, respectively, where 
 (6)
(6) -
(iv)
Calculate the
 canonical variables
canonical variables  and
and  ,
,  (7)
(7) -
(v)
The extracted feature
 can be calculated using
can be calculated using  .
. -
vi)
 .
.
-
(i)
-
7.
Initialize \({\mathbb S} \leftarrow \emptyset \).
-
8.
Repeat the following three steps until
 , where
, where  .
.-
(i)
If
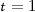 , calculate the relevance
, calculate the relevance  , otherwise calculate the significance
, otherwise calculate the significance  where
where  , of all
, of all  -th extracted feature
-th extracted feature  ,
,  and
and  . \({\mathbb D}\) denotes the decision attribute set. Discard that
. \({\mathbb D}\) denotes the decision attribute set. Discard that  , if it has zero significance with at least one of the selected features of \({\mathbb S}\).
, if it has zero significance with at least one of the selected features of \({\mathbb S}\). -
(ii)
If
 , select a feature
, select a feature  as
as 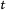 -th feature for which
-th feature for which 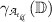 is maximum. Otherwise, the feature
is maximum. Otherwise, the feature  has to be selected as optimal for which
has to be selected as optimal for which  is maximum.
is maximum. -
(iii)
 and
and  .
.
-
(i)
-
9.
Stop.
4 Experimental Results and Discussion
In the current research work, the multimodal data set, named Ovarian Serous Cystadenocarcinoma (OV), is used with three different modalities, namely, gene expression, protein expression, and DNA methylation. The data set is downloaded from TCGA. It has 379 samples with two categories: 51 samples of grade 2 and 328 samples of grade 3. This data set contains expressions of 17,814 genes and 222 proteins, and \(\beta \) values of 27,578 methylated DNAs. Total 2000 top-ranked features, based on their variances, are taken from both gene and methylation data in the current study. To evaluate the performance of different algorithms, both support vector machine (SVM) and nearest neighbor algorithm (NNA) are used. To compute the classification accuracy and F1 score of different approaches, 10-fold cross-validation is performed. A set of correlated features is first generated for each training set. Then, both SVM and NNA are trained with this feature set. The correlated features which are selected for the training set are used to generate test set. Finally, the class label of the test sample is predicted using the SVM and NNA. Twenty five top-ranked correlated features are selected for the analysis.
In the proposed method, both relevance and significance of an extracted feature are computed using rough hypercuboid (RH) approach [6]. However, mutual information (MI) as well as rough sets (RS) with fuzzy discretization can also be used to compute these two measures. In order to establish the importance of rough hypercuboid (RH) approach over rough sets (RS) and mutual information (MI), extensive experimental results are reported in Table 1 for three pairs of modalities. All the results reported in Table 1 establish the fact that the rough hypercuboid equivalence partition matrix based approach performs better than other approaches, irrespective of the pair of modalities and classifier used. In 12 cases, out of total 24 cases, rough hypercuboid equivalence partition matrix based approach performs significantly better and in remaining 12 cases it is better but not significant. This analysis establishes the importance of rough hypercuboid approach over other methods in proposed method.
The performance of the proposed feature extraction algorithm is compared in this section with that of some existing CCA based algorithms, namely, principal component analysis (PCA), CCA, RCCA, FRCCA, several variants of SRCCA using t-test (\(\mathrm SRCCA_{TT}\)) [2], Wilcoxon rank sum test (\(\mathrm SRCCA_{WR}\)) [2], and Wilks’s lambda test (\(\mathrm SRCCA_{WL}\)) [2], CuRSaR [7] and FaRoC [8]. The regularization parameters  and
and  are varied within [0.0, 1.0] with 0.1 as common difference.
are varied within [0.0, 1.0] with 0.1 as common difference.
The box and whisker plots, tables of means, standard deviations, and \(\mathrm{p}\)-value computed through paired-t (one-tailed) test are used to study the performance of different algorithms and the proposed algorithm. Fig. 1 shows the box and whisker plots for classification accuracy and F1 score. On the other hand, the means, standard deviations and \(\mathrm{p}\)-values of accuracy and F1 score for all the methods are reported in Tables 2 and 3. The best mean values are marked in bold in these tables. The experimental results are presented on three pairs of modalities, namely, gene-protein, gene-DNA methylation, and protein-DNA methylation. All the results, presented in Fig. 1 and Tables 2 and 3, establish the fact that the proposed method attains the best mean classification accuracy and F1 score in all the cases, irrespective of the pairs of modalities, and classifiers used. The results, reported in Fig. 1 and Tables 2 and 3, demonstrate that the proposed algorithm performs significantly better than other algorithms in 83 cases out of total 108 cases, considering 0.05 as the level of significance. In remaining 25 cases, it is better but not significant.
5 Conclusion
In present days, the ‘large  small n’ problem becomes a common issue in genetics research, medical studies, risk management, and other fields. If n is very small compared to
small n’ problem becomes a common issue in genetics research, medical studies, risk management, and other fields. If n is very small compared to  , the features become highly collinear, which leads to ill-conditioned of the covariance matrix. The current research work deals with this ‘small n large
, the features become highly collinear, which leads to ill-conditioned of the covariance matrix. The current research work deals with this ‘small n large  ’ problem to overcome the singularity issue of the covariance matrices. The effectiveness of the proposed algorithm, along with a comparison with other algorithms, has been demonstrated considering three different modalities, namely, gene expression, protein expression, and DNA methylation. The concept of hypercuboid equivalence partition matrix is found to be successful in extracting relevant and significant features from high dimensional multimodal real-life data sets.
’ problem to overcome the singularity issue of the covariance matrices. The effectiveness of the proposed algorithm, along with a comparison with other algorithms, has been demonstrated considering three different modalities, namely, gene expression, protein expression, and DNA methylation. The concept of hypercuboid equivalence partition matrix is found to be successful in extracting relevant and significant features from high dimensional multimodal real-life data sets.
References
Cruz-Cano, R., Lee, M.T.: Fast regularized canonical correlation analysis. Comput. Stat. Data Anal. 70, 88–100 (2014)
Golugula, A., Lee, G., Master, S.R., Feldman, M.D., Tomaszewski, J.E., Speicher, D.W., Madabhushi, A.: Supervised regularized canonical correlation analysis: integrating histologic and proteomic measurements for predicting biochemical recurrence following prostate surgery. BMC Bioinform. 12, 483 (2011)
Gou, Z., Fyfe, C.: A canonical correlation neural network for multicollinearity and functional data. Neural Netw. 17(2), 285–293 (2004)
Hotelling, H.: Relations between two sets of variates. Biometrika 28(3/4), 321–377 (1936)
Lanckriet, G.R.G., Bie, T.D., Cristianini, N., Jordan, M.I., Noble, W.S.: A statistical framework for genomic data fusion. Bioinformatics 20(16), 2626–2635 (2004)
Maji, P.: A rough hypercuboid approach for feature selection in approximation spaces. IEEE Trans. Knowl. Data Eng. 26(1), 16–29 (2014)
Maji, P., Mandal, A.: Multimodal omics data integration using max relevance-max significance criterion. IEEE Trans. Biomed. Eng. (2016). doi:10.1109/TBME.2016.2624823
Mandal, A., Maji, P.: FaRoC: fast and robust supervised canonical correlation analysis for multimodal omics data. IEEE Trans. Cybern. (2017). doi:10.1109/TCYB.2017.2685625
Pawlak, Z.: Rough Sets: Theoretical Aspects of Reasoning about Data. Kluwer Academic Publishers, Dordrecht, Boston and London (1991)
Schafer, J., Strimmer, K.: A shrinkage approach to large-scale covariance matrix estimation and implications for functional genomics. Stat. Appl. Genet. Mol. Biol. 4(1), 1–32 (2005)
Vinod, H.D.: Canonical ridge and econometrics of joint production. J. Econometrics 4(2), 147–166 (1976)
Author information
Authors and Affiliations
Corresponding author
Editor information
Editors and Affiliations
Rights and permissions
Copyright information
© 2017 Springer International Publishing AG
About this paper
Cite this paper
Mandal, A., Maji, P. (2017). A New Method to Address Singularity Problem in Multimodal Data Analysis. In: Shankar, B., Ghosh, K., Mandal, D., Ray, S., Zhang, D., Pal, S. (eds) Pattern Recognition and Machine Intelligence. PReMI 2017. Lecture Notes in Computer Science(), vol 10597. Springer, Cham. https://doi.org/10.1007/978-3-319-69900-4_6
Download citation
DOI: https://doi.org/10.1007/978-3-319-69900-4_6
Published:
Publisher Name: Springer, Cham
Print ISBN: 978-3-319-69899-1
Online ISBN: 978-3-319-69900-4
eBook Packages: Computer ScienceComputer Science (R0)




 and
and  , of
, of  and
and  , respectively.
, respectively. , of
, of  and
and  .
. and
and  using (
using ( ,
,  and
and  using (
using ( and
and  of
of  and
and  , respectively, along with corresponding eigenvectors
, respectively, along with corresponding eigenvectors  and
and  .
.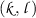 -th regularization parameters of
-th regularization parameters of  and
and  , where
, where  and
and  .
. .
. using (
using ( basis vectors
basis vectors  and
and  , which are the eigenvectors of
, which are the eigenvectors of  and
and 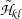 , respectively, where
, respectively, where 

 canonical variables
canonical variables  and
and  ,
, 
 can be calculated using
can be calculated using  .
. .
. , where
, where  .
.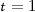 , calculate the relevance
, calculate the relevance  , otherwise calculate the significance
, otherwise calculate the significance  where
where  , of all
, of all  -th extracted feature
-th extracted feature  ,
,  and
and  .
.  , if it has zero significance with at least one of the selected features of
, if it has zero significance with at least one of the selected features of  , select a feature
, select a feature  as
as 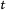 -th feature for which
-th feature for which 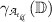 is maximum. Otherwise, the feature
is maximum. Otherwise, the feature  has to be selected as optimal for which
has to be selected as optimal for which  is maximum.
is maximum. and
and  .
.
