Abstract
Several cryptographic schemes and applications are based on functions that are both reasonably efficient to compute and moderately hard to invert, including client puzzles for Denial-of-Service protection, password protection via salted hashes, or recent proof-of-work blockchain systems. Despite their wide use, a definition of this concept has not yet been distilled and formalized explicitly. Instead, either the applications are proven directly based on the assumptions underlying the function, or some property of the function is proven, but the security of the application is argued only informally. The goal of this work is to provide a (universal) definition that decouples the efforts of designing new moderately hard functions and of building protocols based on them, serving as an interface between the two.
On a technical level, beyond the mentioned definitions, we instantiate the model for four different notions of hardness. We extend the work of Alwen and Serbinenko (STOC 2015) by providing a general tool for proving security for the first notion of memory-hard functions that allows for provably secure applications. The tool allows us to recover all of the graph-theoretic techniques developed for proving security under the older, non-composable, notion of security used by Alwen and Serbinenko. As an application of our definition of moderately hard functions, we prove the security of two different schemes for proofs of effort (PoE). We also formalize and instantiate the concept of a non-interactive proof of effort (niPoE), in which the proof is not bound to a particular communication context but rather any bit-string chosen by the prover.
You have full access to this open access chapter, Download conference paper PDF
Similar content being viewed by others
Keywords
These keywords were added by machine and not by the authors. This process is experimental and the keywords may be updated as the learning algorithm improves.
1 Introduction
Several cryptographic schemes and applications are based on (computational) problems that are “moderately hard” to solve. One example is hashing passwords with a salted, moderately hard-to-compute hash function and storing the hash in the password file of a login server. Should the password file become exposed through an attack, the increased hardness of the hash function relative to a standard one increases the effort that the attacker has to spend to recover the passwords in a brute-force attack [33, 48, 51]. Another widely-cited example of this approach originates in the work of Dwork and Naor [28], who suggested the use of a so-called pricing function, supposedly moderately hard to compute, as a countermeasure for junk mail: the sender of a mail must compute a moderately hard function (MoHF) on an input that includes the sender, the receiver, and the mail body, and send the function value together with the message, as otherwise the receiver will not accept the mail. This can be viewed as a proof of effortFootnote 1 (PoE), which, in a nutshell, is a 2-party (interactive) proof system where the verifier accepts if and only if the prover has exerted a moderate amount of effort during the execution of the protocol. Such a PoE can be used to meter access to a valuable resource like, in the case of [28], the attention of a mail receiver. As observed by the authors, requiring this additional effort would introduce a significant obstacle to any spammer wishing to flood many receivers with unsolicited mails. Security was argued only informally in the original work. A line of follow-up papers [1, 27, 29] provides a formal treatment and proves security for protocols that are intuitively based on functions that are moderately hard to compute on architectures with limited cache size.
PoEs have many applications beyond combatting spam mail. One widely discussed special case of PoE protocols are so-called cryptographic puzzles (or client puzzles, e.g. [12, 21, 22, 36, 37, 40, 52, 54]), which are mainly targeted at protecting Internet servers from Denial-of-Service attacks by having the client solve the puzzle before the server engages in any costly operation. These PoEs have the special form of consisting of a single pair of challenge and response messages (i.e., one round of communication), and are mostly based on either inverting a MoHF [40], or finding an input to an MoHF that leads to an output with a certain number of trailing zeroes [2]. More recently, cryptocurrencies based on distributed transaction ledgers that are managed through a consensus protocol based on PoEs have emerged, most prominently Bitcoin [49] and Ethereum [19], and are again based on MoHFs. In a nutshell, to append a block of transactions to the ledger, a so-called miner has to legitimate the block by a PoE, and as long as miners that control a majority of a computing power are honest, the ledger remains consistent [34].
The notions of hardness underlying the MoHFs that have been designed for the above applications vary widely. The earliest and still most common one is computational hardness in terms of the number of computation steps that have to be spent to solve the problem [22, 28, 40, 49]. Other proposals exploit the limited size of fast cache in current architectures and are aimed at forcing the processor to access the slower main memory [1, 27, 29], the use of large amounts of memory during the evaluation of the function [10, 33, 51], or even disk space [30].
Given the plethora of work (implicitly or explicitly) designing and using MoHFs, one question soon comes to mind: is it possible to use the MoHF designed in one work in the application context of another? The current answer is sobering. Either the security notion for the MoHF is not quite sufficient for proving the security of the targeted applications. Or security of the application is proven directly without separating out the properties used from the underlying MoHF.
For example, in the domain of memory-hard functions—an increasingly common type of MoHF first motivated by Percival in [51]—the security of MoHF applications is generally argued only informally. Indeed, this likely stems from the fact that proposed definitions seem inadequate for the task. As argued by Alwen and Serbinenko [10], the hardness notion used by Percival [51] and Forler et al. [33] is not sufficient in practical settings because it disregards that an attacker may amortize the effort over multiple evaluations of the function, or use inherently parallel computational capabilities as provided by a circuit. Yet the definition of [10], while taking these into account, is also not (known to be) useful in proving the security of higher-level protocols, because it requires high average-case, instead of worst-case, complexity. Worse, like all other MoHF definitions in the literature (e.g. [3, 15]), it focuses only on the hardness of evaluating the function; indeed, in most cases the functions modified to append their inputs to their outputs would be considered to have the same complexity as the original ones, but become trivially invertible. However, all applications present the adversary with the task of inverting the MoHF in some form.
In other areas, where the application security is explicitly proven [1, 27, 29], this is done directly with out separating out the properties of the underlying MoHF. This means that (a) the MoHF (security) cannot easily be “extracted” from the paper and used in other contexts, and (b) the protocols cannot easily be instantiated with other MoHFs. Furthermore, the security definitions come with a hard-wired notion of hardness, so it is a priori even more difficult to replace the in-built MoHF with one for a different type of hardness.
Consequently, as already discussed by Naor in his 2003 invited lecture [50], what is needed is a unifying theory of MoHFs. The contribution of this paper is a step toward this direction. Our goal is to design an abstract notion of MoHF that is flexible enough to model various types of functions for various hardness notions considered in the literature, but still expressive enough to be useful in a wide range of applications. We propose such a definition, show (with varying degrees of formality) that existing constructions for various types of hardness instantiate it, and show how it can be used in various application scenarios. Not all proof-of-work schemes, however, fall into the mold of the ones covered in this work. For example the recently popular Equihash [16] has a different form.Footnote 2
More Details on Related Work. We briefly summarize related papers beyond those referenced above. A detailed overview can be found in the full version [11].
After the initial work of Dwork and Naor [28], most subsequent work on MoHFs is based on hash functions, such as using the plain hash function [2] or iterating the function to increase the hardness of inverting it. Iteration seems to first appear in the Unix crypt function [48] and analyzed by Yao and Yin [56] and Bellare et al. [14]. A prefixing scheme for iteration has been discussed and analyzed by Demay et al. [26]. The definitions of [14, 26] are conceptually similar to ours, as they are also based on indifferentiability. Their definitions, however, are restricted to the complexity measure of counting the number of random-oracle invocations.
Based on memory-bound functions, which aim at forcing the processor to access the (slower) main memory because the data needed to compute the functions do not fit into the (fast but small) cache, proofs-of-effort have been developed and analyzed in [1, 27, 29]. The rough idea is that during the computation of the function one has to access various position in a random-looking array that is too large to fit into cache. We discuss the reduction that will be necessary to make those functions useful in our framework in Sect. 5.
For memory-hard functions, which rely on a notion of hardness aimed at ensuring that application-specific integrated circuits (ASICs) have as little advantage (in terms of dollar per rate of computation) over general-purpose hardware, the first security notion of memory-hard functions was given by Percival [51]. The definition asks for a lower bound on the product of memory and time used by an algorithm evaluating the function on any single input. This definition was refined by Alwen and Serbinenko [10] by modeling parallel algorithms as well as the amortized Cumulative Memory Complexity (aCMC) of the algorithms. aCMC was further refined by Alwen and Blocki [3] to account for possible trade-offs of decreasing memory consumption at the added cost of increased logic gates resulting in the notion of amortized Energy Complexity (aEC).
Our Contributions and Outline of the Paper. The starting point of our MoHF definition is the observation that—on the one hand—many instantiations of MoHFs are based on hash functions and analyzed in the random-oracle model, and—on the other hand—many applications also assume that a MoHF behaves like a random oracle. More concretely, we base our definition on indifferentiability from a random oracle [47], and describe each “real-world setting” according to the computational model underlying the MoHF.
Section 2 covers preliminaries; in particular we recall the notion of indifferentiability and introduce an abstract notion of computational cost and resource-bounded computation. In Sect. 3, we describe our new indifferentiability-based definition of MoHF in terms of the real and ideal models considered. Next, in Sect. 4, we instantiate the MoHF definition for the case of memory-hard functions. This section contains the main technical result of the paper, an extension of the pebbling reduction of Alwen and Serbinenko [10] to our stricter MoHF definition. In Sect. 5, we discuss then discuss how other types of moderately hard functions from the literature are captured in our framework, in particular weak memory-hard functions, memory-bound functions, and one-time computable functions. In Sect. 6, we describe a (composable) security definition for PoE. We present an ideal-world description of a PoE; a functionality where the prover can convince the verifier in a certain bounded number of sessions. As this definition starts from the ideal-world description of a MoHF as described above, it can be easily composed with every type of MoHF in our framework. We consider two types of PoE—one based on function inversion, and the other one on hash trail. In Sect. 7, we then continue to describing an analogous definition for a non-interactive proof of effort (niPoE), and again give an instantiation based on hash trail. In Sect. 8, we discuss the composition of the MoHF definition and the PoE and niPoE applications more concretely.
2 Preliminaries
We use the sets \({\mathbb {N}}:=\{1,2,\ldots \}\), and \({\mathbb {Z}} _{\ge c}:=\{c,c+1,\ldots \}\cap {\mathbb {Z}} \) to denote integers greater than or equal to c. Similarly we write [a, c] to denote \(\{a, a+1, \ldots ,c\}\) and [c] for the set [1, c]. For a set S, we use the notation  to denote that x is chosen uniformly at random from the set S. For arbitrary set \({\mathbb {I}} \) and \(n\in {\mathbb {N}} \) we write \({\mathbb {I}} ^{{\times n}}\) to denote the n-wise cross product of \({\mathbb {I}} \). We refer to sets of functions (or distributions) as function (or distribution) families.
to denote that x is chosen uniformly at random from the set S. For arbitrary set \({\mathbb {I}} \) and \(n\in {\mathbb {N}} \) we write \({\mathbb {I}} ^{{\times n}}\) to denote the n-wise cross product of \({\mathbb {I}} \). We refer to sets of functions (or distributions) as function (or distribution) families.
2.1 Reactive Discrete Systems
For an input set \(\mathbb {X}\) and an output set \(\mathbb {Y}\), a reactive discrete \((\mathbb {X}, \mathbb {Y})\) -system repeatedly takes as input a value (or query) \(x_i \in \mathbb {X}\) and responds with a value \(y_i \in \mathbb {Y}\), for \(i\in \{1,2,\dots \}\). Thereby, each output \(y_i\) may depend on all prior inputs \(x_1, \dots , x_i\). As discussed by Maurer [43], reactive discrete systems are exactly modeled by the notion of a random system, that is, the conditional distribution \(\mathsf {p}_{Y_i | X^i Y^{i-1}}\) of each output (random variable) \(Y_i \in \mathbb {Y}\) given all previous inputs \(X_1,\dots ,X_i \in \mathbb {X}\) and outputs \(Y_1,\dots ,Y_{i-1} \in \mathbb {Y}\) of the system.
Discrete reactive systems can have multiple interfaces, where each interface is labeled by an element in some set \(\mathbb {I}\). We then formally consider \((\mathbb {I} \times \mathbb {X}, \mathbb {I} \times \mathbb {Y})\)-systems, where providing an input \(x\in \mathbb {X}\) at interface \(i\in \mathbb {I}\) then means evaluating the system on input \((i,x)\in \mathbb {I}\times \mathbb {X}\), and the resulting output \((i',y)\in \mathbb {Y}\) means that the value y is provided as a response at the interface \(i'\in \mathbb {I}\). We generally denote reactive discrete systems by upper-case calligraphic letters such as \(\mathcal S^{\textsc {}}\) or \(\mathcal T^{\textsc {}}\) or by lower-case Greek letters such as \({{\pi }_{}} \) or \({{\sigma }} \).
A configuration of systems is a set of systems which are connected via their interfaces. Any configuration of systems can again be seen as a system that provides all unconnected interfaces to its environment. Examples are shown in Fig. 1, where Fig. 1a shows a two-interface system \({{\pi }_{}} \) connected to the single interface of another system \(\mathcal R^{\textsc {}}\), and Fig. 1b shows a two-interface system \({{\pi }_{}} \) connected to the \(\mathrm {priv}\)-interface of the system \(\mathcal S^{\textsc {}}\). The latter configuration is denoted by the term \({{{\pi }_{}}}^{\mathrm {priv}}\mathcal S^{\textsc {}}\). Finally, Fig. 1c shows a similar setting, but where additionally a distinguisher (or environment) \({ D } \) is attached to both interfaces of \({{{\sigma }}}^{\mathrm {pub}}\mathcal T^{\textsc {}}\). This setting is denoted as \({ D } ({{{\sigma }}}^{\mathrm {pub}}\mathcal T^{\textsc {}})\) and is further discussed in Sect. 2.2.
2.2 Indifferentiability
The main definitions in this work are based on the indifferentiability framework of Maurer et al. [46, 47]. We define the indifferentiability notion in this section.
Indifferentiability. Left: Distinguisher \({ D } \) connected to protocol \({{\pi }_{}} \) using the \(\mathrm {priv}\)-interface of the real-world resource \(\mathcal S^{\textsc {}}\), denoted \({ D } \left( {{{\pi }_{}}}^{\mathrm {priv}}\mathcal S^{\textsc {}}\right) \). Right: Distinguisher \({ D } \) connected to simulator \({{\sigma }} \) attached to the \(\mathrm {pub}\)-interface of the ideal-world resource \(\mathcal T^{\textsc {}}\), denoted \({ D } \left( {{{\sigma }}}^{\mathrm {pub}}\mathcal T^{\textsc {}}\right) \).
Indifferentiability of a protocol or scheme \({{\pi }_{}} \), which using certain resources \(\mathcal S^{\textsc {}}\), from resource \(\mathcal T^{\textsc {}}\) requires that there exists a simulator \({{\sigma }} \) such that the two systems \({{{\pi }_{}}}^{\mathrm {pub}}\mathcal S^{\textsc {}}\) and \({{{\sigma }}}^{\mathrm {pub}}\mathcal T^{\textsc {}}\) are indistinguishable, as depicted in Fig. 2. The indistinguishability is defined via a distinguisher \({ D } \), a special system that interacts with either \({{{\pi }_{}}}^{\mathrm {priv}}\mathcal S^{\textsc {}}\) or \({{{\sigma }}}^{\mathrm {pub}}\mathcal T^{\textsc {}}\) and finally outputs a bit. In the considered “real-world” setting with \({{{\pi }_{}}}^{\mathrm {priv}}\mathcal S^{\textsc {}}\), the distinguisher \({ D } \) has direct access to the \(\mathrm {pub}\)-interface of \(\mathcal S^{\textsc {}}\), but the \(\mathrm {priv}\)-interface is accessible only through \({{\pi }_{}} \). In the considered “ideal-world” setting with \({{{\sigma }}}^{\mathrm {pub}}\mathcal T^{\textsc {}}\), \({ D } \) has direct access to the \(\mathrm {priv}\)-interface of \(\mathcal T^{\textsc {}}\), but the \(\mathrm {pub}\)-interface is accessible only through \({{\sigma }} \). The advantage of the distinguisher is now defined to be the difference in the probability that \({ D } \) outputs some fixed value, say 1, in the two settings, more formally,
Intuitively, if the advantage is small, then, for the honest parties, the real-world resource \(\mathcal S^{\textsc {}}\) is at least as useful (when using it via \({{\pi }_{}} \)) as the ideal-world resource \(\mathcal T^{\textsc {}}\). Conversely, for the adversary the real world is at most as useful as the ideal world. Put differently, from the perspective of the honest parties, the real world is at least as safe as the ideal world. So any application that makes use of \(\mathcal T^{\textsc {}}\) can instead use \({{{\pi }_{}}}^{\mathrm {priv}}\mathcal S^{\textsc {}}\). This leads to the following definition.
Definition 1 (Indifferentiability)
Let \({{\pi }_{}} \) be a protocol and \(\mathcal S^{\textsc {}},\mathcal T^{\textsc {}}\) be resources, and let \(\varepsilon > 0\). Then \({{{\pi }_{}}}^{\mathrm {priv}}\mathcal S^{\textsc {}}\) is \(\varepsilon \)-indifferentiable from \(\mathcal T^{\textsc {}}\), if
with \({{{\pi }_{}}}^{\mathrm {priv}}\mathcal S^{\textsc {}}\approx _{\varepsilon } {{{\sigma }}}^{\mathrm {pub}}\mathcal T^{\textsc {}}\) defined as \(\forall { D }: \ \varDelta ^{{ D }}\left( {{{\pi }_{}}}^{\mathrm {priv}}\mathcal S^{\textsc {}},{{{\sigma }}}^{\mathrm {pub}}\mathcal T^{\textsc {}}\right) \le \varepsilon \).
2.3 Oracle Functions and Oracle Algorithms
We explore several constructions of hard-to-compute functions that are defined via a sequence of calls to an oracle. To make this dependency explicit, we use the following notation. For sets D and R, a random oracle (RO) H is a random variable distributed uniformly over the function family \({\mathbb {H}} = \{ h: D \rightarrow R\}\).
Definition 2 (Oracle functions)
For (implicit) oracle set \({\mathbb {H}} \), an oracle function \(f^{(\cdot )}\) (with domain D and range R), denoted \(f^{(\cdot )}:D \rightarrow R\), is a set of functions indexed by oracles \(h\in {\mathbb {H}} \) where each \(f^h\) maps \(D \rightarrow R\).
We fix a concrete function in the set \(f^{(\cdot )}\) by fixing an oracle \(h\in {\mathbb {H}} \) to obtain function \(f^{h}:D \rightarrow R\). More generally, if \(\mathbf {f}=(f^{(\cdot )}_1, \ldots , f^{(\cdot )}_n)\) is an n-tuple of oracle functions then we write \(\mathbf {f}^h\) to denote the n-tuple \((f^h_1, \ldots , f^h_n)\).
For an algorithm \({\mathtt {A}} \) we write \({\mathtt {A}} ^h\) to make explicit that \({\mathtt {A}} \) has access to oracle h during its execution. We sometimes refer to algorithms that expect such access as oracle algorithm. We leave the precise model of computation for such algorithms unspecified for now as these will vary between concrete notions of MoHFs.
Example 1
The prefixed hash chain of length \(c\in {\mathbb {N}} \) is an oracle function as
An algorithm \({\mathtt {A}} ^\textsc {hc}\) that computes a hash chain of length c is described as initially evaluating \({h} \) at the input \(1 \Vert x\), and then iteratively \((c-1)\) times on the outputs of the previous round, prefixing with the round index. \(\Diamond \)
2.4 Computation and Computational Cost
One main goal of this paper is to introduce a unifying definitional framework for MoHFs. For any concrete type of MoHF, we have to quantify the (real-world) resources required for performing computations such as evaluating the function.
Cost Measures. For the remainder of this section, we let \((\mathcal {V},0,+,\le )\) be a commutative group with a partial order \(\le \) such that the operation “\(+\)” is compatible with the partial order “\(\le \)”, meaning that \(\forall a,b,c \in \mathcal {V}: a \le b \Rightarrow a \,+\, c \le b \,+\, c\). More concretely, we could consider \(\mathcal {V}= {\mathbb {Z}} \) or \(\mathcal {V}= {\mathbb {R}} \), but also \(\mathcal {V}= {\mathbb {R}} ^n\) for some \(n\in {\mathbb {N}} \) if the computational cost cannot be quantified by a single value, for instance if we want to measure both the computational effort and the memory required to perform the task. We generally use the notation  .
.
The Cost of Computation. We later describe several MoHFs for differing notions of effort, where the hardness is defined using the following complexity notion based on a generic cost function. Intuitively a cost function assigns a non-negative real number as a cost to a given execution of an algorithm \({\mathtt {A}} \). More formally, let \({\mathbb {A}} \) be some set of algorithms (in some fixed computational model). Then an \({\mathbb {A}} \)
-cost function has the form \(\mathsf{{cost}}: {{\mathbb {A}}} \times \{0,1\}^* \times \{0,1\}^* \rightarrow \mathcal {V}_{\ge 0}\). The first argument is an algorithm, the second fixes the input to the execution and the third fixes the random coins of the algorithm (and, in the ROM, also the random coins of the RO). Thus any such triple completely determines an execution which is then assigned a cost. Concrete examples include measuring the number of RO calls made by \({\mathtt {A}} \) during the execution, the number of cache misses during the computation [27, 29] or the amount of memory (in bits) used to store intermediate values during the computation [10]. We write \(y \mathrel {{\overset{{\mathsf {a}}}{\twoheadleftarrow }}} {\mathtt {A}} (x;{\$})\) if the algorithm \({\mathtt {A}} \) computes the output \(y \in \{0,1\}^*\), when given input \(x\in \{0,1\}^*\) and random coins  , with computation cost \({\mathsf {a}} \in \mathcal {V}\).
, with computation cost \({\mathsf {a}} \in \mathcal {V}\).
For concreteness we continue developing the example of a hash-chain of length c by defining an appropriate cost notion.
Example 2
Let \({\mathtt {A}} \) be an oracle algorithm as in Example 1. The cost of evaluating the algorithm \({\mathtt {A}} \) is measured by the number \(b\in {\mathbb {N}} =\mathcal {V}\) of queries to the oracle that can be made during the evaluation of \({\mathtt {A}} \). Therefore, we write

if \({\mathtt {A}} \) computes y from x with b calls to the oracle \({h} \). For the algorithm \({\mathtt {A}} ^\textsc {hc}\) computing the prefixed hash chain of length \(c\in {\mathbb {N}} \), the cost of each evaluation is c and therefore obviously independent of the choice of random oracle, so simply writing  is well-defined. \(\Diamond \)
is well-defined. \(\Diamond \)
2.5 A Model for Resource-Bounded Computation
In this section, we describe generically how we model resource-bounded computation in the remainder of this work. The scenario we consider in the following section has a party specify an algorithm and evaluate it, possibly repeatedly on different inputs. We want to model that evaluating the algorithm incurs a certain computational cost and that the party has bounded resources to evaluate the algorithm—depending on the available resources—only for a bounded number of times, or maybe not at all. Our approach consists of specifying a computation device to which an algorithm \({\mathtt {A}} \) can be input. Then, one can evaluate the algorithm repeatedly by providing inputs \(x_1,\dots ,x_k\) to the device, which evaluates the algorithm \({\mathtt {A}} \) on each of the inputs. Each such evaluation incurs a certain computational cost, and as long as there are still resources available for computation, the device responds with the proper outputs \(y_1 = {\mathtt {A}} (x_1), y_2 = {\mathtt {A}} (x_2), \dots \). Once the resources are exhausted, the device always responds with the special symbol \(\bot \). In the subsequent part of this paper, we will often refer to the computation device as the “computation resource.”
The above-described approach can be used to model arbitrary types of algorithms and computational resources. Examples for such resources include the memory used during the computation (memory-hardness) or the number of computational steps incurred during the execution (computational hardness). Resources may also come in terms of “oracles” or “sub-routines” called by the algorithms, such as a random oracle, where we may want to quantify the number of queries to the oracle (query hardness).
As a concrete example, we describe the execution of an algorithm whose use of resources accumulates over subsequent executions:Footnote 3
-
1.
Let \(b \in \mathcal {V}\) be the resources available to the party and \(j = 1\).
-
2.
Receive input \(x_j \in \{0,1\}^*\) from the party.
-
3.
Compute \(y_j \mathrel {{\overset{c}{\twoheadleftarrow }}} {\mathtt {A}} (x_j)\), for \(c \in \mathcal {V}\). If \(c \ge b\) then set \(b \leftarrow 0\) and output \(\bot \). Otherwise, set \(b \leftarrow b - c\) and output \(y_j\). Set \(j \leftarrow j + 1\) and go to step 2.
We denote the resource that behaves as described above for the specific case of oracle algorithms that are allowed to make a bounded number \(b\in {\mathbb {N}} \) of oracle queries by \(\mathcal S^{\textsc {oa}}_{b}\). For concreteness we show how to define an appropriate computational resource for reasoning about the hash-chain example.
Example 3
We continue with the setting described in Examples 1 and 2, and consider the hash-chain algorithm \({\mathtt {A}} ^\textsc {hc}\) with a computational resource that is specified by the overall number \(b \in \mathcal {V}= {\mathbb {N}} \) that can be made to the oracle.
In more detail, we consider the resource \(\mathcal S^{\textsc {oa}}_{b}\) described above. Upon startup, \(\mathcal S^{\textsc {oa}}_{b}\) samples a uniform  . Upon input of the oracle algorithm \({\mathtt {A}} \) (the type described in Example 1) into the computation resource, the party can query \(x_1,x_2,\dots \) and the algorithm \({\mathtt {A}} \) is evaluated, with access to h, on all inputs until b queries to h have been made, and subsequently only returns \(\bot \).
. Upon input of the oracle algorithm \({\mathtt {A}} \) (the type described in Example 1) into the computation resource, the party can query \(x_1,x_2,\dots \) and the algorithm \({\mathtt {A}} \) is evaluated, with access to h, on all inputs until b queries to h have been made, and subsequently only returns \(\bot \).
For algorithm \({\mathtt {A}} ^\textsc {hc}\), chain length c, and resource \(\mathcal S^{\textsc {oa}}_{b}\) with \(b\in {\mathbb {N}} \), the algorithm can be evaluated \(\left\lfloor b/c \right\rfloor \) times before all queries are answered with \(\bot \). \(\Diamond \)
3 Moderately Hard Functions
In this section, we combine the concepts introduced in Sect. 2 and state our definition of moderately hard function. The existing definitions of MoHF can be seen as formalizing that, with a given amount of resources, the function can only be evaluated a certain (related) number of times. Our definition is different in that it additionally captures that even an arbitrary computation with the same amount of resources cannot provide more (useful) results about the function than making the corresponding number of evaluations. This stronger statement is essential for proving the security of applications.
We base the definition of MoHFs on the notion of indifferentiability discussed in Sect. 2.2. In particular, the definition is based on the indistinguishability of a real and an ideal execution that we describe below. Satisfying such a definition will then indeed imply the desired statement, i.e., that the best the adversary can do is evaluate the function in the forward direction, and additionally that for each of these evaluations it must spend a certain amount of resources.
The real-world resource consists of resource-bounded computational devices that can be used to evaluate certain types of algorithms; one such resource at the \(\mathrm {priv}\)- and one at the \(\mathrm {pub}\)-interface. For such a resource \(\mathcal S^{\textsc {}}\) with bounds specified by \({\mathbf {l}},{\mathbf {r}} \in {\mathbb {P}} \), for some parameter space \({\mathbb {P}} \) that is specified by \(\mathcal S^{\textsc {}}\), for the \(\mathrm {priv}\)- and \(\mathrm {pub}\)-interfaces, respectively, we usually write \(\mathcal S^{\textsc {}}_{{\mathbf {l}},{\mathbf {r}}}\). The protocol system \({{\pi }_{}} \) used by the honest party initially inputs an algorithm  to \(\mathcal S^{\textsc {}}_{{\mathbf {l}},{\mathbf {r}}}\), further inputs \(x_1,x_2,\dots \) from \({ D } \) to \({{\pi }_{}} \) are simply forwarded to \(\mathcal S^{\textsc {}}_{{\mathbf {l}},{\mathbf {r}}}\), and the responses are given back to \({ D } \). Moreover, \({ D } \) can use the \(\mathrm {pub}\)-interface of \(\mathcal S^{\textsc {}}_{{\mathbf {l}},{\mathbf {r}}}\) to input an algorithm \({\mathtt {A}} '\) and evaluate it.
to \(\mathcal S^{\textsc {}}_{{\mathbf {l}},{\mathbf {r}}}\), further inputs \(x_1,x_2,\dots \) from \({ D } \) to \({{\pi }_{}} \) are simply forwarded to \(\mathcal S^{\textsc {}}_{{\mathbf {l}},{\mathbf {r}}}\), and the responses are given back to \({ D } \). Moreover, \({ D } \) can use the \(\mathrm {pub}\)-interface of \(\mathcal S^{\textsc {}}_{{\mathbf {l}},{\mathbf {r}}}\) to input an algorithm \({\mathtt {A}} '\) and evaluate it.
The ideal-world resource also has two interfaces \(\mathrm {priv}\) and \(\mathrm {pub}\). We consider only moderately hard functions with uniform outputs; therefore, the ideal-world resource \(\mathcal T^{\textsc {rro}}_{}\) we consider essentially implements a random function \(D \rightarrow R\) and allows at both interfaces simply to query the random function. (In more detail, \(\mathcal T^{\textsc {rro}}_{}\) is defined as initially choosing a uniformly random function \(f: D\rightarrow R\) and then, upon each input \(x \in D\) at either \(\mathrm {priv}\) or \(\mathrm {pub}\), respond with \(f(x)\in R\) at the same interface.) We generally consider resources \(\mathcal T^{\textsc {rro}}_{a,b}\) for \(a, b\in {\mathbb {N}} \), which is the same as a resource \(\mathcal T^{\textsc {rro}}_{}\) allowing a queries at the \(\mathrm {priv}\) and b queries at the \(\mathrm {pub}\)-interface. All exceeding queries are answered with the special symbol \(\bot \) (Fig. 4).
It is easy to see that the resource \(\mathcal T^{\textsc {rro}}_{a,b}\) is one-way: it is a random oracle to which a bounded number of queries can be made.
Before we provide a more detailed general definitions, we complete the hash-chain example by instantiating an appropriate security notion.
Example 4
We extend Example 3 where the algorithm \({\mathtt {A}} ^\textsc {hc}\) evaluates a hash-chain of length c on its input by defining the natural security notion such an algorithm achieves. The real-world resource \(\mathcal S^{\textsc {2oa}}_{a,b}\), with \(a,b\in {\mathbb {N}} \), behaves as a resource \(\mathcal S^{\textsc {oa}}_{a}\) at the \(\mathrm {priv}\)- and as a resource \(\mathcal S^{\textsc {oa}}_{b}\) at the \(\mathrm {pub}\)-interface. That is \(\mathcal S^{\textsc {2oa}}_{a,b}\) first samples a random function \(h \in {\mathbb {H}} \) uniformly, and then uses this for the evaluation of algorithms input at both interfaces \(\mathrm {priv}\) and \(\mathrm {pub}\) analogously to \(\mathcal S^{\textsc {oa}}_{a}\) and \(\mathcal S^{\textsc {oa}}_{B}\), respectively.
The converter system \({{\pi }_{\textsc {hc}}} \) initially inputs \({\mathtt {A}} ^\textsc {hc}\) into \(\mathcal S^{\textsc {2oa}}_{a,b}\); which is a resource that allows for evaluating such algorithms at both interfaces \(\mathrm {priv}\) and \(\mathrm {pub}\). As \(\mathcal S^{\textsc {2oa}}_{a,b}\) allows for a oracle queries for \({\mathtt {A}} ^\textsc {hc}\), the system \({{{\pi }_{\textsc {hc}}}}^{\mathrm {priv}}\mathcal S^{\textsc {2oa}}_{a,b}\) allows for \(\left\lfloor a/c \right\rfloor \) complete evaluations of \({\mathtt {A}} ^\textsc {hc}\) at the \(\mathrm {priv}\)-interface. The resource \(\mathcal T^{\textsc {rro}}_{a',b'}\) is a random oracle that can be queried at both interfaces \(\mathrm {priv}\) and \(\mathrm {pub}\) (and indeed the outside interface provided by \({{\pi }_{}} \) is of that type). The simulator \({{\sigma }} \), therefore, will initially accept an algorithm \({\mathtt {A}} '\) as input and then evaluate \({\mathtt {A}} '\) with simulating the queries to h potentially using queries to \(\mathcal T^{\textsc {rro}}_{a',b'}\). In particular, we can rephrase the statement about (prefixed) iteration of random oracles of Demay et al. [26] as followsFootnote 4: with \({{\pi }_{\textsc {hc}}} \) being the system that inputs the algorithm \({\mathtt {A}} ^\textsc {hc}\), and \(\mathcal S^{\textsc {2oa}}_{a,b}\) the resource that allows a and b evaluations of h at the \(\mathrm {priv}\)- and \(\mathrm {pub}\)-interfaces, respectively, \({{{\pi }_{\textsc {hc}}}}^{\mathrm {priv}}\mathcal S^{\textsc {2oa}}_{a,b}\) is \((b \cdot 2^{-w})\)-indifferentiable, where w is the output width of the oracle, from \(\mathcal T^{\textsc {rro}}_{a',b'}\) allowing \(a' = \left\lfloor a/c \right\rfloor \) queries at the \(\mathrm {priv}\)- and \(b' = \left\lfloor b/c \right\rfloor \) queries at the \(\mathrm {pub}\)-interface. \(\Diamond \)
The security statement ensures both that the honest party is able to perform its tasks using the prescribed algorithm and resource, and that the adversary cannot to perform more computations than allowed by its resources. We emphasize that the ideal execution in Example 4 will allow both the honest party and the adversary to query a random oracle for some bounded number of times. The fact that in the real execution the honest party can answer the queries with its bounded resource corresponds to the efficient implementation of the MoHF. The fact that any adversarial algorithm that has a certain amount of resources available can be “satisfied” with a bounded number of queries to the ideal random oracle means that the adversarial algorithm cannot gain more knowledge than by evaluating the ideal function for that number of times. Therefore, Example 4 models the basic properties that we require from a MoHF.
The security statement for an MoHF with naïve algorithm  has the following form. Intuitively, for resource limits \(({\mathbf {l}}, {\mathbf {r}})\), the real model with those limits and the ideal model with limits \(({\mathsf {a}} ({\mathbf {l}}),{\mathsf {b}} ({\mathbf {r}}))\) are \(\varepsilon \)-indistinguishable, for some \(\varepsilon = \varepsilon ({\mathbf {l}},{\mathbf {r}})\). I.e., there is a simulator \({{\sigma }} \) such that no distinguisher \({ D } \) can tell the two models apart with advantage \(>\varepsilon \).
has the following form. Intuitively, for resource limits \(({\mathbf {l}}, {\mathbf {r}})\), the real model with those limits and the ideal model with limits \(({\mathsf {a}} ({\mathbf {l}}),{\mathsf {b}} ({\mathbf {r}}))\) are \(\varepsilon \)-indistinguishable, for some \(\varepsilon = \varepsilon ({\mathbf {l}},{\mathbf {r}})\). I.e., there is a simulator \({{\sigma }} \) such that no distinguisher \({ D } \) can tell the two models apart with advantage \(>\varepsilon \).
We recall that the role of \({{\sigma }} \) is to “fool” \({ D } \) into thinking it is interacting with \({{A}} \) in the real model. We claim that this forces \({{\sigma }} \) to be aware of the concrete parameters \({\mathbf {r}} \) of the real world \({ D } \) is supposedly interacting with. Indeed, one strategy \({ D } \) may employ is to provide code \({\mathtt {A}} \) at the \(\mathrm {pub}\)-interface which consumes all available computational resources. In particular, using this technique \({ D } \) will obtain a view encoding \({\mathbf {r}} \). Thus it had better be that \({{\sigma }} \) is able to produce a similar encoding itself. Thus in the following definition we allow \({{\sigma }} \) to depend on the choice of \({\mathbf {r}} \). Conversely, no such dependency between \({\mathbf {l}} \) and \({{\sigma }} \) is needed.Footnote 5
For many applications, we also want to parametrize the function by a hardness parameter \({\mathbf {n}} \in {\mathbb {N}} \). In that case we consider a sequence of oracle functions \(f^{(\cdot )}_{\mathbf {n}} \) and algorithms  (which we will often want to be uniform) and also the functions \({\mathsf {a}}, {\mathsf {b}}, \varepsilon \) must be defined separately for each \({\mathbf {n}} \in {\mathbb {N}} \). This leads us to the following definition.
(which we will often want to be uniform) and also the functions \({\mathsf {a}}, {\mathsf {b}}, \varepsilon \) must be defined separately for each \({\mathbf {n}} \in {\mathbb {N}} \). This leads us to the following definition.
Definition 3 (MoHF security)
For each \({\mathbf {n}} \in {\mathbb {N}} \), let \(f_{\mathbf {n}} ^{(\cdot )}\) be an oracle function and  be an algorithm for computing \(f^{(\cdot )}\), let \({\mathbb {P}} \) be a parameter space and \({\mathsf {a}},{\mathsf {b}}: {\mathbb {P}} \times {\mathbb {N}} \rightarrow {\mathbb {N}} \), and let \(\varepsilon : {\mathbb {P}} \times {\mathbb {P}} \times {\mathbb {N}} \rightarrow {\mathbb {R}} _{\ge 0}\). Then, for a family of models \(\mathcal S^{\textsc {}}_{{\mathbf {l}},{\mathbf {r}}}\),
be an algorithm for computing \(f^{(\cdot )}\), let \({\mathbb {P}} \) be a parameter space and \({\mathsf {a}},{\mathsf {b}}: {\mathbb {P}} \times {\mathbb {N}} \rightarrow {\mathbb {N}} \), and let \(\varepsilon : {\mathbb {P}} \times {\mathbb {P}} \times {\mathbb {N}} \rightarrow {\mathbb {R}} _{\ge 0}\). Then, for a family of models \(\mathcal S^{\textsc {}}_{{\mathbf {l}},{\mathbf {r}}}\),  is a \(({\mathsf {a}},{\mathsf {b}},\varepsilon )\)-secure moderately hard function family in the \(\mathcal S^{\textsc {}}_{{\mathbf {l}},{\mathbf {r}}}\)-model if
is a \(({\mathsf {a}},{\mathsf {b}},\varepsilon )\)-secure moderately hard function family in the \(\mathcal S^{\textsc {}}_{{\mathbf {l}},{\mathbf {r}}}\)-model if

The function family is called uniform if  is a uniform algorithm. The function family is asymptotically secure if \(\varepsilon ({\mathbf {l}},{\mathbf {r}},\cdot )\) is a negligible function in the third parameter for all values of \({\mathbf {r}},{\mathbf {l}} \in {\mathbb {P}} \).
is a uniform algorithm. The function family is asymptotically secure if \(\varepsilon ({\mathbf {l}},{\mathbf {r}},\cdot )\) is a negligible function in the third parameter for all values of \({\mathbf {r}},{\mathbf {l}} \in {\mathbb {P}} \).
We sometimes use the definition with a fixed hardness parameter \({\mathbf {n}} \). Note also that the definition is fundamentally different from resource-restricted indifferentiability [25] in that there the simulator is restricted, as the idea is to preserve the same complexity (notion).
Further Discussion on the Real Model. In the real model, the resource described in Fig. 3 is available to the (honest) party at the \(\mathrm {priv}\)-interface and the adversarial party at the \(\mathrm {pub}\)-interface. Since our goal is to model different types of computational hardness of specific tasks, that is, describe the amount of resources needed to perform these tasks, the nature of the remaining resources will naturally vary depending on the particular type of hardness being modeled. For example, when modeling memory-hardness, the computation resource would limit the amount of memory available during the evaluation, and a bound on the computational power available to the party would correspond to defining computational hardness. Each resource is parametrized by two values \({\mathbf {l}} \) and \({\mathbf {r}} \) (from some arbitrary parameter space \({\mathbb {P}} \)) denoting limits on the amount of the resources available to the parties at the \(\mathrm {priv}\)- and \(\mathrm {pub}\)-interfaces, respectively.Footnote 6 Beyond the local computation resources described above, oracle algorithms have access to an oracle that is chosen initially in the resource according to the prescribed distribution and the same instance is made available to the algorithms at all interfaces. In this work, the algorithms will always have access to a random oracle, i.e. a resource that behaves like a random function \({h} \).
We generally denote the real-world resource by the letter \(\mathcal S^{\textsc {}}\) and use the superscript to further specify the type of computational resource and the subscript for the resource bounds, as \(\mathcal S^{\textsc {2oa}}_{a,b}\) in Example 4, where \({\mathbb {P}} = {\mathbb {N}} \), \({\mathbf {l}} = a\) and \({\mathbf {r}} = b\).
Both interfaces \(\mathrm {priv}\) and \(\mathrm {pub}\) of the real-world resource expect as an input a program that will be executed using the resources specified at the respective interface. Suppose we wish to make a security statement about the hardness of a particular MoHF with the naïve algorithm  . Besides the resources themselves, the real world contains a system \({{\pi }_{}} \) that simply inputs
. Besides the resources themselves, the real world contains a system \({{\pi }_{}} \) that simply inputs  to be executed. Following the specification in Fig. 3, the execution in the real model can be described as follows:
to be executed. Following the specification in Fig. 3, the execution in the real model can be described as follows:
-
Initially, \( D \) is activated and can evaluate
 on inputs of its choice by providing inputs at the \(\mathrm {priv}\)-interface.Footnote 7
on inputs of its choice by providing inputs at the \(\mathrm {priv}\)-interface.Footnote 7
-
Next, \( D \) can provide as input an algorithm \({\mathtt {A}} \) at the \(\mathrm {pub}\)-interface, and evaluate \({\mathtt {A}} \) on one input x. The computation resource will evaluate \({\mathtt {A}} \) on input x.
-
Next, \( D \) can again provide queries at the \(\mathrm {priv}\)-interface to evaluate the algorithms
 (until the resources are exhausted).
(until the resources are exhausted). -
Eventually, \( D \) outputs a bit (denoting its guess at whether it just interacted with the real world or not) and terminates.
At first sight, it might appear counter-intuitive that we allow the algorithm \({\mathtt {A}} \) input at \(\mathrm {pub}\) to be evaluated only once, and not repeatedly, which would be stronger. The reason is that, for most complexity measures we are interested in, such as for memory-hard functions, continuous interaction with the environment \({ D } \) would allow \({\mathtt {A}} \) to “outsource” relevant resource-use to \({ D } \), and contradict our goal of precisely measuring \({\mathtt {A}} \)’s resource consumption (and thereby sometimes render non-trivial statements impossible). This restriction can be relaxed wherever possible, as in Example 4.
Further Discussion on Ideal Model. The (ideal-world) resource \(\mathcal T^{\textsc {}}\) also has a \(\mathrm {priv}\)- and a \(\mathrm {pub}\)-interface. In our definition of a MoHF, the ideal-world resource is always of the type \(\mathcal T^{\textsc {rro}}_{a,b}\) with \(a,b\in {\mathbb {N}} \), that is, a random oracle that allows a queries at the \(\mathrm {priv}\)- and b queries at the \(\mathrm {pub}\)-interface. The \(\mathrm {priv}\)-interface can be used by the distinguisher to query the oracle, while the \(\mathrm {pub}\)-interface is accessed by the simulator system \({{\sigma }} \) whose job it is to simulate the \(\mathrm {pub}\)-interface of the real model consistently.
More precisely, for statements about parametrized real-world resources, we consider a class of ideal resources \(\mathcal T^{\textsc {rro}}_{{\mathsf {a}},{\mathsf {b}}}\) characterized by two functions \({\mathsf {a}} \) and \({\mathsf {b}} \) which map elements of \({\mathbb {P}} \) to \({\mathbb {N}} \). For any concrete real model given by parameters \(({\mathbf {l}}, {\mathbf {r}})\) we compare with the concrete ideal model with resource \(\mathcal T^{\textsc {rro}}_{{\mathsf {a}} ({\mathbf {l}}),{\mathsf {b}} ({\mathbf {r}})}\) parametrized by \(({\mathsf {a}} ({\mathbf {l}}), {\mathsf {b}} ({\mathbf {r}}))\). These numbers denote an upper bound on the number of queries to the random oracle permitted on the \(\mathrm {priv}\)- and \(\mathrm {pub}\)-interfaces, respectively. In particular, after \({\mathsf {a}} ({\mathbf {l}})\) queries on the \(\mathrm {priv}\)-interface all future queries on that interface are responded to with \(\bot \) (and similarly for the \(\mathrm {pub}\)-interface with the limit \({\mathsf {b}} ({\mathbf {r}})\)).
To a distinguisher \( D \), an execution with the ideal model looks as follows:
-
Initially, \( D \) is activated, and can make queries to \(\mathcal T^{\textsc {rro}}_{{\mathsf {a}} ({\mathbf {l}}),{\mathsf {b}} ({\mathbf {r}})}\) at the \(\mathrm {priv}\)-interface. (After \({\mathsf {a}} ({\mathbf {l}})\) queries \(\mathcal T^{\textsc {rro}}_{{\mathsf {a}} ({\mathbf {l}}),{\mathsf {b}} ({\mathbf {r}})}\) always responds with \(\bot \).)
-
Next, \( D \) can provide as input an algorithm \({\mathtt {A}} \) at the \(\mathrm {pub}\)-interface. Overall, the simulator \({{\sigma }} \) can make at most \({\mathsf {b}} ({\mathbf {r}})\) queries to \(\mathcal T^{\textsc {rro}}_{{\mathsf {a}} ({\mathbf {l}}),{\mathsf {b}} ({\mathbf {r}})}\).
-
Next, \( D \) can make further queries to \(\mathcal T^{\textsc {rro}}_{{\mathsf {a}} ({\mathbf {l}}),{\mathsf {b}} ({\mathbf {r}})}\) on the \(\mathrm {priv}\)-interface.
-
Finally, \( D \) outputs a bit (denoting its guess at whether it just interacted with the real world or not) and terminates.
An ideal model is outlined in Fig. 5 with \(\mathrm {priv}\) and \(\mathrm {pub}\) resource limits \(a'\) and \(b'\) respectively.
4 Memory-Hard Functions
Moving beyond the straightforward example of an MoHF based on computational hardness developed during the above examples, we describe more advanced types of MoHFs in this and the next section. Each one is based on a different complexity notion and computational model. For each one, we describe one (or more) constructions. Moreover, for the first two we provide a powerful tool for constructing provably secure MoHFs of those types. We begin, in this section, with memory-hard functions (MHF).
In the introduction, we discussed shortcomings of the existing definitions of MHFs. We address these concerns by instantiating MHFs within our general MoHF framework and providing a pebbling reduction with which we can “rescue” the MHF constructions [5, 6, 10] and security proofs [5, 6] of several recent MHFs from the literature. More generally, the tool is likely to prove useful in the future as new, more practical graphs are developed [5] and/or new labeling functions are developed beyond an ideal compression function. (For more details what is meant by “rescue” we refer to discussion immediately after Theorem 1.)
4.1 The Parallel ROM
To define an MHF, we consider a resource-bounded computational device \(\mathcal S^{\textsc {}}\) with a \(\mathrm {priv}\)- and a \(\mathrm {pub}\)-interface capturing the pROM (adapted from [8]). Let \(w\in {\mathbb {N}} \). Upon startup,  samples a fresh random oracle
samples a fresh random oracle  with range \(\{0,1\}^w\). Now, on both interfaces,
with range \(\{0,1\}^w\). Now, on both interfaces,  accepts as input a pROM algorithm \({\mathtt {A}} \) which is an oracle algorithm with the following behavior.
accepts as input a pROM algorithm \({\mathtt {A}} \) which is an oracle algorithm with the following behavior.
A state is a pair \(({\tau }, \mathbf{{s}})\) where data \({\tau } \) is a string and \(\mathbf{{s}} \) is a tuple of strings. The output of step i of algorithm \({\mathtt {A}} \) is an output state \({\bar{{\sigma _{}}}} _{i} = ({\tau } _{i}, \mathbf{{q}} _{i})\) where \(\mathbf{{q}} _i = [q_i^1,\ldots ,q_i^{z_i}]\) is a tuple of queries to h. As input to step \(i+1\), algorithm \({\mathtt {A}} \) is given the corresponding input state \({\sigma _{}} _{i} = ({\tau } _{i}, h(\mathbf{{q}} _{i}))\), where \(h(\mathbf{{q}} _i) = [h(q_i^1), \ldots , h(q_i^{z_i})]\) is the tuple of responses from h to the queries \(\mathbf{{q}} _i\). In particular, for a given h and random coins of \({\mathtt {A}} \), the input state \({\sigma _{}} _{i+1}\) is a function of the input state \({\sigma _{}} _{i}\). The initial state \({\sigma _{}} _{0}\) is empty and the input \(x_{\mathsf{{in}}}\) to the computation is given a special input in step 1.
For a given execution of a pROM, we are interested in the following complexity measure. We denote the bit-length of a string s by |s|. The length of a state \({\sigma _{}} =({\tau },\mathbf{{s}})\) with \(\mathbf{{s}} =(s^1, s^2, \ldots , s^y)\) is \(|{\sigma _{}} | = |{\tau } | + \sum _{i\in [y]} |s^i|\). The cumulative memory complexity (CMC) of an execution is the sum of the lengths of the states in the execution. More precisely, let us consider an execution of algorithm \({\mathtt {A}} \) on input \(x_{\mathsf{{in}}}\) using coins \({\$} \) with oracle h resulting in \(z\in {\mathbb {Z}} _{\ge 0}\) input states \({\sigma _{}} _{1}, \ldots , {\sigma _{}} _{z}\), where \({\sigma _{}} _{i} = ({\tau } _i,\mathbf{{s}} _i)\) and \(\mathbf{{s}} _i = (s_i^1, s_i^2, \ldots , s_i^{y_j})\). Then the cumulative memory complexity (CMC) of the execution is

while the total number of RO calls is \(\sum _{i\in [z]} y_j\). More generally, the CMC (and total number of RO calls) of several executions is the sum of the CMC (and total RO calls) of the individual executions.
We now describe the resource constraints imposed by  on the pROM algorithms it executes. To quantify the constraints,
on the pROM algorithms it executes. To quantify the constraints,  is parametrized by a left and a right tuple from the following parameter space \({{\mathbb {P}} ^{\textsc {prom}}} = ({\mathbb {Z}} _{\ge 0})^2\) describing the constraints for the \(\mathrm {priv}\) and \(\mathrm {pub}\) interfaces respectively. In particular, for parameters \((q, m)\in {{\mathbb {P}} ^{\textsc {prom}}} \), the corresponding pROM algorithm is allowed to make a total of q RO calls and use CMC at most m summed up across all of the algorithms executions.Footnote 8
is parametrized by a left and a right tuple from the following parameter space \({{\mathbb {P}} ^{\textsc {prom}}} = ({\mathbb {Z}} _{\ge 0})^2\) describing the constraints for the \(\mathrm {priv}\) and \(\mathrm {pub}\) interfaces respectively. In particular, for parameters \((q, m)\in {{\mathbb {P}} ^{\textsc {prom}}} \), the corresponding pROM algorithm is allowed to make a total of q RO calls and use CMC at most m summed up across all of the algorithms executions.Footnote 8
As usual for memory-hard functions, to ensure that the honest algorithm can be run on realistic devices,  restricts the algorithms on the \(\mathrm {priv}\)-interface to be sequential. That is, the algorithms can make only a single call to h per step. Technically, in any execution, for any step j it must be that \(y_j \le 1\). No such restriction is placed on the adversarial algorithm reflecting the power (potentially) available to such a highly parallel device as an ASIC.
restricts the algorithms on the \(\mathrm {priv}\)-interface to be sequential. That is, the algorithms can make only a single call to h per step. Technically, in any execution, for any step j it must be that \(y_j \le 1\). No such restriction is placed on the adversarial algorithm reflecting the power (potentially) available to such a highly parallel device as an ASIC.
We conclude the section with the formal definition of a memory-hard function in the pROM. The definition is a particular instance of an MoHF defined in Definition 3 formulated in terms of exact security.
Definition 4 ((Parallel) memory-hard function)
For each \({\mathbf {n}} \in {\mathbb {N}} \), let \(f_{\mathbf {n}} ^{(\cdot )}\) be an oracle function and  be a pROM algorithm for computing \(f^{(\cdot )}\). Consider the function families:
be a pROM algorithm for computing \(f^{(\cdot )}\). Consider the function families:
Then  is called an \(({\mathsf {a}},{\mathsf {b}},{\epsilon })\)-memory-hard function (MHF) if \(\forall w\in {\mathbb {N}} \) F is an \(({\mathsf {a}} _w,{\mathsf {b}} _w,{\epsilon } _w)\)-secure moderately hard function family for
is called an \(({\mathsf {a}},{\mathsf {b}},{\epsilon })\)-memory-hard function (MHF) if \(\forall w\in {\mathbb {N}} \) F is an \(({\mathsf {a}} _w,{\mathsf {b}} _w,{\epsilon } _w)\)-secure moderately hard function family for  .
.
Data-(In)dependent MHFs. An important distinction in the literature of memory-hard functions concerns the memory-access pattern of  . In particular, if the pattern is independent of the input x then we call this a data-independent MHF (iMHF) and otherwise we call it an data-dependent MHF (dMHF). The advantage of an iMHF is that the honest party running
. In particular, if the pattern is independent of the input x then we call this a data-independent MHF (iMHF) and otherwise we call it an data-dependent MHF (dMHF). The advantage of an iMHF is that the honest party running  is inherently more resistant to certain side-channel attacks (such as cache-timing attacks) which can lead to information leakage about the input x. When the MHF is used for, say, password hashing on a login server this can be a significant concern. Above, we have chosen to not make the addressing mechanism used to store a state \({\sigma _{}} \) explicit in
is inherently more resistant to certain side-channel attacks (such as cache-timing attacks) which can lead to information leakage about the input x. When the MHF is used for, say, password hashing on a login server this can be a significant concern. Above, we have chosen to not make the addressing mechanism used to store a state \({\sigma _{}} \) explicit in  , as it would significantly complicate the exposition with little benefit. Yet, we remark that doing so would definitely be possible within the wider MoHF framework presented here if needed. Moreover the tools for constructing MHFs below actually construct iMHFs.
, as it would significantly complicate the exposition with little benefit. Yet, we remark that doing so would definitely be possible within the wider MoHF framework presented here if needed. Moreover the tools for constructing MHFs below actually construct iMHFs.
4.2 Graph Functions
Now that we have a concrete definition in mind, we turn to constructions. We first define a large class of oracle functions (called graph functions) which have appeared in various guises in the literature [10, 29, 31] (although we differ slightly in some details which simplify later proofs). This allows us to prove the main result of this section; namely a “pebbling reduction” for graph functions. That is, for a graph function F based on some graph G, we show function families \(({\mathsf {a}}, {\mathsf {b}}, {\epsilon })\) depending on G, for which function F is an MHF.
We start by formalizing (a slight refinement of) the usual notion of a graph function (as it appears in, say, [10, 31]). For this, we use the following common notation and terminology. For a directed acyclic graph (DAG) \(G=(V,E)\), we call a node with no incoming edges a source and a node with no outgoing edges a sink. The in-degree of a node is the number of its incoming edges and the in-degree of G is the maximum in-degree of any of its nodes. The parents of a node v are the set of nodes with outgoing edges leading to v. We also implicitly associate the elements of V with unique strings.Footnote 9
A graph function makes use of a oracle \(h\in {\mathbb {H}} _w\) defined over bit strings. Technically, we assume an implicit prefix-free encoding such that h is evaluated on unique strings. Inputs to h are given as distinct tuples of strings (or even tuples of tuples of strings). For example, we assume that h(0, 00), h(00, 0), and h((0, 0), 0) all denote distinct inputs to h.
Definition 5 (Graph function)
Let function \(h:\{0,1\}^* \rightarrow \{0,1\}^w\in {\mathbb {H}} _w\) and DAG \(G=(V,E)\) have source nodes \(\{v^{{\mathsf {in}}}_1, \ldots , v^{{\mathsf {in}}}_a\}\) and sink nodes \((v^{{\mathsf {out}}}_1, \ldots , v^{{\mathsf {out}}}_z)\). Then, for inputs \({\mathbf{x}} = (x_1,\ldots ,x_a) \in (\{0,1\}^*)^{\times a}\), the \((h, {\mathbf{x}})\)-labeling of G is a mapping \(\mathsf{{lab}}: V \rightarrow \{0,1\}^w\) defined recursively to be:
where \(\{v_1, \ldots , v_d\}\) are the parents of v arranged in lexicographic order. The graph function (of G and \({\mathbb {H}} _w\)) is the oracle function
which maps \({\mathbf{x}} \mapsto (\mathsf{{lab}}(v^{{\mathsf {out}}}_1), \ldots , \mathsf{{lab}}(v^{{\mathsf {out}}}_z))\) where \(\mathsf{{lab}}\) is the \((h,{\mathbf{x}})\)-labeling of G.
The above definition differs from the one in [10] in two ways. First, it considers graphs with multiple source and sink nodes. Second it prefixes all calls to h with the input \({\mathbf{x}} \). This ensures that, given any pair of distinct inputs \({\mathbf{x}} _1\ne {\mathbf{x}} _2\), no call to h made by \(f_G({\mathbf{x}} _1)\) is repeated by \(f_G({\mathbf{x}} _2)\). Intuitively, this ensures that finding collisions in h can no longer help avoiding making a call to h for each new label being computed. Technically, it simplifies proofs as we no longer need to compute and carry along the probability of such a collision. We remark that this is merely a technicality and if, as done in practice, the prefixing (of both \({\mathbf{x}} \) and the node v) is omitted, security will only degrade by a negligible amount.Footnote 10
The naïve Algorithm. The naïve oracle algorithm  for \(f_G\) computes one label of G at a time in topological order appending the result to its state. If G has \(|V|=n\) nodes then
for \(f_G\) computes one label of G at a time in topological order appending the result to its state. If G has \(|V|=n\) nodes then  will terminate in n steps making at 1 call to h per step, for a total of n calls, and will never store more than \(w(i-1)\) bits in the data portion of its state in the ith round. In particular for all inputs \({\mathbf{x}} \), oracles h (and coins \({\$} \)) we have that
will terminate in n steps making at 1 call to h per step, for a total of n calls, and will never store more than \(w(i-1)\) bits in the data portion of its state in the ith round. In particular for all inputs \({\mathbf{x}} \), oracles h (and coins \({\$} \)) we have that  . Therefore, in the definition of an MHF we can set \({\mathsf {a}} _w(q,m) = \min ({\left\lfloor q/n\right\rfloor },{\left\lfloor 2m/wn(n-1)\right\rfloor })\). It remains to determine how to set \({\mathsf {b}} _w\) and \({\epsilon } _w\), which is the focus of the next section.
. Therefore, in the definition of an MHF we can set \({\mathsf {a}} _w(q,m) = \min ({\left\lfloor q/n\right\rfloor },{\left\lfloor 2m/wn(n-1)\right\rfloor })\). It remains to determine how to set \({\mathsf {b}} _w\) and \({\epsilon } _w\), which is the focus of the next section.
4.3 A Parallel Memory-Hard MoHF
In this section, we prove a pebbling reduction for memory hardness of a graph function \(f_G\) in the pROM. To this end, we first recall the parallel pebbling game over DAGs and associated cumulative pebbling complexity (CPC).
The Parallel Pebbling Game. The sequential version of the following pebbling game first appeared in [24, 38] and the parallel version in [10]. Put simply, the game is a variant of the standard black-pebbling game where pebbles can be placed according to the usual rules but in batches of moves performed in parallel rather than one at a time sequentially.
Definition 6 (Pebbling a graph)
Let \(G= (V,E)\) be a DAG and \(T,S \subseteq V\) be node sets. Then a (legal) pebbling of G (with starting configuration S and target T) is a sequence \(P=(P_0,\ldots ,P_t)\) of subsets of V such that:
-
1.
\(P_0 \subseteq S\).
-
2.
Pebbles are added only when their predecessors already have a pebble at the end of the previous step.
$$ \forall i \in [t]\,\,\,\,\,\, \forall (x,y)\in E\,\,\,\,\,\,\forall y \in P_i \setminus P_{i-1} \,\,\,\,\,\,\,\,\,\,\,\, x \in P_{i-1} .$$ -
3.
At some point every target node is pebbled (though not necessarily simultaneously).
$$ \forall x \in T\,\,\,\,\,\, \exists z \le t \,\,\,\,\,\,\,\,\,\,\,\, x\in P_z .$$
We call a pebbling of G complete if \(S=\emptyset \) and T is the set of sink nodes of G.
We call a pebbling sequential if no more than one new pebble is placed per step,
In this simple model of computation we are interested in the following complexity notion for DAGs taken from [10].
Definition 7 (Cumulative pebbling complexity)
Let G be a DAG, \(P=(P_0,\ldots ,P_t)\) be an arbitrary pebbling of G, and \(\Pi \) be the set of all complete pebblings of G. Then the (pebbling) cost of P and the cumulative pebbling complexity (CPC) of G are defined respectively to be:
A Pebbling Reduction for Memory-Hard Functions. We are now ready to formally state and prove the main technical result: a security statement showing a graph function to be an MHF for parameters \(({\mathsf {a}},{\mathsf {b}},{\epsilon })\) expressed in terms of the CPC of the graph and the number of bits in the output of h.
Theorem 1 (Pebbling reduction)
Let \(G_n=(V_n,E_n)\) be a DAG of size \(|V_n|=n\). Let  be the graph functions for \(G_n\) and their naïve oracle algorithms. Then, for any \(\lambda \ge 0\), F is an \(({\mathsf {a}},{\mathsf {b}},{\epsilon })\)-memory-hard function where
be the graph functions for \(G_n\) and their naïve oracle algorithms. Then, for any \(\lambda \ge 0\), F is an \(({\mathsf {a}},{\mathsf {b}},{\epsilon })\)-memory-hard function where
We note that \(\mathsf{{cpc}}\) charges for keeping pebbles on G which, intuitively, models storing the label of a node in the data component of an input state. However the complexity notion \(\mathsf{{cmc}}\) for the pROM also charges for the responses to RO queries included in input states. We discuss three options to address this discrepancy.
-
1.
Modify our definition of the pROM to that used in [10]. There, the \({i}^{th}\) batch of queries \(\mathbf{{q}} _i\) to h is made during step i. So the state stored between steps only contains the data component \({\tau } _i\). Thus \(\mathsf{{cmc}}\) in that model is more closely modeled by \(\mathsf{{cpc}}\). While the techniques used below to prove Theorem 1 carry over essentially unchanged to that model, we have opted to not go with that approach as we believe the version of the pROM used here (and in [7]) more closely captures computation for an ASIC. That is, it better models the constraint that during an evaluation of the hash function(s) a circuit must store any remaining state it intends to make use of later in separate registers. Moreover, given the depth of the circuit of hash functions used to realize h, at least one register per output bit of h will be needed.Footnote 11
-
2.
Modify the notion of \(\mathsf{{cpc}}\) to obtain \(\mathsf{{cpc}}'\), which also charges for new pebbles being placed on the graph. That is use \(\mathsf{{cpc}}' = \mathsf{{cpc}}+ \sum _{i}|P_i \setminus P_{i-1}|\) as the pebbling cost.Footnote 12 Such a notion would more closely reflect the way \(\mathsf{{cmc}}\) is defined in this work. In particular, it would allow for a tighter lower bound in Theorem 1, since for any graph \(\mathsf{{cpc}}' \ge \mathsf{{cpc}}\). Moreover, it would be easy to adapt the proof of Theorem 1 to accommodate \(\mathsf{{cpc}}'\). Indeed, (using the terminology from the proof of Theorem 1) in the ex-post-facto pebbling P of an execution, a node \(v\not \in P^x_{i-1}\) is only added to \(P^x_i\) if it becomes necessary for x at time i. By definition, this can only happen if there is a correct call for (x, v) in the input state \({\sigma _{}} _{i}\). Thus, we are guaranteed that for each time step i it holds that \(\sum _{i} \sum _{x} |P^x_i \setminus P^x_{i-1}| \le y_i\), where \(y_i\) is the number of queries to h in input state \({\sigma _{}} _{i}\). So we can indeed modify the second claim in the proof to also add the quantity \(\sum _{x} |P^x_i \setminus P^x_{i-1}|\) to the left side of the inequality. The downside of this approach is that using \(\mathsf{{cpc}}'\) in Theorem 1 would mean that it is no longer (immediately) clear if we can use any past results from the literature about \(\mathsf{{cpc}}\).
-
3.
The third option, which we have opted for in this work, is to borrow from the more intuitive formulation of the pROM of [7] while sticking with the traditional pebbling complexity notion of \(\mathsf{{cpc}}\). We do this because, on the one hand, for any graph \(\mathsf{{cpc}}' \le 2\mathsf{{cpc}}\), so at most a factor of 2 is lost the tightness of Theorem 1 when using \(\mathsf{{cpc}}\) instead of \(\mathsf{{cpc}}'\). Yet on the other hand, for \(\mathsf{{cpc}}\) we already have constructions of graphs with asymptotically maximal \(\mathsf{{cpc}}\) as well as a variety of techniques for analyzing the \(\mathsf{{cpc}}\) of graphs. In particular we have upper and lower bounds for the \(\mathsf{{cpc}}\) of arbitrary DAGs as well as for many specific graphs (and graph distributions) used in the literature as the basis for interesting graph functions [3, 4, 6, 9, 10]. Thus we have opted for this route so as to (A) strengthen the intuition underpinning the model of computation, (B) leave it clear that Theorem 1 can be used in conjunction with all of the past concerning \(\mathsf{{cpc}}\) while (C) only paying a small price in the tightness of the bound we show in that theorem.
The remainder of this subsection is dedicated to proving the theorem. For simplicity we will restrict ourselves to DAGs with a single source \(v_{\in }\) and sink \(v_{\mathsf{{out}}}\) but this only simplifies notation. The more general case for any DAG is identical. The rough outline of the proof is as follows. We begin by describing a simulator \({{\sigma }} \) as in Definition 3, whose goal is to simulate the \(\mathrm {pub}\)-interface of  to a distinguisher \({ D } \) while actually being connected to the \(\mathrm {pub}\)-interface of \(\mathcal T^{\textsc {rro}}_{}\). In a nutshell, \({{\sigma }} \) will emulate the algorithm \({\mathtt {A}} \) it is given by \({ D } \) internally by emulating a copy of
to a distinguisher \({ D } \) while actually being connected to the \(\mathrm {pub}\)-interface of \(\mathcal T^{\textsc {rro}}_{}\). In a nutshell, \({{\sigma }} \) will emulate the algorithm \({\mathtt {A}} \) it is given by \({ D } \) internally by emulating a copy of  to it. \({{\sigma }} \) will keep track of the RO calls made by \({\mathtt {A}} \) and, whenever \({\mathtt {A}} \) has made all the calls corresponding to a complete and legal (x, h)-labeling of G, then \({{\sigma }} \) will query \(\mathcal T^{\textsc {rro}}_{}\) at point x and return the result to \({\mathtt {A}} \) as the result of the final RO call for that labeling.
to it. \({{\sigma }} \) will keep track of the RO calls made by \({\mathtt {A}} \) and, whenever \({\mathtt {A}} \) has made all the calls corresponding to a complete and legal (x, h)-labeling of G, then \({{\sigma }} \) will query \(\mathcal T^{\textsc {rro}}_{}\) at point x and return the result to \({\mathtt {A}} \) as the result of the final RO call for that labeling.
To prove that \({{\sigma }} \) achieves this goal (with high probability) we introduce a generalization of the pebbling game, called an m-color pebbling, and state a trivial lemma showing that the cumulative m-color pebbling complexity of a graph is m times the CC of the graph. Next, we define a mapping between a sequence of RO calls made during an execution in the pROM (such as that of \({\mathtt {A}} \) being emulated by \({{\sigma }} \)) and an m-coloring P of G. We prove a lemma stating that, w.h.p., if m distinct I/O pairs for \(f_G\) were produced during the execution, then P is legal and complete. We also prove a lemma upper-bounding the pebbling cost of P in terms of the CMC (and number of calls made to the RO) of the execution. But since the pebbling cost of G cannot be smaller than \(m \cdot \mathsf{{cpc}}(G)\), this gives us a lower bound on the memory cost of any such execution, as desired. Indeed, any algorithm in the pROM that violates our bound on memory cost with too high probability implies the existence of a pebbling of G with too low pebbling cost, contradicting the pebbling complexity of G. But this means that when \({{\sigma }} \) limits CMC (and number of RO calls) of the emulation of \({\mathtt {A}} \) accordingly, then w.h.p. we can upper-bound the number of calls \({{\sigma }} \) will need to \(\mathcal T^{\textsc {rro}}_{}\).
To complete the proof, we have to show that using the above statements about \({{\sigma }} \) imply that indifferentiability holds. Indeed, the simulation, conditioned on the events that no lucky queries occur and that the simulator does not need excessive queries, is perfect. Therefore, the distinguishing advantage can be bounded by the probability of provoking either of those events, which can be done by the above statements about \({{\sigma }} \). A detailed proof can be found in the full version [11].
5 Other Types of MoHFs
Besides MHFs, several other types of MoHFs have been considered in the literature. In this section, we briefly review weak memory-hard functions and memory-bound functions. A discussion of one-time computable functions and uncomputable functions is given in Sect. 5.3.
5.1 Weak Memory-Hard Functions
A class of MoHFs considered in the literature that are closely related to MoHFs are weak MoHFs. Intuitively, they differ from MoHFs only in that they also restrict adversaries to being sequential.Footnote 13 On the one hand, it may be easier to construct such functions compared to full blown MoHF. In fact, for the data-independent variant of MoHFs, [3] proves that a graph function based on a DAG of size n always has \(\mathsf{{cmc}}\) of \(O(wn^2/\log (n))\) (ignoring \(\log \log \) factors). Yet, as discussed below, the results of [33, 42] and those described below show that we can build W-MoHFs from similar DAGs with sequential  of \(\mathcal {O}(2n^2)\). Put differently, W-MoHFs allow for strictly more memory consumption per call to the RO than is possible with MoHFs. This is valuable since the limiting factor for an adversary is often the memory consumption while the cost for honest parties to enforce high memory consumption is the number of calls they must perform to the RO.
of \(\mathcal {O}(2n^2)\). Put differently, W-MoHFs allow for strictly more memory consumption per call to the RO than is possible with MoHFs. This is valuable since the limiting factor for an adversary is often the memory consumption while the cost for honest parties to enforce high memory consumption is the number of calls they must perform to the RO.
We capture weak MoHFs in the MoHFframework by restricting the real world resource-bounded computational device  to the sequential random oracle model (sROM). Given this definition we can now easily adapt the pebbling reduction of Theorem 1 to obtain a tool for constructing W-MoHFs, which has some immediate implications. In [42], Lengaur and Tarjan prove that the DAGs underlying the two graph functions Catena Dragonfly and Butterfly [33] have
to the sequential random oracle model (sROM). Given this definition we can now easily adapt the pebbling reduction of Theorem 1 to obtain a tool for constructing W-MoHFs, which has some immediate implications. In [42], Lengaur and Tarjan prove that the DAGs underlying the two graph functions Catena Dragonfly and Butterfly [33] have  . In [33], the authors extend these results to analyze the \(\mathsf{{scpc}}\) of stacks of these DAGs. By combining those results with the pebbling reduction for the sROM, we obtain parameters \(({\mathsf {a}},{\mathsf {b}},{\epsilon })\) for which the Catena functions are provably W-MoHFs. Similar implications hold for the pebbling analysis done for the Balloon Hashing function in [18]. Weak memory hard functions are discussed in more detail in the full version [11].
. In [33], the authors extend these results to analyze the \(\mathsf{{scpc}}\) of stacks of these DAGs. By combining those results with the pebbling reduction for the sROM, we obtain parameters \(({\mathsf {a}},{\mathsf {b}},{\epsilon })\) for which the Catena functions are provably W-MoHFs. Similar implications hold for the pebbling analysis done for the Balloon Hashing function in [18]. Weak memory hard functions are discussed in more detail in the full version [11].
5.2 Memory-Bound Functions
Another important notion of MoHF from the literature has been considered in [27, 29]. These predate MHFs and are based on the observation that while computation speeds vary greatly across real-world computational devices, this is much less so for memory-access speeds. Under the assumption that time spent on a computation correlates with the monetary cost of the computation, this observation motivates measuring the cost of a given execution by the number of cache misses (i.e., memory accesses) made during the computation. A function that requires a large number of misses, regardless of the algorithm used to evaluate the function, is called a memory-bound function.
Memory-Bound Functions as MoHFs. We show how to formalize memory-bound functions in the MoHF framework. In particular, we describe the real-world resource-bounded computational device  . It makes use of RO with w-bits of output and is parametrized by 6 positive integers \({{\mathbb {P}} ^{\textsc {mb}}} = {\mathbb {N}} ^{\times 6}\). That is, following the model of [29], an algorithm \({\mathtt {A}} \), executed by
. It makes use of RO with w-bits of output and is parametrized by 6 positive integers \({{\mathbb {P}} ^{\textsc {mb}}} = {\mathbb {N}} ^{\times 6}\). That is, following the model of [29], an algorithm \({\mathtt {A}} \), executed by  with parameters \((m,b,s,{\omega },c,q)\), makes a sequence of calls to the RO and has access to a two tiered memory consisting of a cache of limited size and a working memory (as large as needed). The memory is partitioned into m blocks of b bits each, while cache is divided into s words of \({\omega } \) bits each. When \({\mathtt {A}} \) requests a location in memory, if the location is already contained in cache, then \({\mathtt {A}} \) is given the value for free, otherwise the block of memory containing that location is fetched into cache. The algorithm is permitted a total of q calls to the RO and c fetches (i.e. cache misses) across all executions.
with parameters \((m,b,s,{\omega },c,q)\), makes a sequence of calls to the RO and has access to a two tiered memory consisting of a cache of limited size and a working memory (as large as needed). The memory is partitioned into m blocks of b bits each, while cache is divided into s words of \({\omega } \) bits each. When \({\mathtt {A}} \) requests a location in memory, if the location is already contained in cache, then \({\mathtt {A}} \) is given the value for free, otherwise the block of memory containing that location is fetched into cache. The algorithm is permitted a total of q calls to the RO and c fetches (i.e. cache misses) across all executions.
In [27, 29] the authors describe such functions (with several parameters each) and prove that the hash-trail construction applied to these functions results in a PoE for a notion of “effort” captured by memory-boundedness. (See Sect. 6 for more on the hash-trail construction and PoEs). We conjecture that the proofs in those works carry over to the notion of memory-bound MoHFs described above (using some of the techniques at the end of the proof of Theorem 1). Yet, we believe that a more general pebbling reduction (similar to Theorem 1) is possible for the above definition. Such a theorem would allow us to construct new and improved memory-bound functions. (On the one hand, the function described in [27] has a large description—many megabytes—while the function in [29] is based on superconcentrators which can be somewhat difficult to implement in practice with optimal constants.) In any case, we believe investigating memory-bound functions as MoHFs to be an interesting and tractable line of future work.
5.3 One-Time Computable and Uncomputable Functions
Another—less widely used—notion of MoHFs appearing in the literature are one-time computable functions [31]. Intuitively, these are sets of T pseudo-random functions (PRFs) \(f_1,\ldots ,f_T\) with long keys (where T is an a priori fixed, arbitrary number). An honest party can evaluate each function \(f_i\) exactly once, using a device with limited memory containing these keys. On such a device, evaluating the \({i}^{th}\) PRF provably requires deleting all of the first i keys. Therefore, if an adversary (with arbitrary memory and computational power) can only learn a limited amount of information about the internal state of the device, then regardless of the computation performed on the device, the adversary will never learn more than one input/output pair per PRF. The authors describe the intuitive application of a password-storage device secure against dictionary attacks. An advantage of using the MoHF framework to capture one-time computable functions could be proving security for such an application (using the framework’s composition theorem).
We describe a model for one-time computable functions and uncomputable functions in Sect. 5, where we also sketch a new (hypothetical) application for one-time computable functions in the context of anonymous digital payment systems. We discuss this notion in more detail in the full version [11].
6 Interactive Proofs of Effort
One important practical application of MoHFs are proofs of effort (PoE), where the effort may correspond to computation, memory, or other types of resources that the hardness of which can be used in higher-level protocols to require one party, the prover, to spend a certain amount of resources before the other party, the verifier, has checked this spending and allows the protocol to continue.
6.1 Definition
Our composable definition of PoE is based on the idea of constructing an “ideal” proof-of-effort functionality from the bounded assumed resources the parties have access to in the real setting. Our Definition 3 for MoHFs can already be seen in a similar sense: from the assumed (bounded) resources available to the parties, evaluating the MoHF constructs a shared random function that can be evaluated for some bounded number of times. In the following, we describe the assumed and constructed resources that characterize a PoE.
The Goal of PoE Protocols. The high-level guarantees provided by a PoE to higher-level protocols can be described as follows. Prover \(P\) and verifier \(V\) interact in some number \(n\in {\mathbb {N}} \) of sessions, and in each of the sessions verifier \(V\) expects to be “convinced” by prover \(P\)’s spending of effort. Prover \(P\) can decide how to distribute the available resources toward convincing verifier \(V\) over the individual sessions; if prover \(P\) does not have sufficient resources to succeed in all sessions, then \(P\) can distribute its effort over the sessions. Verifier \(V\)’s protocol provides as output a bit that is 1 in all sessions where the prover attributed sufficient resources, and 0 otherwise. We formalize these guarantees in the resource \({\mathsf {POE}}\) that we describe in more detail below.

The resource \({\mathsf {POE}}\) that formalizes the guarantee achieved by the PoE in a given real-world setting is parametrized by values \(\underline{a},\overline{a},n\in {\mathbb {N}} \) and \(\phi : {\mathbb {N}} \rightarrow {\mathbb {R}} _{\ge 0}\), and is written as \({\mathsf {POE}}_{\phi ,n}^{{\overline{a}},{\underline{a}}} = ({\mathsf {POE}}_{\phi ,n}^{\underline{a}}, {\mathsf {POE}}_{\phi ,n}^{\overline{a}})\). For an honest prover \(P\), the parameter \(\underline{a}\in {\mathbb {N}} \) describes the overall number of “attempts” that \(P\) can take. For a dishonest prover \(P\), the same is described by the parameter \(\overline{a}\in {\mathbb {N}} \).Footnote 14 The success probability of a prover in each session depends on the computational resources spent in that session and can be computed as \(\phi (a)\), where \(a\in {\mathbb {N}} \) is the number of proof attempts in that session.
The “real-world” Setting for PoE Protocols. The PoE protocols we consider in this work are based on the evaluation of an MoHF, which, following Definition 3, can be abstracted as giving the prover and the verifier access to a shared uniform random function \(\mathcal T^{\textsc {rro}}_{}\) that they can evaluate for a certain number of times. We need to consider both the case where the prover is honest (to formalize that the PoE can be achieved with a certain amount of resources) and the case where the prover is dishonest (to formalize that not much more can be achieved by a dishonest prover). In addition to \(\mathcal T^{\textsc {rro}}_{}\), for \(n\) protocol sessions, the prover and verifier can also access n pairs of channels for bilateral communication, which we denote by \(\left[ \longrightarrow , \longleftarrow \right] ^n\) in the following. (This insecure communication resource is implicit in some composable frameworks such as Canetti’s UC [20].)
The resource specifies a bound \(\underline{b}\in {\mathbb {N}} \) for the number of queries that the verifier can make to \(\mathcal T^{\textsc {rro}}_{}\), and bounds \(\underline{a},\overline{a}\in {\mathbb {N}} \) for the cases where the prover is honest and dishonest, respectively. Considering the case \(\underline{a}\le \overline{a}\) makes sense because only loose bounds on the prover’s available resources may be known.
The Security Definition. Having described the real-world and ideal-world settings, we are now ready to state the security definition. This definition will consider the above-described cases where the prover is honest (this requires that the proof can be performed efficiently) and where the prover is dishonest (this requires that each proof need at least a certain effort), while we restrict our treatment to the case of honest verifiers. The security definition below follows the construction notion introduced in [45] for this specific case. The protocol and definition can additionally be extended by a hardness parameter \({\mathbf {n}} \) analogously to Definition 3.
Definition 8
A protocol \(\pi = (\pi _1,\pi _2)\) is a \((\phi ,n,\underline{b},\varepsilon )\)-proof of effort with respect to simulator \({{\sigma }} \) if for all \(\underline{a},\overline{a}\in {\mathbb {N}} \),
and
The reason for the term \(\overline{a}+n\) is that the dishonest prover can in each session decide to send a guess without verifying its correctness locally.
While the definition is phrased using the language of constructive cryptography [44, 45], it can intuitively also be viewed as a statement in Canetti’s UC framework [20].Footnote 15 For this, one would however have to additionally require the correctness formalized in the first equation of Definition 8, because UC-security would only correspond to the second equation.
6.2 Protocols
The PoE protocols we discuss in this section are interactive and start by the verifier sending a challenge to the prover, who responds with a solution. The verifier then checks this solution; an output bit signifies acceptance or rejection. There are several ways to build a scheme for PoE from an MoHF; we describe two particular schemes in this section.
Function Inversion. A simple PoE can be built on the idea of having the prover invert the MoHF on a given output value. This output value is obtained by evaluating the function on a publicly known and efficiently sampleable distribution over the input space, such as the uniform distribution over a certain subset.
Construction 1
The protocol is parametrized by a set \(D \subseteq \left\{ 0,1\right\} ^*\). For each session \(1\le i\le n\), it proceeds as follows:
-
1.
The verifier samples
 , queries \(y_i \leftarrow \mathcal T^{\textsc {rro}}_{}(i,x_i)\), and sends \(y_i\) to the prover.
, queries \(y_i \leftarrow \mathcal T^{\textsc {rro}}_{}(i,x_i)\), and sends \(y_i\) to the prover. -
2.
When activated in session i, the prover checks the nextFootnote 16 possible input value \(x' \in D\) for whether \(\mathcal T^{\textsc {rro}}_{}(i,x')=y_i\). If equality holds, send \(x'\) to the verifier and output 1 locally. Otherwise, output 0 locally.
-
3.
Receiving the value \(x' \in D\) in session i, the verifier accepts iff \(\mathcal T^{\textsc {rro}}_{}(i,x') = y_i\). When activated in session i, output 1 if accepted, and 0 otherwise.
Steps 1 and 3 comprise the verifier’s protocol \(\chi \), whereas step 2 describes the prover’s protocol \(\xi \). For this protocol, we show the following theorem. The proof is deferred to the full version [11].
Theorem 2
Define  . If \(\underline{b}> 2n\), then the described protocol \((\xi ,\chi )\) is a \((\phi , n, \underline{b}, 0)\)-proof of effort, with \(\phi : j \mapsto \zeta _{j} + \frac{1 - \zeta _{j}}{|R|}\). The simulator is described in the proof.
. If \(\underline{b}> 2n\), then the described protocol \((\xi ,\chi )\) is a \((\phi , n, \underline{b}, 0)\)-proof of effort, with \(\phi : j \mapsto \zeta _{j} + \frac{1 - \zeta _{j}}{|R|}\). The simulator is described in the proof.
Hash Trail. The idea underlying PoEs based on a hash trail is that it is difficult to compute a value such that the output of a given hash function on input this value satisfies a certain condition; usually one asks for a preimage x of a function \(f_i\) such that the output string \(f_i(x): \{0,1\}^m\rightarrow \{0,1\}^k\) starts with some number \(d\) of 0’s, where \(d\in \{1,\dots ,k\}\) can be chosen to adapt the (expected) effort necessary to provide a solution. For simplicity and to save on the number of parameters, we assume for the rest of the chapter that \(d\), the hardness parameter of the moderately hard function, is also the bit-length of the output.
Construction 2
The protocol is parametrized by sets \(D, N \subseteq \left\{ 0,1\right\} ^*\) and hardness parameter \(d\in {\mathbb {N}} \). For each session \(1\le i\le n\), it proceeds as follows:
-
1.
The verifier samples uniform
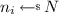 and sends \(n_i\) to the prover.
and sends \(n_i\) to the prover. -
2.
When activated, the prover chooses one value \(x' \in D\) uniformly at random (but without collisions), computes \(y \leftarrow \mathcal T^{\textsc {rro}}_{}(i, n_i, x_i)\), and checks whether \(y[1,\dots ,d] = 0^d\). If equality holds, send \(x'\) to the verifier and output 1 locally. Otherwise, output 0 locally.
-
3.
Receiving the value \(x' \in D\) from the prover, the verifier accepts iff \(y' \leftarrow \mathcal T^{\textsc {rro}}_{}(i , n_i , x')\) satisfies \(y'[1,\dots ,d] = 0^d\). When activated, output 1 if the protocol has accepted and 0 otherwise.
To capture the described scheme as a pair of algorithms \((\xi ,\chi )\) as needed for our security definition, we view steps 1 and 3 as the algorithm \(\chi \), whereas step 2 describes the algorithm \(\xi \). For this protocol, we show the following theorem. The proof is deferred to the full version [11].
Theorem 3
Let \(d\in {\mathbb {N}} \) be the hardness parameter and \(\underline{b}> n\). Then the described protocol \((\xi ,\chi )\) is a \((2^{-d},\underline{b},n,0)\)-proof of effort. The simulator \({{\sigma }} \) is described in the proof.
7 Non-interactive Proofs of Effort
The PoE protocols in Sect. 6.2 require the prover and the verifier to interact, because the verifier has to generate a fresh challenge for the prover in each session to prevent the prover from re-using (parts of) proofs in different sessions. This interaction is inappropriate in several settings, because it either imposes an additional round-trip on protocols (such as in key establishment) or because a setting may be inherently non-interactive, such as sending e-mail. In this section, we describe a non-interactive variant of PoE that can be used in such scenarios. Each proof is cryptographically bound to a certain value, and the higher-level protocol has to make sure that this value is bound to the application so that proofs cannot be re-used.
Although non-interactive PoE (niPoE) have appeared previously in certain applications, and have been suggested for fighting spam mail [1, 27,28,29], to the best of our knowledge they have not been formalized as a tool of their own right.
7.1 Definition
Our formalization of non-interactive PoE (niPoE) follows along the same lines as the one for the interactive proofs. The main difference is that while for interactive proofs, it made sense to some notion of session to which the PoE is associated and in which the verifier sends the challenge, this is not the case for niPoE. Instead, we consider each niPoE as being bound to some particular statement \(s \in \left\{ 0,1\right\} ^*\). This statement s is useful for binding the PoE to a particular context: in the combatting-spam scenario this could be a hash of the message to be sent, in the DoS-protection for key exchange this could be the client’s key share.
For consistency with Sect. 6, the treatment in this section is simplified to deal with either only honest or only dishonest provers. The case where both honest and dishonest provers occur simultaneously is deferred to full version [11].
The Goal of niPoE Protocols. The constructed resource is similar to the resource \({\mathsf {POE}}{}{}\) described in Sect. 6.1, with the main difference that each proof is not bound to a session \(i\in {\mathbb {N}} \), but rather to a statement \(s\in \mathcal S\subseteq \left\{ 0,1\right\} ^*\). Consequently, the resource \({\mathsf {NIPOE}}{}{}\) takes as input at the \(P\)-interface statements \(s\in \mathcal S\), and returns 1 if the proof succeeded and 0 otherwise. Upon an activation at the verifier’s interface \(V\), if for any statement \(s\in \mathcal S\) a proof has been successful, the resource outputs this s, and it outputs \(\bot \) otherwise. An output \(s \not = \bot \) has the meaning that the party at the \(P\)-interface has spent enough effort for the particular statement s. Similarly to \({\mathsf {POE}}{}{}\), the resource \({\mathsf {NIPOE}}{}{}\) is parametrized by a bound \(a\in {\mathbb {N}} \) on the number of proof attempts and a performance function \(\phi : {\mathbb {N}} \rightarrow {\mathbb {R}} _{\ge 0}\), but additionally the number of verification attempts \(\underline{b}\in {\mathbb {N}} \) at the verifier is a parameter. The resource is denoted as \({\mathsf {NIPOE}}^{a}_{\phi ,\underline{b}}\). The behavior of this resource is described in more formally below. There are two inputs for a dishonest prover \(P\) that need further explanation:
-
\((\mathsf {copy}, s)\): This corresponds to sending a proof to \(V\). Prover \(V\) is convinced if the proof was successful (i.e., \(e_s = 1\)), and has to spend one additional evaluation of \(\mathcal T^{\textsc {rro}}_{}\), so the corresponding counter is increased (\(d \leftarrow d + 1\)).
-
\((\mathsf {spend})\): \(E\) forces \(V\) to spend one additional evaluation of \(\mathcal T^{\textsc {rro}}_{}\), for instance by sending an invalid proof. This decreases the number of verifications that \(V\) can still do (\(d \leftarrow d + 1\)).

The “real-world” Setting for niPoE Protocols. The main difference between PoE and niPoE is that a PoE requires bidirectional communication, which in Sect. 6.1 we described by the channels \(\longrightarrow \) and \(\longleftarrow \) available in each session. A niPoE only requires communication from the prover to the verifier, which we denote by the channel \(\longrightarrow \). Additionally, and as in the PoE case, the proof also requires computational resources, which are again formalized by the shared resource \(\mathcal T^{\textsc {rro}}_{\underline{a},\underline{b}}\).
The Security Definition. The definition of niPoE security is analogous to the one for PoE.
Definition 9
A protocol \(\pi = (\pi _1,\pi _2)\) is a non-interactive \((\phi ,\underline{b},\varepsilon )\)-proof-of-effort with respect to simulator \({{\sigma }} \) if for all \(\underline{a},\overline{a}\in {\mathbb {N}} \),
and
7.2 Protocol
Our protocol for niPoE is similar to the one in Construction 2. Instead of binding the solution to a session identifier chosen by the server, however, the identifier is chosen by the client. This makes sense for instance in the setting of sending electronic mail where the PoE can be bound to a hash of the message, or in Denial-of-Service protection in the TLS setting, where the client can bind the proof to its ephemeral key share.
Construction 3
The protocol is parametrized by sets \(D, \mathcal S \subseteq \left\{ 0,1\right\} ^*\) and a hardness parameter \(d\in {\mathbb {N}} \). It proceeds as follows:
-
1.
On input a statement \(s\in \mathcal S\), the prover chooses \(x\in D\) uniformly at random (but without collisions with previous attempts for the same s), computes \(y \leftarrow \mathcal T^{\textsc {rro}}_{}(s, x)\), and checks whether \(y[1,\dots ,d] = 0^d\). If equality holds, send (s, x, y) to the verifier and output 1 locally, otherwise output 0.
-
2.
Upon receiving \((s',x',y) \in \mathcal S\times D \times R\), the verifier accepts s iff \(y' \leftarrow \mathcal T^{\textsc {rro}}_{}(s', x')\) satisfies \(y = y'\) and \(y'[1,\dots ,d] = 0^d\). If the protocol is activated by the receiver and there is an accepted value \(s'\in \mathcal S\), then output \(s'\).
To capture the described scheme as a pair of converters \((\xi ,\chi )\) as needed for our security definition, we view step 2 as the converter \(\chi \), whereas step 1 describes the converter \(\xi \). For this protocol, we show the following theorem. The proof is deferred to the full version [11].
Theorem 4
Let \(d\in {\mathbb {N}} \) the hardness parameter. Then the described protocol \((\xi ,\chi )\) is a non-interactive \((2^{-d},\underline{b},0)\)-proof-of-effort.
8 Combining the Results
Before we can compose the MoHFs proven secure according to Definition 3 with the application protocols described in Sects. 6 and 7 using the respective composition theorem [44, 45], we have to resolve one apparent incompatibility. The indifferentiability statement according to Definition 3 is not immediately applicable in the case with two honest parties, as required in the availability conditions of Definitions 8 and 9, where both the prover and verifier are honest.Footnote 17 We further explain how to resolve this issue in the full version [11]; the result is that for stateless algorithms, Definition 3 immediately implies the analogous statement for resources with more honest interfaces, written \(\mathcal S^{\textsc {}}_{{\mathbf {l}} _1,{\mathbf {l}} _2,{\mathbf {r}}}\) and \(\mathcal T^{\textsc {rro}}_{a_1,a_2,b}\), which have two “honest” interfaces \(\mathrm {priv} _1\) and \(\mathrm {priv} _2\).
We can then immediately conclude the following corollary from composition theorem [44, 45] by instantiating it with the schemes of Definitions 3 and 8. In more detail, for an \(({\mathsf {a}},{\mathsf {b}},\varepsilon )\)-MoHF in some model, and a proof of effort parametrized by \(\phi \), the composition of the MoHF and the PoE construct the PoE resource described above with \({\mathsf {a}} \) attempts allowed to the prover \(P\), and consequently \(\alpha + n\) attempts for the dishonest prover and n sessions. An analogous corollary holds for the niPoEs.
Corollary 1
Let  , \({\mathsf {a}},{\mathsf {b}}: {\mathbb {P}} \rightarrow {\mathbb {N}} \), and \(\varepsilon : {\mathbb {P}} \times {\mathbb {P}} \rightarrow {\mathbb {R}} _{\ge 0}\) as in Definition 3, and let \((\xi ,\chi )\) be a \((\phi ,n,\underline{b},\varepsilon ')\)-proof of effort. Then
, \({\mathsf {a}},{\mathsf {b}}: {\mathbb {P}} \rightarrow {\mathbb {N}} \), and \(\varepsilon : {\mathbb {P}} \times {\mathbb {P}} \rightarrow {\mathbb {R}} _{\ge 0}\) as in Definition 3, and let \((\xi ,\chi )\) be a \((\phi ,n,\underline{b},\varepsilon ')\)-proof of effort. Then
with \(P=\mathrm {priv} _1\) and \(V=\mathrm {priv} _2\), for all \({\mathbf {l}} _1,{\mathbf {l}} _2\in {\mathbb {P}} \), and where \({\bot }^{\mathrm {pub}}{\mathcal S^{\textsc {}}_{{\mathbf {l}} _1,{\mathbf {l}} _2,{\mathbf {r}}}}\) means that the \(\mathrm {pub}\)-interface is not accessible to the distinguisher. Additionally,
with \(P=\mathrm {pub} \) and \(V=\mathrm {priv} _2\), for all \({\mathbf {r}},{\mathbf {l}} _2\in {\mathbb {P}} \), and where \(\tilde{{\sigma }} \) is the composition of the two simulators guaranteed by Definitions 3 and 8.
9 Open Questions
We discuss several interesting open questions raised by this work. The topic of moderately hard functions is an active topic of research both in terms of definitions and constructions and so many practically interesting (and used) moderately hard function constructions and proof-of-effort protocols could benefit from a more formal treatment (e.g. Equihash [16], CryptoNight, Ethash). Many of these will likely result in novel instantiates of the MoHF framework which we believe to be of independent interest as this requires formalizing new security goals motivated by practical considerations. In terms of new moderately hard functions, the recent work of Biryukov and Perrin [17] introduces several new constructions for use in hardening more conventional cryptographic primitives against brute-force attacks. For this type of application, a composable security notion of moderate hardness such as the one in this work would lend itself well to analyzing the effect on the cryptographic primitives being hardened. Other examples of recent proof-of-effort protocols designed to for particular higher-level applications in mind are the results in [13, 23, 32, 35]. In each case, at most standalone security of the higher-level application can be reasoned about so using the framework in this paper could help improve the understanding of the applications composition properties.
A natural question that arises from how the framework is currently formulated is whether the ideal-world resource could be relaxed. While modeling the ideal resource as a random oracle does make proving security for applications using the MoHF easier it seems to moot ever proving security for any candidate MoHF outside the random oracle model. However, it would be nice to show some form of moderate hardness based on other assumptions or, ideally, even unconditionally. Especially in the domain of client-puzzles several interesting constructions already exists based on various computational hardness assumptions [39, 41, 53, 55].
Notes
- 1.
We intentionally use the term effort instead of work since the latter is often associated with computational work, while a MoHF in our framework may be based on spending other types of resources such as memory.
- 2.
Nevertheless, we conjecture that Equihash could also be analyzed in out framework. In particular, if we can always model the underlying hash function used by Equihash as a (trivially secure) MoHF. Then, by assuming the optimality of Wagner’s collision finding algorithm (as done in [16]) one could compute the parameters for which Equihash gives rise to our proof-of-effort definition in Sect. 6. We leave this line of reasoning for future work.
- 3.
An example of this type of resource restriction is the cumulative number of oracle calls that the algorithm can make. Other resources may have different characteristics, such as a bound on the maximum amount of simultaneous memory use during the execution of the algorithm; which does not accumulate over multiple executions.
- 4.
- 5.
We remark that in contrast to, say, non-black box simulators, we are unaware of any actual advantage of this independence between \({{\sigma }} \) and \({\mathbf {l}} \).
- 6.
These parameters may specify bounds in terms of the cost function discussed above.
- 7.
Once the resources at the \(\mathrm {priv}\)-interface are exhausted, no further useful information is gained by \( D \) in making additional evaluation calls for
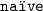 .
. - 8.
In particular, for the algorithm input on the adversarial interface \(\mathrm {pub}\) the single permitted execution can consume at most \({\mathbf {r}} \) resources while for the honest algorithm input on \(\mathrm {priv}\) the total consumed resources across all execution can be at most \({\mathbf {l}} \).
- 9.
For example, we can associate \(v\in V\) with the binary representation of its position in an arbitrary fixed topological ordering of G.
- 10.
Prefixing ensures domain separation; that is random oracle calls in a labeling are unique to that input. However, if inputs are chosen independently of the RO then finding two inputs that share an oracle call requires finding a collision in the RO. To concentrate on the more fundamental and novel aspects of the proofs below, we have chosen to instead assume full prefixing. A formal analysis with less prefixing can be found in [10].
- 11.
Note that any signal entering a circuit at the beginning of a clock cycle that does not reach a memory cell before the end of a clock cycle is lost. Yet, hash functions so complex and clock cycles so short that it is unrealistic to assume an entire evaluation of h can be performed within a single cycle.
- 12.
\(\mathsf{{cpc}}'\) is essentially the special case of “energy complexity” for \(R=1\) in [3].
- 13.
If the adversary is restricted to using general-purpose CPUs and not ASICs or FPGAs with their massive parallelism, this restriction may be reasonable.
- 14.
For the numbers \(\underline{a},\overline{a}\in {\mathbb {N}} \) it may hold that \(\overline{a}> \underline{a}\) because one may only know rough bounds on the available resources (at least \(\underline{a}\), at most \(\overline{a}\)).
- 15.
One main difference is that UC is tailored toward asymptotic statements. As UC a priori allows the environment to create arbitrarily many instances of all protocols and functionalities, making the precise concrete statements we aim for becomes difficult.
- 16.
We assume that the elements in D are ordered, e.g. lexicographically.
- 17.
The verifier is always considered honest in our work.
References
Abadi, M., Burrows, M., Manasse, M., Wobber, T.: Moderately hard, memory-bound functions. ACM Trans. Internet Technol. 5(2), 299–327 (2005)
Back, A.: Hashcash - A Denial of Service Counter-Measure (2002)
Alwen, J., Blocki, J.: Efficiently computing data-independent memory-hard functions. In: Robshaw, M., Katz, J. (eds.) CRYPTO 2016. LNCS, vol. 9815, pp. 241–271. Springer, Heidelberg (2016). https://doi.org/10.1007/978-3-662-53008-5_9
Alwen, J., Blocki, J.: Towards practical attacks on Argon2i and balloon hashing. In: EuroS&P 2017 (2017)
Alwen, J., Blocki, J., Harsha, B.: Practical graphs for optimal side-channel resistant memory-hard functions. Cryptology ePrint Archive, Report 2017/443 (2017). http://eprint.iacr.org/2017/443
Alwen, J., Blocki, J., Pietrzak, K.: Depth-robust graphs and their cumulative memory complexity. In: Coron, J.-S., Nielsen, J.B. (eds.) EUROCRYPT 2017. LNCS, vol. 10212, pp. 3–32. Springer, Cham (2017). https://doi.org/10.1007/978-3-319-56617-7_1. https://eprint.iacr.org/
Alwen, J., Chen, B., Kamath, C., Kolmogorov, V., Pietrzak, K., Tessaro, S.: On the complexity of scrypt and proofs of space in the parallel random oracle model. In: Fischlin, M., Coron, J.-S. (eds.) EUROCRYPT 2016. LNCS, vol. 9666, pp. 358–387. Springer, Heidelberg (2016). https://doi.org/10.1007/978-3-662-49896-5_13
Alwen, J., Chen, B., Pietrzak, K., Reyzin, L., Tessaro, S.: Scrypt is maximally memory-hard. In: Coron, J.-S., Nielsen, J.B. (eds.) EUROCRYPT 2017. LNCS, vol. 10212, pp. 33–62. Springer, Cham (2017). https://doi.org/10.1007/978-3-319-56617-7_2
Alwen, J., Gaži, P., Kamath, C., Klein, K., Osang, G., Pietrzak, K., Reyzin, L., Rolínek, M., Rybár, M.: On the memory-hardness of data-independent password-hashing functions. Cryptology ePrint Archive, Report 2016/783 (2016)
Alwen, J., Serbinenko, V.: High parallel complexity graphs and memory-hard functions. In: STOC (2015)
Alwen, J., Tackmann, B.: Moderately hard functions: definition, instantiations, and applications moderately hard functions. Cryptology ePrint Archive, September 2017
Aura, T., Nikander, P., Leiwo, J.: DOS-resistant authentication with client puzzles. In: Christianson, B., Malcolm, J.A., Crispo, B., Roe, M. (eds.) Security Protocols 2000. LNCS, vol. 2133, pp. 170–177. Springer, Heidelberg (2001). https://doi.org/10.1007/3-540-44810-1_22
Ball, M., Rosen, A., Sabin, M., Vasudevan, P.N.: Proofs of useful work. Cryptology ePrint Archive, Report 2017/203 (2017). http://eprint.iacr.org/2017/203
Bellare, M., Ristenpart, T., Tessaro, S.: Multi-instance security and its application to password-based cryptography. In: Safavi-Naini, R., Canetti, R. (eds.) CRYPTO 2012. LNCS, vol. 7417, pp. 312–329. Springer, Heidelberg (2012). https://doi.org/10.1007/978-3-642-32009-5_19
Biryukov, A., Khovratovich, D.: Tradeoff cryptanalysis of memory-hard functions. In: Iwata, T., Cheon, J.H. (eds.) ASIACRYPT 2015. LNCS, vol. 9453, pp. 633–657. Springer, Heidelberg (2015). https://doi.org/10.1007/978-3-662-48800-3_26
Biryukov, A., Khovratovich, D.: Equihash: asymmetric proof-of-work based on the generalized birthday problem. Ledger J. 2, 1–11 (2017)
Biryukov, A., Perrin, L.: Symmetrically and asymmetrically hard cryptography (full version). Cryptology ePrint Archive, Report 2017/414 (2017). http://eprint.iacr.org/2017/414
Boneh, D., Corrigan-Gibbs, H., Schechter, S.: Balloon hashing: a memory-hard function providing provable protection against sequential attacks. In: Cheon, J.H., Takagi, T. (eds.) ASIACRYPT 2016. LNCS, vol. 10031, pp. 220–248. Springer, Heidelberg (2016). https://doi.org/10.1007/978-3-662-53887-6_8
Buterin, V., Di Lorio, A., Hoskinson, C., Alisie, M.: Ethereum: a distributed cryptographic leger (2013). http://www.ethereum.org/
Canetti, R.: Universally composable security: a new paradigm for cryptographic protocols. In: Proceedings of the 42nd IEEE Symposium on Foundations of Computer Science, pp. 136–145. IEEE (2001)
Canetti, R., Halevi, S., Steiner, M.: Hardness amplification of weakly verifiable puzzles. In: Kilian, J. (ed.) TCC 2005. LNCS, vol. 3378, pp. 17–33. Springer, Heidelberg (2005). https://doi.org/10.1007/978-3-540-30576-7_2
Chen, L., Morrissey, P., Smart, N.P., Warinschi, B.: Security notions and generic constructions for client puzzles. In: Matsui, M. (ed.) ASIACRYPT 2009. LNCS, vol. 5912, pp. 505–523. Springer, Heidelberg (2009). https://doi.org/10.1007/978-3-642-10366-7_30
Chepurnoy, A., Duong, T., Fan, L., Zhou, H.S.: Twinscoin: a cryptocurrency via proof-of-work and proof-of-stake. Cryptology ePrint Archive, Report 2017/232 (2017). http://eprint.iacr.org/2017/232
Cook, S.A.: An observation on time-storage trade off. In: STOC, pp. 29–33 (1973)
Demay, G., Gaži, P., Hirt, M., Maurer, U.: Resource-restricted indifferentiability. In: Johansson, T., Nguyen, P.Q. (eds.) EUROCRYPT 2013. LNCS, vol. 7881, pp. 664–683. Springer, Heidelberg (2013). https://doi.org/10.1007/978-3-642-38348-9_39
Demay, G., Gaži, P., Maurer, U., Tackmann, B.: Query-complexity amplification for random oracles. In: Lehmann, A., Wolf, S. (eds.) ICITS 2015. LNCS, vol. 9063, pp. 159–180. Springer, Cham (2015). https://doi.org/10.1007/978-3-319-17470-9_10
Dwork, C., Goldberg, A., Naor, M.: On memory-bound functions for fighting spam. In: Boneh, D. (ed.) CRYPTO 2003. LNCS, vol. 2729, pp. 426–444. Springer, Heidelberg (2003). https://doi.org/10.1007/978-3-540-45146-4_25
Dwork, C., Naor, M.: Pricing via processing or combatting junk mail. In: Brickell, E.F. (ed.) CRYPTO 1992. LNCS, vol. 740, pp. 139–147. Springer, Heidelberg (1993). https://doi.org/10.1007/3-540-48071-4_10
Dwork, C., Naor, M., Wee, H.: Pebbling and proofs of work. In: Shoup, V. (ed.) CRYPTO 2005. LNCS, vol. 3621, pp. 37–54. Springer, Heidelberg (2005). https://doi.org/10.1007/11535218_3
Dziembowski, S., Faust, S., Kolmogorov, V., Pietrzak, K.: Proofs of space. In: Gennaro, R., Robshaw, M. (eds.) CRYPTO 2015. LNCS, vol. 9216, pp. 585–605. Springer, Heidelberg (2015). https://doi.org/10.1007/978-3-662-48000-7_29
Dziembowski, S., Kazana, T., Wichs, D.: One-time computable self-erasing functions. In: Ishai, Y. (ed.) TCC 2011. LNCS, vol. 6597, pp. 125–143. Springer, Heidelberg (2011). https://doi.org/10.1007/978-3-642-19571-6_9
Eckey, L., Faust, S., Loss, J.: Efficient algorithms for broadcast and consensus based on proofs of work. Cryptology ePrint Archive, Report 2017/915 (2017). http://eprint.iacr.org/2017/915
Forler, C., Lucks, S., Wenzel, J.: Catena: a memory-consuming password scrambler. Cryptology ePrint Archive, Report 2013/525 (2013)
Garay, J., Kiayias, A., Leonardos, N.: The bitcoin backbone protocol: analysis and applications. In: Oswald, E., Fischlin, M. (eds.) EUROCRYPT 2015. LNCS, vol. 9057, pp. 281–310. Springer, Heidelberg (2015). https://doi.org/10.1007/978-3-662-46803-6_10
Garay, J.A., Kiayias, A., Panagiotakos, G.: Proofs of work for blockchain protocols. Cryptology ePrint Archive, Report 2017/775 (2017). http://eprint.iacr.org/2017/775
Groza, B., Petrica, D.: On chained cryptographic puzzles. In: SACI, pp. 25–26 (2006)
Groza, B., Warinschi, B.: Cryptographic puzzles and DoS resilience, revisited. DCC 73(1), 177–207 (2014)
Hewitt, C.E., Paterson, M.S.: Record of the project MAC. In: Conference on Concurrent Systems and Parallel Computation, pp. 119–127. ACM, New York (1970)
Jerschow, Y.I., Mauve, M.: Non-parallelizable and non-interactive client puzzles from modular square roots. In: ARES, pp. 135–142. IEEE (2011)
Juels, A., Brainard, J.G.: Client puzzles: a cryptographic countermeasure against connection depletion attacks. In: NDSS (1999)
Karame, G.O., Čapkun, S.: Low-cost client puzzles based on modular exponentiation. In: Gritzalis, D., Preneel, B., Theoharidou, M. (eds.) ESORICS 2010. LNCS, vol. 6345, pp. 679–697. Springer, Heidelberg (2010). https://doi.org/10.1007/978-3-642-15497-3_41
Lengauer, T., Tarjan, R.E.: Asymptotically tight bounds on time-space trade-offs in a pebble game. J. ACM 29(4), 1087–1130 (1982)
Maurer, U.: Indistinguishability of random systems. In: Knudsen, L.R. (ed.) EUROCRYPT 2002. LNCS, vol. 2332, pp. 110–132. Springer, Heidelberg (2002). https://doi.org/10.1007/3-540-46035-7_8
Maurer, U.: Constructive cryptography – a new paradigm for security definitions and proofs. In: Mödersheim, S., Palamidessi, C. (eds.) TOSCA 2011. LNCS, vol. 6993, pp. 33–56. Springer, Heidelberg (2012). https://doi.org/10.1007/978-3-642-27375-9_3
Maurer, U., Renner, R.: Abstract cryptography. In: ICS (2011)
Maurer, U., Renner, R.: From indifferentiability to constructive cryptography (and back). In: Hirt, M., Smith, A. (eds.) TCC 2016. LNCS, vol. 9985, pp. 3–24. Springer, Heidelberg (2016). https://doi.org/10.1007/978-3-662-53641-4_1
Maurer, U., Renner, R., Holenstein, C.: Indifferentiability, impossibility results on reductions, and applications to the random oracle methodology. In: Naor, M. (ed.) TCC 2004. LNCS, vol. 2951, pp. 21–39. Springer, Heidelberg (2004). https://doi.org/10.1007/978-3-540-24638-1_2
Morris, R., Thompson, K.: Password security: a case history. Commun. ACM 22(11), 594–597 (1979)
Nakamoto, S.: Bitcoin: A Peer-to-Peer Electronic Cash System (2009)
Naor, M.: Moderately hard functions: from complexity to spam fighting. In: Pandya, P.K., Radhakrishnan, J. (eds.) FSTTCS 2003. LNCS, vol. 2914, pp. 434–442. Springer, Heidelberg (2003). https://doi.org/10.1007/978-3-540-24597-1_37
Percival, C.: Stronger key derivation via sequential memory-hard functions. In: BSDCan 2009 (2009)
Price, G.: A general attack model on hash-based client puzzles. In: Paterson, K.G. (ed.) Cryptography and Coding 2003. LNCS, vol. 2898, pp. 319–331. Springer, Heidelberg (2003). https://doi.org/10.1007/978-3-540-40974-8_26
Rivest, R.L., Shamir, A., Wagner, D.A.: Time-lock puzzles and timed-release Crypto. Technical report, Cambridge, MA, USA (1996)
Stebila, D., Kuppusamy, L., Rangasamy, J., Boyd, C., Gonzalez Nieto, J.: Stronger difficulty notions for client puzzles and denial-of-service-resistant protocols. In: Kiayias, A. (ed.) CT-RSA 2011. LNCS, vol. 6558, pp. 284–301. Springer, Heidelberg (2011). https://doi.org/10.1007/978-3-642-19074-2_19
Tritilanunt, S., Boyd, C., Foo, E., González Nieto, J.M.: Toward non-parallelizable client puzzles. In: Bao, F., Ling, S., Okamoto, T., Wang, H., Xing, C. (eds.) CANS 2007. LNCS, vol. 4856, pp. 247–264. Springer, Heidelberg (2007). https://doi.org/10.1007/978-3-540-76969-9_16
Yao, F.F., Yin, Y.L.: Design and analysis of password-based key derivation functions. In: Menezes, A. (ed.) CT-RSA 2005. LNCS, vol. 3376, pp. 245–261. Springer, Heidelberg (2005). https://doi.org/10.1007/978-3-540-30574-3_17
Author information
Authors and Affiliations
Corresponding author
Editor information
Editors and Affiliations
Rights and permissions
Copyright information
© 2017 International Association for Cryptologic Research
About this paper
Cite this paper
Alwen, J., Tackmann, B. (2017). Moderately Hard Functions: Definition, Instantiations, and Applications. In: Kalai, Y., Reyzin, L. (eds) Theory of Cryptography. TCC 2017. Lecture Notes in Computer Science(), vol 10677. Springer, Cham. https://doi.org/10.1007/978-3-319-70500-2_17
Download citation
DOI: https://doi.org/10.1007/978-3-319-70500-2_17
Published:
Publisher Name: Springer, Cham
Print ISBN: 978-3-319-70499-9
Online ISBN: 978-3-319-70500-2
eBook Packages: Computer ScienceComputer Science (R0)










 on inputs of its choice by providing inputs at the
on inputs of its choice by providing inputs at the  (until the resources are exhausted).
(until the resources are exhausted). , queries
, queries 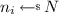 and sends
and sends 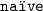 .
.