Abstract
In Attribute-Based Signatures (ABS; first defined by Maji, Prabhakaran and Rosulek, CT-RSA 2011) an authority can generate multiple signing keys, where each key is associated with an attribute x. Messages are signed with respect to a constraint f, such that a key for x can sign messages respective to f only if \(f(x) = 0\). The security requirements are unforgeability and key privacy (signatures should not expose the specific signing key used). In (single-hop) Homomorphic Signatures (HS; first defined by Boneh and Freeman, PKC 2011), given a signature for a data-set x, one can evaluate a signature for the pair (f(x), f), for functions f. In context-hiding HS, evaluated signatures do not reveal information about the original (pre-evaluated) signatures.
In this work we start by showing that these two notions are in fact equivalent. The first implication of this equivalence is a new lattice-based ABS scheme for polynomial-depth circuits, based on the HS construction of Gorbunov, Vaikuntanathan and Wichs (GVW; STOC 2015).
We then construct a new ABS candidate from a worst case lattice assumption (\(\mathrm {SIS}\)), with different parameters. Using our equivalence again, now in the opposite direction, our new ABS implies a new lattice-based HS scheme with different parameter trade-off, compared to the aforementioned GVW.
R. Tsabary—Supported by the Israel Science Foundation (Grant No. 468/14) and Binational Science Foundation (Grant No. 712307).
You have full access to this open access chapter, Download conference paper PDF
Similar content being viewed by others
1 Introduction
In a standard digital signature scheme an authority generates a public verification key \(\mathsf{vk}\) and a secret signing key \(\mathsf{sk}\). Given \(\mathsf{sk}\), it is possible to sign any message, and signatures can be verified publicly with \(\mathsf{vk}\). Recent works study more powerful notions of digital signatures, where the authority can generate multiple signing keys, each with limited signing permissions. An example use case is when an organization wants to allow its employees to sign on behalf of its name, while controlling which messages each employee can sign. A signature should not reveal any information about the signing permissions of the signer, other than whether he is allowed to sign the message corresponding to the same signature. In stronger notions, the signature should not reveal any information about the identity of the signer. Main notions of this form are attribute-based signatures (ABS) [MPR11], policy-based signatures (PBS) [BF14], constrained signatures (CS) [BZ14] and functional signatures (FS) [BGI14]. In this work we use a slightly modified definition of constrained signatures, with two flavors that capture ABS and PBS for languages in \(\mathbf {P}\).
In a homomorphic signatures (HS) scheme, given a signature for a data-set x, one can evaluate a signature for the pair (f(x), f), for any f in the supported function space of the scheme. Context-hiding HS has the security guarantee that an evaluated signature does not reveal information about the original (pre-evaluated) signature. In particular, it does not reveal x. Context-hiding homomorphic signatures are useful, for example, when one wants to prove that he has a signature for a data-set which satisfies some condition, without revealing the data-set itself. We show in this work that CS is equivalent to context-hiding 1-hop HS.
1.1 Overview
Two flavors of CS will be alternately used throughout this work. In key-policy constrained signatures, each signing key \(\mathsf{sk}_f\) is associated with a circuit \(f : \{0,1\}^* \rightarrow \{0,1\}\), which we refer to as the constraint, and a key \(\mathsf{sk}_f\) can sign an attribute \(x \in \{0,1\}^*\) only if \(f(x) = 0\). In message-policy constrained signatures, each key is associated with an attribute \(x \in \{0,1\}^*\), and a key \(\mathsf{sk}_x\) can sign a constraint \(f : \{0,1\}^* \rightarrow \{0,1\}\) only if \(f(x) = 0\). Message-policy CS is equivalent to attribute-based signatures, and key-policy CS is equivalent policy-based signatures for languages in \(\mathbf {P}\) Footnote 1. When presented as two flavors of a single primitive, we can take advantage of the similarities and alternately use the definition that best fits the context. Note that the flavors are interchangeable up to switching the constraint space and attribute space.
Security. We consider two aspects of security – unforgeability and key privacy. Unforgeability requires that an adversary cannot sign a message which it does not have a permission to sign, even after seeing other signatures. We also define a relaxed notion where the adversary has only a single key, and a selective notion where the adversary has to announce the message for which it is going to forge a signature before seeing any public data. Key privacy bounds the information revealed by a signature regarding the key that was used to produce it. In the strongest notion, key-hiding privacy, the signature completely hides the key. In particular, it is impossible to determine whether two signatures were derived from the same key. In constraint-hiding privacy (or attribute-hiding privacy, in the message-policy flavor) we only aim to hide the constraint (or to hide the attribute, in the message-policy flavor), possibly leaving the identity of the signing key public. We note that without any privacy requirements, CS are trivial to achieve using standard signatures.
Delegation. A CS scheme can be extended to support key delegation. In this setting, a party with a singing key \(\mathsf{sk}_f\) can derive a signing key \(\mathsf{sk}_{(f,g)}\) that is authorized to sign a message x only when \(f(x) = 0\) and \(g(x) = 0\). Note that the permissions of \(\mathsf{sk}_{(f,g)}\) are never stronger than the permissions of \(\mathsf{sk}_f\), since otherwise the scheme is forgeable.
Motivation. CS is weaker than PBS for \(\mathbf {NP}\) but strong enough for some of the motivations that lead to the study of PBS, such as constructing group signatures and attribute-based signatures. See the applications discussion in [BF14] for details. We exploit this gap and construct CS with a different approach than previous results that were using variations of NIZK. Indeed, as noted in [BF14], PBS for general languages in \(\mathbf {NP}\) implies simulation-extractable NIZK proofs. We also see in this work a contribution to the understanding of homomorphic signatures – prior to this work there was only a single known construction of (leveled) fully HS [GVW15].
1.2 Results
Unforgeability Amplification. In our first construction we assume a (key-policy) CS scheme with single-key-selective unforgeability. This notion is captured by a security game where the adversary is only allowed to query for a single key \(\mathsf{sk}_f\), and it has to announce f before seeing any public data. It wins if it manages to forge a signature for an attribute x that is not authorized by f, i.e. where \(f(x) = 1\). We use a standard signatures scheme to construct a (key-policy) CS scheme with full unforgeability. The downside of this general amplification is the loss in key privacy – while the new CS scheme is constraint-hiding (i.e. it hides the functionality of the signing key, as long as the underlying CS scheme does as well), signatures reveal other key-specific information and therefore it is not key-hiding (i.e. one can learn from a signature the identity of the signing key). The amplification maintains the delegation properties of the underlying CS scheme.
Equivalence of CS and Homomorphic Signatures. We first construct a (message-policy) CS scheme which is single-key-selective unforgeable and key-hiding, from context-hiding 1-hop homomorphic signatures. [GVW15] construct a context-hiding HS scheme which is secure under the Short Integer Solution (\(\mathrm {SIS}\)) hardness assumption. When used as the underlying HS scheme to our construction, this results in a \(\mathrm {SIS}\)-based (message-policy) CS scheme with bounded attribute space, and constraint space of boolean circuits with bounded depth. In the other direction, we construct a selectively-unforgeable context-hiding 1-hop HS scheme from a single-key-selective unforgeable key-hiding (message-policy) CS scheme. As shown in [GVW15], it is possible to amplify the unforgeability of such HS scheme to the adaptive notion.
CS from Lattice Trapdoors. We construct a (key-policy) CS scheme from lattice trapdoors, which is message-selective unforgeable and key-hiding. The key privacy is statistical, and the unforgeability relies on the Short Integers Solution (SIS) hardness assumption. The construction supports attribute space of fixed size and constraint space of boolean circuits with bounded depth. When translated to the message-policy flavor, the attribute space is unbounded and the policy space is bounded in depth and size.
A New Homomorphic Signatures Construction. An immediate conclusion of the above two results is a new lattice-based (leveled) fully homomorphic signatures scheme, where fresh signatures are of fixed size (independent of the signed data-set size), and evaluated signatures grow with the size of the policy description. It means that for any policy with a short description succinctness is maintained.
Two New CS Constructions. Combining the first two results gives a new CS construction – first construct the HS-based (message-policy) CS scheme which is single-key-selective unforgeable, and then amplify it to full unforgeability, while compromising on key privacy. We summarize the different properties of this CS construction and the lattice-based CS construction in the table below. Note that the HS-based scheme is presented in the message-policy flavor, and the lattice-based scheme is presented in the key-policy flavor. Implementing each of them in the opposite flavor will result in a constraint space of bounded depth and size, and an unbounded attribute space.
HS-based message-policy CS | Lattice-based key-policy CS | |
|---|---|---|
Assumption | SIS | SIS |
Attribute space | Fixed | Fixed |
Constraint space | Bounded depth | Bounded depth |
Unforgeability | Full | Message-selective |
Privacy | Constraint-hiding | Key-hiding |
Supports delegation | No | Yes |
1.3 Technical Overview
Definition of CS. A (key-policy) CS scheme consists of 4 algorithms \((\mathsf{Setup},\mathsf{Keygen},\) \(\mathsf{Sign},\mathsf{Ver})\). \(\mathsf{Setup}\) is an initialization algorithm that generates a verification key \(\mathsf{vk}\) and a master signing key \(\mathsf{msk}\). \(\mathsf{Keygen}\) produces constrained signing keys – it takes as input the master signing key \(\mathsf{msk}\) and a constraint f, and outputs a constrained key \(\mathsf{sk}_f\). The signing algorithm \(\mathsf{Sign}\) takes as input an attribute x and a constrained singing key \(\mathsf{sk}_f\), and outputs a signature \(\sigma _{x}\), which is valid if and only if \(f(x) = 0\). The verification algorithm \(\mathsf{Ver}\) takes an attribute x and a signature \(\sigma _{x}\), and either accepts or rejects.
Unforgeability Amplification. We now give a brief description of the amplification. Assume a (key-policy) constrained signatures scheme \(\mathsf{CS}'\) which is single-key-selective unforgeable, constraint-hiding and possibly supports delegation. Let \(\mathsf{S}\) be an existentially unforgeable standard signatures scheme. The construction is as follows. In \(\mathsf{Setup}\), the authority initializes \(\mathsf{S}\) and sets \((\mathsf{vk},\mathsf{msk}) = (\mathsf{S}.\mathsf{vk},\mathsf{S}.\mathsf{sk})\). Every time a key is generated, the authority initializes a fresh instance of \(\mathsf{CS}'\) and generates a constrained key for the desired f under this instance: \((\mathsf{CS}'.\mathsf{vk}',\mathsf{CS}'.\mathsf{sk}'_f)\). It also generates a fresh instance of \(\mathsf{S}:\) \((\mathsf{S}.\mathsf{vk}'',\mathsf{S}.\mathsf{sk}'')\). The authority then signs \((\mathsf{CS}'.\mathsf{vk}',\mathsf{S}.\mathsf{vk}'')\) under the standard scheme \(\mathsf{S}\) using \(\mathsf{msk}= \mathsf{S}.\mathsf{sk}\) and gets \(\mathsf{S}.\sigma _{(\mathsf{vk}',\mathsf{vk}'')}\). The constrained key is therefore \(\mathsf{sk}_f = (\mathsf{CS}'.\mathsf{vk},\mathsf{CS}'.\mathsf{sk}_f,\) \(\mathsf{S}.\mathsf{vk}'',\mathsf{S}.\mathsf{sk}'',\mathsf{S}.\sigma _{(\mathsf{vk}',\mathsf{vk}'')})\). To sign an attribute x with a key of this form, one signs x with \((\mathsf{CS}'.\mathsf{vk},\mathsf{CS}'.\mathsf{sk}_f)\), signs x with \((\mathsf{S}.\mathsf{vk}'',\mathsf{S}.\mathsf{sk}'')\) and outputs these signatures along with \(\mathsf{S}.\sigma _{(\mathsf{vk}',\mathsf{vk}'')}\). Verification is done by verifying the signatures for x under \(\mathsf{CS}'.\mathsf{vk}'\) and \(\mathsf{S}.\mathsf{vk}''\), and verifying \(\mathsf{S}.\sigma _{(\mathsf{vk}',\mathsf{vk}'')}\) under \(\mathsf{S}.\mathsf{vk}\). Since for each instance of \(\mathsf{CS}'\) the authority only generates a single key, the unforgeability for each such instance is maintained. The existential unforgeability of \(\mathsf{S}\) guarantees that it is not possible to forge a signature for an instance of \(\mathsf{CS}'\) that was not initialized by the authority. Note that \(\mathsf{CS}'.\mathsf{vk}\) is a part of the signature, and since this value is different for each key, it reveals the identity of the key. For that reason the construction is not key-hiding but solely constraint-hiding.
CS from Homomorphic Signatures. The construction of (message-policy) CS from context-hiding HS works as follows. The CS authority initializes the HS scheme. In order to produce a CS key for an attribute x, it signs x under the HS scheme and outputs \(\mathsf{sk}_x = \mathsf{HS}.\sigma _x\). A signature for a policy f is derived from \(\mathsf{sk}_x\) by homomorphically evaluating f on \(\mathsf{HS}.\sigma _x\). This results in an HS signature for the pair (f, f(x)). In order to verify one checks the validity of the HS signature, and that \(f(x) = 0\). The context-hiding property of HS ensures that \(\sigma _{(f,f(x))}\) reveals nothing about \(\sigma _x\), and thus the construction is key-hiding.
Homomorphic Signatures from CS. The construction of context-hiding 1-hop HS from (message-policy) CS works as follows. The HS authority initializes the CS scheme. In order to sign a data-set x, generate a CS key for the attribute x and outputs \(\sigma _x = \mathsf{CS}.\mathsf{sk}_x\). To homomorphically evaluate a function f on a signature \(\sigma _{x}\), first compute \(y=f(x)\), then define the function \(f_{y}\) that on input \(x'\) outputs 0 if and only if \(f(x') = y\). Sign the constraint \(f_{y}\) under the \(\mathsf{CS}\) scheme (using \(\mathsf{CS}.\mathsf{sk}_x\)) and output this CS signature: \(\mathsf{HS}.\sigma _{(f,y)} = \mathsf{CS}.\sigma _{f_y}\). In order to verify one checks the validity of the CS signature. The key-hiding property of CS ensures that \(\mathsf{CS}.\sigma _{f_y}\) reveals nothing about \(\mathsf{CS}.\mathsf{sk}_x\), and thus the construction is context-hiding.
CS from Lattice Trapdoors. We use techniques that were developed in [GVW13, BGG+14] for the purpose of attribute-based encryption (ABE). Let \(\ell \) be the attribute length, i.e. \(x\in \{0,1\}^{\ell }\). The constraint space is all the circuits \(f:\{0,1\}^{\ell } \rightarrow \{0,1\}\) of bounded depth. The verification key \(\mathsf{vk}\) consists of a uniformly sampled matrix \(\vec {{\mathbf {{A}}}}= [{\mathbf {{A}}}_1\Vert \dots \Vert {\mathbf {{A}}}_{\ell _{\mathcal{X}}}]\) and a close-to-uniform matrix \({\mathbf {{A}}}\), and the master signing key \(\mathsf{msk}\) is a trapdoor for \({\mathbf {{A}}}\), i.e. \({\mathbf {{{A}}}}^{-1}_{{\tau _0}}\). A valid signature for an attribute x is a non-zero short-entries vector \(\mathbf {{v}}_{x}\) such that \([{\mathbf {{A}}}\Vert \vec {{\mathbf {{A}}}}- x \otimes \mathbf {G}]\cdot \mathbf {{v}}_{x} =\mathbf {{0}}\), where \(\mathbf {G}\) is a special fixed gadget matrix. The constrained signing key \(\mathsf{sk}_f\) respective to a circuit f is a trapdoor \([{\mathbf {{A}}}\Vert {\mathbf {{A}}}_f]^{-1}_{\tau }\), where \({\mathbf {{A}}}_f\) is computed from  and f. Given \(\mathsf{msk}= {\mathbf {{{A}}}}^{-1}_{{\tau _0}}\) it is possible to generate a trapdoor \([{\mathbf {{A}}}\Vert \mathbf {M}]^{-1}_{\tau }\) for any matrix \(\mathbf {M}\), so the authority can generate such keys efficiently. For any pair (x, f), a trapdoor \([{\mathbf {{A}}}\Vert \vec {{\mathbf {{A}}}}- x \otimes \mathbf {G}]^{-1}_{\tau '}\) can be derived from the trapdoor \([{\mathbf {{A}}}\Vert {\mathbf {{A}}}_f - f(x) \mathbf {G}]^{-1}_{\tau }\). This implies that when \(f(x) = 0\), it can be derived from the signing key \(\mathsf{sk}_f = [{\mathbf {{A}}}\Vert {\mathbf {{A}}}_f]^{-1}_{\tau }\). The trapdoor \([{\mathbf {{A}}}\Vert \vec {{\mathbf {{A}}}}- x \otimes \mathbf {G}]^{-1}_{\tau '}\) allows to sample a short vector \(\mathbf {{v}}_{x}\) which is a valid signature for x. Since the signature is sampled from the same distribution regardless of the signing key, the scheme is statistically key-hiding. The proof of message-selective unforgeability is similar to the selective security proof in [BGG+14]. Recall that the adversary has to announce x for which it is going to forge a signature at the beginning of the game. The matrix
and f. Given \(\mathsf{msk}= {\mathbf {{{A}}}}^{-1}_{{\tau _0}}\) it is possible to generate a trapdoor \([{\mathbf {{A}}}\Vert \mathbf {M}]^{-1}_{\tau }\) for any matrix \(\mathbf {M}\), so the authority can generate such keys efficiently. For any pair (x, f), a trapdoor \([{\mathbf {{A}}}\Vert \vec {{\mathbf {{A}}}}- x \otimes \mathbf {G}]^{-1}_{\tau '}\) can be derived from the trapdoor \([{\mathbf {{A}}}\Vert {\mathbf {{A}}}_f - f(x) \mathbf {G}]^{-1}_{\tau }\). This implies that when \(f(x) = 0\), it can be derived from the signing key \(\mathsf{sk}_f = [{\mathbf {{A}}}\Vert {\mathbf {{A}}}_f]^{-1}_{\tau }\). The trapdoor \([{\mathbf {{A}}}\Vert \vec {{\mathbf {{A}}}}- x \otimes \mathbf {G}]^{-1}_{\tau '}\) allows to sample a short vector \(\mathbf {{v}}_{x}\) which is a valid signature for x. Since the signature is sampled from the same distribution regardless of the signing key, the scheme is statistically key-hiding. The proof of message-selective unforgeability is similar to the selective security proof in [BGG+14]. Recall that the adversary has to announce x for which it is going to forge a signature at the beginning of the game. The matrix  is then generated from \({\mathbf {{A}}}\) based on x in such way that it is possible to generate a key for any function f for which \(f(x) = 1\) without \({\mathbf {{{A}}}}^{-1}_{{\tau _0}}\). It is then shown that forging a signature for x implies breaking \(\mathrm {SIS}\) respective to the matrix \({\mathbf {{A}}}\).
is then generated from \({\mathbf {{A}}}\) based on x in such way that it is possible to generate a key for any function f for which \(f(x) = 1\) without \({\mathbf {{{A}}}}^{-1}_{{\tau _0}}\). It is then shown that forging a signature for x implies breaking \(\mathrm {SIS}\) respective to the matrix \({\mathbf {{A}}}\).
1.4 Related Work
Policy-based signatures were introduced in [BF14], where it was also shown that PBS for \(\mathbf {NP}\) can be constructed from NIZK. [CNW16] construct lattice-based PBS in the random oracle model. [MPR11] introduced attribute-based signatures, and suggested a general framework for constructing ABS from NIZK. In [SAH16] ABS for circuits is constructed from bilinear maps. [BK16] construct ABS for threshold functions and (\(\vee \),\(\wedge \))- functions from lattice assumptions. Our construction in Sect. 6 is the first ABS candidate for circuits that does not use NIZK or non-standard assumptions.
[Fuc14, CRV14] define constrained verifiable random functions (CVRF), which are constraint PRFs where given a constraint key one can compute, in addition to the function value, a non-interactive proof for the computed function value, where the proof is key-hiding. ABS can be constructed from CVRF trivially, however the pseudo-randomness property of known CVRF constructions implies single-key unforgeability of the derived ABS. [Fuc14, CRV14] show existence of CVRFs for poly-sized circuits, where the constructions assume mulitilinar-maps and the multilinear DDH assumption respectively.
Homomorphic signatures were constructed in [BF11, CFW14] for polynomials, and later in [GVW15] for boolean circuits. [LTWC16] define multi-key homomorphic signatures and show how to derive ABS from it. [FMNP16] define multi-key homomorphic MACS and signatures, and extend the [GVW15] HS construction to support multi-key evaluation.
Other notions of digital signatures with fine-grained control over signing permissions are functional signatures (FE) [BGI14] and delegatable functional signatures [BMS16]. In FE, a key respective to a function f can sign a message y if and only if the signer provides a preimage x such that \(f(x) = y\). When the function space consists of efficiently invertible functions, finding such x is trivial whenever it exists, and FE can be derived from (key-policy) CS: a FE key for f will be a CS key for the function that computes \(f\circ f^{-1}\) and returns 0 if and only if the output is equal to the input.
2 Preliminaries
2.1 Digital Signatures
Definition 1
((Standard) Signature Scheme). A signature scheme is a tuple of PPT algorithms \((\mathsf{Setup},\mathsf{Sign},\mathsf{Ver})\) with the following syntax.
-
\(\mathsf{Setup}(1^{\lambda }) \rightarrow (\mathsf{vk},\mathsf{sk})\) takes as input the security parameter \(\lambda \) and outputs a verification key \(\mathsf{vk}\) and a signing key \(\mathsf{sk}\).
-
\(\mathsf{Sign}(\mathsf{sk}, m) \rightarrow \sigma _m\) takes as input a signing key \(\mathsf{sk}\) and a message m, and outputs a signature \(\sigma _m\) for m.
-
\(\mathsf{Ver}_{\mathsf{vk}}(m,\sigma _m)\) takes as input a message m and a signature \(\sigma _m\), and either accepts or rejects.
Correctness. The scheme is correct for a message space \(\mathcal{M}\), if for all \(m\in \mathcal{M}\) it holds that \(\mathsf{Ver}_{\mathsf{vk}}(m,\mathsf{Sign}(\mathsf{sk},m)) = accept\), where \((\mathsf{sk},\mathsf{vk}) \leftarrow \mathsf{Setup}(1^{\lambda })\).
Existential Unforgeability. The scheme is existentially unforgeable for a message space \(\mathcal{M}\) if every PPTM adversary \(\mathcal{A}\) has no more than negligible advantage in the following game:
-
1.
The challenger computes \((\mathsf{sk},\mathsf{vk}) \leftarrow \mathsf{Setup}(1^{\lambda })\) and sends \(\mathsf{vk}\) to \(\mathcal{A}\).
-
2.
\(\mathcal{A}\) makes queries: it sends \(m \in \mathcal{M}\) and gets in response \(\sigma _m \leftarrow \mathsf{Sign}(m,\mathsf{sk})\).
-
3.
\(\mathcal{A}\) wins if it manages to output \((m^*,\sigma _{m^*})\) such that \(\mathsf{Ver}_{\mathsf{vk}}(m^*,\sigma _{m^*}) = accept\), where \(m^* \ne m\) for any signature queried by \(\mathcal{A}\) for a message \(m\in \mathcal{M}\).
2.2 Short Integer Solution (SIS)
Below is the definition and hardness assumption of SIS, as phrased in [Pei16].
Definition 2
(Short Integer Solution ( \(\mathrm {SIS}_{n,q,B,m}\) )). Given a uniformly random matrix \(\mathbf {A}\in \mathbb {Z}_q^{n \times m}\), find a nonzero integer vector \(\mathbf {{r}} \in \mathbb {Z}^m\) of norm \(\left\| {\mathbf {{r}}} \right\| _{\infty } \le B\) such that \({\mathbf {{A}}}\mathbf {{r}} = \mathbf {{0}}\).
Theorem 1
[Ajt96, Mic04, MR07, MP13]. For any \(m= \mathrm{poly}(n)\), \(B> 0\), and sufficiently large \(q \ge B \cdot \mathrm{poly}(n)\), solving \(\mathrm {SIS}_{n,q,B,m}\) with non-negligible probability is at least as hard as solving the decisional approximate shortest vector problem \(\mathsf{GapSVP}_{\gamma }\) and the approximate shortest independent vectors problem \(\mathsf{SIVP}_{\gamma }\) on arbitrary n-dimensional lattices (i.e., in the worst case) with overwhelming probability, for some \(\gamma = B \cdot \mathrm{poly}(n)\).
2.3 Lattice Trapdoors
Let \(n,q\in \mathbb {Z}\), \(\mathbf {g}= (1, 2, 4, \ldots , 2^{\lceil \log q \rceil -1}) \in \mathbb {Z}_q^{\lceil \log q \rceil }\) and \(m = n \lceil \log q \rceil \). The gadget matrix \(\mathbf {G}\) is defined as the diagonal concatenation of \(\mathbf {g}\) n times. Formally, \(\mathbf {G}= \mathbf {g}\otimes \mathbf {I}_n \in \mathbb {Z}_q^{n\times m}\). For any \(t \in \mathbb {Z}\), the function \(\mathbf {G}^{-1}: \mathbb {Z}_q^{n\times t} \rightarrow \{0,1\}^{m\times t}\) expands each entry \(a \in \mathbb {Z}_q\) of the input matrix into a column of size \(\lceil \log q \rceil \) consisting of the bits representation of a. For any matrix \(\mathbf {A}\in \mathbb {Z}_q^{n\times t}\), it holds that \(\mathbf {G}\cdot {\mathbf {{G}}}^{-1}({\mathbf {A}}) =~\mathbf {A}\).
The (centered) discrete Gaussian distribution over \(\mathbb {Z}^m\) with parameter \(\tau \), denoted \(D_{\mathbb {Z}^m, \tau }\), is the distribution over \(\mathbb {Z}^m\) where for all \(\mathbf {{x}}\), \(\Pr [\mathbf {{x}}] \propto e^{-\pi \left\| {\mathbf {{x}}} \right\| ^2/\tau ^2}\). Let \(n,m,q \in {\mathbb N}\) and consider a matrix \({\mathbf {{A}}}\in \mathbb {Z}_q^{n \times m}\). For all \(\mathbf {{v}} \in \mathbb {Z}_q^n\) we let \({\mathbf {{{A}}}}^{-1}_{{\tau }}(\mathbf {{v}})\) denote the random variable whose distribution is the Discrete Gaussian \(D_{\mathbb {Z}^m,\tau }\) conditioned on \({\mathbf {{A}}}\cdot {\mathbf {{{A}}}}^{-1}_{{\tau }}(\mathbf {{v}}) = \mathbf {{v}}\).
A \(\tau \)-trapdoor for \({\mathbf {{A}}}\) is a procedure that can sample from a distribution within \(2^{-n}\) statistical distance of \({\mathbf {{{A}}}}^{-1}_{{\tau }}(\mathbf {{v}})\) in time \(\mathrm{poly}(n,m,\log q)\), for any \(\mathbf {{v}} \in \mathbb {Z}_q^n\). We slightly overload notation and denote a \(\tau \)-trapdoor for \({\mathbf {{A}}}\) by \({\mathbf {{{A}}}}^{-1}_{{\tau }}\). The following properties had been established in a long sequence of works.
Corollary 1
(Trapdoor Generation [Ajt96, MP12]). There exists an efficiently computable value \(m_0 = O(n \log q)\) and an efficient procedure \(\mathsf{TrapGen}(1^n,q,m)\) such that for all \(m \ge m_0\) outputs \(({\mathbf {{A}}}, {\mathbf {{{A}}}}^{-1}_{{\tau _0}})\), where \({\mathbf {{A}}}\in \mathbb {Z}_q^{n \times m}\) is \(2^{-n}\)-uniform and \(\tau _0 = O(\sqrt{n \log q \log n})\).
We use the most general form of trapdoor extension as formalized in [MP12].
Theorem 2
(Trapdoor Extension [ABB10, MP12]). Given \(\bar{{\mathbf {{A}}}}\in \mathbb {Z}_q^{n \times m}\) with a trapdoor \(\bar{{\mathbf {{A}}}}^{-1}_{\tau }\), and letting \(\bar{{\mathbf {{B}}}}\in \mathbb {Z}_q^{n \times m'}\) be s.t. \(\bar{{\mathbf {{A}}}}= \bar{{\mathbf {{B}}}}{\mathbf {{S}}}\pmod {q}\) where \({\mathbf {{S}}}\in \mathbb {Z}^{m' \times m}\) with largest singular value \(s_1({\mathbf {{S}}})\), then \((\bar{{\mathbf {{A}}}}^{-1}_{\tau }, {\mathbf {{S}}})\) can be used to sample from \(\bar{{\mathbf {{B}}}}^{-1}_{\tau '}\) for any \(\tau ' \ge \tau \cdot s_1({\mathbf {{S}}})\).
A few additional important corollaries are derived from this theorem. We recall that \(s_1({\mathbf {{S}}}) \le \sqrt{m'm} \left\| {{\mathbf {{S}}}} \right\| _{\infty }\) and that a trapdoor \(\mathbf {G}^{-1}_{O(1)}\) is trivial. The first is a trapdoor extension that follows by taking \({\mathbf {{S}}} = [\mathbf {I}_{m'} \Vert {\mathbf {{0}}}_{m}]^T\).
Corollary 2
Given \({\mathbf {{A}}}\in \mathbb {Z}_q^{n \times m'}\), with a trapdoor \({\mathbf {{A}}}^{-1}_{\tau }\), it is efficient to generate a trapdoor \([{\mathbf {{A}}}\Vert {\mathbf {{B}}}]^{-1}_{\tau '}\) for all \({\mathbf {{B}}}\in \mathbb {Z}_q^{n \times m}\), for any \(m \in {\mathbb N}\) and any \(\tau ' \ge \tau \).
Next is a trapdoor extension that had been used extensively in prior work. It follows from Theorem 2 with \({\mathbf {{S}}}= [-{\mathbf {{R}}}^T \Vert \mathbf {I}_m]^T\).
Corollary 3
Given \({\mathbf {{A}}}\in \mathbb {Z}_q^{n \times m'}\), and \({\mathbf {{R}}}\in \mathbb {Z}^{m' \times m}\) with \(m=n\lceil \log q \rceil \), it is efficient to compute \([{\mathbf {{A}}}\Vert {\mathbf {{A}}}{\mathbf {{R}}}+ \mathbf {G}]^{-1}_{\tau }\) for \(\tau = O(\sqrt{m m'}\left\| {{\mathbf {{R}}}} \right\| _{\infty })\).
Note that by taking \({\mathbf {{A}}}\) uniform and \({\mathbf {{R}}}\) to be a high entropy small matrix, e.g. uniform in \(\{-1,0,1\}\), and relying on the leftover hash lemma, Corollary 1 is in fact a special case of this one.
It is also possible to permute trapdoors in the following manner.
Corollary 4
Given \([{\mathbf {{A}}}_1 \Vert \dots \Vert {\mathbf {{A}}}_t]^{-1}_{\tau }\) and a permutation \(\rho :\mathbb {Z}_t \rightarrow \mathbb {Z}_t\), it is efficient to compute \([{\mathbf {{A}}}_{\rho (1)} \Vert \dots \Vert {\mathbf {{A}}}_{\rho (t)}]^{-1}_{\tau }\).
2.4 Lattice Evaluation
The following is an abstraction of the evaluation procedure in recent LWE based FHE and ABE schemes, that developed in a long sequence of works [ABB10, MP12, GSW13, AP14, BGG+14, GVW15]. We use a similar formalism to [BV15, BCTW16] but slightly rename the functions.
Theorem 3
There exist efficient deterministic algorithms \(\mathsf{EvalF}\) and \(\mathsf{EvalFX}\) such that for all \(n,q,\ell \in \mathbb {N}\), and for any sequence of matrices \(\vec {{\mathbf {{A}}}}= (\mathbf {A}_1,\ldots ,\mathbf {A}_\ell ) \in (\mathbb {Z}_q^{n \times n\lceil \log q \rceil })^{\ell }\), for any depth d boolean circuit \(f: \{0,1\}^\ell \rightarrow \{0,1\}\) and for every \(\mathbf {{x}}= (x_1, \ldots , x_\ell ) \in \{0,1\}^\ell \), the outputs  and
and  are both in \(\mathbb {Z}^{(\ell n \lceil \log q \rceil ) \times n\lceil \log q \rceil }\) and it holds that \(\left\| {\mathbf {H}_f} \right\| _{\infty }, \left\| {\mathbf {H}_{f,x}} \right\| _{\infty } \le (2 n \lceil \log q \rceil )^{d}\) and \( (\vec {{\mathbf {{A}}}}- \mathbf {{x}}\otimes \mathbf {G}) \cdot \mathbf {H}_{f,\mathbf {{x}}} = \vec {{\mathbf {{A}}}}\cdot \mathbf {H}_f - f(\mathbf {{x}}) \mathbf {G}\pmod {q}\).
are both in \(\mathbb {Z}^{(\ell n \lceil \log q \rceil ) \times n\lceil \log q \rceil }\) and it holds that \(\left\| {\mathbf {H}_f} \right\| _{\infty }, \left\| {\mathbf {H}_{f,x}} \right\| _{\infty } \le (2 n \lceil \log q \rceil )^{d}\) and \( (\vec {{\mathbf {{A}}}}- \mathbf {{x}}\otimes \mathbf {G}) \cdot \mathbf {H}_{f,\mathbf {{x}}} = \vec {{\mathbf {{A}}}}\cdot \mathbf {H}_f - f(\mathbf {{x}}) \mathbf {G}\pmod {q}\).
3 Definition of Constrained Signatures (CS)
We now define constrained signatures, along with a number of security notions that will be used throughout this work. The definitions are presented in the key-policy flavor. See Appendix A for definitions in the message-policy flavor. Lastly we define key delegation in the context of constrained signatures.
Definition 3
((Key-Policy) Constrained Signatures). Let \(\mathcal{X}\) be an attribute space and \(\mathcal{F}\) be a function space of the form \(f\in \mathcal{F}\Longrightarrow f : \mathcal{X}' \rightarrow \{0,1\}\) where \(\mathcal{X}' \subseteq \mathcal{X}\). A constrained signatures scheme for \((\mathcal{X},\mathcal{F})\) is a tuple of algorithms:
-
\(\mathsf{Setup}(1^{\lambda }) \rightarrow (\mathsf{msk},\mathsf{vk})\) takes as input the security parameter \(\lambda \) and possibly a description of \((\mathcal{X},\mathcal{F})\), and outputs a master signing key \(\mathsf{msk}\) and a public verification key \(\mathsf{vk}\).
-
\(\mathsf{Keygen}(f,\mathsf{msk}) \rightarrow \mathsf{sk}_f\) takes as input a function \(f \in \mathcal{F}\) and the master signing key \(\mathsf{msk}\), and outputs a signing key \(\mathsf{sk}_f\).
-
\(\mathsf{Sign}(x,\mathsf{sk}_f) \rightarrow \sigma _{x}\) takes as input an attribute \(x \in \mathcal{X}\) and a signing key \(\mathsf{sk}_f\), and outputs a signature \(\sigma _{x}\).
-
\(\mathsf{Ver}_{\mathsf{vk}}(x, \sigma _{x}) \rightarrow \{accept, reject\}\) takes as input an attribute \(x\in \mathcal{X}\) and a signature \(\sigma _{x}\), and either accepts or rejects.
Correctness. The scheme is correct if for all \(x\in \mathcal{X}\) and \(f \in \mathcal{F}\) for which \(f(x) = 0\), it holds that with all but negligible probability \(\mathsf{Ver}_{\mathsf{vk}}(x,\sigma _{x}) = accept\), where \((\mathsf{msk},\mathsf{vk}) \leftarrow \mathsf{Setup}(1^{\lambda })\) and \(\sigma _{x} = \mathsf{Sign}(x,\mathsf{Keygen}(f,\mathsf{msk}))\).
Privacy. Privacy bounds the information revealed by a signature about the signing key that was used to produce it. We define two notions of privacy. In constraint-hiding privacy, a signature should not reveal the signing key’s functionality f, however it might be possible to retrieve other information such as whether two signatures were produced using the same key. In key-hiding privacy, a signature should not reveal any information at all about the signing key.
Definition 4
(Privacy of (Key-Policy) Constrained Signatures). The scheme is constraint-hiding if any \(\textsc {ppt}\) adversary \(\mathcal{A}\) has no more than negligible advantage in the following game.
-
1.
The challenger computes and outputs \((\mathsf{msk},\mathsf{vk}) \leftarrow \mathsf{Setup}(1^{\lambda })\).
-
2.
\(\mathcal{A}\) sends \((f_0,f_1,x)\) such that \(f_0(x) = f_1(x) = 0\).
-
3.
The challenger computes \(\mathsf{sk}_{f_0} = \mathsf{Keygen}(f_0,\mathsf{msk})\) and \(\mathsf{sk}_{f_1} = \mathsf{Keygen}(f_1,\mathsf{msk})\). It then samples \(b {\mathop {\leftarrow }\limits ^{\scriptscriptstyle {\$}}}\{0,1\}\) and computes \(\sigma _{x,b} \leftarrow \mathsf{Sign}(x,\mathsf{sk}_{f_b})\). It sends \(\sigma _{x,b}\) to \(\mathcal{A}\).
-
4.
\(\mathcal{A}\) outputs \(b' \in \{0,1\}\) and wins if and only if \(b' = b\).
The scheme is key-hiding if any \(\textsc {ppt}\) adversary \(\mathcal{A}\) has no more than negligible advantage in the above game, where in step 3 the challenger sends \((\mathsf{sk}_{f_0},\mathsf{sk}_{f_1},\sigma _{x,b})\) to \(\mathcal{A}\).
Unforgeability. We consider full unforgeability vs. message-selective unforgeability. These notions are caputred by a security game between a challenger and an adversary. In the full unforgeability game, the adversary can adaptively make queries of three types: (1) query for constrained keys, (2) query for signatures under a specified constraint, and (3) query for signatures that are generated with an existing key from a type (2) query. In order to win the adversary has to forge a signature for an attribute \(x^*\) that is not authorized by any of the queried keys, and does not appear in any of the type (2) and (3) signature queries. In the message-selective game, the adversary has to announce \(x^*\) before seeing the verification key. The construction in Sect. 6 is message-selective unforgeable.
Definition 5
(Unforgeability of (Key-Policy) Constrained Signatures). The scheme is fully unforgeable if every PPTM adversary \(\mathcal{A}\) has no more than negligible advantage in the following game:
-
1.
The challenger computes \((\mathsf{msk},\mathsf{vk}) \leftarrow \mathsf{Setup}(1^{\lambda })\) and sends \(\mathsf{vk}\) to \(\mathcal{A}\).
-
2.
\(\mathcal{A}\) makes queries of three types:
-
Key Queries. \(\mathcal{A}\) sends \(f\in \mathcal{F}\) and gets back \(\mathsf{sk}_f\leftarrow \mathsf{Keygen}(f,\mathsf{msk})\).
-
Signature Queries. \(\mathcal{A}\) sends \((f,x)\in \mathcal{F}\times \mathcal{X}\) such that \(f(x) = 0\). The challenger computes \(\mathsf{sk}_f \leftarrow \mathsf{Keygen}(f,\mathsf{msk})\) and sends back \(\sigma _{x} \leftarrow \mathsf{Sign}(x,\mathsf{sk}_f)\).
-
Repeated Signature Queries. \(\mathcal{A}\) sends \(i \in {\mathbb N}\) and \(x \in \mathcal{X}\). If there were less than i signature queries at this point of the game, the challenger returns \(\perp \). Otherwise, let f denote the constraint that was sent at the ith signature query and let \(\mathsf{sk}_f\) denote the key that was generated by the challenger when answering this query. If \(f(x) \ne 0\), the challenger returns \(\perp \). Otherwise it returns \(\sigma _{x} \leftarrow \mathsf{Sign}(x,\mathsf{sk}_f)\).
-
-
3.
\(\mathcal{A}\) wins if it manages to output \((x^*,\sigma _{x^*})\) such that \(\mathsf{Ver}_{\mathsf{vk}}(x^*,\sigma _{x^*}) = accept\) and the following restrictions hold:
-
For any key queried by \(\mathcal{A}\) respective to \(f \in \mathcal{F}\), it holds that \(f(x^*) = 1\).
-
For any signature \(\sigma _x\) queried by \(\mathcal{A}\), it holds that \(x \ne x^*\).
-
The scheme is message-selective unforgeable if any PPT \(\mathcal{A}\) that announces \(x^*\) before seeing \(\mathsf{vk}\) has no more than negligible advantage in the game.
We also define a relaxed notion, single-key-selective unforgeability, which is useful as a building block towards full unforgeability, as shown in Sect. 4. In this security game, the adversary is restricted to a single key query and no signatures queries. It also has to announce the queried constraint at the beginning of the game.
Definition 6
(Single-Key-Selective Unforgeability of (Key-Policy) Constrained Signatures). The scheme is single-key-selective unforgeable if every PPTM adversary \(\mathcal{A}\) has no more than negligible advantage in the following game:
-
1.
\(\mathcal{A}\) sends \(f^* \in \mathcal{F}\) to the challenger.
-
2.
The challenger computes \((\mathsf{msk},\mathsf{vk}) \leftarrow \mathsf{Setup}(1^{\lambda })\) and \(\mathsf{sk}_{f^*} \leftarrow \mathsf{Keygen}(f^*,\mathsf{msk})\), and sends \((\mathsf{vk},\mathsf{sk}_{f^*})\) to \(\mathcal{A}\).
-
3.
\(\mathcal{A}\) wins if it manages to output \((x^*,\sigma _{(x^*)})\) such that \(\mathsf{Ver}_{\mathsf{vk}}(x^*,\sigma _{x^*}) = accept\) and \(f^*(x^*) = 1\).
3.1 Key Delegation
Given a key \(\mathsf{sk}_f\) for a constraint \(f \in \mathcal{F}\), it might be useful to generate a key with limited capabilities, i.e. a key \(\mathsf{sk}_{(f,g)}\) for a constraint that requires \(f(x) = 0\) and \(g(x) = 0\) for some function \(g \in \mathcal{F}\). In this setting, any attribute \(x \in \mathcal{X}\) that can be signed by \(\mathsf{sk}_{(f,g)}\) can also be signed by \(\mathsf{sk}_f\), but the other direction is not guaranteed since it might be the case that \(f(x)=0\) but \(g(x) = 1\). Key delegation can therefore be though of as restricting the signing permissions of a given key.
We now give a formal definition of the key delegation algorithm, along with definitions for correctness, privacy and unforgeability. Note that it captures multiple levels of delegation. The unforgeability game is analogouse to the non-delegatable unforgeability game, where the adversary can in addition query for delegated keys.
Definition 7
(Delegation of (Key-Policy) Constrained Signatures). A constrained signatures scheme \(\mathsf{CS}= (\mathsf{Setup},\mathsf{Keygen},\mathsf{Sign},\mathsf{Ver})\) with attribute space \(\mathcal{X}\), function space \(\mathcal{F}\) and key space \(\mathcal{K}\) supports delegation if there exists a PPT algorithm \(\mathsf{DelKey}\) with the syntax
-
\(\mathsf{DelKey}(\mathsf{sk}_{(f_1,\dots ,f_{t})},f_{t+1}) \rightarrow \mathsf{sk}_{(f_1,\dots ,f_{t+1})}\): takes as input a constrained key \(\mathsf{sk}_{(f_1,\dots ,f_{t})}\in \mathcal{K}\) and a function \(f_{t+1} \in \mathcal{F}\), and outputs a delegated constrained key \(\mathsf{sk}_{(f_1,\dots ,f_{t+1})} \in \mathcal{K}\).
such that it satisfies correctness, privacy and unforgeability as defined below. For any \(t \ge 1\) and \(F = (f_1,\dots ,f_t) \in \mathcal{F}^t\), write \(F(x) = 0\) to denote that \(f \in F \Rightarrow f(x) = 0\). Moreover, denote \(\mathsf{sk}_{F} = \mathsf{sk}_{(f_1,\dots ,f_{t})}\), where \(\forall i \in [2\dots t]: \mathsf{sk}_{(f_1,\dots ,f_i)} = \mathsf{DelKey}(\mathsf{sk}_{(f_1,\dots ,f_{i-1})},f_i)\) and \(\mathsf{sk}_{f_1} = \mathsf{Keygen}(f_1,\mathsf{msk})\) for some \((\mathsf{msk},\mathsf{vk}) \leftarrow \mathsf{Setup}(1^{\lambda })\) which is clear from the context.
Correctness. Consider \((\mathsf{msk},\mathsf{vk}) \leftarrow \mathsf{Setup}(1^{\lambda })\). The scheme is correct for a function family \(\mathcal{F}\) and attribute space \(\mathcal{X}\), if for all \(t \in {\mathbb N}\), \((x,F) \in \mathcal{X}\times \mathcal{F}^t\) for which \(F(x) = 0\), it holds with all but negligible probability that \(\mathsf{Ver}_{\mathsf{vk}}(x,\mathsf{Sign}(x,\mathsf{sk}_{F})) = accept\).
Privacy. The scheme is constraint-hiding if any \(\textsc {ppt}\) adversary \(\mathcal{A}\) has no more than negligible advantage in the following game.
-
1.
The challenger computes and outputs \((\mathsf{msk},\mathsf{vk}) \leftarrow \mathsf{Setup}(1^{\lambda })\).
-
2.
\(\mathcal{A}\) sends \((t,F_0,F_1,x)\), where \(\forall b \in \{0,1\}: F_b = (f^b_1,\dots ,f^b_{t})\) and \(F_b(x) = 0\).
-
3.
The challenger computes \(\mathsf{sk}_{F_0}\) and \(\mathsf{sk}_{F_1}\). It then samples \(b {\mathop {\leftarrow }\limits ^{\scriptscriptstyle {\$}}}\{0,1\}\) and computes \(\sigma _{x,b} \leftarrow \mathsf{Sign}(x,\mathsf{sk}_{F_b})\). It sends \(\sigma _{x,b}\) to \(\mathcal{A}\).
-
4.
\(\mathcal{A}\) outputs \(b' \in \{0,1\}\) and wins if and only if \(b' = b\).
The scheme is key-hiding if any \(\textsc {ppt}\) adversary \(\mathcal{A}\) has no more than negligible advantage in the above game, where in step 3 the challenger sends \((\mathsf{sk}_{F_0},\mathsf{sk}_{F_1},\sigma _{x,b})\) to \(\mathcal{A}\).
Full Unforgeability. The scheme is fully unforgeable if every PPTM adversary \(\mathcal{A}\) has no more than negligible advantage in the following game:
-
1.
The challenger computes \((\mathsf{msk},\mathsf{vk}) \leftarrow \mathsf{Setup}(1^{\lambda })\) and sends \(\mathsf{vk}\) to \(\mathcal{A}\).
-
2.
\(\mathcal{A}\) makes queries of three types:
-
Key Queries. \(\mathcal{A}\) sends \(t\in {\mathbb N}\), \(F\in \mathcal{F}^t\) and gets back \(\mathsf{sk}_F\).
-
Signature Queries. \(\mathcal{A}\) sends \(t\in {\mathbb N}\), \((F,x)\in \mathcal{F}^t \times \mathcal{X}\) such that \(F(x) = 0\). The challenger computes \(\mathsf{sk}_F\) as described above and returns \(\sigma _{x} \leftarrow \mathsf{Sign}(x,\mathsf{sk}_F)\).
-
Repeated Signature Queries. \(\mathcal{A}\) sends \(i \in {\mathbb N}\) and \(x\in \mathcal{X}\). If there were less than i signature queries at this point of the game, the challenger returns \(\perp \). Otherwise, let F denote the set of constraints that was sent at the ith signature query and let \(\mathsf{sk}_F\) denote the key that was generated by the challenger when answering this query. If \(\exists f \in F\) s.t. \(f(x) \ne 0\), the challenger returns \(\perp \). Otherwise it returns \(\sigma _{x} \leftarrow \mathsf{Sign}(x,\mathsf{sk}_f)\).
-
-
3.
\(\mathcal{A}\) wins if it manages to output \((x^*,\sigma _{x^*})\) such that \(\mathsf{Ver}_{\mathsf{vk}}(x^*,\sigma _{x^*}) = accept\) and the following restrictions hold:
-
For any key queried by \(\mathcal{A}\) respective to \(t\in {\mathbb N}\), \(F\in \mathcal{F}^t\), it holds that \(\exists f \in F\) such that \(f(x^*) = 1\).
-
For any signature \(\sigma _x\) queried by \(\mathcal{A}\), it holds that \(x \ne x^*\).
-
Message-Selective Unforgeability. The scheme maintains message-selective unforgeability if any PPT \(\mathcal{A}\) that announces \(x^*\) before seeing \(\mathsf{vk}\) has no more than negligible advantage in the game.
Single-Key-Selective Unforgeability. The scheme is single-key-selective unforgeable if every PPTM adversary \(\mathcal{A}\) has no more than negligible advantage in the following game:
-
1.
\(\mathcal{A}\) sends \(t \in {\mathbb N}, F \in \mathcal{F}^t\) to the challenger.
-
2.
The challenger computes \((\mathsf{msk},\mathsf{vk}) \leftarrow \mathsf{Setup}(1^{\lambda })\) and \(\mathsf{sk}_F\), and sends \((\mathsf{vk},\mathsf{sk}_F)\) to \(\mathcal{A}\).
-
3.
\(\mathcal{A}\) wins if it manages to output \((x^*,\sigma _{x^*})\) such that \(\mathsf{Ver}_{\mathsf{vk}}(x^*,\sigma _{x^*}) = accept\) and \(\exists f \in F\) such that \(f(x^*) = 1\).
4 From Single-Key-Selective Unforgeability to Full Unforgeability
We show how any standard digital signatures scheme can be used to amplify the security guarantee of a (key-policy) CS scheme from single-key-selective to full unforgeability. This comes with a partial loss in key privacy – while the underlying scheme might be either key-hiding or solely constraint-hiding, the amplified scheme reveals key-specific information as part of the signature, and thus it is only constraint-hiding.
Let \(\mathsf{CS}= (\mathsf{Setup}',\mathsf{Keygen}',\mathsf{Sign}',\mathsf{Ver}')\) be a single-key selectively unforgeable constraint-hiding constrained signature scheme with attribute space \(\mathcal{X}'\), constraint space \(\mathcal{F}'\) and verification-key space \(\mathcal{V}\mathcal{K}'\). Let \(\mathsf{S}=(\mathsf{S}.\mathsf{Setup},\mathsf{S}.\mathsf{Sign},\mathsf{S}.\mathsf{Ver})\) be a standard signature scheme with verification-key space \(\mathcal{V}\mathcal{K}\) and message space \(\mathcal{X}\) such that \(\mathcal{V}\mathcal{K}' \times \mathcal{V}\mathcal{K}\subseteq \mathcal{X}\). The construction is as follows.
-
\(\mathsf{Setup}(1^{\lambda })\). Compute \((\mathsf{S}.\mathsf{vk},\mathsf{S}.\mathsf{sk}) \leftarrow \mathsf{S}.\mathsf{Setup}(1^{\lambda })\). Output \(\mathsf{vk}= \mathsf{S}.\mathsf{vk}\) and \(\mathsf{msk}= \mathsf{S}.\mathsf{sk}\).
-
\(\mathsf{Keygen}(f,\mathsf{msk})\). Generate \((\mathsf{vk}',\mathsf{msk}') \leftarrow \mathsf{Setup}'(1^{\lambda })\). Compute \(k'_f \leftarrow \mathsf{Keygen}'(\mathsf{msk}',f)\). Generate \((\mathsf{vk}'',\mathsf{sk}'') \leftarrow \mathsf{S}.\mathsf{Setup}(1^{\lambda })\). Sign \((\mathsf{vk}',\mathsf{vk}'')\) using \(\mathsf{msk}\): \(\sigma _{(\mathsf{vk}',\mathsf{vk}'')} \leftarrow \mathsf{S}.\mathsf{Sign}(\mathsf{S}.\mathsf{sk},(\mathsf{vk}',\mathsf{vk}''))\). Output \(k_f = (\mathsf{vk}',k'_f, \mathsf{vk}'',\mathsf{sk}'',\sigma _{(\mathsf{vk}',\mathsf{vk}'')})\).
-
\(\mathsf{Sign}(x,k_f)\). Compute \(\sigma '_{x}= \mathsf{Sign}'(x,k'_f)\) and \(\sigma ''_{x} = \mathsf{S}.\mathsf{Sign}(\mathsf{sk}'',x)\). Output \(\sigma _{x} = (\mathsf{vk}',\sigma '_{x},\mathsf{vk}'',\sigma ''_{x},\sigma _{(\mathsf{vk}',\mathsf{vk}'')})\).
-
\(\mathsf{Ver}_{\mathsf{vk}}(x,\sigma _{x})\). Accept only if \(\mathsf{S}.\mathsf{Ver}(\sigma _{(\mathsf{vk}',\mathsf{vk}'')},(\mathsf{vk}',\mathsf{vk}'')) = accept\), \(\mathsf{Ver}'_{\mathsf{vk}'}(x,\sigma '_{x}) = accept\) and \(\mathsf{S}.\mathsf{Ver}_{\mathsf{vk}''}(x,\sigma ''_{x}) = accept\).
Lemma 1
(Correctness). The scheme is correct for \((\mathcal{F}',\mathcal{X}')\).
Proof
Fix \(x\in \mathcal{X}'\) and \(f \in \mathcal{F}'\) such that \(f(x) = 0\), and consider \((\mathsf{msk},\mathsf{vk}) \leftarrow \mathsf{Setup}(1^{\lambda })\) and \(\sigma _{x} = \mathsf{Sign}(x,\mathsf{Keygen}(f,\mathsf{msk}))\). Denote \(\sigma _{x} = (\mathsf{vk}',\sigma '_{x},\mathsf{vk}'',\sigma ''_{x},\sigma _{(\mathsf{vk}',\mathsf{vk}'')})\), then by \(\mathsf{Sign}\) and \(\mathsf{Keygen}\) it holds that \(\sigma _{x}' = \mathsf{Sign}'(x,k_f') = \mathsf{Sign}'(x,\mathsf{Keygen}'(\mathsf{msk}',f))\), and since \(f(x) = 0\) it holds that \(\mathsf{Ver}'_{\mathsf{vk}'}(\sigma '_{x},x)=accept\) by the correctness of \(\mathsf{CS}'\). Moreover, \(\mathsf{S}.\mathsf{Ver}_{\mathsf{vk}''}(x,\sigma ''_{x}) = \mathsf{S}.\mathsf{Ver}_{\mathsf{vk}''}(x,\mathsf{S}.\mathsf{Sign}(\mathsf{sk}'',x) = accept\) and \(\mathsf{S}.\mathsf{Ver}(\sigma _{(\mathsf{vk}',\mathsf{vk}'')},\) \((\mathsf{vk}',\mathsf{vk}'')) = \mathsf{S}.\mathsf{Ver}(\mathsf{S}.\mathsf{Sign}(\mathsf{S}.\mathsf{sk},(\mathsf{vk}',\mathsf{vk}'')),(\mathsf{vk}',\mathsf{vk}'')) = accept\) by the correctness of \(\mathsf{S}\). Therefore, \(\mathsf{Ver}_{\mathsf{vk}}(x,m,\sigma _{x})\) accepts.
Lemma 2
(Privacy). The scheme is constraint-hiding for \((\mathcal{F}',\mathcal{X}')\).
Proof
Assume towards contradiction an adversary \(\mathcal{A}\) that wins the constraint-hiding privacy game with some significant probability, and use it to break the constraint-hiding privacy of \(\mathsf{CS}\) as follows:
-
1.
Receive \((\mathsf{vk}',\mathsf{msk}') \leftarrow \mathsf{Setup}'(1^{\lambda })\) from the \(\mathsf{CS}\) challenger.
-
2.
Compute \((\mathsf{S}.\mathsf{vk},\mathsf{S}.\mathsf{sk}) \leftarrow \mathsf{S}.\mathsf{Setup}(1^{\lambda })\) and send \((\mathsf{msk}= \mathsf{S}.\mathsf{sk},\mathsf{vk}= \mathsf{S}.\mathsf{vk})\) to \(\mathcal{A}\).
-
3.
\(\mathcal{A}\) returns \((f_0,f_1,x)\) such that \(f_0(x) = f_1(x) = 0\). Forward \((f_0,f_1,x)\) to the \(\mathsf{CS}\) challenger.
-
4.
The \(\mathsf{CS}\) challenger samples \(b {\mathop {\leftarrow }\limits ^{\scriptscriptstyle {\$}}}\{0,1\}\) and returns \(\sigma '_{x,b}\). Now generate \((\mathsf{vk}'',\mathsf{sk}'') \leftarrow \mathsf{S}.\mathsf{Setup}(1^{\lambda })\), sign \((\mathsf{vk}',\mathsf{vk}'')\) with the standard signature scheme: \(\sigma _{(\mathsf{vk}',\mathsf{vk}'')} \leftarrow \mathsf{S}.\mathsf{Sign}(\mathsf{S}.\mathsf{sk},(\mathsf{vk}',\mathsf{vk}''))\), sign x with the standard signature scheme: \(\sigma ''_{x} \leftarrow \mathsf{S}.\mathsf{Sign}(\mathsf{sk}'',x)\) and send to \(\mathcal{A}\) the signature \(\sigma _{x,b} = (\mathsf{vk}',\sigma '_{x,b},\mathsf{vk}'',\sigma ''_{x},\sigma _{(\mathsf{vk}',\mathsf{vk}'')})\).
-
5.
Get \(b'\) from \(\mathcal{A}\) and forward it to the \(\mathsf{CS}\) challenger. Clearly, any advantage of \(\mathcal{A}\) induces an advantage of the reduction.
Lemma 3
(Unforgeability). The scheme is fully unforgeable for \((\mathcal{F}',\mathcal{X}')\).
Proof
Assume towards contradiction an adversary \(\mathcal{A}\) that wins the security game. We show that it can be used to break either \(\mathsf{S}\) or \(\mathsf{CS}\). Let \(\mathcal{Q}_{key},\mathcal{Q}_{sig},\mathcal{Q}_{rep}\) be the sets of key queries, signature queries and repeated signature queries made by \(\mathcal{A}\) during the security game. Recall that \(\mathcal{Q}_{key} \in \mathcal{F}'\), \(\mathcal{Q}_{sig} \in \mathcal{F}' \times \mathcal{X}'\) and \(\mathcal{Q}_{rep} \in {\mathbb N}\times \mathcal{X}'\). In particular, each query \(q_i \in \mathcal{Q}_{key} \bigcup \mathcal{Q}_{sig}\) contains an element \(f_i \in \mathcal{F}\). Moreover, every response of the challenger (whether it is a key or a signature) contains a pair \((\mathsf{vk}'_i,\mathsf{vk}''_i)\) that is generated during \(\mathsf{Keygen}(f_i,\mathsf{msk})\). \(\mathcal{A}\) wins the game, it therefore outputs a successful forgery \((x^*,\sigma _{x^*})\), where \(\sigma _{x^*} = (\mathsf{vk}'_*,\sigma '_{x^*},\mathsf{vk}''_*,\sigma ''_{x^*},\sigma _{(\mathsf{vk}'_*,\mathsf{vk}''_*)})\). Since \(\mathsf{Ver}_{\mathsf{vk}}(x^*,\sigma _{(x^*,m^*)}) = accept\), it holds that \(\mathsf{S}.\mathsf{Ver}(\sigma _{\mathsf{vk}'_*},\mathsf{vk}'_*)\) accepts, \(\mathsf{Ver}'_{\mathsf{vk}'_*}(x^*,\sigma '_{x^*})\) accepts and \(\mathsf{S}.\mathsf{Ver}_{\mathsf{vk}''}(x^*,\sigma ''_{x^*})\) accepts. Consider three cases:
-
If \(\exists q_i \in \mathcal{Q}_{key}\) such that \((\mathsf{vk}'_i,\mathsf{vk}_i'') = (\mathsf{vk}'_*,\mathsf{vk}''_*)\), then \((x^*,\sigma '_{x^*})\) is a valid forgery to the \(\mathsf{CS}\) instance that was initialized during \(\mathsf{Keygen}(f_i,\mathsf{msk})\). Note that since \(q_i \in \mathcal{Q}_{key}\), \(f_i(x^*) = 1\). We show a reduction from the selective-single-key security game of \(\mathsf{CS}\) to this game:
-
1.
Initialize \((\mathsf{S}.\mathsf{vk},\mathsf{S}.\mathsf{sk}) \leftarrow \mathsf{S}.\mathsf{Setup}(1^{\lambda })\) as in the real scheme and send \(\mathsf{S}.\mathsf{vk}\) to \(\mathcal{A}\).
-
2.
Queries phase:
-
Answer all queries except of the ith as in the real unforgeability game.
-
Upon receiving form \(\mathcal{A}\) the query \(q_i \in \mathcal{Q}_{key}\), send \(f_i\) to the ith \(\mathsf{CS}\) challenger and get back \((\mathsf{vk}'_i,k'_{f_i})\). Generate \((\mathsf{vk}''_i,\mathsf{sk}''_i) \leftarrow \mathsf{S}.\mathsf{Setup}(1^{\lambda })\), sign \((\mathsf{vk}'_i,\mathsf{vk}''_i)\) with the standard scheme: \(\sigma _{(\mathsf{vk}'_i,\mathsf{vk}''_i)} \leftarrow \mathsf{S}.\mathsf{Sign}(\mathsf{S}.\mathsf{sk},(\mathsf{vk}'_i,\mathsf{vk}''_i))\). Send to \(\mathcal{A}\) the key \(k_{f_i} = (\mathsf{vk}'_i,k'_{f_i},\mathsf{vk}_i'',\mathsf{sk}_i'',\sigma _{(\mathsf{vk}'_i,\mathsf{vk}''_i)})\).
-
-
3.
When \(\mathcal{A}\) sends the forgery \((x^*,\sigma _{x^*})\), send \((x^*,\sigma '_{x^*})\) to the ith \(\mathsf{CS}\) challenger to win the selective-single-key game.
-
1.
-
If \(\exists q_i \in \mathcal{Q}_{sig}\) such that \((\mathsf{vk}'_i,\mathsf{vk}_i'') = (\mathsf{vk}'_*,\mathsf{vk}''_*)\), then \((x^*,\sigma ''_{x^*})\) is a valid forgery to the \(\mathsf{S}\) instance that was initialized during \(\mathsf{Keygen}(f_i,\mathsf{msk})\). Note that \(\forall q_i \in \mathcal{Q}_{sig}\), where \(q_i = (f_i,x_i)\), it holds that \(x_i \ne x^*\). We show a reduction from the security game of \(\mathcal{S}\) to this game:
-
1.
Initialize \((\mathsf{S}.\mathsf{vk},\mathsf{S}.\mathsf{sk}) \leftarrow \mathsf{S}.\mathsf{Setup}(1^{\lambda })\) as in the real scheme and send \(\mathsf{S}.\mathsf{vk}\) to \(\mathcal{A}\).
-
2.
Queries phase:
-
Answer all queries up to \(q_i\) as in the real unforgeability game.
-
Upon receiving form \(\mathcal{A}\) the query \(q_i \in \mathcal{Q}_{sig}\), instantiate a game against the ith \(\mathsf{S}\) challenger and get \(\mathsf{vk}_i''\). Query a signature for \(x_i\) and get back \(\sigma ''_{x_i}\). Generate \((\mathsf{vk}'_i,\mathsf{msk}'_i) \leftarrow \mathsf{Setup}'(1^{\lambda })\) and \(k'_{f_i} \leftarrow \mathsf{Keygen}'(\mathsf{msk}_i',f_i)\), sign \(\sigma _{x_i}' \leftarrow \mathsf{Sign}'(x_i,k'_{f_i})\). Sign \((\mathsf{vk}'_i,\mathsf{vk}''_i)\) with the standard signature scheme: \(\sigma _{(\mathsf{vk}'_i,\mathsf{vk}''_i)} \leftarrow \mathsf{S}.\mathsf{Sign}(\mathsf{S}.\mathsf{sk},(\mathsf{vk}'_i,\mathsf{vk}''_i))\). Send \(\mathcal{A}\) the signature \(\sigma _{x_i} = (\mathsf{vk}'_i,\sigma '_{x_i},\mathsf{vk}_i'',\sigma _{x_i}'',\sigma _{(\mathsf{vk}'_i,\mathsf{vk}''_i)})\).
-
Answer all queries as in the real game, except of repeated signature queries that reference \(q_i\). For these, do as described above with the same \(\mathsf{vk}'_i, \mathsf{vk}''_i,\sigma _{(\mathsf{vk}'_i, \mathsf{vk}''_i)}, k'_{f_i}\).
-
-
3.
When \(\mathcal{A}\) sends the forgery \((x^*,\sigma _{x^*})\), send \((x^*,\sigma ''_{x^*})\) to the ith \(\mathsf{S}\) challenger to win the game.
-
1.
-
Otherwise \(\forall q_i \in \mathcal{Q}_{key}\bigcup \mathcal{Q}_{sig}\) \((\mathsf{vk}'_i,\mathsf{vk}_i'') \ne (\mathsf{vk}'_*,\mathsf{vk}''_*)\), and thus \((\sigma _{(\mathsf{vk}'_*,\mathsf{vk}''_*)},(\mathsf{vk}'_*,\mathsf{vk}''_*))\) is a valid forgery to \(\mathsf{S}\). We show a reduction from the security game of \(\mathsf{S}\) to this game:
-
1.
Receive \(\mathsf{S}.\mathsf{vk}\) from the \(\mathsf{S}\) challenger and send it to \(\mathcal{A}\).
-
2.
Answer queries from \(\mathcal{A}\) as in the real game, except the way \(\sigma _{(\mathsf{vk}'_i,\mathsf{vk}''_i)}\) is computed: instead of signing \((\mathsf{vk}'_i,\mathsf{vk}''_i)\) with \(\mathsf{msk}= \mathsf{S}.\mathsf{sk}\) (which we don’t have), query the \(\mathsf{S}\) challenger and get \(\sigma _{(\mathsf{vk}'_i,\mathsf{vk}''_i)}\).
-
3.
When \(\mathcal{A}\) sends the forgery \((x^*,\sigma _{x^*})\), send \((\sigma _{(\mathsf{vk}'_*,\mathsf{vk}''_*)},(\mathsf{vk}'_*,\mathsf{vk}''_*))\) to the \(\mathsf{S}\) challenger to win the game.
-
1.
4.1 Key Delegation
If the underlying scheme \(\mathsf{CS}\) supports delegation, i.e. there exists an algorithm \( \mathsf{DelKey}'(k'_{(f_1,\dots ,f_{t})}, f_{t+1}) \rightarrow k'_{(f_1,\dots ,f_{t},f_{t+1})} \) and \(\mathsf{CS}\) is correct, constraint-hiding and single-key-selectively unforgeable as per Definition 7, then also the amplified construction is. The amplified delegation algorithm delegates the key of \(\mathsf{CS}\). It also initializes a new instance of \(\mathsf{S}\) with each delegation, which is used either to sign x, when the key is used in \(\mathsf{Sign}\), or to sign the verification keys of every two neighboring delegation levels, when the key is delegated.
-
\(\mathsf{DelKey}(\mathsf{sk}_{(f_1,\dots ,f_{t})},f_{t+1})\) takes a key \(\mathsf{sk}_{(f_1,\dots ,f_{t})} = (\mathsf{vk}',k'_{(f_1,\dots ,f_{t})},\{\mathsf{vk}''_i\}_{i \in [t]},\mathsf{sk}''_t,\) \( \sigma _{(\mathsf{vk}',\mathsf{vk}''_1)},\{\sigma _{(\mathsf{vk}''_i,\mathsf{vk}''_{i+1})}\}_{i \in [t-1]})\) and a constraint \(f_{t+1} \in \mathcal{F}'\). It computes \(k'_{(f_1,\dots ,f_{t},f_{t+1})} \leftarrow \mathsf{DelKey}'(k'_{(f_1,\dots ,f_{t})}, f_{t+1})\). It then generates \((\mathsf{sk}''_{t+1},\mathsf{vk}''_{t+1}) \leftarrow \mathsf{S}.\mathsf{Setup}(1^{\lambda })\), signs \(\sigma _{(\mathsf{vk}''_t,\mathsf{vk}''_{t+1})} \leftarrow \mathsf{S}.\mathsf{Sign}(\mathsf{sk}''_t,(\mathsf{vk}''_t,\mathsf{vk}''_{t+1}))\) and outputs \(\mathsf{sk}_{(f_1,\dots ,f_{t},f_{t+1})} = (\mathsf{vk}',k'_{(f_1,\dots ,f_{t+1})},\) \(\{\mathsf{vk}''_i\}_{i \in [t+1]},\mathsf{sk}''_{t+1}, \sigma _{(\mathsf{vk}',\mathsf{vk}''_1)},\{\sigma _{(\mathsf{vk}''_i,\mathsf{vk}''_{i+1})}\}_{i \in [t]})\).
-
\(\mathsf{Sign}(x,\mathsf{sk}_{(f_1,\dots ,f_{t})})\) takes a key \(\mathsf{sk}_{(f_1,\dots ,f_{t})} = (\mathsf{vk}',k'_{(f_1,\dots ,f_{t})},\{\mathsf{vk}''_i\}_{i \in [t]},\mathsf{sk}''_t, \sigma _{(\mathsf{vk}',\mathsf{vk}''_1)},\) \(\{\sigma _{(\mathsf{vk}''_i,\mathsf{vk}''_{i+1})}\}_{i \in [t-1]})\) and an attribute \(x\in \mathcal{X}'\). It computes \(\sigma '_{x} \leftarrow \mathsf{Sign}'(x,k'_{(f_1,\dots ,f_{t})})\) and \(\sigma ''_{x} \leftarrow \mathsf{S}.\mathsf{Sign}(\mathsf{sk}_t'',x)\). It outputs \(\sigma _{x} = (\mathsf{vk}',\sigma '_{x},\{\mathsf{vk}''_i\}_{i \in [t]},\sigma ''_{x},\sigma _{(\mathsf{vk}',\mathsf{vk}''_1)},\{\sigma _{(\mathsf{vk}''_i,\mathsf{vk}''_{i+1})}\}_{i \in [t-1]})\).
-
\(\mathsf{Ver}_{\mathsf{vk}}(x,\sigma _{x})\) accepts only when all of the following conditions hold: \(\mathsf{Ver}_{\mathsf{vk}'}'(x,\sigma '_{x})\) accepts; \(\mathsf{S}.\mathsf{Ver}_{\mathsf{S}.\mathsf{vk}}(\sigma _{(\mathsf{vk}',\mathsf{vk}''_1)},(\mathsf{vk}',\mathsf{vk}''_1))\) accepts; \(\forall i \in [t-1]\), \(\mathsf{S}.\mathsf{Ver}_{\mathsf{vk}_i''}(\sigma _{(\mathsf{vk}''_i,\mathsf{vk}''_{i+1})},(\mathsf{vk}''_i,\mathsf{vk}''_{i+1}))\) accepts; \(\mathsf{S}.\mathsf{Ver}_{\mathsf{vk}''_t}(\sigma ''_{x},x)\) accepts.
See Appendix B for correctness, privacy and unforgeability proofs.
5 Equivalence of CS and Homomorphic Signatures
5.1 Recap on Homomorphic Signatures
Our starting point is a (single-data selectively secure) homomorphic signature scheme, which is also context hiding. We use a simplified version of the definition in [GVW15] that suffices for our needs.
Definition 8
(Single-Data Homomorphic Signature). A single-data homomorphic signature scheme is a 4-tuple of PPT algorithms \((\mathsf{HS}.\mathsf{Setup},\mathsf{HS}.\mathsf{Sign},\) \(\mathsf{HS}.\mathsf{Eval},\mathsf{HS}.\mathsf{Ver})\) with the following syntax.
-
\(\mathsf{HS}.\mathsf{Setup}(1^{\lambda }) \rightarrow (\mathsf{vk},\mathsf{sk})\) takes as input the security parameter \(\lambda \) and possibly a description of the data-set space \(\mathcal{X}\) and the functions space \(\mathcal{G}\). It outputs a verification key \(\mathsf{vk}\) and a signing key \(\mathsf{sk}\).
-
\(\mathsf{HS}.\mathsf{Sign}(\mathsf{sk}, x) \rightarrow \sigma _x\) takes as input a signing key \(\mathsf{sk}\) and a data-set \(x\in \mathcal{X}\), and outputs a signature \(\sigma _x\).
-
\(\mathsf{HS}.\mathsf{Eval}(g,x,\sigma _x) \rightarrow \sigma _{(g,g(x))}\) takes as input a data-set \(x\in \mathcal{X}\) and a function \(g \in \mathcal{G}\) such that g(x) is defined, and a signature \(\sigma _x\). It outputs a signature for the pair (g, g(x)): \(\sigma _{(g,g(x))}\).
-
\(\mathsf{HS}.\mathsf{Ver}_{\mathsf{vk}}(g,y,\sigma _{(g,y)})\) takes as input a function \(g \in \mathcal{G}\), a value y and a signature \(\sigma _{(g,y)}\), and either accepts or rejects.
Correctness. The scheme is correct for a function family \(\mathcal{G}\) and data-set space \(\mathcal{X}\) if for all \(x\in \mathcal{X}\) and \(g \in \mathcal{G}\) such that g(x) is defined, it holds that \(\mathsf{HS}.\mathsf{Ver}_{\mathsf{vk}}(g,g(x),\) \(\sigma _{(g,g(x))}) = accept\), where \(\sigma _{(g,g(x))} = \mathsf{HS}.\mathsf{Eval}(g,x,\sigma _x)\), \(\sigma _x = \mathsf{HS}.\mathsf{Sign}(\mathsf{sk},x)\) and \((\mathsf{vk},\mathsf{sk}) \leftarrow \mathsf{HS}.\mathsf{Setup}(1^{\lambda })\).
Single-Data Selective Unforgeability. Fix \(\mathcal{X},\mathcal{G}\) and consider the following game between an adversary \(\mathcal{A}\) and a challenger:
-
\(\mathcal{A}\) sends \(x\in \mathcal{X}\) to the challenger.
-
The challenger computes \((\mathsf{sk},\mathsf{vk}) \leftarrow \mathsf{HS}.\mathsf{Setup}(1^{\lambda })\) and \(\sigma _x \leftarrow \mathsf{HS}.\mathsf{Sign}_{vk}(\mathsf{sk},x)\). It sends to \(\mathcal{A}\) the values \((\mathsf{vk},\sigma _x)\).
-
\(\mathcal{A}\) outputs \((g,y,\sigma _{(g,y)})\). It wins if \(g \in \mathcal{G}\), \(\mathsf{HS}.\mathsf{Ver}_{\mathsf{vk}}(g,y,\sigma _{(g,y)})=accept\) and \(y \ne g(x)\).
The scheme is secure for \(\mathcal{X},\mathcal{G}\) if any PPT \(\mathcal{A}\) has no more than negligible advantage in this game.
Context Hiding. The scheme is context hiding for \(\mathcal{X},\mathcal{G}\) if any \(\textsc {ppt}\) adversary \(\mathcal{A}\) has no more than negligible advantage in the following game.
-
1.
The challenger computes and outputs \((\mathsf{sk},\mathsf{vk}) \leftarrow \mathsf{HS}.\mathsf{Setup}(1^{\lambda })\).
-
2.
\(\mathcal{A}\) sends \((g,x_0,x_1) \in \mathcal{G}\times \mathcal{X}\times \mathcal{X}\) such that \(g(x_0) = g(x_1)\). Denote this value by y.
-
3.
The challenger computes \(\sigma _{x_0} \leftarrow \mathsf{HS}.\mathsf{Sign}(\mathsf{sk},x_0)\) and \(\sigma _{x_1} \leftarrow \mathsf{HS}.\mathsf{Sign}(\mathsf{sk},x_1)\). It then samples \(b {\mathop {\leftarrow }\limits ^{\scriptscriptstyle {\$}}}\{0,1\}\) and computes \(\sigma _{(g,y)} \leftarrow \mathsf{HS}.\mathsf{Eval}(g,x_b,\sigma _{x_b})\). It sends \((\sigma _{x_0},\sigma _{x_1},\sigma _{(g,y)})\) to \(\mathcal{A}\).
-
4.
\(\mathcal{A}\) outputs \(b' \in \{0,1\}\) and wins if and only if \(b' = b\).
Note that the correctness requirement also captures the validity of a non-evaluated signature: a signature \(\sigma _x\) for a data-set \(x\in \mathcal{X}\) can be verified bit-by-bit using the functions \(\{g_i\}_{i\in [\left| {x} \right| ]}\), where \(g_i(x)\) outputs the ith bit of x. The context hiding property requires that an evaluated signature will not reveal anything about the original (pre-evaluated) signature, other than the evaluation result along with a signature for it.
5.2 Constrained Signatures from Homomorphic Signatures
In this section we construct a (message-policy) CS scheme from context-hiding homomorphic signatures. We assume that the underlying HS scheme is context-hiding and single data-set unforgeable, and show that the resulting CS scheme is single-key-selective unforgeable and key-hiding. Combined with the security amplification from Sect. 4 (which downgrades the key privacy), this results in a scheme that is fully unforgeable and attribute-hiding.
Let \(\mathsf{HS}= (\mathsf{Setup},\mathsf{Sign},\mathsf{Eval},\mathsf{Ver})\) be a homomorphic signature scheme with data-space \(\mathcal{X}\) and functions space \(\mathcal{F}\). We construct \(\mathsf{CS}= (\mathsf{Setup},\mathsf{Keygen},\mathsf{Sign},\mathsf{Ver})\) for \((\mathcal{X},\mathcal{F})\).
-
\(\mathsf{CS}.\mathsf{Setup}(1^{\lambda })\). Initialize the \(\mathsf{HS}\) scheme \((\mathsf{HS}.\mathsf{sk},\mathsf{HS}.\mathsf{vk})\leftarrow \mathsf{HS}.\mathsf{Setup}(1^{\lambda })\) and output \(\mathsf{vk}= \mathsf{HS}.\mathsf{vk}\) and \(\mathsf{msk}= \mathsf{HS}.\mathsf{sk}\).
-
\(\mathsf{CS}.\mathsf{Keygen}(x,\mathsf{msk})\). Sign x using \(\mathsf{HS}\): \(\mathsf{HS}.\sigma _x \leftarrow \mathsf{HS}.\mathsf{Sign}(\mathsf{HS}.\mathsf{sk}, x)\). Output \(\mathsf{sk}_x = \mathsf{HS}.\sigma _x\).
-
\(\mathsf{CS}.\mathsf{Sign}(f,\mathsf{sk}_x)\). Use \(\sigma _x\) to homomorphically compute a context-hiding signature for \(y = f(x)\). That is, compute and output \(\sigma _{f}= \mathsf{HS}.\sigma _{(f,f(x))} \leftarrow \mathsf{HS}.\mathsf{Eval}(f, x, \sigma _x)\).
-
\(\mathsf{CS}.\mathsf{Ver}_{\mathsf{vk}}(f,\sigma _{f})\). Accept if and only if \(\mathsf{HS}.\mathsf{Ver}_{\mathsf{vk}} (f,0,\sigma _{f})\) accepts.
Lemma 4
(Correctness). The scheme is correct for \((\mathcal{F},\mathcal{X})\).
Proof
Fix \((x,f) \in \mathcal{X}\times \mathcal{F}\) such that \(f(x) = 0\). Consider \((\mathsf{msk},\mathsf{vk}) \leftarrow \mathsf{CS}.\mathsf{Setup}(1^{\lambda })\), \(\mathsf{sk}_x \leftarrow \mathsf{CS}.\mathsf{Keygen}(x,\mathsf{msk})\) and \(\sigma _{f} = \mathsf{CS}.\mathsf{Sign}(f,\mathsf{sk}_x)\). Then it holds that \(\sigma _{f} \leftarrow \mathsf{HS}.\mathsf{Eval}(f,x,\mathsf{HS}.\mathsf{Sign}(\mathsf{HS}.\mathsf{sk},x))\). We need to show that \(\mathsf{Ver}_{\mathsf{vk}}(f,\sigma _{f}) = accept\), i.e. that \(\mathsf{HS}.\mathsf{Ver}_{\mathsf{vk}} (f,0,\mathsf{HS}.\sigma _{(f,f(x))})\) accepts. Indeed, \(f(x) = 0\) by assumption, thus the result follows by the correctness of \(\mathsf{HS}\).
Lemma 5
(Privacy). The scheme is key-hiding for \((\mathcal{F},\mathcal{X})\).
Proof
Assume towards contradiction an adversary \(\mathcal{A}_c\) that wins the privacy game with noticeable advantage and use it to break the context hiding property of the underlying \(\mathsf{HS}\) scheme as follows:
-
1.
Receive \((\mathsf{HS}.\mathsf{sk},\mathsf{HS}.\mathsf{vk}) \leftarrow \mathsf{HS}.\mathsf{Setup}(1^{\lambda })\) from the \(\mathsf{HS}\) challenger and forward it to \(\mathcal{A}_c\) as \((\mathsf{msk},\mathsf{vk})\).
-
2.
Receive from \(\mathcal{A}_c\) a tuple \((x_0,x_1,f)\) such that \(f(x_0) = f(x_1) = 0\). Forward \((x_0,x_1,f)\) to the \(\mathsf{HS}\) challenger.
-
3.
Receive from the \(\mathsf{HS}\) challenger the challenge \((\mathsf{HS}.\sigma _{x_0},\mathsf{HS}.\sigma _{x_1},\mathsf{HS}.\sigma _{(f,0)})\) and forward it to \(\mathcal{A}_c\) as \((\mathsf{sk}_{x_0},\mathsf{sk}_{x_1},\sigma _{f})\).
-
4.
Get \(b'\) from \(\mathcal{A}_c\) and forward it to the \(\mathsf{HS}\) challenger. Clearly, any advantage of \(\mathcal{A}_c\) induces an advantage of the reduction.
Lemma 6
(Unforgeability). The scheme is single-key-selectively unforgeable for \((\mathcal{F},\mathcal{X})\).
Proof
Consider the CS single-key selective security game against an adversary \(\mathcal{A}_c\). Let \(x \in \mathcal{X}\) be the attribute sent by \(\mathcal{A}_c\), and assume towards contradiction that it wins the game. Then \(\mathcal{A}_c\) outputs \((f,\sigma _{f})\) such that \(\mathsf{CS}.\mathsf{Ver}_{\mathsf{vk}}(f,\sigma _{f}) = accept\) and \(f(x) \ne 0\). Such adversary can be used to break the unforgeability of \(\mathsf{HS}\):
-
1.
Upon receiving x from \(\mathcal{A}_c\), send it to the \(\mathsf{HS}\) challenger.
-
2.
The \(\mathsf{HS}\) challenger sends back \(\mathsf{HS}.\mathsf{vk}\) and \(\mathsf{HS}.\sigma _{x} = \mathsf{HS}.\mathsf{Sign}(\mathsf{HS}.\mathsf{sk}, x)\), which is exactly \((\mathsf{vk}, \mathsf{sk}_{x})\) that we have to send to \(\mathcal{A}_c\).
-
3.
\(\mathcal{A}_c\) sends back \((f, \sigma _{f})\) such that \(\mathsf{Ver}_{\mathsf{vk}}(f,\sigma _{f}) = accept\) and \(f(x) \ne 0\). Denoting \(\sigma _{f} = \mathsf{HS}.\sigma _{(f,f(x))}\), it means that \(\mathsf{HS}.\mathsf{Ver}_{\mathsf{vk}}(f,0,\mathsf{HS}.\sigma _{(f,f(x))}) = accept\) while \(f(x) \ne 0\), therefore \(\mathsf{HS}.\sigma _{(f_{m},f_m(x))}\) is a successful forgery against \(\mathsf{HS}\).
5.3 Homomorphic Signatures from Constrained Signatures
We show how to construct a context-hiding 1-hop homomorphic signatures scheme from (message-policy) CS. We assume that the underlying CS scheme is single-key-selective unforgeable and key-hiding, and show that the resulting HS scheme is context-hiding and selectively unforgeable. As shown in [GVW15], it is possible to construct an adaptively unforgeable HS scheme from a selectively unforgeable HS scheme.
Let \(\mathsf{CS}= (\mathsf{Setup},\mathsf{Keygen},\mathsf{Sign},\mathsf{Ver})\) be a constrained signatures scheme with attribute space \(\mathcal{X}\) and constraint space \(\mathcal{F}\). We construct \(\mathsf{HS}= (\mathsf{Setup},\mathsf{Sign},\mathsf{Eval},\mathsf{Ver})\) for data-set space \(\mathcal{X}\) and functions space \(\mathcal{G}: \mathcal{X}\rightarrow \mathcal{Y}\), where the requirement is that for any \((g,y) \in \mathcal{G}\times \mathcal{Y}\), it holds that \(f_{(g,y)} \in \mathcal{F}\), where \(f_{(g,y)}: \mathcal{X}\rightarrow \{0,1\}\) is a function that on input x returns 0 if and only if \(g(x) = y\).
-
\(\mathsf{HS}.\mathsf{Setup}(1^{\lambda })\). Initialize the \(\mathsf{CS}\) scheme: compute \((\mathsf{CS}.\mathsf{msk},\mathsf{CS}.\mathsf{vk})\leftarrow \mathsf{CS}.\mathsf{Setup}(1^{\lambda })\). Output \(\mathsf{vk}= \mathsf{CS}.\mathsf{vk}\) and \(\mathsf{sk}= \mathsf{CS}.\mathsf{msk}\).
-
\(\mathsf{HS}.\mathsf{Sign}(x,\mathsf{sk})\). Compute and output \(\sigma _x = \mathsf{CS}.\mathsf{sk}_x \leftarrow \mathsf{CS}.\mathsf{Keygen}(x,\mathsf{CS}.\mathsf{msk})\).
-
\(\mathsf{HS}.\mathsf{Eval}(g,\sigma _x)\). Let \(y = g(x)\). Define the circuit \(f_{(g,y)}: \mathcal{X}\rightarrow \{0,1\}\) that on input x returns 0 if and only if \(g(x) = y\). Use \(\mathsf{CS}.\mathsf{sk}_x\) to sign the policy \(f_{(g,y)}\). That is, compute and output \(\sigma _{(g,y)} = \mathsf{CS}.\sigma _{f_{(g,y)}} \leftarrow \mathsf{CS}.\mathsf{Sign}(f_{(g,y)}, \mathsf{CS}.\mathsf{sk}_x)\).
-
\(\mathsf{HS}.\mathsf{Ver}_{\mathsf{vk}}(g,y,\sigma _{(g,y)})\). Accept if and only if \(\mathsf{CS}.\mathsf{Ver}_{\mathsf{vk}} (f_{(g,y)},\mathsf{CS}.\sigma _{f_{(g,y)}})\) accepts.
Lemma 7
(Correctness). The scheme is correct for \((\mathcal{G},\mathcal{X})\).
Proof
Fix \((x,g) \in \mathcal{X}\times \mathcal{G}\). Consider \((\mathsf{sk},\mathsf{vk}) \leftarrow \mathsf{HS}.\mathsf{Setup}(1^{\lambda })\), \(\sigma _x \leftarrow \mathsf{HS}.\mathsf{Sign}(x,\mathsf{sk})\) and \(\sigma _{(g,y)} = \mathsf{HS}.\mathsf{Eval}(g,\sigma _x)\), where \(y = g(x)\). Then it holds that \(\sigma _{(g,y)} = \mathsf{CS}.\sigma _{f_{(g,y)}} = \mathsf{CS}.\mathsf{Sign}(f_{(g,y)}, \mathsf{CS}.\mathsf{sk}_x)\), where \(\mathsf{CS}.\mathsf{sk}_x \leftarrow \mathsf{CS}.\mathsf{Keygen}(x,\mathsf{CS}.\mathsf{msk})\). We need to show that \(\mathsf{HS}.\mathsf{Ver}_{\mathsf{vk}}(g,y,\sigma _{(g,y)}) = accept\), i.e. that \(\mathsf{CS}.\mathsf{Ver}_{\mathsf{vk}} (f_{(g,y)},\mathsf{CS}.\sigma _{f_{(g,y)}})\) accepts. Indeed, \(g(x) = y\) and therefore \(f_{(g,y)}(x) =0 \), and thus \(\mathsf{CS}.\mathsf{Ver}_{\mathsf{vk}} (f_{(g,y)},\mathsf{CS}.\sigma {_{f_{(g,y)}}})\) accepts by the correctness of \(\mathsf{CS}\).
Lemma 8
(Privacy). The scheme is context-hiding for \(({\mathcal {G}},{\mathcal {X}})\).
Proof
Assume towards contradiction an adversary \({\mathcal {A}}_h\) that wins the context-hiding game with noticeable advantage, and use it to break the key-privacy the underlying \({\mathsf{MPCS}}\) scheme as follows:
-
1.
Receive \((\mathsf{CS}.\mathsf{msk},\mathsf{CS}.\mathsf{vk}) \leftarrow \mathsf{CS}.\mathsf{Setup}(1^{\lambda })\) from the \(\mathsf{CS}\) challenger and forward it to \(\mathcal{A}_h\) as \((\mathsf{sk},\mathsf{vk})\).
-
2.
Receive from \(\mathcal{A}_h\) a tuple \((g,x_0,x_1)\) such that \(g(x_0) = g(x_1)\) and denote this value by y. Forward \((x_0,x_1,f_{(g,y)})\) to the \(\mathsf{CS}\) challenger.
-
3.
Receive from the \(\mathsf{CS}\) challenger the challenge \((\mathsf{CS}.\mathsf{sk}_{x_0},\mathsf{CS}.\mathsf{sk}_{x_1},\mathsf{CS}.\sigma _{f_{(g,y)}})\) and forward it to \(\mathcal{A}_h\) as \((\sigma _{x_0},\sigma _{x_1},\sigma _{(g,y)})\).
-
4.
Get \(b'\) from \(\mathcal{A}_h\) and forward it to the \(\mathsf{CS}^y\) challenger. Clearly, any advantage of \(\mathcal{A}_h\) induces an advantage of the reduction.
Lemma 9
(Unforgeability). The scheme is single-data selectively unforgeable for \(({\mathcal {G}},{\mathcal {X}})\).
Proof
Consider the HS single-data selective unforgeability game against an adversary \({\mathcal {A}}_h\). Let \(x \in {\mathcal {G}}\) be the data-set sent by \(\mathcal{A}_h\), and assume towards contradiction that it wins the game. Then \(\mathcal{A}_h\) outputs \((g,y,\sigma _{(g,y)})\) such that \(\mathsf{HS}.\mathsf{Ver}_{\mathsf{vk}}(g,y,\sigma _{(g,y)}) = accept\) and \(g(x) \ne y\). Such adversary can be used to break the unforgeability of \({\mathsf{MPCS}}\):
-
1.
Upon receiving x from \(\mathcal{A}_h\), send it to the \(\mathsf{CS}\) challenger.
-
2.
The \(\mathsf{CS}\) challenger sends back \(\mathsf{CS}.\mathsf{sk}_{x} = \mathsf{CS}.\mathsf{Keygen}(\mathsf{CS}.\mathsf{msk}, x)\) and \(\mathsf{CS}.\mathsf{vk}\), which is exactly \(( \sigma _{x},\mathsf{vk})\) that we have to send to \(\mathcal{A}_h\).
-
3.
\(\mathcal{A}_h\) sends back \((g,y, \sigma _{(g,y)})\) such that \(\mathsf{HS}.\mathsf{Ver}_{\mathsf{vk}}(g,y,\sigma _{(g,y)}) = accept\) and \(g(x) \ne y\). Denoting \(\sigma _{(g,y)} = \mathsf{CS}.\sigma _{f_{(g,y)}}\), it means that \(\mathsf{CS}.\mathsf{Ver}_{\mathsf{vk}}(f_{(g,y)},\mathsf{CS}.\sigma _{f_{(g,y)}}) = accept\), however \(g(x) \ne y\) and therefore \(f_{(g,y)}(x) \ne 0\), thus \(\mathsf{CS}.\sigma _{f_{(g,y)}}\) is a successful forgery against \(\mathsf{CS}\).
6 CS Construction from Lattice Trapdoors
In this section we construct a (key-policy) CS scheme from lattices trapdoors, using techniques that were developed in [GVW13, BGG+14]. The resulting scheme supports a fixed attribute space, and the constraint space consists of boolean circuits with a bound on depth. We prove message-selective unforgeability based on the \(\mathrm {SIS}\) hardness assumption, and statistical key-hiding. Lastly we show how to extend the scheme to support key delegation.
The initialization parameters are \((\ell ,d)\), where the attribute space is \(\mathcal{X}= \{0,1\}^{\ell }\) and the constraint space is all d-depth bounded circuits \(\mathcal{F}_d =\{f : \{0,1\}^{\ell } \rightarrow \{0,1\}\}\).
6.1 The Scheme
Initialize the parameters \(n,m,m',q,B,\tau _0,\tau _k,\tau _s\) respective to \(\lambda ,d,\ell \) as described below.
-
\(\mathsf{Setup}(1^{\lambda }) \rightarrow (\mathsf{msk},\mathsf{vk})\): Generate a matrix \({\mathbf {{A}}}\in \mathbb {Z}_q^{n \times m'}\) with its trapdoor \({\mathbf {{{A}}}}^{-1}_{{\tau _0}}\) (see Corollary 1). Sample uniformly a matrix \(\vec {{\mathbf {{A}}}}{\mathop {\leftarrow }\limits ^{\scriptscriptstyle {\$}}}\mathbb {Z}_q^{n \times (m \times \ell )}\). Output
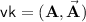 and \(\mathsf{msk}= {\mathbf {{{A}}}}^{-1}_{{\tau _0}}\).
and \(\mathsf{msk}= {\mathbf {{{A}}}}^{-1}_{{\tau _0}}\). -
\(\mathsf{Keygen}_{\mathsf{vk}}(f,\mathsf{msk}) \rightarrow \mathsf{sk}_f\): Compute
 (see Theorem 3) and \({\mathbf {{A}}}_f = \vec {{\mathbf {{A}}}}\cdot {\mathbf {{H}}}_f\), then use \({\mathbf {{{A}}}}^{-1}_{{\tau _0}}\) to compute \(\mathsf{sk}_f = [{\mathbf {{A}}}\Vert {\mathbf {{A}}}_f]^{-1}_{\tau _k}\) (see Corollary 2).
(see Theorem 3) and \({\mathbf {{A}}}_f = \vec {{\mathbf {{A}}}}\cdot {\mathbf {{H}}}_f\), then use \({\mathbf {{{A}}}}^{-1}_{{\tau _0}}\) to compute \(\mathsf{sk}_f = [{\mathbf {{A}}}\Vert {\mathbf {{A}}}_f]^{-1}_{\tau _k}\) (see Corollary 2). -
\(\mathsf{Sign}_{ \mathsf{pp}}(x,\mathsf{sk}_f) \rightarrow \sigma _{x}\): If \(f(x) \ne 0\) return \(\perp \). Otherwise, compute
 (see Theorem 3). Note that by this theorem, \( [\vec {{\mathbf {{A}}}}-x \otimes \mathbf {G}]\cdot {\mathbf {{H}}}_{f,x} = {\mathbf {{A}}}_f -f(x)\mathbf {G}= {\mathbf {{A}}}_f \). Now apply trapdoor extension (see Theorem 2) with $$ \bar{{\mathbf {{A}}}}= [{\mathbf {{A}}}\Vert {\mathbf {{A}}}_f], \quad \bar{{\mathbf {{B}}}}= [{\mathbf {{A}}}\Vert \vec {{\mathbf {{A}}}}- x \otimes \mathbf {G}], \quad {\mathbf {{S}}}= \left[ \begin{array}{cc} \mathbf {I}_{m^{\prime }} &{} {\mathbf {{0}}} \\ {\mathbf {{0}}} &{} {\mathbf {{H}}}_{f,x} \end{array} \right] $$
(see Theorem 3). Note that by this theorem, \( [\vec {{\mathbf {{A}}}}-x \otimes \mathbf {G}]\cdot {\mathbf {{H}}}_{f,x} = {\mathbf {{A}}}_f -f(x)\mathbf {G}= {\mathbf {{A}}}_f \). Now apply trapdoor extension (see Theorem 2) with $$ \bar{{\mathbf {{A}}}}= [{\mathbf {{A}}}\Vert {\mathbf {{A}}}_f], \quad \bar{{\mathbf {{B}}}}= [{\mathbf {{A}}}\Vert \vec {{\mathbf {{A}}}}- x \otimes \mathbf {G}], \quad {\mathbf {{S}}}= \left[ \begin{array}{cc} \mathbf {I}_{m^{\prime }} &{} {\mathbf {{0}}} \\ {\mathbf {{0}}} &{} {\mathbf {{H}}}_{f,x} \end{array} \right] $$(using \(\mathsf{sk}_f = [{\mathbf {{A}}}\Vert {\mathbf {{A}}}_f]_{\tau _k}^{-1} = \bar{{\mathbf {{A}}}}_{\tau _k}^{-1}\)), and achieve \(\bar{{\mathbf {{B}}}}^{-1}_{\tau _s} = [{\mathbf {{A}}}\Vert \vec {{\mathbf {{A}}}}- x \otimes \mathbf {G}]^{-1}_{\tau _s}\). Sample \(\sigma _{x} {\mathop {\leftarrow }\limits ^{\scriptscriptstyle {\$}}}[{\mathbf {{A}}}\Vert \vec {{\mathbf {{A}}}}-x \otimes \mathbf {G}]^{-1}_{\tau _s}(\mathbf {{0}})\) and output \(\sigma _{x}\). Note that by Theorem 3, \({\mathbf {{H}}}_{f,x} \in \mathbb {Z}^{\ell m \times m}\) and \(\left\| {{\mathbf {{H}}}_{f,x}} \right\| _{\infty } \le (2m)^{d}\), and thus the largest singular value \(s_1({\mathbf {{S}}}) = \max \{1, s_1({\mathbf {{H}}}_{f,x})\} \le \sqrt{\ell }2^dm^{d+1}\). Hence \(\tau _k \cdot s_1({\mathbf {{S}}}) \le \tau _s = \tau _k \cdot \sqrt{\ell }2^dm^{d+1}\), as required by the conditions of Theorem 2.
-
\(\mathsf{Ver}_{ \mathsf{pp}}(x, \sigma _{x}) \rightarrow \{accept, reject\}\): Output accept if and only if the following conditions hold: \(\sigma _{x} \ne \perp \), \(\sigma _{x} \ne \mathbf {{0}}\), \([{\mathbf {{A}}}\Vert \vec {{\mathbf {{A}}}}-x \otimes \mathbf {G}]\cdot \sigma _{x} = \mathbf {{0}}\) and \(\left\| {\sigma _{x}} \right\| _{\infty }\le B\).
Choice of Parameters. The \(\mathrm {SIS}\) parameters \(n,q,B'\) are chosen according to constraints from the correctness and security analyses that follow. We require that \(n \ge \lambda \), \(q\le 2^n\) and recall that \(\ell = \mathrm{poly}(\lambda ) \le 2^n\). We set \(m = n \lceil \log q \rceil \), \(m' = \max \{m_0, (n+1)\lceil \log q \rceil + 2\lambda \}\), where \(m_0\) is as required by \(\mathsf{TrapGen}\) (see Corollary 1), \(\tau _0 = O(\sqrt{n \lceil \log q \rceil \log {n}})\) as required by \(\mathsf{TrapGen}\) (see Corollary 1), \(\tau _k = \max \{ \sqrt{m'}\ell 2^d m^{1.5+d}, \tau _0\}\), \(\tau _s = \tau _k \cdot \sqrt{\ell }2^dm^{d+1}\), \(B = \tau _s\sqrt{m' +\ell \cdot m}\), and we require that \( (\ell m + 1) B \le B' \), i.e. that \( (\ell m + 1) \sqrt{m'}\ell ^{1.5} 2^{2d} m^{2d+2.5}\sqrt{m' +\ell \cdot m} \le B' \), while keeping \(\mathrm {SIS}_{n,q,B',m'}\) hard as per Theorem 1. These constraints can be met by setting \(n = d^{\frac{1}{\epsilon }} + \ell \), \(B' = 2^{n^{\epsilon }}\) and then choosing q accordingly based on Theorem 1. Note that it guarantees that indeed \(q \le 2^n\) and \( (\ell m + 1) \sqrt{m'}\ell ^{1.5} 2^{2d} m^{2d+2.5}\sqrt{m' +\ell \cdot m} \le B'. \)
Correctness and Security. We prove correctness and security for the attribute space \(\mathcal{X}= \{0,1\}^{\ell }\) and function family \(\mathcal{F}_d = \{ f: \{0,1\}^{\ell } \rightarrow \{0,1\}\}\) of circuits with depth at most d.
Lemma 10
(Correctness). The scheme is correct for \((\mathcal{X},\mathcal{F})\).
Proof
Fix \(x\in \mathcal{X}\) and \(f \in \mathcal{F}\) for which \(f(x) = 0\), and consider \((\mathsf{msk},\mathsf{vk}) \leftarrow \mathsf{Setup}(1^{\lambda })\) and \(\sigma _{x} = \mathsf{Sign}_{\mathsf{vk}}(x,\mathsf{Keygen}_{\mathsf{vk}}(f,\mathsf{msk}))\). Then since \(f(x) = 0\), \(\sigma _{x} \in [{\mathbf {{A}}}\Vert \vec {{\mathbf {{A}}}}-x \otimes \mathbf {G}]^{-1}_{\tau _s}(\mathbf {{0}})\) and therefore \([{\mathbf {{A}}}\Vert \vec {{\mathbf {{A}}}}-x\otimes \mathbf {G}]\cdot \sigma _{x} = 0\). By the properties of lattice trapdoors, samples from \([{\mathbf {{A}}}\Vert \vec {{\mathbf {{A}}}}-x \otimes \mathbf {G}]^{-1}_{\tau _s}(\mathbf {{0}})\) are within \(2^{-n}\) statistical distance from a discrete Gaussian distribution over \(\mathbb {Z}_q^{m' + \ell \cdot m}\) with parameter \(\tau _s\). Therefore, with all but \(2^{-(m' + \ell \cdot m)} = \mathrm{negl}(\lambda )\) probability, \(\left\| {\sigma _{(x,m)}} \right\| _{\infty } \le \tau _s \sqrt{m' + \ell \cdot m} = B\) and hence \(\mathsf{Ver}_{\mathsf{vk}}(x,\sigma _{x}) = accept\).
Lemma 11
(Privacy). The scheme is statistically key-hiding for \((\mathcal{X},\mathcal{F})\).
Proof
Consider the key-hiding privacy game from Definition 4. Change the way that \(\sigma _{x,b}\) is generated in the challenge: use \(\mathsf{msk}= {\mathbf {{{A}}}}^{-1}_{{\tau _0}}\) to compute \([{\mathbf {{A}}}\Vert \vec {{\mathbf {{A}}}}-x \otimes \mathbf {G}]^{-1}_{\tau _s}\) (note that \(\tau _s \ge \tau _0\) and see Corollary 2), then sample and output \(\sigma _{x,b} {\mathop {\leftarrow }\limits ^{\scriptscriptstyle {\$}}}[{\mathbf {{A}}}\Vert \vec {{\mathbf {{A}}}}-x \otimes \mathbf {G}]^{-1}_{\tau _s}(\mathbf {{0}})\). The distribution from which \(\sigma _{x,b}\) is sampled remains the same, therefore this change is statistically indistinguishable. In this setting, the challenge is independent of b and thus any adversary has no advantage in the game.
Lemma 12
(Unforgeability). The scheme is message-selective unforgeable for \((\mathcal{X},\mathcal{F})\).
Proof
The proof proceeds with a sequence of hybrids and follows similar lines to [BGG+14].
Hybrid \({\mathcal {H}}_{0}\). The message-selective unforgeability game from Definition 5.
Hybrid \({\mathcal {H}}_{1}\). Upon receiving \(x^*\), the challenger generates \(\mathsf{vk}\) as follows: it generates \({\mathbf {{A}}}\) along with \({\mathbf {{{A}}}}^{-1}_{{\tau _0}}\) as before, then it samples a matrix \(\vec {{\mathbf {{R}}}}_A {\mathop {\leftarrow }\limits ^{\scriptscriptstyle {\$}}}{\{0,1\}}^{m'\times \ell _{\mathcal{X}} m}\) and computes \(\vec {{\mathbf {{A}}}}= {\mathbf {{A}}}\vec {{\mathbf {{R}}}}_A + x^* \otimes \mathbf {G}\). Indistinguishability follows from the extended leftover hash lemma, since \(m' \ge (n+1) \lceil \log q \rceil + 2 \lambda \) and \({\mathbf {{A}}}\) is statistically-close to uniform by Corollary 1.
Hybrid \({\mathcal {H}}_{2}\). Change the way that the challenger answers key queries. Let f be a query, then \(f(x^*) = 1\) and thus \(f(x^*) = 1\), thus by Theorem 3
Hence \([{\mathbf {{A}}}\Vert {\mathbf {{A}}}_f] = [{\mathbf {{A}}}\Vert {\mathbf {{A}}}\cdot \vec {{\mathbf {{R}}}}_A \cdot {\mathbf {{H}}}_{f,x^*} + \mathbf {G}]\), and by Corollary 3 it is possible to compute \(\mathsf{sk}_f = [{\mathbf {{A}}}\Vert {\mathbf {{A}}}_f]^{-1}_{\tau _k} = [{\mathbf {{A}}}\Vert {\mathbf {{A}}}\cdot \vec {{\mathbf {{R}}}}_A \cdot {\mathbf {{H}}}_{f,x^*} + \mathbf {G}]^{-1}_{\tau _k}\) given \({\mathbf {{A}}},\vec {{\mathbf {{R}}}}_A\) and \({\mathbf {{H}}}_{f,x^*}\), since \(\left\| {{\mathbf {{H}}}_{f,x}} \right\| _{\infty } \le (2m)^{d}\) and thus
The distribution of \(\mathsf{sk}_f\) remains the same, thus the hybrids are statistically indistinguishable.
Hybrid \({\mathcal {H}}_{3}\). Change the way that the challenger answers signature queries. Let (f, x) be a query, then \(x \ne x^*\) and \(f(x) = 0\). Consider the function \(f_{x}:\{0,1\}^{\ell } \rightarrow \{0,1\}\) that returns 0 if the input is x, and 1 otherwise. Then since \(x\ne x^*\), \(f_{x}(x^*) = 1\), hence we can generate a \(\mathsf{sk}_{f_x}\) respective to the function \(f_x\) as described in the previous hybrid. In this hybrid we compute a signature for x using this \(\mathsf{sk}_{f_x}\), i.e. output \(\mathsf{Sign}_{\mathsf{vk}}(x,\mathsf{sk}_{f_x})\). Since \(f_{x}(x)= 0\) and the scheme is statistically constraint-hiding, this change is statistically indistinguishable.
Hybrid \({\mathcal {H}}_{4}\). Change the way that the challenger answers repeated signature queries. Let \((i,x) \in {\mathbb N}\times \mathcal{X}\) be a query. Compute and output \(\mathsf{Sign}_{\mathsf{vk}}(x,\mathsf{sk}_{f_x})\), where \(\mathsf{sk}_{f_x}\) is as described above. Since the scheme is statistically key-hiding, this change is statistically indistinguishable.
Hybrid \({\mathcal {H}}_{5}\). At this point the challenger does not use \({\mathbf {{{A}}}}^{-1}_{{\tau _0}}\) anymore. We switch to sampling \({\mathbf {{A}}}\) uniformly without \({\mathbf {{{A}}}}^{-1}_{{\tau _0}}\), which is statistically indistinguishable by Corollary 1.
Finally we show that if \(\mathcal{A}\) wins the game in this hybrid then it breaks \(\mathrm {SIS}_{n,q,B'}\): Let \({\mathbf {{A}}}\) be a \(\mathrm {SIS}_{n,q,B',m'}\) challenge. Initialize a game against \(\mathcal{A}\) as in this hybrid using the matrix \({\mathbf {{A}}}\). Assume that \(\mathcal{A}\) produces a valid forgery \(\sigma _{x^*}\) for \(x^*\). Then \(\sigma _{x^*} \ne \mathbf {{0}}\), \(\left\| {\sigma _{x^*}} \right\| _{\infty } \le B\) and
Since
\([\mathbf {I}\Vert \vec {{\mathbf {{R}}}}_A]\cdot \sigma _{x^*}\) is a valid solution to \(\mathrm {SIS}_{n,q,B',m'}\).
6.2 Adding Key Delegation
It is possible to extend the construction to support key delegation as per Definition 7. We define an alternative \(\mathsf{Sign}^{del}\) algorithm along with a new \(\mathsf{DelKey}\) algorithm. Note that by definition each key maintains its delegation history: an ordered list of constraints which define the permissions of the key. Upon computing \(\mathsf{DelKey}_{\mathsf{vk}}(\mathsf{sk}_{(f_1,\dots ,f_{t})},f_{t+1}) \rightarrow \mathsf{sk}_{(f_1,\dots ,f_{t+1})}\), the delegated key \(\mathsf{sk}_{(f_1,\dots ,f_{t+1})}\) contains the constraints list of \(\mathsf{sk}_{(f_1,\dots ,f_{t})}\) and the new constraint \(f_{t+1}\). The scheme should be parameterized with an upper bound \(t'\) to the delegation depth (i.e. the list length). The other parameters are initialized as before, with the only differences \(\tau _s = \tau _k \cdot \sqrt{\ell t'}2^dm^{d+1}\) and \(n = d^{\frac{1}{\epsilon }} + \ell t'\). Hence the scheme can be initializes with any \(t' = \mathrm{poly}(\lambda )\).
-
\(\mathsf{DelKey}_{\mathsf{vk}}(\mathsf{sk}_{(f_1,\dots ,f_{t})},f_{t+1}) \rightarrow \mathsf{sk}_{(f_1,\dots ,f_{t+1})}\): Recall that when \(t = 1\), \(\mathsf{sk}_f = [{\mathbf {{A}}}\Vert {\mathbf {{A}}}_f]^{-1}_{\tau _k}\). Assume that for any \(t \ge 1\), \( \mathsf{sk}_{f_1,\dots ,f_{t}}= [{\mathbf {{A}}}\Vert {\mathbf {{A}}}_{f_1} \Vert \dots \Vert {\mathbf {{A}}}_{f_t}]^{-1}_{\tau _k} \), and compute the new key as follows: Compute
 (see Theorem 3) and \({\mathbf {{A}}}_{f_{t+1}} = \vec {{\mathbf {{A}}}}\cdot {\mathbf {{H}}}_{f_{t+1}}\), then use \([{\mathbf {{A}}}\Vert {\mathbf {{A}}}_{f_1} \Vert \dots \Vert {\mathbf {{A}}}_{f_t}]^{-1}_{\tau _k}\) to compute and output \(sk_{f_1,\dots ,f_{t+1}}= [{\mathbf {{A}}}\Vert {\mathbf {{A}}}_{f_1} \Vert \dots \Vert {\mathbf {{A}}}_{f_{t+1}}]^{-1}_{\tau _k}\) (see Corollary 2).
(see Theorem 3) and \({\mathbf {{A}}}_{f_{t+1}} = \vec {{\mathbf {{A}}}}\cdot {\mathbf {{H}}}_{f_{t+1}}\), then use \([{\mathbf {{A}}}\Vert {\mathbf {{A}}}_{f_1} \Vert \dots \Vert {\mathbf {{A}}}_{f_t}]^{-1}_{\tau _k}\) to compute and output \(sk_{f_1,\dots ,f_{t+1}}= [{\mathbf {{A}}}\Vert {\mathbf {{A}}}_{f_1} \Vert \dots \Vert {\mathbf {{A}}}_{f_{t+1}}]^{-1}_{\tau _k}\) (see Corollary 2). -
\(\mathsf{Sign}_{ \mathsf{pp}}(x, sk_{f_1,\dots ,f_{t}}) \rightarrow \sigma _x\): If \(\exists i \in [t]\) s.t. \(f_i(x) \ne 0\), return \(\perp \). Otherwise, for \(i\in [t]\) compute
 (see Theorem 3). Note that by this theorem, \( [\vec {{\mathbf {{A}}}}-x \otimes \mathbf {G}]\cdot {\mathbf {{H}}}_{f_i,x} = {\mathbf {{A}}}_{f_i} -f_i(x)\mathbf {G}= {\mathbf {{A}}}_{f_i} -f_i(x)\mathbf {G}= {\mathbf {{A}}}_{f_i} \). Now apply the Trapdoor Extension Theorem (2) with $$\begin{aligned} \bar{{\mathbf {{A}}}}= [ {\mathbf {{A}}}\Vert {\mathbf {{A}}}_{f_1} \Vert \dots \Vert {\mathbf {{A}}}{_{f_t}}], \quad \bar{{\mathbf {{B}}}}= [ {\mathbf {{A}}}\Vert {\vec {{\mathbf {A}}}} - x \otimes \mathbf {G}], \quad {\mathbf {{S}}}= \left[ \begin{array}{lllll} {\mathbf {I}}_{{m}^{\prime }} &{} {\mathbf {0}} &{} \dots &{} {\mathbf {0}} \\ {\mathbf {0}} &{} {\mathbf {H}}{_{f_1,x}} &{} \dots &{} {\mathbf {H}}{_{f_t,x}} \end{array}\right] \end{aligned}$$
(see Theorem 3). Note that by this theorem, \( [\vec {{\mathbf {{A}}}}-x \otimes \mathbf {G}]\cdot {\mathbf {{H}}}_{f_i,x} = {\mathbf {{A}}}_{f_i} -f_i(x)\mathbf {G}= {\mathbf {{A}}}_{f_i} -f_i(x)\mathbf {G}= {\mathbf {{A}}}_{f_i} \). Now apply the Trapdoor Extension Theorem (2) with $$\begin{aligned} \bar{{\mathbf {{A}}}}= [ {\mathbf {{A}}}\Vert {\mathbf {{A}}}_{f_1} \Vert \dots \Vert {\mathbf {{A}}}{_{f_t}}], \quad \bar{{\mathbf {{B}}}}= [ {\mathbf {{A}}}\Vert {\vec {{\mathbf {A}}}} - x \otimes \mathbf {G}], \quad {\mathbf {{S}}}= \left[ \begin{array}{lllll} {\mathbf {I}}_{{m}^{\prime }} &{} {\mathbf {0}} &{} \dots &{} {\mathbf {0}} \\ {\mathbf {0}} &{} {\mathbf {H}}{_{f_1,x}} &{} \dots &{} {\mathbf {H}}{_{f_t,x}} \end{array}\right] \end{aligned}$$(using \(\mathsf{sk}_f = \bar{{\mathbf {{A}}}}_{\tau _k}^{-1}\)), and achieve \(\bar{{\mathbf {{B}}}}^{-1}_{\tau _s} = [{\mathbf {{A}}}\Vert \vec {{\mathbf {{A}}}}- x \otimes \mathbf {G}]^{-1}_{\tau _s}\). Finally sample and output \(\sigma _{x} {\mathop {\leftarrow }\limits ^{\scriptscriptstyle {\$}}}[{\mathbf {{A}}}\Vert \vec {{\mathbf {{A}}}}- x \otimes \mathbf {G}]^{-1}_{\tau _s}(\mathbf {{0}})\). Note that by Theorem 3, \(\forall i \in [t]: {\mathbf {{H}}}_{f_i,x} \in \mathbb {Z}^{\ell m \times m}\) and \(\left\| {{\mathbf {{H}}}_{f_i,x}} \right\| _{\infty } \le (2m)^{d}\), and thus the largest singular value \(s_1({\mathbf {{S}}}) \le \sqrt{\ell t}2^dm^{d+1}\). Hence \(\tau _k \cdot s_1({\mathbf {{S}}}) \le \tau _k \cdot \sqrt{\ell t'}2^dm^{d+1} = \tau _s\), as required by the conditions of Theorem 2.
Correctness and Security. Correctness and statistical key-hiding can be proved the same way as in the non-delegatable scheme, since for each x the valid signatures distribution remains the same: \([{\mathbf {{A}}}\Vert \vec {{\mathbf {{A}}}}-x \otimes \mathbf {G}]^{-1}_{\tau _s}(\mathbf {{0}})\). We now prove message-selective unforgeability as per Definition 7.
Lemma 13
The scheme is message-selective unforgeable for \((\mathcal{X},\mathcal{F})\).
Proof
We first define the procedure \(\mathsf{PermuteKey}(\mathsf{sk}_{f_1,\dots ,f_{t}},\rho ) \rightarrow \mathsf{sk}_{f_{\rho (1)},\dots ,f_{\rho (t)}}\) that takes as input a signing key \(\mathsf{sk}_{f_1,\dots ,f_{t}}\) and a permutation \(\rho : \mathbb {Z}_t \rightarrow \mathbb {Z}_t\), and outputs a key of the permuted constraints \(\mathsf{sk}_{f_{\rho (1)},\dots ,f_{\rho (t)}}\). \(\mathsf{PermuteKey}\) works as follows: Recall that \(\mathsf{sk}_{f_1,\dots ,f_{t}}= [{\mathbf {{A}}}\Vert {\mathbf {{A}}}_{f_1} \Vert \dots \Vert {\mathbf {{A}}}_{f_t}]^{-1}_{\tau _k}\), thus by Corollary 4, it is efficient to compute \(\mathsf{sk}_{f_{\rho (1)},\dots ,f_{\rho (t)}}= [{\mathbf {{A}}}\Vert {\mathbf {{A}}}_{f_{\rho (1)}} \Vert \dots \Vert {\mathbf {{A}}}_{f_{\rho (t)}}]^{-1}_{\tau _k}\).
The security proof goes by reduction to the security of the non-delegatable scheme. Assume an adversary \(\mathcal{A}_{del}\) that wins the delegation security game, and use it to win the security game without delegation against a challenger \(\mathsf{Challenger}\) as follows:
-
1.
Receive \(x^*\) from \(\mathcal{A}_{del}\) and forward it to \(\mathsf{Challenger}\).
-
2.
Receive \(\mathsf{vk}\) from \(\mathsf{Challenger}\) and forward it to \(\mathcal{A}_{del}\).
-
3.
Answer \(\mathcal{A}_{del}\)’s queries as follows:
-
If the query is a key query, i.e. it is of the form \(t \in {\mathbb N}\), \(F\in \mathcal{F}^t\) such that \(\exists f \in F\) for which \(f(x^*) = 1\), request \(\mathsf{sk}_{f_i}\) from \(\mathsf{Challenger}\). Then compute \( \mathsf{sk}_{(f,F/f)}\) using \(\mathsf{DelKey}\) \(\left| {F} \right| -1\) times and \(\mathsf{sk}_{f}\). Finally compute \(\mathsf{sk}_{F}\) using \(\mathsf{PermuteKey}\) and \( \mathsf{sk}_{(f,F/f)}\), and send it to \(\mathcal{A}_{del}\).
-
If the query is a signature query, i.e. it is of the form \(t \in {\mathbb N}\), \((F,x) \in \mathcal{F}^t \times \mathcal{X}\) such that \(x\ne x^*\) and \(\forall f\in F: f(x) = 0\), request \(\sigma _{x}\) from \(\mathsf{Challenger}\) using an arbitrary \(f\in F\), i.e. send (x, f) and get back \(\sigma _{x}\). Forward the signature to \(\mathcal{A}_{del}\). Recall that in the unforgeability game, those queries should be answered by computing \(\sigma _{x} \leftarrow \mathsf{Sign}(x,\mathsf{sk}_F)\). Since the construction is key-hiding, this is indistinguishable to \(\mathcal{A}_{del}\).
-
If the query is a repeated signature query, i.e. it is of the form \(i \in {\mathbb N}\), \(x \in \mathcal{X}\) such that \(x \ne x^*\) and the ith signature query \((F_i,x_i)\) satisfies \(\forall f \in F_i: f(x) = 0\), answer it as described above as if it were a signature query of the form \((F_i,x)\). Recall that in the unforgeability game, those queries should be answered by computing \(\sigma _{x} \leftarrow \mathsf{Sign}(x,\mathsf{sk}_{F_i})\), where \(\mathsf{sk}_{F_i}\) is a key that was generated when the ith signature query was answered. Since the construction is key-hiding, this is indistinguishable to \(\mathcal{A}_{del}\).
-
-
4.
Get a forgery \(\sigma _{x^*}\) from \(\mathcal{A}_{del}\) and forward it to \(\mathsf{Challenger}\).
If \(\mathcal{A}_{del}\) wins the game then also the reduction does, with contradiction to the security of the non-delegatable scheme.
Notes
References
Agrawal, S., Boneh, D., Boyen, X.: Lattice basis delegation in fixed dimension and shorter-ciphertext hierarchical IBE. In: Rabin, T. (ed.) CRYPTO 2010. LNCS, vol. 6223, pp. 98–115. Springer, Heidelberg (2010). https://doi.org/10.1007/978-3-642-14623-7_6
Ajtai, M.: Generating hard instances of lattice problems (extended abstract). In: Miller, G.L. (ed.) Proceedings of the Twenty-Eighth Annual ACM Symposium on the Theory of Computing, Philadelphia, Pennsylvania, USA, 22–24 May 1996, pp. 99–108. ACM (1996)
Alperin-Sheriff, J., Peikert, C.: Faster bootstrapping with polynomial error. In: Garay, J.A., Gennaro, R. (eds.) CRYPTO 2014. LNCS, vol. 8616, pp. 297–314. Springer, Heidelberg (2014). https://doi.org/10.1007/978-3-662-44371-2_17
Brakerski, Z., Cash, D., Tsabary, R., Wee, H.: Targeted homomorphic attribute-based encryption. In: Hirt, M., Smith, A. (eds.) TCC 2016. LNCS, vol. 9986, pp. 330–360. Springer, Heidelberg (2016). https://doi.org/10.1007/978-3-662-53644-5_13
Boneh, D., Freeman, D.M.: Linearly homomorphic signatures over binary fields and new tools for lattice-based signatures. In: Catalano, D., Fazio, N., Gennaro, R., Nicolosi, A. (eds.) PKC 2011. LNCS, vol. 6571, pp. 1–16. Springer, Heidelberg (2011). https://doi.org/10.1007/978-3-642-19379-8_1
Bellare, M., Fuchsbauer, G.: Policy-based signatures. In: Krawczyk, H. (ed.) PKC 2014. LNCS, vol. 8383, pp. 520–537. Springer, Heidelberg (2014). https://doi.org/10.1007/978-3-642-54631-0_30
Boneh, D., Gentry, C., Gorbunov, S., Halevi, S., Nikolaenko, V., Segev, G., Vaikuntanathan, V., Vinayagamurthy, D.: Fully key-homomorphic encryption, arithmetic circuit ABE and compact garbled circuits. In: Nguyen, P.Q., Oswald, E. (eds.) EUROCRYPT 2014. LNCS, vol. 8441, pp. 533–556. Springer, Heidelberg (2014). https://doi.org/10.1007/978-3-642-55220-5_30
Boyle, E., Goldwasser, S., Ivan, I.: Functional signatures and pseudorandom functions. In: Krawczyk, H. (ed.) PKC 2014. LNCS, vol. 8383, pp. 501–519. Springer, Heidelberg (2014). https://doi.org/10.1007/978-3-642-54631-0_29
El Bansarkhani, R., El Kaafarani, A.: Post-quantum attribute-based signatures from lattice assumptions. Cryptology ePrint Archive, Report 2016/823 (2016). http://eprint.iacr.org/2016/823
Backes, M., Meiser, S., Schröder, D.: Delegatable functional signatures. In: Cheng, C.-M., Chung, K.-M., Persiano, G., Yang, B.-Y. (eds.) PKC 2016. LNCS, vol. 9614, pp. 357–386. Springer, Heidelberg (2016). https://doi.org/10.1007/978-3-662-49384-7_14
Brakerski, Z., Vaikuntanathan, V.: Constrained key-homomorphic PRFs from standard lattice assumptions - or: how to secretly embed a circuit in your PRF. In: Dodis, Y., Nielsen, J.B. (eds.) TCC 2015. LNCS, vol. 9015, pp. 1–30. Springer, Heidelberg (2015). https://doi.org/10.1007/978-3-662-46497-7_1
Boneh, D., Zhandry, M.: Multiparty key exchange, efficient traitor tracing, and more from indistinguishability obfuscation. In: Garay, J.A., Gennaro, R. (eds.) CRYPTO 2014. LNCS, vol. 8616, pp. 480–499. Springer, Heidelberg (2014). https://doi.org/10.1007/978-3-662-44371-2_27
Catalano, D., Fiore, D., Warinschi, B.: Homomorphic signatures with efficient verification for polynomial functions. In: Garay, J.A., Gennaro, R. (eds.) CRYPTO 2014. LNCS, vol. 8616, pp. 371–389. Springer, Heidelberg (2014). https://doi.org/10.1007/978-3-662-44371-2_21
Cash, D., Hofheinz, D., Kiltz, E., Peikert, C.: Bonsai trees, or how to delegate a lattice basis. J. Cryptol. 25(4), 601–639 (2012)
Cheng, S., Nguyen, K., Wang, H.: Policy-based signature scheme from lattices. Des. Codes Cryptogr. 81, 43–74 (2016)
Chandran, N., Raghuraman, S., Vinayagamurthy, D.: Constrained pseudorandom functions: verifiable and delegatable (2014). http://eprint.iacr.org/2014/522
Fiore, D., Mitrokotsa, A., Nizzardo, L., Pagnin, E.: Multi-key homomorphic authenticators. In: Cheon, J.H., Takagi, T. (eds.) ASIACRYPT 2016. LNCS, vol. 10032, pp. 499–530. Springer, Heidelberg (2016). https://doi.org/10.1007/978-3-662-53890-6_17
Fuchsbauer, G.: Constrained verifiable random functions. In: Abdalla, M., De Prisco, R. (eds.) SCN 2014. LNCS, vol. 8642, pp. 95–114. Springer, Cham (2014). https://doi.org/10.1007/978-3-319-10879-7_7
Gentry, C., Peikert, C., Vaikuntanathan, V.: Trapdoors for hard lattices and new cryptographic constructions. In: Dwork, C. (ed.) Proceedings of the 40th Annual ACM Symposium on Theory of Computing, Victoria, British Columbia, Canada, 17–20 May 2008, pp. 197–206. ACM (2008)
Gentry, C., Sahai, A., Waters, B.: Homomorphic encryption from learning with errors: conceptually-simpler, asymptotically-faster, attribute-based. In: Canetti, R., Garay, J.A. (eds.) CRYPTO 2013. LNCS, vol. 8042, pp. 75–92. Springer, Heidelberg (2013). https://doi.org/10.1007/978-3-642-40041-4_5
Gorbunov, S., Vaikuntanathan, V., Wee, H.: Attribute-based encryption for circuits. In: Boneh, D., Roughgarden, T., Feigenbaum, J. (eds.) Symposium on Theory of Computing Conference, STOC 2013, Palo Alto, CA, USA, 1–4 June 2013, pp. 545–554. ACM (2013)
Gorbunov, S., Vaikuntanathan, V., Wichs, D.: Leveled fully homomorphic signatures from standard lattices. In: Servedio, R.A., Rubinfeld, R. (eds.) Proceedings of the Forty-Seventh Annual ACM on Symposium on Theory of Computing, STOC 2015, Portland, OR, USA, 14–17 June 2015, pp. 469–477. ACM (2015)
Lai, R.W.F., Tai, R.K.H., Wong, H.W.H., Chow, S.S.M.: A zoo of homomorphic signatures: multi-key and key-homomorphism (2016). http://eprint.iacr.org/2016/834
Micciancio, D.: Almost perfect lattices, the covering radius problem, and applications to ajtais connection factor. SIAM J. Comput. 34(1), 118–169 (2004)
Micciancio, D., Peikert, C.: Trapdoors for lattices: simpler, tighter, faster, smaller. In: Pointcheval, D., Johansson, T. (eds.) EUROCRYPT 2012. LNCS, vol. 7237, pp. 700–718. Springer, Heidelberg (2012). https://doi.org/10.1007/978-3-642-29011-4_41
Micciancio, D., Peikert, C.: Hardness of SIS and LWE with small parameters. In: Canetti, R., Garay, J.A. (eds.) CRYPTO 2013. LNCS, vol. 8042, pp. 21–39. Springer, Heidelberg (2013). https://doi.org/10.1007/978-3-642-40041-4_2
Maji, H.K., Prabhakaran, M., Rosulek, M.: Attribute-based signatures. In: Kiayias, A. (ed.) CT-RSA 2011. LNCS, vol. 6558, pp. 376–392. Springer, Heidelberg (2011). https://doi.org/10.1007/978-3-642-19074-2_24
Micciancio, D., Regev, O.: Worst-case to average-case reductions based on gaussian measures. SIAM J. Comput. 37(1), 267–302 (2007)
Peikert, C.: A decade of lattice cryptography. Found. Trends Theor. Comput. Sci. 10, 283–424 (2016)
Sakai, Y., Attrapadung, N., Hanaoka, G.: Attribute-based signatures for circuits from bilinear map. In: Cheng, C.-M., Chung, K.-M., Persiano, G., Yang, B.-Y. (eds.) PKC 2016. LNCS, vol. 9614, pp. 283–300. Springer, Heidelberg (2016). https://doi.org/10.1007/978-3-662-49384-7_11
Author information
Authors and Affiliations
Corresponding author
Editor information
Editors and Affiliations
Appendices
A Definitions of Message-Policy CS
Definition 9
((Message-Policy) Constrained Signatures). Let \(\mathcal{X}\) be an attribute space and \(\mathcal{F}\) be a function space of the form \(f\in \mathcal{F}\Longrightarrow f : \mathcal{X}' \rightarrow \{0,1\}\) where \(\mathcal{X}' \subseteq \mathcal{X}\). A constrained signatures scheme for \((\mathcal{X},\mathcal{F})\) is a tuple of algorithms:
-
\(\mathsf{Setup}(1^{\lambda }) \rightarrow (\mathsf{msk},\mathsf{vk})\) takes as input the security parameter \(\lambda \) and possibly a description of \((\mathcal{X},\mathcal{F})\), and outputs a master signing key \(\mathsf{msk}\) and a public verification key \(\mathsf{vk}\).
-
\(\mathsf{Keygen}(x,\mathsf{msk}) \rightarrow \mathsf{sk}_x\) takes as input an attribute \(x \in \mathcal{X}\) and the master signing key \(\mathsf{msk}\), and outputs a signing key \(\mathsf{sk}_x\).
-
\(\mathsf{Sign}(f, \mathsf{sk}_f) \rightarrow \sigma _{f}\) takes as input a policy \(f \in \mathcal{F}\) and a signing key \(\mathsf{sk}_x\), and outputs a signature \(\sigma _{f}\).
-
\(\mathsf{Ver}_{\mathsf{vk}}(f, \sigma _{f}) \rightarrow \{accept, reject\}\) takes as input a policy \(f\in \mathcal{F}\) and a signature \(\sigma _{f}\), and either accepts or rejects.
Correctness. The scheme is correct if for all \(x\in \mathcal{X}\) and \(f \in \mathcal{F}\) for which \(f(x) =~0\), it holds that with all but negligible probability \(\mathsf{Ver}_{\mathsf{vk}}(f,\sigma _{f}) = accept\), where \((\mathsf{msk},\mathsf{vk}) \leftarrow \mathsf{Setup}(1^{\lambda })\) and \(\sigma _{f} = \mathsf{Sign}(f,\mathsf{Keygen}(x,\mathsf{msk}))\).
Definition 10
(Privacy of (Message-Policy) Constrained Signatures). The scheme is attribute-hiding if any \(\textsc {ppt}\) adversary \(\mathcal{A}\) has no more than negligible advantage in the following game.
-
1.
The challenger computes and outputs \((\mathsf{msk},\mathsf{vk}) \leftarrow \mathsf{Setup}(1^{\lambda })\).
-
2.
\(\mathcal{A}\) sends \((x_0,x_1,f)\) such that \(f(x_0) = f(x_1) = 0\).
-
3.
The challenger computes \(\mathsf{sk}_{x_0} = \mathsf{Keygen}(x_0,\mathsf{msk})\) and \(\mathsf{sk}_{x_1} = \mathsf{Keygen}(x_1,\mathsf{msk})\). It then samples \(b {\mathop {\leftarrow }\limits ^{\scriptscriptstyle {\$}}}\{0,1\}\) and computes \(\sigma _{f,b} \leftarrow \mathsf{Sign}(f,\mathsf{sk}_{x_b})\). It sends \(\sigma _{f,b}\) to \(\mathcal{A}\).
-
4.
\(\mathcal{A}\) outputs \(b' \in \{0,1\}\) and wins if and only if \(b' = b\).
The scheme is key-hiding if any \(\textsc {ppt}\) adversary \(\mathcal{A}\) has no more than negligible advantage in the above game, where in step 2 the challenger sends \((\mathsf{sk}_{x_0},\mathsf{sk}_{x_1},\sigma _{f,b})\) to \(\mathcal{A}\).
Definition 11
(Unforgeability of (Message-Policy) Constrained Signatures). The scheme is fully unforgeable if every PPTM adversary \(\mathcal{A}\) has no more than negligible advantage in the following game:
-
1.
The challenger computes \((\mathsf{msk},\mathsf{vk}) \leftarrow \mathsf{Setup}(1^{\lambda })\) and sends \(\mathsf{vk}\) to \(\mathcal{A}\).
-
2.
\(\mathcal{A}\) makes queries of three types:
-
Key Queries. \(\mathcal{A}\) sends \(x\in \mathcal{X}\) and gets back \(\mathsf{sk}_x\leftarrow \mathsf{Keygen}(x,\mathsf{msk})\).
-
Signature Queries. \(\mathcal{A}\) sends \((f,x)\in \mathcal{F}\times \mathcal{X}\) such that \(f(x) = 0\). The challenger computes \(\mathsf{sk}_x \leftarrow \mathsf{Keygen}(x,\mathsf{msk})\) and sends back \(\sigma _{f} \leftarrow \mathsf{Sign}(f,\mathsf{sk}_x)\).
-
Repeated Signature Queries. \(\mathcal{A}\) sends \(i \in {\mathbb N}\) and \(f \in \mathcal{F}\times \mathcal{M}\). If there were less than i signature queries at this point of the game, the challenger returns \(\perp \). Otherwise, let x denote the attribute that was sent at the ith signature query and let \(\mathsf{sk}_x\) denote the key that was generated by the challenger when answering this query. If \(f(x) \ne 0\), the challenger returns \(\perp \). Otherwise it returns \(\sigma _{f} \leftarrow \mathsf{Sign}(f,\mathsf{sk}_x)\).
-
-
3.
\(\mathcal{A}\) wins if it manages to output \((f^*,\sigma _{f^*})\) such that \(\mathsf{Ver}_{\mathsf{vk}}(f^*,\sigma _{f^*}) = accept\) and the following restrictions hold:
-
For any key queried by \(\mathcal{A}\) respective to \(x \in \mathcal{X}\), it holds that \(f^*(x) = 1\).
-
For any signature \(\sigma _f\) queried by \(\mathcal{A}\), it holds that \(f \ne f^*\).
-
The scheme maintains message-selective unforgeability if any PPT \(\mathcal{A}\) that announces \(f^*\) before seeing \(\mathsf{vk}\) has no more than negligible advantage in the game.
Definition 12
(Single-Key-Selective Unforgeability of (Message-Policy) Constrained Signatures). The scheme is single-key selectively unforgeable if every PPTM adversary \(\mathcal{A}\) has no more than negligible advantage in the following game:
-
1.
\(\mathcal{A}\) sends \(x^* \in \mathcal{F}\) to the challenger.
-
2.
The challenger computes \((\mathsf{msk},\mathsf{vk}) \leftarrow \mathsf{Setup}(1^{\lambda })\) and \(\mathsf{sk}_{x^*} \leftarrow \mathsf{Keygen}(x^*,\mathsf{msk})\), and sends \((\mathsf{vk},\mathsf{sk}_{x^*})\) to \(\mathcal{A}\).
-
3.
\(\mathcal{A}\) wins if it manages to output \((f^*,\sigma _{f^*})\) such that \(\mathsf{Ver}_{\mathsf{vk}}(f^*,\sigma _{f^*}) = accept\) and \(f^*(x^*) = 1\).
B Proofs for Sect. 4.1
For any \(t \ge 1\) and \(F = (f_1,\dots ,f_t) \in \mathcal{F}^t\), write \(F(x) = 0\) to denote that \(f \in F \Rightarrow f(x) = 0\). Moreover, denote \(\mathsf{sk}_{F} = \mathsf{sk}_{(f_1,\dots ,f_{t})}\), where \(\forall i \in [2\dots t]: \mathsf{sk}_{(f_1,\dots ,f_i)} = \mathsf{DelKey}(\mathsf{sk}_{(f_1,\dots ,f_{i-1})},f_i)\) and \(\mathsf{sk}_{f_1} = \mathsf{Keygen}(f_1,\mathsf{msk})\) for some \((\mathsf{msk},\mathsf{vk}) \leftarrow \mathsf{Setup}(1^{\lambda })\) which is clear from the context.
Lemma 14
(Correctness). The scheme from Sect. 4.1 is correct for \((\mathcal{F}',\mathcal{X}')\).
Proof
Fix \(x\in \mathcal{X}'\), \(t \in {\mathbb N}\) and \(F \in \mathcal{F}'^t\) such that \(F(x) = 0\), and consider \((\mathsf{msk},\mathsf{vk}) \leftarrow \mathsf{Setup}(1^{\lambda })\). Consider \(\mathsf{sk}_F\) as described above and \(\sigma _{x} = \mathsf{Sign}(x,\mathsf{sk}_F)\).
Denote
then by \(\mathsf{Sign}\), \(\mathsf{Keygen}\) and \(\mathsf{DelKey}\) it holds that \(\sigma _{x}' = \mathsf{Sign}'(x,\mathsf{sk}'_F)\), and since \(F(x) = 0\) it holds that \(\mathsf{Ver}'_{\mathsf{vk}'}(\sigma '_{x},x)=accept\) by the correctness of \(\mathsf{CS}'\). Moreover,
and for all \(i = 1.\dots t-1\),
by the correctness of \(\mathsf{S}\). Therefore, \(\mathsf{Ver}_{\mathsf{vk}}(x,\sigma _{x})\) accepts.
Lemma 15
(Privacy). The scheme from Sect. 4.1 is constraint-hiding for \((\mathcal{F}',\mathcal{X}')\).
Proof
Assume towards contradiction an adversary \(\mathcal{A}\) that wins the constraint-hiding privacy game with some significant probability, and use it to break the constraint-hiding privacy of \(\mathsf{CS}\) as follows:
-
1.
Receive \((\mathsf{vk}',\mathsf{msk}') \leftarrow \mathsf{Setup}'(1^{\lambda })\) from the \(\mathsf{CS}\) challenger.
-
2.
Compute \((\mathsf{S}.\mathsf{vk},\mathsf{S}.\mathsf{sk}) \leftarrow \mathsf{S}.\mathsf{Setup}(1^{\lambda })\) and send \((\mathsf{msk}= \mathsf{S}.\mathsf{sk},\mathsf{vk}= \mathsf{S}.\mathsf{vk})\) to \(\mathcal{A}\).
-
3.
\(\mathcal{A}\) returns \((t,F_0,F_1,x)\), where \(\forall b \in \{0,1\}: F_b = (f^b_1,\dots ,f^b_{t})\) and \(F_b(x) = 0\). Forward \((t,F_0,F_1,x)\) to the \(\mathsf{CS}\) challenger.
-
4.
The \(\mathsf{CS}\) challenger samples \(b {\mathop {\leftarrow }\limits ^{\scriptscriptstyle {\$}}}\{0,1\}\) and returns \(\sigma '_{x,b}\).
Now for \(i \in [t]\) generate \((\mathsf{vk}''_1,\mathsf{sk}''_t) \leftarrow \mathsf{S}.\mathsf{Setup}(1^{\lambda })\), sign \((\mathsf{vk}',\mathsf{vk}''_1)\) with the standard signature scheme: \(\sigma _{(\mathsf{vk}',\mathsf{vk}''_1)} \leftarrow \mathsf{S}.\mathsf{Sign}(\mathsf{S}.\mathsf{sk},(\mathsf{vk}',\mathsf{vk}''_1))\) and for each \(i \in [t-1]\) sign \(\sigma _{(\mathsf{vk}''_i,\mathsf{vk}''_{i+1})} \leftarrow \mathsf{S}.\mathsf{Sign}(\mathsf{S}.\mathsf{sk}''_i,(\mathsf{vk}''_i,\mathsf{vk}''_{i+1}))\). Finally sign \(\sigma ''_{x} \leftarrow \mathsf{S}.\mathsf{Sign}(\mathsf{sk}''_t,x)\) and send to \(\mathcal{A}\) the signature \(\sigma _{x,b} = (\mathsf{vk}',\sigma '_{x,b},\{\mathsf{vk}''_i\}_{i \in [t]},\sigma ''_{x},\sigma _{(\mathsf{vk}',\mathsf{vk}''_1)},\) \(\{\sigma _{(\mathsf{vk}''_i,\mathsf{vk}''_{i+1})}\}_{i \in [t-1]})\).
-
5.
Get \(b'\) from \(\mathcal{A}\) and forward it to the \(\mathsf{CS}\) challenger. Clearly, any advantage of \(\mathcal{A}\) induces an advantage of the reduction.
Lemma 16
(Unforgeability). The scheme from Sect. 4.1 is fully unforgeable for \((\mathcal{F}',\mathcal{X}')\).
Proof
Assume towards contradiction an adversary \(\mathcal{A}\) that wins the security game. We show that it can be used to break either \(\mathsf{S}\) or \(\mathsf{CS}\). Let \(\mathcal{Q}_{key},\mathcal{Q}_{sig},\mathcal{Q}_{rep}\) be the sets of key queries, signature queries and repeated signature queries made by \(\mathcal{A}\) during the security game. Recall that each query \(q_i \in \mathcal{Q}_{key}\) is of the form \((t_i,(f^i_1,\dots ,f^i_{t_i}))\) and each query \(q_i \in \mathcal{Q}_{sig}\) is of the form \((t_i,(f^i_1,\dots ,f^i_{t_i},x_i))\), where \(t_i \in \mathbb {Z}, f^i_j \in \mathcal{F}', x_i \in \mathcal{X}'\). In particular, each query \(q_i \in \mathcal{Q}_{key} \bigcup \mathcal{Q}_{sig}\) contains a set \((f^i_1,\dots ,f^i_{t_i}) \in \mathcal{F}'^{t_i}\). Moreover, every response of the challenger (whether it is a key or a signature) contains a tuple \((\mathsf{vk}'^i,\{\mathsf{vk}''^i_j\}_{j \in [t_i]})\) that is generated during \(\mathsf{Keygen}\) and \(\mathsf{DelKey}\). \(\mathcal{A}\) wins the game, it therefore outputs a successful forgery \((x^*,\sigma _{x^*})\), where \(\sigma _{x^*} = (\mathsf{vk}'^*,\sigma '_{x^*},\{\mathsf{vk}''^*_{j}\}_{j=1\dots t},\sigma ''_{x^*},\) \(\sigma _{(\mathsf{vk}'^*,\mathsf{vk}''^*_{1})},\{\sigma _{(\mathsf{vk}''^*_{j},\mathsf{vk}''^*_{j+1})}\}_{j=1\dots t-1})\). Consider three cases:
-
If \(\exists q_i \in \mathcal{Q}_{key}\) such that \((\mathsf{vk}'^i,\{\mathsf{vk}''^i_j\}_{j \in [t_i]}) = (\mathsf{vk}'^*,\{\mathsf{vk}''^*_j\}_{j \in [t_i]})\), then \((x^*,\sigma '_{x^*})\) is a valid forgery to the delegatable \(\mathsf{CS}\) instance that was initialized during \(\mathsf{Keygen}(f_i,\mathsf{msk})\). Note that since \(q_i \in \mathcal{Q}_{key}\), \(\exists j \in [1\dots t_i]\) such that \(f^i_j(x^*) = 1\), therefore \((t_i, f^i_1,\dots ,f^i_{t_i})\) is a valid delegated-key query to the underlying \(\mathsf{CS}\) challenger. We show a reduction from the selective-single-key security game of \(\mathsf{CS}\) to this game:
-
1.
Initialize \((\mathsf{S}.\mathsf{vk},\mathsf{S}.\mathsf{sk}) \leftarrow \mathsf{S}.\mathsf{Setup}(1^{\lambda })\) as in the real scheme and send \(\mathsf{S}.\mathsf{vk}\) to \(\mathcal{A}\).
-
2.
Queries phase:
-
Answer all queries except of the ith as in the real unforgeability game.
-
Upon receiving form \(\mathcal{A}\) the query \(q_i \in \mathcal{Q}_{key}\), send \((t_i, f^i_1,\dots ,f^i_{t_i})\) to the ith \(\mathsf{CS}\) challenger and get back \((\mathsf{vk}'_i,k'_{(f^i_1,\dots ,f^i_{t_i})})\). For \(j \in [t_i]\), generate \((\mathsf{vk}''^i_j,\mathsf{sk}''^i_j) \leftarrow \mathsf{S}.\mathsf{Setup}(1^{\lambda })\). Compute \(\sigma _{(\mathsf{vk}'_i,\mathsf{vk}''^i_1)} \leftarrow \mathsf{S}.\mathsf{Sign}(\mathsf{S}.\mathsf{sk},(\mathsf{vk}'_i,\mathsf{vk}''^i_1))\) and for each \(j \in [1\dots t_i-1]\) compute \(\sigma _{(\mathsf{vk}''^i_j,\mathsf{vk}''^i_{j+1})}\leftarrow \mathsf{S}.\mathsf{Sign}(\mathsf{sk}''^i_j,(\mathsf{vk}''^i_j,\mathsf{vk}''^i_{j+1}))\). Send to \(\mathcal{A}\) the key \(\mathsf{sk}_{(f^i_1,\dots ,f^i_{t_i})} = (\mathsf{vk}'_i,k'_{(f^i_1,\dots ,f^i_{t_i})},\{\mathsf{vk}''^i_j\}_{j \in [t_i]},\mathsf{sk}''^i_{t_i}, \sigma _{(\mathsf{vk}'_i,\mathsf{vk}''^i_1)},\) \(\{\sigma _{(\mathsf{vk}''^i_j,\mathsf{vk}''^i_{j+1})}\}_{j \in [t_i-1]})\).
-
-
3.
When \(\mathcal{A}\) sends the forgery \((x^*,\sigma _{x^*})\), send \((x^*,\sigma '_{x^*})\) to the ith \(\mathsf{CS}\) challenger to win the selective-single-key game.
-
1.
-
If \(\exists q_i \in \mathcal{Q}_{sig}\) such that \((\mathsf{vk}'^i,\{\mathsf{vk}''^i_j\}_{j \in [t_i]}) = (\mathsf{vk}'^*,\{\mathsf{vk}''^*_j\}_{j \in [t_i]})\), then \((x^*,\sigma ''_{x^*})\) is a valid forgery to the \(\mathsf{S}\) instance that was initialized during \(\mathsf{DelKey}(k'_{(f^i_1,\dots ,f^i_{t_i-1})},f^i_{t_i})\). Note that \(\forall q_i \in \mathcal{Q}_{sig}\), it holds that \(x_i \ne x^*\). We show a reduction from the security game of \(\mathcal{S}\) to this game:
-
1.
Initialize \((\mathsf{S}.\mathsf{vk},\mathsf{S}.\mathsf{sk}) \leftarrow \mathsf{S}.\mathsf{Setup}(1^{\lambda })\) as in the real scheme and send \(\mathsf{S}.\mathsf{vk}\) to \(\mathcal{A}\).
-
2.
Queries phase:
-
Answer all queries up to \(q_i\) as in the real unforgeability game.
-
Upon receiving form \(\mathcal{A}\) the query \(q_i \in \mathcal{Q}_{sig}\), compute \(k'_{(f^i_1,\dots ,f^i_{t_i-1})}\) as in the real game, then instantiate a game against the \(\mathsf{S}\) challenger and get \(\mathsf{vk}''^i_{t_i}\). Query a signature for \((x_i,m_i)\) and get back \(\sigma ''_{(x_i,m_i)}\). Sign \(\sigma _{(\mathsf{vk}''^i_{t_i-1},\mathsf{vk}''^i_{t_i})} \leftarrow \mathsf{S}.\mathsf{Sign}(\mathsf{sk}''^i_{t_i-1},(\mathsf{vk}''^i_{t_i-1},\mathsf{vk}''^i_{t_i}))\). Compute \(k'_{(f^i_1,\dots ,f^i_{t_i})}\leftarrow \mathsf{DelKey}'(k'_{(f^i_1,\dots ,f^i_{t_i-1})},f^i_{t_i})\) and \(\sigma _{(x_i,m_i)}' \leftarrow \mathsf{Sign}'(x_i,m_i,k'_{(f^i_1,\dots ,f^i_{t_i})})\). Send to \(\mathcal{A}\): \(\sigma _{x_i} = (\mathsf{vk}'_i,\sigma '_{x_i},\{\mathsf{vk}''^i_{j}\}_{j \in [t_i]},\sigma ''_{(x_i,m_i)},\sigma _{(\mathsf{vk}'_i,\mathsf{vk}''^i_{1})},\{\sigma _{(\mathsf{vk}''^i_{j},\mathsf{vk}''^i_{j+1})}\}_{j \in [t_i-1]})\).
-
Answer all queries as in the real game, except of repeated signature queries that reference \(q_i\). For these, do as described above with the values \(\mathsf{vk}'_i\), \(\{\mathsf{vk}''^i_{j}\}_{j \in [t_i]}\), \(\sigma _{(\mathsf{vk}'_i, \mathsf{vk}''^i_1)}\), \(\{\sigma _{(\mathsf{vk}''^i_{j},\mathsf{vk}''^i_{j+1})}\}_{j \in [t_i-1]}\), \(k'_{(f^i_1,\dots ,f^i_{t_i})}\) that were generated when \(q_i\) was answered.
-
-
3.
When \(\mathcal{A}\) sends the forgery \((x^*,\sigma _{x^*})\), send \((x^*,\sigma ''_{x^*})\) to the ith \(\mathsf{S}\) challenger to win the game.
-
1.
-
If \(\forall d \in [1\dots t_i]\) and \(\forall q_i \in \mathcal{Q}_d^* = \{q_i \in \mathcal{Q}_{key} \bigcup \mathcal{Q}_{sig} : (\mathsf{vk}'_i,\{\mathsf{vk}''^i_j\}_{j=1\dots d-1}) = (\mathsf{vk}'_*,\{\mathsf{vk}''^*_j\}_{j=1\dots d-1}) \}\) it holds that \(\mathsf{vk}''^*_d \ne \mathsf{vk}''^i_d\), then \((\sigma _{(\mathsf{vk}''^*_{d-1},\mathsf{vk}''^*_{d})},((\mathsf{vk}''^*_{d-1},\mathsf{vk}''^*_{d}))\) is a valid forgery to the \(\mathsf{S}\) instance with the verification key \(\mathsf{vk}''^*_{d-1}=\mathsf{vk}''^i_{d-1}\). The reduction follows similar lines to the reduction from the previous case.
-
Otherwise \(\forall q_i \in \mathcal{Q}_{key}\bigcup \mathcal{Q}_{sig}\) \((\mathsf{vk}'_i,\mathsf{vk}''^i_1) \ne (\mathsf{vk}'_*,\mathsf{vk}''^*_{1})\), and thus \((\sigma _{(\mathsf{vk}'_*,\mathsf{vk}''^*_1)},(\mathsf{vk}'_*,\mathsf{vk}''^*_1))\) is a valid forgery to \(\mathsf{S}\). We show a reduction from the security game of \(\mathsf{S}\) to this game:
-
1.
Receive \(\mathsf{S}.\mathsf{vk}\) from the \(\mathsf{S}\) challenger and send it to \(\mathcal{A}\).
-
2.
Answer queries from \(\mathcal{A}\) as in the real game, except the way \(\sigma _{(\mathsf{vk}'_*,\mathsf{vk}''^*_1)}\) is computed: instead of signing \((\mathsf{vk}'_*,\mathsf{vk}''^*_1)\) with \(\mathsf{msk}= \mathsf{S}.\mathsf{sk}\), query the \(\mathsf{S}\) challenger and get \(\sigma _{(\mathsf{vk}'_*,\mathsf{vk}''^*_1)}\).
-
3.
When \(\mathcal{A}\) sends the forgery \((x^*,\sigma _{x^*})\), send \((\sigma _{(\mathsf{vk}'_*,\mathsf{vk}''^*_1)},(\mathsf{vk}'_*,\mathsf{vk}''^*_1))\) to the \(\mathsf{S}\) challenger to win the game.
-
1.
Rights and permissions
Copyright information
© 2017 International Association for Cryptologic Research
About this paper
Cite this paper
Tsabary, R. (2017). An Equivalence Between Attribute-Based Signatures and Homomorphic Signatures, and New Constructions for Both. In: Kalai, Y., Reyzin, L. (eds) Theory of Cryptography. TCC 2017. Lecture Notes in Computer Science(), vol 10678. Springer, Cham. https://doi.org/10.1007/978-3-319-70503-3_16
Download citation
DOI: https://doi.org/10.1007/978-3-319-70503-3_16
Published:
Publisher Name: Springer, Cham
Print ISBN: 978-3-319-70502-6
Online ISBN: 978-3-319-70503-3
eBook Packages: Computer ScienceComputer Science (R0)





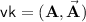 and
and  (see Theorem
(see Theorem  (see Theorem
(see Theorem  (see Theorem
(see Theorem  (see Theorem
(see Theorem 