Abstract
Verifiable random functions (VRFs) are pseudorandom functions where the owner of the seed, in addition to computing the function’s value y at any point x, can also generate a non-interactive proof \(\pi \) that y is correct, without compromising pseudorandomness at other points. Being a natural primitive with a wide range of applications, considerable efforts have been directed towards the construction of such VRFs. While these efforts have resulted in a variety of algebraic constructions (from bilinear maps or the RSA problem), the relation between VRFs and other general primitives is still not well understood.
We present new constructions of VRFs from general primitives, the main one being non-interactive witness-indistinguishable proofs (NIWIs). This includes:
-
A selectively-secure VRF assuming NIWIs and non-interactive commitments. As usual, the VRF can be made adaptively-secure assuming subexponential hardness of the underlying primitives.
-
An adaptively-secure VRF assuming (polynomially-hard) NIWIs, noninteractive commitments, and (single-key) constrained pseudorandom functions for a restricted class of constraints.
The above primitives can be instantiated under various standard assumptions, which yields corresponding VRF instantiations, under different assumptions than were known so far. One notable example is a non-uniform construction of VRFs from subexponentially-hard trapdoor permutations, or more generally, from verifiable pseudorandom generators (the construction can be made uniform under a standard derandomization assumption). This partially answers an open question by Dwork and Naor (FOCS ’00).
The construction and its analysis are quite simple. Both draw from ideas commonly used in the context of indistinguishability obfuscation.
You have full access to this open access chapter, Download conference paper PDF
Similar content being viewed by others
1 Introduction
Verifiable random functions (VRFs), introduced by Micali et al. [39], are pseudorandom functions (PRFs) [27] where it is possible to verify that a given output y corresponds to a correct evaluation of the function on any given input x. Such a VRF is associated with a secret key \(SK\) and a corresponding public verification key \(VK\). The secret key allows anyone to compute the function \(y=\mathsf{VRF.Eval}_{SK}(x)\) at any point x, and also to compute a proof \(\pi _{x,y}\) that y was computed correctly. Here, by “computed correctly”, we mean that any verification key \(VK^*\), even a maliciously chosen one, is a commitment to the entire function—it uniquely determines the value y of the function at any point x, and accepting proofs only exist for this value y. The pseudorandomness requirement generalizes that of plain PRFs—the value y of the function at any point x should be pseudorandom, even after evaluating the function and obtaining proofs of correctness for an arbitrary polynomial number of points \(\left\{ x_i\ne x\right\} \). The standard definition is adaptive, allowing the point x to be chosen at any point, and we can also consider a selective definition, where the adversary chooses the challenge x, before getting the verification key \(VK\), and before any evaluation query.
Constructions. VRFs are a natural primitive with a variety of applications (listed for instance in [1]), and considerable effort has been invested in the pursuit of constructions, aiming to diversify and simplify the underlying assumptions [1, 11, 12, 19, 21, 22, 26, 33, 35, 36, 38, 39]. Despite the progress made, almost all known constructions are of an algebraic nature, and are based directly either on the (strong) RSA assumption, or on different assumptions related to bilinear (or multilinear) maps. Attempts to construct VRFs from more general assumptions have been limited to constructions from VRF-suitable identity-based encryption [1], or from indistinguishability obfuscation (IO) and injective one-way functions [45]. In both cases, concrete instantiations are, again, only known based on bilinear or multilinear maps.Footnote 1 Alternatively, weak VRFs, which are the verifiable analog of weak PRFs [42], can be constructed from (doubly enhanced) trapdoor permutations [16].
In terms of barriers, VRFs imply [29] non-interactive zero-knowledge proofs (NIZKs) [10], and accordingly constructing VRFs from symmetric-key primitives like one-way functions, or collision-resistant hashing, seems out of reach for existing techniques. In contrast, NIZKs can be constructed from (doubly enhanced) trapdoor permutations (TDPs) [6, 24, 28], and we may hope that so can VRFs. As possible evidence that this is a false hope, Fiore and Schröder show that there is no black-box reduction from VRFs to (doubly enhanced) TDPs [25].
1.1 This Work
We present new constructions of VRFs from general assumptions, the main one being non-interactive witness-indistinguishable proofs (NIWIs), which were introduced by Barak et al. [4].
Our most basic result is a selectively-secure construction based on NIWIs, non-interactive commitments, and puncturable PRFs [13, 15, 37, 45] (these are in turn implied by one-way functions and thus also by non-interactive commitments). As usual, adaptive security of the construction can be shown assuming all primitives are subexponentially-secure.
Theorem 1
(informal). Assuming the existence of NIWIs and non-interactive commitments, there exist selectively-secure VRFs. Further assuming subexponential hardness of these primitives, there exist adaptively-secure VRFs.
Aiming to avoid subexponential assumptions, our more general construction replaces puncturable PRFs with more general types of single-key constrained PRF (CPRFs) [13, 15, 37] and achieves adaptive security from polynomial assumptions.
Theorem 2
(informal). Assuming the existence of NIWIs, non-interactive commitments, and single-key CPRFs (for some restricted class of constraints), there exist adaptively-secure VRFs.
Given the reliance on generic primitives, the above theorems already allow (and may further allow in the future) to base VRFs on different assumptions. We now review the (generic and specific) assumptions under which the above primitives are known, and derive corresponding corollaries. (For now, we focus on the implications of the theorems. We recall the definitions of NIWIs and CPRFs later, in the technical overview.)
NIWIs. Dwork and Naor [23] gave a non-uniform construction of NIWIs from NIZKs (which can be constructed from doubly enhanced TDPs). Barak et al. [4] showed that the construction can be made uniform assuming also the existence of a problem solvable in deterministic time \(2^{O(n)}\) with non-deterministic circuit complexity \(2^{\varOmega (n)}\). The latter is a worst-case assumption previously used to derandomize AM [40], and can be seen as an extension of the assumption that \(\mathbf{EXP}\not \subseteq \mathbf{NP/poly}\) (see further discussion in [4]). Groth et al. [32] then constructed NIWIs based on standard assumptions on bilinear maps such as the Decision Linear (DLIN) assumption, the Symmetric External Diffie Hellman (SXDH) assumption, or the Subgroup Decision Assumption. In [8], NIWIs are constructed from IO and one-way permutations.
Non-interactive Commitments. Such commitments are known from any family of injective one-way functions [9]. Naor [41] gave a non-uniform construction from plain one-way functions, which can be made uniform under the same derandomization assumption mentioned above [4].
CPRFs. Theorem 2 relies on single-key CPRFs for certain specific classes of constraints (see the technical outline below). It can be instantiated either by the CPRFs of Brakerski and Vaikuntanathan [17], based on LWE and 1D-SIS, or from those of Boneh and Zhandry, based on IO [14]. We also give new instantiations under the DDH assumption.Footnote 2
We can now combine the above in different ways to get instantiations of (adaptively-secure) VRFs from different assumptions, several of which were previously unknown. For example:
-
A non-uniform construction from subexponential hardness of (doubly enhanced) TDPs. This should be contrasted with the black-box barrier of Fiore and Schróder mentioned above. The barrier does not apply to this construction both due to non-uniformity, and also non-black-box use of some of the underlying primitives, such as the commitments or puncturable PRFs.
-
By instantiating these TDPs with a variant of the Rabin construction [28], we get a non-uniform construction from subexponential hardness of Factoring. This should be compared with the construction from subexponential hardness of strong RSA [39]. (We can avoid subexponential hardness relying on DDH or LWE and 1D-SIS. We can further make the construction uniform under the above mentioned derandomization assumption.)
-
Constructions from simple assumptions on bilinear groups, such as DLIN or SXDH. Indeed, the past decade has seen gradual progress toward this goal, starting from [38], through [1, 11, 12, 21, 22, 35, 36], and culminating in [33], with a construction from the n-Linear assumption. While the result obtained here does not improve on [33], it provides a quite different solution.
-
A construction from polynomially hard IO and one-way permutations. In comparison, the existing construction mentioned above [45] required subexponential hardness for adaptive security.
An Equivalence Between Nonuniform VRFs, VPRGs, and NIZKs. Dwork and Naor [23] defined a verifiable version of pseudo-random generators (VPRGs) and showed their equivalence to NIZKs. Such VPRGs (or NIZKs) are implied (even by selectively-secure) VRFs. Dwork and Naor raised the question of whether the converse holds: do VPRGs imply VRFs? (Analogously to the fact that PRGs imply PRFs.) Our result shows that for non-uniform constructions this is indeed the case—VPRGs imply selectively-secure VRFs (or adaptively-secure if they are subexponentially-hard). For uniform constructions, we only establish this equivalence conditioned on the mentioned derandomization assumption.
1.2 Techniques
We now explain the main ideas behind our constructions.
A Naïve Idea: NIWIs instead of NIZKs. Our starting point is the simple construction of VRFs in the common random string model [39]—to construct a VRF, let the verification key \(VK\) be a commitment \(\textsf {c}=\textsf {Com}(\mathsf {F})\) to a function \(\mathsf {F}\) drawn at random from a PRF family [27], and store \(\mathsf {F}\) along with the commitment randomness as the private evaluation key \(SK\). The value of the function at any point x is simply \(y=\mathsf {F}(x)\), and the proofs of correctness \(\pi _{x,y}\) are simply NIZKs that y is consistent with the commitment \(\textsf {c}\).
This solution works as expected, but requires a common random string. Aiming to get a construction in the plain model, a natural direction is to replace NIZKs with NIWIs, which exist in the plain model and still offer some level of privacy. Concretely, NIWIs guarantee absolute soundness (convincing proofs for false statements simply do not exist), and witness indistinguishability—a proof for a statement with multiple witnesses leaks no information about which witness was used in the proof; namely, proofs that use different witnesses are computationally indistinguishable. It is not hard see, however, that this relaxed privacy guarantee does not allow using NIWIs as is in the above solution. Indeed, since \(\mathsf {F}\) is uniquely determined by the commitment \(\textsf {c}\), a NIWI proof may very well leak it in full, without ever compromising witness indistinguishability.
Indeed, leveraging witness indistinguishability would require a different function commitment mechanism that would not completely determine the underlying description of the function \(\mathsf {F}\). This may appear to conflict with the uniqueness requirement of VRFs, which in the naïve construction was guaranteed exactly due to the fact that the commitment fixes the function’s description. However, we observe that there is still some wiggle room here—uniqueness of VRFs only requires that the functionality \(\left\{ \mathsf {F}(x)\right\} _x\) is fixed (rather than the description \(\mathsf {F}\) of the function). Our solution will take advantage of this fact.
Function Commitments: Indistinguishability instead of Simulation. At high level, our first step is to consider, and instantiate, a function commitment mechanism so that on one hand, any verification key \(VK^*\) completely determines the underlying function, but on the other hand, does not leak which specific (circuit) description is used in the commitment. The second step will be to show that such function commitments can be combined with appropriate PRFs to obtain VRFs.
This approach bears similarity to a common approach in obfuscation-based applications. There, typically, a given application easily follows from the simulation-based notion of virtual black-box obfuscation. The challenge is to recover the application using the weaker indistinguishability-based notion of IO, which hides which circuit was obfuscated (among different circuit descriptions for the same function). In our context, the NIZK-based VRF solution corresponds to simulation-based function commitments where the verification key, function values, and proofs can all be efficiently simulated given black-box access to the underlying function, in which case, any PRF would be enough to get VRFs. Our challenge will be to obtain VRFs from an indistinguishability-based notion of function commitments. Indeed, our second step will rely on techniques from the IO regime, such as puncturing [45]. Details follow.
Step 1: Indistinguishability-Based Function Commitments. The function commitment notion we consider requires that verification keys \(VK,VK'\) corresponding to two circuits \(\mathsf {F},\mathsf {F}'\) would be indistinguishable given evaluations \(y_i\), with proofs of consistency \(\pi _{x_i,y_i}\), for an arbitrary polynomial number of points \(x_i\), provided that the circuits agree on these points, namely \(\mathsf {F}(x_i)=\mathsf {F}'(x_i)\). This is on top of the usual binding requirement saying that any verification key \(VK^*\) uniquely determines the underlying function (but not its circuit description).
This notion is dual and equivalent to a notion of functional (bit-string) commitments considered in [2, Appendix G] where the commitment is to an input x, and evaluations correspond to \(f_i(x)\) for different functions \(f_i\). In [2], such functional commitments are constructed from single-ciphertext verifiable functional encryption (SCT-VFE), which in turn is constructed from commitments, NIWIs, and plain, non-verifiable, SCT-FE (known from one-way functions [30, 44]). This, in particular, gives an instantiation for the required function commitments.
Here we give a simple construction of the required function commitments directly from NIWIs and commitments (avoiding FE altogether). Concretely, a verification key \(VK\) for a circuit \(\mathsf {F}\) consists of three commitments \((\textsf {c}_1,\textsf {c}_2,\textsf {c}_3)\) to the circuit \(\mathsf {F}\). The secret key \(SK\) consists of \(\mathsf {F}\) and the randomness for the commitments. To prove correctness of \(y=\mathsf {F}(x)\), we give a NIWI that y is consistent with two out of the three commitments; namely, there exist \(1\le i<j\le 3\) so that \(\textsf {c}_i,\textsf {c}_j\) are commitments to circuits \(\mathsf {F}_i,\mathsf {F}_j\), and \(y=\mathsf {F}_i(x)=\mathsf {F}_j(x)\).
The binding of commitments and soundness of NIWIs, guarantee that any verification key corresponds to at most a single function, which at any point returns the majority value of the functions underlying the commitments (for malicious verification keys, a majority may not exist, in which case no value will be accepted). At the same time, the required indistinguishability can be shown by a simple hybrid argument. Throughout this argument, NIWI proofs use as the witness the randomness and underlying plaintext for any two of the three commitments, allowing to invoke the hiding of the third commitment. For example, at first, proofs will use the randomness for \(\textsf {c}_1\) and \(\textsf {c}_2\), allowing to change the third commitment \(\textsf {c}_3\) from the circuit \(\mathsf {F}\) to the circuit \(\mathsf {F}'\). Then, assuming \(\mathsf {F}'\) and \(\mathsf {F}\) agree on all evaluation queries \(x_i\), we can rely on witness-indistinguishability, and now use instead the randomness for two different commitments, say \(\textsf {c}_1\) and \(\textsf {c}_3\) to compute NIWI proofs. Now, we can change \(\textsf {c}_2\) to \(\mathsf {F}'\), and so on.
Step 2: From Function Commitments to VRFs. Our construction of VRFs then proceeds by combining function commitments such as those above with carefully chosen PRFs. Indeed, while we might not be able to use any PRF (as in the simulation-based function commitments from NIZKs), the indistinguishability guarantee that we have suggests a natural solution. Specifically, if we could replace the committed PRF circuit \(\mathsf {F}\), with a circuit \(\mathsf {F}'\) that agrees with \(\mathsf {F}\) on all of the adversary’s evaluation queries \(x_i\), and yet does not leak information on the function’s value \(\mathsf {F}(x)\) at the challenge point x, then we could satisfy the pseudorandomness requirement of VRFs. Can we generate such a circuit \(\mathsf {F}'\) ? We first observe that in the case of a selective adversary (that announces the challenge x before even getting the verification key), we certainly can—via puncturable PRFs [13, 15, 37]. Recall that in such PRFs, we can puncture the PRF circuit \(\mathsf {F}\) at any point x, so that the new punctured circuit \(\mathsf {F}'_{\left\{ x\right\} }\) retains the functionality of \(\mathsf {F}\) at any point other than x, whereas the value \(\mathsf {F}(x)\) at the punctured point x remains pseudorandom.
Concretely, our security reduction will use any selective adversary against the VRF to break the pseudorandomness at the punctured point x. The reduction will generate a commitment (namely, verification key) for the punctured \(\mathsf {F}'_{\left\{ x\right\} }\), and use this punctured circuit to compute the answers \((y_i,\pi _{x_i,y_i})\), for all the queries \(x_i\ne x\). By the function-commitment indistinguishability, the adversary could not distinguish between this and the real VRF experiment where the unpunctured \(\mathsf {F}\) would be used, as the two completely agree on all evaluations points \(x_i\). Accordingly, any successful adversary in the VRF game can be used by the reduction to distinguish \(\mathsf {F}(x)\) from a truly random output.
Adaptive Security via Constrained PRFs. As mentioned, selective security implies adaptive security if we assume subexponential hardness—the reduction basically guesses the challenge, incurring a \(2^{|x|}\) security loss. To obtain adaptive security from polynomial assumptions, we follow a common path in adaptive-security proofs, relying on the idea of partitioning. Roughly speaking, the idea is that instead of guessing the challenge (which is successful with exponentially-small probability), the reduction guesses a partition \((S, X\) \(\setminus \) \( S)\) of the query space X, aiming that with noticeable (rather than exponentially-small) probability, all evaluation queries \(x_i\) will fall outside S, but the challenge x will fall inside S.
In our case, given such a partition scheme, we aim to follow the same approach as above (for the selective case), only that now instead of creating a circuit \(\mathsf {F}'_{\left\{ x\right\} }\) that is punctured at a single point, we would like to create a circuit \(\mathsf {F}'_S\) that is punctured at the entire set S; namely, it retains the functionality of \(\mathsf {F}\) on any point in \(X\) \(\setminus \) \(S\), but the value \(\mathsf {F}(x)\) is pseudorandom for any \(x\in S\). This more general notion is indeed known as constrained PRFs (CPRF). Here we only need single-key CPRFs in the sense that security holds in the presence of a single constrained PRF. Also, we do not need constraining for arbitrary sets S, but just for the sets S in the support of the partition scheme we use. We give three examples of such partition schemes, one that aligns with the common notion of admissible hash functions [11], a second one that generalizes admissible hashing to large alphabets, and a third one based on universal hashing [18]. As stated in the previous subsection, we demonstrate corresponding CPRFs based on different (polynomial) assumptions. Overall, the construction is exactly the same as before only that we instantiate the PRF with a CPRF for constrained sets in the support of one of the above partition schemes.Footnote 3
Fulfilling the above approach involves certain technical subtleties, most of which are common to typical partitioning proofs. One notorious issue concerns the fact that, while overall noticeable, the probability of successful partition may vary with how the adversary chooses its queries. In particular, it may potentially be the case that conditioned on a successful partition, the adversary’s advantage in the VRF game becomes negligible (see more elaborate discussion in [46]). There are several approaches for dealing with this in the literature (the most common one is perhaps the artificial abort technique in [46]). We follow an approach suggested by Jager [36] of requiring that the partition schemes in use are balanced in the sense that the probability of partition does not change by much over different choices of queries. See further details in Sects. 2.4 and 3.3.
1.3 Concurrent and Subsequent Work
In concurrent and independent work, Goyal et al. [31] present a similar approach for constructing VRFs. The general construction and underlying primitives are essentially the same as ours. There are some differences regarding the instantiations provided for the underlying primitives and the presentation. We summarize the symmetric difference below.
-
Underlying Primitives. In terms of CPRF instantiations, apart from the instantiations common to both works, they give an instantiation based on the Phi-Hiding assumption, and we give an instantiations based on the DDH assumption. They also give new instantiations for commitment schemes based on LWE and LPN, which we do not.
-
Presentation and Abstractions. For modularity, we chose to use the abstraction of function commitments. Effectively, the same function commitment construction is present in both works. Also, to get adaptive security, they rely on the standard notion of admissible hash functions, whereas we chose to consider a somewhat more general notion of partition schemes, with the aim of giving more flexibility when designing corresponding CPRFs; indeed, this allows us to get our DDH-based instantiation.
-
Analysis. To prove adaptive security, they use the technique of artificial aborts [46], whereas we instead use a slightly stronger notion of partition schemes (or admissible hash functions) that are also balanced [36]. (The balance property does not require any additional assumptions and is essentially obtained for free in the considered constructions).
In a subsequent note [3], Badrinarayanan et al. suggest an alternative construction of VRFs from single-ciphertext verifiable functional-encryption (SCT-VFE). Their construction can be interpreted as following our two-step construction where the first step—function commitments—is realized using SCT-VFE (the second step, of using puncturable or constrained PRFs, is identical). As mentioned, SCT-VFE was constructed in [2] from commitments, NIWIs, and plain (non-verifiable) SCT-FE. We give a simple construction of the required function commitments directly from NIWIs and commitments.
Organization. In Sect. 2, we define the primitives used in this work. In Sect. 3, we present the main construction and its analysis. In Sect. 4, we discuss possible instantiations, induced by different partition schemes and CPRFs. Some of the basic definitions and proofs are Omitted and can be found in the full version.
2 Preliminaries
In this section, we give the basic definitions used throughout the paper. For lack of space, some of the standard definitions can be found in the full version.
2.1 Verifiable Random Functions
We define verifiable random functions (VRFs).
Definition 1
(VRF [39]). Let n, m, k be polynomially bounded functions. A verifiable random function \(\mathsf {VRF}=(\mathsf {VRF.Gen},\mathsf{VRF.Eval},\mathsf {VRF.P},\mathsf {VRF.V})\) consists of the following polynomial-time algorithms:
-
a probabilistic key sampler \(\mathsf {VRF.Gen}(1^\lambda )\) that given a security parameter \(1^\lambda \) outputs a secret key \(SK\) and public verification key \(VK\in \{0,1\}^{k(\lambda )}\),
-
an evaluator \(\mathsf{VRF.Eval}_{SK}(x)\) that given the secret key and \(x\in \{0,1\}^{n(\lambda )}\) outputs \(y\in \{0,1\}^{m(\lambda )}\),
-
a prover \(\mathsf {VRF.P}_{SK}(x)\) that given x and the secret key produces a proof \(\pi \) that y is consistent with the verification key \(VK\),
-
and verifier \(\mathsf {VRF.V}_{VK}(\pi ,x,y)\) that verifies the proof.
We make the following requirements:
-
1.
Completeness: For every security parameter \(\lambda \in \mathbb {N}\) and input \(x\in \{0,1\}^{n(\lambda )}\),
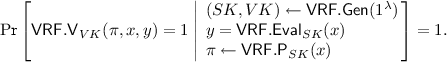
-
2.
Uniqueness: For every security parameter \(\lambda \in \mathbb {N}\), input \( x\in \{0,1\}^{n(\lambda )}\), and arbitrary verification key \(VK^*\in \{0,1\}^{k(\lambda )}\), there exists at most a single \(y\in \{0,1\}^{m(\lambda )}\) for which there exists an accepting proof \(\pi \). That is,
$$\begin{aligned} \text {if} \qquad \mathsf {VRF.V}_{VK^*}(\pi _0,x,y_0)=\mathsf {VRF.V}_{VK^*}(\pi _1,x,y_1)=1 \qquad \text {then} \qquad y_0=y_1. \end{aligned}$$ -
3.
Adaptive Indistinguishability: For any adversary \(\mathcal {A}(1^\lambda )\), consider the following game \(\mathcal {G}_\mathcal {A}^{\mathsf{vrf}}\):
-
(a)
The VRF challenger samples \((SK,VK)\leftarrow \mathsf {VRF.Gen}(1^\lambda )\), and sends \(VK\) to \(\mathcal {A}\).
-
(b)
\(\mathcal {A}\) submits to a challenger evaluation queries \(x_1,\dots ,x_Q\), and gets back from the challenger \((y_1,\pi _1),\dots ,(y_Q,\pi _Q)\), where \(y_i=\mathsf{VRF.Eval}_{SK}(x_i)\), \(\pi _i \leftarrow \mathsf {VRF.P}(x_i,SK)\).
-
(c)
At any point, including between evaluation queries, \(\mathcal {A}\) may submit a challenge input \(x_*\in \{0,1\}^{n(\lambda )}\). The challenger then sets \(y^0_* = \mathsf{VRF.Eval}_{SK}(x_*), y^1_* \leftarrow \{0,1\}^{m(\lambda )}\), samples \(b\leftarrow \{0,1\}\), and sends \(y^b_*\) to \(\mathcal {A}\). (The adversary \(\mathcal {A}\) may then make additional evaluation queries.)
-
(d)
At the end, \(\mathcal {A}\) outputs a guess \(b'\). The result of the game \(\mathcal {G}^{\mathsf{vrf}}_\mathcal {A}(\lambda )\) is 1 if \(b'=b\), and 0 otherwise.
We say that \(\mathcal {A}\) is admissible if in the above game it is always the case that
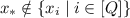 . We require that any polynomial-size admissible adversary wins the game with negligible advantage: $$\begin{aligned} \mathsf {Adv}_\mathcal {A}^{\mathsf{vrf}}:= \left| \Pr \left[ \mathcal {G}^\mathsf{vrf}_\mathcal {A}(\lambda )=1\right] -\frac{1}{2}\right| \le \mathrm {negl}(\lambda ). \end{aligned}$$
. We require that any polynomial-size admissible adversary wins the game with negligible advantage: $$\begin{aligned} \mathsf {Adv}_\mathcal {A}^{\mathsf{vrf}}:= \left| \Pr \left[ \mathcal {G}^\mathsf{vrf}_\mathcal {A}(\lambda )=1\right] -\frac{1}{2}\right| \le \mathrm {negl}(\lambda ). \end{aligned}$$We say that the VRF satisfies Selective Indistinguishability (rather than adaptive) if \(\mathcal {A}\) submits the challenge query \(x_*\) at the beginning of the game, before getting \(VK\) and making any evaluation query.
-
(a)
2.2 Sets with Efficient Representation
We consider collections of sets with efficient representation.
Definition 2
(Efficient Representation of Sets). \(\mathcal {S}=\left\{ \mathcal {S}_\lambda \right\} _{\lambda \in \mathbb {N}}\) is a collection of sets with efficient representation if there is a polynomial \(\mathrm {poly}\) such that any set \(S\in \mathcal {S}_\lambda \) can be represented by a circuit \(C_S\) of size \(\mathrm {poly}(\lambda )\) such that \(C_S(s)=1\) if \(s\in S\) and \(C_S(s)=0\) otherwise. We further require that given \(C_S\), it is possible to efficiently sample some \(s \in S\).
It will be convenient to identify any set \(S\) with its circuit representation \(C_S\). In particular, when an algorithm gets as input a set \(S\) that is super-polynomially large, we mean that it gets as input its efficient representation \(C_S\).
2.3 Constrained Pseudo-Random Functions
We next define constrained pseudo-random functions (CPRFs).
Definition 3
(Constrained \(\mathbf{PRF}\)s [13, 15, 37]). Let n, m, k be polynomially-bounded functions. Let \(\mathcal {S}=\left\{ \mathcal {S}_\lambda \subseteq 2^{\{0,1\}^{n(\lambda )}}\right\} _{\lambda \in \mathbb {N}}\) be a collection of sets with efficient representation. A constrained PRF \(\mathsf {CPRF}= (\mathsf {CPRF.Gen},\mathsf{CPRF.Eval},\mathsf {CPRF.Cons})\) for \(\mathcal {S}\) consists of the following polynomial-time algorithms:
-
a probabilistic key sampler \(\mathsf {CPRF.Gen}(1^\lambda )\) that given a security parameter \(1^\lambda \) outputs a key \(K\in \{0,1\}^{k(\lambda )}\),
-
an evaluator \(\mathsf{CPRF.Eval}_K(x)\) that given as input the key \(K\) and \(x\in \{0,1\}^{n(\lambda )}\) outputs \(y\in \{0,1\}^{m(\lambda )}\),
-
and a constraining algorithm that given as input the key \(K\) and a set \(S\in \mathcal {S}_\lambda \), outputs a constrained key \(K_{S}\in \{0,1\}^{k(\lambda )}\).
We make the following requirements:
-
1.
Functionality: For every security parameter \(\lambda \in \mathbb {N}\), set \(S\in \mathcal {S}_\lambda \), and input \(x\in \{0,1\}^{n(\lambda )}\) \(\setminus \) \(S\),

-
2.
(Single-Key) Indistinguishability: For any adversary \(\mathcal {B}(1^\lambda )\), consider the following game \(\mathcal {G}_\mathcal {B}^{\mathsf{cprf}}\):
-
(a)
\(\mathcal {B}\) submits a constraint \(S\) to a CPRF challenger.
-
(b)
The CPRF challenger samples \(K\leftarrow \mathsf {CPRF.Gen}(1^\lambda )\), computes a constrained key \(K_{S} \leftarrow \mathsf {CPRF.Cons}(K,S)\), and sends \(K_{S}\) to \(\mathcal {B}\).
-
(c)
\(\mathcal {B}\), given \(K_S\), chooses a challenge input \(x_*\in \{0,1\}^{n(\lambda )}\), and sends it to the challenger.
-
(d)
The challenger sets \(\begin{array}{l} y^0_* = \mathsf{CPRF.Eval}_K(x_*),\\ y^1_*\leftarrow \{0,1\}^{m(\lambda )}\end{array}\), samples \(b\leftarrow \{0,1\}\), and sends \(y^b_*\) to \(\mathcal {B}\).
-
(e)
\(\mathcal {B}\), given \(y^b_*\), outputs a guess \(b'\). The result of the game \(\mathcal {G}^{\mathsf{cprf}}_\mathcal {B}(\lambda )\) is 1 if \(b'=b\), and 0 otherwise.
We say that \(\mathcal {B}\) is admissible if in the above game it is always the case that \(S\in \mathcal {S}_\lambda \) and \(x_* \in S\). We require that any polynomial-size admissible adversary wins the game with negligible advantage:
$$\begin{aligned} \mathsf {Adv}_\mathcal {B}^{\mathsf{cprf}}:= \left| \Pr \left[ \mathcal {G}^\mathsf{cprf}_\mathcal {B}(\lambda )=1\right] -\frac{1}{2}\right| \le \mathrm {negl}(\lambda ). \end{aligned}$$ -
(a)
Remark 1
(Key Size). In the above definition, constrained keys and unconstrained keys have the same description size k. Furthermore, we have a single evaluation algorithm for both constrained and unconstrained keys. Both of these assumptions are without loss of generality and are just meant to simplify presentation in our construction.
Remark 2
(Computational Functionality). We can also consider a relaxed computational functionality requirement [17], which essentially says that inputs outside the constrained set \(S\), on which functionality isn’t preserved, may exist, but are hard to find. Formally,
-
1.
Computational Functionality: For any polynomial-size adversary \(\mathcal {A}\), any \(\lambda \in \mathbb {N},\) and any \(S\in \mathcal {S}_\lambda \):
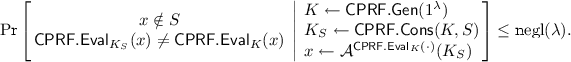
2.4 Partition Schemes
We define partition schemes, which generalize the concept of admissible hash functions [11] often used in the literature to prove adaptive security.
Such a scheme for a domain \(\{0,1\}^n\) provides a way to efficiently encode any element \(x\in \{0,1\}^n\) to an element \(\widehat{x} = \mathsf {PAR.Enc}(x)\) in a new domain \(\{0,1\}^{\widehat{n}}\). The new domain is associated with a partition sampler \(\mathsf{PAR.Gen}\) that samples a partition \((S,\overline{S})\), where \(\overline{S}=\{0,1\}^{\widehat{n}}\) \(\setminus \) \(S\). The main guarantee is that for any set of \(Q\) elements \(X \subseteq \{0,1\}^n\) and any \(x_* \notin X\), with high probability \(\widehat{x}_*\in S\) and \(\widehat{X} \subseteq \overline{S}\); namely, \(x_*\) and X are split by the partition. We shall further require that the scheme is balanced, roughly meaning that the probability that the above occurs does not change much between different choices of \((X,x_*)\). This property was suggested in [36] for admissible hash functions as an alternative to the artificial abort technique in partition-based proofs [46], inspired by [5].
Definition 4
(Partition Schemes). Let \(n,\widehat{n}\) be polynomially bounded functions, \(\tau <1\) an inverse-polynomial function, and \(\mathcal {S}=\left\{ \mathcal {S}_\lambda \subseteq 2^{\{0,1\}^{\widehat{n}(\lambda )}}\right\} _{\lambda \in \mathbb {N}}\) a collection of sets with efficient representation. A partition scheme \(\mathsf {PAR}=(\mathsf {PAR.Enc},\mathsf{PAR.Gen})\) parameterized by \((n,\widehat{n},\tau ,\mathcal {S})\) consists of the following polynomial-time algorithms
-
a deterministic encoder \(\mathsf {PAR.Enc}(x)\) that maps any \(x\in \{0,1\}^{n(\lambda )}\) to \(\widehat{x}\in \{0,1\}^{\widehat{n}(\lambda )}\)
-
a probabilistic sampler \(\mathsf{PAR.Gen}(1^\lambda ,Q,\delta )\) that given security parameter \(1^\lambda \), integer \(Q\), and balance parameter \(\delta \), outputs a set \(S\in \mathcal {S}_\lambda \), interpreted as a partition \((S,\overline{S})\) of \(\{0,1\}^{\widehat{n}(\lambda )}\).Footnote 4
Fix \(\lambda ,Q\in \mathbb {N},\delta <1\). Let \(\mathcal {X}\) be a distribution on pairs \((X,x_*)\) such that \(X:=\left( x_1,\dots ,x_Q\right) \in \{0,1\}^{n(\lambda )\times Q}\) and \(x_*\in \{0,1\}^{n(\lambda )}\) \(\setminus \) \(X\). We define the probability that \((X,x_*)\) are split by the sampled partition:

For every \(\lambda ,Q\in \mathbb {N}, \delta <1\), and any two distributions \(\mathcal {X},\mathcal {X}'\) as above, we require:
-
1.
Probable Partitioning:
$$\begin{aligned} P_{\mathcal {X}}(\lambda ,Q,\delta ) \ge \tau (\lambda ,Q,\delta ^{-1}) =\left( \frac{\delta }{Q\cdot \lambda }\right) ^{O(1)}, \end{aligned}$$ -
2.
Balance:
$$\begin{aligned} 1-\delta \le \frac{P_{\mathcal {X}}(\lambda ,Q,\delta )}{P_{\mathcal {X}'}(\lambda ,Q,\delta )} \le 1+\delta . \end{aligned}$$
Remark 3
(Admissible Hash Functions). Admissible hash functions [11] are a special case of partition schemes where the partitions considered are of a specific kind—namely S is always the set of all strings that contain a certain substring (we call these substring matching in Sect. 4). For our construction, we may use other partition schemes as well (we give such an example in Sect. 4).
We also note that the balance requirement is inspired by the definition in [36] for balanced admissible hash functions. There, the requirements of probable partition and balanced are unified to one requirement. We find that the above formulation captures the balance requirement in a somewhat more intuitive way.
3 The Construction
In this section, we present our VRF construction. For this purpose we first define and construct verifiable function commitments. We then use this primitive in conjunction with constrained PRFs to obtain our VRFs.
3.1 A Verifiable Function Commitment
We define verifiable function commitment schemes (VFCs). At high-level such a scheme has a similar syntax to that of a VRF, it allows to commit to a function and then verify its uniquely determined values. Security of such commitments says that commitments to two circuits \(C_0,C_1\) remain indistinguishable, as long as the attacker only sees evaluations (with proofs) on inputs x such that \(C_0(x)=C_1(x)\).
Definition 5
(Verifiable Function Commitment). Let n, m, k be polynomially bounded functions. A verifiable function commitment \(\mathsf {VFC}=(\mathsf {VFC.Gen},\mathsf {VFC.P},\mathsf {VFC.V})\) consists of the following polynomial-time algorithms:
-
a probabilistic key sampler \(\mathsf {VFC.Gen}(1^\lambda ,C)\) that given a security parameter \(1^\lambda \) and a circuit \(C\) \(:\{0,1\}^{n(\lambda )}\rightarrow \{0,1\}^{m(\lambda )}\) outputs a secret key \(SK\) and public verification key \(VK\in \{0,1\}^{k(\lambda )}\),
-
a prover \(\mathsf {VFC.P}_{SK}(x)\) that given x and the secret key produces a proof \(\pi \) that \(y=C(x)\) is consistent with the verification key \(VK\),
-
and verifier \(\mathsf {VFC.V}_{VK}(\pi ,x,y)\) that verifies the proof.
We make the following requirements (the first two analogous to those of a VRF):
-
1.
Completeness: For every security parameter \(\lambda \in \mathbb {N}\), input \(x\in \{0,1\}^{n(\lambda )}\), and circuit C,
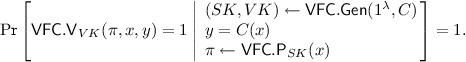
-
2.
Uniqueness: For every security parameter \(\lambda \in \mathbb {N}\), input \( x\in \{0,1\}^{n(\lambda )}\), and arbitrary verification key \(VK^*\in \{0,1\}^{k(\lambda )}\), there exists at most a single \(y\in \{0,1\}^{m(\lambda )}\) for which there exists an accepting proof \(\pi \). That is,
$$\begin{aligned} \text {if} \qquad \mathsf {VFC.V}_{VK^*}(\pi _0,x,y_0)=\mathsf {VFC.V}_{VK^*}(\pi _1,x,y_1)=1 \qquad \text {then} \qquad y_0=y_1. \end{aligned}$$ -
3.
Indistinguishability: For any adversary \(\mathcal {A}(1^\lambda )\), consider the following game \(\mathcal {G}_\mathcal {A}^{\mathsf{vfc}}\):
-
(a)
\(\mathcal {A}\) submits to the challenger two circuits \(C_0,C_1\).
-
(b)
The challenger samples \(b\leftarrow \{0,1\}\), \((SK,VK)\leftarrow \mathsf {VFC.Gen}(1^\lambda ,C_b)\), and sends \(VK\) to \(\mathcal {A}\).
-
(c)
\(\mathcal {A}\) submits to a challenger evaluation queries \(x_1,\dots ,x_Q\), and gets back from the challenger \(\pi _1,\dots ,\pi _Q\), where \(\pi _i \leftarrow \mathsf {VFC.P}(x_i,SK)\).
-
(d)
At the end, \(\mathcal {A}\) outputs a guess \(b'\). The result of the game \(\mathcal {G}^{\mathsf{vfc}}_\mathcal {A}(\lambda )\) is 1 if \(b'=b\), and 0 otherwise.
We say that \(\mathcal {A}\) is admissible if in the above game the circuits \(C_0,C_1\) map \(\{0,1\}^{n(\lambda )}\) to \(\{0,1\}^{m(\lambda )}\) are of the same size and \(C_0(x_i)= C_1(x_i)\) for all \(i \in [Q]\). We require that any polynomial-size admissible adversary wins the game with negligible advantage:
$$\begin{aligned} \mathsf {Adv}_\mathcal {A}^{\mathsf{vfc}}:= \left| \Pr \left[ \mathcal {G}^\mathsf{vfc}_\mathcal {A}(\lambda )=1\right] -\frac{1}{2}\right| \le \mathrm {negl}(\lambda ). \end{aligned}$$ -
(a)
We now show how to construct such a VFC.
Ingredients:
-
A non-interactive commitment \(\textsf {Com}\).
-
A non-interactive witness-indistinguishable proof system \(\mathsf {NIWI}\).
The Construction:
-
The key sampler \(\mathsf {VRF.Gen}(1^\lambda ,C)\):
-
Compute three commitments \(\left\{ \textsf {c}_i:= \textsf {Com}(C;r_i)\right\} _{i\in [3]}\), using randomness \(r_i\leftarrow \{0,1\}^\lambda \).
-
Output the secret key \(SK= (C,r_2,r_3)\) and public key \(VK= (\textsf {c}_1,\textsf {c}_2,\textsf {c}_3)\).
-
-
The prover \(\mathsf {VRF.P}_{SK}(x)\):
-
Construct the statement \(\varPsi = \varPsi (\textsf {c}_1,\textsf {c}_2,\textsf {c}_3,x,y)\) asserting that y is consistent with the function value given by the majority of the commitments:
$$\begin{aligned} \exists ((i,r_i,C_{i}),(j,r_j,C_{j})) : \begin{array}{l} 1\le i<j\le 3,\\ \textsf {c}_i = \textsf {Com}(C_i;r_i),\textsf {c}_j = \textsf {Com}(C_j;r_j),\\ y= C_i(x) = C_j(x). \end{array} \end{aligned}$$ -
Output a NIWI proof \(\pi \leftarrow \mathsf {NIWI.P}(\varPsi ,(2,r_2,C),(3,r_3,C),1^\lambda )\) for the statement \(\varPsi \), using the commitment randomness \(r_2,r_3\) and the circuit C as the witness.
-
-
The verifier \(\mathsf {VRF.V}_{VK}(\pi ,x,y)\):
-
Construct \(\varPsi \) as above.
-
Run the NIWI verifier \(\mathsf {NIWI.V}(\pi ,\varPsi )\) and output the same answer.
-
Completeness and Uniqueness. The completeness of the scheme follows readily from the completeness of the NIWI system. The uniqueness follows from the perfect binding of the commitment as well as the soundness of the NIWI. Indeed, given the verification key \(VK= (\textsf {c}_1,\textsf {c}_2,\textsf {c}_3)\), binding implies that for each commitment \(\textsf {c}_i\), there exists at most a single circuit \(C_i\) such that \(\textsf {c}_i\) is a valid commitment to \(C_i\). Thus, also for any input x, each \(\textsf {c}_i\) is consistent with at most a single value \(y_i = C_i(x)\). By the soundness of the NIWI, any accepted y must be consistent with the majority of value \(y_1,y_2,y_3\).
Indistinguishability. We prove the security of the scheme.
Proposition 1
For any polynomial-size admissible adversary \(\mathcal {A}\), it holds that \(\mathsf {Adv}_\mathcal {A}^{\mathsf{vfc}}(\lambda ) \le \mathrm {negl}(\lambda )\).
The proof proceeds by a standard hybrid argument and is given in the full version.
3.2 The VRF
We now present the VRF construction based on verifiable function commitments and constrained pseudorandom functions. We first list the required ingredients.
Ingredients:
-
A partition scheme \(\mathsf {PAR}\) parameterized by \((n,\widehat{n},\tau ,\mathcal {S})\) for a collection of sets \(\mathcal {S}=\left\{ \mathcal {S}_\lambda \right\} _{\lambda \in \mathbb {N}}\) with efficient representation.
-
A constrained pseudo-random function \(\mathsf {CPRF}\) for the collection \(\mathcal {S}\), mapping \(\widehat{n}\) bits to m bits. (For simplicity, we assume perfect functionality. We later observe that the construction works also given computational functionality.)
-
A verifiable function commitment \(\mathsf {VFC}\) for circuits mapping \(\widehat{n}\) bits to m bits.
The Construction:
-
The key sampler \(\mathsf {VRF.Gen}(1^\lambda )\):
-
Sample a CPRF key \(K\leftarrow \mathsf {CPRF.Gen}(1^\lambda )\), and consider the circuit \(C_K(\cdot ) = \mathsf{CPRF.Eval}_K(\cdot )\).
-
Sample VFC keys \(({\overline{SK}},{\overline{VK}}) \leftarrow \mathsf {VFC.Gen}(1^\lambda ,C_K)\).
-
Output the secret key \(SK= (K,\overline{SK})\) and public key \(VK= \overline{VK}\).
-
-
The evaluator \(\mathsf{VRF.Eval}_{SK}(x)\):
-
Compute \(\widehat{x} = \mathsf {PAR.Enc}(x)\).
-
Output \(y:=\mathsf{CPRF.Eval}_K(\widehat{x})\).
-
-
The prover \(\mathsf {VRF.P}_{SK}(x)\):
-
Output a VFC proof \(\pi \leftarrow \mathsf {VFC.P}_{\overline{SK}}(\widehat{x})\) for the consistency of \(y=C_K(\widehat{x})\) with \(\overline{VK}\).
-
-
The verifier \(\mathsf {VRF.V}_{VK}(\pi ,x,y)\):
-
Run the VFC verifier \(\mathsf {VFC.V}_{\overline{VK}}(\pi ,\widehat{x},y)\) and output the same answer.
-
Completeness and Uniqueness. Completeness and uniqueness follow readily from those of the VFC.
3.3 Security Analysis
We now prove the security of the VRF constructed above. Concretely, given an admissible adversary \(\mathcal {A}\) against the VRF, we construct an admissible adversary \(\mathcal {B}\) against the underlying constrained PRF. Throughout, we assume that \(\mathcal {A}\) makes (w.l.o.g exactly) \(Q=Q(\lambda )\) evaluation queries in the VRF game, for some polynomially bounded \(Q(\lambda )\), and denote its advantage \(\mathsf {Adv}_\mathcal {A}^\mathsf{vrf}(\lambda )\) by \(\delta =\delta (\lambda )\).
The CPRF adversary. Adversary \(\mathcal {B}(1^\lambda )\) operates as follows:
-
1.
Initializes a variable \(\mathsf {result}= \mathtt {succ}\).
-
2.
Invokes \(\mathsf{PAR.Gen}(1^\lambda ,Q,\delta )\) to sample a partition set \(S\in \mathcal {S}_\lambda \).
-
3.
Submits \(S\) to the CPRF challenger as the constraint, and obtains a constrained key \(K_S\).
-
4.
It now emulates \(\mathcal {A}\) in \(\mathcal {G}^\mathsf{vrf}_\mathcal {A}\) as follows:
-
(a)
Computes the constrained evaluation circuit \(C_{K_S}(\cdot ) = \mathsf{CPRF.Eval}_{K_{S}}(\cdot )\), samples corresponding VFC keys \((\overline{SK},\overline{VK}) \leftarrow \mathsf {VFC.Gen}(1^\lambda ,C_{K_S})\), and sends \(VK= \overline{VK}\) to \(\mathcal {A}\).
-
(b)
When \(\mathcal {A}\) makes an evaluation query \(x_i\in \{0,1\}^n\), for \(i\in [Q]\),
-
i.
\(\mathcal {B}\) computes the encoding \(\widehat{x}_i\) of \(x_i\).
-
ii.
If \(\widehat{x}_i \in S\), sets \(\mathsf {result}= \mathtt {fail}\), and jumps to the last step 4d.
-
iii.
Otherwise, computes \(y_i = C_{K_{S}}(\widehat{x}_i)\), and a VFC proof \(\pi _i \leftarrow \mathsf {VFC.P}_{SK}(\widehat{x}_i)\) that \(y_i\) is consistent with \(\overline{VK}\). Sends \((y_i,\pi _i)\) to \(\mathcal {A}\).
-
i.
-
(c)
When \(\mathcal {A}\) makes the challenge query \(x_* \in \{0,1\}^n\),
-
i.
As before, \(\mathcal {B}\) computes the encoding \(\widehat{x}_*\) of \(x_*\).
-
ii.
If \(\widehat{x}_* \notin S\), sets \(\mathsf {result}= \mathtt {fail}\), and jumps to the last step 4d.
-
iii.
Otherwise, submits \(\widehat{x}_*\) to the CPRF challenger as the challenge query, obtains \(y_*^b\), and sends it to \(\mathcal {A}\) as the VRF challenge.
-
i.
-
(d)
At the end of the game, if \(\mathsf {result}= \mathtt {fail}\), \(\mathcal {B}\) acts as follows:
-
i.
If a challenge query \(\widehat{x}_*\) has not yet been submitted to the CPRF challenger (due to a pre-challenge failure in step 4(b)ii or 4(c)ii), samples some \(z \in S\) and submits it as the challenge. Disregards the challenger’s answer.
-
ii.
Outputs a random guess \(b'\leftarrow \{0,1\}\).
If \(\mathsf {result}=\mathtt {succ}\), \(\mathcal {B}\) obtains a guess \(b'\) from \(\mathcal {A}\), and outputs \(b'\).
-
i.
-
(a)
Note that \(\mathcal {B}\) is admissible by construction (it always respects the constraint S). We now show that the advantage of \(\mathcal {B}\) in the CPRF game is as large as the advantage \(\delta \) of \(\mathcal {A}\) in the VRF game, up to some loss \(\tau \) that depends on the partition scheme (the guaranteed partition probability).
Proposition 2
\(\mathsf {Adv}_\mathcal {B}^{\mathsf{cprf}}(\lambda ) \ge \tau (\lambda ,Q,\delta ^{-1}) \cdot \frac{\delta }{2}-\mathrm {negl}(\lambda )\ge \left( \frac{\delta }{\lambda \cdot Q}\right) ^{O(1)} -\mathrm {negl}(\lambda )\).
Proof
To prove the claim we examine a sequence of hybrid CPRF games \(\left\{ \mathcal {G}_\alpha ^\mathsf{cprf}\right\} \), each with a corresponding adversary \(\mathcal {B}_\alpha \) and challenger \(\mathcal {CH}_\alpha \), which slightly augment the adversary and challenger of the previous hybrid. In all games, as in the original CPRF game, the result of the game is 1 if and only if the adversary \(\mathcal {B}_\alpha \) guesses correctly the challenge bit, i.e. \(b'=b\).
Hybrid \(\mathcal {G}_0^\mathsf{cprf}\) : This corresponds to the game \(\mathcal {G}_{\mathcal {B}}^\mathsf{cprf}\) described above. Namely \(\mathcal {B}_0\) is the above described \(\mathcal {B}\) and \(\mathcal {CH}_0\) is the usual CPRF challenger.
Hybrid \(\mathcal {G}_1^\mathsf{cprf}\) : In this game, the CPRF challenger \(\mathcal {CH}_1\) also provides \(\mathcal {B}_1\) with the unconstrained key \(K\), and \(\mathcal {B}_1\) generates the VFC keys \((\overline{SK},\overline{VK})\leftarrow \mathsf {VFC.Gen}(1^\lambda ,C_K)\) corresponding to the circuit \(C_K(\cdot ) = \mathsf{CPRF.Eval}_K(\cdot )\) instead of the constrained circuit \(C_{K_S}\).
We argue that by the indistinguishability of the VFC scheme
Indeed, any noticeable difference between the games, leads to an efficient distinguisher \(\mathcal {D}\) that can break the VFC scheme. The distinguisher \(\mathcal {D}\) will submit to the VFC challenger the circuits \(C_0=C_{K_S},C_1=C_{K}\), and then will emulate \(\mathcal {B}\) only that instead of generating \((\overline{SK},\overline{VK})\) and the proofs \(\pi _i\) by itself, it will use the verification key \(\overline{VK}\) and proofs \(\pi _i\) given by the VFC challenger. First, note that this always induces an admissible VFC adversary. Indeed, \(\mathcal {B}\) only answers the queries \(x_i\) of \(\mathcal {A}\) as long as they are such that \(\widehat{x}_i\notin S\), meaning that \(C_{K_S}(\widehat{x}_i)=C_{K}(\widehat{x}_i)\). It is left to note that when the challenge bit is b, the emulated \(\mathcal {B}\) acts exactly as \(\mathcal {B}_b\) in \(\mathcal {G}_b^\mathsf{cprf}\).
Hybrid \(\mathcal {G}_2^\mathsf{cprf}\) : In this game, the adversary \(\mathcal {B}_2\) and challenger \(\mathcal {CH}_2\) act differently given evaluation queries \(x_i\), or the challenge query \(x_*\), from the emulated \(\mathcal {A}\). \(\mathcal {B}_2\) does not check right away whether \(\widehat{x}_i \), or \(\widehat{x}_*\) are in \(S\). Instead, first all evaluation queries are answered according to the unconstrained circuit \(C_K\), and the challenge is also answered according to this circuit, or a random string, depending on the challenge bit b. Namely, this part exactly emulates the real VRF game \(\mathcal {G}_\mathcal {A}^\mathsf{vrf}\).
Having finished emulating \(\mathcal {A}\) as above, and recording its output guess \(b'\), \(\mathcal {B}_2\) now checks that for all evaluation queries \(x_i\) made \(\widehat{x}_i \notin S\) and for the challenge query \(\widehat{x}_* \in S\). If this is the case, it outputs the recorded \(b'\) (previously output by \(\mathcal {A}\)) as the guess. Otherwise, it outputs a random guess \(b'\leftarrow \{0,1\}\).
We argue that
Indeed, consider in either game the event \(\mathsf {bad}\) that either \(\widehat{x}_i \in S\) for some evaluation query by \(\mathcal {A}\) or \(\widehat{x}_*\notin S\) for the challenge query by \(\mathcal {A}\). Then, until the first query that induces \(\mathsf {bad}\), the view of \(\mathcal {A}\) in the two experiments is distributed exactly the same. This also implies that \(\mathsf {bad}\) occurs in both experiments with exactly the same probability. Furthermore, if \(\mathsf {bad}\) does occur, then from that point on, \(\mathcal {A}\)’s emulation is disregarded and the two experiments again have exactly the same output distribution, a random \(b'\). The required equality follows.
The Advantage in \(\mathcal {G}_2^\mathsf{cprf}\) . To conclude the proof, we show that
Let us denote by \(\mathsf {win}\) the event that in \(\mathcal {G}_2^\mathsf{cprf}\) the adversary \(\mathcal {A}\) emulated in the first part correctly guesses the challenge bit b. We continue to denote by \(\mathsf {bad}\) the event that either \(\widehat{x}_i \in S\) for some evaluation query by \(\mathcal {A}\) or \(\widehat{x}_*\notin S\) for the challenge query by \(\mathcal {A}\).
Then, we have that

We next note that by the probable partition and balance properties of the underlying partition schemes:

Indeed, \(\overline{\mathsf {bad}}\) is exactly the event of successful partition where \((X=\left\{ x_1,\dots ,x_q\right\} \), \(x_*)\) are sampled according to \(\mathcal {A}\)’s queries in the VRF game. \(\overline{\mathsf {bad}}| \mathsf {win}\) is the event of successful partition when \((X,x_*)\) are sampled from a different distribution—the one induced by \(\mathcal {A}\) in the VRF game, but conditioned on \(\mathcal {A}\) winning.
In addition, since the view of the emulated \(\mathcal {A}\) in \(\mathcal {G}_2^\mathsf{cprf}\) is identical to its view in \(\mathcal {G}_\mathcal {A}^\mathsf{vrf}\), it holds that
It now follows that

Extending the Proof for CPRFs with Computational Functionality. We observe that the proof extends when relying on CPRFs with computational (and not perfect) functionality (Remark 2). First, note that the place where we rely on the functionality of the CPRF is in the transition between \(\mathcal {G}_{0}^\mathsf{cprf}\) to \(\mathcal {G}_{1}^\mathsf{cprf}\). There, to argue that both \(C_K\) and \(C_{K_{S}}\) agree on any \(\mathcal {A}\)-query \(x_i\) (thus making the VCF attacker admissible), we rely on the fact that for \(x_i\notin S\), the two circuits agree. For CPRFs with perfect functionality, this agreement is guaranteed.
To extend the analysis to the case of computational functionality, we will argue that in the above transition, the VCF distinguisher \(\mathcal {D}\) considered still does not violate functionality—namely, it does not output any evaluation query \(x_i \notin S\) such that \(\mathsf{CPRF.Eval}_{K_{S}}(x_i) \ne \mathsf{CPRF.Eval}_K(x_i)\)—except with negligible probability. Concretely, if it outputs with non-negligible probability \(x_i\notin S\) that violates functionality, we can construct from it an adversary that breaks the computational functionality of the CPRF.
First, we argue that if the VCF attacker \(\mathcal {D}\) violates functionality with non-negligible probability when the VCF challenge bit b is chosen at random, then it also does so when we restrict \(b=0\); that is, when VFC keys always correspond to \(C_0=C_{K_S}\). Indeed, until the point that \(\mathcal {D}\) outputs \(x_i\) that violates functionality, the case that \(b=0\) and \(b=1\) are indistinguishable by the VFC guarantee; furthermore, the event that \(x_i\) violates functionality is efficiently testable.
We now observe that in the restricted VFC experiment where \(b=0\), can be perfectly emulated given only the constrained key \(K_S\) and oracle access to \(\mathsf{CPRF.Eval}_K\) (needed to compute the answer to the challenge query). Thus, we can use \(\mathcal {D}\) to break the computational functionality of the CPRF.
4 Instantiations
In this section, we discuss possible instantiations for the underlying partition scheme and constrained PRF. We consider both adaptive security and selective security. For adaptive security, we consider instantiations based on various polynomial assumptions (such as LWE and 1D-SIS, DDH, or IO), or instantiations based on sub-exponential one-way functions. For selective security, we can rely on polynomial one-way functions. (The assumptions mentioned above are those required for appropriate CPRFs. For the CPRFs themselves, we still need NIWIs and non-interactive commitments).
4.1 Adaptive Security from Polynomial Assumptions
To obtain adaptive security from polynomial assumptions, we describe three partition schemes for three different collections of partition sets \(\mathcal {S}\). We then exhibit the existence of CPRFs for these collections based on different assumptions.
Partition Schemes. We give three examples of partition schemes. The first is a code-based scheme that aligns with the common notion of (balanced) admissible hash functions from the literature. The second is a variant of the first to large alphabets (which will be useful later on for simplifying the assumptions behind CPRFs). The third is a simple scheme based on universal hashing [18], which is omitted here and can be found in the full version.
Substring Matching over Binary Alphabet. We first describe an existing partition scheme considered first in [38] for the collection substring matching sets, which aligns with the notion of admissible hash functions. The scheme was also shown to be balanced in [36]. Given that our definition is slightly different than that in [36], and for the sake of completeness, we describe the scheme and its analysis.
-
The partition scheme’s encoding function \(\mathsf {PAR.Enc}(x)\) is any binary error correcting code with constant distance \(c<1\).Footnote 5 Each element \(x\in \{0,1\}^n\) is encoded by an element \(\widehat{x}\in \{0,1\}^{\widehat{n}}\).
-
The collection of sets \(\mathcal {S}_\lambda \) that partitions \(\{0,1\}^{\widehat{n(\lambda )}}\) consists of sets \(S_s\) parameterized by a string \(s \in \left\{ 0,1,\star \right\} ^{\widehat{n(\lambda )}}\) containing wildcard symbols \(\star \). For an element \(z\in \{0,1\}^{\widehat{n(\lambda )}}\), we say that \(z\in S_s\) if every non-wildcard bit of s agrees with z; namely, if \(s_i \ne \star \), then \(s_i=z_i\). We call such a set \(S_s\) a substring matching set.
-
The partition sampler \(\mathsf{PAR.Gen}(1^\lambda ,Q,\delta )\) works as follows:
-
Let \(d:= \log (2Q/\delta )/\log (\frac{1}{1-c})\).
-
Sample a random set of d indices \(D \leftarrow {[\widehat{n}] \atopwithdelims ()d}\).
-
For \(i\in D\) sample \(s_i\leftarrow \{0,1\}\) at random. For \(i\notin D\) set \(s_i=\star \).
-
Output \(S_s\).
-
We will now prove probable partition and balance.
For \((X=(x_1,\dots ,x_Q),x_*)\), and consistently with Definition 4, define:

Further define
First, note that for any fixed \((X=\left\{ x_1,\dots ,x_Q\right\} ,x_*)\) and any \(x_i\in X\), it holds that
Also, for any fixed D,
Combining the first fact, a union bound over all \(x_i\in X\), and the second fact, we have
Thus, probable partitioning holds with \(\tau (\lambda ,Q,\delta ^{-1}) = \left( \delta /Q\right) ^{O(1)}\).
Furthermore, we know that
This in turn implies that
Since for every two distributions \(\mathcal {X},\mathcal {X}'\) on pairs \((X,x_*)\) it holds that
the balance property follows.
Substring Matching over Polynomial Alphabet. We describe a variant of the above that will have a polynomial alphabet and will require supporting d-symbol substrings only for a constant d, which will be useful in the construction of corresponding CPRFs. We shall restrict attention to a relatively simple setting of parameters, which will be enough for our purpose. (Conceivably, setting the parameters more carefully may lead to more efficient constructions.)
-
Let \(\varSigma \supseteq \{0,1\}\) be an alphabet of size \(\sigma = O(n^2)\). The partition scheme’s encoding function \(\mathsf {PAR.Enc}(x)\) is an efficient error correcting code mapping \(\varSigma ^{n}\) to \(\varSigma ^{m}\cong \{0,1\}^{\widehat{n}}\) with distance \(1-\frac{1}{n}\). Each element \(x\in \{0,1\}^n\) is encoded by an element \(\widehat{x}\in \{0,1\}^{\widehat{n}}\). For example, we can take the Reed-Solomon code consisting of degree n polynomials over a field \(\mathbb {F}_{2^k}\) of size \(O(n^2)\) (so \(\widehat{n}=m\times k\)).
-
The collection of sets \(\mathcal {S}_\lambda \) that partitions \(\varSigma ^{m}\cong \{0,1\}^{\widehat{n}}\) consists of sets \(S_s\) parameterized by a string \(\left( s \in \varSigma \cup \left\{ \star \right\} \right) ^{m}\) containing wildcard symbols \(\star \). For an element \(z\in \varSigma ^{m}\), we say that \(z\in S_s\) if every non-wildcard symbol of s agrees with z; namely, if \(s_i \ne \star \), then \(s_i=z_i\). Again, we call such a set \(S_s\) a substring matching set.
-
The partition sampler \(\mathsf{PAR.Gen}(1^\lambda ,Q,\delta )\) works as follows:
-
Let \(d:= \log (2Q/\delta )/\log (n)\). (In our setting, both \(Q/\delta \) and n are polynomial in \(\lambda \) and \(d = O(1)\).)
-
Sample a random set of d indices \(D \leftarrow {[m] \atopwithdelims ()d}\).
-
For \(i\in D\) sample \(s_i\leftarrow \varSigma \) at random. For \(i\notin D\) set \(s_i=\star \).
-
Output \(S_s\).
-
The proof of probable partition and balance naturally generalizes that of the previous partition scheme.
Constrained PRFs. We now discuss possible CPRF instantiations for the above collections.
Existing Constructions. We start by noting that CPRFs for all set collections with efficient representation, with computational functionality, are known based on the standard lattice assumptions—LWE and 1D-SIS [17]. We also note that such CPRFs with perfect correctness are known from indistinguishability obfuscation (IO) [14]. In particular, we can rely on the above CPRFs with either one of the partition schemes presented above.
A Construction for Substring Matching Sets over Binary Alphabet. We now give a construction that can be used together with the first partition scheme for substring matching sets over binary alphabet. The construction is based on the d-power DDH assumption (for logarithmic d), which in turn can be reduced to the subgroup hiding assumption in composite DDH groups [20, 34]. Later on, we will show how to reduce the assumption to plain DDH, by generalizing this construction.
Assumption 41
( d -Power DDH). There exists a polynomial-time sampler \(\mathcal {G}(1^\lambda )\) that outputs a group \(\mathbb {G}\) and \(g\in \mathbb {G}\), such that for any polynomial-size adversary \(\mathcal {A}\), and any \(d(\lambda )=O(\log \lambda )\),

We next describe the construction, which is inspired by the Naor-Reingold PRF [43] and a construction of adaptive puncturable PRFs from [34] from indistinguishability obfuscation and d-Power DDH. The security notion considered in that work is stronger than the one considered in this work (Definition 3), where the constraining set is chosen ahead of time and not adaptively. In particular, it will not require indistinguishability obfuscation and will handle the collection of constraints \(\mathcal {S}\) considered in this section.
For domain \(\{0,1\}^{\widehat{n}}\), the function is defined as follows:
-
Each (unconstrained) key \(K\) consists of \(\widehat{n}\) pairs \(\left( k_{i,b} \leftarrow \mathbb {Z}^{*}_{|\mathbb {G}|}\right) _{i\in [\widehat{n}],b\in \{0,1\}}\), as well as \((\mathbb {G},g)\).
-
The value of the function is given by \(\mathsf{CPRF.Eval}_K(x) = g^{\prod _{i\in [\widehat{n}]}k_{i,x_i}}\).
-
The constraining algorithm \(\mathsf {CPRF.Cons}(K,s)\), given a key \(K\) and a string \(s\in \left\{ 0,1,\star \right\} ^{\widehat{n}}\), with d non-wildcards at positions \(D\subseteq [\widehat{n}]\), works as follows:
-
Samples \(\alpha \leftarrow \mathbb {Z}^*_{\mathbb {G}}\).
-
Outputs a constrained key \(K_{S_s}\) consisting of \((s,\mathbb {G},g,g^\alpha ,\dots ,g^{\alpha ^{d-1}})\) and a new set \(\left( k'_{i,b}\right) _{i,b}\), where
$$\begin{aligned} k'_{i,b} = {\left\{ \begin{array}{ll} \alpha ^{-1} \cdot k_{i,b} &{} i \in D, b=s_i\\ k_{i,b} &{} \text {otherwise}\\ \end{array}\right. }. \end{aligned}$$
-
-
To evaluate the function on \(x\in \{0,1\}^{\widehat{n}}\) \(\setminus \) \(S_s\) using the constrained key \(K_{S_s}\):
-
Let \(d'\) be the number of indices \(i\in D\) such that \(x_i=s_i\) (note that \(d'<d\) since \(x\notin S_s\)).
-
Output \(\left( g^{\alpha ^{d'}}\right) ^{\prod _{i\in [\widehat{n}]}k'_{i,x_i}}\).
-
Functionality. By definition,
Indistinguishability. We now prove the indistinguishability property of the constructed CPRF. Given an (admissible) adversary \(\mathcal {B}\) that breaks the indistinguishability of the CPRF, we construct and adversary \(\mathcal {A}\) that breaks the d-Power DDH assumption with the same advantage.
The breaker \(\mathcal {A}\) . Given \((\mathbb {G},g,g^\alpha ,\dots ,g^{\alpha ^{d-1}},g^{\gamma _b})\), the adversary \(\mathcal {A}\) emulates \(\mathcal {B}\) as follows:
-
1.
When \(\mathcal {B}\) submits \(s\in \left\{ 0,1,\star \right\} ^{\widehat{n}}\) to the CPRF challenger, where s has d non-wildcard entries on an index set \(D\subseteq [\widehat{n}]\), \(\mathcal {A}\) samples \(\left( k'_{i,b}\leftarrow \mathbb {Z}_{|G|}^*\right) _{i,b}\). It then sends \(K_{S_s}:=\left( s,\mathbb {G},g,g^{\alpha },\dots ,g^{\alpha ^{d-1}},\left( k'_{i,b}\right) _{i,b}\right) \) to \(\mathcal {B}\).
-
2.
Then \(\mathcal {B}\) gives \(x\in S_s\) as the challenge query, \(\mathcal {A}\) returns \(g^{{\gamma _b}\prod _{i\in \widehat{n}} k'_{i,x_i}}\).
-
3.
When \(\mathcal {B}\) outputs a guess \(b'\), \(\mathcal {A}\) outputs the same guess.
We observe that the view of the emulated \(\mathcal {B}\) is identical to its view in the CPRF game, where the induced unconstrained key is given by
When \(\gamma _b=\alpha ^d\), this corresponds to the case that the CPRF value is returned, and when \(\gamma _b \leftarrow \mathbb {Z}_{|G|}^*\) is random, this corresponds to the case that a random element \(g^\beta ,\beta \leftarrow \mathbb {Z}^*_{|G|}\) is returned.Footnote 6
It follows that
A Construction for Substring Matching Sets over Polynomial Alphabet. We now give a construction that can be used together with the second partition scheme for substring matching sets over polynomial alphabet. The construction is based on the Generalized Decision Diffie Hellman Assumption (GDDH), which follows from DDH [43].
Assumption 42
(GDDH). There exists a polynomial-time sampler \(\mathcal {G}(1^\lambda )\) that outputs a group \(\mathbb {G}\) and \(g\in \mathbb {G}\), such that for any polynomial-size adversary \(\mathcal {A}\), and any \(d =O(1)\),Footnote 7

We next describe the construction, which is a carefully augmented variant of the previous construction. At first, it might be tempting to use the previous CPRF construction (with binary substring matching partition) as before, only that instead of using the same pad \(\alpha \), we would use independent pads \(\alpha _1,\dots ,\alpha _d\) for each of the d padded coordinates. The problem with this approach is that the constrained key will need to include all the elements  . Here, as long as we use the first partition scheme, over binary alphabet, \(d \approx \log Q/\delta \). Thus, the size of the above set is roughly \(Q/\delta \), which is too large. (It is a polynomial in \(\lambda \), but a polynomial that depends on the adversary’s number of queries and advantage, which are not apriori bounded. Before, this was not an issue as we only considered the set of all powers of the same element \(\alpha \).)
. Here, as long as we use the first partition scheme, over binary alphabet, \(d \approx \log Q/\delta \). Thus, the size of the above set is roughly \(Q/\delta \), which is too large. (It is a polynomial in \(\lambda \), but a polynomial that depends on the adversary’s number of queries and advantage, which are not apriori bounded. Before, this was not an issue as we only considered the set of all powers of the same element \(\alpha \).)
To circumvent the above we use the second partition scheme presented over a polynomial alphabet that has a constant d. This requires a natural augmentation of the construction, which we present now.
For domain \(\{0,1\}^{\widehat{n}} \cong \varSigma ^m\), where \(\varSigma \) is of size \(\sigma =O(n^2)\), the function is defined as follows:
-
Each (unconstrained) key \(K\) consists of an \(m\times \sigma \) matrix \(\left( k_{i,j} \leftarrow \mathbb {Z}^{*}_{|\mathbb {G}|}\right) _{i\in [m],j\in \varSigma }\), as well as \(\mathbb {G},g\).
-
The value of the function on \(x\in \varSigma ^m\) is given by \(\mathsf{CPRF.Eval}_K(x) = g^{\prod _{i\in [m]} k_{i,x_i}}\).
-
The constraining algorithm \(\mathsf {CPRF.Cons}(K,s)\), given a key \(K\) and a string \(s\in \left( \varSigma \cup \left\{ \star \right\} \right) ^{m}\), with d non-wildcards at positions \(\left\{ i_1,\dots ,i_d\right\} =D\subseteq [m]\), works as follows:
-
Samples \(\alpha _{i_1},\dots ,\alpha _{i_d} \leftarrow \mathbb {Z}^*_{\mathbb {G}}\).
-
Outputs a constrained key \(K_{S_s}\) consisting of
 , and a new set \(\left( k'_{i,j}\right) _{i,j}\), where $$\begin{aligned} k'_{i,j} = {\left\{ \begin{array}{ll} \alpha ^{-1}_i \cdot k_{i,j} &{} i \in D, j=s_i\\ k_{i,j} &{} \text {otherwise}\\ \end{array}\right. }. \end{aligned}$$
, and a new set \(\left( k'_{i,j}\right) _{i,j}\), where $$\begin{aligned} k'_{i,j} = {\left\{ \begin{array}{ll} \alpha ^{-1}_i \cdot k_{i,j} &{} i \in D, j=s_i\\ k_{i,j} &{} \text {otherwise}\\ \end{array}\right. }. \end{aligned}$$
-
-
To evaluate the function on \(x\in \varSigma ^m \setminus S_s\) using the constrained key \(K_{S_s}\):
-
Let \(D'\subseteq D\) be the subset of indices such that \(x_i=s_i\) (note that \(D' \ne D\) since \(x\notin S_s\)).
-
Output \(\left( g^{\prod _{\ell \in D'}\alpha _{i_\ell }}\right) ^{\prod _{i\in [m]} k'_{i,x_i}}\).
-
First, we note that as long as \(d\le c\log n\) for some fixed constant c, all the algorithms, including the constraining algorithm run in fixed polynomial time as required. When combining this scheme with the substring matching partition scheme over large alphabets, it is always the case that \(d = O(1) \ll \log n\). Proving functionality and security of the CPRF is similar to the previous CPRF (from d-power DDH), and can be found in the full version.
Remark 4
(Resulting VRFs from Bilinear Maps). Using the above construction, we get VRFs from simple assumptions on bilinear maps—DLIN and SXDH. Indeed, both SXDH and DLIN imply DDH in plain (non-bilinear) groups,Footnote 8 as required for the above CPRFs, as well as commitments and NIWIs.
Remark 5
(Verifiable Unpredictable Function from Factoring). We note that a computational (rather than decisional) version of GDH holds assuming it is hard to factor Blum integers [7]. In this version, the value \(g^{\prod _{\ell \in D} \alpha _{i_{\ell }}}\) is only unpredictable and not necessarily pseudorandom. It is not hard to see that the same construction as above, would give in this case a corresponding notion of unpredictable CPRFs. Plugging this in our general construction would readily give a Verifiable Unpredictable Function [39], instead of a VRF.
4.2 Selective Security
We now discuss how to obtain selective security based on plain puncturable PRFs, instead of the more general CPRFs considered above. As usual, this also gives an adaptively-secure constructions assuming subexponential hardness.
Puncturable PRFs are a special case of constrained PRFs where the collection of sets \(\mathcal {S}\) includes singletons \(S_x =\left\{ x\right\} \); namely, every constrained key \(K_{\left\{ x\right\} }\) allows computing the PRF everywhere, but at the point x. As shown in [13, 15, 37], the GGM [27] PRF yield puncturable PRFs. In particular, (subexponential) puncturable PRFs can be constructed from (subexponential) one-way functions.
Recall that in the case of selective security (see Definition 3), the VRF adversary announces the challenge query \(x_*\) ahead of time, before obtaining the verification key, or performing any evaluation query. In this case, we can avoid using partition schemes, and replace use puncturable PRFs as our CPRFs. Alternatively, we can think of a trivial partition scheme for the collection of singletons where the encoding is the identity, and the partition sampler also gets the challenges \(x_*\) as input, and outputs it as the partition, corresponding to the case that successful partition occurs with probability \(\tau =1\). The same analysis as in Sect. 3.3 now applies.
By taking all the underlying primitives to be subexponentially hard (say \(2^{\lambda ^{\varepsilon }}\)-hard), the scheme is adaptively secure (when setting the underlying security parameter to \(n^{1/\varepsilon }\)). This follows by a standard reduction (see for example [1]).
Notes
- 1.
The construction based on IO is also limited to either selective security, or reliance on subexponential hardness.
- 2.
We also give a simpler construction under the stronger d-power DDH assumption.
- 3.
In the body, we further allow the partition scheme to involve some encoding of the input space X into a more structured input space \(\widehat{X}\), and then consider applying the CPRF and partitioning for encoded inputs in the new space \(\widehat{X}\). See Definition 4 and Sect. 3 for more details.
- 4.
We note that the set S has efficient representation in terms of \(\lambda \), and does not grow with \(Q,\delta ^{-1}\). Indeed, throughout this paper, \(Q,\delta ^{-1}\), will be arbitrary polynomials in \(\lambda \) that depend on the adversary. In our partition schemes, the representation of sets will only scale with \(\min \left\{ \log (Q/\delta ),n(\lambda )\right\} \).
- 5.
Recall that in a code with (relative) distance c, each two codewords agree on at most a c-fraction of symbols.
- 6.
The above distribution is not necessarily random over strings. In any natural instantiation of the group, e.g. as a prime order group for a large prime, or a composite group of smooth order, \(g^\beta \) is also random in the group \(\mathbb {G}\). In any case, and as usual, if one insists, on outputting a random string, we can further apply a randomness extractor (see for example, [43]).
- 7.
This is a weaker variant of the usual GDDH assumption where d may be polynomial (and the elements are given by an oracle). This weaker variant will be sufficient for us.
- 8.
For SXDH, DDH holds in the based groups. For DLIN, DDH holds in the target group. We thank Brent Waters for pointing out this last fact.
References
Abdalla, M., Catalano, D., Fiore, D.: Verifiable random functions: relations to identity-based key encapsulation and new constructions. J. Cryptol. 27(3), 544–593 (2014)
Badrinarayanan, S., Goyal, V., Jain, A., Sahai, A.: Verifiable functional encryption. In: Cheon, J.H., Takagi, T. (eds.) ASIACRYPT 2016. LNCS, vol. 10032, pp. 557–587. Springer, Heidelberg (2016). https://doi.org/10.1007/978-3-662-53890-6_19
Badrinarayanan, S., Goyal, V., Jain, A., Sahai, A.: A note on VRFs from verifiable functional encryption. Cryptology ePrint Archive 2017/051 (2017)
Barak, B., Ong, S.J., Vadhan, S.P.: Derandomization in cryptography. SIAM J. Comput. 37(2), 380–400 (2007)
Bellare, M., Ristenpart, T.: Simulation without the artificial abort: simplified proof and improved concrete security for waters’ IBE scheme. In: Joux, A. (ed.) EUROCRYPT 2009. LNCS, vol. 5479, pp. 407–424. Springer, Heidelberg (2009). https://doi.org/10.1007/978-3-642-01001-9_24
Bellare, M., Yung, M.: Certifying permutations: noninteractive zero-knowledge based on any trapdoor permutation. J. Cryptol. 9(3), 149–166 (1996)
Biham, E., Boneh, D., Reingold, O.: Breaking generalized Diffie-Hellmann modulo a composite is no easier than factoring. Inf. Process. Lett. 70(2), 83–87 (1999)
Bitansky, N., Paneth, O.: ZAPs and non-interactive witness indistinguishability from indistinguishability obfuscation. In: Dodis, Y., Nielsen, J.B. (eds.) TCC 2015. LNCS, vol. 9015, pp. 401–427. Springer, Heidelberg (2015). https://doi.org/10.1007/978-3-662-46497-7_16
Blum, M.: Coin flipping by telephone. In: IEEE Workshop on Communications Security Advances in Cryptology: A Report on CRYPTO 1981, Santa Barbara, California, USA, pp. 11–15, 24–26 August 1981
Blum, M., De Santis, A., Micali, S., Persiano, G.: Noninteractive zero-knowledge. SIAM J. Comput. 20(6), 1084–1118 (1991)
Boneh, D., Boyen, X.: Secure identity based encryption without random oracles. In: Franklin, M. (ed.) CRYPTO 2004. LNCS, vol. 3152, pp. 443–459. Springer, Heidelberg (2004). https://doi.org/10.1007/978-3-540-28628-8_27
Boneh, D., Montgomery, H.W., Raghunathan, A.: Algebraic pseudorandom functions with improved efficiency from the augmented cascade. In: Proceedings of the 17th ACM Conference on Computer and Communications Security, CCS 2010, Chicago, Illinois, USA, pp. 131–140, 4–8 October 2010
Boneh, D., Waters, B.: Constrained pseudorandom functions and their applications. In: Sako, K., Sarkar, P. (eds.) ASIACRYPT 2013. LNCS, vol. 8270, pp. 280–300. Springer, Heidelberg (2013). https://doi.org/10.1007/978-3-642-42045-0_15
Boneh, D., Zhandry, M.: Multiparty key exchange, efficient traitor tracing, and more from indistinguishability obfuscation. In: Garay, J.A., Gennaro, R. (eds.) CRYPTO 2014. LNCS, vol. 8616, pp. 480–499. Springer, Heidelberg (2014). https://doi.org/10.1007/978-3-662-44371-2_27
Boyle, E., Goldwasser, S., Ivan, I.: Functional signatures and pseudorandom functions. In: Krawczyk, H. (ed.) PKC 2014. LNCS, vol. 8383, pp. 501–519. Springer, Heidelberg (2014). https://doi.org/10.1007/978-3-642-54631-0_29
Brakerski, Z., Goldwasser, S., Rothblum, G.N., Vaikuntanathan, V.: Weak verifiable random functions. In: Reingold, O. (ed.) TCC 2009. LNCS, vol. 5444, pp. 558–576. Springer, Heidelberg (2009). https://doi.org/10.1007/978-3-642-00457-5_33
Brakerski, Z., Vaikuntanathan, V.: Constrained key-homomorphic PRFs from standard lattice assumptions. In: Dodis, Y., Nielsen, J.B. (eds.) TCC 2015. LNCS, vol. 9015, pp. 1–30. Springer, Heidelberg (2015). https://doi.org/10.1007/978-3-662-46497-7_1
Carter, L., Wegman, M.N.: Universal classes of hash functions. J. Comput. Syst. Sci. 18(2), 143–154 (1979)
Chandran, N., Raghuraman, S., Vinayagamurthy, D.: Constrained pseudorandom functions: verifiable and delegatable. Cryptology ePrint Archive, 2014/522 (2014)
Chase, M., Meiklejohn, S.: Déjà Q: using dual systems to revisit q-type assumptions. In: Nguyen, P.Q., Oswald, E. (eds.) EUROCRYPT 2014. LNCS, vol. 8441, pp. 622–639. Springer, Heidelberg (2014). https://doi.org/10.1007/978-3-642-55220-5_34
Dodis, Y.: Efficient construction of (distributed) verifiable random functions. In: Desmedt, Y.G. (ed.) PKC 2003. LNCS, vol. 2567, pp. 1–17. Springer, Heidelberg (2003). https://doi.org/10.1007/3-540-36288-6_1
Dodis, Y., Yampolskiy, A.: A verifiable random function with short proofs and keys. In: Vaudenay, S. (ed.) PKC 2005. LNCS, vol. 3386, pp. 416–431. Springer, Heidelberg (2005). https://doi.org/10.1007/978-3-540-30580-4_28
Dwork, C., Naor, M.: ZAPs and their applications. SIAM J. Comput. 36(6), 1513–1543 (2007)
Feige, U., Lapidot, D., Shamir, A.: Multiple noninteractive zero knowledge proofs under general assumptions. SIAM J. Comput. 29(1), 1–28 (1999)
Fiore, D., Schröder, D.: Uniqueness is a different story: impossibility of verifiable random functions from trapdoor permutations. In: Cramer, R. (ed.) TCC 2012. LNCS, vol. 7194, pp. 636–653. Springer, Heidelberg (2012). https://doi.org/10.1007/978-3-642-28914-9_36
Fuchsbauer, G.: Constrained verifiable random functions. In: Abdalla, M., Prisco, R. (eds.) SCN 2014. LNCS, vol. 8642, pp. 95–114. Springer, Cham (2014). https://doi.org/10.1007/978-3-319-10879-7_7
Goldreich, O., Goldwasser, S., Micali, S.: How to construct random functions. J. ACM 33(4), 792–807 (1986)
Goldreich, O., Rothblum, R.D.: Enhancements of trapdoor permutations. J. Cryptol. 26(3), 484–512 (2013)
Goldwasser, S., Ostrovsky, R.: Invariant signatures and non-interactive zero-knowledge proofs are equivalent. In: Brickell, E.F. (ed.) CRYPTO 1992. LNCS, vol. 740, pp. 228–245. Springer, Heidelberg (1993). https://doi.org/10.1007/3-540-48071-4_16
Gorbunov, S., Vaikuntanathan, V., Wee, H.: Functional encryption with bounded collusions via multi-party computation. In: Safavi-Naini, R., Canetti, R. (eds.) CRYPTO 2012. LNCS, vol. 7417, pp. 162–179. Springer, Heidelberg (2012). https://doi.org/10.1007/978-3-642-32009-5_11
Goyal, R., Hohenberger, S., Koppula, V., Waters, B.: A generic approach to constructing and proving verifiable random functions. Cryptology ePrint Archive 2017/21 (2017)
Groth, J., Ostrovsky, R., Sahai, A.: New techniques for noninteractive zero-knowledge. J. ACM 59(3), 11 (2012)
Hofheinz, D., Jager, T.: Verifiable random functions from standard assumptions. In: Kushilevitz, E., Malkin, T. (eds.) TCC 2016. LNCS, vol. 9562, pp. 336–362. Springer, Heidelberg (2016). https://doi.org/10.1007/978-3-662-49096-9_14
Hohenberger, S., Koppula, V., Waters, B.: Adaptively secure puncturable pseudorandom functions in the standard model. In: Iwata, T., Cheon, J.H. (eds.) ASIACRYPT 2015. LNCS, vol. 9452, pp. 79–102. Springer, Heidelberg (2015). https://doi.org/10.1007/978-3-662-48797-6_4
Hohenberger, S., Waters, B.: Constructing verifiable random functions with large input spaces. In: Gilbert, H. (ed.) EUROCRYPT 2010. LNCS, vol. 6110, pp. 656–672. Springer, Heidelberg (2010). https://doi.org/10.1007/978-3-642-13190-5_33
Jager, T.: Verifiable random functions from weaker assumptions. In: Dodis, Y., Nielsen, J.B. (eds.) TCC 2015. LNCS, vol. 9015, pp. 121–143. Springer, Heidelberg (2015). https://doi.org/10.1007/978-3-662-46497-7_5
Kiayias, A., Papadopoulos, S., Triandopoulos, N., Zacharias, T.: Delegatable pseudorandom functions and applications. In: Sadeghi, A.-R., Gligor, V.D., Yung, M. (eds.) 20th Conference on Computer and Communications Security, ACM CCS 2013, pp. 669–684. ACM Press, Berlin (2013)
Lysyanskaya, A.: Unique signatures and verifiable random functions from the DH-DDH separation. In: Yung, M. (ed.) CRYPTO 2002. LNCS, vol. 2442, pp. 597–612. Springer, Heidelberg (2002). https://doi.org/10.1007/3-540-45708-9_38
Micali, S., Rabin, M.O., Vadhan, S.P.: Verifiable random functions. In: 40th Annual Symposium on Foundations of Computer Science, FOCS 1999, New York, NY, USA, pp. 120–130, 17–18 October 1999
Miltersen, P.B., Vinodchandran, N.V.: Derandomizing Arthur-Merlin games using hitting sets. In: 40th Annual Symposium on Foundations of Computer Science, FOCS 1999, New York, NY, USA, pp. 71–80, 17–18 October 1999
Naor, M.: Bit commitment using pseudorandomness. J. Cryptol. 4(2), 151–158 (1991)
Naor, M., Reingold, O.: Synthesizers and their application to the parallel construction of pseudo-random functions. J. Comput. Syst. Sci. 58(2), 336–375 (1999)
Naor, M., Reingold, O.: Number-theoretic constructions of efficient pseudo-random functions. J. ACM 51(2), 231–262 (2004)
Sahai, A., Seyalioglu, H.: Worry-free encryption: functional encryption with public keys. In: Proceedings of the 17th ACM Conference on Computer and Communications Security, CCS 2010, Chicago, Illinois, USA, pp. 463–472, 4–8 October 2010
Sahai, A., Waters, B.: How to use indistinguishability obfuscation: deniable encryption, and more. In: Shmoys, D.B. (ed.) 46th Annual ACM Symposium on Theory of Computing, pp. 475–484. ACM Press, New York (2014)
Waters, B.: Efficient identity-based encryption without random oracles. In: Cramer, R. (ed.) EUROCRYPT 2005. LNCS, vol. 3494, pp. 114–127. Springer, Heidelberg (2005). https://doi.org/10.1007/11426639_7
Acknowledgements
Member of the Check Point Institute of Information Security. Supported by the Alon Young Faculty Fellowship. Part of this research was done while at MIT. Supported by NSF Grants CNS-1350619 and CNS-1414119 and DARPA and ARO under Contract No. W911NF-15-C-0236. Any opinions, findings and conclusions or recommendations expressed in this material are those of the author(s) and do not necessarily reflect the views of the DARPA and ARO. Part of this research was done while visiting Tel Aviv University and supported by the Leona M. & Harry B. Helmsley Charitable Trust and Check Point Institute for Information Security.
Author information
Authors and Affiliations
Corresponding author
Editor information
Editors and Affiliations
Rights and permissions
Copyright information
© 2017 International Association for Cryptologic Research
About this paper
Cite this paper
Bitansky, N. (2017). Verifiable Random Functions from Non-interactive Witness-Indistinguishable Proofs. In: Kalai, Y., Reyzin, L. (eds) Theory of Cryptography. TCC 2017. Lecture Notes in Computer Science(), vol 10678. Springer, Cham. https://doi.org/10.1007/978-3-319-70503-3_19
Download citation
DOI: https://doi.org/10.1007/978-3-319-70503-3_19
Published:
Publisher Name: Springer, Cham
Print ISBN: 978-3-319-70502-6
Online ISBN: 978-3-319-70503-3
eBook Packages: Computer ScienceComputer Science (R0)





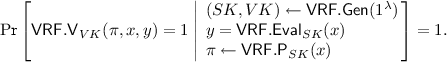
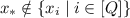 . We require that any polynomial-size admissible adversary wins the game with negligible advantage:
. We require that any polynomial-size admissible adversary wins the game with negligible advantage: 
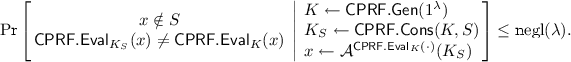
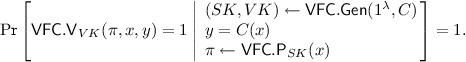
 , and a new set
, and a new set 