Optimal-Rate Non-Committing Encryption

Abstract

Non-committing encryption (NCE) was introduced in order to implement secure channels under adaptive corruptions in situations when data erasures are not trustworthy. In this paper we are interested in the rate of NCE, i.e. in how many bits the sender and receiver need to send per plaintext bit.

In initial constructions the length of both the receiver message, namely the public key, and the sender message, namely the ciphertext, is $m\cdot \mathrm {poly}(\lambda )$ for an m-bit message, where $\lambda$ is the security parameter. Subsequent work improve efficiency significantly, achieving rate $\mathrm {poly}\log (\lambda )$.

We show the first construction of a constant-rate NCE. In fact, our scheme has rate $1 + o(1)$, which is comparable to the rate of plain semantically secure encryption. Our scheme operates in the common reference string (CRS) model. Our CRS has size $\mathrm {poly}(m\cdot \lambda )$, but it is reusable for an arbitrary polynomial number of m-bit messages. In addition, ours is the first NCE construction with perfect correctness. We assume one way functions and indistinguishability obfuscation for circuits.

This work was done [in part] while the authors were visiting the Simons Institute for the Theory of Computing, supported by the Simons Foundation and by the DIMACS/Simons Collaboration in Cryptography through NSF grant #CNS-1523467.

R. Canetti—Supported in addition by the NSF MACS project and ISF Grant 1523/14. The author is a member of Check Point Institute for Information Security.

O. Poburinnaya—Supported in addition by the NSF MACS project and NSF grant 1421102.

M. Raykova—Supported by NSF grants 1421102, 1633282, 1562888, DARPA W911NF-15-C-0236, W911NF-16-1-0389.

1 Introduction

Informally, non-committing, or adaptively secure, encryption (NCE) is an encryption scheme for which it is possible to generate a dummy ciphertext which is indistinguishable from a real one, but can later be opened to any message [CFGN96]. This primitive is a central tool in building adaptively secure protocols: one can take an adaptively secure protocol in secure channels setting and convert it into adaptively secure protocol in computational setting by encrypting communications using NCE. In particular, NCE schemes are secure under selective-opening attacks [DNRS99].

This additional property of being able to open dummy ciphertexts to any message has its price in efficiency: while for plain semantically secure encryption we have constructions with $O(\lambda )$-size, reusable public and secret keys for security parameter $\lambda$, and $m+\mathrm {poly}(\lambda )$ size ciphertext for m-bit messages, non-committing encryption has been far from being that efficient. Some justification for this state of affairs is the lower bound of Nielsen [Nie02], which shows that the secret key of any NCE has to be at least m where m is the overall number of bits decrypted with this key. Still, no bound is known on the size of the public key or the ciphertext.

In this paper we focus on building NCE with better efficiency: specifically, we optimize the rate of NCE, i.e. the total amount of communication sent per single bit of a plaintext.

1.1 Prior Work

The first construction of adaptively secure encryption, presented by Beaver and Haber [BH92], is interactive (3 rounds) and relies on the ability of parties to reliably erase parts of their internal state. An adaptively secure encryption that does not rely on secure erasures, or non-committing encryption, is presented in [CFGN96]. The scheme requires only two messages, just like standard encryption, and is based on joint-domain trapdoor permutations. It requires both the sender and the receiver to send $\varTheta (\lambda ^2)$ bits per each bit of a plaintext. Subsequent work has focused on reducing rate and number of rounds. Beaver [Bea97] and Damgård and Nielsen [DN00] propose a 3-round NCE protocol from, respectively, DDH and a simulatable PKE (which again can be built from similar assumptions to those of [CFGN96]) with $m\,\cdot \,\varTheta (\lambda ^2)$ bits overall communication for m bit messages, but only $m\cdot \varTheta (\lambda )$ bits from sender to receiver. These results were improved by Choi et al. [CDMW09] who reduce the number of rounds to two, which matches optimal number of rounds since non-interactive NCE is impossible [Nie02]. Also they reduced simulatable PKE assumption to a weaker trapdoor simulatable PKE assumption; such a primitive can be constructed from factoring. A recent work of Hemenway et al. [HOR15] presented a two-round NCE construction based on the $\varPhi$-hiding assumption which has $\varTheta (m\log m)+\mathrm {poly}(\lambda )$ ciphertext size and $m\cdot \varTheta (\lambda )$ communication from receiver to sender. In a concurrent work, Hemenway et al. [HORR16] show how to build NCE with rate $\mathrm {poly}\log (\lambda )$ under the ring-LWE assumption.

We remark that the recent results on adaptively secure multiparty computation (MPC) from indistinguishability obfuscation in the common reference string (CRS) model [CGP15, GP15, DKR15] do not provide an improvement of NCE rate. Specifically, [CGP15, DKR15] already use NCE as a building block in their constructions, and the resulting NCE is as inefficient as underlying NCE. The scheme by Garg and Polychroniadou [GP15] does not use NCE, but their second message is of size $\mathrm {poly}(m\lambda )$ due to the statistically sound non-interactive zero knowledge proof involved.

Another line of work focuses on achieving better parameters for weaker notions of NCE where the adversary sees the internal state of only one of the parties (receiver or sender). Jarecki and Lysyanskaya [JL00] propose a scheme which is non-committing for the receiver only, which has two rounds and ciphertext expansion factor 3 (i.e., the ciphertext size is $3m+\mathrm {poly}(\lambda )$), under DDH assumption. Furthermore, their public key is also short and thus their scheme achieves rate 4. Hazay and Patra [HP14] build a constant-rate NCE which is secure as long as only one party is corrupted, which was later modified by [HLP15] to obtain a constant-rate NCE in the partial erasure model, meaning that security would hold even with both parties corrupted, as long as one party is allowed to erase. Canetti et al. [CHK05] construct a constant-rate NCE with erasures, meaning that the sender has to erase encryption randomness, and the receiver has to erase the randomness used for the initial key generation. Their NCE construction has rate 13.

1.2 Our Results

We present two NCE schemes with constant-rate in the programmable CRS model. We first present a simpler construction which gives us rate 13, and then, using more sophisticated techniques, we construct the second scheme with rate $1 + o(1)$.

Our first construction is given by a rate-preserving transformation from any NCE with erasures to full NCE, assuming indistinguishability obfuscation ($i\mathcal {O}$) and one way functions (OWFs). The known construction of constant-rate NCE with erasures [CHK05] requires decisional composite residuosity assumption and has rate 13.

Our second construction assumes only $i\mathcal {O}$ and OWFs and achieves rate $1 + o(1)$. To be more precise, the public key, which is the first protocol message in our scheme, has the size $O(\lambda )$. The ciphertext, which is the second message, has the size $O(\lambda ) + |m|$. The CRS size is $O(\mathrm {poly}(m\lambda ))$, but the CRS is reusable for any polynomially-many executions without an a priori bound on the number of executions. Thus when the length |m| of a plaintext is large, the scheme has overall rate that approaches 1.

In addition, this NCE scheme is the first to guarantee perfect correctness. Note that NCE in the plain model cannot be perfectly correct, and therefore some setup assumption is necessary to achieve this property.

1.3 Construction and Proof Techniques

Definition of NCE. Before describing our construction, we recall what a non-committing encryption is in more detail. Such a scheme consists of algorithms $(\mathsf {Gen}, \mathsf {Enc}, \mathsf {Dec}, \mathsf {Sim})$, which satisfy usual correctness and security requirements. Additionally, the scheme should remain secure even if the adversary first decides to see the communications in the protocol and later corrupt the parties. This means that the simulator should be able to generate a dummy ciphertext $c_f$ (without knowing which message it encrypts). Later, upon corruption of the parties, the simulator learns a message m, and it should generate internal state of the parties consistent with m and $c_f$ - namely, encryption randomness of the sender and generation randomness of the receiver.

First attempts and our first construction. Recall that the recent puncturing technique adds a special trapdoor to a program, which allows to “explain” any input-output behavior of a program, i.e. to generate randomness consistent with a given input-output pair [SW14, DKR15]. Given such a technique, we could try to build NCE as follows. Start from any rate-efficient non-committing encryption scheme in a model with erasures. Obfuscate key generation algorithm $\mathsf {Gen}$ and put it in the CRS. The protocol then proceeds as follows: the receiver runs $\mathsf {Gen}$, obtains (pk, sk), sends pk to the sender, gets back c and decrypts it with sk. In order to allow simulation of the receiver, augment $\mathsf {Gen}$ with a trapdoor which allows a simulator to come up with randomness for $\mathsf {Gen}$ consistent with (pk, sk). However, this approach doesn’t allow to simulate the sender.

One natural way to allow simulation of the sender is to modify $\mathsf {Gen}$: instead of outputting pk, it should output an obfuscated encryption algorithm $E = i\mathcal {O}(\mathsf {Enc}[pk])$ with the public key hardwired, and the receiver should send E (instead of pk) to the sender in round 1. In the simulation $\mathsf {Enc}[pk]$ can be augmented with a trapdoor, thus allowing to simulate the sender. The problem is that this scheme is no longer efficient: in all known constructions the trapdoor (and therefore the whole program E) has the size of at least $\lambda |m|$, meaning that the rate is at least $\lambda$ (this is due to the fact that this trapdoor uses a punctured PRF applied to the message m, and, to the best of our knowledge, in all known constructions of PPRFs the size of a punctured key is at least $\lambda |m|$).

Another attempt to allow simulation of the sender is to add to the CRS an obfuscated encryption program $E' = i\mathcal {O}(\mathsf {Enc}(pk, m, r))$, augmented with a trapdoor in the simulation. Just like in the initial scheme, the receiver should send pk to the sender; however, instead of computing c directly using pk, the sender should run obfuscated program $E'$ on pk, m and r. This scheme allows to simulate both the sender and the receiver, and at the same time keeps communication as short as in the original PKE. However, we can only prove selective security, meaning that the adversary has to commit to the challenge message m before it sees the CRS. This is a limitation of the puncturing technique being used: in the security proof the input to the program $\mathsf {Enc}$, including message m, has to be hardwired into the program.

We get around this issue by using another level of indirection, similar to the approach taken by [KSW14] to obtain adaptive security. Instead of publishing $E' = i\mathcal {O}(\mathsf {Enc}(pk, m, r))$ in the CRS, we publish a program $\mathsf {Gen}\mathsf {Enc}$ which generates $E'$ and outputs it. The protocol works as follows: the receiver uses $\mathsf {Gen}$ to generate (pk, sk) and sends pk to the sender. The sender runs $\mathsf {Gen}\mathsf {Enc}$ and obtains $E'$, and then executes $E'(pk, m, r) \rightarrow c$ and sends c back to the receiver. Note that $\mathsf {Gen}\mathsf {Enc}$ doesn’t take m as input, therefore there is no need to hardwire m into CRS and in particular there is no need to know m at the CRS generation step.

When this scheme uses [CHK05] as underlying NCE with erasures, it has rate 13. The scheme from [CHK05] additionally requires the decisional composite residuosity assumption.

Our second construction. We give another construction of NCE, which achieves nearly optimal rate. That is, the amount of bits sent is $|m| + \mathrm {poly}(\lambda )$, and by setting m to be long enough, we can achieve rate close to 1. The new scheme assumes only indistinguishability obfuscation and one-way functions; there is no need for composite residuosity, used in our previous scheme.

Our construction proceeds in two steps. We first construct a primitive which we call same-public-key non-committing encryption with erasures, or seNCE for short; essentially this is a non-committing encryption secure with erasures, but there is an additional technical requirement on public keys. Our seNCE scheme will have short ciphertexts, i.e. ciphertext size is $m+\mathrm {poly}(\lambda )$. However, the public keys will still be long, namely $\mathrm {poly}(m\lambda )$.

The second step in our construction is to transform any seNCE into a full NCE scheme such that the ciphertext size is preserved and the public key size depends only on security parameter. We achieve this at the cost of adding a CRS.

Same-public-key NCE with erasures (seNCE). As a first step we construct a special type of non-committing encryption which we can realize in the standard model (without a CRS). This NCE scheme has the following additional properties:

• security with erasures: the receiver is allowed to erase its generation randomness (but not sk); the sender is allowed to erase its encryption randomness. (This means that sk is the only information the adversary expects to see upon corrupting both parties.)

• same public key: the generation and simulation algorithms executed on the same input r produce the same public keys.

Construction of seNCE. The starting point for our seNCE construction is the PKE construction from $i\mathcal {O}$ by Sahai and Waters [SW14]. Similarly to that approach we set our public key to be an obfuscated program with a key k inside, which takes as inputs message m and randomness r and outputs a ciphertext $c = (c_1, c_2) = (\mathsf {prg}(r), \mathsf {F}_k(\mathsf {prg}(r)) \oplus m)$, where $\mathsf {F}$ is a pseudorandom function (PRF). However, instead of setting k to be a secret key, we set the secret key to be an obfuscated program (with k hardwired) which takes an input $c = (c_1, c_2)$ and outputs $\mathsf {F}_k(c_1) \oplus c_2$. Once the encryption and decryption programs are generated, the key k and the randomness used for the obfuscations are erased, and the only thing the receiver keeps is its secret key. Note that ciphertexts in the above scheme have length $m+\mathrm {poly}(\lambda )$.

To see that this construction is secure with erasures, consider the simulator that sets a dummy ciphertext $c_f$ to be a random value. To generate a fake decryption key $sk_f$, which behaves like a real secret key except that it decrypts $c_f$ to a challenge message m, the simulator obfuscates a program (with $m, c_f, k$ hardwired) that takes as input $(c_1, c_2)$ and does the following: if $c_1 = c_{f1}$ then the program outputs $c_{f2} \oplus c_2 \oplus m$, otherwise the output is $\mathsf {F}_k(c_1) \oplus c_2$. Encryption randomness of the sender, as well as k and obfuscation randomness of the receiver, are erased and do not need to be simulated. (Note that the simulated secret key is larger than the real secret key. So, to make sure that the programs have the same size, the real secret key has to be padded appropriately.)

Furthermore, the scheme has the same-public-key property: The simulated encryption key is generated in exactly the same way as the honest encryption key.

Note that this scheme has perfect correctness.

From seNCE to full NCE. Our first step is to enhance the given seNCE scheme, such that the scheme remains secure even when the sender is not allowed to erase its encryption randomness. Specifically, following ideas from the deniable encryption of Sahai and Waters [SW14], we add a trapdoor branch to the encryption program, i.e. the public key. This allows the simulator to create fake randomness $r_{f, \mathsf {Enc}}$, which activates this trapdoor branch and makes the program output $c_f$ on input m. In order to create such randomness, the simulator generates $r_{f, \mathsf {Enc}}$ as an encryption (using a scheme with pseudorandom ciphertexts¹) of an instruction for the program to output $c_f$. The program will first try to decrypt $r_{f, \mathsf {Enc}}$ and check whether it should output $c_f$ via trapdoor branch, or execute a normal branch instead.

The above construction of enhanced seNCE still has the following shortcomings. First, its public key (recall that it is an encryption program) is long: the program has to be padded to be at least of size $\mathrm {poly}(\lambda ) \cdot |m|$, since in the proof the keys for the trapdoor branch are punctured and have an increased size, and therefore the size of an obfuscated program is $\mathrm {poly}(m\lambda )$.² Second, the simulator still cannot simulate the randomness which the receiver used to generate its public key, e.g. keys for the trapdoor branch and randomness for obfuscation. Third, the scheme is only selectively secure, meaning that the adversary has to fix the message before it sees a public key. This is due to the fact that our way for explaining a given output (i.e. trapdoor branch mechanism) requires hardwiring the message inside the encryption program in the proof.

We resolve these issues by adding another “level of indirection” for the generation of obfuscated programs. Specifically, we introduce a common reference string that will contain two obfuscated programs, called $\mathsf {GenEnc}$ and $\mathsf {GenDec}$, which are generated independently of the actual communication of the protocol and can be reused for unboundedly many messages. The CRS allows the sender and the receiver to locally and independently generate their long public and private keys for the underlying enhanced seNCE while communicating only a short token. Furthermore, we will only need to puncture these programs at points which are unrelated to the actual encrypted and decrypted messages. The protocol proceeds as follows.

Description of our protocol. The receiver chooses randomness $r_{\mathsf {GenDec}}$ and runs a CRS program $\mathsf {GenDec}(r_{\mathsf {GenDec}})$. This program uses $r_{\mathsf {GenDec}}$ to sample a short token t. Next the program uses this token t to internally compute a secret generation randomness $r_\mathsf {seNCE}$, from which it derives (pk, sk) pair for underlying seNCE scheme. Finally, the program outputs (t, sk). In round 1 the receiver sends the token t (which therefore is a short public key of the overall NCE scheme) to the sender.

The sender generates its own randomness $r_{\mathsf {GenEnc}}$ and runs a CRS program $\mathsf {GenEnc}(t, r_{\mathsf {GenEnc}})$. $\mathsf {Gen}\mathsf {Enc}$, in the same manner as $\mathsf {GenDec}$, first uses t to generate secret $r_\mathsf {seNCE}$ and sample (the same) key pair (pk, sk) for the seNCE scheme. Further, $\mathsf {GenEnc}$ generates trapdoor keys and obfuscation randomness, which it uses to compute a public key program $\mathsf {P}_\mathsf {Enc}[pk]$ of enhanced seNCE, which extends the underlying seNCE public key with a trapdoor as described above. $\mathsf {P}_\mathsf {Enc}[pk]$ is the output of $\mathsf {GenEnc}$. After obtaining $\mathsf {P}_\mathsf {Enc}$, the sender chooses encryption randomness $r_{\mathsf {Enc}}$ and runs $c \leftarrow \mathsf {P}_\mathsf {Enc}[pk](m, r_{\mathsf {Enc}})$. In its response message, the sender sends c to the receiver, who decrypts it using sk.

Correctness of this scheme follows from correctness of the seNCE scheme, since at the end a message is being encrypted and decrypted using the seNCE scheme. To get some idea of why security holds, note that the seNCE generation randomness $r_\mathsf {seNCE}$ is only computed internally by the programs. This value is never revealed to the adversary, and therefore can be thought of as being “erased”. In particular, if we had a VBB obfuscation, we could almost immediately reduce security of our scheme to security of seNCE. Due to the fact that we only have $i\mathcal {O}$, the actual security proof becomes way more intricate.

To see how we resolved the three issues from above (namely, with the length of the public key, with simulating the receiver, and with selective security), note:

• (a) The only information communicated between sender and receiver is the short token t which depends only on the security parameter, and the ciphertext c which has size $\mathrm {poly}(\lambda ) + |m|$. Thus the total communication is $\mathrm {poly}(\lambda ) + |m|$.

• (b) The simulator will show slightly modified programs with trapdoor branches inside; they allow the simulator to “explain” the randomness for any desired output, thus allowing it to simulate internal state of both parties.

• (c) We no longer need to hardwire message-dependent values into the programs in the CRS, which previously made security only selective. Indeed, in a real world the inputs and outputs of these programs no longer depend on the message sent. They still do depend on the message in the ideal world (for instance, the output of $\mathsf {GenDec}$ is $sk_m$); however, due to the trapdoor branches in the programs it is possible for the simulator to encode $sk_m$ into randomness $r_\mathsf {GenDec}$ rather than the program $\mathsf {GenDec}$ itself. Therefore m can be chosen adaptively after seeing the CRS (and the public key).

To give more details about adaptivity issues which come up in the analysis of the simulator, let us look closely at the following three parts of the proof:

• Starting from a real execution, the first step is to switch real sender generation randomness $r_\mathsf {GenEnc}$ to fake randomness $r_{f, \mathsf {GenEnc}}$ (which “explains” a real output $\mathsf {P}_\mathsf {Enc}$). During this step we need to hardwire $\mathsf {P}_\mathsf {Enc}$ inside $\mathsf {GenEnc}$, which can be done, since $\mathsf {P}_\mathsf {Enc}$ doesn’t depend on m yet.

• Later in the proof we need to switch real encryption randomness $r_\mathsf {Enc}$ to fake randomness $r_{f, \mathsf {Enc}}$. During this step we need to hardwire m into $\mathsf {P}_\mathsf {Enc}$. However, at this point $\mathsf {P}_\mathsf {Enc}$ is not hardwired into the program $\mathsf {GenEnc}$; instead it is being encoded into randomness $r_\mathsf {GenEnc}$, and therefore it needs to be generated only when the sender is corrupted (which means that the simulator learns m and can create $\mathsf {P}_\mathsf {Enc}$ with m hardwired).

• Eventually we need to switch real seNCE values pk, c, sk to simulated $pk, c_f, sk_f$. Before we can do this, we have to hardwire pk into $\mathsf {GenEnc}$. Luckily, in the underlying seNCE game the adversary is allowed to choose m after it sees pk, and therefore the requirement to hardwire pk into the CRS program doesn’t violate adaptive security.

In the proof of our NCE we crucially use the same public-key property of underlying seNCE: Our programs use the master secret key MSK to compute the generation randomness $r_{\mathsf {seNCE}}$ from token t, and then sample seNCE keys (pk, sk) using this randomness. In the proof we hardwire pk in the CRS, then puncture $\mathsf {MSK}$ and choose $r_{\mathsf {seNCE}}$ at random. Next we switch the seNCE values, including the public key pk, to simulated ones. Then we choose $r_{\mathsf {seNCE}}$ as a result of a PRF, and unhardwire pk. In order to unhardwire (now simulated) pk from the program and compute $(pk, sk) = \mathsf {F}_\mathsf {MSK}(r_\mathsf {seNCE})$ instead, simulated pk generated from $r_{\mathsf {seNCE}}$ should be exactly the same as the real public key pk which the program normally produces by running $\mathsf {seNCE}.\mathsf {Gen}(r_{\mathsf {seNCE}})$. This ensures that the programs with and without pk hardwired have the same functionality, and thus security holds by $i\mathcal {O}$.

An additional interesting property of this transformation is that it preserves the correctness of underlying $\mathsf {seNCE}$ scheme, meaning that if seNCE is computationally (statistically, perfectly) correct, then the resulting NCE is also computationally (statistically, perfectly) correct. Therefore, when instantiated with our perfectly correct $\mathsf {seNCE}$ scheme presented earlier, the resulting $\mathsf {NCE}$ achieves perfect correctness. To the best of our knowledge, this is the first $\mathsf {NCE}$ scheme with such property.

Shrinking the secret key. The secret key in the above scheme consists of an obfuscated program D, where D is the secret key (i.e. decryption program) for the $\mathsf {seNCE}$ scheme, together with some padding that will leave room to “hardwire”, in the hybrid distributions in the proof of security, the |m|-bit plaintext m into D. Overall, the description size of D is $|m|+O(\lambda )$; when using standard IO, this means that the obfuscated version of D is of size $\mathrm {poly}(|m|\lambda )$.

Still, using the succinct Turing and RAM machine obfuscation of [KLW15, CHJV15, BGL+15, CH15] it is possible to obtain program obfuscation where the size of the obfuscated program is the size of the original program plus a polynomial in the security parameter. This can be done in a number of ways. One simple way is to generate the following (short) obfuscated TM machine OU: The input is expected to contain a description of a program that is one-time-padded, and then authenticated using a signed accumulator as in [KLW15], all with keys expanded from an internally known short key. The machine decrypts, authenticates, and then runs the input circuit. Now, to obfuscate a program, simply one time pad the program, authenticate it, and present it alongside machine OU with the authentication information and keys hardwired.

Augmented explainability compiler. In order to implement the trapdoor branch in the proof of our NCE scheme, we use among other things the “hidden sparse triggers” method of Sahai and Waters [SW14]. This method proved to be useful in other applications as well, and Dachman-Soled et al. [DKR15] abstracted it into a primitive called “explainability compiler”. Roughly speaking, explainability compiler turns a randomized program into its “trapdoored” version, such that it becomes possible, for those who know faking keys, to create fake randomness which is consistent with a given input-output pair.

We use a slightly modified version of this primitive, which we call an augmented explainability compiler. The difference here is that we can use the original (unmodified) program in the protocol, and only in the proof replace it with its trapdoor version. This is important for perfect correctness of NCE: none of the programs $\mathsf {GenEnc}$, $\mathsf {GenDec}$, and $\mathsf {Enc}$ in the real world contain trapdoor branches (indeed, if there was a trapdoor branch in, say, encryption program $\mathsf {Enc}$, it would be possible that an honest sender accidentally chooses randomness which contains an instruction to output an encryption of 0, making the program output this encryption of 0 instead of an encryption of m).

Organization. In Sect. 2 we define the different variants of non-committing encryption, as well as other primitives we use. In Sect. 3 we define and construct an augmented explainability compiler, used in the construction of our NCE. Our optimal-rate NCE and a sketch of security proof are described in Sect. 4.

2 Preliminaries

2.1 Non-committing Encryption and Its Variants

Non-committing encryption. Non-committing encryption is an adaptively secure encryption scheme, i.e., it remains secure even if the adversary decides to see the ciphertext first and only later corrupt parties. This means that the simulator should be able to first present a “dummy” ciphertext without knowing what the real message m is. Later, when parties are corrupted and the simulator learns m, the simulator should be able to present receiver decryption key (or receiver randomness) which decrypts dummy c to m and sender randomness under which m is encrypted to c.

Definition 1

A non-committing encryption scheme for a message space $M = \left\{ 0,1\right\} ^l$ is a tuple of algorithms $(\mathsf {Gen}, \mathsf {Enc}, \mathsf {Dec}, \mathsf {Sim})$, such that correctness and security hold:

• Correctness: For all $m \in M$

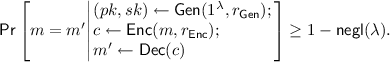
• Security: An adversary cannot distinguish between real and simulated ciphertexts and internal state even if it chooses message m adaptively depending on the public key pk. More concretely, no PPT adversary $\mathcal {A}$ can win the following game with more than negligible advantage:

A challenger chooses random $b \in \left\{ 0, 1\right\}$. If $b = 0$, it runs the following experiment (real):

• 1. It chooses randomness $r_{\mathsf {Gen}}$ and creates $(pk, sk) \leftarrow \mathsf {Gen}(1^\lambda , r_{\mathsf {Gen}})$. It shows pk to the adversary.

• 2. The adversary chooses message m.

• 3. The challenger chooses randomness $r_{\mathsf {Enc}}$ and creates $c \leftarrow \mathsf {Enc}(pk, m; r_{\mathsf {Enc}})$. It shows $(c, r_{\mathsf {Enc}}, r_{\mathsf {Gen}})$ to the adversary.

If $b = 1$, the challenger runs the following experiment (simulated):

• 1. It runs $(pk^s, c^s) \leftarrow \mathsf {Sim}(1^\lambda )$. It shows $pk^s$ to the adversary.

• 2. The adversary chooses message m.

• 3. The challenger runs $(r^s_{\mathsf {Enc}}, r^s_{\mathsf {Gen}}) \leftarrow \mathsf {Sim}(m)$ and shows $(c^s, r^s_{\mathsf {Enc}}, r^s_{\mathsf {Gen}})$ to the adversary.

The adversary outputs a guess $b'$ and wins if $b = b'$.

Note that we allow $\mathsf {Sim}$ to be interactive, and in addition we omit its random coins.

In this definition we only spell out the case where both parties are corrupted, and all corruptions happen after the execution and simultaneously. Indeed, if any of the parties is corrupted before the ciphertext is sent, then the simulator learns m and can present honest execution of the protocol; therefore we concentrate on the case where corruptions happen afterwards. Next, m is the only information the simulator needs, and after learning it (regardless of which party was corrupted) the simulator can already simulate both parties; thus we assume that corruptions of parties happen simultaneously. Finally, without loss of generality we assume that both parties are corrupted: if only one or no party is corrupted, then the adversary sees strictly less information in the experiment, and therefore cannot distinguish between real execution and simulation, as long as the scheme is secure under our definition.

Note that this definition only allows parties to encrypt a single message under a given public key. This is due to impossibility result of Nielsen [Nie02], who showed that a secret key of any NCE can support only bounded number of ciphertexts. If one needs to send many messages, it can run several instances of a protocol (each with a fresh pair of keys). Security for this case can be shown via a simple hybrid argument.

Non-committing encryption in a programmable common reference string model. In this work we build NCE in a CRS model, meaning that both parties and the adversary are given access to a CRS, and the simulator, in addition to simulating communications and parties’ internal state, also has to simulate the CRS. Before giving a formal definition, we briefly discuss possible variants of this definition.

Programmable CRS. One option is to consider a global (non-programmable) CRS model, where the CRS is given to the simulator, or local (programmable) CRS model, where the simulator is allowed to generate a CRS. The first variant is stronger and more preferable, but in our construction the simulator needs to know underlying trapdoors and we therefore focus on a weaker definition.

Reusable CRS. Given the fact that in a non-committing encryption a public key can be used to send only bounded number of bits, a bounded-use CRS would force parties to reestablish CRS after sending each block of messages. Since sampling a CRS is usually an expensive operation, it is good to be able to generate a CRS which can be reused for any number of times set a priori. It is even better to have a CRS which can be reused any polynomially many times without any a priori bound. In our definition we ask a CRS to be reusable in this stronger sense.

Security of multiple executions. Unlike NCE in the standard model, in the CRS model single-execution security of NCE does not immediately imply multi-execution security. Indeed, in a reduction to a single-execution security we would have to, given a challenge and a CRS, simulate other executions. But we cannot do this since we didn’t generate this CRS ourselves and do not know trapdoors. Therefore in our definition we explicitly require that the protocol remains secure even when the adversary sees many executions with the same CRS.

Definition 2

An NCE scheme for a message space $M = \left\{ 0,1\right\} ^l$ in a common reference string model is a tuple of algorithms $(\mathsf {GenCRS}, \mathsf {Gen},$ $\mathsf {Enc}, \mathsf {Dec}, \mathsf {Sim})$ which satisfy correctness and security.

Correctness: For all $m \in M$

If this probability is equal to 1, then we say that the scheme is perfectly correct.³

Security: For any PPT adversary $\mathcal {A}$, advantage of $\mathcal {A}$ in distinguishing the following two cases is negligible:

A challenger chooses random $b \in \left\{ 0, 1\right\}$. If $b = 0$, it runs the following experiment (real):

First it generates a CRS as $\mathsf {CRS}\leftarrow \mathsf {GenCRS}(1^\lambda , l)$. $\mathsf {CRS}$ is given to the adversary. Next the challenger does the following, depending on the adversary’s request:

• On a request to initiate a protocol instance with session ID $\mathsf {id}$, the challenger chooses randomness $r_{\mathsf {Gen}, \mathsf {id}}$ and creates $(pk_\mathsf {id}, sk_\mathsf {id}) \leftarrow \mathsf {Gen}(1^\lambda , \mathsf {CRS}, r_{\mathsf {Gen}, \mathsf {id}})$. It shows $pk_\mathsf {id}$ to the adversary.

• On a request to encrypt a message $m_\mathsf {id}$ in a protocol instance with session ID $\mathsf {id}$, the challenger chooses randomness $r_{\mathsf {Enc}, \mathsf {id}}$ and creates $c_\mathsf {id}\leftarrow \mathsf {Enc}(pk_\mathsf {id}, m_\mathsf {id}; r_{\mathsf {Enc}, \mathsf {id}})$. It shows $c_\mathsf {id}$ to the adversary.

• On a request to corrupt the sender of a protocol instance with ID $\mathsf {id}$, the challenger shows $r_{\mathsf {Enc}, \mathsf {id}}$ to the adversary.

• On a request to corrupt the receiver of a protocol instance with ID $\mathsf {id}$, the challenger shows $r_{\mathsf {Gen}, \mathsf {id}}$ to the adversary.

If $b = 1$, it runs the following experiment (simulated):

First it generates a CRS as $\mathsf {CRS}^s \leftarrow \mathsf {Sim}(1^\lambda , l)$. $\mathsf {CRS}^s$ is given to the adversary. Next the challenger does the following, depending on the adversary’s request:

• On a request to initiate a protocol instance with session ID $\mathsf {id}$, the challenger runs $(pk^s_\mathsf {id}, c^s_\mathsf {id}) \leftarrow \mathsf {Sim}(1^\lambda )$ and shows $pk_\mathsf {id}^s$ to the adversary.

• On a request to encrypt a message $m_\mathsf {id}$ in a protocol instance with session ID $\mathsf {id}$, the challenger shows $c^s_\mathsf {id}$ to the adversary.

• On a request to corrupt the sender of a protocol instance with ID $\mathsf {id}$, the challenger shows $r^s_{\mathsf {Enc}, \mathsf {id}} \leftarrow \mathsf {Sim}(m_\mathsf {id})$ to the adversary.

• On a request to corrupt the receiver of a protocol instance with ID $\mathsf {id}$, the challenger shows $r^s_{\mathsf {Gen}, \mathsf {id}}\leftarrow \mathsf {Sim}(m_\mathsf {id})$ to the adversary.

The adversary outputs a guess $b'$ and wins if $b = b'$.

Constant rate NCE. The rate of an NCE scheme is how many bits the sender and receiver need to communicate in order to transmit a single bit of a plaintext: NCE scheme for a message space $M = \left\{ 0, 1\right\} ^l$ has rate $f(l, \lambda )$, if $(|pk| + |c|) / l = f(l, \lambda )$. If $f(l, \lambda )$ is a constant, the scheme is said to have constant rate.

Same-public-key non-committing encryption with erasures (seNCE). Here we define a different notion of NCE which we call same-public-key non-committing encryption with erasures (seNCE). First, such a scheme allows parties to erase unnecessary information: the sender is allowed to erase its encryption randomness, and the receiver is allowed to erase its generation randomness $r_{\mathsf {Gen}}$ (but not its public or secret key). Furthermore, this scheme should have “the same public key” property, which says that both real generation and simulated generation algorithms should output exactly the same public key pk, if they are executed with the same random coins.

Definition 3

The same-public-key non-committing encryption with erasures (seNCE) for a message space $M = \left\{ 0,1\right\} ^l$ is a tuple of algorithms $(\mathsf {Gen}, \mathsf {Enc}, \mathsf {Dec}, \mathsf {Sim})$, such that correctness, security, and the same-public-key property hold:

• Correctness: For all $m \in M$

• Security with erasures: No PPT adversary $\mathcal {A}$ can win the following game with more than negligible advantage:

  A challenger chooses random $b \in \left\{ 0, 1\right\}$. If $b = 0$, it runs a real experiment:

  • 1. The challenger chooses randomness $r_{\mathsf {Gen}}$ and creates $(pk, sk) \leftarrow \mathsf {Gen}(1^\lambda , r_{\mathsf {Gen}})$. It shows pk to the adversary.

  • 2. The adversary chooses a message m.

  • 3. The challenger chooses randomness $r_{\mathsf {Enc}}$ and creates $c \leftarrow \mathsf {Enc}(pk, m; r_{\mathsf {Enc}})$. It shows c to the adversary.

  • 4. Upon corruption request, the challenger shows to the adversary the secret key sk.

  If $b = 1$, the challenger runs a simulated experiment:

  • 1. A challenger generates simulated public key and ciphertext $(pk^s, c^s) \leftarrow \mathsf {Sim}(1^\lambda )$⁴. It shows $pk^s$ to the adversary.

  • 2. The adversary chooses a message m.

  • 3. The challenger shows the ciphertext $c^s$ to the adversary.

  • 4. Upon corruption request, the challenger runs $sk^s \leftarrow \mathsf {Sim}(m)$ and shows to the adversary simulated secret key $sk^s$.

  The adversary outputs a guess $b'$ and wins if $b = b'$.

• The same public key: For any r if $\mathsf {Gen}(1^\lambda , r) = (pk, sk); \mathsf {Sim}(1^\lambda , r) = (pk_f, c_f)$, then $pk = pk_f$.

2.2 Puncturable Pseudorandom Functions and Their Variants

Puncturable PRFs. In puncrurable PRFs it is possible to create a key that is punctured at a set S of polynomial size. A key k punctured at S (denoted $k\{S\}$) allows evaluating the PRF at all points not in S. Furthermore, the function values at points in S remain pseudorandom even given $k\{S\}$.

Definition 4

A puncturable pseudorandom function family for input size $n(\lambda )$ and output size $m(\lambda )$ is a tuple of algorithms $\{ \mathsf {Sample}, \mathsf {Puncture}, \mathsf {Eval}\}$ such that the following properties hold:

• Functionality preserved under puncturing: For any PPT adversary A which outputs a set $S \subset \left\{ 0, 1\right\} ^n$, for any $x \not \in S$,

  $$\begin{aligned} \mathsf {Pr}[F_k(x) = F_{k\{S\}}( x) : k \leftarrow \mathsf {Sample}(1^\lambda ), k\{S\} \leftarrow \mathsf {Puncture}(k, S)] = 1. \end{aligned}$$

• Pseudorandomness at punctured points: For any PPT adversaries $A_1, A_2$, define a set S and state $\mathsf {state}$ as $(S, \mathsf {state}) \leftarrow A_1(1^\lambda )$. Then

  $$\begin{aligned} \mathsf {Pr}[A_2(\mathsf {state}, S, k\{S\}, F_k(S))] - \mathsf {Pr}[A_2(\mathsf {state}, S, k\{S\}, U_{|S| \cdot m(\lambda )})] < \mathsf {negl}(\lambda ), \end{aligned}$$

  where $F_k(S)$ denotes concatenated PRF values on inputs from S, i.e. $F_k(S) = \{ F_k(x_i) : x_i \in S\}$.

The GGM PRF [GGM84] satisfies this definition.

Statistically injective puncturable PRFs. Such PRFs are injective with overwhelming probability over the choice of a key. Sahai and Waters [SW14] show that if $\mathsf {F}$ is a puncturable PRF where the output length is large enough compared to the input length, and h is 2-universal hash function, then $\mathsf {F}'_{k, h} = \mathsf {F}_k(x) \oplus h(x)$ is a statistically injective puncturable PRF.

Extracting puncturable PRFs. Such PRFs have a property of a strong extractor: even when a full key is known, the output of the PRF is statistically close to uniform, as long as there is enough min-entropy in the input. Sahai and Waters [SW14] showed that if the input length is large enough compared to the output length, then such PRF can be constructed from any puncturable PRF $\mathsf {F}$ as $\mathsf {F}'_{k, h} = h(\mathsf {F}_k(x))$, where h is 2-universal hash function.

3 Augmented Explainability Compiler

In this section we describe a variant of an explainability compiler of [DKR15]. This compiler is used in our construction of NCE, as discussed in the introduction.

Roughly speaking, explainability compiler modifies a randomized program such that it becomes possible, for those who know faking keys, to create fake randomness $r_f$ which is consistent with a given input-output pair. Explainability techniques were first introduced by Sahai and Waters [SW14] as a method to obtain deniability for encryption (there they were called “a hidden sparse trigger meachanism”). Later Dachman-Soled, Katz and Rao [DKR15] generalized these ideas and introduced a notion of explainability compiler.

We modify this primitive for our construction and call it an “augmented explainability compiler”. Before giving a formal definition, we briefly describe it here. Such a compiler $\mathsf {Comp}$ takes a randomized algorithm $\mathsf {Alg}(input; u)$ with input input and randomness u and outputs three new algorithms:

• $\mathsf {Comp}.\mathsf {Rerand}(\mathsf {Alg})$ outputs a new algorithm ${\mathsf {Alg}'}(input; r)$ which is a “rerandomized” version of $\mathsf {Alg}$. Namely, $\mathsf {Alg}'$ first creates fresh randomness u using a PRF on input (input, r) and then runs $\mathsf {Alg}$ with this fresh randomness u.

• $\mathsf {Comp}.\mathsf {Trapdoor}(\mathsf {Alg})$ outputs a new algorithm ${\mathsf {Alg}''}(input; r)$ which is a “trapdoored” version of $\mathsf {Alg}'$, which allows to create randomness consistent with a given output: namely, before executing $\mathsf {Alg}'$, $\mathsf {Alg}''$ interprets its randomness r as a ciphertext and tries to decrypt it using internal key. If it succeeds and r encrypts an instruction to output output, then $\mathsf {Alg}''$ complies. Otherwise it runs $\mathsf {Alg}'$.

• $\mathsf {Comp}.\mathsf {Explain}(\mathsf {Alg})$ outputs a new algorithm $\mathsf {Explain}(input, output)$ which outputs randomness for algorithm $\mathsf {Alg}''$ consistent with given input and output. It uses an internal key to encrypt an instruction to output output on an input input, and outputs the resulting ciphertext.

Definition 5

An augmented explainability compiler $\mathsf {Comp}$ is an algorithm which takes as input algorithm $\mathsf {Alg}$ and randomness and outputs programs $\mathsf {P}_\mathsf {Rerand}, \mathsf {P}_\mathsf {Trapdoor}, \mathsf {P}_\mathsf {Explain}$, such that the following properties hold:

• Indistinguishability of the source of the output. For any input it holds that

  $$\begin{aligned} \{ (\mathsf {P}_\mathsf {Trapdoor}, \mathsf {P}_\mathsf {Explain}, output): r \leftarrow U, output \leftarrow \mathsf {Alg}(input; r)\} \end{aligned}$$

  and

  $$\begin{aligned} \{ (\mathsf {P}_\mathsf {Trapdoor}, \mathsf {P}_\mathsf {Explain}, output): r \leftarrow U, output \leftarrow \mathsf {P}_\mathsf {Trapdoor}(input; r)\} \end{aligned}$$

  are indistinguishable.

• Indistinguishability of programs with and without a trapdoor. $\mathsf {P}_\mathsf {Rerand}$ and $\mathsf {P}_\mathsf {Trapdoor}$ are indistinguishable.

• Selective explainability. Any PPT adversary has only negligible advantage in winning the following game:

  • 1. Adv fixes an input $input^*$;

  • 2. The challenger runs $\mathsf {P}_{\mathsf {Rerand}}, \mathsf {P}_{\mathsf {Trapdoor}}, \mathsf {P}_{\mathsf {Explain}} \leftarrow \mathsf {Comp}(\mathsf {Alg})$;

  • 3. It chooses random $r^*$ and computes $output^* \leftarrow \mathsf {P}_{\mathsf {Trapdoor}}(input^*; r^*)$;

  • 4. It chooses random $\rho$ and computes fake $r^*_f \leftarrow \mathsf {P}_{\mathsf {Explain}}(input^*, output^*; \rho )$

  • 5. It chooses random bit b. If $b = 0$, it shows $(\mathsf {P}_{\mathsf {Trapdoor}}, \mathsf {P}_{\mathsf {Explain}}, output^*, r^*)$, else it shows $(\mathsf {P}_{\mathsf {Trapdoor}}, \mathsf {P}_{\mathsf {Explain}}, output^*, r^*_f)$

  • 6. Adv outputs $b'$ and wins if $b = b'$.

Differences between [DKR15] compiler and our construction. For the reader familiar with [SW14, DKR15], we briefly describe the differences.

First, we split compiling procedure into two parts: the first part, rerandomization, adds a PRF to the program $\mathsf {Alg}$, such that the program uses randomness $\mathsf {F}(input, r)$ instead of r. The second part adds a trapdoor branch to rerandomized program. This is done for a cleaner presentation of the proof.

Second, we slightly change a trapdoor branch activation mechanism: together with faking keys we hardwire an image S of a pseudorandom generator into the program. Whenever this program decrypts fake r, it follows instructions inside r only if these instructions contain a correct preimage of S. This trick allows us to first change S to random and then to indistinguishably “delete” the whole trapdoor branch from the program. Thus it becomes possible to use a program without a trapdoor in the protocol (and only in the proof change it to its trapdoor version), which is crucial for achieving perfect correctness.

Fig. 1.

Explainability compiler and programs used.

Construction. Our explainability compiler is described in Fig. 1. It takes as input algorithm $\mathsf {Alg}$ and randomness r. It uses r to sample keys $\mathsf {Ext}$ (for an extracting PRF), f (for a special encryption scheme called puncturable deterministic encryption, or $\mathsf {PDE}$[SW14]), as well as random s, and randomness for $i\mathcal {O}$. It sets $S = \mathsf {prg}(s)$. Then it obfuscates programs $\mathsf {Rerand}[\mathsf {Alg}, \mathsf {Ext}]$, $\mathsf {Trapdoor}[\mathsf {Alg}, \mathsf {Ext}, f, S]$, and $\mathsf {Explain}[f, s]$. It outputs these programs.

Theorem 1

Algorithm $\mathsf {Comp}$ presented in Fig. 1 is an augmented explainability compiler.

The proof of security can be found in the full version of the paper.

4 Optimal-Rate Non-committing Encryption in the CRS Model

In this section we show how to construct a fully non-committing encryption with rate $1+o(1)$. A crucial part of our protocol is the underlying seNCE scheme with short ciphertexts, which we will transform into a full NCE in Sect. 4.2.

4.1 Same-Public-Key Non-committing Encryption with Erasures

In this section we present our construction of the same-public-key non-committing encryption with erasures (seNCE for short) (defined in Sect. 2, Definition 3), which is a building block in our construction of a full fledged NCE.

Fig. 2.

seNCE protocol

Inspired by Sahai and Waters [SW14] way of converting a secret key encryption scheme into a public-key encryption, we set our public key to be an obfuscated encryption algorithm $pk = i\mathcal {O}(\mathsf {Enc}[k])$ (see Fig. 2). To allow the simulator to generate a fake secret key, we apply the same trick to the secret key: we set the secret key to be an obfuscated decryption algorithm with hardcoded PRF key, namely $sk = i\mathcal {O}(\mathsf {Dec}[k])$. In other words, the seNCE protocol proceeds as follows: the receiver generates the obfuscated programs pk, sk and then erases generation randomness, including the key k. Then it sends pk to the sender; the sender encrypts its message m, erases his encryption randomness, and sends back the resulting ciphertext c, which the receiver decrypts with sk. We present the detailed description of the seNCE protocol in Fig. 2.

Theorem 2

The scheme given on Fig. 2 is the same-public-key non-committing encryption scheme with erasures, assuming indistinguishability obfuscation for circuits and one way functions. In addition, it has ciphertexts (the second message in the protocol) of size $\mathrm {poly}(\lambda ) + |m|$.The protocol is also perfectly correct.

Proof

We show that the scheme from Fig. 2. is a seNCE and has short ciphertexts.

Perfect correctness. The underlying secret key encryption scheme is perfectly correct, since $\mathsf {Dec}(\mathsf {Enc}(m, r)) = \mathsf {F}_k(c_1) \oplus (\mathsf {F}_k(c_1) \oplus m) = m$. Due to perfect correctness of $i\mathcal {O}$, our seNCE protocol is also perfectly correct.

Security with erasures: We need to show that real and simulated pk, c, sk are indistinguishable, even when the adversary can choose m adaptively after seeing pk.

• 1. Real experiment. In this experiment $\mathsf {P}_{\mathsf {Enc}}$ and $\mathsf {P}_{\mathsf {Dec}}$ are generated honestly using $\mathsf {Gen}$, $c^*$ is a ciphertext encrypting $m^*$ with randomness $r^*$, i.e. $c_1^* = \mathsf {prg}(r^*)$, $c_2^* = F_k(c_1^*) \oplus m^*$.

• 2. Hybrid 1. In this experiment $c_1^*$ is generated at random instead of $\mathsf {prg}(r^*)$. Indistinguishability from the previous hybrid follows by security of the PRG.

• 3. Hybrid 2. In this experiment we puncture key k in both programs $\mathsf {Enc}$ and $\mathsf {Dec}$, more specifically, we obfuscate programs $\mathsf {P}_{\mathsf {Enc}} = i\mathcal {O}(\mathsf {Enc}$:$1[k\{c_1^*\}])$, $\mathsf {P}_{\mathsf {Dec}} = i\mathcal {O}(\mathsf {SimDec}[k\{c_1^*\},$ $c^*, m^*])$. We claim that functionality of these programs is the same as that of $\mathsf {Enc}$ and $\mathsf {Dec}$:

  Indeed, in $\mathsf {Enc}$:1 (defined in Fig. 4), $c_1^*$ is random and thus with high probability it is outside the image of the PRG; therefore no input r results in evaluating $\mathsf {F}$ at the punctured point $c_1^*$, and we can puncture safely. In $\mathsf {SimDec}$ (defined in Fig. 3), if $c_1 \ne c_1^*$, then the program behaves exactly like the original one (i.e. computes $F_k(c_1) \oplus c_2$); if $c_1 = c_1^*$, then $\mathsf {SimDec}$ outputs $c_2^* \oplus c_2 \oplus m = (F_k(c_1^*) \oplus m) \oplus c_2 \oplus m = F_k(c_1^*) \oplus c_2$, which is exactly what $\mathsf {Dec}$ outputs when $c_1 = c_1^*$. Note that $c_1^*$ is random (and thus independent of m), therefore $\mathsf {pk}= \mathsf {Enc}$:$1[k\{c_1^*\}]$ can be generated before the message $m^*$ is fixed.

  Indistinguishability from the previous hybrid follows by the security of $i\mathcal {O}$.

• 4. Hybrid 3. In this hybrid we switch $c_2^*$ from $\mathsf {F}_k(c_1^*) \oplus m^*$ to random. This hybrid relies on the indistinguishability between punctured value $F_k(c_1^*)$ and a truly random value, even given a punctured key $k\{c_1^*\}$.

  Indeed, to reconstruct this hybrid, first choose random $c_1^*$ and get $k\{c_1^*\}$ and $val^*$ (which is either random or $F_k(c_1^*)$) from the PPRF challenger. Show obfuscated $\mathsf {Enc}:1[k\{c_1^*\}]$ as a public key. When the adversary fixes message $m^*$, set $c_2^* = val^* \oplus m^*$ and upon corruption show obfuscated $\mathsf {SimDec}[k\{c_1^*\}, c^*, m^*]$. If $val^*$ is truly random, then $c_2^* = val^* \oplus m^*$ is distributed uniformly and thus we are in hybrid 3. If $val^*$ is the actual PRF value, then $c_2^* = F_k(c_1^*) \oplus m^*$ and we are in hybrid 2.

  Indistinguishability holds by security of a punctured PRF.

• 5. Hybrid 4 (Simulation). In this hybrid we unpuncture the key k in both programs and show $\mathsf {P}_{\mathsf {Enc}} \leftarrow i\mathcal {O}(\mathsf {Enc}[k])$, $\mathsf {P}_{\mathsf {Dec}} \leftarrow i\mathcal {O}(\mathsf {SimDec}[k, c^*, m^*])$.

  This is without changing the functionality of the programs: Indeed, in $\mathsf {Enc}$ no random input r results in $\mathsf {prg}(r) = c_1^*$, thus we can remove the puncturing. In $\mathsf {Dec}$:1 due to preceding “if” no input c causes evaluation of $F_{k\{c_1^*\}}$, thus we can unpuncture it as well.

  The indistinguishability from the previous hybrid follows by the security if the $i\mathcal {O}$.

Fig. 3.

seNCE simulator.

Fig. 4.

Program Enc:1 used in the proof.

We observe that the last hybrid is indeed the simulation experiment described in Fig. 3: $c^*$ is a simulated ciphertext since $c_1^*$ is random, $c_2^* = \mathsf {F}_k(c_1^*)$, $\mathsf {P}_{\mathsf {Enc}}$ is honestly generated, and $\mathsf {P}_{\mathsf {Dec}}$ is a simulated key $\mathsf {SimDec}[k, c^*, m^*]$, which decrypts $c^*$ to $m^*$. Thus, we have shown that this scheme is non-committing with erasures.

The same public key. Both real generation algorithm $\mathsf {Gen}$ and the simulator on randomness $r_{\mathsf {Gen}} = (r_1, r_2, r_3)$ produce exactly the same public key $pk = i\mathcal {O}(Enc[r_1]; r_2)$.

Efficiency: Our PRG should be length-doubling to ensure that its image is sparse. Thus $|c_1| = 2\lambda$, and $|c_2| = |m|$. Thus the size of our ciphertext is $2\lambda + |m|$.

4.2 From seNCE to Full NCE

In this section we show how to transform any seNCE (for instance, seNCE constructed in Sect. 4.1) into full non-committing encryption in the CRS model. We start with a brief overview of the construction:

Construction. Our CRS contains algorithms $\mathsf {Comp}.\mathsf {Rerand}(\mathsf {GenEnc})$ and $\mathsf {Comp}.\mathsf {Rerand}$ $(\mathsf {GenDec})$ which share master secret key $\mathsf {MSK}$. Both programs can internally generate the parameters for the underlying seNCE scheme using their $\mathsf {MSK}$ and then output an encryption program or a decryption key. More specifically, $\mathsf {GenDec}$ takes a random input, produces generation token t and then uses this token and $\mathsf {MSK}$ to generate randomness $r_{\mathsf {NCE}}$ for $\mathsf {seNCE}.\mathsf {Gen}$. Then the program samples $\mathsf {seNCE}$ keys pk, sk from $r_\mathsf {NCE}$. It outputs the token t and the generated decryption key sk for a seNCE scheme. The receiver keeps sk for itself and sends the token t to the sender.

$\mathsf {GenEnc}$, given a token t, can produce (the same) pair (pk, sk) and outputs an algorithm $\mathsf {Comp}.\mathsf {Rerand}(\mathsf {Enc}_{pk})$, which has pk hardwired. This algorithm takes a message m and outputs its encryption c, which the sender sends back to the receiver. Then receiver decrypts it using sk.

We present our full NCE protocol and its building block functions $\mathsf {GenEnc}$, $\mathsf {GenDec}$, $\mathsf {Enc}$ in Fig. 5.

Fig. 5.

The NCE protocol.

Theorem 3

Assuming $\mathsf {Comp}$ is a secure explainability compiler, $\mathsf {seNCE}$ is a secure same-public-key NCE with erasures with a ciphertext size $O(\mathrm {poly}(\lambda )) + m$, and assuming one-way functions, the described construction is a constant-rate non-committing public key encryption scheme in a common reference string model. Assuming perfect correctness of underlying $\mathsf {seNCE}$ and $\mathsf {Comp}$, our NCE scheme is also perfectly correct.

4.3 Proof of the Theorem 3

Proof

We first show correctness of the scheme. Next we present a simulator and argue that the scheme is secure. Finally we argue that the scheme is constant-rate.

Correctness. The presented scheme is perfectly correct, as long as the underlying $\mathsf {seNCE}$ and $\mathsf {Comp}$ are perfectly correct: First, due to perfect correctness of $\mathsf {Comp}$, using compiled versions $\mathsf {Comp}.\mathsf {Rerand}(\mathsf {GenEnc})$, $\mathsf {Comp}.\mathsf {Rerand}(\mathsf {GenDec})$, $\mathsf {Comp}.\mathsf {Rerand}(\mathsf {Enc})$ is as good as the using original programs. Next, both the sender and receiver generate public and secret $\mathsf {seNCE}$ keys as $(pk, sk) \leftarrow \mathsf {seNCE}.\mathsf {Gen}(F_{\mathsf {MSK}}(t))$. The sender also generates c, which is an encryption of m under pk, which is decrypted under sk by receiver. Thus the scheme is as correct as the underlying $\mathsf {seNCE}$ scheme is.

Since the protocol for $\mathsf {seNCE}$ which we give in Sect. 4.1 has perfect correctness, the overall $\mathsf {NCE}$ scheme, when instantiated with our $\mathsf {seNCE}$ protocol from Sect. 4.1, also achieves perfect correctness.

Description of the Simulator. In this subsection we first explain which variables the adversary sees and then describe our simulator.

The view of the adversary. The view of the adversary consists of the CRS (programs $\mathsf {P}^*_{\mathsf {GenEnc}}, \mathsf {P}^*_{\mathsf {GenDec}}$), as well as the communication and the internal states of several protocol instances. Namely, for each protocol instance the adversary sees the following variables:

• 1. The first protocol message $t^*$, after which the adversary assigns an input m for this protocol instance;

• 2. The second protocol message $c^*$;

• 3. The sender internal state $r^*_{\mathsf {Enc}}, r^*_{\mathsf {GenEnc}}$;

• 4. The receiver internal states $r^*_{\mathsf {GenDec}}$.

Other values, such as $\mathsf {P}^*_{\mathsf {Enc}}$ and $sk^*$, can be obtained by the adversary by running programs in the CRS: $\mathsf {P}^*_{\mathsf {Enc}} \leftarrow \mathsf {P}^*_{\mathsf {GenEnc}}(t^*, r^*_{\mathsf {GenEnc}})$, $(sk^*, t^*) \leftarrow \mathsf {P}^*_{\mathsf {GenDec}}(r^*_{\mathsf {GenDec}})$.

Simulation. The simulator runs the compiler $\mathsf {Comp}$ on programs $\mathsf {Enc}, \mathsf {GenEnc}, \mathsf {GenDec}$ and sets a simulated CRS to be a description of programs $\mathsf {Comp}.\mathsf {Trapdoor}(\mathsf {GenEnc})$, $\mathsf {Comp}.\mathsf {Trapdoor}(\mathsf {GenDec})$. The difference from the real-world CRS is that these simulated programs have a trapdoor branch inside them, which allows the simulator to produce randomness such that a program outputs a desired output on this randomness.

The simulator keeps programs $\mathsf {Expl}_{\mathsf {Enc}} = \mathsf {Comp}.\mathsf {Explain}(\mathsf {Enc})$,

$\mathsf {Expl}_{\mathsf {GenEnc}} =\mathsf {Comp}.\mathsf {Explain}(\mathsf {GenEnc}), \mathsf {Expl}_{\mathsf {GenDec}} = \mathsf {Comp}.\mathsf {Explain}(\mathsf {GenDec})$ for later use.

• CRS generation. The simulator sets the CRS to be a description of programs $\mathsf {P}^*_{\mathsf {GenEnc}} = \mathsf {Comp}.\mathsf {Trapdoor}(\mathsf {GenEnc})$, $\mathsf {P}^*_{\mathsf {GenDec}} = \mathsf {Comp}.\mathsf {Trapdoor}(\mathsf {GenDec})$.

  Next the simulator responds to requests of the adversary. The adversary can interactively ask to setup a new execution of the protocol (where the input m can be chosen based on what the adversary has already learn from other executions), or ask to deliver messages or corrupt parties in protocols which are already being executed. Below we describe what our simulator does in each case:

• Simulation of the first message. If the receiver is already corrupted, then the simulator generates the first message by choosing random $r^*_\mathsf {GenDec}$ and running $(t^*, sk^*) \leftarrow \mathsf {P}^*_{\mathsf {GenDec}}(r^*_\mathsf {GenDec})$. Otherwise the simulator chooses random $t^*$ as the first message.

• Simulation of the second message. If either the sender or the receiver is already corrupted, then the simulator learns m and therefore can generate the second message honestly. If neither the sender nor the receiver in this execution are corrupted by this moment, the simulator runs $(pk_f^*, c^*_f) \leftarrow \mathsf {seNCE}.\mathsf {Sim}(\mathsf {F}_\mathsf {MSK}(t^*))$ and gives $c^*_f$ to the adversary as the second message.

• Simulation of the sender internal state. If either the sender or the receiver had been corrupted before the second message was sent, then the simulator has generated the second message honestly and can thus show true sender randomness.

  Otherwise it first generates a program $\mathsf {P}^*_\mathsf {Enc}= \mathsf {Comp}.\mathsf {Trapdoor}(\mathsf {Enc}[\mathsf {pk}_f^*])$ with simulated $pk_f^*$ hardwired inside. Next it encodes $m^*, c^*_f$ into sender encryption randomness, i.e. sets $r^*_{f, \mathsf {Enc}} \leftarrow \mathsf {Expl}_{\mathsf {Enc}}(m^*, c^*_f; \rho _3)$ for random $\rho _3$; so that $P^*_\mathsf {Enc}$ on input $(m^*, r^*_{f, \mathsf {Enc}})$ outputs $c^*_f$.

  Finally, it encodes $\mathsf {P}^*_\mathsf {Enc}$ into $r^*_{f, \mathsf {GenEnc}}$, i.e. sets the sender’s generation randomness $r^*_{f,\mathsf {GenEnc}} \leftarrow \mathsf {Expl}_{\mathsf {GenEnc}}(t^*, \mathsf {P}^*_{\mathsf {Enc}}; \rho _2)$ for random $\rho _2$, so that $\mathsf {P}^*_\mathsf {GenEnc}$ outputs $\mathsf {P}^*_\mathsf {Enc}$ on input $(t^*, r^*_{f, \mathsf {GenEnc}})$.

  The pair $(r^*_{f, \mathsf {GenEnc}}, r^*_{f, \mathsf {Enc}})$ is set to be the sender internal state.

• Simulation of the receiver internal state. If the corruption happens before the first message is sent, then the simulator has generated the first message honestly and thus can show true receiver internal state.

  If corruption happens after the first message, but before the second, then the first message $t^*$ was generated at random. In this case the simulator computes $sk^* \leftarrow \mathsf {seNCE}.\mathsf {Gen}(F_\mathsf {MSK}(t^*))$. It encodes $(t^*, sk^*)$ into receiver randomness, i.e. sets $r^*_{f, \mathsf {GenDec}} \leftarrow \mathsf {Expl}_{\mathsf {GenDec}}(t^*, sk^*; \rho _1)$ for random $\rho _1$, so that $P^*_\mathsf {GenDec}$ on input $r^*_{f, \mathsf {GenDec}}$ outputs $(t^*, sk^*)$.

  If corruption happens after the second message, then the simulator runs $\mathsf {seNCE}$ simulator and gets fake secret key $sk^*_f$ which decrypts dummy $c^*_f$ to $m^*$, chosen by the adversary. Next it encodes $(t^*, sk^*_f)$ into receiver randomness, i.e. sets $r^*_{f, \mathsf {GenDec}} \leftarrow \mathsf {Expl}_{\mathsf {GenDec}}(t^*, sk^*_f; \rho _1)$ for random $\rho _1$, so that $P^*_\mathsf {GenDec}$ on input $r^*_{f, \mathsf {GenDec}}$ outputs $(t^*, sk^*_f)$.

Fig. 6.

Simulation.

Note that simulation of each protocol instance is independent of simulation of other protocol instances (except for the fact that they share the same CRS). Therefore in order to keep the description of the simulator simple enough, in Fig. 6 we present a detailed description of the simulator for a single execution only; it can be trivially generalized to a multiple-execution case according to what is written above. In addition, the simulator is presented for a difficult case, i.e. when nobody is corrupted by the time the ciphertext is sent, and therefore the simulator has to present a dummy c and later open it to a correct m.

Next we outline the intuition for the security proof and after that provide the detailed description of the hybrids.

Overview of the Analysis of the Simulator. Before presenting hybrids, let us give a roadmap of the proof: Starting from the real execution, we first switch the programs in the CRS: instead of compiling them with $\mathsf {Comp}.\mathsf {Rerand}$, we compile them using $\mathsf {Comp}.\mathsf {Trapdoor}$; in other words, we add trapdoor branches to the programs in the CRS, in order to allow creating fake randomness which explains a given output. Next we change what the simulator shows as internal states of the parties: instead of showing their real randomness, the simulator shows fake randomness (which explains outputs of programs from a real execution, i.e. this randomness explains honestly generated $sk^*$, $c^*$, and $P^*_\mathsf {Enc}$). Our next step is to puncture the key $\mathsf {MSK}\{t^*\}$ in both CRS programs. This allows us to switch seNCE generation randomness $r^*_{\mathsf {NCE}}$ from $\mathsf {F}_\mathsf {MSK}(t^*)$ to a random value; this means that $\mathsf {seNCE}$ parameters $(pk^*, sk^*)$ are now freshly generated and do not depend on the rest of an experiment anymore. Therefore we can use security of $\mathsf {seNCE}$ and switch seNCE values $(pk^*, c^*, sk^*)$ from real to simulated (in particular, the simulator hardwires these simulated $c^*_f, sk^*_f$ into fake randomness, instead of hardwiring real-execution $c^*, sk^*$). Next we undo previous hybrids: we set $r^*_{\mathsf {NCE}}$ as the result of $\mathsf {F}_\mathsf {MSK}(t^*)$, and then unpuncture $\mathsf {MSK}\{t^*\}$ in both CRS programs.

In security proof we will be using the following properties of explainability compiler $\mathsf {Comp}$ for any algorithm $\mathsf {Alg}$:

• 1. Indistinguishability of programs with and without trapdoor branch;

  $\mathsf {Comp}.\mathsf {Rerand}(\mathsf {Alg}) \approx \mathsf {Comp}.\mathsf {Trapdoor}(\mathsf {Alg})$.

• 2. Indistinguishability of explanations:

  given programs $\mathsf {P}(x; r) = \mathsf {Comp}.\mathsf {Trapdoor}(\mathsf {Alg})$ and $\mathsf {Expl}= \mathsf {Comp}.\mathsf {Explain}(\mathsf {Alg})$, it is impossible to distinguish between real randomness and input (x, r) and fake randomness $(x, r_f \leftarrow \mathsf {Comp}.\mathsf {Expl}(x, \mathsf {P}(x, r))$. In particular, evaluating $\mathsf {P}(x; r_f)$ results in $\mathsf {P}(x, r)$, with the only difference that the computation $\mathsf {P}(x; r_f)$ uses the trapdoor branch, which is however undetectable.

• 3. Indistinguishability of source of the output:

  given programs $\mathsf {P}(x; r) = \mathsf {Comp}.\mathsf {Trapdoor}(\mathsf {Alg})$ and $\mathsf {Expl}= \mathsf {Comp}.\mathsf {Explain}(\mathsf {Alg})$, it is infeasible to tell whether a given output y was obtained by running original program $\mathsf {Alg}$ or its compiled version $\mathsf {Comp}.\mathsf {Trapdoor}(\mathsf {Alg})$.

We omit proofs of these statements, since they generally follow the proofs of explainability compiler in previous works [DKR15], with some adaptations for our scenario (such as added indistinguishablity of programs with and without a trapdoor). Formal proofs appear in the full version of our paper.

We now briefly describe each hybrid. The full description with detailed security reductions is given in the full version of the paper.

• Hybrid 0. We start with a real execution of the protocol.

• Hybrids 1a–1b. We change how we generate the CRS programs: instead of obtaining them as $\mathsf {Comp}.\mathsf {Rerand}(\mathsf {GenEnc})$ and $\mathsf {Comp}.\mathsf {Rerand}(\mathsf {GenDec})$, we generate them as $\mathsf {Comp}.\mathsf {Trapdoor}(\mathsf {GenEnc})$ and $\mathsf {Comp}.\mathsf {Trapdoor}(\mathsf {GenDec})$. Security holds by indistinguishability of programs with and without trapdoor branch.

  Next for every execution i, in which the receiver is corrupted between the first and the second messages, we run hybrids $2_i - 3_i$.

  $\bullet$ :

  Hybrid 2 $_i$. Instead of showing the real randomness $r^*_{\mathsf {GenDec}}$, the simulator shows fake $r^*_{f,\mathsf {GenDec}}$, which encodes $t^*, sk^*$. These experiments are indistinguishable because of the indistinguishability of explanation: indeed, $\mathsf {P}^*_\mathsf {GenDec}$ on both inputs $r^*_{\mathsf {GenDec}}$ and $r^*_{f, \mathsf {GenDec}}$ outputs $t^*, sk^*$, therefore true randomness $r^*_{\mathsf {GenDec}}$ is indistinguishable from randomness $r^*_{f,\mathsf {GenDec}}$, which explains the output $t^*, sk^*$.

  Note that since there is no non-random input to our program $\mathsf {P}_{\mathsf {GenDec}}$, it is enough to use the selective indistinguishability of explanation.

  $\bullet$ :

  Hybrid 3 $_i$. We set $t^* = \mathsf {prg}(w^*)$ for random $w^*$ and then compute $sk^*$ as $(pk^*, sk^*) \leftarrow \mathsf {seNCE}.\mathsf {Gen}(F_\mathsf {MSK}(t^*))$. In other words, we compute $(t^*, \mathsf {sk}^*)$ as the result of running $\mathsf {GenDec}$ instead of $\mathsf {Comp}.\mathsf {Trapdoor}(\mathsf {GenDec})$. Indistinguishability holds by indistinguishability of the source of the output for the compiler $\mathsf {Comp}$ and program $\mathsf {GenDec}$.

  $\bullet$ :

  Hybrid 4 $_i$. Finally we set $t^*$ to be randomly chosen instead of being the result of $\mathsf {prg}(w^*)$. Security follows from security of the $\mathsf {prg}$.

  This is the simulation for the case when the receiver is corrupted between the first and the second message.

  For every execution i, in which both corruptions happen after the second message is sent, we run hybrids $2_{i} - 5h_{i}$.

• Hybrid $2_i$. Instead of showing the real randomness $r^*_{\mathsf {GenEnc}}$, the simulator shows fake $r^*_{f,\mathsf {GenEnc}}$, which encodes $t^*, \mathsf {P}^*_{\mathsf {Enc}}$. These experiments are indistinguishable because of the indistinguishability of explanation: indeed, $\mathsf {P}^*_\mathsf {GenEnc}$ on both inputs $t^*, r^*_{\mathsf {GenEnc}}$ and $t^*, r^*_{f, \mathsf {GenEnc}}$ outputs $P^*_\mathsf {Enc}$, and by the theorem true randomness $r^*_{\mathsf {GenEnc}}$ is indistinguishable from fake randomness $r^*_{f,\mathsf {GenEnc}}$ which explains $P^*_\mathsf {Enc}$ on input $t^*$. Note that non-random input to our program $\mathsf {P}_{\mathsf {GenEnc}}$ is $t^*$, obtained by running $t^* \leftarrow P^*_{\mathsf {GenDec}}(r^*_{\mathsf {GenDec}})$ for random $r^*_{\mathsf {GenDec}}$, i.e., it can be generated before a CRS is shown to the adversary. Thus it is enough to use the selective indistinguishability of explanation.

• Hybrid $3_i$. In the next step instead of showing the real $r^*_{\mathsf {GenDec}}$, the simulator shows fake $r^*_{f,\mathsf {GenDec}}$, which encodes $t^*, sk^*$. These experiments are indistinguishable because of the indistinguishability of explanation: indeed, $\mathsf {P}^*_\mathsf {GenDec}$ on both inputs $r^*_{\mathsf {GenDec}}$ and $r^*_{f, \mathsf {GenDec}}$ outputs $t^*, sk^*$, therefore true randomness $r^*_{\mathsf {GenDec}}$ is indistinguishable from randomness $r^*_{f,\mathsf {GenDec}}$, which explains the output $t^*, sk^*$ on empty non-random input.

  Note that since there is no non-random input to our program $\mathsf {P}_{\mathsf {GenDec}}$, it is enough to use the selective indistinguishability of explanation.

• Step 4$_i$. Next global step is to switch random $r^*_{\mathsf {Enc}}$ to fake $r^*_{f, \mathsf {Enc}}$ which encodes $(m^*, c^*)$. We do this in several steps:

  • Hybrid 4a$_i$. We obtain $t^*, sk^*$ by running $\mathsf {GenDec}$ on random $w^*$ instead of running $\mathsf {P}^*_\mathsf {GenDec}= \mathsf {Comp}.\mathsf {Trapdoor}(\mathsf {GenDec})$ on $r^*_\mathsf {GenDec}$. Indistinguishability holds by indistinguishability of a source of the output for programs $\mathsf {GenDec}$ and $\mathsf {Comp}.$ $\mathsf {Trapdoor}(\mathsf {GenDec})$.

  • Hybrid 4b$_i$. We choose $t^*$ at random instead of choosing it as $\mathsf {prg}(w^*$) for random $w^*$. $(\mathsf {pk}^*, \mathsf {sk}^*)$ are then obtained from $r^*_\mathsf {NCE}= \mathsf {F}_\mathsf {MSK}(t^*)$. Indistinguishability holds by security of a $\mathsf {prg}$.

  • Hybrid 4c$_i$. We generate $\mathsf {P}^*_{\mathsf {Enc}}$ by running $\mathsf {GenEnc}$ on $t^*$ and random $e^*$, instead of running $\mathsf {P}^*_\mathsf {GenEnc}= \mathsf {Comp}.\mathsf {Trapdoor}(\mathsf {GenEnc})$ on $(t^*, r^*_{\mathsf {GenEnc}})$. Security holds by indistinguishability of source of the output for programs $\mathsf {GenEnc}$ and $\mathsf {Comp}.\mathsf {Trapdoor}(\mathsf {GenEnc})$.

  • Hybrid 4d$_i$. We generate the program $\mathsf {P}^*_\mathsf {Enc}\leftarrow \mathsf {Comp}.\mathsf {Trapdoor}(\mathsf {Enc}[\mathsf {pk}^*])$ instead of $\mathsf {Comp}.\mathsf {Rerand}(\mathsf {Enc}[\mathsf {pk}^*])$. Security holds by indistinguishability of programs with and without trapdoor branch for program $\mathsf {Enc}$.

  • Hybrid 4e$_i$. In this step we finally change $r^*_{\mathsf {Enc}}$ to $r^*_{f, \mathsf {Enc}}$ as follows: we first create a CRS and give it to the adversary. Then we generate random $t^*$ and show $t^*$ to the adversary as the first message in the protocol. Next the adversary fixes an input $m^*$. Then we generate $pk^*, sk^*$ as $\mathsf {seNCE}.\mathsf {Gen}(F_\mathsf {MSK}(t^*))$ and give $\mathsf {Enc}() = \mathsf {seNCE}.\mathsf {Enc}_{pk^*}()$ to the explainability challenger as the underlying program. The challenger chooses random $e^*$, runs $\mathsf {Comp}(\mathsf {Enc}; e^*)$ and gives us either $(r^*_{\mathsf {Enc}}, m^*, c^*, \mathsf {P}^*_{\mathsf {Enc}})$ or $(r^*_{f, \mathsf {Enc}}, m^*, c^*, \mathsf {P}^*_{\mathsf {Enc}})$, where $r^*_\mathsf {Enc}$ is random, $\mathsf {P}^*_\mathsf {Enc}= \mathsf {Comp}.\mathsf {Trapdoor}(\mathsf {Enc}; e^*)$, $c^* = \mathsf {P}^*_\mathsf {Enc}(m^*; r^*_\mathsf {Enc})$, and $r^*_{f, \mathsf {Enc}}$ encodes $m^*, c^*$. We show the given $c^*$ as the second message in the protocol. Once asked to open the internal state, we present the given $r^*_{\mathsf {Enc}}$ or $r^*_{f, \mathsf {Enc}}$, generate $r^*_{\mathsf {GenEnc}}$ explaining the given $\mathsf {P}^*_{\mathsf {Enc}}$, and generate $r^*_{\mathsf {GenDec}}$ explaining $(t^*, sk^*)$.

    We can rely on the selective indistinguishability of explanation for program $\mathsf {Comp}.\mathsf {Trapdoor}(\mathsf {Enc})$ since at the moment when we need to see the challenge in explanation game (i.e., when we need to show $c^*$ to the adversary), $\mathsf {P}^*_{\mathsf {Enc}}$’s input $m^*$ is already fixed.

• Step 5$_i$. Our next global step is to change the underlying seNCE values to simulated. We proceed in several steps:

  • Hybrids 5a$_i$–5b$_i$. We puncture $\mathsf {MSK}$ at $t^*$. In $\mathsf {P}^*_\mathsf {GenDec}$ we can puncture immediately, since due to the sparseness of the length-doubling $\mathsf {prg}$, $t^*$ lies outside of the prg image and therefore $\mathsf {F}_\mathsf {MSK}$ is never called at $t^*$. In $\mathsf {P}^*_\mathsf {GenEnc}$ we hardwire $pk^*$ and use it whenever $t = t^*$; otherwise, we use the punctured key $\mathsf {MSK}\{t^*\}$ to generate $r_{\mathsf {NCE}}$ and then sample pk.

  • Hybrid 5c$_i$. Once $\mathsf {MSK}\{t^*\}$ is punctured, we can choose the generation randomness for underlying seNCE scheme $r^*_{\mathsf {NCE}}$ at random.

  • Hybrids 5d$_i$. We generate $c^*$ as a result of running $\mathsf {Enc}$ on $m^*$ and random $u^*$ instead of running $\mathsf {P}^*_\mathsf {Enc}= \mathsf {Comp}.\mathsf {Trapdoor}(\mathsf {Enc})$ on $(m^*; r^*_\mathsf {Enc})$. We rely on indistinguishability of the source of the output for program $\mathsf {Enc}$.

  • Hybrid 5e$_i$. Next we switch the seNCE values from real to simulated: namely, $c^*_f$ is now simulated and $sk^*_f$ is now a simulated key decrypting $c^*_f$ to $m^*$. We rely on the security of the underlying seNCE. Here we crucially use the fact that in the underlying NCE scheme $pk^*$ is shown before the adversary chooses a message, since we hardwire this $pk^*$ into the CRS (in $\mathsf {P}^*_\mathsf {GenEnc}$).

  • Hybrid 5f$_i$. We switch back $r^*_{\mathsf {NCE}}$ to be the result of $\mathsf {F}_{\mathsf {MSK}}(t^*)$.

  • Hybrid 5g$_i$-5h $_i$. We unpuncture $\mathsf {MSK}\{t^*\}$ in $\mathsf {P}^*_\mathsf {GenEnc}$ and $\mathsf {P}^*_\mathsf {GenDec}$ and remove the hardwired $pk^*$ from $\mathsf {P}^*_\mathsf {GenEnc}$. To remove hardwired $pk^*$, we crucially use the fact that $pk^*$, although simulated, is the same as real $pk^*$, generated from randomness $\mathsf {F}_{\mathsf {MSK}}(t^*)$, which is guaranteed by the same-public-key property of seNCE.

This concludes the overview of hybrids. For the detailed description of the hybrids with security reductions, see the full version of the paper.

Fig. 7.

Size dependency graph between different variables, when underlying seNCE is instantiated with our construction from Sect. 4.1. Notation: $i\mathcal {O}(s)$ for size s means the resulting size of an obfuscated program of the initial approximate size s. Dependencies due to obfuscation are drawn as fat blue arrows. Green boxes mark CRS, yellow boxes mark randomness used for extracting PRF, and blue denotes variables which are sent in the protocol. Arrows for t are shown dashed for easier tracking. Red dashed rectangles with size in the top right corner denote a “size group”, e.g. any variable inside $i\mathcal {O}(\lambda m)$ box is as large as an obfuscated program of initial size $\lambda m$. (Color figure online)

Sizes in Our Construction. Our construction has a lot of size dependencies. We present a size diagram on Fig. 7, assuming our implementation of explainability compiler based on $i\mathcal {O}$ and puncturable deterministic encryption ($\mathsf {PDE}$). There all sizes are grouped in “complexity classes”. Here we outline several main dependencies:

• if a fake randomness has values encoded, it should be longer than these values, but not much longer. Namely, if underlying encoded message has size l, then the size of the plaintext for $\mathsf {PDE}$ (which consists of encoded message, secret s and $\mathsf {prg}(\rho )$) is $l + 3\lambda$, and the size of $\mathsf {PDE}$ ciphertext should be at least 4 times bigger (the latter is because explainability compiler uses statistically injective PRF). Therefore randomness and encoded value are in the same “complexity class”.

• if a key is punctured on some input, its size is at least $\lambda |input|$.

• size of an obfuscated program is significantly larger than the size of the original program (polynomial in original size s and security parameter $\lambda$).

Note that all dependencies in the graph are due to the “hardwired values”, i.e. due to the fact that some values should be hardcoded into programs, or messages should be encrypted into ciphertexts. In particular, the same length restrictions remain even when succinct $i\mathcal {O}$ for TM or RAM [CHJV15, CH15, KLW15] is used.

Note that the dependency graph is acyclic, and variables which we actually send over the channel - t and c - are in the very top of the graph. This means that we can set length of t and m to be a security parameter, and then set lengths of other variables as large as needed by following edges in dependency graph.