Stability Analysis of ECOC Kernel Machines

Abstract

Error correcting output codes kernel machines (ECOC kernel machines) are ensemble of kernel machines based on ECOC decomposition methods. How to improve the generalization capability of this framework is an open problem. In this paper, we discussed the condition for generalization in terms of the stability property of ECOC kernel machines. Here we provide a proof for the result that an ECOC kernel machine has the pointwise hypothesis stability. This stability property can be calculated by training on the training dataset once and has clear and meaningful formulation. It can be applied to tune the kernel parameters in model selection and design good matrixes for ECOC kernel machines.

1 Introduction

Many real-world pattern recognition applications are aim to map the instances into a set of classes. To deal with such problems, the efficient way is to decompose the multiclass problems into a set of binary classification problems [1]. In this case, many techniques addressing the binary classification task can be used to solve the complex multiclass problems. There are many different approaches for recasting the multiclass problem into a series of smaller binary classification tasks, such as one-versus-all (OVA), one-versus-one (OVO) [2, 3], and error correcting output codes (ECOC) [4, 5]. One-versus-all which is the simplest approach considers the comparison between each class and the others, and takes the maximum output as the final classification decision. One-versus-one approach addresses the comparison of all possible pairs of classes, and obtains the final classification result by means of a voting procedure. Error correcting output codes (ECOC) is a general framework to achieve this decomposition, which was presented by Dietterich and Bakiri [4]. Due to the error correcting capability [6,7,8], ECOC has been successfully applied to a wide range of applications [9,10,11,12].

When the ECOC framework is applied in practice, we expect that this framework will have an accuracy classification result. Generally speaking, training the learning algorithms on the empirical datasets to predict the unlabeled samples precisely is one of the key points for machine learning. The ECOC framework can be seen as a special learning algorithm, which is an ensemble of some binary classifiers. How to improve and evaluate the generalization capability of this framework is an open problem and some works have been done. Masulli and Valentini [13] attempted to analyze the main factors affecting the effectiveness of ECOC methods experimentally, and their analysis showed that all these factors concurred to the effectiveness of ECOC methods in a not straightforward way and interacted between them. Garcia-Pedrajas and Fyfe [14] proposed an evolutionary approach to the design of output codes, which took five different aspects into account, but it was difficult to define an apparent relationship between these aspects and the generalization ability of ECOC methods. These results underscore the difficulty of this problem.

On the other hand, some works focused on just one or two aspects that were related to generalization performance of ECOC methods. Pujol and Radeva [15] focused on obtaining the partitions which had the maximum class discrimination. Escalera and Tax [16] used the subclass information to guarantee that the base classifier can split each subgroup of classes. Ali-Bagheri [17, 18] aimed to improve independency among base classifiers using different feature subsets for each base classifiers. Angel-Bautista and Escalera [19] presented a novel genetic strategy to obtain the better dichotomizers. These works provide us some new ways to the ECOC framework research. However, it is a pity that there is little formal justification to support these improvements. The previous works show that it is difficult to determine what is the intrinsic factors affecting the effectiveness of ECOC methods.

To improve the generalization capability of ECOC framework, what we need to do is to go back to the nature of ECOC framework. The nature is it is just a special learning algorithm. Note that in this case, we do not discuss the decoding strategy. A central question for machine learning is to determine conditions under which a learning algorithm will generalize from its finite training set to novel samples [20]. A milestone in learning theory was empirical risk minimization (ERM) based on minimizing the training error. Furthermore, Valentini [21] proposed the upper bounds on the training error of ECOC kernel machines. In this case, the problem is changed to how to minimize the difference between the training error and the generalization error. Fortunately, Poggio and Rifkin [20] discussed the conditions for generalization in terms of a precise stability property of the learning process. Bousquet and Elisseeff [22] showed how to use the stability to derive bounds on the generalization error based on the training error. The stability of a learning algorithm can be a bridge between the training error and the generalization error, and as a powerful tool in ECOC framework research.

In other word, if the learning algorithm has minimization training error and is more stable, the learning algorithm can have better generalization capability. It is our purpose in this paper to discuss the stability of ECOC framework with kernel machines. The most contribution of our work is that we obtain the result that ECOC kernel machines have pointwise hypothesis stability. This stability can be calculated by training on the training dataset once, and has clear and meaningful formulation. It can be applied to tune the kernel parameters in model selection and design good matrixes for ECOC kernel machines.

The rest of this paper is organized as follows: Sect. 2 provides a brief introduction to the ECOC decomposition methods and background on kernel machines. The pointwise hypothesis stability of ECOC kernel machines is explained in detail in Sect. 3. In Sect. 4, some applications of pointwise hypothesis stability are presented. Finally, Sect. 5 draws the main conclusions of the paper.

2 ECOC Kernel Machines

2.1 ECOC

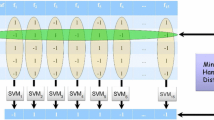
The ECOC framework consists of two stages: encoding and decoding. At the coding stage, the main task is to construct a coding matrix. Each column of the coding matrix is the bipartition (groups of classes), which indicates one binary problem. Each row of the coding matrix is the codeword for each class, where the bit implies the label of the class for a binary problem [23]. The base classifier is obtained by training the binary problem. Binary ECOC is the original framework. It has two symbols $\left\{ { + 1, - 1} \right\}$ in the coding matrix, which represent the negative class and the positive class in one binary problem. When the coding step attracted special attention, Allwen et al. [5] introduced zero as the third symbol, which indicated that the corresponding class would be ignored for a binary problem. The classical ECOCs are shown in Fig. 1.

Fig. 1.

Four classical ECOCs, binary ECOC: (a) one-versus-all; (c) dense random; ternary ECOC: (b) one-versus-one; (d) sparse random

In Fig. 1, the white, black and gray regions of the coding matrix stand for the symbol “1”, “−1” and “0” respectively. For example, in Fig. 1(c) when classifier $f_{1}$ is trained, classes $C_{1}$ and $C_{4}$ are seen as the positive class and classes $C_{2}$ and $C_{3}$ as the negative class. In the same way, finally, we obtain a classifier vector $\left\{ {f_{1} ,f_{2} ,f_{3} ,f_{4} } \right\}$.

Given a test sample, the base classifiers output a codeword. Note that the obtained codeword cannot take the value zero since the output of the base classifier is “+1” or “−1”. At the decoding stage, this codeword is compared with the codewords defined in the coding matrix, and the test sample is assigned to the class corresponding to the closest codeword. Usually, this comparison is implemented by the Hamming and the Euclidean decoding distance. Specially, Allwen et al. [5] showed the advantage of using a loss-based function of the margin of the output of the base classifier. For example, in Fig. 1(c) given the test sample $X$, the classifier vector output a codeword $\left\{ {x_{1} ,x_{2} ,x_{3} ,x_{4} } \right\}$. Then, the final classification result is obtained by a given decoding strategy.

2.2 Kernel Machines

We assume that the training set is $Z^{m} = \left\{ {\left( {x_{i} ,y_{i} } \right)_{i = 1}^{m} \in \left\{ {X \times \left\{ { - 1,1} \right\}} \right\}^{m} } \right\}$ and $\ell :R \to R$ is a loss function. Kernel machines are the minimizers of functionals of the form

$$ F\left[ {f;Z^{m} } \right] = \frac{1}{m}\sum\limits_{i = 1}^{m} {\ell \left( {y_{i} f\left( {x_{i} } \right)} \right)} + \lambda \left\| f \right\|_{K}^{2} $$

(1)

where $\lambda$ is a positive constant named regularization parameter. The minimization of functional in (1) is done in a Reproducing Kernel Hilbert Space (RKHS) $\mathcal{H}$ defined by a symmetric and positive definite kernel $K:X \times X \to R$, and $\left\| f \right\|_{K}^{2}$ is the norm of a function $f:X \to R$ belonging to $\mathcal{H}$.

If $\ell$ is convex, the minimizer of functional in (1) is unique and has the form

$$ f\left( x \right) = \sum\limits_{i = 1}^{m} {\alpha_{i} y_{i} K\left( {x_{i} ,x} \right)} $$

(2)

The coefficients $\alpha_{i}$ are computed by solving an optimization problem whose form is determined by the loss function $\ell$. For example, in SVMs, the soft-margin loss is $\ell \left( {yf\left( x \right)} \right) = \left| {1 - yf\left( x \right)} \right|_{ + }$, where $\left| x \right|_{ + } = x$ if $x > 0$ and zero otherwise. In this case, the $\alpha_{i}$ is the solution of a quadratic programming problem with constraints $\alpha_{i} \in \left[ {0,1/2m\lambda } \right]$. A peculiar property of an SVM is that, usually, only few data points have nonzero coefficients $\alpha_{i}$. These points are named support vectors.

3 Pointwise Hypothesis Stability of ECOC Kernel Machines

3.1 Pointwise Hypothesis Stability

The stability of one learning algorithm can be used to get bounds on the generalization error [22]. Here we focus on the stability with respect to changes in the training set. Firstly, we introduce some notations.

A training dataset is given as follows

$$ S = \left\{ {\text{z}_{1} = \left( {x_{1} ,y_{1} } \right), \ldots ,z_{m} = \left( {x_{m} ,y_{m} } \right)} \right\} $$

(3)

By removing the $i$th element, the changed training dataset is given as:

$$ S^{\backslash i} = \left\{ {z_{1} , \ldots ,z_{i - 1} ,z_{i + 1} , \ldots ,z_{m} } \right\} $$

(4)

Then, we denote by $f$ the function trained on the set $S$, and $f^{\backslash i}$ the function trained on the set $S^{\backslash i}$. The definition of pointwise hypothesis stability is given in Definition 1.

Definition 1 (Pointwise Hypothesis Stability).

An algorithm $A$ has pointwise hypothesis stability $\delta$ with respect to the loss function $\ell$ if the following holds

$$ \forall S \in Z^{m} ,\,\forall i \in \left\{ {1, \cdots ,m} \right\},\,{\rm E}_{S} \left[ {\left| {\ell \left( {f,z_{i} } \right) - \ell \left( {f^{\backslash i} ,z_{i} } \right)} \right|} \right] \le \delta $$

(5)

3.2 Multiclass Loss Function

Based on Definition 1, the loss function of ECOC kernel machines is needed. Let the coding matrix be $M \in \left\{ { - 1,0,1} \right\}^{k \times l}$, where $k$ is the number of class and $l$ is the number of binary classifier. $m_{ps}$ is the code bit which indicates the label of class $p$ in the $s$ th binary classifier. The vector function formed by the binary classifiers is $f\left( x \right) = \left\{ {f_{1} \left( x \right), \cdots ,f_{l} \left( x \right)} \right\}$.

The multiclass margin of a sample $\left( {x_{i} ,y_{i} } \right) \in X \times \left\{ {1, \cdots ,k} \right\}$ can be written as [24]

$$ g\left( {x_{i} ,y_{i} } \right) = d_{L} \left( {m_{p} ,f\left( {x_{i} } \right)} \right) - d_{L} \left( {m_{{y_{i} }} ,f\left( {x_{i} } \right)} \right) $$

(6)

where $d_{L} \left( {m_{p} ,f\left( {x_{i} } \right)} \right) = \sum\limits_{s = 1}^{l} {L\left( {m_{ps} f_{s} \left( {x_{i} } \right)} \right)}$ is the linear loss-based decoding function with $L\left( {m_{ps} f_{s} \left( {x_{i} } \right)} \right) = - m_{ps} f_{s} \left( {x_{i} } \right)$, and $p = \arg \mathop {\hbox{min} }\limits_{{q \ne y_{i} }} d_{L} \left( {m_{q} ,f\left( {x_{i} } \right)} \right)$.

Note that the multiclass margin is positive when sample $x_{i}$ is classified correctly. Considering a loss function is typically a nondecreasing function of the margin, the linear-margin loss function can be defined as $\ell \left( {f,z} \right) = - g\left( {x,y} \right)$.

3.3 Pointwise Hypothesis Stability of ECOC Kernel Machines

In this section, we present the proof of pointwise hypothesis stability of ECOC kernel machines. To this end, we first need the following lemma [24].

Lemma 1.

Let $f$ be the kernel machine as defined in (2) obtained by solving (1). Let $f^{\backslash i}$ be the solution of (1) found when the data point $\left( {x_{i} ,y_{i} } \right)$ is removed from the training set. We have

$$ y_{i} f\left( {x_{i} } \right) - \alpha_{i} G_{ii} \le y_{i} f^{\backslash i} \left( {x_{i} } \right) \le y_{i} f\left( {x_{i} } \right) $$

(7)

where $G_{ij} = K\left( {x_{i} ,x_{j} } \right)$.

By applying Lemma 1 simultaneously to each kernel machine used in the ECOC procedure, Inequality (7) can be rewritten as

$$ f_{s}^{\backslash i} \left( {x_{i} } \right) = f_{s} \left( {x_{i} } \right) - \lambda_{s} m_{{y_{i} s}} ,\quad s \in \left\{ {1, \cdots ,l} \right\} $$

(8)

where $\lambda_{s}$ is a parameter in $\left[ {0,\alpha_{i}^{s} G_{ii}^{s} } \right]$.

Theorem 1.

Let $M \in \left\{ { - 1,1} \right\}^{k \times l}$ be the code matrix and $f_{s} \left( x \right) = \sum\nolimits_{i = 1}^{m} {\alpha_{i}^{s} m_{{y_{i} s}} K^{s} \left( {x_{i} ,x} \right)}$ be the $s$ th binary classifier, where $\alpha_{i} \in \left[ {0,C} \right]$ with $C = {1 \mathord{\left/ {\vphantom {1 {\left( {2m\lambda } \right)}}} \right. \kern-0pt} {\left( {2m\lambda } \right)}}$. The multiclass loss function is $\ell \left( {f,z} \right) = - g\left( {x,y} \right)$. Let $\kappa = \max_{s} \max_{i} G_{ii}^{s} = \max_{s} \max_{i} K^{s} \left( {x_{i} ,x_{i} } \right)$. $f$ is the vector function derived by the ECOC kernel machines based on the coding matrix $M$. Decoding strategy is set as linear loss-based decoding function. $\theta \left( \cdot \right)$ is the Heavyside function: $\theta \left( x \right) = 1$ if $x > 0$ and zero otherwise. Thus, ECOC kernel machines have pointwise hypothesis stability with

$$ {\rm E}_{S} \left[ {\left| {\ell \left( {f,z_{i} } \right) - \ell \left( {f^{\backslash i} ,z_{i} } \right)} \right|} \right] \le \frac{2\kappa C}{m}\sum\limits_{i = 1}^{m} {\sum\limits_{s = 1}^{l} {\theta \left( {\alpha_{i}^{s} } \right)} } $$

(9)

Proof.

In order to prove that ECOC kernel machines has pointwise hypothesis stability, we have to find the bound for ${\rm E}_{S} \left[ {\left| {\ell \left( {f,z_{i} } \right) - \ell \left( {f^{\backslash i} ,z_{i} } \right)} \right|} \right]$. Firstly, for $\forall S \in Z^{m} ,\,\forall z_{i} = \left( {x_{i} ,y_{i} } \right) \in S$, we have

$$ {\rm E}_{S} \left[ {\left| {\ell \left( {f,z_{i} } \right) - \ell \left( {f^{\backslash i} ,z_{i} } \right)} \right|} \right] = \frac{1}{m}\sum\limits_{i = 1}^{m} {\left| {\ell \left( {f,z_{i} } \right) - \ell \left( {f^{\backslash i} ,z_{i} } \right)} \right|} = \frac{1}{m}\sum\limits_{i = 1}^{m} {\left| {g\left( {x_{i} ,y_{i} } \right) - g^{\backslash i} \left( {x_{i} ,y_{i} } \right)} \right|} $$

So, if we want to bound ${\rm E}_{S} \left[ {\left| {\ell \left( {f,z_{i} } \right) - \ell \left( {f^{\backslash i} ,z_{i} } \right)} \right|} \right]$, firstly we can bound $\left| {g\left( {x_{i} ,y_{i} } \right) - g^{\backslash i} \left( {x_{i} ,y_{i} } \right)} \right|$.

The above problem can be divided into two parts. On one hand, from the definition of $g\left( {x,y} \right)$ and linear loss-based decoding function, we have

$$ g^{\backslash i} \left( {x_{i} ,y_{i} } \right) = m_{{y_{i} }} f^{\backslash i} \left( {x_{i} } \right) - m_{{p^{\backslash i} }} f^{\backslash i} \left( {x_{i} } \right) $$

(10)

where $p^{\backslash i} = \arg \mathop {\hbox{max} }\limits_{{q \ne y_{i} }} m_{q} f^{\backslash i} \left( {x_{i} } \right)$.

$$ g\left( {x_{i} ,y_{i} } \right) = m_{{y_{i} }} f\left( {x_{i} } \right) - m_{p} f\left( {x_{i} } \right) $$

(11)

where $p = \arg \mathop {\hbox{max} }\limits_{{q \ne y_{i} }} m_{q} f\left( {x_{i} } \right)$.

Moreover, from the definition of $p$, we can get

$$ m_{p} f\left( {x_{i} } \right) \ge m_{{p^{\backslash i} }} f\left( {x_{i} } \right) $$

(12)

(11) minus (10), there is

$$ g\left( {x_{i} ,y_{i} } \right) - g^{\backslash i} \left( {x_{i} ,y_{i} } \right) = \sum\limits_{s = 1}^{l} {\left[ {m_{{y_{i} s}} f_{s} \left( {x_{i} } \right) - m_{ps} f_{s} \left( {x_{i} } \right) - m_{{y_{i} s}} f_{s}^{\backslash i} \left( {x_{i} } \right) + m_{{p^{\backslash i} s}} f_{s}^{\backslash i} \left( {x_{i} } \right)} \right]} $$

(13)

Now, applying (8), we can get

$$ \begin{aligned} g\left( {x_{i} ,y_{i} } \right) - g^{\backslash i} \left( {x_{i} ,y_{i} } \right) & = \sum\limits_{s = 1}^{l} {\left[ {m_{{y_{i} s}} f_{s} \left( {x_{i} } \right) - m_{ps} f_{s} \left( {x_{i} } \right) - m_{{y_{i} s}} \left( {f_{s} \left( {x_{i} } \right) - \lambda_{s} m_{{y_{i} s}} } \right) + m_{{p^{\backslash i} s}} \left( {f_{s} \left( {x_{i} } \right) - \lambda_{s} m_{{y_{i} s}} } \right)} \right]} \\ & = \sum\limits_{s = 1}^{l} {\left[ {\left( {m_{{p^{\backslash i} s}} - m_{ps} } \right)f_{s} \left( {x_{i} } \right) + \left( {m_{{y_{i} s}} - m_{{p^{\backslash i} s}} } \right)\lambda_{s} m_{{y_{i} s}} } \right]} \\ \end{aligned} $$

(14)

Considering (12), we can write the following inequality

$$ g\left( {x_{i} ,y_{i} } \right) - g^{\backslash i} \left( {x_{i} ,y_{i} } \right) \le \sum\limits_{s = 1}^{l} {\left( {m_{{y_{i} s}} - m_{{p^{\backslash i} s}} } \right)\lambda_{s} m_{{y_{i} s}} } \le \sum\limits_{s = 1}^{l} {2\lambda_{s} \le \sum\limits_{s = 1}^{l} {2\alpha_{i}^{s} G_{ii}^{s} } } \le 2\kappa \sum\limits_{s = 1}^{l} {\alpha_{i}^{s} } $$

(15)

Note that the second inequality is just because of $m_{{y_{i} s}} \in \left\{ { - 1,1} \right\}$, and then

$$ 0 \le \left( {m_{{y_{i} s}} - m_{{p^{\backslash i} s}} } \right)m_{{y_{i} s}} \le 2 $$

(16)

Considering $\alpha_{i}^{s} \in \left[ {0,C} \right]$, and $\alpha_{i}^{s} > 0$ indicates $z_{i}$ is a support vector, for $\forall \left( {x_{i} ,y_{i} } \right) \in S$,

$$ g\left( {x_{i} ,y_{i} } \right) - g^{\backslash i} \left( {x_{i} ,y_{i} } \right) \le 2\kappa \sum\limits_{s = 1}^{l} {\alpha_{i}^{s} } \le 2\kappa C\sum\limits_{s = 1}^{l} {\theta \left( {\alpha_{i}^{s} } \right)} $$

(17)

On the other hand, due to (16) and $\lambda_{s} \ge 0$, we have

$$ \sum\limits_{s = 1}^{l} {\left( {m_{{y_{i} s}} - m_{{p^{\backslash i} s}} } \right)\lambda_{s} m_{{y_{i} s}} } \ge 0 $$

(18)

From (14), we can get

$$ \begin{aligned} g\left( {x_{i} ,y_{i} } \right) - g^{\backslash i} \left( {x_{i} ,y_{i} } \right) & \ge \sum\limits_{s = 1}^{l} {\left( {m_{{p^{\backslash i} s}} - m_{ps} } \right)f_{s} \left( {x_{i} } \right)} \\ & = \sum\limits_{s = 1}^{l} {\left[ {m_{{p^{\backslash i} s}} f_{s} \left( {x_{i} } \right) - m_{{p^{\backslash i} s}} f_{s}^{\backslash i} \left( {x_{i} } \right)} \right]} + \sum\limits_{s = 1}^{l} {\left[ {m_{{p^{\backslash i} s}} f_{s}^{\backslash i} \left( {x_{i} } \right) - m_{ps} f_{s} \left( {x_{i} } \right)} \right]} \\ & \ge \sum\limits_{s = 1}^{l} {\left[ {m_{{p^{\backslash i} s}} f_{s} \left( {x_{i} } \right) - m_{{p^{\backslash i} s}} f_{s}^{\backslash i} \left( {x_{i} } \right)} \right]} + \sum\limits_{s = 1}^{l} {\left[ {m_{ps} \left( {f_{s}^{\backslash i} \left( {x_{i} } \right) - f_{s} \left( {x_{i} } \right)} \right)} \right]} \\ & = \sum\limits_{s = 1}^{l} {\left[ {m_{{p^{\backslash i} s}} \left( {f_{s} \left( {x_{i} } \right) - f_{s}^{\backslash i} \left( {x_{i} } \right)} \right)} \right]} - \sum\limits_{s = 1}^{l} {\left[ {m_{ps} \left( {f_{s} \left( {x_{i} } \right) - f_{s}^{\backslash i} \left( {x_{i} } \right)} \right)} \right]} \\ & = \sum\limits_{s = 1}^{l} {\left( {m_{{p^{\backslash i} s}} - m_{ps} } \right)\lambda_{s} m_{{y_{i} s}} } \\ \end{aligned} $$

(19)

Moreover, $\lambda_{s} \ge 0$ and $\left( {m_{{p^{\backslash i} s}} - m_{ps} } \right)m_{{y_{i} s}} \ge - 2$, the following inequalities are given

$$ g\left( {x_{i} ,y_{i} } \right) - g^{\backslash i} \left( {x_{i} ,y_{i} } \right) \ge \sum\limits_{s = 1}^{l} {\left( {m_{{p^{\backslash i} s}} - m_{ps} } \right)\lambda_{s} m_{{y_{i} s}} \ge - 2\sum\limits_{s = 1}^{l} {\lambda_{s} } \ge - 2\kappa \sum\limits_{s = 1}^{l} {\alpha_{i}^{s} } } $$

(20)

So, for $\forall \left( {x_{i} ,y_{i} } \right) \in S$,

$$ g\left( {x_{i} ,y_{i} } \right) - g^{\backslash i} \left( {x_{i} ,y_{i} } \right) \ge - 2\kappa \sum\limits_{s = 1}^{l} {\alpha_{i}^{s} } \ge - 2\kappa C\sum\limits_{s = 1}^{l} {\theta \left( {\alpha_{i}^{s} } \right)} $$

(21)

And then, we get the bound

$$ \forall i \in \left\{ {1, \cdots ,m} \right\},\quad \left| {g\left( {x_{i} ,y_{i} } \right) - g^{\backslash i} \left( {x_{i} ,y_{i} } \right)} \right| \le 2\kappa C\sum\limits_{s = 1}^{l} {\theta \left( {\alpha_{i}^{s} } \right)} $$

(22)

Finally, we prove that ECOC kernel machines has pointwise hypothesis stability with

$$ {\rm E}_{S} \left[ {\left| {\ell \left( {f,z_{i} } \right) - \ell \left( {f^{\backslash i} ,z_{i} } \right)} \right|} \right] \le \frac{2\kappa C}{m}\sum\limits_{i = 1}^{m} {\sum\limits_{s = 1}^{l} {\theta \left( {\alpha_{i}^{s} } \right)} } $$

■

Remark.

The parameters $\alpha_{i}^{s}$ indicate if point $x_{i}$ is a support vector for the $s$ th kernel machine, which depend on the solution of the machines trained on the full dataset (so training the machines once will suffice). Our result indicates that pointwise hypothesis stability $\delta$ is related with all samples in the training set. For binary ECOC the number of training samples of every dichotomy is the same, thus, there exists parameter $\alpha_{i}$ for every $z_{i}$ . But, for ternary ECOC the number of training samples of every dichotomy is different, thus, many training samples are not considered in the training phase of a kernel machine. Considering the parameters $\alpha_{i}$ indicate if point $x_{i}$ is a support vector, so, the parameters $\alpha_{i}$ for these ignored points can be seen as zero just as that these points are not support vectors for kernel machines. This hypothesis is an open problem and will be discussed in our future work.

4 Application of Pointwise Hypothesis Stability

In this section, we introduce two aspects of application of pointwise hypothesis stability: model selection and good coding matrixes design for ECOC kernel machines.

4.1 Model Selection

When a coding matrix $M$ is given, in order to have a better generalization performance we should tune the kernel parameters to find the better binary classifiers. Importantly, we need to evaluate the generalization error to check if the tuned kernel parameter is the best one. However, it is difficult to calculate the generalization error, due to the unknown distribution of the data. We have to estimate the generalization error from the available dataset. This available dataset is often defined as the training dataset. On the training dataset we can only obtain the training error or the empirical error. Previously, the better classifier is selected by empirical error minimization, which is known as empirical risk minimization (ERM). But this always leads to an overfitting problem, which means that although the classifier has the minimum empirical error, it has a bad generalization performance. There must be a gap between the empirical error and the generalization error. Fortunately, Bousquet and Elisseeff [22] have given the relation between stability and generalization. They give the generalization error bound in Theorem 2. That is to say the difference between the empirical error and the generalization error can be measured by the stability of a learning algorithm.

Theorem 2.

For any learning algorithm $A$ with pointwise hypothesis stability $\delta$ with respect to a loss function $\ell$ such that $0 \le \ell \left( {f,z} \right) \le B$, we have

$$ R\left( {A,S} \right) \le R_{emp} \left( {A,S} \right) + \sqrt {\frac{{B^{2} + 12Bm\delta }}{2m}} $$

(23)

where $R\left( {A,S} \right)$ is the generalization error and $R_{emp} \left( {A,S} \right)$ is the empirical error.

Note that for a loss function we can always find a suitable upper bound, for example, a large enough bound. Considering we tune the kernel parameters with the same loss function, the upper bound can be seen as a constant argument. In this case, the generalization error bound is just affected by the empirical error on the training dataset and the pointwise hypothesis stability of the learning algorithm.

In order to present the application of pointwise hypothesis stability in model selection, we carry out the experiments on the UCI datasets [25]. Table 1 shows a summary of the datasets used in the experiments. We take the experiment on the vowel dataset as an instance. To reduce the computational complexity, we use 10-fold cross validation to split the whole dataset into 10 parts, and select one part as the training dataset and another part as the test dataset. Moreover, we do not discuss the parameter $C$ which is related to the regularization parameter $\lambda$, and treat it as a constant argument. SVMs are trained on a Gaussian kernel $K\left( {x,x_{i} } \right) = \exp \left\{ { - {{\left| {x - x_{i} } \right|^{2} } \mathord{\left/ {\vphantom {{\left| {x - x_{i} } \right|^{2} } {\sigma^{2} }}} \right. \kern-0pt} {\sigma^{2} }}} \right\}$. So, we have $\kappa = \max_{s} \max_{i} G_{ii}^{s} = \max_{s} \max_{i} K^{s} \left( {x_{i} ,x_{i} } \right) = 1$. In this case, computing the pointwise hypothesis stability means computing the average number of support vectors for each sample on all binary classifiers. Note that we focus on searching for the best value of the kernel parameter $\sigma$ of the Gaussian kernel. Finally, the parameters are set as $C = 10$ and $\sigma \in \left[ {0.1,4} \right]$ sampled with step 0.1. The used coding strategy is one-versus-all. Figure 2 shows the experimental result.

Table 1. Summary of the used datasets.

Fig. 2.

Experimental result on the vowel dataset

Figure 2(c) plots the training error against different kernel parameter $\sigma$. We can observe that when the kernel parameter $\sigma$ is smaller than 1.3, the training error is the minimum value, equal to zero. However, in Fig. 2(b) the test error is not at the least level, although there is a downward trend. This is just the overfitting problem. In other word, the minimum training error not always leads to the minimum test error. Intuitively, if we combine two figures together [Fig. 2(a) and (c)], the combination will have the same trend with the test error, which is just a validation to Theorem 2. To finish this combination, we calculate the proportion that the number of support vectors for each sample takes on the number of binary classifiers, which can be seen as the possibility of being a support vector for each sample, and regard it as the pointwise hypothesis stability. Refer to Theorem 2, Fig. 2(d) shows the estimation of generalization error against different kernel parameter $\sigma$. We can observe that the minimum of the generalization error estimate is very close to the minimum of the test error, although there is a slight deviation. Moreover, Fig. 3 shows the comparison between the generalization error and the test error on several UCI datasets. The comparison result shows that the generalization error estimated by pointwise hypothesis stability can be used to select the better value of kernel parameter in the model selection.

Fig. 3.

Comparison between the generalization error and the test error

4.2 Good Coding Matrixes Design

On the other hand, the coding matrix design problem is that given a set of binary classifiers, finding a matrix which has better generalization performance. Crammer and Singer [26] have proven that this problem is NP-complete. As an alternative way, many works have focused on the problem dependent design for coding matrixes, such as, Discriminant ECOC [15] and Subclass ECOC [16], which can be a promising approach in the future. For the moment, these problem dependent designs are implemented to achieve a specific criterion. For example, Discriminant ECOC is designed to maximize a discriminative criterion, and Subclass ECOC is designed to guarantee that the base classifier is capable of splitting each subgroup of classes. In this case, the key point for problem dependent design is to find a criterion, which will lead to a better generalization performance. However, there is less formal justification to find it. The difficulty for the problem dependent design is that there is no an apparent relationship between the generalization performance and the property of coding matrix. That is to say if we know which property of coding matrix will lead to a better generalization performance, we can take this property as the criterion in the problem dependent design, such as, the discriminative criterion.

Fortunately, we think that pointwise hypothesis stability will make a certain process for the problem dependent design. Theorem 2 shows the difference between the generalization error and the empirical error. It is sure that if we reduce this difference, we will obtain the better generalization performance. Note that in this paper we do not discuss how to get minimum empirical error, because this problem needs a more detailed work. Just as in Sect. 4.1, we also take the upper bound for the loss function as the constant argument. So, the difference is just affected by pointwise hypothesis stability of the learning algorithm. In this case, the minimization for this difference is equal to the minimization for pointwise hypothesis stability.

Refer to Theorem 1, pointwise hypothesis stability for ECOC kernel machines can be written as follows:

$$ \delta = \frac{2\kappa C}{m}\sum\limits_{i = 1}^{m} {\sum\limits_{s = 1}^{l} {\theta \left( {\alpha_{i}^{s} } \right)} } $$

(24)

Considering that we just take care the coding matrix design, parameters, such as, $\kappa ,C,m$, can be seen as the constant arguments. So, pointwise hypothesis stability is determined by $\sum\nolimits_{s = 1}^{l} {\theta \left( {\alpha_{i}^{s} } \right)}$.

Note that $l$ is the codeword length or the number of binary classifiers. Now we discuss that when the codeword length is given, what we should do to minimize the pointwise hypothesis stability. In this case, $\sum\nolimits_{s = 1}^{l} {\theta \left( {\alpha_{i}^{s} } \right)}$ can be seen as the possibility for one sample $\left( {x_{i} ,y_{i} } \right)$ to be support vectors among all binary classifiers. Reducing the pointwise hypothesis stability means to reduce the possibility for all samples in the training dataset. On the other hand, the support vectors are the samples on the separating surface. In other word, the separating surface is represented by the support vectors. Complex separating surface needs more support vectors, which often means that the two class groups are difficult to be split. If two class groups have maximum class discrimination, the separating surface will be simple and the possibility for one sample to be a support vector will be reduced. That is to say if we want to reduce the pointwise hypothesis stability and have a better generalization performance for ECOC kernel machines, we should design the coding matrix which has high discrimination power. This also validates that the Discriminant ECOC has the advantage to have better generalization performance.

In order to validate the relationship between the discriminative criterion in problem dependent design of coding matrix and the pointwise hypothesis stability, we carry out a simple experiment on the synthetic dataset. The synthetic dataset generated randomly has four classes. There are 100 samples for each class. The feature vector of each class has two dimensions: Feature1 and Feature2. The probability density function for each class is defined as follows:

$$ p\left( {x|class_{i} } \right) = \frac{1}{{2\pi \left| {\Sigma _{i} } \right|^{1/2} }}\exp \left[ { - \frac{1}{2}\left( {x - \mu_{i} } \right)^{T}\Sigma _{i}^{ - 1} \left( {x - \mu_{i} } \right)} \right]\quad i = 1,2, \cdots 4 $$

(25)

where the parameters are shown in Table 2. Figure 4 shows the distribution of four classes.

Table 2. Parameters for synthetic dataset

Fig. 4.

The synthetic dataset with four classes

Simply, we take the design of one column of the coding matrix into consideration. In this experiment, we compare two columns with different discrimination power. Intuitively, in Fig. 4 we can observe that the class groups $\left\{ {\left\{ {Class1,Class2} \right\},\left\{ {Class3,Class4} \right\}} \right\}$ can be split more easily than the class groups $\left\{ {\left\{ {Class1,Class3} \right\},\left\{ {Class2,Class4} \right\}} \right\}$. So, one column is set as $P1 = \left[ {1, - 1,1, - 1} \right]^{T}$ and the other column is set as $P2 = \left[ {1,1, - 1, - 1} \right]^{T}$, with more class discrimination. The pointwise hypothesis stability for each column is calculated by the proportion that the support vectors take up all the samples in the synthetic dataset, which is proportional to the possibility of one sample to be a support vector. Figure 5 shows the fluctuation curves of pointwise hypothesis stability of two columns against different experiment times. We can see that the pointwise hypothesis stability of $P2$ is smaller than that of $P1$. This experiment proves that the maximization of discriminative criterion can lead to have smaller pointwise hypothesis stability, which may lead to a better generalization performance finally.

Fig. 5.

Pointwise hypothesis stability of two columns

However, the design of good coding matrix is a complex problem, which is determined by many different factors, such as, the codeword length and the minimum hamming distance. Furthermore, these factors may work in an intersectant way. For example, if we only achieve the minimum pointwise hypothesis stability, maybe we will get a bad training error rate. So, the design of good coding matrix needs a tradeoff among several factors or criterions.

5 Conclusion

We provide a proof for the result that an ECOC kernel machines has the pointwise hypothesis stability. In our proof, the stability is determined by the coefficients which can be calculated by training the machines once on the training dataset, and it is easy to be applied in practice. Note that the stability can be seen as the difference between the training error and the generalization error. Minimizing this gap can help to reduce the generalization error. Finally, the applications of this stability in model selection and good coding matrixes design for ECOC kernel machines are presented. How to take both the training error and pointwise hypothesis stability into consideration in good coding matrixes design will be a meaningful direction to get better generalization capability, which will be discussed in our future research works.