Keywords

1 Introduction and Related Work

Infrared image identifies the thermal and hidden targets, it can unaffected by the external influences and occlusion, but it is poor contrast and details. In contrast, visible image can provide higher contrast and rich details, but its quality is easily affected by light intensity, occlusion and the impact of surroundings. Fuse the two type images can get a more informative image, it has been widely used in military reconnaissance, target recognition, society security and other fields [1].

Therefore, to fuse the different sensor images, there exits many algorithms which can be classified into two types: spatial domain and transform domain. The traditional algorithms fuse images based on spatial domain mainly, such as weighted average, principal component analysis [2] (PCA), gradient transform [3], contrast transform [4] and other algorithms. This kind of algorithms are simple and efficient. But the fused image is lack of image information and details, the edges of targets are not perfect.

To this end, scholars began to fuse images based on transform domain. The first transform domain algorithm is based on the wavelet transform domain [5], image can be decomposed into a low coefficient and a series of high level coefficients via wavelet transform. Those coefficients preserve the important information of the image, but high level coefficients express three directions only, so there are flaws in the details of performance. For the problem of wavelet transform, more transform domain fusion methods are proposed, such as Curvelet transform [6], contourlet transform [7] can decompose the image into more directions on different scales. Those methods perform well in processing the details, but the filter kernel is complex and hard to calculation. Guo and Labate proposed Shearlet transform [8, 9], this multi-scales geometric analysis is simple and effective, express the details and edges better.

Fusion methods based on the transform domain [10,11,12] enhance the quality of the details in fused image significantly, but their results are widespread lack of contrast information. Generally, the infrared image is larger than visible image in intensity, so most of those methods may lose a lot of information of visible image. Because those methods mainly use the coefficients directed without considering the connection between the coefficients, fused image contrast in not enough.

Summarizing the above problems, it is significant to proposed a novel transform. Hence, we try to proposed a novel transform named NSSCT to fuse infrared and visible images in this paper. Firstly, we introduce the framework of image fusion and build the NSSCT coefficients. Then, the fusion image achieved by the proposed rules in different coefficients. Finally, the experiment results prove that the performance of proposed fusion method.

2 Fusion Scheme and NSSCT

2.1 Framework for Image Fusion

In order to obtain a more informative fused image, the fused image should retain both hidden target information and contrast information. So we use NSSCT to decompose the infrared image and visible image, NSSCT is presented in the next section, obtain the coefficients which contain contrast information. Foinr the low coefficients, extract the saliency map to enhance the saliency target; for the high level coefficients fuse them to enhance the contrast of fused image. The schematic of proposed method is shown below (Fig. 1).

Fig. 1.
figure 1

Schematic diagram of the proposed method

Full size image

2.2 Non-subsampled Shearlet-Contrast Transform

NSST

Shearlet transform [8] is a multi-scales geometric analysis tool proposed by Guo and Labate. The direction filter kernel is simple, for the high level coefficients, there are more directions and is steerable.

For a two-dimensional affine system, it is constructed as:

$$ \xi_{AB} (\psi ) = \{ \psi_{j,l,k} (x) = \left| {\det A} \right|^{j/2} \,\psi (B^{l} A^{j} x - k):j,l{ \in }Z,k{ \in }Z^{2} \} $$
(1)

where \( \psi { \in }L^{2} (R^{2} ) \), L is the integrable space, R is the set of real numbers, and Z is the set of integers. A and B are 2 × 2 reversible matrix, j is the decomposition level, l is the number of each decomposition direction, k is the transform parameter.

Suppose that ξ AB (ψ) satisfies the Parseval assumption (tight support condition) for any function \( f{ \in }L^{2} (R^{2} ) \), as:

$$ \sum\limits_{j,l,k} {| < f,\psi_{j,l,k} > |^{2} } = ||f||^{2} $$
(2)

Then, the ψ j,l,k is the synthetic wavelet. Matrix A controls the scale and matrix B controls the direction. In general, \( A = \left[ {\begin{array}{*{20}c} 4 & 0 \\ 0 & 2 \\ \end{array} } \right] \) and \( B = \left[ {\begin{array}{*{20}c} 1 & 1 \\ 0 & 1 \\ \end{array} } \right] \) in the Shearlet transform.

NSST is based on the Shearlet transform using nonsubsampled scaling and direction filter processing. NSST is considered to be the optimal approximation of sparse representation for image. Hence, a lot of methods [13, 14] based on NSST are proposed, the results perform well in reserve image details and edges, but most of those methods use the coefficients directed, so the results is short of contrast.

NSSCT

Because of the lack of contrast in fusion results, we analyze the coefficients by NSST, and build a novel transform named NSSCT.

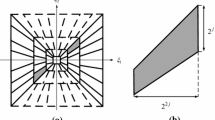
The image F is decomposed into a low coefficient I L and a series of high level coefficients [G 1 , G 2 …G i …G n ]. For any adjacent high level coefficients, the coefficients direction of the scale i + 1 is double as more as the scale i. An example in shown in Fig. 2.

Fig. 2.
figure 2

The adjacent levels coefficients

Full size image

Figure 2 shows the results of the first scale high level coefficients G 1 and the second scale high level coefficients G 2 after decompose the image Lena. It is easily to know that the lower level coefficients can be the background of the higher level coefficients.

It is obvious also that \( G_{1}^{1} \) is correlate with \( G_{2}^{1} \) and \( G_{2}^{2} \), but uncorrelated with other coefficients inlevel 2. So we calculate the correlation [15] between G 1 and G 2 . The Fig. 3 show the results.

Fig. 3.
figure 3

The value of correlation between adjacent coefficients

Full size image

It is apparently in Fig. 3 that lower level coefficients correlate with the two higher coefficients which are similar direction. In order to improve the contrast information of the fused images, it is necessary to make the relevant scales contain the contrast information of the images. To obtain the contrast information needs compare the adjacent scales. At that time, we need transform the coefficients to ensure the consistency and numbers between the adjacent scales. Hence, the coefficients of G 2 are transformed as:

$$ G_{2}^{1*} = G_{2}^{1} \odot G_{2}^{2} $$
(3)

Before explain the operation \( \odot \) we will analyze the process to calculate the hig level coefficients.

$$ G_{j}^{l} = \left\langle {f,\psi_{j,l,k}^{(d)} } \right\rangle = 2^{{\frac{3j}{2}}} \int\limits_{{R^{2} }} {\hat{f}(\xi )\overline{{V(2^{ - 2j} \xi )W_{j,l}^{(d)} (\xi )}} e^{{2\pi i\xi A_{d}^{ - j} B_{d}^{ - l} k}} d\xi } $$
(4)

For \( G_{2}^{l} \), it is in the right frequency domain, so d = 0. The parameter j = 2 and l = 1. Hence, the direction of the coefficients is determined by l. The definition of V and W parameters in (7) is given in [9, 10]. We calculate the \( G_{2}^{1*} \) to explain the operation \( \odot \).

$$ \begin{aligned} G_{2}^{1*} & = G_{2}^{1} \odot G_{2}^{2} \\ & = \left\langle {f,\psi_{2,1}^{(0)} } \right\rangle \odot \left\langle {f,\psi_{2,2}^{(0)} } \right\rangle \\ & = 2^{3} \int\limits_{{R^{2} }} {\hat{f}(\xi )\overline{{V(2^{ - 2} \xi )}} e^{{2\pi i\xi A_{0}^{ - 1} }} (W_{2,1}^{(d)} (\xi )e^{{B_{0}^{ - l} }} \odot W_{2,2}^{(d)} (\xi )e^{{B_{0}^{ - 2} }} )d\xi } \\ \end{aligned} $$
(5)

There are two coefficients \( G_{2}^{1} \) and \( G_{2}^{2} \) which are the same scale but different directions. Hence, when calculate the \( G_{2}^{1*} \), the direction filter W and the matrix B is most important. So we calculate it as:

$$ W_{j,l}^{(d)} (\xi )e^{{B_{0}^{ - l} }} \odot W_{j,l + 1}^{(d)} (\xi )e^{{B_{0}^{ - l + 1} }} = \left\{ {\begin{array}{*{20}l} {(\psi_{2} (2^{j} \frac{{\xi_{2} }}{{\xi_{1} }} - l/2) \times D_{0} (\xi ) + \psi_{2} (2^{j} \frac{{\xi_{1} }}{{\xi_{2} }} - l/2 + 1) \times D_{1} (\xi ))e^{{B_{0}^{ - l} }} } \hfill & {if,l = - 2^{j - 1} } \hfill \\ {(\psi_{2} (2^{j} \frac{{\xi_{2} }}{{\xi_{1} }} - l/2) \times D_{0} (\xi ) + \psi_{2} (2^{j} \frac{{\xi_{1} }}{{\xi_{2} }} - l/2 - 1) \times D_{1} (\xi ))e^{{B_{0}^{ - l} }} } \hfill & {if,l = 2^{j - 1} - 1} \hfill \\ {(\psi_{2} (2^{j} \frac{{\xi_{2} }}{{\xi_{1} }} - l/2))e^{{B_{0}^{ - l} }} \,otherwise} \hfill & {} \hfill \\ \end{array} } \right. $$
(6)

In (6), \( \psi_{2} \) is the direction component of the Shearlet transform, \( D_{0} (\xi ) \) and \( D_{1} (\xi ) \) are the support frame of the Shearlet. Then, we can get the \( G_{2}^{1*} \), the other coefficients can be calculated as above equations.

In order to preserve the contrast information, we contrast the coefficients which are different scales but are similarity in direction. So that the contrast information will be contained in the coefficients.

$$ \left\{ {\begin{array}{*{20}l} {G_{i}^{k} = \frac{{G_{i + 1}^{k\,*} }}{{G_{i}^{k} }} - I} \hfill & {if,N > i \ge 1} \hfill \\ {G_{i}^{k} = G_{i}^{k} } \hfill & {if,i = N} \hfill \\ \end{array} (0 < k < 2^{i - 1} )} \right. $$
(7)

3 Fusion Rules

3.1 Rule of High Level Coefficients

Based on the (4), (5) and (6), we have obtained the new coefficients. The new coefficients reflect the contrast and details information, to enhance the contrast and preserve the details, it is necessary to calculate the fusion coefficients in different region. Thus, \( G_{i}^{k} (I_{r} ) \) and \( G_{i}^{k} (V_{i} ) \), which are high level coefficients at level i and direction k of infrared and visible respectively, with approximation value can be considered to be redundant data. It means that they both are the details or regions with similar contrast, hence, it is applicative to obtain the fused coefficients by weighted summation. On the other hand, \( G_{i}^{k} (I_{r} ) \) and \( G_{i}^{k} (V_{i} ) \) with different characteristics which means that one of them are details or region with high contrast, the larger should be preserve. Thus, a threshold σ should be set. The specific calculate rule is shown as:

$$ G_{i}^{k} (fus) = \left\{ {\begin{array}{*{20}l} {\omega *G_{i}^{k} (I_{r} ) + \omega *G_{i}^{k} (V_{i} )} \hfill & {\left| {H(G_{i}^{k} (I_{r} )) - H(G_{i}^{k} (V_{i} ))} \right| < \sigma } \hfill \\ {\;\;\;\;\;\;\;\;\;\;G_{i}^{k} (I_{r} )} \hfill & {H(G_{i}^{k} (I_{r} )) - H(G_{i}^{k} (V_{i} )) > \sigma } \hfill \\ {\;\;\;\;\;\;\;\;\;\;G_{i}^{k} (V)} \hfill & {H(G_{i}^{k} (I_{r} )) - H(G_{i}^{k} (V_{i} )) < - \sigma } \hfill \\ \end{array} } \right. $$
(8)

where \( G_{i}^{k} (fus) \) denotes the fused coefficients. H(.) denotes the calculate of normalization. σ is the threshold to control different regions, in this paper, σ is set to 0.8. \( \omega = 1 - \omega \), \( \omega \) is a parameter to control fusion weights, the calculate of \( \omega \) as:

$$ \omega = \frac{{H(G_{i}^{k} (I_{r} ))}}{{H(G_{i}^{k} (I_{r} )) + H(G_{i}^{k} (V_{i} ))}} $$
(9)

After the fusion, we obtain the fused high level coefficients which preserve details and contrast, the fused image can avoid lacking of information.

3.2 Rule of Low Level Coefficients

The low level coefficients is the overview of source image, which contains the main information of the target and entropy of the image. To enhance the quality of the fused image, the fusion rule should based on the saliency [16] of the target.

Hence, we calculate the value of saliency for the image,

$$ S_{i} = 1 - \exp \{ - \frac{1}{M}\sum\limits_{m = 1}^{M} {\frac{{d_{inensity} (p_{i} ,p_{j}^{m} )}}{{1 + \varepsilon \bullet d_{position} (p_{i} ,p_{j}^{m} )}}} \} $$
(10)

In the (10), p i and p j denotes pixel patch which size is 3 × 3 centered on pixel i and j respectively. \( d_{inensity} (p_{i} ,p_{j}^{{}} ) \) denotes the intensity distance between the two pixel patches, and is calculated by the difference between the average value of the two pixel patches. \( d_{position} (p_{i} ,p_{j}^{{}} ) \) denotes the difference of Euler distances between two pixel patches. ε is a parameter to control the value saliency in pixel i, in this paper, ε is set to 0.6. (10) shows that intensity distance is positive correlation with the S i , and Euler distance is negative correlation with the S i . The value of S i shows the saliency in the image, the more larger, the more salient. So the rule of low coefficient fusion need to compare the value of saliency.

$$ L_{i} (fus) = \, \left\{ {\begin{array}{*{20}l} {L_{i} (I_{r} ) + \beta \bullet S_{i} (I_{r} )} \hfill & {H(S_{i} (I_{r} )) - H(S_{i} (V_{i} )) > \sigma_{L} } \hfill \\ {L_{i} (V_{i} ) + \beta \bullet S_{i} (V_{i} )} \hfill & {H(S_{i} (I_{r} )) - H(S_{i} (V_{i} )) < - \sigma_{L} } \hfill \\ {\alpha (L_{i} (I_{r} ) + \beta \bullet S_{i} (I_{r} )) + \alpha (L_{i} (V_{i} ) + \beta \bullet S_{i} (V_{i} ))} \hfill & {otherwise} \hfill \\ \end{array} } \right. $$
(11)

There are also necessary to build a threshold \( \sigma_{L} \) to distinguish different regions for different fusion rule, to make the target more salient, the \( \sigma_{L} \) need to be smaller than σ, \( \sigma_{L} \) is set to 0.5.

4 Experimental Results

4.1 Experiment Setting

To evaluate the performance of the proposed methods on image fusion, we select two sets of infrared images and visible image in this experiment and compare the performance between PCA [2], GT [3], CP [4], DWT [5] SAL (saliency) [17], NSCT [11] and NSST [12]. The number of levels in our method is 5.

4.2 Subjective Visual Test

Figure 4 shows the comparison on image with target. (a) and (b) are the source infrared and visible image, (c)–(j) are fused image by PCA, DWT, CP, GT, SAL, NSCT, NSST, and proposed methods, respectively. The targets in results are marked by blue rectangle and details of roof are marked by red rectangle. Target in proposed result is more saliency than PCA and NSST, compared with DWT, NSCT, SAL and GT results, the target are less bright, but those results are too bright to cover the contrast and details for the targets. It is also obvious that proposed result contain more details in the red rectangles. The results of PCA, DWT, SAL and NSCT brings the halo effects in the red rectangles. The CP results perform well in contrast of image, but is lack of some edges information, the result by the proposed methods perform better than it.

Fig. 4.
figure 4

The first set of experimental results (Color figure online)

Full size image

Figure 5 shows the comparison on image with more details and different contrast between infrared and visible images. (a) and (b) are the source infrared and visible image, (c)–(j) are fused image by PCA, DWT, CP, GT, SAL, NSCT, NSST, and proposed methods, respectively.

Fig. 5.
figure 5

The second set of experimental results (Color figure online)

Full size image

The person targets in results are marked by green rectangle, the details of the seat within the store are marked by blue rectangle, and the texts in the roof are marked by red rectangle. The results by the proposed methods is superior to the other methods in the contrast. In the green rectangle, the results by the PCA, DWT, GT, SAL, NSCT are lack of contrast information, those results extract the most information form the infrared image, but the contrast information is mainly contained in visible image. The results by the NSST preserve the details well, but in the bule rectangle, it is fuzzy because of less contrast. CP methods perform well for the contrast of the image, but the details of the text in the roof are insufficient. So, the performance of the proposed methods is the best among those methods.

4.3 Quantitative Tests

To compare the performance on image fusion by above methods with quantitative measurement, the measure indexes of image quality (Q) [18], edge quality (Q e ) [19] and mutual information (MI) [20] are used in this paper (Table 1).

Table 1. Quantitative comparison for Fig. 4
Full size table

It is obvious that proposed method achieves the largest value of Q and Q e among other methods, which demonstrates that or method performs well in contrast and details of the fused image. The PCA result achieves larger value of MI for Fig. 5, because of the similar structure to visible, but loss the information of target from the infrared image (Table 2).

Table 2. Quantitative comparison for Fig. 5
Full size table

5 Conclusion

Fused image has been widely used in many fields. But contrast loss and edge blurring limit its future development in industry application. To improve its quality, we construct a novel transform to decompose the image. For the high level coefficients, we fuse them to enhance the details and contrast; fuse the low level coefficients to enhance the salient of the target in source image. In addition, the experiment with subjective visual and quantitative tests show that the proposed methods can preserve details on the edges and enhance contrast of the image.