Abstract
Attrapadung (Eurocrypt 2014) proposed a generic framework called pair encoding to simplify the design and proof of security of CPA-secure predicate encryption (PE) in composite order groups. Later Attrapadung (Asiacrypt 2016) extended this idea in prime order groups. Yamada et al. (PKC 2011, PKC 2012) and Nandi et al. (ePrint Archive: 2015/457, AAECC 2017) proposed generic conversion frameworks to achieve CCA-secure PE from CPA-secure PE provided the encryption schemes have properties like delegation or verifiability. The delegation property is harder to achieve and verifiability based conversion degrades the decryption performance due to a large number of additional pairing evaluations. Blömer et al. (CT-RSA 2016) proposed a direct fully CCA-secure predicate encryption in composite order groups but it was less efficient as it needed a large number of pairing evaluations to check ciphertext consistency. As an alternative, Nandi et al. (ePrint Archive: 2015/955) proposed a direct conversion technique in composite order groups. We extend the direct conversion technique of Nandi et al. in the prime order groups on the CPA-secure PE construction by Attrapadung (Asiacrypt 2016) and prove our scheme to be CCA-secure in a quite different manner. Our first direct CCA-secure predicate encryption scheme requires exactly one additional ciphertext component and three additional units of pairing evaluation during decryption. The second construction requires exactly three additional ciphertext components but needs only one additional unit pairing evaluation during decryption. This is a significant improvement over conventional approach for CPA-to-CCA conversion in prime order groups.
Access this chapter
Tax calculation will be finalised at checkout
Purchases are for personal use only
Similar content being viewed by others
Notes
- 1.
- 2.
Suppose given ciphertext is \({\overline{\varvec{\mathrm{C}}}}=(\mathrm {\overline{\mathrm{C}}}_0,\varvec{\mathrm{C}})\) where \(\mathrm {\overline{\mathrm{C}}}_0= {{ g}_1}^{(\xi \mathbf {W}_{n+1}+\mathbf {W}_{n+2})c_1+{\mathbf {B}}\Big ({\begin{matrix}{\mathbf {0}}\\ \tau \end{matrix}}\Big )}\) for some \(\tau \in {\mathbb {Z}}_p\) and \(\mathrm{C}_1={ g}_1^{c_1}\). Note that it satisfies the verification in Eq. (1) as can be seen in Lemma 1. However, as the simulator knows \(\mathbf {W}_{n+1}\) and \(\mathbf {W}_{n+2}\), it can compute \(L={{ g}_1}^{(\xi \mathbf {W}_{n+1}+\mathbf {W}_{n+2})c_1}\). Therefore it gets hold of \({ g}_1^{{\mathbf {B}}\Big ({\begin{matrix}{\mathbf {0}}\\ \tau \end{matrix}}\Big )}\) by computing \(\mathrm {\overline{\mathrm{C}}}_0/L\). Since, \({\mathbf {B}}\) and \({\mathbf {Z}}\) are simulated exactly as Lemma 2 (see the Setup of Lemma 2), and \({\mathcal {B}}_1\) implicitly sets
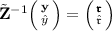 to compute \(i^{th}\) altKey,
to compute \(i^{th}\) altKey,  evaluation will allow the simulator to decide the \({\mathcal {D}}_d{\text {-MatDH}}\) problem instance. Thus, under \({\mathcal {D}}_d{\text {-MatDH}}\) assumption, the adversary can’t make such decryption query. Therefore any decryption query \({\mathcal {A}}\) makes, to satisfy Eq. (1), the queried ciphertext \({\overline{\varvec{\mathrm{C}}}}\) must follow the relation that \(\mathrm {\overline{\mathrm{C}}}_0={{ g}_1}^{(\xi \mathbf {W}_{n+1}+\mathbf {W}_{n+2})c_1}\) and \(\mathrm{C}_1={ g}_1^{c_1}\) where \(\xi =\mathcal {H}(\varvec{\mathrm{C}})\).
evaluation will allow the simulator to decide the \({\mathcal {D}}_d{\text {-MatDH}}\) problem instance. Thus, under \({\mathcal {D}}_d{\text {-MatDH}}\) assumption, the adversary can’t make such decryption query. Therefore any decryption query \({\mathcal {A}}\) makes, to satisfy Eq. (1), the queried ciphertext \({\overline{\varvec{\mathrm{C}}}}\) must follow the relation that \(\mathrm {\overline{\mathrm{C}}}_0={{ g}_1}^{(\xi \mathbf {W}_{n+1}+\mathbf {W}_{n+2})c_1}\) and \(\mathrm{C}_1={ g}_1^{c_1}\) where \(\xi =\mathcal {H}(\varvec{\mathrm{C}})\).
References
Boneh, D., Franklin, M.: Identity-based encryption from the Weil pairing. In: Kilian, J. (ed.) CRYPTO 2001. LNCS, vol. 2139, pp. 213–229. Springer, Heidelberg (2001). https://doi.org/10.1007/3-540-44647-8_13
Waters, B.: Dual system encryption: realizing fully secure IBE and HIBE under simple assumptions. In: Halevi, S. (ed.) CRYPTO 2009. LNCS, vol. 5677, pp. 619–636. Springer, Heidelberg (2009). https://doi.org/10.1007/978-3-642-03356-8_36
Attrapadung, N.: Dual system encryption via doubly selective security: framework, fully secure functional encryption for regular languages, and more. In: Nguyen, P.Q., Oswald, E. (eds.) EUROCRYPT 2014. LNCS, vol. 8441, pp. 557–577. Springer, Heidelberg (2014). https://doi.org/10.1007/978-3-642-55220-5_31
Wee, H.: Dual system encryption via predicate encodings. In: Lindell, Y. (ed.) TCC 2014. LNCS, vol. 8349, pp. 616–637. Springer, Heidelberg (2014). https://doi.org/10.1007/978-3-642-54242-8_26
Attrapadung, N.: Dual system encryption framework in prime-order groups via computational pair encodings. In: Cheon, J.H., Takagi, T. (eds.) ASIACRYPT 2016. LNCS, vol. 10032, pp. 591–623. Springer, Heidelberg (2016). https://doi.org/10.1007/978-3-662-53890-6_20
Chen, J., Gay, R., Wee, H.: Improved dual system ABE in prime-order groups via predicate encodings. In: Oswald, E., Fischlin, M. (eds.) EUROCRYPT 2015. LNCS, vol. 9057, pp. 595–624. Springer, Heidelberg (2015). https://doi.org/10.1007/978-3-662-46803-6_20
Chen, J., Wee, H.: Dual system groups and its applications – compact HIBE and more. Cryptology ePrint Archive, Report 2014/265 (2014). http://eprint.iacr.org/2014/265
Agrawal, S., Chase, M.: A study of pair encodings: predicate encryption in prime order groups. In: Kushilevitz, E., Malkin, T. (eds.) TCC 2016. LNCS, vol. 9563, pp. 259–288. Springer, Heidelberg (2016). https://doi.org/10.1007/978-3-662-49099-0_10
Agrawal, S., Chase, M.: Simplifying design and analysis of complex predicate encryption schemes. Cryptology ePrint Archive, Report 2017/233 (2017). http://eprint.iacr.org/2017/233
Yamada, S., Attrapadung, N., Hanaoka, G., Kunihiro, N.: Generic constructions for chosen-ciphertext secure attribute based encryption. In: Catalano, D., Fazio, N., Gennaro, R., Nicolosi, A. (eds.) PKC 2011. LNCS, vol. 6571, pp. 71–89. Springer, Heidelberg (2011). https://doi.org/10.1007/978-3-642-19379-8_5
Yamada, S., Attrapadung, N., Santoso, B., Schuldt, J.C.N., Hanaoka, G., Kunihiro, N.: Verifiable predicate encryption and applications to CCA security and anonymous predicate authentication. In: Fischlin, M., Buchmann, J., Manulis, M. (eds.) PKC 2012. LNCS, vol. 7293, pp. 243–261. Springer, Heidelberg (2012). https://doi.org/10.1007/978-3-642-30057-8_15
Nandi, M., Pandit, T.: Generic conversions from CPA to CCA secure functional encryption. Cryptology ePrint Archive, Report 2015/457 (2015). http://eprint.iacr.org/
Nandi, M., Pandit, T.: Verifiability-based conversion from CPA to CCA-secure predicate encryption. J. Appl. Algebra Eng. Commun. Comput., 1–26 (2017). https://doi.org/10.1007/s00200-017-0330-2
Blömer, J., Liske, G.: Construction of fully CCA-secure predicate encryptions from pair encoding schemes. In: Sako, K. (ed.) CT-RSA 2016. LNCS, vol. 9610, pp. 431–447. Springer, Cham (2016). https://doi.org/10.1007/978-3-319-29485-8_25
Nandi, M., Pandit, T.: On the power of pair encodings: Frameworks for predicate cryptographic primitives. Cryptology ePrint Archive, Report 2015/955 (2015). http://eprint.iacr.org/2015/955
Freeman, D.M.: Converting pairing-based cryptosystems from composite-order groups to prime-order groups. In: Gilbert, H. (ed.) EUROCRYPT 2010. LNCS, vol. 6110, pp. 44–61. Springer, Heidelberg (2010). https://doi.org/10.1007/978-3-642-13190-5_3
Boyen, X., Mei, Q., Waters, B.: Direct chosen ciphertext security from identity-based techniques. In: ACM Conference on Computer and Communications Security, CCS 2005, pp. 320–329. ACM (2005). https://doi.org/10.1145/1102120.1102162
Canetti, R., Halevi, S., Katz, J.: Chosen-ciphertext security from identity-based encryption. In: Cachin, C., Camenisch, J.L. (eds.) EUROCRYPT 2004. LNCS, vol. 3027, pp. 207–222. Springer, Heidelberg (2004). https://doi.org/10.1007/978-3-540-24676-3_13
Chatterjee, S., Mukherjee, S., Pandit, T.: CCA-secure predicate encryption from pair encoding in prime order groups: generic and efficient. Cryptology ePrint Archive, Report 2017/657 (2017). http://eprint.iacr.org/2017/657
Lewko, A., Okamoto, T., Sahai, A., Takashima, K., Waters, B.: Fully secure functional encryption: attribute-based encryption and (hierarchical) inner product encryption. In: Gilbert, H. (ed.) EUROCRYPT 2010. LNCS, vol. 6110, pp. 62–91. Springer, Heidelberg (2010). https://doi.org/10.1007/978-3-642-13190-5_4
Author information
Authors and Affiliations
Corresponding author
Editor information
Editors and Affiliations
Rights and permissions
Copyright information
© 2017 Springer International Publishing AG
About this paper
Cite this paper
Chatterjee, S., Mukherjee, S., Pandit, T. (2017). CCA-secure Predicate Encryption from Pair Encoding in Prime Order Groups: Generic and Efficient. In: Patra, A., Smart, N. (eds) Progress in Cryptology – INDOCRYPT 2017. INDOCRYPT 2017. Lecture Notes in Computer Science(), vol 10698. Springer, Cham. https://doi.org/10.1007/978-3-319-71667-1_5
Download citation
DOI: https://doi.org/10.1007/978-3-319-71667-1_5
Published:
Publisher Name: Springer, Cham
Print ISBN: 978-3-319-71666-4
Online ISBN: 978-3-319-71667-1
eBook Packages: Computer ScienceComputer Science (R0)





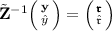 to compute
to compute  evaluation will allow the simulator to decide the
evaluation will allow the simulator to decide the