Abstract
A cryptographic hash function is a function \(H:\{0,1\}^{*}\rightarrow \{0,1\}^{n}\), that takes an arbitrary long input and transforms it to an n-bit output, while keeping some basic properties that ensure its security. Because they are very useful in computer security, cryptographic hash functions are amongst the most important primitives in the modern cryptography.
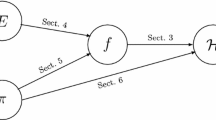
The Merkle-Damgård structure is an iterative construction for transforming a compression function \(f:\{0,1\}^{n}\times \{0,1\}^{m}\rightarrow \{0,1\}^{n}\) into a hash function, and it is widely used by different hash functions such as MD4, MD5, SHA0 and SHA1. Some generic attacks on this structure were presented in the last 15 years. Some of these attacks use the diamond structure, first introduced by Kelsey and Kohno in the herding attack. This structure is a complete binary tree that allows \(2^{k}\) different inputs to lead to the same hash value, and it used in numerous attacks on the Merkle-Damgård structure. Following the herding attack, other papers analyzed and optimized the diamond structure. The best time complexity of constructing a diamond structure to date is about \(a \cdot 2^{\frac{n+k}{2}+2}\) for \(a\approx 2.732\).
In this work we suggest a new and simple method for constructing a diamond structure with better time complexity of \(c\,\cdot \,2^{\frac{n+k}{2}+2}\) for \(c\approx 1.254\). We present a pseudo-code for this new method, and a recursive formulation of it. We also present analysis supported by experiments of our new method.
Access this chapter
Tax calculation will be finalised at checkout
Purchases are for personal use only
Similar content being viewed by others
Notes
- 1.
It is common to set \(2^{\ell }-1\) as the maximal length of a message.
- 2.
He should consider the length of the prefix P, or at least the maximum length of it, and if the real length is less than he considered, he can add some blocks to the \(M_{link}\) block, which will defined in the second phase.
- 3.
The degree of each vertex follows a Poisson distribution with a mean of 2. Thus, for each vertex, the probability that it is an isolated vertex is \(e^{-2}\), and thus we expect to about \(2^{k}\cdot e^{-2}\) isolated vertices.
- 4.
Blackburn et al. [6] discuss another model to represent the diamond construction: Sampling With Replacement Random Intersection Graph \(G_{SWR}(\nu ,m,L)\) random graph, defined as follow: Let V be a set of vertices where \(|V|=\nu \) (in our case \(\nu =2^{k}\)), and F be a colors set where \(|F|=m\) (in our case \(m=2^{n}\)). For each vertex \(v\in V\) generate a subset \(F_{v}\subset F\) by sampling uniformly with replacement L colors from F (in Kelsey-Kohno’s case \(L=2^{\frac{n-k+1}{2}}\)). Finally, \((v,u)\in E\iff F_{v}\cap F_{u}\ne \phi \). They achieve from this model the same results as from the G(n, p) model.
- 5.
Although usually we are looking for collisions, this requirement about the cardinality of \(H_{k,0}\) is needed for their analysis. Later, by our method, we will show how to use such collisions. If there are collisions, they replace the appropriate message blocks one by one until the required cardinality is obtained.
- 6.
If not, they replace some message blocks one by one until it is obtained.
- 7.
We note that the analysis of [20] uses a slightly different definition of a, but for more natural comparison with previous methods, we took a as the coefficient of \(2^{\frac{n+k}{2}+2}\).
- 8.
We tested this idea on more cases: when \(|E|\sim Poi(a\cdot |V|), a = 0.5 + \frac{t}{20},\forall t\in \{0,1,2,\dots ,19\}\). The difference between the results in the Kelsey-Kohno’s case and the best results is quite small (less than one standard deviation).
- 9.
It is easy to see that if we switch to the Blackburn et al. process earlier, the expected length of the diamond will decrease.
- 10.
We note that the mean value of the experiment is greater than those of the recursion by a few standard deviation units. This difference is a subject for a future research.
- 11.
We note that the mean value of the experiment is greater than those of the recursion by a few s.d. units. This difference is a subject for a future research.
References
Andreeva, E., Bouillaguet, C., Dunkelman, O., Fouque, P., Hoch, J.J., Kelsey, J., Shamir, A., Zimmer, S.: New second-preimage attacks on hash functions. J. Cryptol. 29(4), 657–696 (2016)
Aronson, J., Frieze, A., Pittel, B.G.: Maximum matchings in sparse random graphs: Karp-Sipser revisited. Random Struct. Algorithms 12, 111–178 (1998)
Barham, M., Dunkelman, O., Lucks, S., Stevens, M.: New second preimage attacks on dithered hash functions with low memory complexity. In: Avanzi, R., Heys, H. (eds.) Selected Areas in Cryptography – SAC 2016. LNCS, vol. 10532, pp. 247–263. Springer, Cham (2017). https://doi.org/10.1007/978-3-319-69453-5_14
Bertoni, G., Daemen, J., Peeters, M., Van Assche, G.: Keccak sponge function family main document. Submiss. NIST (Round 2) 3, 30 (2009)
Biham, E., Chen, R., Joux, A., Carribault, P., Lemuet, C., Jalby, W.: Collisions of SHA-0 and reduced SHA-1. In: Cramer [8], pp. 36–57
Blackburn, S.R., Stinson, D.R., Upadhyay, J.: On the complexity of the herding attack and some related attacks on hash functions. Des. Codes Crypt. 64(1–2), 171–193 (2012)
Brassard, G. (ed.): CRYPTO 1989. LNCS, vol. 435. Springer, New York (1990). https://doi.org/10.1007/0-387-34805-0
Cramer, R. (ed.): EUROCRYPT 2005. LNCS, vol. 3494. Springer, Heidelberg (2005). https://doi.org/10.1007/b136415
Damgård, I.: A design principle for hash functions. In: Brassard [7], pp. 416–427
Dean, R.D.: Formal aspects of mobile code security. Ph.D. thesis, Princeton University, Princeton (1999)
Erdös, P., Rényi, A.: On the evolution of random graphs. Publ. Math. Inst. Hung. Acad. Sci 5, 17–61 (1960)
Erdös, P., Rényi, A.: On the strength of connectedness of a random graph. Acta Math. Hung. 12(1–2), 261–267 (1961)
Erdös, P., Rényi, A.: On the existence of a factor of degree one of a connected random graph. Acta Math. Hung. 17(3–4), 359–368 (1966)
Hoch, Y.Z.: Security analysis of generic iterated hash functions. Ph.D. thesis, Weizmann Institute of Science, Rehovot, Israel (2009)
Joux, A.: Multicollisions in iterated hash functions. Application to cascaded constructions. In: Franklin, M. (ed.) CRYPTO 2004. LNCS, vol. 3152, pp. 306–316. Springer, Heidelberg (2004). https://doi.org/10.1007/978-3-540-28628-8_19
Karp, R.M., Sipser, M.: Maximum matchings in sparse random graphs. In: 22nd Annual Symposium on Foundations of Computer Science, Nashville, Tennessee, USA, 28–30 October 1981, pp. 364–375. IEEE Computer Society (1981)
Kelsey, J., Kohno, T.: Herding hash functions and the Nostradamus attack. In: Vaudenay, S. (ed.) EUROCRYPT 2006. LNCS, vol. 4004, pp. 183–200. Springer, Heidelberg (2006). https://doi.org/10.1007/11761679_12
Kelsey, J., Schneier, B.: Second preimages on n-bit hash functions for much less than 2\(^{\rm n}\) work. In: Cramer [8], pp. 474–490
Klima, V.: Finding MD5 collisions on a notebook PC using multi-message modifications. Cryptology ePrint Archive, Report 2005/102 (2005)
Kortelainen, T.: On iteration-based security flaws in modern hash functions. Ph.D. thesis, University of Oulu, Finland (2014)
Kortelainen, T., Kortelainen, J.: On diamond structures and Trojan message attacks. In: Sako, K., Sarkar, P. (eds.) ASIACRYPT 2013. LNCS, vol. 8270, pp. 524–539. Springer, Heidelberg (2013). https://doi.org/10.1007/978-3-642-42045-0_27
Merkle, R.C.: One way hash functions and DES. In: Brassard [7], pp. 428–446
Rivest, R.L.: Abelian square-free dithering for iterated hash functions. Presented at ECRYPT hash function workshop, Cracow, 21 June 2005, and at the cryptographic hash workshop, Gaithersburg, Maryland, 1 November 2005, August 2005
Sasaki, Y., Aoki, K.: Finding preimages in full MD5 faster than exhaustive search. In: Joux, A. (ed.) EUROCRYPT 2009. LNCS, vol. 5479, pp. 134–152. Springer, Heidelberg (2009). https://doi.org/10.1007/978-3-642-01001-9_8
Stevens, M.: Attacks on hash functions and applications. Ph.D. thesis, Leiden University (2012)
Stevens, M., Sotirov, A., Appelbaum, J., Lenstra, A., Molnar, D., Osvik, D.A., de Weger, B.: Short chosen-prefix collisions for MD5 and the creation of a rogue CA certificate. In: Halevi, S. (ed.) CRYPTO 2009. LNCS, vol. 5677, pp. 55–69. Springer, Heidelberg (2009). https://doi.org/10.1007/978-3-642-03356-8_4
Wang, X., Lai, X., Feng, D., Chen, H., Yu, X.: Cryptanalysis of the hash functions MD4 and RIPEMD. In: Cramer [8], pp. 1–18
Wang, X., Yin, Y.L., Yu, H.: Finding collisions in the full SHA-1. In: Shoup, V. (ed.) CRYPTO 2005. LNCS, vol. 3621, pp. 17–36. Springer, Heidelberg (2005). https://doi.org/10.1007/11535218_2
Wang, X., Yu, H.: How to break MD5 and other hash functions. In: Cramer [8], pp. 19–35
Acknowledgements
The research of Ariel Weizmann was supported by the European Research Council under the ERC starting grant agreement n. 757731 (LightCrypt) and by the BIU Center for Research in Applied Cryptography and Cyber Security in conjunction with the Israel National Cyber Bureau in the Prime Minister’s Office. The second author was supported in part by the Israeli Science Foundation through grant No. 827/12.
Author information
Authors and Affiliations
Corresponding author
Editor information
Editors and Affiliations
Rights and permissions
Copyright information
© 2017 Springer International Publishing AG
About this paper
Cite this paper
Weizmann, A., Dunkelman, O., Haber, S. (2017). Efficient Construction of Diamond Structures. In: Patra, A., Smart, N. (eds) Progress in Cryptology – INDOCRYPT 2017. INDOCRYPT 2017. Lecture Notes in Computer Science(), vol 10698. Springer, Cham. https://doi.org/10.1007/978-3-319-71667-1_9
Download citation
DOI: https://doi.org/10.1007/978-3-319-71667-1_9
Published:
Publisher Name: Springer, Cham
Print ISBN: 978-3-319-71666-4
Online ISBN: 978-3-319-71667-1
eBook Packages: Computer ScienceComputer Science (R0)