Abstract
We consider a problem, which we call secure grouping, of dividing a number of parties into some subsets (groups) in the following manner: Each party has to know the other members of his/her group, while he/she may not know anything about how the remaining parties are divided (except for certain public predetermined constraints, such as the number of parties in each group). In this paper, we construct an information-theoretically secure protocol using a deck of physical cards to solve the problem, which is jointly executable by the parties themselves without a trusted third party. Despite the non-triviality and the potential usefulness of the secure grouping, our proposed protocol is fairly simple to describe and execute. Our protocol is based on algebraic properties of conjugate permutations. A key ingredient of our protocol is our new techniques to apply multiplication and inverse operations to hidden permutations (i.e., those encoded by using face-down cards), which would be of independent interest and would have various potential applications.
Access this chapter
Tax calculation will be finalised at checkout
Purchases are for personal use only
Similar content being viewed by others
Notes
- 1.
In some card games, the dealer announces one of the cards (e.g., “
 ”) and then the player having this card becomes the dealer’s partner. However, now the dealer cannot know who is the partner, though the partner him/herself can know that he/she is the dealer’s partner; hence the condition of secure grouping is not achieved.
”) and then the player having this card becomes the dealer’s partner. However, now the dealer cannot know who is the partner, though the partner him/herself can know that he/she is the dealer’s partner; hence the condition of secure grouping is not achieved. - 2.
Note that this sequence of number cards is obtained by moving, for each \(k = 1,2,\dots ,7\), the k-th card
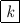 to the \(\sigma (k)\)-th position. For example, if \(\sigma (k) = k+1\) for \(1 \le k \le 6\) and \(\sigma (7) = 1\), then the resulting card sequence is
to the \(\sigma (k)\)-th position. For example, if \(\sigma (k) = k+1\) for \(1 \le k \le 6\) and \(\sigma (7) = 1\), then the resulting card sequence is  .
. - 3.
Usually, we define coding rules such as
 and
and  since the card-based protocol normally uses Boolean values. If the usual Boolean encoding rule is used instead of the number cards, the secure grouping protocol can still be executed. In the case the number of cards increases \(2\lceil \log _2{n} \rceil \) times larger.
since the card-based protocol normally uses Boolean values. If the usual Boolean encoding rule is used instead of the number cards, the secure grouping protocol can still be executed. In the case the number of cards increases \(2\lceil \log _2{n} \rceil \) times larger.
References
Crépeau, C., Kilian, J.: Discreet solitary games. In: Stinson, D.R. (ed.) CRYPTO 1993. LNCS, vol. 773, pp. 319–330. Springer, Heidelberg (1994). https://doi.org/10.1007/3-540-48329-2_27
Boer, B.: More efficient match-making and satisfiability The Five Card Trick. In: Quisquater, J.-J., Vandewalle, J. (eds.) EUROCRYPT 1989. LNCS, vol. 434, pp. 208–217. Springer, Heidelberg (1990). https://doi.org/10.1007/3-540-46885-4_23
Ishikawa, R., Chida, E., Mizuki, T.: Efficient card-based protocols for generating a hidden random permutation without fixed points. In: Calude, C.S., Dinneen, M.J. (eds.) UCNC 2015. LNCS, vol. 9252, pp. 215–226. Springer, Cham (2015). https://doi.org/10.1007/978-3-319-21819-9_16
Koch, A., Walzer, S., Härtel, K.: Card-based cryptographic protocols using a minimal number of cards. In: Iwata, T., Cheon, J.H. (eds.) ASIACRYPT 2015. LNCS, vol. 9452, pp. 783–807. Springer, Heidelberg (2015). https://doi.org/10.1007/978-3-662-48797-6_32
Mizuki, T.: Efficient and secure multiparty computations using a standard deck of playing cards. In: Foresti, S., Persiano, G. (eds.) CANS 2016. LNCS, vol. 10052, pp. 484–499. Springer, Cham (2016). https://doi.org/10.1007/978-3-319-48965-0_29
Mizuki, T., Asiedu, I.K., Sone, H.: Voting with a logarithmic number of cards. In: Mauri, G., Dennunzio, A., Manzoni, L., Porreca, A.E. (eds.) UCNC 2013. LNCS, vol. 7956, pp. 162–173. Springer, Heidelberg (2013). https://doi.org/10.1007/978-3-642-39074-6_16
Mizuki, T., Kumamoto, M., Sone, H.: The five-card trick can be done with four cards. In: Wang, X., Sako, K. (eds.) ASIACRYPT 2012. LNCS, vol. 7658, pp. 598–606. Springer, Heidelberg (2012). https://doi.org/10.1007/978-3-642-34961-4_36
Mizuki, T., Shizuya, H.: A formalization of card-based cryptographic protocols via abstract machine. Int. J. Inf. Sec. 13(1), 15–23 (2014)
Mizuki, T., Shizuya, H.: Practical card-based cryptography. In: Ferro, A., Luccio, F., Widmayer, P. (eds.) FUN 2014. LNCS, vol. 8496, pp. 313–324. Springer, Cham (2014). https://doi.org/10.1007/978-3-319-07890-8_27
Mizuki, T., Sone, H.: Six-card secure AND and four-card secure XOR. In: Deng, X., Hopcroft, J.E., Xue, J. (eds.) FAW 2009. LNCS, vol. 5598, pp. 358–369. Springer, Heidelberg (2009). https://doi.org/10.1007/978-3-642-02270-8_36
Mizuki, T., Uchiike, F., Sone, H.: Securely computing XOR with 10 cards. Australas. J. Comb. 36, 279–293 (2006)
Nakai, T., Tokushige, Y., Misawa, Y., Iwamoto, M., Ohta, K.: Efficient card-based cryptographic protocols for millionaires’ problem utilizing private permutations. In: Foresti, S., Persiano, G. (eds.) CANS 2016. LNCS, vol. 10052, pp. 500–517. Springer, Cham (2016). https://doi.org/10.1007/978-3-319-48965-0_30
Niemi, V., Renvall, A.: Secure multiparty computations without computers. Theor. Comput. Sci. 191(1–2), 173–183 (1998)
Nishida, T., Hayashi, Y., Mizuki, T., Sone, H.: Card-based protocols for any boolean function. In: Jain, R., Jain, S., Stephan, F. (eds.) TAMC 2015. LNCS, vol. 9076, pp. 110–121. Springer, Cham (2015). https://doi.org/10.1007/978-3-319-17142-5_11
Nishida, T., Mizuki, T., Sone, H.: Securely computing the three-input majority function with eight cards. In: Dediu, A.-H., Martín-Vide, C., Truthe, B., Vega-Rodríguez, M.A. (eds.) TPNC 2013. LNCS, vol. 8273, pp. 193–204. Springer, Heidelberg (2013). https://doi.org/10.1007/978-3-642-45008-2_16
Nishimura, A., Hayashi, Y., Mizuki, T., Sone, H.: An implementation of non-uniform shuffle for secure multi-party computation. In: Proceedings of the 3rd ACM International Workshop on ASIA Public-Key Cryptography, AsiaPKC@AsiaCCS, Xi’an, China, 30 May–03 June 2016, pp. 49–55 (2016)
Shinagawa, K., Mizuki, T., Schuldt, J.C.N., Nuida, K., Kanayama, N., Nishide, T., Hanaoka, G., Okamoto, E.: Multi-party computation with small shuffle complexity using regular polygon cards. In: Au, M.-H., Miyaji, A. (eds.) ProvSec 2015. LNCS, vol. 9451, pp. 127–146. Springer, Cham (2015). https://doi.org/10.1007/978-3-319-26059-4_7
Shinagawa, K., Mizuki, T., Schuldt, J., Nuida, K., Kanayama, N., Nishide, T., Hanaoka, G., Okamoto, E.: Secure multi-party computation using polarizing cards. In: Tanaka, K., Suga, Y. (eds.) IWSEC 2015. LNCS, vol. 9241, pp. 281–297. Springer, Cham (2015). https://doi.org/10.1007/978-3-319-22425-1_17
Shinagawa, K., Mizuki, T., Schuldt, J.C.N., Nuida, K., Kanayama, N., Nishide, T., Hanaoka, G., Okamoto, E.: Secure computation protocols using polarizing cards. IEICE Trans. 99-A(6), 1122–1131 (2016)
Stiglic, A.: Computations with a deck of cards. Theor. Comput. Sci. 259(1–2), 671–678 (2001)
Ueda, I., Nishimura, A., Hayashi, Y., Mizuki, T., Sone, H.: How to implement a random bisection cut. In: Martín-Vide, C., Mizuki, T., Vega-Rodríguez, M.A. (eds.) TPNC 2016. LNCS, vol. 10071, pp. 58–69. Springer, Cham (2016). https://doi.org/10.1007/978-3-319-49001-4_5
Acknowledgement
We thank the members of Shin-Akarui-Angou-Benkyou-Kai for their helpful comments. In particular we would like to thank Shuichi Katsumata for his helpful comments. A part of this work is supported by JST CREST grant number JPMJCR1688.
Author information
Authors and Affiliations
Corresponding author
Editor information
Editors and Affiliations
Rights and permissions
Copyright information
© 2017 Springer International Publishing AG
About this paper
Cite this paper
Hashimoto, Y., Shinagawa, K., Nuida, K., Inamura, M., Hanaoka, G. (2017). Secure Grouping Protocol Using a Deck of Cards. In: Shikata, J. (eds) Information Theoretic Security. ICITS 2017. Lecture Notes in Computer Science(), vol 10681. Springer, Cham. https://doi.org/10.1007/978-3-319-72089-0_8
Download citation
DOI: https://doi.org/10.1007/978-3-319-72089-0_8
Published:
Publisher Name: Springer, Cham
Print ISBN: 978-3-319-72088-3
Online ISBN: 978-3-319-72089-0
eBook Packages: Computer ScienceComputer Science (R0)





 ”) and then the player having this card becomes the dealer’s partner. However, now the dealer cannot know who is the partner, though the partner him/herself can know that he/she is the dealer’s partner; hence the condition of secure grouping is not achieved.
”) and then the player having this card becomes the dealer’s partner. However, now the dealer cannot know who is the partner, though the partner him/herself can know that he/she is the dealer’s partner; hence the condition of secure grouping is not achieved.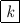 to the
to the  .
. and
and  since the card-based protocol normally uses Boolean values. If the usual Boolean encoding rule is used instead of the number cards, the secure grouping protocol can still be executed. In the case the number of cards increases
since the card-based protocol normally uses Boolean values. If the usual Boolean encoding rule is used instead of the number cards, the secure grouping protocol can still be executed. In the case the number of cards increases