Abstract
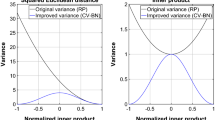
The technique of random projection is one of dimension reduction, where high dimensional vectors in \(\mathbb R^D\) are projected down to a smaller subspace in \(\mathbb R^k\). Certain forms of distances or distance kernels such as Euclidean distances, inner products [10], and \(l_p\) distances [12] between high dimensional vectors are approximately preserved in this smaller dimensional subspace. Word vectors which are represented in a bag of words model can thus be projected down to a smaller subspace via random projections, and their relative similarity computed via distance metrics. We propose using marginal information and Bayesian probability to improve the estimates of the inner product between pairs of vectors, and demonstrate our results on actual datasets.
Access this chapter
Tax calculation will be finalised at checkout
Purchases are for personal use only
Similar content being viewed by others
References
Achlioptas, D.: Database-friendly random projections: Johnson-Lindenstrauss with binary coins. J. Comput. Syst. Sci. 66(4), 671–687 (2003). https://doi.org/10.1016/S0022-0000(03)00025-4
Agustí, P., Traver, V.J., Pla, F.: Bag-of-words with aggregated temporal pair-wise word co-occurrence for human action recognition. Pattern Recogn. Lett. 49(C), 224–230 (2014). https://doi.org/10.1016/j.patrec.2014.07.014
Ailon, N., Chazelle, B.: The fast Johnson-Lindenstrauss transform and approximate nearest neighbors. SIAM J. Comput. 39(1), 302–322 (2009). https://doi.org/10.1137/060673096
Ball, K.: An elementary introduction to modern convex geometry. Flavors Geom. 31, 1–58 (1997). http://library.msri.org/books/Book31/files/ball.pdf
Boutsidis, C., Gittens, A.: Improved matrix algorithms via the subsampled randomized hadamard transform. CoRR abs/1204.0062 (2012). http://arxiv.org/abs/1204.0062
Fosdick, B.K., Raftery, A.E.: Estimating the correlation in bivariate normal data with known variances and small sample sizes. Am. Stat. 66(1), 34–41 (2012). http://EconPapers.repec.org/RePEc:taf:amstat:v:66:y:2012:i:1:p:34--41
Guyon, I., Gunn, S., Ben-Hur, A., Dror, G.: Result analysis of the NIPS 2003 feature selection challenge. In: Saul, L.K., Weiss, Y., Bottou, L. (eds.) Advances in Neural Information Processing Systems, vol. 17, pp. 545–552. MIT Press (2005). http://papers.nips.cc/paper/2728-result-analysis-of-the-nips-2003-feature-selection-challenge.pdf
Kang, K., Hooker, G.: Random projections with control variates. In: Proceedings of the 6th International Conference on Pattern Recognition Applications and Methods: ICPRAM, vol. 1, pp. 138–147. INSTICC, ScitePress (2017)
Lecun, Y., Bottou, L., Bengio, Y., Haffner, P.: Gradient-based learning applied to document recognition. In: Proceedings of the IEEE, pp. 2278–2324 (1998)
Li, P., Hastie, T.J., Church, K.W.: Improving random projections using marginal information. In: Lugosi, G., Simon, H.U. (eds.) COLT 2006. LNCS (LNAI), vol. 4005, pp. 635–649. Springer, Heidelberg (2006). https://doi.org/10.1007/11776420_46
Li, P., Hastie, T.J., Church, K.W.: Very sparse random projections. In: Proceedings of the 12th ACM SIGKDD International Conference on Knowledge Discovery and Data Mining, KDD 2006, pp. 287–296. ACM, New York (2006). http://doi.acm.org/10.1145/1150402.1150436
Li, P., Mahoney, M.W., She, Y.: Approximating higher-order distances using random projections. CoRR abs/1203.3492 (2012). http://arxiv.org/abs/1203.3492
Lichman, M.: UCI machine learning repository (2013). http://archive.ics.uci.edu/ml
Maqueda, A.I., Ruano, A., del Blanco, C.R., Carballeira, P., Jaureguizar, F., García, N.: Novel multi-feature bag-of-words descriptor via subspace random projection for efficient human-action recognition. In: 2015 12th IEEE International Conference on Advanced Video and Signal Based Surveillance (AVSS), pp. 1–6, August 2015
Murphy, K.P.: Machine Learning: A Probabilistic Perspective. MIT Press, Cambridge (2012)
Nadaraya, E.A.: On estimating regression. Theory Probab. Appl. 9(1), 141–142 (1964)
Perrone, V., Jenkins, P.A., Spano, D., Teh, Y.W.: Poisson random fields for dynamic feature models (2016). arXiv e-prints: arXiv:1611.07460
Vempala, S.S.: The Random Projection Method, DIMACS Series in Discrete Mathematics and Theoretical Computer Science, vol. 65. American Mathematical Society, Providence, R.I. (2004). Appendice pp. 101–105. http://opac.inria.fr/record=b1101689
Acknowledgements
We thank the reviewers who provided us with many helpful comments. We hope we have addressed most of these comments in this version of the paper where possible. This research was supported by the SUTD Faculty Fellow Award.
Author information
Authors and Affiliations
Corresponding author
Editor information
Editors and Affiliations
Rights and permissions
Copyright information
© 2018 Springer International Publishing AG
About this paper
Cite this paper
Kang, K. (2018). Random Projections with Bayesian Priors. In: Huang, X., Jiang, J., Zhao, D., Feng, Y., Hong, Y. (eds) Natural Language Processing and Chinese Computing. NLPCC 2017. Lecture Notes in Computer Science(), vol 10619. Springer, Cham. https://doi.org/10.1007/978-3-319-73618-1_15
Download citation
DOI: https://doi.org/10.1007/978-3-319-73618-1_15
Published:
Publisher Name: Springer, Cham
Print ISBN: 978-3-319-73617-4
Online ISBN: 978-3-319-73618-1
eBook Packages: Computer ScienceComputer Science (R0)