Skip to main content
Springer Nature Link
Log in

A Walk in the Clouds: Routing Through VNFs on Bidirected Networks

  • Conference paper
  • First Online:
Algorithmic Aspects of Cloud Computing (ALGOCLOUD 2017)

Part of the book series: Lecture Notes in Computer Science ((LNTCS,volume 10739))

Included in the following conference series:

  • 505 Accesses

Abstract

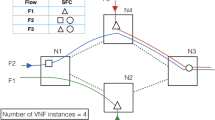
The virtualization of network functions enables innovative new network services which can be deployed quickly and at low cost on (distributed) cloud computing infrastructure. This paper initiates the algorithmic study of the fundamental underlying problem of how to efficiently route traffic through a given set of Virtualized Network Functions (VNFs). We are given a link-capacitated network \(G=(V,E)\), a source-destination pair \((s,t)\in V^2\) and a set of waypoints \(\mathscr {W} \subset V\) (the VNFs). In particular, we consider the practically relevant but rarely studied case of bidirected networks. The objective is to find a (shortest) route from s to t such that all waypoints are visited. We show that the problem features interesting connections to classic combinatorial problems, present different algorithms, and derive hardness results.

This is a preview of subscription content, log in via an institution to check access.

Access this chapter

Log in via an institution

Subscribe and save

Springer+ Basic
$34.99 /Month
  • Get 10 units per month
  • Download Article/Chapter or eBook
  • 1 Unit = 1 Article or 1 Chapter
  • Cancel anytime
Subscribe now

Buy Now

Chapter
USD 29.95
Price excludes VAT (USA)
  • Available as PDF
  • Read on any device
  • Instant download
  • Own it forever

Tax calculation will be finalised at checkout

Purchases are for personal use only

Institutional subscriptions

Similar content being viewed by others

Notes

  1. 1.

    See http://www.topology-zoo.org/.

References

  1. Amiri, S.A., Foerster, K.-T., Jacob, R., Schmid, S.: Charting the Complexity Landscape of Waypoint Routing. arXiv preprint arXiv:1705.00055 (2017)

  2. Amiri, S.A., Foerster, K.-T., Schmid, S.: Walking through waypoints. arXiv preprint arXiv:1708.09827 (2017)

  3. Archer, A., Bateni, M.H., Hajiaghayi, M.T., Karloff, H.J.: Improved approximation algorithms for prize-collecting steiner tree and TSP. SIAM J. Comput. 40(2), 309–332 (2011)

    Article  MathSciNet  MATH  Google Scholar 

  4. Arora, S., Grigni, M., Karger, D.R., Klein, P.N., Woloszyn, A.: A polynomial-time approximation scheme for weighted planar graph TSP. In: Proceedings of SODA (1998)

    Google Scholar 

  5. Bansal, N., Lee, K.-W., Nagarajan, V., Zafer, M.: Minimum congestion mapping in a cloud. In: Proceedings of PODC (2011)

    Google Scholar 

  6. Bellman, R.: Dynamic programming treatment of the travelling salesman problem. J. ACM 9(1), 61–63 (1962)

    Article  MathSciNet  MATH  Google Scholar 

  7. Björklund, A., Husfeld, T., Taslaman, N.: Shortest cycle through specified elements. In: Proceedings of SODA (2012)

    Google Scholar 

  8. Björklund, A., Husfeldt, T.: Shortest two disjoint paths in polynomial time. In: Esparza, J., Fraigniaud, P., Husfeldt, T., Koutsoupias, E. (eds.) ICALP 2014. LNCS, vol. 8572, pp. 211–222. Springer, Heidelberg (2014). https://doi.org/10.1007/978-3-662-43948-7_18

    Google Scholar 

  9. Byrka, J., Grandoni, F., Rothvoß, T., Sanità, L.: Steiner tree approximation via iterative randomized rounding. J. ACM 60(1), 6:1–6:33 (2013)

    Article  MathSciNet  MATH  Google Scholar 

  10. Chanas, P.: Reseaux ATM: conception et optimisation. Ph.D. thesis, University of Grenoble (1998)

    Google Scholar 

  11. Christofides, N.: Worst-case analysis of a new heuristic for the travelling salesman problem. Technical report 388, Graduate School of Industrial Administration, Carnegie Mellon University (1976)

    Google Scholar 

  12. Cormen, T.H., Leiserson, C.E., Rivest, R.L., Stein, C.: Introduction to Algorithms, 3rd edn. MIT Press, Cambridge (2009)

    MATH  Google Scholar 

  13. Edmonds, J., Johnson, E.: Matching: a well-solved class of linear programs. In: Combinatorial Structures and their Applications: Proceedings of the Calgary Symposium, pp. 88–92. Gordon and Breach, New York (1970)

    Google Scholar 

  14. ETSI: Network functions virtualisation - introductory white paper. White Paper, October 2013

    Google Scholar 

  15. Even, G., Medina, M., Patt-Shamir, B.: On-line path computation and function placement in SDNs. In: Bonakdarpour, B., Petit, F. (eds.) SSS 2016. LNCS, vol. 10083, pp. 131–147. Springer, Cham (2016). https://doi.org/10.1007/978-3-319-49259-9_11

    Chapter  Google Scholar 

  16. Even, G., Rost, M., Schmid, S.: An approximation algorithm for path computation and function placement in SDNs. In: Suomela, J. (ed.) SIROCCO 2016. LNCS, vol. 9988, pp. 374–390. Springer, Cham (2016). https://doi.org/10.1007/978-3-319-48314-6_24

    Chapter  Google Scholar 

  17. Fortune, S., Hopcroft, J.E., Wyllie, J.: The directed subgraph homeomorphism problem. Theor. Comput. Sci. 10, 111–121 (1980)

    Article  MathSciNet  MATH  Google Scholar 

  18. Garey, M.R., Johnson, D.S.: Computers and Intractability: A Guide to the Theory of NP-Completeness. W. H. Freeman, New York (1979)

    MATH  Google Scholar 

  19. Hartert, R., Vissicchio, S., Schaus, P., Bonaventure, O., Filsfils, C., Telkamp, T., Francois, P.: A declarative and expressive approach to control forwarding paths in carrier-grade networks. In: Proceedings of SIGCOMM (2015)

    Google Scholar 

  20. Held, M., Karp, R.M.: The traveling-salesman problem and minimumspanning trees: Part II. Math. Program. 1(1), 6–25 (1971)

    Article  MATH  Google Scholar 

  21. Sherry, J., et al.: Making middleboxes someone else’s problem: network processing as a cloud service. In: Proceedings of ACM SIGCOMM (2012)

    Google Scholar 

  22. Jarry, A., Pérennes, S.: Disjoint paths in symmetric digraphs. Discrete Appl. Math. 157(1), 90–97 (2009)

    Article  MathSciNet  MATH  Google Scholar 

  23. Jarry, A.: Multiflows in symmetric digraphs. Discrete Appl. Math. 160(15), 2208–2220 (2012)

    Article  MathSciNet  MATH  Google Scholar 

  24. Karpinski, M., Lampis, M., Schmied, R.: New inapproximability bounds for TSP. J. Comput. Syst. Sci. 81(8), 1665–1677 (2015)

    Article  MathSciNet  MATH  Google Scholar 

  25. Kawarabayashi, K., Kobayashi, Y., Reed, B.A.: The disjoint paths problem in quadratic time. J. Comb. Theor. Ser. B 102(2), 424–435 (2012)

    Article  MathSciNet  MATH  Google Scholar 

  26. Khuller, S., Mitchell, S.G., Vazirani, V.V.: Processor efficient parallel algorithms for the two disjoint paths problem and for finding a kuratowski homeomorph. SIAM J. Comput. 21(3), 486–506 (1992)

    Article  MathSciNet  MATH  Google Scholar 

  27. Khuller, S., Schieber, B.: Efficient parallel algorithms for testing k-connectivity and finding disjoint s-t paths in graphs. SIAM J. Comput. 20(2), 352–375 (1991)

    Article  MathSciNet  MATH  Google Scholar 

  28. Klein, P.N.: A subset spanner for planar graphs, with application to subset TSP. In: Proceedings of STOC (2006)

    Google Scholar 

  29. Klein, P.N., Marx, D.: A subexponential parameterized algorithm for subset TSP on planar graphs. In: Proceedings of SODA (2014)

    Google Scholar 

  30. Lukovszki, T., Schmid, S.: Online admission control and embedding of service chains. In: Scheideler, C. (ed.) Structural Information and Communication Complexity. LNCS, vol. 9439, pp. 104–118. Springer, Cham (2015). https://doi.org/10.1007/978-3-319-25258-2_8

    Chapter  Google Scholar 

  31. Napper, J., Haeffner, W., Stiemerling, M., Lopez, D.R., Uttaro, J.: Service Function Chaining Use Cases in Mobile Networks. Internet-draft, IETF (2016)

    Google Scholar 

  32. Naves, G., Sebö, A.: Multiflow feasibility: an annotated tableau. In: Cook, W., Lovász, L., Vygen. J. (eds.) Research Trends in Combinatorial Optimization, pp. 261–283. Springer, Heidelberg (2009). https://doi.org/10.1007/978-3-540-76796-1_12

  33. Sköldström, P., et al.: Towards unified programmability of cloud and carrier infrastructure. In: Proceedings of EWSDN (2014)

    Google Scholar 

  34. Soulé, R., et al.: Merlin: a language for provisioning network resources. In: Proceedings of ACM CoNEXT (2014)

    Google Scholar 

  35. Robertson, N., Seymour, P.D.: Graph minors .XIII. The disjoint paths problem. J. Comb. Theor. Ser. B 63(1), 65–110 (1995)

    Article  MathSciNet  MATH  Google Scholar 

  36. Robins, G., Zelikovsky, A.: Tighter bounds for graph steiner tree approximation. SIAM J. Discrete Math. 19(1), 122–134 (2005)

    Article  MathSciNet  MATH  Google Scholar 

  37. Saltzer, J.H., Reed, D.P., Clark, D.D.: End-to-end arguments in system design. ACM Trans. Comput. Syst. (TOCS) 2(4), 277–288 (1984)

    Article  Google Scholar 

  38. Sebö, A., van Zuylen, A.: The salesman’s improved paths: A 3/2+1/34 approximation. In: Proceedings of FOCS (2016)

    Google Scholar 

  39. Vachani, R., Shulman, A., Kubat, P., Ward, J.: Multicommodity flows in ring networks. INFORMS J. Comput. 8(3), 235–242 (1996)

    Article  MATH  Google Scholar 

Download references

Acknowledgements

Klaus-Tycho Foerster is supported by VILLUM FONDEN project ReNet and Mahmoud Parham by AAU’s PreLytics project.

Author information

Authors and Affiliations

  1. Aalborg University, Aalborg, Denmark

    Klaus-Tycho Foerster, Mahmoud Parham & Stefan Schmid

Authors
  1. Klaus-Tycho Foerster
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Mahmoud Parham
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. Stefan Schmid
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Mahmoud Parham .

Editor information

Editors and Affiliations

  1. IST AUSTRIA, Klosterneuburg, Austria

    Dan Alistarh

  2. University of Athens, Athens, Greece

    Alex Delis

  3. University of Cyprus, Nicosia, Greece

    George Pallis

Rights and permissions

Reprints and permissions

Copyright information

© 2018 Springer International Publishing AG

About this paper

Check for updates. Verify currency and authenticity via CrossMark

Cite this paper

Foerster, KT., Parham, M., Schmid, S. (2018). A Walk in the Clouds: Routing Through VNFs on Bidirected Networks. In: Alistarh, D., Delis, A., Pallis, G. (eds) Algorithmic Aspects of Cloud Computing. ALGOCLOUD 2017. Lecture Notes in Computer Science(), vol 10739. Springer, Cham. https://doi.org/10.1007/978-3-319-74875-7_2

Download citation

  • DOI: https://doi.org/10.1007/978-3-319-74875-7_2

  • Published:

  • Publisher Name: Springer, Cham

  • Print ISBN: 978-3-319-74874-0

  • Online ISBN: 978-3-319-74875-7

  • eBook Packages: Computer ScienceComputer Science (R0)

Publish with us

Policies and ethics