Abstract
A period is the difference between the volumes of two semi-algebraic sets. Recent research has located their worst-case complexity in low levels of the Grzegorczyk Hierarchy. The present work introduces, analyzes, and evaluates three rigorous algorithms for rigorously computing periods: a deterministic, a randomized, and a ‘transcendental’ one.
Based on ideas presented at CCA 2017, this work was supported by the National Research Foundation of Korea (grant NRF-2017R1E1A1A03071032) and the International Research & Development Program of the Korean Ministry of Science and ICT (grant NRF-2016K1A3A7A03950702). We thank the anonymous referees for feedback!
Access this chapter
Tax calculation will be finalised at checkout
Purchases are for personal use only
Notes
- 1.
Of course the specific periods \(\pi \) and \(\ln (2)\) admit other, more efficient algorithms.
References
Bailey, D.H.: Jonathan Borwein: experimental mathematician. Exp. Math. 26(2), 125–129 (2017)
Berenbrink, P., Czumaj, A., Steger, A., Vöcking, B.: Balanced allocations: the heavily loaded case. SIAM J. Comput. 35(6), 1350–1385 (2006)
Becher, V., Daicz, S., Chaitin, G.: A highly random number. In: Calude, C.S., Dinneen, M.J., Sburlan, S. (eds.) Combinatorics, Computability and Logic. Discrete Mathematics and Theoretical Computer Science, pp. 55–68. Springer, London (2001). https://doi.org/10.1007/978-1-4471-0717-0_6
Brattka, V., Gherardi, G., Hölzl, R.: Las Vegas computability and algorithmic randomness. In: Mayr, E.W., Ollinger, N. (eds.) 32nd International Symposium on Theoretical Aspects of Computer Science (STACS 2015). Leibniz International Proceedings in Informatics (LIPIcs), vol. 30, pp. 130–142. Schloss Dagstuhl-Leibniz-Zentrum für Informatik, Dagstuhl (2015)
Flum, J., Grohe, M.: Parameterized Complexity Theory. Texts in Theoretical Computer Science. An EATCS Series. Springer, Heidelberg (2006). https://doi.org/10.1007/3-540-29953-X
Heintz, J., Recio, T., Roy, M.-F.: Algorithms in real algebraic geometry and applications to computational geometry. In: Goodman, J.E., Pollack, R., Steiger, W. (eds.) Discrete and Computational Geometry: Papers from the DIMACS Special Year. DIMACS Series in Discrete Mathematics and Theoretical Computer Science, vol. 6, pp. 137–164. DIMACS/AMS (1990)
Kanada, Y.:
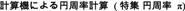 . J. Math. Cult. 1(1), 72–83 (2003)
. J. Math. Cult. 1(1), 72–83 (2003)Kratsch, D., Fomin, F.V.: Exact Exponential Algorithms. Texts in Theoretical Computer Science. An EATCS Series. Springer, Heidelberg (2010). https://doi.org/10.1007/978-3-642-16533-7
Ko, K.-I.: Complexity Theory of Real Functions. Progress in Theoretical Computer Science. Birkhäuser, Boston (1991). https://doi.org/10.1007/978-1-4684-6802-1
Koiran, P.: The real dimension problem is NPR-complete. J. Complex. 15(2), 227–238 (1999)
Kutylowski, M.: Small Grzegorczyk classes. J. Lond. Math. Soc. 36(2), 193–210 (1987)
Kontsevich, M., Zagier, D.: Periods. In: Engquist, B., Schmid, W. (eds.) Mathematics Unlimited – 2001 and Beyond, pp. 771–808. Springer, Heidelberg (2001). https://doi.org/10.1007/978-3-319-50926-6_12
Meer, K.: Optimization and approximation problems related to polynomial system solving. In: Proceedings of the 2nd Conference on Computability in Europe (CiE 2006), pp. 360–367 (2006)
Mitzenmacher, M., Upfal, E.: Probability and Computing - Randomized Algorithms and Probabilistic Analysis. Cambridge University Press, New York (2005)
Müller, N.T.: The iRRAM: exact arithmetic in C++. In: Blanck, J., Brattka, V., Hertling, P. (eds.) CCA 2000. LNCS, vol. 2064, pp. 222–252. Springer, Heidelberg (2001). https://doi.org/10.1007/3-540-45335-0_14
Müller, N.T., Ziegler, M.: From calculus to algorithms without errors. In: Hong, H., Yap, C. (eds.) ICMS 2014. LNCS, vol. 8592, pp. 718–724. Springer, Heidelberg (2014). https://doi.org/10.1007/978-3-662-44199-2_107
Papadimitriou, C.H.: Computational Complexity. Addison-Wesley, Boston (1994)
Popescu-Pampu, P.: What is the Genus?. LNM, vol. 2162. Springer, Cham (2016). https://doi.org/10.1007/978-3-319-42312-8
Ritchie, R.W.: Classes of predictably computable functions. Trans. Am. Math. Soc. 106(1), 139–173 (1963)
Skordev, D.: On the subrecursive computability of several famous constants. J. Univers. Comput. Sci. 14(6), 861–875 (2008)
Skordev, D., Weiermann, A., Georgiev, I.: \(M^2\)-computable real numbers. J. Logic Comput. 22(4), 899–925 (2012)
Turing, A.M.: On computable numbers, with an application to the “Entscheidungsproblem”. Proc. Lond. Math. Soc. 42(2), 230–265 (1937)
Tent, K., Ziegler, M.: Computable functions of reals. Münster J. Math. 3, 43–65 (2010)
Viu-Sos, J.: A semi-canonical reduction for periods of Kontsevich-Zagier. arXiv:1509.01097 (2017)
Weihrauch, K.: Computable Analysis. Texts in Theoretical Computer Science. An EATCS Series. Springer, Heidelberg (2000). https://doi.org/10.1007/978-3-642-56999-9
Yoshinaka, M.: Periods and elementary real numbers. arXiv:0805.0349 (2008)
Author information
Authors and Affiliations
Corresponding author
Editor information
Editors and Affiliations
Rights and permissions
Copyright information
© 2018 Springer International Publishing AG, part of Springer Nature
About this paper
Cite this paper
Cho, J., Park, S., Ziegler, M. (2018). Computing Periods\(\ldots \) . In: Rahman, M., Sung, WK., Uehara, R. (eds) WALCOM: Algorithms and Computation. WALCOM 2018. Lecture Notes in Computer Science(), vol 10755. Springer, Cham. https://doi.org/10.1007/978-3-319-75172-6_12
Download citation
DOI: https://doi.org/10.1007/978-3-319-75172-6_12
Published:
Publisher Name: Springer, Cham
Print ISBN: 978-3-319-75171-9
Online ISBN: 978-3-319-75172-6
eBook Packages: Computer ScienceComputer Science (R0)


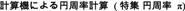 . J. Math. Cult. 1(1), 72–83 (2003)
. J. Math. Cult. 1(1), 72–83 (2003)