Abstract
A Local Optima Network represents fitness landscape connectivity within the space of local optima as a mathematical graph. In certain other complex networks or graphs there have been recent observations made about inherent self-similarity. An object is said to be self-similar if it shows the same patterns when measured at different scales; another word used to convey self-similarity is fractal. The fractal dimension of an object captures how the detail observed changes with the scale at which it is measured, with a high fractal dimension being associated with complexity. We conduct a detailed study on the fractal nature of the local optima networks of a benchmark combinatorial optimisation problem (NK Landscapes). The results draw connections between fractal characteristics and performance by three prominent metaheuristics: Iterated Local Search, Simulated Annealing, and Tabu Search.
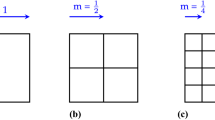
The original version of this chapter was revised: Figure 4 was corrected. The erratum to this chapter is available at https://doi.org/10.1007/978-3-319-77449-7_13
This is a preview of subscription content, log in via an institution to check access.
Access this chapter
Tax calculation will be finalised at checkout
Purchases are for personal use only
Similar content being viewed by others
References
Weinberger, E.D., Stadler, P.F.: Why some fitness landscapes are fractal. J. Theor. Biol. 163(2), 255–275 (1993)
Ochoa, G., Tomassini, M., Vérel, S., Darabos, C.: A study of NK landscapes’ basins and local optima networks. In: Proceedings of the 10th Annual Conference on Genetic and Evolutionary Computation, pp. 555–562. ACM (2008)
Mandelbrot, B.: How long is the coast of Britain? Statistical self-similarity and fractional dimension. Science 156(3775), 636–638 (1967). http://www.sciencemag.org/content/156/3775/636.abstract
Song, C., Gallos, L.K., Havlin, S., Makse, H.A.: How to calculate the fractal dimension of a complex network: the box covering algorithm. J. Stat. Mech: Theory Exp. 2007(03), P03006 (2007)
Stadler, P.F.: Fitness landscapes. In: Lässig, M., Valleriani, A. (eds.) Biological Evolution and Statistical Physics. Lecture Notes in Physics, vol. 585, pp. 183–204. Springer, Heidelberg (2002). https://doi.org/10.1007/3-540-45692-9_10
Weinberger, E.: Correlated and uncorrelated fitness landscapes and how to tell the difference. Biol. Cybern. 63(5), 325–336 (1990)
Locatelli, M.: On the multilevel structure of global optimization problems. Comput. Optim. Appl. 30(1), 5–22 (2005)
Zelinka, I., Zmeskal, O., Saloun, P.: Fractal analysis of fitness landscapes. In: Richter, H., Engelbrecht, A. (eds.) Recent Advances in the Theory and Application of Fitness Landscapes. ECC, vol. 6, pp. 427–456. Springer, Heidelberg (2014). https://doi.org/10.1007/978-3-642-41888-4_15
Thomson, S.L., Daolio, F., Ochoa, G.: Comparing communities of optima with funnels in combinatorial fitness landscapes. In: Proceedings of the Genetic and Evolutionary Computation Conference, GECCO 2017, pp. 377–384. ACM, New York (2017). http://doi.acm.org/10.1145/3071178.3071211
Cahon, S., Melab, N., Talbi, E.G.: Paradiseo: a framework for the reusable design of parallel and distributed metaheuristics. J. Heuristics 10(3), 357–380 (2004)
Acknowledgements
This work is supported by the Leverhulme Trust (award number RPG-2015-395) and by the UK’s Engineering and Physical Sciences Research Council (grant number EP/J017515/1). We gratefully acknowledge that all network data used during this research were obtained from [2].
Author information
Authors and Affiliations
Corresponding author
Editor information
Editors and Affiliations
Rights and permissions
Copyright information
© 2018 Springer International Publishing AG, part of Springer Nature
About this paper
Cite this paper
Thomson, S.L., Verel, S., Ochoa, G., Veerapen, N., McMenemy, P. (2018). On the Fractal Nature of Local Optima Networks. In: Liefooghe, A., López-Ibáñez, M. (eds) Evolutionary Computation in Combinatorial Optimization. EvoCOP 2018. Lecture Notes in Computer Science(), vol 10782. Springer, Cham. https://doi.org/10.1007/978-3-319-77449-7_2
Download citation
DOI: https://doi.org/10.1007/978-3-319-77449-7_2
Published:
Publisher Name: Springer, Cham
Print ISBN: 978-3-319-77448-0
Online ISBN: 978-3-319-77449-7
eBook Packages: Computer ScienceComputer Science (R0)