Skip to main content
Springer Nature Link
Log in

A Comparison of Accuracy and Efficiency of Parallel Solvers for Fractional Power Diffusion Problems

  • Conference paper
  • First Online:
Parallel Processing and Applied Mathematics (PPAM 2017)

Part of the book series: Lecture Notes in Computer Science ((LNTCS,volume 10777))

  • 1581 Accesses

Abstract

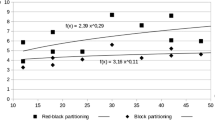
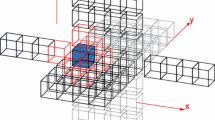
In this paper, we construct and investigate parallel solvers for three dimensional problems described by fractional powers of elliptic operators. The main aim is to make a scalability analysis of parallel versions of several state of the art solvers. The originality of this work is that we also consider the accuracy of the selected numerical algorithms. For comparison of accuracy, we use solutions obtained solving the test problem by the Fourier algorithm. Such analysis enables to compare the efficiency of the proposed parallel algorithms depending on the required accuracy of solution and on a number of processes used in computations.

This is a preview of subscription content, log in via an institution to check access.

Access this chapter

Log in via an institution

Subscribe and save

Springer+ Basic
$34.99 /Month
  • Get 10 units per month
  • Download Article/Chapter or eBook
  • 1 Unit = 1 Article or 1 Chapter
  • Cancel anytime
Subscribe now

Buy Now

Chapter
USD 29.95
Price excludes VAT (USA)
  • Available as PDF
  • Read on any device
  • Instant download
  • Own it forever

Tax calculation will be finalised at checkout

Purchases are for personal use only

Institutional subscriptions

Similar content being viewed by others

References

  1. Bonito, A., Pasciak, J.: Numerical approximation of fractional powers of elliptic operators. Math. Comput. 84, 2083–2110 (2015)

    Article  MathSciNet  MATH  Google Scholar 

  2. Harizanov, S., Lazarov, R., Margenov, S., Marinov, P., Vutov, Y.: Optimal solvers for linear systems with fractional powers of sparse SPD matrices. Numer. Linear Algebra Appl. e2167 (2018). https://doi.org/10.1002/nla.2167

  3. Nochetto, R., Otárola, E., Salgado, A.: A PDE approach to fractional diffusion in general domains: a priori error analysis. Found. Comput. Math. 15(3), 733–791 (2015)

    Article  MathSciNet  MATH  Google Scholar 

  4. Nochetto, R., Otárola, E., Salgado, A.: A PDE approach to numerical fractional diffusion. In: Proceedings of the 8th ICIAM, Beijing, China, pp. 211–236 (2015)

    Google Scholar 

  5. Vabishchevich, P.: Numerical solving unsteady space-fractional problems with the square root of an elliptic operator. Math. Model. Anal. 21(2), 220–238 (2016)

    Article  MathSciNet  Google Scholar 

  6. Čiegis, R., Tumanova, N.: On construction and analysis of finite difference schemes for pseudoparabolic problems with nonlocal boundary conditions. Math. Modell. Anal. 19(2), 281–297 (2014)

    Article  MathSciNet  Google Scholar 

  7. Čiegis, R., Starikovičius, V., Margenov, S.: On parallel numerical algorithms for fractional diffusion problems. In: Third NESUS Workshop, IICT-BAS, Sofia, Bulgaria, 6–7 Oct 2016, NESUS, ICT COST Action IC1305 (2016)

    Google Scholar 

  8. Čiegis, R., Starikovičius, V., Margenov, S., Kriauzienė, R.: Parallel solvers for fractional power diffusion problems. Concurr. Comput.: Pract. Exp. 25(24) (2017). https://doi.org/10.1002/cpe.4216

  9. Falgout, R.D., Yang, U.M.: Hypre: a library of high performance preconditioners. In: Sloot, P.M.A., Hoekstra, A.G., Tan, C.J.K., Dongarra, J.J. (eds.) ICCS 2002. LNCS, vol. 2331, pp. 632–641. Springer, Heidelberg (2002). https://doi.org/10.1007/3-540-47789-6_66

    Chapter  Google Scholar 

  10. Falgout, R., Jones, J., Yang, U.: The design and implementation of hypre, a library of parallel high performance preconditioners. In: Bruaset, A.M., Tveito, A. (eds.) Numerical Solution of Partial Differential Equations on Parallel Computers. LNCSE, pp. 267–294. Springer, Heidelberg (2006). https://doi.org/10.1007/3-540-31619-1_8

    Chapter  Google Scholar 

  11. Čiegis, R., Starikovičius, V., Tumanova, N., Ragulskis, M.: Application of distributed parallel computing for dynamic visual cryptography. J. Supercomput. 72(11), 4204–4220 (2016)

    Article  Google Scholar 

Download references

Acknowledgment

The work of authors was supported by EU under the COST programme Action IC1305, “Network for Sustainable Ultrascale Computing (NESUS)”. The third author has been partially supported by the Bulgarian National Science Fund under Grant BNSF-DN12/1.

Author information

Authors and Affiliations

  1. Vilnius Gediminas Technical University, Saulėtekis avenue 11, LT10223, Vilnius, Lithuania

    Raimondas Čiegis, Vadimas Starikovičius & Rima Kriauzienė

  2. Institute of Information and Communication Technologies, Bulgarian Academy of Sciences, Acad. G. Bonchev street, bl. 25A, 1113, Sofia, Bulgaria

    Svetozar Margenov

  3. Vilnius University Institute of Mathematics and Informatics, Akademijos street 4, 08663, Vilnius, Lithuania

    Rima Kriauzienė

Authors
  1. Raimondas Čiegis
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Vadimas Starikovičius
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. Svetozar Margenov
    View author publications

    You can also search for this author in PubMed Google Scholar

  4. Rima Kriauzienė
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Raimondas Čiegis .

Editor information

Editors and Affiliations

  1. Czestochowa University of Technology, Czestochowa, Poland

    Roman Wyrzykowski

  2. University of Tennessee, Knoxville, Tennessee, USA

    Jack Dongarra

  3. University of Southern California, Marina Del Rey, California, USA

    Ewa Deelman

  4. Czestochowa University of Technology, Czestochowa, Poland

    Konrad Karczewski

Rights and permissions

Reprints and permissions

Copyright information

© 2018 Springer International Publishing AG, part of Springer Nature

About this paper

Check for updates. Verify currency and authenticity via CrossMark

Cite this paper

Čiegis, R., Starikovičius, V., Margenov, S., Kriauzienė, R. (2018). A Comparison of Accuracy and Efficiency of Parallel Solvers for Fractional Power Diffusion Problems. In: Wyrzykowski, R., Dongarra, J., Deelman, E., Karczewski, K. (eds) Parallel Processing and Applied Mathematics. PPAM 2017. Lecture Notes in Computer Science(), vol 10777. Springer, Cham. https://doi.org/10.1007/978-3-319-78024-5_8

Download citation

  • DOI: https://doi.org/10.1007/978-3-319-78024-5_8

  • Published:

  • Publisher Name: Springer, Cham

  • Print ISBN: 978-3-319-78023-8

  • Online ISBN: 978-3-319-78024-5

  • eBook Packages: Computer ScienceComputer Science (R0)

Publish with us

Policies and ethics