Abstract
Hahn’s celebrated embedding theorem asserts that linearly ordered Abelian groups embed in the lexicographic product of real groups [13]. In this paper the partial-lexicographic product construction is introduced, a class of residuated monoids, namely, group-like FL\(_e\)-chains which possess finitely many idempotents are embedded into finite partial-lexicographic products of linearly ordered Abelian groups, that is, Hahn’s theorem is extended to this residuated monoid class. As a side-result, the finite strong standard completeness of the logic \(\mathbf{IUL}^{fp}\) is announced.
S. Jenei—The present scientific contribution is dedicated to the \(650^{th}\) anniversary of the foundation of the University of Pécs, Hungary, and was supported by the GINOP 2.3.2-15-2016-00022 grant.
Access this chapter
Tax calculation will be finalised at checkout
Purchases are for personal use only
Notes
- 1.
Real groups are very specific in the class of residuated lattices.
- 2.
In the more general modern terminology.
- 3.
FL-algebras are also called pointed residuated lattices or pointed residuated lattice-ordered monoids.
- 4.
Integrality means that the unit element of the multiplication is the greatest element of the underlying universe.
- 5.
Also called FL\(_{ew}\)-algebras.
- 6.
He called it reducible.
- 7.
In the sense of Clifford.
- 8.
Divisibility is the dual notion of being naturally ordered. For residuated integral monoids, divisibility is equivalent to the continuity of the semigroup operation in the order topology provided that the underlying chain is densely-ordered.
- 9.
In the sense of Aglianò-Montagna.
- 10.
A common generalization of ordinal sums and direct products.
- 11.
It was proved for a wider class of algebras.
- 12.
Absorbent continuity is a weakened version of the naturally ordered property.
- 13.
Weakly real chains are densely-ordered chains with two additional properties.
- 14.
A stronger statement was proved there for at most countable algebras. However, the part of the proof, which is about the densification step does not use this assumption.
- 15.
Or its dual notion, divisibility.
- 16.
That is, all elements are comparable with the unit element of the monoidal operation.
- 17.
Sometimes the lattice operators are replaced by their induced ordering \(\le \) in the signature, in particular, if an FL\(_e\)-chain is considered, that is, if the ordering is linear.
- 18.
That is, there exists a binary operation
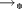 such that
such that 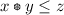 if and only if
if and only if 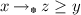 ; this equivalence is called residuation condition or adjointness condition, (
; this equivalence is called residuation condition or adjointness condition, ( ) is called an adjoint pair. Equivalently, for any x, z, the set
) is called an adjoint pair. Equivalently, for any x, z, the set 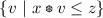 has its greatest element, and
has its greatest element, and  is defined as this element:
is defined as this element: 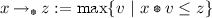 .
. - 19.
We use the word monoid to mean semigroup with unit element.
- 20.
Lattice-ordered Abelian groups equipped with
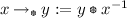 and \(f:=t\) are group-like FL\(_e\)-algebras.
and \(f:=t\) are group-like FL\(_e\)-algebras. - 21.
We set \(\max (\emptyset )=t\).
- 22.
We mean that \((X\setminus X_1)*(X\setminus X_1)\subseteq X\setminus X_1\) holds.
- 23.
We remark that the only choice for \(\mathbf X_1\) is \(\mathbf X_{\tau =t}\), see Definition 5.
- 24.
We mean that for \(x\in X_1\), it holds true that \(x\notin \{ x_\uparrow ,x_\downarrow \}\subset X_1\) (\(\downarrow \) and \(\uparrow \) are computed in X).
- 25.
Just like at item (0), the only choice for \(\mathbf X_1\) is \(\mathbf X_{\tau =t}\), provided that it is discrete, see Definition 5.
- 26.
The rank of an involutive FL\(_e\)-algebra is positive if \(t>f\), negative if \(t<f\), and 0 if \(t=f\).
- 27.
In the spirit of Theorem 1 we identify linearly ordered Abelian groups by cancellative, group-like FL\(_e\)-chains here.
- 28.
References
Aczél, J.: Lectures on Functional Equations and Their Applications. Academic Press, New York/London (1966)
Aglianò, P., Montagna, F.: Varieties of BL-algebras I: general properties. J. Pure Appl. Algebra 181(2–3), 105–129 (2003)
Ánh, P.N., Márki, L., Vámos, P.: Divisibility theory in commutative rings: Bezout monoids. Trans. Am. Math. Soc. 364, 3967–3992 (2012)
Bosbach, B.: Concerning bricks. Acta Math. Acad. Sci. Hung. 38, 89–104 (1981)
Bosbach, B.: Concerning semiclans. Arch. Math. 37, 316–324 (1981)
Bosbach, B.: Komplementäre halbgruppen. axiomatik und arithmetik. Fund. Math. 64, 257–287 (1969)
Bosbach, B.: Residuation groupoids and lattices. Stud. Sci. Math. Hung. 13, 433–451 (1978)
Cignoli, R., D’Ottaviano, I.M.L., Mundici, D.: Algebraic Foundations of Many-Valued Reasoning. Kluwer, Dordrecht (2000)
Clifford, A.H.: Naturally linearly ordered commutative semigroups. Am. J. Math. 76(3), 631–646 (1954)
Conrad, P.F., Harvey, J., Holland, W.C.: The Hahn embedding theorem for lattice-ordered groups. Trans. Am. Math. Soc. 108, 143–169 (1963)
Fuchs, L.: Partially Ordered Algebraic Systems. Pergamon Press, Oxford/London/New York/Paris (1963)
Galatos, N., Jipsen, P., Kowalski, T., Ono, H.: Residuated Lattices: An Algebraic Glimpse at Substructural Logics. Studies in Logic and the Foundations of Mathematics, vol. 151. Elsevier, New York City (2007)
Hahn, H.: Über die nichtarchimedischen Grössensysteme. S.-B. Akad. Wiss. Wien. IIa 116, 601–655 (1907)
Hájek, P.: Metamathematics of Fuzzy Logic. Kluwer Academic Publishers, Dordrecht (1998)
Horžík, R.: Algebraic semantics: semilinear FL-algebras. In: Cintula, P., Hájek, P., Noguera, C. (eds.) Handbook of Mathematical Fuzzy Logic, pp. 283–353. College Publications, London (2011)
Hölder, O.: Die Axiome der Quantität und die Lehre vom Mass. In: Berichte über die Verhandlungen der Königlich Sachsischen Gesellschaft der Wissenschaften zu Leipzig, Mathematisch-Physische Classe, vol. 53, pp. 1–64 (1901)
Jenei, S.: On the geometry of associativity. Semigroup Forum 74(3), 439–466 (2007)
Jenei, S.: On the structure of rotation-invariant semigroups. Arch. Math. Log. 42, 489–514 (2003)
Jenei, S.: Structural description of a class of involutive uninorms via skew symmetrization. J. Log. Comput. 21(5), 729–737 (2011)
Jenei, S., Montagna, F.: A proof of standard completeness of Esteva and Godo’s monoidal logic MTL. Stud. Log. 70(2), 184–192 (2002)
Jenei, S., Montagna, F.: A classification of certain group-like FL\(_e\)-chains. Synthese 192(7), 2095–2121 (2015)
Jenei, S., Montagna, F.: Erratum to “a classification of certain group-like FL\(_e\)-chains”. Synthese 193(1), 313–313 (2016)
Jipsen, P., Montagna, F.: Embedding theorems for classes of GBL-algebras. J. Pure Appl. Algebra 214(9), 1559–1575 (2010)
Johnstone, P.T.: Stone Spaces. Cambridge University Press, Cambridge (1982)
Metcalfe, G., Montagna, F.: Substructural fuzzy logics. J. Symb. Log. 72(3), 834–864 (2007)
Mostert, P.S., Shields, A.L.: On the structure of semigroups on a compact manifold with boundary. Ann. Math. 65, 117–143 (1957)
Tsinakis, C., Wille, A.M.: Minimal varieties of involutive residuated lattices. Stud. Log. 83(1–3), 407–423 (2006)
Ward, M., Dilworth, R.P.: Residuated lattices. Trans. Am. Math. Soc. 45, 335–354 (1939)
Author information
Authors and Affiliations
Corresponding author
Editor information
Editors and Affiliations
Rights and permissions
Copyright information
© 2018 Springer International Publishing AG, part of Springer Nature
About this paper
Cite this paper
Jenei, S. (2018). On the Structure of Group-Like FL\(_e\)-chains. In: Medina, J., et al. Information Processing and Management of Uncertainty in Knowledge-Based Systems. Theory and Foundations. IPMU 2018. Communications in Computer and Information Science, vol 854. Springer, Cham. https://doi.org/10.1007/978-3-319-91476-3_21
Download citation
DOI: https://doi.org/10.1007/978-3-319-91476-3_21
Published:
Publisher Name: Springer, Cham
Print ISBN: 978-3-319-91475-6
Online ISBN: 978-3-319-91476-3
eBook Packages: Computer ScienceComputer Science (R0)


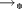 such that
such that 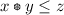 if and only if
if and only if 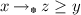 ; this equivalence is called residuation condition or adjointness condition, (
; this equivalence is called residuation condition or adjointness condition, ( ) is called an adjoint pair. Equivalently, for any x, z, the set
) is called an adjoint pair. Equivalently, for any x, z, the set 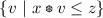 has its greatest element, and
has its greatest element, and  is defined as this element:
is defined as this element: 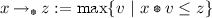 .
.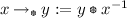 and
and