Abstract
Statistical learning of relations between entities is a popular approach to address the problem of missing data in Knowledge Graphs. In this work we study how relational learning can be enhanced with background of a special kind: event logs, that are sequences of entities that may occur in the graph. Events naturally appear in many important applications as background. We propose various embedding models that combine entities of a Knowledge Graph and event logs. Our evaluation shows that our approach outperforms state-of-the-art baselines on real-world manufacturing and road traffic Knowledge Graphs, as well as in a controlled scenario that mimics manufacturing processes.
You have full access to this open access chapter, Download conference paper PDF
Similar content being viewed by others
1 Introduction
Knowledge Graphs (KGs) nowadays power many important applications including Web searchFootnote 1, question answering [3], machine learning [19], data integration [10], entity disambiguation and linking [5, 8]. A KG is typically defined as a collection of triples \( \langle entity,predicate,entity\rangle \) that form a directed graph where nodes are entities and edges are labeled with binary predicates (relations). Examples of large-scale KGs range from general-purpose such as Yago [24] and DBPedia [12] to domain specific ones such as Siemens [10] and Statoil [9] corporate KGs.
Large-scale KGs are often automatically constructed and highly incomplete [6] in the sense that they are missing certain triples. Due to their size and the speed of growth, manual completion of such KGs is infeasible. In order to address this issue, a number of relational learning approaches for automatic KG completion have been recently proposed, see [6, 16] for an overview. Many of these approaches are based on learning representations, or embeddings, of entities and relations [4, 17, 22]. It was shown that the quality of embeddings can be significantly improved if the embedding’s vector space is enriched with additional information from an external source, such as a corpora of natural language text [27] or structural knowledge such as rules [25] or type constraints [11].
An important type of external knowledge that is common in practice and to the best of our knowledge has not been explicitly considered so far is event log data. Events naturally appear in many applications including social networks, smart cities, and manufacturing. In social networks the nodes of a KG can be people and locations, and edges can be friendship relations and places of birth [30], while an event log for a person can be a sequence of (possibly repetitive) places that the person has visited. In smart cities a KG can model traffic [21] by representing cameras, traffic lights, and road topology, while an event log for one day can be a sequence of traffic signals where jams or accidents have occurred. In smart manufacturing an event log can be a sequence of possible states, e.g., overheating or low power of machines such as conveyors, and these logs can be emitted during a manufacturing process.
In this work we define an event log for a KG as a set of sequences constituted of entities (possibly with repetitions) that may occur in the KG as nodes. Moreover, we assume that not every entity from a KG, but only what we call event entities can occur in logs. In the above: visited cities, traffic signals, and alarms are event entities. As we see later in the paper this separation of entities in a KG into event and non-event is important and practically motivated. We now illustrate an industrial KG and event log.
Example 1
Consider an industrial KG that is inspired by a Siemens automated factory, that we will use later on for experiments, and that contains information about factory equipment, products, as well as materials and processes to produce the products. The KG was semi-automatically generated by parsing heterogeneous spreadsheets and other semi-structured data repositories and it is incomplete. In Fig. 1 we depict a small excerpt from this KG where solid lines denote relations that are in the KG while dashed – the missing relations. The KG contains the topology of the conveyors A, B, and C and says that two of them (A and B) are connected to each other: \(\langle ConveyorA, connectedTo, ConveyorB\rangle \). The KG also stores operator control specifications, in particular, event entities that the equipment can emit during operation. For example, CoilJam, is an event entity and it can be emitted by conveyor C, i.e., \(\langle CoilJam, hasSource, ConveyorC\rangle \). Event entities have further semantics described by the typing, e.g. CoilJam is of type JamAlarm, severity levels, and possible emitting source locations. At the same time, the KG misses the facts that the conveyors A and C are connected in the factory; that BoardJam is of type JamAlarm, and HighEnergy (HE) has the source \( ConveyorA \) and is of type EnergyEvent.
Additionally, in the example, we assume that an event log recorded during the operation of the factory consists of three following sequences over event entities:
Observe that the event log suggests that a jam typically occurs after a sequence of two consecutive low energy consumption (LE) events. \(\square \)
An event log gives external knowledge to the KG by specifying frequent sequential patterns on the KG’s entities. These patterns capture some processes that the nodes of a KG can be involved in, i.e., manufacturing with machines described by the KG, traveling by a person mentioned in the KG, or traffic around traffic signals. This type of external knowledge has conceptual differences from text corpora where KG entities are typically described in a natural language and where occurrences of KG entities do not necessarily correspond to any process. Events are also different from rules or constraints that introduce formal restrictions on some relations.
The goal of this work is to understand how event logs can enhance relational learning for KGs. We address this problem by proposing an Event-enhanced Knowledge Learning (EKL) approach for KG completion that intuitively has two sub–steps:
-
1.
Event alignment, where event entities are aligned in a low-dimensional vector space that reflects sequential similarity, and
-
2.
KG completion, where the KG is extended with missing edges that can be either event-specific, e.g., such as the type edge between BoardJam and JamAlarm in Example 1, or not event-specific, e.g., such as connectedTo between ConveyorA and ConveyorC in Example 1.
Observe, the event logs directly influence the first step while also indirectly the second step of EKL. Hence, we expect a collective learning effect in a sense that the overall KG completion can benefit from event alignment, and vice versa.
Example 2
During the first step EKL will align BoardJam and CoilJam to be similar. In the second step EKL will accordingly adjust entities ConveyorC and ConveyorB and then predict that ConveyorA is likely to also be connected to ConveyorC. Intuitively the missing link between the conveyors can be inferred from the sequential pattern in the event log: the log tells us that both BoardJam and CoilJam occur as a consequence of two consecutive LE events and therefore exhibit similar semantics. This similarity is carried to conveyor entities B and C, which leads to an increased likelihood that they both follow the same entity ConveyorA. \(\square \)
Note that the prediction of event-specific missing links is not the standard task for relational learning since we are predicting links within the background. Moreover, our approach can address the zero-shot scenario, where some event entities only appear in the event log, but they are novel to the KG (it is marked with red in Fig. 1). E.g., HE in Example 1 corresponds to an entity that is missing in the KG, that has to be aligned during the first step of EKL and then linked to ConveyorA as well as to its type during the second step of EKL. Thus, EKL can also populate a KG with new (unseen) entities.
The contributions of our work are as follows:
-
Several EKL approaches to KG completion that comprise
-
two model architectures that allow to combine (representations of) a KG and an event log for simultaneous training of both representations;
-
three models for event logs that reflect different notions of event context.
-
-
An extensive evaluation of our approach and comparison to a state-of-the-art baseline on real-world data from a factory, on smart city traffic data, and controlled experiment data. Our results show that we significantly outperform two state-of-the-art baselines and the advantages are most visible for predicting links between entities that reflect the sequential process nature within the KG.
Finally, note that we presented a very preliminary version of this work as a short in-use paper [20]. Here we are significantly different from [20] and extend it, since [20] does not describe our EKL models and it only focusses on several simple KG extension scenarios that we do not study here.
2 Existing Methods for KG Completion
We now review the problem of KG completion and the existing methods to address it, following the standard problem definition, c.f. [4, 22, 26]. Let \(\mathcal {E} \) be a finite set of (all possible) entities and \(\mathcal {R} \) a finite set of relations. A KG \(\mathcal {K} \) is a set of triples \(\langle h, r, t\rangle \), where \( h,t \in \mathcal {E} \) and \( r \in \mathcal {R} \). Given a KG \(\mathcal {K} \) and a triple \(\langle h, r, \_\rangle \) (resp. \(\langle \_, r, t\rangle \)) where ‘\(\_\)’ denotes a missing entity, the KG completion problem is to predict the missing t (resp. h) by computing for each \(e\,{\in }\,\mathcal {E} \) a score \(f(\langle h{,} r{,} e\rangle )\) (resp. \(f(\langle e{,} r{,} t\rangle )\)) that reflects the likelihood of the triple \(\langle h{,} r{,} e\rangle \) (resp. \(\langle e{,} r{,} t\rangle \)) being in the KG.
Statistical Relational Learning for KG Completion. Statistical relational learning has gained a lot of attention by the research community, including translation-based models [4, 26], latent tensor factorization [18], neural tensor networks [23] and others (see e.g., [16] for an overview). In this work we focus on translation-based models. They address the KG completion problem by reducing it to a representation learning task where the main goal is to represent entities h, t and relations r occurring in \(\mathcal {K} \) in a low-dimensional, say d-dimensional, vector space \(\mathbf {h}, \mathbf {t}, \mathbf {r} \in \mathbb {R}^d\), which define the model parameter matrices \(\mathbf {W}_{\mathcal {E}} \in \mathbb {R}^{|\mathcal {E} | \times d}\) and \(\mathbf {W}_{\mathcal {R}} \in \mathbb {R}^{|\mathcal {R} | \times d}\) respectively. These parameters are typically referred to as latent representations or simply embeddings.
Such KG representations have been shown to be effectively learned by using a ranking loss with the objective that true triples should be ranked before false/unknown ones according to the scoring function. This learning objective is formulated as minimizing a margin-based ranking loss:
where \(f(\cdot )\) is some scoring function that operates on the entity and relation embeddings \(\mathbf {h,r,t}\) and \(\mathbf {h',r,t'}\) from N, which is a set of negative examples, i.e. presumably false triples not contained in \(\mathcal {K} \). This loss is minimized when the true triples outscore the false ones by a constant margin \(\gamma \). In practice the training is done using mini-batches of \(\mathcal {K} \), instead of iterating over all triples, together with stochastic-gradient descent (SGD), since this introduces more variance in the embedding parameter updates and can prevent early convergence in local optima.
For example, in the TransE model [4], given \(\mathcal {K} \) such f relies on distance or similarity between vectors. Intuitively, TransE follows the intuition that there is a linear relation for triples \(\mathbf {h} + \mathbf {r} \approx \mathbf {t}\), hence the scoring function is defined as a dissimilarity measure (e.g. \(\ell ^2\)-norm) \(f(\mathbf {h},\mathbf {r},\mathbf {t}) = \Vert \mathbf {h} + \mathbf {r} - \mathbf {t}\Vert _2^2\). This means that translating entity h with relation r should end up close to its tail entity t in the latent d-dimensional space. In order to prevent overfitting, the magnitudes of parameters in TransE are normalized after each mini-batch to unit-norm vectors, i.e. \(\forall e \in \mathcal {E}: \Vert \mathbf {e}\Vert = 1\).
Enhancing KG Learning with Background Knowledge. It was shown that traditional representation learning can be improved using background knowledge. Most prominently, external text corpora can be used as background [27,28,29, 31]. The main approaches follow the idea of computing two separate representations of entities: a text-based and a KG-based one. There are two proposals to combine both representations:
-
1.
include a linear combination layer to directly modify \(\mathbf {h}\), \(\mathbf {r}\), and \(\mathbf {t}\) in \(\mathcal {L}_{\mathcal {K}}\) of Eq. 1, or
-
2.
add a dedicated learning objective for text-based representations to \(\mathcal {L}_{\mathcal {K}}\).
The TEKE model [27] follows the first proposal, by incorporating textual context of entities into a KG by exploiting a co-occurrence network of entities and words in the text thus defining a combination between pre-trained language model word embeddings and KG entities. It includes \(\mathbf {n}(h)\) as the weight-averaged neighborhood word vector representation of an entity h and then applies a linear combination \(\mathbf {\hat{h}} = \mathbf {A}\mathbf {n}(h) + \mathbf {h}\) to make up the final entity representation used in triple scoring. Furthermore, TEKE uses a weighted average of the merged neighborhood word embeddings for pairs of entities h, t in the text as \(\mathbf {n}(h,t)\) to transform the relation embeddings \(\mathbf {\hat{r}} = \mathbf {B}\mathbf {n}(h,t) + \mathbf {r}\).
The DKRL [29] follows the second proposal and adds three \(\mathcal {L}^i_{\mathcal {K}}\) to the objective for text-based representations, where \(\mathcal {L}^1_{\mathcal {K}}\) uses a translation objective within text-based representations, \(\mathcal {L}^2_{\mathcal {K}}\) is a mixed translation from text-based to KG-based and \(\mathcal {L}^3_{\mathcal {K}}\) from KG-based to text-based. Intuitively, DKRL considers correlation between entities within \(\mathcal {K} \), between \(\mathcal {K} \) and the text and within the text. The text embeddings are learned using a continuous bag of words or a deep convolutional neural network. The KG and the text-based representations are then jointly optimized.
SSP [28, 31] also follow the second proposal and exploit the semantic information about KG’s entities given in the form of textual entity descriptions. The SSP method strengthens the effect of text descriptions by performing the embedding process in the semantic subspace and a topic model for entity text descriptions. They combine the objective of KG embeddings \(\mathcal {L} _{\mathcal {K}}\) and of text embeddings \(\mathcal {L} _{\mathcal {S}}\) using the joint formulation:
where, \(\alpha \) is a hyper-parameter used as a weighting factor. The main advantage of this approach is that the simultaneous training of both objective functions within an aggregated objective allows both models to influence each other.
3 Event-Enhanced KG Completion
In this section we present our approach to KG completion enhanced with event logs: we start with the problem definition, proceed to limitations of existing approaches to address the problem, propose our adaptation of the joint model formulation to the event-based setting based on \(\mathcal {L}_{\mathcal {K}}\) and \(\mathcal {L}_{\mathcal {S}}\), and define several ways to combine \(\mathcal {L}_{\mathcal {K}}\) and \(\mathcal {L}_{\mathcal {S}}\).
3.1 Problem Definition
Let \(\mathcal {X} \, {\subseteq }\, \mathcal {E} \) be a set of event entities. An event log s is a finite sequence \( {(}e_1,{\cdots },e_{m}{)} \) of entities from \(\mathcal {X} \) and a sequence dataset \(\mathcal {S} \) a set \(\{ s_1,\,{\cdots },\,s_n \}\) of event logs. E.g., an event log \(( LE{,}HE{,}BoardJam{,}ShutdownA )\) is generated by machines during operation.
The event-enhanced KG completion problem is, given a KG \(\mathcal {K} \), a sequence dataset \(\mathcal {S} \), and a triple \(\langle h, r, \_\rangle \) (resp. \(\langle \_, r, t\rangle \)), to predict the missing t (resp. h) by exploiting both \(\mathcal {K} \) and \(\mathcal {S} \) for the computation of a score \(f(\langle h, r, e\rangle )\) (resp. \(f(\langle e, r, t\rangle )\)) for each \(e \in \mathcal {E} \). We consider three variations of the event-enhanced completion problem with respect to the entities h, t in the given/predicted triple: the first setting corresponds to the standard KG completion problem, while the other two are specific for our scenario.
-
1.
non-event entities: neither given nor predicted entities of \(\langle h, r, \_\rangle \) (resp. \(\langle \_, r, t\rangle \)) are from \(\mathcal {X} \), as in \(\langle ConveyorA, connectedTo, ConveyorB\rangle \) from Example 1,
-
2.
event entities known by KG: each given or predicted event entity of \(\langle h, r, \_\rangle \) (resp. \(\langle \_, r, t\rangle \)) is in \(\mathcal {K} \), as in \(\langle BoardJam, type, JamAlarm\rangle \) from Example 1,
-
3.
event entities unknown by KG: either given or predicted event entity of \(\langle h, r, \_\rangle \) (resp. \(\langle \_, r, t\rangle \)), does not appear in \(\mathcal {K} \), as for HE from Example 1. This corresponds to the problem of zero-shot learning.
3.2 Limitation of Existing Methods
We now discuss why the existing background-enhanced learning approaches are insufficient or cannot be naturally applied at all to our setting. Approaches of the first kind such as TEKE rely on the assumption that all entities of the KG should also appear in the background. This assumption is critical to TEKE’s enhancement of \(\mathbf {B}\mathbf {n}(h,t)\), which is undefined if either h or t have no text representation. In our setting only the event entities occur in the background and in applications such as manufacturing only a small fragment of KG entities are actually event entities. Moreover, TEKE relies only on mere co-occurrences of words and KG entities in the text corpora and ignores the sequential correlation among entity occurrences. Approaches of the second kind including DKRL and SSP require that a dedicated piece of background, that is, a text corpus, is attached to each individual entity of the KG, while in our setting all event entities share a single event log, i.e. the same background is attached to every event entity. Although the convolutional version of DKRL is able to respect sequential correlation between the words in the entity description, it can not be directly applied to sequences of event entities, since this requires a different embedding objective. Instead of using the final output of the last convolutional layer as representation of the entity, we need to learn representations of the actual tokens in the sequence. The same limitations hold for the topic model of SSP, which also requires a dedicated background for each entity in the KG.
We note that that is a body of work on Business Process Mining that we see as relevant to our work since manufacturing can be seen as a business process. The exact nature of relation requires further study and it as a future work.
3.3 Adaptation of Joint Model Formulation
Observe that in our setting the KG embedding objective function is dominated by non-event entities, i.e., pre-trained event embeddings would be continuously marginalized during training. Thus, we see the joint training objective in Eq. 2 for SSP where there is an explicit definition of the background for learning as the most natural approach for our context and adapt to the idea of simultaneous training of both objective functions.
At the same time, adaptation of Eq. 2 to our setting is a non-trivial task that requires to carefully design three ingredients: (i) an embedding model \(\mathcal {L}_{\mathcal {K}}\) (ii) an embedding model \(\mathcal {L}_{\mathcal {S}}\) (iii) a way to connect the two models for simultaneous training. In our work we do not develop a new \(\mathcal {L} _{\mathcal {K}}\) and exploit TransE as \(\mathcal {L} _{\mathcal {K}}\). The reason is that for our setting it is a good compromise between computational efficiency and quality of prediction.
In the remaining part of the section we start with our novel proposal on how to combine the embeddings of \(\mathcal {L}_{\mathcal {K}}\) and \(\mathcal {L}_{\mathcal {S}}\), and then present our new models for event embeddings \(\mathcal {L}_{\mathcal {S}}\) that we refer to as event-enhanced knowledge learning (EKL).
3.4 Combining \(\mathcal {L}_{\mathcal {K}}\) and \(\mathcal {L}_{\mathcal {S}}\)
We now propose two architectures to combine \(\mathcal {L}_{\mathcal {K}}\) and \(\mathcal {L}_{\mathcal {S}}\). The first, shared, is specific for our setting and different from what was used for text enhanced learning, while the second, combined, is inspired by TEKE.
Shared Architecture. In contrast to text-enhanced KG embeddings, in our setting both the KG and the background contain exclusively entities from \(\mathcal {E} \). Hence, we can directly employ an architecture that uses a single shared entity representation for both \(\mathcal {L}_{\mathcal {K}}\) and \(\mathcal {L}_{\mathcal {S}}\). In such a shared architecture one can define an identity connection between event entity embeddings \(\mathbf {e}\) and \(\mathbf {h,t}\), the entity embeddings in the KG, i.e. the event embedding matrix \(\mathbf {W}_{\mathcal {X}}\) is the \(|\mathcal {X} |\)-by-d submatrix of \(\mathbf {W}_{\mathcal {E}}\). During training, the gradients of both objective functions are averaged and therefore simultaneously updated.
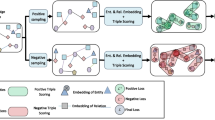
Figure 2a illustrates this approach on a simplistic example. Starting at the bottom, given an event sequence and a KG we simultaneously proceed with both objectives \(\mathcal {L}_{\mathcal {K}}\) and \(\mathcal {L}_{\mathcal {S}}\) as follows: The event entities of the event sequence are directed to the event embedding model using a shared entity representation. In the example the input event \( Event1 \) uses the vector representation \(\mathbf {e_1}\). In parallel, head and tail entities h, t of the input triples from the KG on the right-hand side are also taken from the shared entity embedding matrix resulting in \(\mathbf {h}\) and \(\mathbf {t}\) respectively. The shared aspect is further indicated with the dashed representations stating that \(\mathbf {h} = \mathbf {e_1}\). Note that the representation of the relation r in the input triple is not affected, since relation embeddings are used exclusively in the KG embedding model in \(f(\mathbf {h}, \mathbf {r}, \mathbf {t})\). On top of each embedding model the calculation of the actual objective function \(\mathcal {L}_{\mathcal {S}}\) and \(\mathcal {L}_{\mathcal {K}}\) is carried out and combined according to \(\mathcal {L}_{joint}\) with negative event sample \(\mathbf {e_{neg}}\) and negative entity sample \(\mathbf {t}'\).
Combined Architecture. The shared architecture proposes a very compact and efficient model with only few parameters. In correspondence to TEKE, we also propose a more flexible combined architecture that allows two separate representations of \(\mathbf {W}_{\mathcal {X}}\) and \(\mathbf {W}_{\mathcal {E}}\), however, without relying on the co-occurrence of head and tail entity. More precisely, given \(\mathbf {e}\) from \(\mathbf {W}_{\mathcal {X}}\) and \(\mathbf {h}\) from \(\mathbf {W}_{\mathcal {E}}\), we define \(\hat{\mathbf {h}}\) with a custom combination operator denoted as \(\mathbf {h} \otimes \mathbf {e}\) as follows:
where \(\mathbf {a_r}\) and \(\mathbf {b_r}\) are trainable weighting vectors for each relation r and \(\odot \) is the Hadamard product. Intuitively, this allows the model to adjust the influence of event embeddings on the KG entity embeddings specifically for each relation in a weighted average fashion. Figure 2b shows this combination leading to \(\hat{\mathbf {h}}\) being fed into the triple scoring functions.
Note that both of the above proposed architectures are very general, as in fact any KG embedding model, e.g. factorization-based, can be ‘plugged’ in them.
3.5 Defining \(\mathcal {L}_{\mathcal {S}}\) via Negative Sampling
As for the event embeddings, we first propose to learn event embedding parameters that are given by \(\mathbf {W}_{\mathcal {X}}\) using the following negative sampling adapted softmax loss objective:
where \(\sigma \) is the sigmoid function, \(\mathbf {e}, \mathbf {e_{neg}}\) are the vector representations of the target event and a negative sample event of an additional parameter matrix for the softmax prediction respectively, whereas \(\mathbf {c}\) is the representation of the context of the target event, i.e. some of its predecessors and successors in the event log. Intuitively, this loss is minimized when the context representations consistently have higher similarity to the actual target compared to the negative sample. The notion of context is critical for such definition of \(\mathcal {L}_{\mathcal {S}}\) and we propose two models of context where we assume that the further an event appears from a given one, the lower is their dependency. We model this assumption by selecting a sliding window of size \( m \), which stores only those events that potentially can have effect on each other.
\(\mathbf{EKL}_{{\varvec{Full}}}\) Model. In the full model, we define the context as the target’s predecessors and successors in a sliding window. This is conceptually shown in Fig. 3a, where a sliding window contains a target event entity in the center and its neighboring events (i.e., context) are the center event’s possible causes and effects. The goal is to predict the target event based on the representations of its causes and effects. Following this intuition, we define the context operation for a given context target \(e_i\) in a window of size m:
where \(\oplus \) represents the vector concatenation operation. Since the resulting vector from the concatenation is of size \(\mathbb {R}^{(m-1)\cdot d}\), the size of the vector that represents the target entity \(\mathbf {e}\) for classification in the softmax has to be adapted as well, i.e., \(\mathbf {e} \in \mathbb {R}^{(m-1)\cdot d}\). Note that the actual entity representations preserve their original size in the d-dimensional space, hence the only additional parameters are needed for the prediction of each \(\mathbf {e}\). Therefore, we can still ensure the efficient training of event sequence embeddings. The window size m is added as an additional hyper-parameter.
\(\mathbf{EKL}_{{\varvec{Cause}}}\) Model. Further we also address the case where only the causing events may have influence on the target. In order to preserve the predictive information that a sequence of events inherently possesses, we propose to concatenate the representation of the \(m-1\) event predecessors to predict a given target event, i.e. the m-th event in the window. Formally this can be denoted as \(\mathbf {c_i} = \bigoplus _{j=1}^{m-1} \mathbf {e}_{i-j}\). In Fig. 3b we illustrate this idea again for a generic sequence window of event entities. Observe that the target event here is always the last one in the window.
Note that negative sampling in EKL\(_{\textit{Full}}\) and EKL\(_{\textit{Cause}}\) should be done with care. In order to avoid an accidental inclusion of dependent events as negatives, we make sure that the negative sample is always taken from outside of the complete sequence, i.e. after a certain time threshold before and after the target event.
3.6 Defining \(\mathcal {L}_{\mathcal {S}}\) via Autoencoders: EKL\(_{\textit{Auto}}\) Model
Sequence modeling is usually closely related to Recurrent Neural Networks (RNNs). Based on previous experiments it was known that RNNs do not yield good representations of the events for our datasets. Another natural way to learn representations of event sequences is to resort to the family of autoencoder models. The goal here is to encode the sequence s to a latent representation and then to try decoding this back, hence, the latent encoding needs to conserve the sequential information within a low-dimensional vector. Formally, our event embedding objective is the mean-squared error of the original sequence and its decoding:
where \(\mathbf {s} = [\mathbf {e_1}, \mathbf {e_2}, \cdots , \mathbf {e_m}]\) is the stacked vector representation of s and \(\phi \circ \omega \) is the encoder-decoder function chain. In this work we use a convolutional autoencoder [13] with different filter sizes (adapted to the window size) on the stacked vectors of the sequence, i.e. for one filter \(\mathbf {W}_f\) we have: \(\omega (\mathbf {s}) = \sigma (\mathbf {s} \star \mathbf {W}_f + b)\) and \(\phi (\mathbf {h}) = \sigma (\mathbf {h} \star \mathbf {\tilde{W}}_f + c)\), where \(\star \) is the convolution operator, \(\sigma \) is the sigmoid activation function, \(\mathbf {\tilde{W}}_f\) is the flipped filter matrix, and b and c are bias terms.
4 Evaluation
We have implemented both of our architectures for event-enhanced KG completion into a system prototypeFootnote 2 employing the TransE model with the original max-margin objective and negative sampling techniques in TensorFlow [1]. In contrast to the original implementation provided by the authors, our TensorFlow models use a more efficient training technique from [15] exploiting the AdaGrad variant of stochastic gradient-descent [7], which has been shown to yield good quality of prediction for other relational learning models, due to its frequency-adaptive weighting of updates [17].
The AdaGrad technique is beneficial for parameter updates of entities that are only sparsely connected in the KG, and on the other hand, it prevents overfitting for densely connected entities. As suggested for TransE [4], all embeddings were initialized by sampling from a uniform distribution \(U[-\frac{6}{\sqrt{d}}, \frac{6}{\sqrt{d}}]\). In terms of negative sampling we employ the random replacement of head or tail entities relying on the closed-world assumption and the Bernoulli sampling proposed in [26].
4.1 Evaluation Protocol
We evaluated our three novel approaches for event representations, i.e., EKL\(_{\textit{Auto}}\), EKL\(_{\textit{Full}}\) and EKL\(_{\textit{Cause}}\), together with the two architectures (shared and combined) for KG completion by comparing them to plain TransE and the state-of-the-art TEKE model, precisely the TransE-based TEKE_E version, as a baseline for incorporating events, which are in the TEKE case treated as common text corpus and pre-trained using the word2vec skipgram model [14]. In each of the experiments, the original KG is split into a training (70% of the original KG), validation (10%) and test (20%) sets. Final results on quality of prediction are calculated based on the test set, for which we report two commonly-used evaluation metrics:
-
Mean Rank: the average rank of the entities (head and tail) that would have been the correct ones;
-
Hits@ N : the portion of ranks within N highest ranked entities for \(N \in \{1, 3, 10\}\).
The mean rank in our experiments corresponds to the filtered version that has been originally proposed in [4], i.e. in the test set when ranking a particular triple \(\langle h,r,t\rangle \), all \(\langle h,r,t'\rangle \) triples with \(t\ne t'\) are removed. Employing grid search through the hyper-parameters we determine the best configuration by mean rank on the validation set with early stopping over a maximum of 100 epochs.
4.2 Dataset Descriptions
Our experiments were performed on two real-world datasets enriched with event sequences: manufacturing and traffic. The statistical details of these datasets are presented in Table 1, where we report the total number of triples \(|\mathcal {K} |\), the number of sequences \(|\mathcal {S} |\), the total number of entities \(|\mathcal {E} |\) with the number of event entities stated in brackets and the number of relations \(|\mathcal {R} |\). We made both datasets and the corresponding sequences available online, see the Github link above.
Manufacturing Dataset. The first dataset is an excerpt of a real-world manufacturing KG from an automated factory that stores data about production equipment, product-part descriptions, and production processes. It models several automated production lines and contains entities corresponding to equipments, products, material, and processes connected via different domain-specific relations, e.g. connectedTo, madeOf, follows. The events are messages collected from a subset of the production machines, i.e. machine event logs. These are mostly alarms and warnings reporting about critical states of the production process, e.g. alarms about jams at the material intake of a machine. Some event sequences were known not to influence each other; these bring noise to the embeddings. To avoid this situation, we pre-processed the raw sequences of events by splitting them into multiple disjoint ones based on a maximum time gap that was given by domain experts. This does not bias the embeddings to any of the models, since it just removes spurious correlations. Then, we set the following parameters: mini-batch size to 32 samples; \(d \in \{40, 60, 80\}\) as embedding size; and \(\eta \in \{0.01, 0.05, 0.1\}\) as learning rate. For the event embeddings, we set the context window size \(m \in \{2, 3, 4, 5\}\) for EKL\(_{\textit{Cause}}\) and EKL\(_{\textit{Auto}}\), \(m\in \{3, 5, 7, 9\}\) for EKL\(_{\textit{Full}}\) and \(\alpha \in \{0.1, 0.5, 1.0\}\). The number of negative samples for all event embedding models was empirically set to 8.
Traffic Dataset. Here we took a fragment of the CityPulse data collectionFootnote 3 that was used in the smart city applications [2] for monitoring traffic with sensors placed on several locations in the area of Aarhus in Denmark. From this dataset we engineered a KG consisting of the sensor locations, streets, routes, and point of interest locations with typing information crawled from the Google places APIFootnote 4. The event data is based on the observed vehicle counts for different routes, e.g. IncreasedTrafficEvent between two streets. Since connected streets as well as similar localities (e.g., schools) should intuitively exhibit a similar traffic pattern, the events may be used to complete the data about street connections and locality information. This dataset is particularly challenging and interesting, as the number of entities is higher than the number of overall facts, witnessing the KG sparsity. To cope with the large number of entities and triples in the KG, we set the mini-batch size to 64 samples and the embedding size d from \(\{60, 80, 100\}\), while keeping the rest of the hyper-parameters the same as in the previous scenario.
4.3 Evaluation Results
Overall KG Completion. In Table 2 we report the results for the variations (1) and (2) of the event-enhanced KG completion problem from Sect. 3.1. As expected, our EKL models significantly outperform TEKE and TransE in both settings. We report that EKL\(_{\textit{Cause}}\) in the shared architecture shows the best results in terms of mean rank and the first two hits metrics in the manufacturing case. The shared entity embeddings are highly beneficial for the other EKL models as well and show significant improvements compared to the TEKE_E model. In this case, TEKE_E performs even worse than default TransE, confirming that mere co-occurrence between events does not contribute to the completion. However, in the traffic scenario TEKE_E shows much stronger results compared to TransE, but using our combined architecture achieves consistently better results, as in terms of mean rank EKL\(_{\textit{Full}}\) outperforms the rest. On the other hand, the EKL\(_{\textit{Auto}}\) model has highest hits@1 for both datasets using the shared embeddings, therefore it is the most specific model, but cannot generalize as well as EKL\(_{\textit{Full}}\) and EKL\(_{\textit{Cause}}\).
Impact on Relations. Table 3 (top right and left) contains the mean rank for every KG relation achieved by the best EKL and TEKE_E model on the manufacturing and traffic data. For the manufacturing scenario the relations that are semantically closer to events benefit from the sequential embeddings more than others and we expected this effect. E.g., the improvement for the connectedTo relation that links equipments to each other is more evident than for other relations like materials partonomy isPartOf. The additional knowledge given by the sequences also propagates to the process-oriented follows relation, for which the significant improvement over TEKE is observed. Similar conclusions can be made about the traffic scenario. Here, again the EKL\(_{\textit{Cause}}\) model performs exceptionally well on the hasStartPoint relation, while for less event-dependent relations such as locatedAt the difference of EKL compared to TEKE is less apparent.
Further evaluation is focused on the manufacturing scenario, since this dataset has richer semantics in terms of relations and typing of event entities.
Impact of Window Size. In Table 3 (bottom, left) we examine the impact of the window size on the overall mean rank performance of our models. One can observe that capturing the sequential nature of the event entities is sensitive to the window size parameter. In our manufacturing scenario the EKL\(_{\textit{Cause}}\) model performs very well for small window sizes, and the results deteriorate after the window size of 4. In the preparation of EKL\(_{\textit{Full}}\) the window size must always be an odd number, therefore the window size here is increased by two. It can be observed that EKL\(_{\textit{Full}}\) needs a slightly larger window to capture the context, and shows best performance at a window size of 7. In case of EKL\(_{\textit{Auto}}\) we see a deterioration after window size 3.
Zero-Shot Learning. The zero-shot learning (variation (3) of the event-enhanced KG completion problem in Sect. 3.1) addresses the case when triples about event entities present in the test set are not in the training KG, hence their links to known entities in the KG can only be inferred through their sequential occurrence.
To evaluate the effectiveness of our EKL models in a zero-shot learning setting, we have accordingly designed tailored KG test sets, by varying the percentage of the out-of-KG event entities in the test set (10%, 30%, and 50% of the overall set of event entity triples). Furthermore, we also vary the percentage of out-of-KG event entities in the event log, where 100% indicates that every out-of-KG entity of the test set has been observed at least once in one of the sequences. The results of our experiments are reported in Fig. 4a. Note that in the setting on the right, when 50% of all event entities are solely present in the test set, the EKL\(_{\textit{Full}}\) model consistently outperforms all other approaches w.r.t. mean rank. In other settings, as the sequence dataset proportion is increased, EKL\(_{\textit{Full}}\) shows best improvement and ends up with the lowest mean rank eventually.
It appears that EKL\(_{\textit{Full}}\) is more stable at capturing typing and location of events, due to its incorporation of future context, compared to EKL\(_{\textit{Cause}}\) and EKL\(_{\textit{Auto}}\). On the other hand, all EKL models significantly outperform TEKE in all zero-shot settings and seem to converge with less data. We argue that this is due to their ability to capture sequential correlations inside the event logs and the joint optimization.
Controlled Topology of Processes. In our real-world manufacturing scenario the process entities reflect the topology of physical equipment in the factory. Since our experiments witness that EKL does the best predictions for relations that reflect this topology, we designed a controlled scenario where we can validate how the changes in topology affect quality of prediction.
To this end we chose six relations that naturally determine manufacturing topology: follows, isA, hasSource, involvedEquipment, hasComponent, and connectsTo. We scaled the topology in two dimensions: structure of the processes and number of events. This gave us four KGs, each describing a complex tree-shaped manufacturing process, where one concrete piece of manufacturing equipment is attached to each node of the tree and multiple events are attached to each piece of equipment. These KGs are described in Table 3 (bottom right), where BF stands for branching factor.
We now describe the concrete procedure that we followed to generate these KGs. First, we set the branching factor of the process varying from 2 to 5 and the depth of the process. The intuition behind the branching factor is that, starting from a root process step, the successor steps can be partly executed in parallel and the branching controls this degree of parallelism, which is a common characteristic of real-world processes in manufacturing, road traffic, etc. E.g., in a manufacturing case a particular preparation process may have a fixed set of three successor process steps (branching factor three) each performing a different operation in parallel to the others. Second, for each process we iteratively constructed the process-tree starting from the root, until the process depth, by randomly selecting the number of children in each node to be at most the branching factor. Using the process-tree, we generate corresponding equipment entities participating in the process. Then, using multiple random walks through the process-tree (with restart) we simulated 50, 000 (\(|\mathcal {S} | = 50,000\)) event occurrences that are linked to the equipment of the process. Each random walk follows successor process entities from the root to the end with uniform probability for all successors and a small probability of staying in the current process. Hence, we end up with multiple cause and effect event patterns in the sequence data instead of having a purely linear chaining. Note that the relative amount of event entities to overall entities in the KG stays roughly at \(30\%\).
Again, we compared our three event-enhanced KG embedding models to TEKE_E. The results are presented in Fig. 4b. Observe that, as the branching increases, the more all EKL models outperform TEKE_E, since the alignment of process and machine entities no longer follows a linear sequence, which is hard to capture without considering sequential correlations. In general, EKL\(_{\textit{Full}}\) seems to be the most effective event embedding model in terms of adapting to the non-linear process chains, while we conjecture that EKL\(_{\textit{Auto}}\) might be more prone to overfit to linear sequences.
5 Conclusions
We proposed EKL, a novel method for event-enhanced learning of knowledge graph embeddings by jointly modeling representations of KGs and event logs consisting of sequences of event entities. Our approach has many applications across domains such as manufacturing, smart cities, and social networks. More specifically, we proposed two different architectures, using a single shared entity embedding layer and another one using combined embeddings for joint optimization. Furthermore, we presented several event embedding models with various notions of context concatenation and an event sequence Autoencoder model. Evaluation on two real-world scenarios and a controlled experiment showed the effectiveness of our approach compared to the state-of-the-art TEKE model. Especially process-oriented parts of KGs exhibit significantly improved completion performance when provided with event embeddings. Our EKL models are also capable of zero-shot learning, in which event entities are not linked to the KG. The scaled zero-shot experiments showed that EKL models significantly improve handling of zero-shot event entities in the KG completion.
Notes
- 1.
- 2.
Source code of EKL: http://github.com/NetherNova/event-kge.
- 3.
iot.ee.surrey.ac.uk:8080/datasets.html.
- 4.
developers.google.com/maps/documentation/javascript/places.
References
Abadi, M., Barham, P., Chen, J., Chen, Z., et al.: TensorFlow : a system for large-scale machine learning. In: OSDI (2016)
Ali, M.I., Gao, F., Mileo, A.: CityBench: a configurable benchmark to evaluate RSP engines using smart city datasets. In: Arenas, M., et al. (eds.) ISWC 2015. LNCS, vol. 9367, pp. 374–389. Springer, Cham (2015). https://doi.org/10.1007/978-3-319-25010-6_25
Bordes, A., Chopra, S., Weston, J.: Question answering with subgraph embeddings. In: EMNLP, pp. 615–620 (2014)
Bordes, A., Usunier, N., García-Durán, A., Weston, J., Yakhnenko, O.: Translating embeddings for modeling multi-relational data. In: NIPS, pp. 2787–2795 (2013)
Cucerzan, S.: Large-scale named entity disambiguation based on Wikipedia data. In: EMNLP-CoNLL, pp. 708–716 (2007)
Dong, X., Gabrilovich, E., Heitz, G., Horn, W., Lao, N., Murphy, K., Strohmann, T., Sun, S., Zhang, W.: Knowledge vault: a web-scale approach to probabilistic knowledge fusion. In: ACM SIGKDD, pp. 601–610 (2014)
Duchi, J.C., Hazan, E., Singer, Y.: Adaptive subgradient methods for online learning and stochastic optimization. J. Mach. Learn. Res. 12, 2121–2159 (2011)
Hachey, B., Radford, W., Nothman, J., Honnibal, M., Curran, J.R.: Evaluating entity linking with Wikipedia. Artif. Intell. 194, 130–150 (2013)
Kharlamov, E., Hovland, D., Skjæveland, M.G., Bilidas, D., Jiménez-Ruiz, E., Xiao, G., Soylu, A., Lanti, D., Rezk, M., Zheleznyakov, D., Giese, M., Lie, H., Ioannidis, Y.E., Kotidis, Y., Koubarakis, M., Waaler, A.: Ontology based data access in Statoil. JWS 44, 3–36 (2017)
Kharlamov, E., Mailis, T., Mehdi, G., Neuenstadt, C., Özçep, Ö.L., Roshchin, M., Solomakhina, N., Soylu, A., Svingos, C., Brandt, S., Giese, M., Ioannidis, Y.E., Lamparter, S., Möller, R., Kotidis, Y., Waaler, A.: Semantic access to streaming and static data at Siemens. JWS 44, 54–74 (2017)
Krompaß, D., Baier, S., Tresp, V.: Type-constrained representation learning in knowledge graphs. In: Arenas, M., et al. (eds.) ISWC 2015. LNCS, vol. 9366, pp. 640–655. Springer, Cham (2015). https://doi.org/10.1007/978-3-319-25007-6_37
Lehmann, J., Isele, R., Jakob, M., Jentzsch, A., Kontokostas, D., Mendes, P.N., Hellmann, S., Morsey, M., van Kleef, P., Auer, S., Bizer, C.: Dbpedia - a large-scale, multilingual knowledge base extracted from Wikipedia. Semant. Web 6(2), 167–195 (2015)
Masci, J., Meier, U., Cireşan, D., Schmidhuber, J.: Stacked convolutional auto-encoders for hierarchical feature extraction. In: Honkela, T., Duch, W., Girolami, M., Kaski, S. (eds.) ICANN 2011. LNCS, vol. 6791, pp. 52–59. Springer, Heidelberg (2011). https://doi.org/10.1007/978-3-642-21735-7_7
Mikolov, T., Chen, K., Corrado, G., Dean, J.: Distributed representations of words and phrases and their compositionality. In: NIPS, pp. 1–9 (2013)
Minervini, P., Fanizzi, N., D’Amato, C., Esposito, F.: Scalable learning of entity and predicate embeddings for knowledge graph completion. In: ICMLA, pp. 162–167 (2015)
Nickel, M., Murphy, K., Tresp, V., Gabrilovich, E.: A review of relational machine learning for knowledge graphs. Proc. IEEE 104(1), 11–33 (2016)
Nickel, M., Rosasco, L., Poggio, T.A.: Holographic embeddings of knowledge graphs. In: AAAI, pp. 1955–1961 (2016)
Nickel, M., Tresp, V., Kriegel, H.P.: A three-way model for collective learning on multi-relational data. In: ICML (2011)
Ringsquandl, M., Lamparter, S., Brandt, S., Hubauer, T., Lepratti, R.: Semantic-guided feature selection for industrial automation systems. In: Arenas, M., et al. (eds.) ISWC 2015. LNCS, vol. 9367, pp. 225–240. Springer, Cham (2015). https://doi.org/10.1007/978-3-319-25010-6_13
Ringsquandl, M., Lamparter, S., Kharlamov, E., Lepratti, R., Stepanova, D., Kroeger, P., Horrocks, I.: On event-driven learning of knowledge in smart factories: the case of siemens. In: IEEE Big Data (2017)
Santos, H., Dantas, V., Furtado, V., Pinheiro, P., McGuinness, D.L.: From data to city indicators: a knowledge graph for supporting automatic generation of dashboards. In: Blomqvist, E., Maynard, D., Gangemi, A., Hoekstra, R., Hitzler, P., Hartig, O. (eds.) ESWC 2017. LNCS, vol. 10250, pp. 94–108. Springer, Cham (2017). https://doi.org/10.1007/978-3-319-58451-5_7
Shi, B., Weninger, T.: ProjE : embedding projection for knowledge graph completion. In: AAAI 2017, pp. 1–14 (2017)
Socher, R., Chen, D., Manning, C.D., Ng, A.Y.: Reasoning with neural tensor networks for knowledge base completion. In: NIPS, pp. 1–10 (2013)
Suchanek, F.M., Kasneci, G., Weikum, G.: YAGO: a core of semantic knowledge. In: Proceedings of WWW, pp. 697–706 (2007)
Wang, Q., Wang, B., Guo, L.: Knowledge base completion using embeddings and rules. In: IJCAI, pp. 1859–1866 (2015)
Wang, Z., Zhang, J., Feng, J., Chen, Z.: Knowledge graph embedding by translating on hyperplanes. In: AAAI, pp. 1112–1119 (2014)
Wang, Z., Li, J.Z.J.: Text-enhanced representation learning for knowledge graph. In: IJCAI, pp. 1293–1299 (2016)
Xiao, H., Huang, M., Meng, L., Zhu, X.: SSP: semantic space projection for knowledge graph embedding with text descriptions. In: AAAI, pp. 1–10 (2017)
Xie, R., Liu, Z., Jia, J., Luan, H., Sun, M.: Representation learning of knowledge graphs with entity descriptions. In: IJCAI, pp. 2659–2665 (2016)
Yang, Z., Tang, J., Cohen, W.W.: Multi-modal bayesian embeddings for learning social knowledge graphs. In: IJCAI, pp. 2287–2293 (2016)
Zhong, H., Zhang, J., Wang, Z., Wan, H., Chen, Z.: Aligning knowledge and text embeddings by entity descriptions. In: EMNLP, pp. 267–272 (2015)
Acknowledgements
This work was partially supported by the EPSRC projects DBOnto,MaSI\(^3\) and ED\(^3\).
Author information
Authors and Affiliations
Corresponding author
Editor information
Editors and Affiliations
Rights and permissions
Copyright information
© 2018 Springer International Publishing AG, part of Springer Nature
About this paper
Cite this paper
Ringsquandl, M. et al. (2018). Event-Enhanced Learning for KG Completion. In: Gangemi, A., et al. The Semantic Web. ESWC 2018. Lecture Notes in Computer Science(), vol 10843. Springer, Cham. https://doi.org/10.1007/978-3-319-93417-4_35
Download citation
DOI: https://doi.org/10.1007/978-3-319-93417-4_35
Published:
Publisher Name: Springer, Cham
Print ISBN: 978-3-319-93416-7
Online ISBN: 978-3-319-93417-4
eBook Packages: Computer ScienceComputer Science (R0)