Control Variates as a Variance Reduction Technique for Random Projections

Abstract

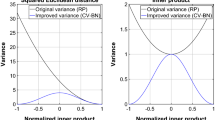
Control variates are used as a variance reduction technique in Monte Carlo integration, making use of positively correlated variables to bring about a reduction of variance for estimated data. By storing the marginal norms of our data, we can use control variates to reduce the variance of random projection estimates. We demonstrate the use of control variates in estimating the Euclidean distance and inner product between pairs of vectors, and give some insight on our control variate correction. Finally, we demonstrate our variance reduction through experiments on synthetic data and the arcene, colon, kos, nips datasets. We hope that our work provides a starting point for other control variate techniques in further random projection applications.

Appendix

We use the following lemma for ease of computation of first and second moments.

Lemma 2

Suppose we have a sequence of terms $\{t_i\}_{i=1}^p = \{a_ir_i\}_{i=1}^p$ for $\mathbf{a} = (a_1,a_2,\ldots , a_p)$, $\{s_i\}_{i=1}^p = \{b_ir_i\}_{i=1}^p$ for $\mathbf{b} = (b_1,b_2,\ldots , b_p)$ and $r_i$ i.i.d. random variables with $\mathbb E[r_i] = 0$, $\mathbb E[r_i^2] = 1$ and finite third, and fourth moments, denoted by $\mu _3, \mu _4$ respectively. Then:

$$\begin{aligned} \mathbb E\left[ \left( \sum _{i=1}^p t_i\right) ^2\right]&= \sum _{i=1}^p a_i^2 = \Vert \mathbf{a}\Vert _2^2\end{aligned}$$

(59)

$$\begin{aligned} \mathbb E\left[ \left( \sum _{i=1}^p t_i\right) ^4\right]&= \mu _4 \sum _{i=1}^p a_i^4 + 6 \sum _{u=1}^{p-1}\sum _{v=u+1}^p a_u^2a_v^2 \end{aligned}$$

(60)

$$\begin{aligned} \mathbb E\left[ \left( \sum _{i=1}^p s_i\right) \left( \sum _{i=1}^p t_i\right) \right]&= \sum _{i=1}^p a_ib_i = \langle \mathbf{a}, \mathbf{b} \rangle \end{aligned}$$

(61)

$$\begin{aligned} \mathbb E\left[ \left( \sum _{i=1}^p s_i\right) ^2\left( \sum _{i=1}^p t_i\right) ^2\right]&= \sum _{i=1}^p a_i^2b_i^2 + \sum _{i \ne j}a_i^2b_j^2 + 4\sum _{u=1}^{p-1}\sum _{v=u+1}^p a_ub_ua_vb_v \end{aligned}$$

(62)

The motivation for this lemma is that we do expansion of terms of the above four forms to prove our theorems.