Development of Scalable Three-Dimensional Elasto-Plastic Nonlinear Wave Propagation Analysis Method for Earthquake Damage Estimation of Soft Grounds

Abstract

In soft complex grounds, earthquakes cause damages with large deformation such as landslides and subsidence. Use of elasto-plastic models as the constitutive equation of soils is suitable for evaluation of nonlinear wave propagation with large ground deformation. However, there is no example of elasto-plastic nonlinear wave propagation analysis method capable of simulating a large-scale soil deformation problem. In this study, we developed a scalable elasto-plastic nonlinear wave propagation analysis program based on three-dimensional nonlinear finite-element method. The program attains 86.2% strong scaling efficiency from 240 CPU cores to 3840 CPU cores of PRIMEHPC FX10 based Oakleaf-FX [1], with 8.85 TFLOPS (15.6% of peak) performance on 3840 CPU cores. We verified the elasto-plastic nonlinear wave propagation program through convergence analysis, and conducted an analysis with large deformation for an actual soft ground modeled using 47,813,250 degrees-of-freedom.

1 Introduction

Large earthquakes often cause severe damage in cut-and-fill land developed for housing. It is said that earthquake waves are amplified locally by impedance contrast between the cut layer and fill layer, which causes damage. To evaluate this wave amplification, 3D wave propagation analysis with high spatial resolution considering nonlinearity of soil properties is required. Finite-element methods (FEM) are suitable for solving problems with complex geometry, and nonlinear constitutive relations can be implemented. However, large-scale finite-element analysis is computational expensive to assure convergence of the numerical solution.

Efficient use of high performance computers is effective for solving this problem [2, 3]. For example, Ichimura et al. [4] developed a fast and scalable 3D nonlinear wave propagation analysis method based on nonlinear FEM, and was selected as a Gordon Bell Prize Finalist in SC14. Here, computational methods for speeding up the iterative solver was developed, which enabled large-scale analysis on distributed-shared memory parallel supercomputers such as the K computer [5]. In this method, a simple nonlinear model (Ramberg-Osgood model [6] with the Masing rule [7]) was used for the constitutive equation of soils, and the program was used for estimating earthquake damage at sites with complex grounds [8]. However, this simple constitutive equation is insufficient for simulating permanent ground displacement; 3D elasto-plastic constitutive equations are required to conduct reliable nonlinear wave propagation analysis for soft grounds. On the other hand, existing elasto-plastic nonlinear wave propagation analysis programs based on nonlinear FEM for seismic response of soils are not designed for high performance computers, and thus they cannot be used for large scale analyses.

In this study, we develop a scalable 3D elasto-plastic nonlinear wave propagation analysis method based on the highly efficient FEM solver described in [4]. Here, we incorporate a standard 3D elasto-plastic constitutive equation for soft soils (i.e., super-subloading surface Sekiguchi-Ohta EC model [9,10,11]) into this FEM solver. The FEM solver is also extended to conduct self-weight analysis, which is essential for conducting elasto-plastic analysis. This enables large-scale 3D elasto-plastic nonlinear wave propagation analysis, which is required for assuring numerical convergence when computing seismic response of soft grounds.

The rest of the paper is organized as follows. In Sect. 2, we describe the target equation and the developed nonlinear wave propagation analysis method. In Sect. 3, we verify the method through a convergence test, apply the method to an actual site, and measure the computational performance of the method. Section 4 concludes the paper.

2 Methodology

Previous wave propagation analysis based on nonlinear FEM [4] used the Ramberg-Osgood model and Masing rule for the constitutive equation of soils. Instead, we apply an elasto-plastic model (super-subloading surface Sekiguchi-Ohta EC model) to this FEM solver for analyzing large ground deformation. In elasto-plastic nonlinear wave propagation analysis, we first find an initial stress state by conducting initial stress analysis considering gravitational forces, and then conduct nonlinear wave propagation analysis by inputting seismic waves. Since the previous FEM implementation was not able to carry out initial stress analysis and nonlinear wave propagation analysis successively, we extended the solver. In this section, we first describe the target wave propagation problem with the super-subloading surface Sekiguchi-Ohta EC model, and then we describe the developed scalable elasto-plastic nonlinear wave propagation analysis method.

2.1 Target Problem

We use the following equation obtained by discretizing the nonlinear wave equation in the spatial domain by FEM and the time domain by the Newmark-$\beta$ method:

$$\begin{aligned}&\left( \frac{4}{dt^2} \mathbf {M}+\frac{2}{dt} \mathbf {C}^n + \mathbf {K}^n\right) ~\delta \mathbf {u}^{n} \nonumber \\&\qquad \qquad =\mathbf {f}^n- \mathbf {q}^{n-1} + \mathbf {C}^n \mathbf {v}^{n-1} + \mathbf {M}\left( \mathbf {a}^{n-1} + \frac{4}{dt} \mathbf {v}^{n-1}\right) , \end{aligned}$$

(1)

with

$$\begin{aligned} {\left\{ \begin{array}{ll} \mathbf {q}^{n} = \mathbf {q}^{n-1} + \mathbf {K}^n \delta \mathbf {u}^{n},\\ \mathbf {u}^{n} = \mathbf {u}^{n-1} + \delta \mathbf {u}^{n},\\ \mathbf {v}^{n} = - \mathbf {v}^{n-1} + \frac{2}{dt} \delta \mathbf {u}^{n},\\ \mathbf {a}^{n} = - \mathbf {a}^{n-1} - \frac{4}{dt} \mathbf {v}^{n-1} + \frac{4}{dt^2} \delta \mathbf {u}^{n}. \end{array}\right. } \end{aligned}$$

(2)

Here, $\delta \mathbf {u}, \mathbf {u}, \mathbf {v}, \mathbf {a}$, and $\mathbf {f}$ are vectors describing incremental displacement, displacement, velocity, acceleration, and external force, respectively. $\mathbf {M}, \mathbf {C}$, and $\mathbf {K}$ are the mass, damping, and stiffness matrices. dt, and n are the time step increment and the time step number, respectively. In the case that nonlinearity occurs, $\mathbf {C}, \mathbf {K}$ change every time steps. Rayleigh damping is used for the damping matrix $\mathbf {C}$, where the element damping matrix $\mathbf {C}_e^n$ is calculated using the element mass matrix $\mathbf {M}_e$ and the element stiffness matrix $\mathbf {K}_e^n$ as follows:

$$\begin{aligned} \mathbf {C}_e^n = \alpha ^{*} \mathbf {M}_e + \beta ^{*} \mathbf {K}_e^n, \end{aligned}$$

The coefficients $\alpha ^{*}$ and $\beta ^{*}$ are determined by solving the following least-squares equation,

$$\begin{aligned} \mathrm {minimize}\left[ \int ^{f_\mathrm {max}}_{f_\mathrm {min}} \left( h^n - \frac{1}{2}\left( \frac{\alpha ^{*}}{2 \pi f}+ 2 \pi f \beta ^{*} \right) \right) ^2 \mathrm {d}f\right] . \end{aligned}$$

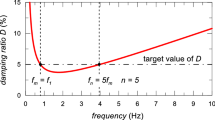
where $f_\mathrm {max}$ and $f_\mathrm {min}$ are the maximum and minimum target frequencies and $h^n$ is the damping ratio at time step n. Small elements are locally generated when modeling complex geometry with solid elements, and therefore satisfying the Courant condition when using explicit time integration methods (e.g., central difference method) leads to small time increments and considerable computational cost. Thus, the Newmark-$\beta$ method is used for time integration with $\beta =1/4, \delta =1/2$ ($\beta$ and $\delta$ are parameters of the Newmark-$\beta$ method). By applying Semi-infinite absorbing boundary conditions to the bottom and side boundaries of the simulation domain, we take dissipation character and semi-infinite character into consideration.

Next we summarize the super-subloading surface Sekiguchi-Ohta EC model [9,10,11], which is one of the 3D elasto-plastic constitutive equations used in nonlinear wave propagation analysis of soils. The super-subloading surface Sekiguchi-Ohta EC model is described using subloading and superloading surfaces summarized in Fig. 1. The subloading surface is a yield surface defined inside of the normal yield surface. It is similar in shape to the normal yield surface and a current stress state is always on it. We can take into account plastic deformation in the normal yield surface and reproduce smooth change from elastic state to plastic state by introducing the subloading surface. On the other hand, the superloading surface is a yield surface defined outside of the normal yield surface. It is similar in shape to the normal yield surface and the subloading surface. Relative contraction of the superloading surface (i.e., the expansion of the normal yield surface) describes the decay of the structure as plastic deformation proceeds. At the end, the superloading surface and the normal yield surface become identical. Similarity ratios of the subloading surface to the superloading surface, of the normal yield surface to the superloading surface are denoted by $R, R^*$, respectively ($0< R \le 1, 0 < R^*\le 1$). 1/R is overconsolidation ratio and R is the index of degree of structure. As plastic deformation proceeds, the subloading surface expands and the superloading surface relatively contracts. The expansion speed $\dot{R}$ and contraction speed $\dot{R^*}$ are calculated as in Fig. 1. $D, \dot{\varvec{\epsilon }^p}$ are the coefficient of dilatancy, the plastic volumetric strain speed and m, a, b, c are the degradation parameters of overconsolidated state and structures state, respectively. Using this R and $R^*$, a yield function of the subloading surface is described as $f\left( \varvec{\sigma }', {\epsilon _v}^p\right)$ in Fig. 1. Here, $M, n_E, \varvec{\sigma }', {\varvec{\sigma }_0}'$ are the critical state parameter, the fitting parameter, the effective stress tensor, the effective initial stress tensor and $\eta ^*, p', q$ are the stress parameter proposed by Sekiguchi and Ohta, the effective mean stress, the deviatoric stress. The following stress-strain relationship is obtained by solving the simultaneous equations in Fig. 1.

(3)

where,

$\mathbf {C}^e (C_{ijkl}^e), \mathbf {C}^{ep}$ are the elasticity tensor, the elasto-plasticity tensor and $K, G, \varLambda , \nu '$ are the bulk modulus, the shear modulus, the irreversibility ratio, the effective Poisson’s ratio, respectively.

Fig. 1.

Governing equation of stress-strain relation and relation of yield surfaces

2.2 Fast and Scalable Elasto-Plastic Nonlinear Analysis Method

In this subsection, we first summarize the solver algorithm in [4] following Algorithm 1. By changing the $\mathbf {K}$ matrix in Algorithm 1 according to the change in the constitutive model, we can expect high computational efficiency when conducting elasto-plastic analyses. In the latter part of the subsection, we describe the initial stress analysis and nonlinear wave propagation analysis procedure.

The majority of the cost in conducting finite-element analysis is in solving the linear equation in Eq. (1). The solver in [4] enables fast and scalable solving of Eq. (1) by using adaptive conjugate gradient (CG) method with multi-grid preconditioning, mixed precision arithmetics, and fast matrix-vector multiplication based on the Element-by-Element method [12, 13]. Instead of storing a fixed preconditioning matrix, the preconditioning equation is solved roughly using an another CG solver. In Algorithm 1, outer loop means the iterative calculation of the CG method solving $\mathbf {A} \mathbf {x} = \mathbf {b}$, and the inner loop means the computation of preconditioning equation (solving $\mathbf{{z}} = \mathbf{{A}}^{-1} \mathbf{{r}}$ by CG method). Since the preconditioning equation needs only be solved roughly, single-precision arithmetic is used in the preconditioner, while double precision arithmetic is used in the outer loop. Furthermore, the multi-grid method is used in the preconditioner to improve convergence in the inner loop itself. Here, a two-step grid with second-order tetrahedral mesh ($\text {FEMmodel}$) and first-order tetrahedral mesh ($\text {FEMmodel}_\text {c}$) is used. Specifically, an initial solution of $\mathbf{{z}} = \mathbf{{A}}^{-1} \mathbf{{r}}$ is estimated by computing $\mathbf{{z}}_c = {\mathbf{{A}}_c}^{-1} \mathbf{{r}}_c$, which reduces the number of iterations in solving $\mathbf{{z}} = \mathbf{{A}}^{-1} \mathbf{{r}}$. In order to reduce memory footprint, memory transfer sizes, and improve load balance, a matrix-free method is used to compute matrix-vector products instead of storing the global matrix on memory. This algorithm is implemented using MPI/OpenMP for computation on distributed-shared memory computers.

We enable initial stress analysis and nonlinear wave propagation analysis successively by changing the right hand side of Eq. (1). The calculation algorithm for each time step of the elasto-plastic nonlinear wave propagation analysis is shown in Algorithm 2. Here, the same algorithm is used for both the initial stress analysis and the wave propagation analysis. In the following, we describe initial stress analysis and nonlinear wave propagation analysis after initial stress analysis.

In this study, we use self-weight analysis as initial stress analysis. Gravity is considered by calculating the external force vector in Eq. (1) as

$$\begin{aligned} \mathbf {f}^n = \mathbf {f}^n + \int \rho g \mathbf {N} \mathrm {d}V, \end{aligned}$$

(4)

where $\rho , g$, and $\mathbf {N}$ are density, gravitational acceleration and the shape function, respectively. We apply the Dirichlet boundary condition by fixing vertical displacement at bottom nodes of the model.

During nonlinear wave propagation analysis, waves are inputted from the bottom of the model. Thus, instead of using Dirichlet boundary conditions at the bottom of the model, we balance gravitational forces by adding reaction force to the bottom of the model obtained at the last step of initial stress analysis (step $t_0$). Here, the reaction force

$$\begin{aligned} - \mathbf {f}^{t_0} + \mathbf {q}^{t_0-1}, \end{aligned}$$

(5)

is added to the bottom nodes of the model in Eq. (1). Here, $\mathbf {f}^{n}$ is calculated as in Eq. (4).

3 Numerical Experiments

3.1 Verification of Proposed Method

As we cannot obtain analytical solutions for elasto-plastic nonlinear wave propagation analysis, we cannot verify the developed program by comparing numerical solutions with analytical solutions. However, we can compare 1D numerical analysis results with the same elasto-plastic constitutive models with 3D numerical analysis results on a horizontally stratified soil structure to verify the consistency between the 1D and 3D analyses as well as the numerical convergence with fine discretization of the analyses. As we use the results of the 1D analysis (stress and velocity) with the same elasto-plastic models as the boundary condition at base and side faces of the 3D model for 3D analyses, we can check the consistency between the 3D and 1D analyses and their numerical convergence by checking the uniformity of 3D analysis results in the $x-y$ plane.

Fig. 2.

Horizontally layered model and ground property

We conducted numerical tests on a horizontally stratified ground structure with soft layer of 10 m thickness on top of bedrock of 40 m thickness. The size of the 3D model was $0\le x\le 16\,\text {m}, 0\le y\le 16\,\text {m}, 0\le z\le 50\,\text {m}$ (Fig. 2). The ground properties of each layer and elasto-plastic parameters of the soft layer are described in Fig. 2. Here, $K_i$ and $K_0$ are the coefficient of initial earth pressure at rest and the coefficient of earth pressure at rest, respectively. We used $h_\mathrm {max} \times 0.01$ for Rayleigh damping of the soft layer. Following previous studies [8], we chose element size ds such that it satisfies

$$\begin{aligned} ds\le {\frac{V_s}{{\chi }f_\mathrm {max}}}. \end{aligned}$$

(6)

Here, $f_\mathrm {max}$ and $\chi$ are the maximum target frequency and the number of elements per wavelength, respectively. $\chi$ is set to ${\chi }>10$ for nonlinear layers and ${\chi }>5$ for linear layers for numerical convergence of the solution. Taking the above conditions into account, we considered two models whose minimum element size is 1 m and 2 m, respectively, and the maximum element size is 8 m in both 1D analysis and 3D analysis. We used the seismic wave observed at the Kobe Marine Meteorological Observatory during the Great Hanshin Earthquake in 1995 (Fig. 3, Kobe wave). We pull back this wave to the bedrock and input it to the bottom of the 3D model. Since the major components of the response is influenced by waves below 2.5 Hz, we conduct analysis targeting frequency range between 0.1 and 2.5 Hz. We first conduct self-weight analysis with $dt = 0.001\,\text {s}\,{\times }$ 700,000 time steps, and then conduct nonlinear wave propagation analysis with $dt = 0.001\,\text {s}\,{\times }$ 40,000 time steps using the Kobe wave. Instead of loading the full gravitational force at the initial step, we increased the gravitational force by 0.000002 times every time step until 500,000 time steps for both the 1D and 3D analyses. For the 3D analysis, we used the Oakleaf-FX system at the University of Tokyo consisting of 4,800 computing nodes each with single 16 core SPARC64 IXfx CPUs (Fujitsu’s PRIMEHPC FX10 massively parallel supercomputer with a peak performance of 1.13 PFLOPS). For the model with minimum element size of 1 m, the degrees-of-freedom was 85,839, and the 3D analysis took 20,619 s using 576 CPU cores (72 MPI processes $\times$ 8 OpenMP threads). For the model with minimum element size of 2 m, the degrees-of-freedom was 14,427, and the 3D analysis took 12,278 s by using 64 CPU cores (8 MPI processes $\times$ 8 OpenMP threads).

Fig. 3.

Input wave

Results of the 1D and 3D analyses are shown in Figs. 4 and 5. From Fig. 4, we can see that the time history of displacement on ground surface for each analysis are almost identical. Figure 5 shows the displacement distribution at surface of the 3D analysis. We can see that the difference of displacement values at each point is converged within about 0.75%. Although not shown, the maximum difference was about 2% for the case with element size of 2 m. We can see that the 3D analysis results converge to the 1D analysis results by using sufficiently small elements (in this case, 1 m elements).

Fig. 4.

Displacement time history at surface for horizontally stratified ground model

Fig. 5.

Displacement on surface for horizontally stratified ground model ($ds = 1\,\text {m}$)

3.2 Application Example

The Kumamoto earthquake occurring successively on September 14 and 16, 2016 caused heavy damage such as landslides and house collapse. At a residential area in the Minamiaso village with large-scale embankment, houses near the valley collapsed due to landslide and some cracks occurred in the east-west direction [14]. In addition, ground subsidence occurred at a residential area little far from the valley. Targeting this residential area, we conducted elasto-plastic nonlinear wave propagation analysis using the developed program.

Fig. 6.

Geometry and ground property of application problem

Fig. 7.

Strong scaling measured for solving 25 time steps of application problem. Numbers in brackets indicate floating-point performance efficiency to hardware peak.

Fig. 8.

Displacement on ground surface. Black arrow indicates the displacement direction in $x-y$ plane.

The FEM model used is shown in Fig. 6. There is no borehole logs in the target area, so we estimate the thickness and shape of the soft layer based on borehole logs measured near the target area. The elevation was based on the digital elevation map of the Geospatial Information Authority of Japan. Finally, we assume the ground consists of two layers. The size of the model was $0\le x\le 720\,\text {m}, 0\le y\le 640\,\text {m}, 0\le z \le$ about $100\,\text {m}$. The ground properties of each layer shown in Fig. 6 were set based on [15]. Here we used $h_\mathrm {max} \times 0.01$ as the Rayleigh damping of the soft layer. Based on the results of Sect. 3.1, we set the minimum element size to 1 m, and the maximum element size to 16 m. The model consisted of 47,813,250 degrees-of-freedom, 15,937,750 nodes, and 11,204,117 tetrahedral elements. We pulled the seismic wave observed at the KiK-net [16] station KMMH16 during the Kumamoto earthquake (Fig. 3, Mashiki wave) to the bedrock and computed the response targeting frequency range between 0.1 and 2.5 Hz. We first conducted self-weight analysis with $dt = 0.001\,{\times }$ 350,000 time steps and then conducted wave propagation analysis with $dt = 0.001\,{\times }$ 55,000 time steps. Here we increased the self-weight by 0.000004 times every time step until full loading at 250,000 time steps.

In order to check the computational performance of the developed program, we measured strong scaling on this model using the first 25 time steps. As shown in Fig. 7, the program attained 86.2% strong scaling efficiency from 240 CPU cores (30 MPI processes $\times$ 8 OpenMP threads) to 3840 CPU cores (480 MPI processes $\times$ 8 OpenMP threads). This enabled 8.85 TFLOPS (15.6% of peak) when using 3840 CPU cores of Oakleaf-FX (480 MPI processes $\times$ 8 OpenMP threads), leading to feasible analysis time of 31 h 13 min (112,388 s) for conducting the whole initial stress and wave propagation analysis. This high peak performance could be attained by the method using matrix free matrix-vector multiplication, single-precision arithmetic and so on indicated in Sect. 2.2.

The magnitude of the displacement in the x, y directions and the displacement distribution in the z direction on ground surface are shown in Fig. 8. From this figure, we can see permanent displacement towards the north valley at part of the soft layer after wave propagation analysis. We can also see large subsidence at the center of the soft layer. These results are effects caused by using the elasto-plastic model into the 3D analysis. By setting more suitable parameters to the soft soil based on site measurements, we can expect improvement of analysis results following the actual phenomenon.

4 Concluding Remarks

In this study, we developed a scalable 3D elasto-plastic nonlinear wave propagation analysis method. We showed its capability of conducting large-scale nonlinear wave propagation analysis with large deformation through a verification analysis, scaling test, and application to the embankment of the Minamiaso village. The program attained high performance on Oakleaf-FX, with 8.85 TFLOPS (15.6% of peak) on 3840 CPU cores. In the future, we plan to apply this method to the seismic response analysis for roads in mountain region and bridges which are prone to seismic damage.