Free Surface Flow Simulation of Fish Turning Motion

Abstract

In this paper, the influence of depth from the free surface of the fish and turning motion will be clarified by numerical simulation. We used Moving-Grid Finite volume method and Moving Computational Domain Method with free surface height function for numerical simulation schemes. Numerical analysis is performed by changing the radius at a certain depth, and the influence of the difference in radius is clarified. Next, analyze the fish that changes its depth and performs rotational motion at the same rotation radius, and clarify the influence of the difference in depth. In any cases, the drag coefficient was a positive value, the side force coefficient was a negative value and the lift coefficient was a smaller value than drag. Analysis was performed with the radius of rotation changed at a certain depth. The depth was changed and the rotational motion at the same rotation radius was analyzed. As a result, it was found the following. The smaller radius of rotation, the greater the lift and side force coefficients. The deeper the fish from free surface, the greater the lift coefficient. It is possible to clarify the influence of depth and radius of rotation from the free surface of submerged fish that is in turning motion on the flow.

1 Introduction

Free surface flows [1] are widely seen in industries. For example, sloshing in the tank [2], mixing in the vessel [3], droplets from the nozzle [4], resin in the injection molding [5] are free surface flows with industrial applications. Focusing, on moving submerged objects, wave power generator [6], moving fish [7,8,9], fish detection in ocean currents are attractive application.In particular, since fish are familiar existence and application to fish robots can be considered in the future, many research has been reported on the flow of free surface with fish [7,8,9]. In general, fish are not limited to linear motion, but always move three-dimensionally including curvilinear motion. Also, when fish escape from enemies, it is known to change the direction of moving by deforming the shape of the fish [7]. In other words, the surface shape change on the fish itself has some influence on the flow fields. Furthermore, for fish swimming near the surface of the water, the movement may influence the free surface as water surface, or the interaction such as the influence on the fish due to the large wave may considered. In other words, when analyzing the swimming phenomenon of fish, it is necessary to simultaneously consider the three-dimensional curved movement, the change of the surface shape of the fish and the shape of the water at the same time, various researches are done. Numerical simulation approaches to these studies can be also be found in several papers. Focusing on what does not consider the influence of the free surface, Yu et al. carried out a three-dimensional simulation to clarify the relationship between how to move fish fins and surrounding flow field [8]. In addition, Kajtar simulates fish with a rigid body connected by a link, and reveals a flow near a free surface of two dimensions by a method of moving a rigid body [9]. However, as far as the authors know, these numerical researches have only studies that do not consider the influence of free surfaces or only one-way motion to fish.

In the view of these backgrounds, it can be said that calculation of curved rotational motion is indispensable in addition or free surface in order to capture more accurate motion of fish near the water surface, but in the past this case is not, we focused on t part and carried out the research. In such free surface flow with moving submerged object, a method for tracking a free surface is important. Among them, the height function method [10] has high computational efficiency. Generally, in free surface flow, there are cases where complicated phenomena such as bubble, droplet and wave entrainment are sometimes presented, which is one of major problems. However, in this paper, we will not consider the influence of breaking in order to make the expression of motion of fish with high flexibility and expansions of analysis area top priority. In simulating such a free surface with fish, since the computational grid moves and deforms according to the change of the free surface and the movement, a method suitable for a computational grid which moves and deforms with time is necessary. Among them, Moving-Grid Finite volume method [11] that strictly satisfies the Geometric Conservation Law, and it was considers suitable. The Moving-Grid Finite volume method has been proposed as a computational scheme suitable for moving grid and has been successfully applied to various unsteady flow problems. For example, this method was applied to the flows with the falling spheres in long pipe [12,13,14] and fluid-rigid bodies interaction problem [15, 16]. Furthermore, using Moving Computational Domain Method (MCD) [17], it is possible to analyze the flow while moving the object freely by moving the entire computational domain including the object.

The purpose of this paper is to perform hydrodynamic analysis when the fish shape submerged objects rotates using the height function method, the Moving-Grid Finite volume method and the Moving Computational Domain method. In this paper, we pay attention to the difference in flow due to the difference in exercise. Therefore, the fish itself shall not be deformed. In this paper, we will clarify the influence of depth from the free surface of the free surface and rotating radius of motion. For this reason, analysis is performed by changing the radius at a certain depth, and the influence of the difference in radius is clarified. Next, analyze the fish that changes its depth and performs rotational motion at the same rotation radius, and clarify the influence of the difference in depth. Based on the finally obtained results, we will state the conclusion.

2 Governing Equations

In this paper, three-dimensional continuity equation and Navier-Stokes equations with gravity force are used as governing equations. Nondimensionalized continuity equation and Navier-Stokes equations are

$$ \frac{\partial u}{\partial x} + \frac{\partial v}{\partial y} + \frac{\partial w}{\partial z} = 0, $$

(1)

$$ \frac{{\partial \varvec{q}}}{\partial t} + \frac{{\partial \varvec{E}}}{\partial x} + \frac{{\partial \varvec{F}}}{\partial y} + \frac{{\partial \varvec{G}}}{\partial z} + \frac{{\partial \varvec{P}_{1} }}{\partial x} + \frac{{\partial \varvec{P}_{2} }}{\partial y} + \frac{{\partial \varvec{P}_{3} }}{\partial z} = \varvec{H}, $$

(2)

where, $x,y,z$ are coordinates, $t$ is time. $u,v,w$ are velocity in $x,y,z$ coordinates, respectively, $\varvec{q}$ is velocity vector, $\varvec{ q} = \left[ {u, v, w} \right]^{T}$. $\varvec{E},\varvec{F},\varvec{G}$ are flux vectors in $x,y,z$ direction, respectively. $\varvec{H}$ is force term including gravity, $\varvec{ H} = \left[ {0,0, - 1/{\text{Fr}}^{2} } \right]^{\varvec{T}}$, ${\text{Fr}}$ is Froude number. $\varvec{P}_{1} ,\varvec{P}_{2} ,\varvec{P}_{3}$ are pressure gradient vectors in $x,y,z$ directions, respectively. Where, flux vectors are

$$ \varvec{E} = \varvec{E}_{a} - \varvec{E}_{v} , \varvec{F} = \varvec{F}_{a} - \varvec{F}_{v} , \varvec{G} = \varvec{G}_{a} - \varvec{G}_{v} , $$

(3)

where, $\varvec{E}_{a} ,\varvec{ F}_{a} ,\varvec{ G}_{a}$ are inviscid flux vectors in $x,y,z$ directions, $\varvec{E}_{v} ,\varvec{ F}_{v} ,\varvec{ G}_{v}$ are viscid flux vectors, respectively. These vectors are

$$ \begin{array}{*{20}c} {\varvec{E}_{a} = \left[ {u^{2} , uv, uw} \right]^{T} ,} & {\varvec{F}_{a} = \left[ {vu, v^{2} , vw} \right]^{T} ,} & {\varvec{G}_{a} = \left[ {wu, wv, w^{2} } \right]^{T} ,} \\ {\varvec{E}_{v} = \frac{1}{\text{Re}}\left[ {u_{x} ,v_{x} , w_{x} } \right]^{T} , } & {\varvec{F}_{v} = \frac{1}{\text{Re}}\left[ {u_{y} ,v_{y} , w_{y} } \right]^{T} ,} & {\varvec{G}_{v} = \frac{1}{\text{Re}}\left[ {u_{z} ,v_{z} , w_{z} } \right]^{T} ,} \\ {\varvec{P}_{1} = \left[ {p, 0, 0} \right]^{T} ,} & {\varvec{P}_{2} = \left[ {0, p, 0} \right]^{T} ,} & {\varvec{P}_{3} = \left[ {0, 0, p} \right]^{T} , } \\ \end{array} $$

(4)

where, $p$ is pressure, ${\text{Re }}$ is Reynolds number, the subscript $x,y,z$ means velocity difference in $x,y,z$ directions. The relational expression of nondimensionalization are

$$ x = \frac{{\bar{x}}}{{\bar{L}_{0} }}, y = \frac{{\bar{y}}}{{\bar{L}_{0} }},z = \frac{{\bar{z}}}{{\bar{L}_{0} }}, u = \frac{{\bar{u}}}{{\bar{U}_{0} }}, v = \frac{{\bar{v}}}{{\bar{U}_{0} }}, w = \frac{{\bar{w}}}{{\bar{U}_{0} }}, p = \frac{{\bar{p}}}{{\bar{\rho }\bar{U}_{0}^{2} }},t = \frac{{\bar{t}}}{{{{\bar{L}_{0} } \mathord{\left/ {\vphantom {{\bar{L}_{0} } {\bar{U}_{0} }}} \right. \kern-0pt} {\bar{U}_{0} }}}}, $$

(5)

where, $^{ - }$ means dimensional number, $\bar{L}_{0} ,\bar{U}_{0} ,\bar{\rho }$ are characteristic length, characteristic velocity and density. ${\text{Re}} = {{\bar{U}_{0} \bar{L}_{0} } \mathord{\left/ {\vphantom {{\bar{U}_{0} \bar{L}_{0} } {\bar{\nu }}}} \right. \kern-0pt} {\bar{\nu }}} , {\text{Fr}} = {{\bar{U}_{0} } \mathord{\left/ {\vphantom {{\bar{U}_{0} } {\sqrt {\bar{g}\bar{L}_{0} } }}} \right. \kern-0pt} {\sqrt {\bar{g}\bar{L}_{0} } }}$, where $\bar{v}$ is kinetic viscosity and $\bar{g}$ is gravitational acceleration.

3 Discretization Method

In discretization method, Moving-Grid Finite volume method [11] was used. This method is based on cell centered finite volume method. In three dimensional flow, space-time unified four dimensional control volume is used.

In this paper, moving grid finite volume method with fractional step method [18] was used for incompressible flows. In this method, there are two computational step and pressure equation. In first step, intermediate velocity is calculated. Pressure is calculated from pressure Poisson equation. In the second step, velocity is corrected from the pressure.

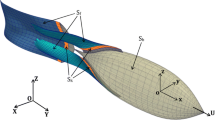
Figure 1 shows schematic drawing of structured four dimensional control volume in space-time unified domain. $\varvec{R}$ is grid position vector, $\varvec{R} = \left[ {x,y,z} \right]^{T}$, where superscript $n$ shows computational step and subscript $i,j,k$ show structured grid point indexes. The red region is computational cell at $n$ computational step, blue region is computational cell at $n + 1$ computational step. The control volume $\varOmega$ is four dimensional polyhedron and formed between the computational cell at $n$ computational step and computational cell at $n + 1$ computational step.

Fig. 1.

Schematics drawing of control volume. (Color figure online)

The Moving-Grid finite volume method was adapted to Eq. (2), the first step is

$$ \varvec{q}^{*} V^{n + 1} - \varvec{q}^{n} V^{n} + \frac{1}{2}\sum\nolimits_{l = 1}^{6} {\left\{ {\left( {\varvec{E}^{*} + \varvec{E}^{n} } \right)\tilde{n}_{x} + \left( {\varvec{F}^{*} + \varvec{F}^{n} } \right)\tilde{n}_{y} + \left( {\varvec{G}^{*} + \varvec{G}^{n} } \right)\tilde{n}_{z} + \left( {\varvec{q}^{*} + \varvec{q}^{n} } \right)\tilde{n}_{t} } \right\}}_{l} \tilde{S}_{l} = V_{\varOmega } \varvec{H,} $$

(6)

where $V_{\varOmega }$ is volume of four dimensional control volume. The superscript index $n$ is computational step, $*$ is sub-iteration step. The $\tilde{n}_{x} , \tilde{n}_{y} ,\tilde{n}_{y} , \tilde{n}_{t}$ are the components of outward unit normal vectors in $x, y, z, t$ coordinate of four dimensional control volume. The subscript $l$ index means computational surface. The $l = 1,2, \ldots ,6$ surface are the surface from $n$ step computational cell and $n + 1$ step computational cell. For example, Fig. 2 shows the computational surface at $l = 2$. The $\tilde{S}_{l}$ is length of normal vector $\tilde{\varvec{n}}$.

Fig. 2.

Schematic drawing of computational surface.

The second step is as follows.

$$ \left( {\varvec{q}^{n + 1} - \varvec{q}^{*} } \right)V^{n + 1} + \sum\nolimits_{l = 1}^{6} {\left( {\varvec{P}_{1}^{n + 1/2} \tilde{n}_{x} + \varvec{P}_{2}^{n + 1/2} \tilde{n}_{y} + \varvec{P}_{3}^{n + 1/2} \tilde{n}_{z} } \right)}_{l} \tilde{S}_{l} = {\mathbf{0}}. $$

(7)

The pressure Poisson equation is as follows.

$$ - D^{*} V^{n + 1} + \sum\nolimits_{l = 1}^{6} {\left( {\frac{{\partial p^{n + 1/2} }}{{\partial x^{n + 1} }}\tilde{n}_{x} + \frac{{\partial p^{n + 1/2} }}{{\partial y^{n + 1} }}\tilde{n}_{y} + \frac{{\partial p^{n + 1/2} }}{{\partial z^{n + 1} }}\tilde{n}_{z} } \right)}_{l} \tilde{S}_{l} = \text{0}. $$

(8)

The $D^{*}$ is defined as follows.

$$ D^{*} = \frac{{\partial u^{*} }}{{\partial x^{n + 1} }} + \frac{{\partial v^{*} }}{{\partial y^{n + 1} }} + \frac{{\partial w^{*} }}{{\partial z^{n + 1} }}. $$

(9)

The computational step is as follows. In the first step, the intermediate velocity $\varvec{q}^{*}$ is solved from Eq. (6). The pressure $p^{n + 1/2}$ is solved from Eq. (8). In the second step, velocity $\varvec{q}^{n + 1}$ is solved from Eq. (7).

4 Numerical Schemes

Numerical schemes are as follows. Equation (2) was divided from fractional step method [18]. The intermediate velocity was calculated using LU-SGS [19] iteratively. The inviscid flux term $\varvec{E}_{a} , \varvec{F}_{a} ,\varvec{G}_{a}$ and moving grid term $\varvec{q}\tilde{n}_{t}$ were evaluated using QUICK [20]. In our computation results, there were not unphysical results or divergence. The viscous term $\varvec{E}_{v} , \varvec{F}_{v} ,\varvec{G}_{v}$ and pressure gradient term $\varvec{P}_{1}^{n + 1/2} , \varvec{P}_{2}^{n + 1/2} ,\varvec{P}_{3}^{n + 1/2}$ were evaluated using centred difference scheme. The pressure Poisson equation Eq. (8) was calculated using Bi-CGSTAB [21] iteratively.

5 Surface Tracking Method

In this paper, the surface height function is used for free surface tracking. Figure 3 shows schematic drawing of free surface height function $h$. In time step $n$, the function $h$ are free surface, $h$ is assumed free surface in the next time step $n + 1$.

Fig. 3.

Schematic drawing of free surface height function.

The surface height equation is

$$ \frac{\partial h}{\partial t} + \left( {u - u_{G} } \right)\frac{\partial h}{\partial x} + \left( {v - v_{G} } \right)\frac{\partial h}{\partial y} = w, $$

(10)

where $u_{G} ,v_{G}$ means the moving velocity in $x,y$ directions respectively. In addition, general coordinate transformation is used. When $\xi , \eta$ are defined as $\xi = \xi \left( {x,y} \right), \eta = \eta \left( {x,y} \right),$

$$ \xi_{x} = \frac{{y_{\eta } }}{J}, \xi_{y} = - \frac{{x_{\eta } }}{J}, \eta_{x} = - \frac{{y_{\xi } }}{J}, \eta_{y} = \frac{{x_{\xi } }}{J}, $$

(11)

where the subscript indexes $x, y, \xi , \eta$ are the derivatives in $x, y, \xi , \eta$ directions, respectively. $J$ means Jacobian, $J = x_{\xi } y_{ \eta } - x_{\eta } y_{ \xi }$.

The Eq. (10) is transformed as

$$ \frac{\partial h}{\partial t} + \left( {U - U_{G} } \right)\frac{\partial h}{\partial \xi } + \left( {V - V_{G} } \right)\frac{\partial h}{\partial \eta } = w, $$

(12)

$$ \begin{array}{*{20}c} {U = \frac{1}{J}\left( {uy_{\eta } - vx_{\eta } } \right),V = \frac{1}{J}\left( { - uy_{\xi } + vx_{\xi } } \right),} \\ {U_{G} = \frac{1}{J}\left( {u_{G} y_{\eta } - v_{G} x_{\eta } } \right),V_{G} = \frac{1}{J}\left( { - u_{G} y_{\xi } + v_{G} x_{\xi } } \right).} \\ \end{array} $$

(13)

The Eq. (12) is not conservation form. For solving this equation, finite difference method is used. The advection term $\left( {U - U_{G} } \right)h_{ \xi } , \left( {V - V_{G} } \right)h_{\eta }$ are evaluated by 1st order upwind difference. The 1st order upwind method has low accuracy. When high order scheme is used, free surface shape tends to be sharp, which causes calculation instability. The 1st order upwind method is used to prevent this phenomenon. The moving velocity components $u_{G} ,v_{G}$ are evaluated by moving grid velocity at grid points. In this paper, surface tension is omitted. The pressure at free surface is fixed by 0.

6 Numerical Results

In this section, we present numerical simulation results for moving submerged fish along a curved path.

6.1 Computational Conditions

This case is to create a shape simulating a fish and to make it rotate. The purpose of this case is to see the difference in the free surface shape and the force acting on the fish by changing the depth from the initial free surface and the radius of rotation of the fish.

Figure 4 shows schematics of computational domain. Figure 5 shows shape of fish. The characteristic length of fish is $L$. The length of fish is $1$, the width is $0.5$ and the height is $0.5$. The length of computational domain is $60$, the width is $20$ and the height is $4$ or $3.5$. The fish position is 20L from forward boundary, centered at width. When the height of computational domain height is $4$, the fish position from initial free surface is $2$. When the height of computational domain height is $3.5$, the fish position from initial free surface is $1.5$.

Fig. 4.

Schematics of computational domain.

Fig. 5.

Shape of fish.

The Reynolds number is 5000, the Froude number is 2, and the time step is 0.002. The grid points are $121\left( {\text{Length}} \right) \times 81\left( {\text{Width}} \right) \times 81\left( {\text{Height}} \right)$. The grid points at the fish surface are $21 \times 21 \times 21$.

Table 1 shows the comparison of our computational cases. The cycle of rotation of fish are 50 and 75. The initial fish depth from free surface is $2$ or $1.5$. Therefore, four cases were analyzed.

Table 1. Computational conditions.

Figure 6 shows schematics of fish motion. It is assumed that the motion condition is linear motion of constant acceleration with acceleration 0.1 up to dimensionless time 10 in the negative direction of the $x$ axis, and then to rotate at speed 1 thereafter. The cycle of rotation is 50 or 75. When the cycle of rotation is 50, the radius of rotation is about 7.96. When the cycle of rotation is 75, the radius of rotation is about 11.9. The Moving Computational Domain method [17] was used, the simulation was performed by moving the entire computational domain including the fish.

Fig. 6.

Schematics of fish motion.

Initial conditions of velocity is $u = v = w = 0$ and pressure is given as a function of height considering hydrostatic pressure.

Boundary conditions are as follows. At the forward boundary, velocity is $u = v = w = 0$, pressure is Neumann boundary condition. Free surface height is fixed by initial free surface height. At the backward boundary, velocity is linear extrapolated, pressure is Neumann boundary condition. Free surface height is Neumann boundary condition. At the fish boundary, velocity is no-slip condition, pressure is Neumann boundary condition. At the bottom wall, velocity is slip condition, pressure is Neumann boundary condition. At the side boundary,velocity is outflow condition, pressure is Neumann boundary condition. Free surface height is Neumann boundary condition. At the free surface boundary, free surface shape is calculated from surface height function equation, velocity is extrapolated, pressure is fixed by $p = 0$.

6.2 Numerical Results

In this section, numerical results are shown. First, we will explain the flow fields.

Figure 7 shows the isosurface where the vorticity magnitude is 5 and free surface shape in Case (a). As for the shape of the free surface, the amount of change from the initial height is emphasized 50 times and displayed. Figure 7(a) shows the results at $t = 10$, deformed with moving. Figures 7(b)–(f) show the results at t = 15 – 35, respectively. In these figures, it is understood that there is a region with large vorticity around the fish. From the viewpoint if the free surface shape, there is a region where the free surface rises at the top of the fish, and it is recessed behind. Furthermore, it can be seen that the shape of the free surface behind the fish.

Fig. 7.

Isosurface of vorticity magnitude and free surface shape (Case (a)).

In the next, we describe the drag, side force and lift acting on the surface of the fish. In this paper, the force acting in the direction opposite to the travelling direction of the fish is defined as a drag force, the force acting in the vertical direction on the motion path is defined as a side force, and the force acting in the depth direction is defines as a lift force. Also, each nondimensionalization one is called a drag coefficient (Cd), a side force coefficient (Cs) and a lift coefficient (Cl). When calculating the lift coefficient, the pressure excluding the influence of gravity are used for calculation.

Figure 8 shows the time history of the drag, side and lift coefficient. As an example, the results of Case (a) are shown, but in all other cases the overall trend was similar. The horizontal axis shows nondimensionalized time, the vertical axis shows the coefficients (Cd, Cs and Cl). Since the rotational motion is started after the dimensionless time 10, it is indicated by the dimensionless time 50 for one cycle from the dimensionless time 10. From Fig. 8, the Cd is always positive value, it is understood that the fish receives the force from the direction of motion. Also the Cl is always a negative value, it is understood that the fish receives the force in the direction of the center of rotation. Furthermore, the Cl is smaller than the other coefficients, and it can be seen that the free surface is less affected by the farther from the fish. It is also understood that these coefficients hardly change with time.

Fig. 8.

Time history of coefficient of drag, side force and lift (Case (a)).

Next, average values of coefficients in cases are shown. Table 2 shows the average values of Cd, Cs and Cl in these cases respectively. The average is the time when the fish has rotated by one cycle. Therefore, Case (a) and (c) are time averaged with dimensionless time 50, and Case (b) and (d) are time averaged by dimensionless time 75.

Table 2. Comparisons of coefficients of drag, side force and lift.

First, from Table 2, it can be seen that the lift coefficient Cl is smaller than the absolute values of the drag coefficient Cd and the side force coefficient Cs. Next, from Table 2, we will consider the influence due to the difference in the cycle of rotation. Cases (a) and (b) are cases with the depth 2, and Case (c) and (d) when the depth is 1.5 when the cycle of rotation only differs. When comparing Case (a) and (b), both coefficients are smaller in Case (b) than in Case (a). This is considered to be due to the fact that the cycle of rotation of Case (b) is longer than the cycle of rotation of Case (a), that is, the radius of rotation is large, so the influence of rotation is reduced in Case (b). Case (c) and Case (d) have the same tendency.

Next, consider the influence of the depth of the fish from the free surface. Case (a) and (c), Case (b) and (d), are cases with the same cycle of rotation. When comparing Case (a) and (c), the lift coefficient is larger in Case (c). In addition, the drag coefficient and the side force coefficient hardly change. This seems to be because Case (c) is more likely to have fish than free surface than Case (a), and Case (c) has greater influence on the lift coefficient. Since the motion path in the same, it is considered that the drag coefficient and the side force coefficient did not change so much. Case (b) and Case (d) have the same tendency.

In conclusion, focusing on the lift coefficient, the lift coefficient is greatly influenced by the radius of rotation and the depth from free surface. When the radius of rotation is small, and when the depth from free surface is small, the lift coefficient is large. The absolute value of the lift coefficient is smaller than the drag and lift coefficients, this is because the lift coefficient is calculated using the pressure excluding the influence of gravity. The computational required for the computation of dimensionless time 10 was 13 h.

7 Conclusions

In this paper, a simulation was conducted with varying depth and radius of rotation in order to clarify the influence of the depth and radius of rotation from the free surface of submerged fish in the low. The conclusion of this paper is summarized below.

• Analysis was performed with the radius of rotation changed at a certain depth. The smaller radius of rotation, the greater the side force and the lift coefficients.

• The depth was changed and the rotational motion at the same rotation radius was analyzed. It was found that the deeper the depth from free surface, the greater the lift coefficient.

• It is possible to clarify the influence of depth from the free surface and radius of rotation of submerged fish that is in rotational motion on the flow.

This work was supported by JSPS KAKENHI Grant Numbers 16K06079, 16K21563.