Abstract
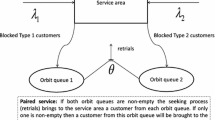
We analyse a priority queueing system with a normal queue (high priority) and an orbit (low priority). Only the first customer in orbit can retry during times that the queue and server are empty (constant retrial policy). In contrast with existing literature, we assume different service time distributions for the high- and low-priority customers. We obtain closed-form expressions for the probability generating function of the number of customers in queue and orbit, in steady state, and for the Laplace Stieltjes transforms of the stationary waiting times of both type of customers.
This is a preview of subscription content, log in via an institution to check access.
Access this chapter
Tax calculation will be finalised at checkout
Purchases are for personal use only
Notes
- 1.
- 2.
Note from Eq. (24) that \(P_2(0,z_1,z_2)\) is independent of \(z_1\).
- 3.
The effective retrial time of class-2 customer starts when the customer is for the first time the head of the orbit and ends when he enters the server.
- 4.
The coefficient of variation of a distribution is defined as the ratio of the standard deviation to the mean.
References
Atencia, I., Moreno, P.: A single-server retrial queue with general retrial times and Bernoulli schedule. Appl. Math. Comput. 162(2), 855–880 (2005)
Choi, B.D., Chang, Y.: Single server retrial queues with priority calls. Math. Comput. Modell. 30, 7–32 (1999)
Cox, D. : The analysis of non-Markovian stochastic processes by the inclusion of supplementary variables. In: Mathematical Proceedings of the Cambridge Philosophical Society, vol. 51, no. 3, pp. 433–441. Cambridge University Press (1955)
Durrett, R.: Essentials of Stochastic Processes. STS. Springer, New York (2012). https://doi.org/10.1007/978-1-4614-3615-7
Farahmand, K.: Single line queue with repeated demands. Queueing Syst. 6(1), 223–228 (1990)
Fayolle, G.: A simple telephone exchange with delayed feedbacks. In: Proceedings of the International Seminar on Teletraffic Analysis and Computer Performance Evaluation, pp. 245–253. North-Holland Publishing Co. (1986)
Gao, S.: A preemptive priority retrial queue with two classes of customers and general retrial times. Oper. Res. Int. J. 15(2), 233–251 (2015)
Gómez-Corral, A.: Stochastic analysis of a single server retrial queue with general retrial times. Naval Res. Logistics (NRL) 46, 561–581 (1999)
Phung-Duc, T., Rogiest, W.: Two way communication retrial queues with balanced call blending. In: Al-Begain, K., Fiems, D., Vincent, J.-M. (eds.) ASMTA 2012. LNCS, vol. 7314, pp. 16–31. Springer, Heidelberg (2012). https://doi.org/10.1007/978-3-642-30782-9_2
Saffer, Z., Yue, W.: Call blending retrial queue with gated type incoming call service. In: 9th International Conference on Queueing Theory and Network Applications, Bellingham, USA, pp. 18–27 (2014)
Walraevens, J., Steyaert, B., Bruneel, H.: Delay characteristics in discrete-time GI-G-1 queues with non-preemptive priority queueing discipline. Perform. Eval. 50(1), 53–75 (2002)
Walraevens, J., Steyaert, B., Bruneel, H.: Performance analysis of a single-server ATM queue with a priority scheduling. Comput. Oper. Res. 30(12), 1807–1829 (2003)
Walraevens, J.: Discrete-time queueing models with priorities. Doctoral dissertation, Ghent University (2004)
Acknowledgments
The authors wish to thank Tuan Phung-Duc and Dieter Claeys for preliminary discussions about the model in this paper.
Author information
Authors and Affiliations
Corresponding author
Editor information
Editors and Affiliations
Rights and permissions
Copyright information
© 2018 Springer International Publishing AG, part of Springer Nature
About this paper
Cite this paper
Devos, A., Walraevens, J., Bruneel, H. (2018). A Priority Retrial Queue with Constant Retrial Policy. In: Takahashi, Y., Phung-Duc, T., Wittevrongel, S., Yue, W. (eds) Queueing Theory and Network Applications. QTNA 2018. Lecture Notes in Computer Science(), vol 10932. Springer, Cham. https://doi.org/10.1007/978-3-319-93736-6_1
Download citation
DOI: https://doi.org/10.1007/978-3-319-93736-6_1
Published:
Publisher Name: Springer, Cham
Print ISBN: 978-3-319-93735-9
Online ISBN: 978-3-319-93736-6
eBook Packages: Computer ScienceComputer Science (R0)