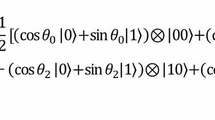Digital Image Processing with Quantum Approaches

Abstract

We devise and analyze illustrative examples of image processing tasks that show the capability of specifically quantum properties to afford enhanced performance inaccessible with classical processing. The quantum approaches here essentially demonstrate and exploit the possibility of parallel processing stemming from superposition of quantum states. The results illustrate the rich potential, yet largely to be explored, of quantum information and computation for image and signal processing.

1 Introduction

Quantum information and computation is an emerging scientific field where specifically quantum phenomena and properties are considered for contributing to information processing and computing. One is naturally lead to the quantum level by miniaturization, integration and the evolution of current information technologies toward their ultimate physical limits. In addition, at the quantum level, specifically novel properties, non-existing classically, arise that can be exploited for information processing with enhanced performance. This current trend of information sciences toward the quantum is specially relevant for signal and image processing. In this report we concentrate on digital image processing. Based on current generic quantum information processing methodologies, we devise and analyze image processing examples with quantum solutions affording enhanced performance that are inaccessible with classical approaches. Beyond these worked out examples of quantum computation on images, more generally we motivate the great specific potential contained in quantum approaches for digital image processing, which yet largely remain to be explored and mastered.

2 Quantum Representation of Images

We consider digital images where at each pixel with spatial coordinates (x, y) the intensity $I(x, y) \in [0, 2^L -1]$ is coded and stored in an L-bit pixel register. An image with size $2^{N_x}\times 2^{N_y}$ pixels is therefore coded by a number $2^{N_x}\times 2^{N_y}$ of L-bit pixel registers. This is a standard classical (non quantum) representation for digital images.

In the quantum domain, each classical bit is replaced by a quantum bit or qubit [1, 2]. Physically, a qubit can be materialized by a quantum object or system endowed with a two-dimensional state (Hilbert) space $\mathcal {H}_2$, such as a photon with its two states of polarization, or an electron with its two states of spin, or an atom or ion with two accessible states (one ground state and one excited state). The two quantum states accessible to the qubit are denoted $\mathinner {|{0}\rangle }$ and $\mathinner {|{1}\rangle }$, and they form an orthonormal basis, the computational basis, for the qubit Hilbert space $\mathcal {H}_2$. An L-qubit register is characterized by a quantum state belonging to the $2^L$-dimensional tensor product space $\mathcal {H}_2^{\otimes L}$ referred to the orthonormal basis $\{\mathinner {|{\vec {z}\,}\rangle } \}$ with the L-bit words $\vec {z} \in \{0, 1 \}^L$. For instance for $L=2$, the orthonormal basis of $\mathcal {H}_2^{\otimes 2}$ is $\{\mathinner {|{00}\rangle }, \mathinner {|{01}\rangle }, \mathinner {|{10}\rangle }, \mathinner {|{11}\rangle }\}$.

A direct quantum representation of the image would replace the L-bit register by an L-qubit register for each pixel, with $2^{N_x}\times 2^{N_y}$ such L-qubit registers for an image with $2^{N_x}\times 2^{N_y}$ pixels. Such a quantum encoding would yield the benefit of a highly integrated representation for the image, supported by elementary physical objects, affording very high density of storage and processing, and huge memory capacities [3]. The measurement of each qubit in the orthonormal basis $\{\mathinner {|{0}\rangle }, \mathinner {|{1}\rangle }\}$ would allow exact deterministic recovery of the pixel intensity I(x, y) at each pixel (x, y). For the sequel, this type of quantum image representation will be called a non-superposed representation; it requires a number $2^{N_x}\times 2^{N_y}$ of L-qubit registers for the image.

The specificities of quantum physics [1] offer the possibility of an even more compact image representation, under the form of a superposed representation. It is possible to place a qubit into an arbitrary superposition of the two orthonormal basis states $\{\mathinner {|{0}\rangle }, \mathinner {|{1}\rangle }\}$, in a quantum state of $\mathcal {H}_2$ denoted $\mathinner {|{\psi }\rangle }=\alpha _0 \mathinner {|{0}\rangle } + \alpha _1 \mathinner {|{1}\rangle }$, provided the state vector $\mathinner {|{\psi }\rangle }$ is kept with unit norm, i.e. the two complex coordinates in $\mathbbm {C}$ verify $|\alpha _0|^2+|\alpha _1|^2 =1$. Quantum theory [1] then stipulates the probabilistic rule (Born rule) that when measured in the orthonormal basis $\{\mathinner {|{0}\rangle }, \mathinner {|{1}\rangle }\}$ of $\mathcal {H}_2$, the quantum state $\mathinner {|{\psi }\rangle }$ is found (projected) in state $\mathinner {|{0}\rangle }$ with probability $|\alpha _0|^2$ or in state $\mathinner {|{1}\rangle }$ with probability $|\alpha _1|^2$. In this way, for instance, an $L=4$-qubit register can be prepared in a state $\mathinner {|{\psi }\rangle }=3^{-1/2}\mathinner {|{0000}\rangle }+3^{-1/2}\mathinner {|{0011}\rangle }+3^{-1/2}\mathinner {|{1111}\rangle }$ of $\mathcal {H}_2^{\otimes 4}$, and upon measurement in the orthonormal basis $\{\mathinner {|{\vec {z}\,}\rangle } \}_{\vec {z}\, \in \{0, 1 \}^4}$ of $\mathcal {H}_2^{\otimes 4}$ it will be found in state $\mathinner {|{0000}\rangle }$ or $\mathinner {|{0011}\rangle }$ or $\mathinner {|{1111}\rangle }$ with equal probability 1 / 3.

In an image of size $2^{N_x}\times 2^{N_y}$ pixels, each of its $2^{N_x}\times 2^{N_y}$ pixel registers can be assigned an address over $N_x+N_y$ bits. In standard classical image representations, the pixel addresses are usually not explicitly coded in actual physical registers. Instead, the coding of the pixel addresses is implicit. It is for instance ensured by the spatial sequencing of the memory locations in a solid-state storage, or by the temporal sequencing of the bit stream in a communication process. The same applies for the $2^{N_x}\times 2^{N_y}$ pixel registers of qubits in a non-superposed quantum representation: the addresses of these registers are implicit and not physically encoded. By contrast, for a superposed quantum representation, one considers registers of $N_x+N_y$ qubits for the addresses of the $2^{N_x}\times 2^{N_y}$ pixels. Such a register has its quantum state in the $(N_x+N_y)$-dimensional space $\mathcal {H}_2^{\otimes (N_x+N_y)} \equiv \mathcal {H}_2^{\otimes N_x} \otimes \mathcal {H}_2^{\otimes N_y}$ and is denoted $\mathinner {|{\vec {x}, \vec {y}\,}\rangle }$, with $\vec {x}$ and $\vec {y}$ respectively $N_x$-bit and $N_y$-bit binary words. At each pixel address $(\vec {x}, \vec {y}\,)$ is an L-qubit register storing the local image intensity $I(\vec {x}, \vec {y}\,)$ and placed in the quantum state of $\mathcal {H}_2^{\otimes L}$ denoted $\mathinner {|{I(\vec {x}, \vec {y}\,)}\rangle }$. In this way, each pixel with its address and intensity is represented by the quantum state $\mathinner {|{\vec {x}, \vec {y}\,}\rangle } \otimes \mathinner {|{I(\vec {x}, \vec {y}\,)}\rangle }$ which belongs to the space $\mathcal {H}_2^{\otimes (N_x+N_y)} \otimes \mathcal {H}_2^{\otimes L}$ materialized by a pixel register of $N_x+N_y+L$ qubits comprising an $(N_x+N_y)$-qubit register for the address and an L-qubit register for the intensity. The specific feature enabled by quantum physics is that one such $(N_x+N_y+L)$-qubit pixel register can be placed in a superposition state of the form

$$\begin{aligned} \mathinner {|{\psi }\rangle }= \Bigl (2^{N_x+N_y} \Bigr )^{-1/2} \sum _{\vec {x} \in \{0, 1 \}^{N_x}} \sum _{\vec {y} \in \{0, 1 \}^{N_y}} \mathinner {|{\vec {x}, \vec {y}\,}\rangle } \otimes \mathinner {|{I(\vec {x}, \vec {y}\,)}\rangle } \;. \end{aligned}$$

(1)

The quantum state $\mathinner {|{\psi }\rangle }$ of Eq. (1) represents a superposition of all the pixel information (address and intensity) for all the $2^{N_x}\times 2^{N_y}$ pixels of the image. This accomplishes a complete (quantum) coding of the whole image, encoded in the quantum state of a single quantum register with $N_x+N_y+L$ qubits. By contrast, we recall that the non-superposed quantum representation requires a number $2^{N_x}\times 2^{N_y}$ of quantum registers with L qubits, much like a classical representation. For instance for a standard image with $2^{10}\times 2^{10}$ pixels and $L=8$-bit intensities, we are comparing one quantum register with 28 qubits for the superposed representation, against $2^{20} \approx 10^6$ quantum registers with 8 qubits for the non-superposed representation. In this way, quantum superposition offers a possibility of huge space reduction compared to a non-superposed quantum or to a classical image representation. Other quantum image representations have been proposed [4], yet the representation of Eq. (1), with the superposition, incorporates an essential quantum feature.

The superposed quantum state $\mathinner {|{\psi }\rangle }$ of Eq. (1) representing the whole image, is a coherent superposition where each pixel intensity $I(\vec {x}, \vec {y}\,)$ is referred to its specific address $\mathinner {|{\vec {x}, \vec {y}\,}\rangle }$ which is orthogonal to all other pixel addresses in $\mathinner {|{\psi }\rangle }$. In this way, each pixel information in $\mathinner {|{\psi }\rangle }$ is perfectly and separately identified. For instance, when the state $\mathinner {|{\psi }\rangle }$ is projected on a specific $\mathinner {|{\vec {x}, \vec {y}\,}\rangle }$, this recovers the local intensity $I(\vec {x}, \vec {y}\,)$; and this holds in the same way for every pixel superposed in state $\mathinner {|{\psi }\rangle }$. There is however a significant limitation with the superposed state $\mathinner {|{\psi }\rangle }$ of Eq. (1), which is inherent to the quantum principles, and which arises when performing measurement on the image encoded by $\mathinner {|{\psi }\rangle }$ of Eq. (1). Although the state $\mathinner {|{\psi }\rangle }$ of Eq. (1) incorporates all the information defining the image, this information cannot be recovered in full in a deterministic way from $\mathinner {|{\psi }\rangle }$. From quantum theory, the measurement of $\mathinner {|{\psi }\rangle }$ takes the form of a projective measurement in the vector space $\mathcal {H}_2^{\otimes (N_x+N_y)} \otimes \mathcal {H}_2^{\otimes L} \ni \mathinner {|{\psi }\rangle }$. When referred to the computational basis of $\mathcal {H}_2^{\otimes (N_x+N_y)} \otimes \mathcal {H}_2^{\otimes L}$, the projective measurement, by the Born rule, has an outcome which occurs at random, as a projection of the state $\mathinner {|{\psi }\rangle }$ in one state of the form $\mathinner {|{\vec {x}, \vec {y}\,}\rangle } \otimes \mathinner {|{I(\vec {x}, \vec {y}\,)}\rangle }$ among the $2^{N_x+N_y}$ such possible states, equiprobably. This provides perfect recovery of the intensity $I(\vec {x}, \vec {y}\,)$ for a pixel at coordinates $(\vec {x}, \vec {y}\,)$ yet selected at random. After such measurement the initial state $\mathinner {|{\psi }\rangle }$ is destroyed, collapsed (projected) into the corresponding basis state of $\mathcal {H}_2^{\otimes (N_x+N_y)} \otimes \mathcal {H}_2^{\otimes L}$; no more information can be recovered for the image. With such drastic information reduction, clearly the superposed state $\mathinner {|{\psi }\rangle }$ of Eq. (1) is not suited for complete recovery, for display for instance, of the whole image information. Nevertheless, this superposed state $\mathinner {|{\psi }\rangle }$ of Eq. (1) has great potential for parallel computation or processing to be performed on the image.

Many tasks in image processing consist in an extreme yet controlled reduction of the information initially contained in the image. For instance, for pattern recognition, the targeted output may be a few bits of information for labeling the recognized class. For image-based manufacturing or access control, the targeted output may be a single bit of information, for a compliant / noncompliant product or an authorized / unauthorized access; or for a malignant or benign alteration in medical imaging. The superposed image representation of Eq. (1) is specially attractive for such tasks. By processing the $(N_x+N_y+L)$-qubit register initialized in state $\mathinner {|{\psi }\rangle }$, one has the ability to process all the pixels of the image simultaneously in parallel. Typically such quantum processings will consist in applying unitary transformations in $\mathcal {H}_2^{\otimes (N_x+N_y+L)}$, to transform unit-norm state vectors such as $\mathinner {|{\psi }\rangle }$ into unit-norm state vectors, possibly complemented by combinations with auxiliary qubit registers. This is the central assignment of quantum computing, which relies on quantum gates, with a few elementary gates which are known to be universal and enable the realization of any arbitrary unitary transformations [1] as envisaged above. Ultimately, after a suitably designed sequence of unitary transformations, a final measurement will extract the few bits of information intended as the result of the quantum computation performed in parallel.

Several algorithms of quantum computation have been introduced to solve some reference computational problems, such as the parallel test of a Boolean function [5], or the search in an unsorted database [6], or the factoring of integers [7], and in each case with quantumly enhanced performance compared to classical solutions. Only very recently has it been specifically considered that the capabilities of quantum computation, such as the parallelism presented above, make it very attractive to tackle digital image processing problems, although this area of imaging largely remains to be explored [8].

3 Quantum Image Processing

3.1 Image Classification

For illustration of quantum approaches for image processing, we consider the processing of a binary image, where at each pixel the intensity is binary. The principles can extended to other types of images, and a binary image can be regarded as a bit plane in images with larger dynamics of intensity. We address a task of image classification, where one is given a binary image which can belong to one of two classes, namely a class of constant images where all the pixels in the image share the same binary intensity (there are only two images in this class), and a class of balanced images with half of the pixels at a given binary intensity and the other half at the opposite intensity, as illustrated in Fig. 1. Classically, it requires to test on average a number of the order of half of the pixels (two pixels in the most favorable case, half of the pixels plus one in the least favorable), i.e. to process half of the pixel registers, to classify the image. By contrast, we will see that with a quantum approach only one pixel register need be tested. A comparable quantum approach is used in the Deutsch-Jozsa quantum algorithm for parallel test of a Boolean function [5], which we transpose here to a task of binary image classification.

Fig. 1.

The two sets of binary images with size $256\times 256$ pixels to be classified. Circled in blue is the set of two constant images. Circled in red are four examples of balanced images with equal number of black and white pixels. The quantum algorithm performs the image classification by processing a single pixel register placed in a superposed quantum state. (Color figure online)

For shorter notation we denote a pixel address as $\vec {a}=(\vec {x}, \vec {y}\,)$ with $\vec {a}$ a binary word of $N_x+N_y=N_a$ bits. At this pixel address is the binary intensity $I(\vec {a} \,)=I(\vec {x}, \vec {y}\,)=0$ or 1. The whole binary image is encoded in a single pixel register comprising $N_a+1$ qubits, with the first $N_a$ qubits as the address register and the last qubit as the intensity register. This $(N_a+1)$-qubit pixel register is placed in the superposed quantum state similar to Eq. (1),

$$\begin{aligned} \mathinner {|{\psi }\rangle }= 2^{-N_a/2}\sum _{\vec {a} \in \{0, 1 \}^{N_a}} \mathinner {|{\vec {a}\,}\rangle } \mathinner {|{I(\vec {a}\,)}\rangle } \;. \end{aligned}$$

(2)

The processing starts by using the intensity register $\mathinner {|{I(\vec {a}\,)}\rangle }$ as the target input to a standard Cnot quantum gate [1] having an auxiliary qubit $\mathinner {|{u}\rangle }$ as its control input. The operation of the Cnot gate is to deliver the two-qubit output Cnot$\bigl (\mathinner {|{I(\vec {a}\,)}\rangle }\mathinner {|{u}\rangle }\bigr )=\mathinner {|{I(\vec {a}\,)\oplus u}\rangle }\mathinner {|{u}\rangle }$, with the XOR operation $\oplus$. When the control input is placed in the superposed state $\mathinner {|{u}\rangle }=2^{-1/2}\bigl (\mathinner {|{0}\rangle }-\mathinner {|{1}\rangle } \bigr )=\mathinner {|{-}\rangle }$, the Cnot gate acts as Cnot$\bigl (\mathinner {|{I(\vec {a}\,)}\rangle }\mathinner {|{-}\rangle }\bigr )=2^{-1/2} \bigl [ \mathinner {|{I(\vec {a}\,)}\rangle } - \mathinner {|{\overline{I}(\vec {a}\,)}\rangle } \bigr ] \mathinner {|{-}\rangle } =(-1)^{I(\vec {a}\,)}\mathinner {|{-}\rangle }\mathinner {|{-}\rangle }$, where $\overline{I}(\vec {a}\,)$ is the binary complement of $I(\vec {a}\,)$.

When this operation takes place with the superposed state $\mathinner {|{\psi }\rangle }$ of Eq. (2), the input $\mathinner {|{\psi }\rangle }\mathinner {|{-}\rangle }$ is taken to the output $\mathinner {|{\psi '}\rangle }\mathinner {|{-}\rangle }$ with the $(N_a+1)$-qubit pixel register ending up in the transformed state

$$\begin{aligned} \mathinner {|{\psi '}\rangle } = 2^{-N_a/2} \sum _{\vec {a} \in \{0, 1 \}^{N_a}} \mathinner {|{\vec {a}\,}\rangle } (-1)^{I(\vec {a}\,)}\mathinner {|{-}\rangle } \;. \end{aligned}$$

(3)

The phase factor $(-1)^{I(\vec {a}\,)}$ occurring in the coherent quantum superposition of Eq. (3) is an important ingredient of the computation. A Hadamard quantum gate [1] performs a unitary transformation whose action on the computational basis of $\mathcal {H}_2$ for a qubit can be expressed as $\mathsf {H} \mathinner {|{v}\rangle }=2^{-1/2}\bigl (\mathinner {|{0}\rangle }+(-1)^v\mathinner {|{1}\rangle } \bigr )$ for $v=0, 1$. A Hadamard gate $\mathsf {H}^{\otimes N_a}$ in dimension $N_a$ is applied on the $N_a$ qubits corresponding to the address part of the $(N_a+1)$-qubit pixel register, while the qubit corresponding to the binary intensity part of the $(N_a+1)$-qubit pixel register is left unchanged. This operates as $\mathsf {H}^{\otimes N_a} \otimes \mathrm {I}_2 \mathinner {|{\psi '}\rangle }=\mathinner {|{\phi }\rangle }\mathinner {|{-}\rangle }$, where $\mathrm {I}_2$ is the identity operator on $\mathcal {H}_2$ for a qubit, and $\mathinner {|{\phi }\rangle }$ is the $N_a$-qubit quantum state defined as

$$\begin{aligned} \mathinner {|{\phi }\rangle }= 2^{-N_a} \sum _{\vec {z} \in \{0, 1 \}^{N_a}} w(\vec {z}\,) \mathinner {|{\vec {z}\,}\rangle } \end{aligned}$$

(4)

with the scalar weight

$$\begin{aligned} w(\vec {z}\,)= \sum _{\vec {a} \in \{0, 1 \}^{N_a}} (-1)^{I(\vec {a}\,)\,\oplus \, \vec {a}\,\vec {z}} \;. \end{aligned}$$

(5)

Now to obtain the result of the processing performing the image classification, a measurement is performed, in the computational basis of $\mathcal {H}_2^{\otimes N_a}$, on the $N_a$ qubits corresponding to the address part of the $(N_a+1)$-qubit pixel register. These $N_a$ qubits are in the superposed state $\mathinner {|{\phi }\rangle }$ of Eq. (4). In $\mathinner {|{\phi }\rangle }$, the weight of the basis state $\mathinner {|{\vec {z}\,}\rangle }=\mathinner {|{\vec {0}\,}\rangle }=\mathinner {|{0}\rangle }^{\otimes N_a}$ according to Eq. (5) is

$$\begin{aligned} w(\vec {z}=\vec {0} \,)= \sum _{\vec {a} \in \{0, 1 \}^{N_a}} (-1)^{I(\vec {a}\,)} \;. \end{aligned}$$

(6)

Now when the binary image is constant, then at all pixel addresses $\vec {a}$ either $I(\vec {a}\,)=0$ or $I(\vec {a}\,)=1$, so that $w(\vec {z}=\vec {0} \,)=\pm 2^{N_a}$. Then, since $\mathinner {|{\phi }\rangle }$ in Eq. (4) is a normalized state, necessarily the other weights $w(\vec {z} \not =\vec {0} \,)$ are zero and $\mathinner {|{\phi }\rangle }=\mathinner {|{\vec {0}\,}\rangle }=\mathinner {|{0}\rangle }^{\otimes N_a}$. So, when the image is constant, measurement of these $N_a$ qubits of the pixel register yields $N_a$ qubits found in state $\mathinner {|{0}\rangle }$.

Conversely, when the binary image is balanced, then Eq. (6) gives $w(\vec {z}=\vec {0} \,)=0$ so that in $\mathinner {|{\phi }\rangle }$ of Eq. (4) the basis state $\mathinner {|{\vec {0}\,}\rangle }=\mathinner {|{0}\rangle }^{\otimes N_a}$ is absent of the superposition; when the $N_a$ qubits are measured, at least one of them is found out of state $\mathinner {|{0}\rangle }$, i.e. found in state $\mathinner {|{1}\rangle }$.

In this way, by processing a single pixel register placed in a superposed quantum state, it can be decided whether the binary image is constant or balanced, and this independently of the number $2^{N_a}$ of pixels in the image. By contrast, a classical approach would require the processing of in the order of $2^{N_a} /2$ pixel registers.

The quantum circuit assembling the quantum gates to implement the image processing is depicted in Fig. 2.

Fig. 2.

Quantum circuit assembling the 2-qubit Cnot gate and the $N_a$-qubit Hadamard gate $\mathsf {H}^{\otimes N_a}$, and performing the quantum image processing.

In Fig. 2 the operation of the quantum circuit is represented during the processing of an arbitrary basis state $\mathinner {|{\vec {a}\,}\rangle } \mathinner {|{I(\vec {a}\,)}\rangle }$ of $\mathcal {H}_2^{\otimes N_a} \otimes \mathcal {H}_2^{}$ entering the linear superposition of Eq. (2) and applied at the circuit input. For the complete image processing, this same input is placed in the linear superposition of Eq. (2) and by virtue of the laws of quantum physics the circuit responds according to the parallel process we described above.

3.2 Image Model Identification

For another illustration of quantum image processing, we consider, for the same type of binary images, the image model where the binary intensity $I(\vec {a}\,)$ at any pixel with address $\vec {a}$ is described by

$$\begin{aligned} I(\vec {a}\,)= \vec {c}\, \vec {a} \oplus b\;. \end{aligned}$$

(7)

Such a model has been considered in [9], as a class of Boolean functions amenable to parallel test by a quantum approach. Here we use this model of Eq. (7) as an image model to be involved in a task analyzed as an image processing. The image model of Eq. (7) is parametrized by $(\vec {c}, b)$, where $\vec {c}$ is a binary word of the size of the pixel address $\vec {a}$, i.e. with $N_a=N_x+N_y$ bits for images of size $2^{N_x} \times 2^{N_y}=2^{N_a}$ pixels. The scalar product $\vec {c}\, \vec {a}$ is accomplished modulo 2 so as to yield the binary result 0 or 1. The parameter $b=0$ or 1 is a single bit. There are therefore $2^{N_a+1}$ distinct parameter configurations, generating a set of $2^{N_a+1}$ distinct binary images through Eq. (7). The parameter b ensures that for each image in the model set (with $b=0$) then its binary complement (with $b=1$) is also an image in the set. Figure 3 presents some examples of binary images with size $256\times 256$ pixels according to the model of Eq. (7). For such images with $N_x=N_y=8$, the model of Eq. (7) generates a set of $2^{17}\approx 10^5$ distinct binary images of size $256\times 256$ pixels.

Fig. 3.

Eight binary images with $256\times 256$ pixels according to the model of Eq. (7). Each image can be identified by processing a single pixel register placed in a superposed quantum state.

The task is then, from the observation of a given image following the model of Eq. (7), to determine the parameter configuration $(\vec {c}, b)$ that produced it. From the observed image, the same process of Eqs. (2)–(5) is applied on the $(N_a+1)$-qubit pixel register placed in the superposed quantum state. One then arrives for the state $\mathinner {|{\phi }\rangle }$ of the $N_a$-qubit register in Eq. (4), at the scalar weight of Eq. (5) now taking the form

$$\begin{aligned} w(\vec {z}\,)= \sum _{\vec {a} \in \{0, 1 \}^{N_a}} (-1)^{\vec {c}\, \vec {a} \, \oplus \, b \,\oplus \, \vec {a}\,\vec {z}} \;. \end{aligned}$$

(8)

Therefore, from Eq. (8), the weight of the state $\mathinner {|{\vec {z}\,}\rangle }=\mathinner {|{\vec {c}\,}\rangle }$ in $\mathinner {|{\phi }\rangle }$ is

$$\begin{aligned} w(\vec {z}=\vec {c} \,)= \sum _{\vec {a} \in \{0, 1 \}^{N_a}} (-1)^{0\,\oplus \, b} =\pm 2^{N_a}\;. \end{aligned}$$

(9)

Since $\mathinner {|{\phi }\rangle }$ in Eq. (4) is a normalized state, necessarily the other weights $w(\vec {z} \not =\vec {c} \,)$ are zero and $\mathinner {|{\phi }\rangle }=\mathinner {|{\vec {c}\,}\rangle }$. So, the measurement in the computational basis of $\mathcal {H}_2^{\otimes N_a}$ of these $N_a$ qubits of the pixel register in state $\mathinner {|{\phi }\rangle }$ yields the $N_a$ bits of the parameter $\vec {c}$. This is the quantum speed-up: by processing a single register with $N_a$ qubits, one can extract the information of the value of $\vec {c}$ among $2^{N_a}$ possible values. Besides, the value of the one-bit parameter b can always be read from the pixel with address $\vec {a}=\vec {0}$ in the original image $I(\vec {a}\,)$, since with the image model of Eq. (7) always $I(\vec {a}=\vec {0}\,)=b$. By contrast, a classical approach would require processing and measuring, instead of one, at least $N_a$ pixel registers taken at $N_a$ specific addresses to determine the $N_a$ bits of $\vec {c}$.

The same quantum circuit presented in Fig. 2 can be used to perform the image identification task. Compared to the task of image classification of Sect. 3.1, the difference here for image identification is that the circuit of Fig. 2 is used on a different input image and the result of the measurement of the output state $\mathinner {|{\phi }\rangle }$ is interpreted differently.

4 Conclusion

The image processing tasks devised and analyzed in Sect. 3 are illustrative examples making clearly visible the specific capabilities of quantum approaches for enhanced solutions. The key feature here is the capability of quantum systems to implement parallel representation and computing via superposed quantum states. In this way, all the pixels forming an image can be handled simultaneously in coherent superposition as if there were only one. This enables reduction of both memory space and computing time. Such faculty of parallel processing by quantum superposition appears specially relevant for digital image processing, along with other specifically quantum properties such as entanglement [1, 10, 11]. In principle, the parallel processing afforded by the quantum superposition can be made accessible to any classical digital images. Starting from a classical digital image, it will be the first task of the quantum processor to realize the superposed representation to support the subsequent parallel processing. There is yet no systematic methodology to identify image processing tasks that could benefit from such quantum approaches for enhanced performance, and a fortiori no systematic methodology for constructing the appropriate quantum algorithms integrating the capabilities and constraints of quantum information. Such quantum methodologies for quantum image and signal processing remain largely to be elaborated. Concomitantly is the on-going development of specialized hardware for implementing the quantum algorithms. Many proposals still in progress have been developed at the laboratory, and there even now exists a commercial quantum computer able to process registers of several hundreds of qubits, although not quite yet under the form of a universal programmable machine. These quantum perspectives embody very rich potential to be explored for information, signal and image processing.