1 Introduction

Our atmosphere is filled with particles that cause several phenomena, which lead to visibility degradation and make the detection of scenes’ objects more difficult. The severity of these phenomena is directly related to the type of particles, their size and their concentrations [13].

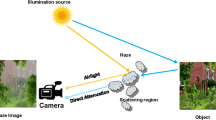
In such conditions, the apparent luminance of any distant object is controlled by two processes that occur concurrently: the light coming from the object is gradually attenuated by scattering and absorption. It is denoted by t. And the airlight A coming from a source of light (e.g. The Sun) and it is scattered by the haze particles toward the observer all along the line of sight [2].

The formation of the image with the degraded visibility at pixel x, is generally modeled as the sum of the scene’s radiance J(x) and the atmospheric light \(A_{\infty }\), weighted by a transmission factor t(x) (Eq. 1). The \(A_{\infty }\) is the airlight scattered by an object located at infinity with respect to the observer.

$$\begin{aligned} I(x)=J(x)t(x) + A_{\infty }(1-t(x)) \end{aligned}$$
(1)

where I(x) is the image formed on the camera’s sensor. The transmission factor t(x) depends on the scene’s depth d (distance to the sensor) and on the scattering coefficient \(\beta \) of the haze, such that \(t(x)= e^{-\beta .d(x)}\) [9]. \(t \in [0, 1]\): when \(t=1\), this means that the total light coming from the imaged object reaches the camera with no attenuation. And when \(t=0\), this indicates that the light coming from the imaged object is totally extinct by the fog. In other words, this happens when the fog is opaque.

An important number of dehazing methods consider the inversion of this simple physical model based on prior assumptions to estimate the unknown parameters and to recover J(x) [10, 12]. Some approaches adjust this model to represent faithfully reality, such as adding a parameter to model noise [7]. However, the majority of single image dehazing methods consider the simplest haze model given in 1. These methods consider the haze model evenly all over the image, even when the conditions greatly change between regions, such as the density of fog at distant objects and the color of objects. This seriously degrades the perceptual quality at these regions after dehazing. One may wonder, if this only due to the hypothesis of the used dehazing method or it is also due to the haze model limitation.

For instance, we consider the aerial view shown in Fig. 1: on the lower half part of the image, there is a soft layer of haze, thus, the light transmitted from the objects to the camera is important. The haze-free image recovered through the haze model inversion shows a visually pleasing natural scene. However, on the very upper part where the haze is heavy, the application of the same model inversion provides surprising estimated colors.

Fig. 1.
figure 1

Hazy image and the correspondant dehazed image processed by the physical based Dark Channel Prior method [6]. The lower half part of the dehazed image shows a good quality in the objects recovery. However, some colored spots appear on the upper part. Images are borrowed from [10]. (Color figure online)

Full size image

In order to investigate the haze model validity over various regions of the image, which means the ability to recover recognized colors after inversion, we use data from the CHIC database [5, 8]. It includes, unlike other databases, a set of real foggy scenes with various fog densities in addition to the original fog-free image. It provides also accurate values of the basically unknown parameters of the haze model, t and \(A_{\infty }\). In Sect. 2, we measure the evolution of chromatic dependencies between the airlight and the objects’ colors through the fog thickness. We use the perceptual correlation as a prior screening of regions over which the dehazing is prone to failure. Accordingly, we identify three critical classes for the haze model validity in Sect. 3 based on the perceptual difference between foggy colors and the airlight. This work is concluded in the last section, where we invite researchers to reconsider the haze model at high densities of fog. In the rest of this paper, we use the term dehazing to denote the haze model inversion.

2 Colorimetric Assessment Through Fog Densities

In our previous study [3], using simulated hazy images, the shift of the color components, hue and saturation, was quantified between the haze-free and the dehazed images. At low fog densities, hue is more accurately recovered than saturation. In order to investigate the consistency between real and simulated foggy images, a comparison between their recovered images was conducted in [4]. It was noted that the convergence model fails to stand for high densities of fog and causes inaccuracies in saturation recovery at low densities.

While previous studies focused mainly on the analysis of dehazing results, we investigate here the possibility to screen the inputs where the convergence is prone to failure. The series of these studies serves on the one hand to restrict the dehazing to the proper regions and to warn of the use of simulated images used recently to train neural network models designed for dehazing [1, 11].

Thus, we use two scenes of several densities of fog taken from CHIC database. The images are shown in Fig. 2.

Fig. 2.
figure 2

Data used in our experiment. They are a subset of the CHIC database generated with a fog machine [5, 8]. First row: Scene A; Second row: Scene B. From left to right: Level 1 (highest fog level); Level 3; Level 5; Level 7; Level 9 (lowest fog level); Fog-free. (Color figure online)

Full size image
Fig. 3.
figure 3

The patches are represented by the corresponding letter in Fig. 4. (Color figure online)

Full size image
Fig. 4.
figure 4

The distribution of r and g coordinates of the ColorChecker patches (Fig. 5) at fog level 7 (red), fog level 9 (green) and fog-free level (blue). The triangle placed at the center is \(A_\infty \). (Color figure online)

Full size image

2.1 Protocol

We investigate the possibility to locate the foggy colors that might be unrecognized after dehazing according to the perceptual difference between the atmospheric light and the foggy colors. We particularly studied the recovery of the colorchecker patches at fog levels. These colorcheckers are placed at the back of the scenes A and B of the CHIC database at 7 and 4.25 m from the camera, respectively (Fig. 2).

For every color patch indicated by the corresponding letters in Fig. 3, we plot the color coordinates in the rg color space, where r, g and b imply the proportion of red, green and blue in the original RGB color, with \(r + g + b = 1\) (Fig. 4). This visualizes the evolution of colors with the increasing fog density towards the atmospheric light \(A_{\infty }\). Then, for each fog density, we performed the inversion of the haze model to recover the haze-free image J, as the unknown parameters t and \(A_\infty \) are calculable in CHIC database. The recovered images are shown in Fig. 5.

2.2 Indicators

Two parameters are calculated to label the behavior of the haze model across fog densities: the color difference parameter \(\varDelta E^{*}_{ab}\) calculated between the airlight and the foggy colors as an indicator to report a possible inaccurate color recovery. We correlate it to the transmission parameter t, which denotes the intensity of fog according to the relation \(t(x)= e^{-\beta .d(x)}\) defined in Sect. 1. The calculation of this parameter is detailed in [5].

2.3 Analysis

For ease of reading of Fig. 4, we only plot the coordinates of the color patches of the fog-free level, level 9 and level 7. This is quite sufficient to note that the evolution of colors towards \(A_{\infty }\) is not linear. From a certain increasing density of fog, color hue shifts toward \(A_{\infty }\) away from the hue line determined by the coordinates of the same color patch at the fog-free level and the slightly foggy level 9. The shift value and its direction are not consistent across colors. This is mainly dependent on the relative position of the fog-free color to \(A_{\infty }\). Thus, at high fog densities, as there are no constant hue lines, the dehazing in RGB color space, implies a shift in the perceived hue that degrades the quality of the dehazed image.

Besides the distribution of colors in RGB color space in which the dehazing is often performed, we depict the perceptual difference between the original fog-free color and \(A_{\infty }\), denoted by \(\varDelta E^{*}_{ab}\). A higher value means a larger noticeable color difference. This depends simultaneously on the colorfulness of the original color and the intensity of fog.

According to Fig. 5, level 5 of fog densities represents a critical edge: above this level, colors are perceptually well recovered. However, at lower levels, from level 1 to level 4, colors are hardly recognized. This is reflected in the \(\varDelta E^{*}_{ab}\) values given in Tables 1 and 2: considering level 5 for both scenes, A and B, colors are quite better recovered for scene B. The corresponding values of \(\varDelta E^{*}_{ab}\) are higher for scene B than for scene A, which underlines a larger difference against the atmospheric light and therefore a better recovery.

This points out an obvious connection between the initial difference between foggy colors and the atmospheric light, on the one hand, and the quality of dehazed colors on the other hand. According to the values provided in Tables 1 and 2, for values below the color difference \(\varDelta E^{*}_{ab}\) \(\in [5, 6]\), dehazing induces an image quality degaradation. Beyond these values, recovered colors are similar to the fog-free original image and the global quality is improved.

Fig. 5.
figure 5

First row: Scene A; Second row: Scene B. Dehazed images of the Macbeth ColorChecker placed at the top of the scenes, at 7 m in scene A and 4.25 m in scene B. They are calculated at different levels of fog. (Color figure online)

Full size image
Table 1. \(\varDelta E^{*}_{ab}\) between atmospheric light and the chromatic patches of the Macbeth ColorChecker at different fog levels of Scene A. For each level we calculate the standard deviation of \(\varDelta E^{*}_{ab}\) of all patches.
Full size table
Table 2. \(\varDelta E^{*}_{ab}\) between atmospheric light and the chromatic patches of the Macbeth ColorChecker at different fog levels of Scene B. For each level we calculate the standard deviation of \(\varDelta E^{*}_{ab}\) of all patches.
Full size table

3 Results

In all of this, we can identify three critical classes for the haze model validity according to the perceptual difference parameter \(\varDelta E^{*}_{ab}\) and the transmission parameter t:

  1. 1.

    A high density of fog, which induces small transmission values, makes all colors almost look alike and close to the atmospheric light (from level 1 to level 4 in CHIC database). At these levels, transmission values are extremely low. They vary between 0 and 0.1. The results do not depend on the objects’ colors. No matter what the color is, it is badly recovered by dehazing.

  2. 2.

    A medium density, which shows up when almost \(20\%\) of the transmitted light reach the camera, induces particular observation. Generally, recovered colors are barely recognized, especially those with the lowest \(\varDelta E^{*}_{ab}\) values, such as the color patches B, E and F (see level 5 in Table 1). Moreover, some patches are hardly discernible after dehazing such as patches E and F, and patches K, L and P.

  3. 3.

    A low density of fog, which guarantees the recognition of the color’s hue. From level 6 to level 9, \(\varDelta E^{*}_{ab}\) values either almost fall in the interval [5, 6] or they are higher. Thus, colors are all easily distinguished from the airlight and they are therefore accurately recovered in hue but with a small bias in the colorfulness, which is not quantified in this study. This is mainly due to the noise, which is excluded from the haze model. Transmission values at such levels are higher than 0.2.

4 Conclusion

In this paper, we investigate the possibility to screen regions where the dehazing is likely to fail in providing correct colors that we believe mandatory to avoid adverse effects. Accordingly, beyond a critical density of fog, the perceptual difference between the atmospheric light and the hazy colors is extremely low. Thus, for any color hidden by fog, it is impossible to retrieve the accurate hue of the fog-free color in the visible range, even if the parameters of the fog model are accurately calculated. At lower fog densities, the innacuracy of the color recovery is mainly due to the noise, which affects particularly the colorfulness of the recovered scene.

The physics based dehazing methods used today should consider seriously the haze model validity. Otherwise, undesirable effects show up at very far objects or in the presence of much fog. Usually, we hardly try to reduce these effects by refining hypothesis, while the model itself is limited.

Future works will focus on the quantification of colors’ shift according to the parameters investigated in this paper and the possible coupling of complementary processing operations to push the haze model limits even further.