A Cooperative Jamming Based Secure Uplink Transmission Scheme for Heterogeneous Networks Supporting D2D Communications

Abstract

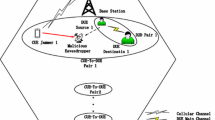
A heterogeneous network supporting D2D communications is a typical framework to cope with data sharing in a cyber physical system. In the network, there exists more interference than traditional cellular networks, which promotes interference cancellation (IC) technologies. Yet, how IC can improve security performance of D2D-enabled networks is still unknown. In addition, how to establish a secure physical transmission link for users in these networks is of great significance. In this paper, with IC or not, we first derive the expressions of the secrecy outage probability in D2D-enabled heterogeneous networks, respectively. Then, according to the transmission constraint and the security constraint, we present two cooperative jamming schemes based on devices in D2D networks for achieving secure uplink of cellular users. In these schemes, we formulate the above secure challenge as an optimization problem with or without fully IC and provide the corresponding optimal solutions to improve the secrecy performance of cellular uplink. Finally, numerical simulation demonstrates that the secure performance of cellular uplink is remarkably enhanced using our cooperative jamming schemes.

Appendices

Appendix A: Proof of Lemma 1

To proof Lemma 1, we first discuss $F_{\gamma _c}(T)\triangleq 1-\mathrm {Pr}^{\mathrm {(N)}}(\gamma _c>T)$ based on the CDF definition. Here, $\mathrm {Pr}^{\mathrm {(N)}}(\gamma _c>T)$ represents the coverage probability of the cellular link without IC capability, which is

$$\begin{aligned} \begin{aligned} \mathrm {Pr}^{\mathrm {(N)}}(\gamma _c> T)&=P\left( \left| h_{cM} \right| ^2>\frac{r_{cM}^{\alpha }T}{p_c}\sum _{k\in \varPhi _{c,d}}p_d\left| h_{kM}\right| ^2r_{kM}^{-\alpha }\right) \\&= \int _{0}^{R}\frac{2r_{cM}}{R^2}\mathcal {L}^{\mathrm {(N)}}\left( \frac{r_{cM}^{\alpha }T}{p_c}\right) \mathrm {d}r_{cM}, \end{aligned} \end{aligned}$$

(12)

where $\mathcal {L}^{\mathrm {(N)}}(s)=E_{\varPhi _{c,d}}\left[ e^{-s\sum _{k\in \varPhi _{c,d}}p_d\left| h_{kM}\right| ^2r_{kM}^{-\alpha }} \right]$ denotes the Laplace transform of s for the scenario without IC capability. Specifically,

$$\begin{aligned} \begin{aligned} \mathcal {L}^{\mathrm {(N)}}(s)\overset{\mathrm {(a)}}{=}&\exp \left\{ -\lambda _{c,d}\int _{R^2}\left( 1-E_h\left[ e^{-sp_d\left| h_{kM}\right| ^2r_{kM}^{-\alpha }}\right] \right) \mathrm {d}r_{kM}\right\} \\ \overset{\mathrm {(b)}}{=}&\exp \left\{ -2\pi \lambda _{c,d}\int _{0}^{\infty }\frac{sp_dr_{kM}}{sp_d+r_{kM}^{\alpha }}\mathrm {d}r_{kM}\right\} \\ =&\exp \left\{ -\pi \lambda _{c,d}(sp_d)^{\frac{2}{\alpha }}\varGamma (1+\frac{2}{\alpha })\varGamma (1-\frac{2}{\alpha })\right\} , \end{aligned} \end{aligned}$$

(13)

where $\mathrm {(a)}$ follows the PDF of PPP, and $\mathrm {(b)}$ holds because of the definition of a surface integral. Accordingly, (12) can be rewritten as follows.

$$\begin{aligned} \mathrm {Pr}^{\mathrm {(N)}}(\gamma _c > T) =\frac{1-e^{-\pi \lambda _{c,d}(\frac{Tp_d}{p_c})^{\frac{2}{\alpha }}\varGamma (1+\frac{2}{\alpha })\varGamma (1-\frac{2}{\alpha })R^2}}{\pi \lambda _{c,d}(\frac{Tp_d}{p_c})^{\frac{2}{\alpha }}\varGamma (1+\frac{2}{\alpha })\varGamma (1-\frac{2}{\alpha })R^2}. \end{aligned}$$

(14)

Next, we can derive the PDF of the most detrimental Eve, $g(\cdot )$, based on the partial differential of the corresponding CDF, $G(\cdot )$. Assuming M as the best SINR of eavesdroppers, $G(M)\triangleq \mathrm {Pr}(\max \gamma _{e}<M)$ can be calculated as follows.

$$\begin{aligned} \begin{aligned} G(M)&= E\left[ \prod _{\varPhi _e}\left( 1-e^{-\frac{r_{ce}^{\alpha }M}{p_c}\sum \limits _{k\in \varPhi _{c,d}}p_d\left| h_{ke}\right| ^2r_{ke}^{-\alpha }}\right) \right] \\&\overset{\mathrm {(a)}}{=}\exp \left\{ -2\pi \lambda _e\int _{0}^{\infty }r_{ce} \mathcal {L}^{\mathrm {(N)}}\left( \frac{r_{ce}^{\alpha }M}{p_c}\right) \mathrm {d}r_{ce}\right\} \\&\overset{\mathrm {(c)}}{=} \exp \left\{ -\frac{\lambda _e}{\lambda _{c,d}(\frac{Mp_d}{p_c})^{\frac{2}{\alpha }}\varGamma (1+\frac{2}{\alpha })\varGamma (1-\frac{2}{\alpha })}\right\} , \end{aligned} \end{aligned}$$

(15)

where $\mathrm {(c)}$ holds by substituting $\mathcal {L}^{\mathrm {(N)}}(\cdot )$.

As a result, the secrecy outage probability of CU$_c$ can be expressed as

$$\begin{aligned} \begin{aligned} P_{\mathrm {SOP}}^{(\mathrm {N})}&=1-\int _{0}^{\infty }\mathrm {Pr}^{\mathrm {(N)}}(\gamma _{c}>\mathrm {Th}(\max \gamma _{e}))\mathrm {d}G(M)\\&=1-\frac{2B}{\alpha A \lambda _{c,d}^2}\int _{0}^{\infty }\frac{1-e^{-A\lambda _{c,d}\mathrm {Th}(x)^{\frac{2}{\alpha }}}}{\mathrm {Th}(x)^{\frac{2}{\alpha }}}\cdot e^{-\frac{B}{\lambda _{c,d}}x^{-\frac{2}{\alpha }}}x^{-1-\frac{2}{\alpha }}\mathrm {d} x, \end{aligned} \end{aligned}$$

(16)

where $A=\pi (\frac{p_d}{p_c})^{\frac{2}{\alpha }}\varGamma (1+\frac{2}{\alpha })\varGamma (1-\frac{2}{\alpha })R^2$ and $B=\frac{\pi \lambda _e R^2}{A}$. And this completes the proof of Lemma 1.

Appendix B: Proof of Lemma 2

Similar to the proof of Lemma 1, we first provide the coverage probability of cellular links with IC capability follows [27].

$$\begin{aligned} \begin{aligned} \mathrm {Pr}^{\mathrm {(I)}}(\gamma _c> T)&=P(\left| h_{cM} \right| ^2>\frac{r_{cM}^{\alpha }T}{p_c}\sum _{k\in \varPhi _{c,d}}p_d\left| h_{kM}\right| ^2r_{kM}^{-\alpha }\varDelta _k)\\&=\int _{0}^{R}\frac{2r_{cM}}{R^2}\mathcal {L}^{\mathrm {(I)}}(\frac{r_{cM}^{\alpha }T}{p_c}) \mathrm {d}r_{cM}, \end{aligned} \end{aligned}$$

(17)

where $\mathcal {L}^{\mathrm {(I)}}(s)=e^{-\lambda _{c,d}2\pi (\phi _1(s)+\phi _2(s)-\phi _3)}$ denotes the Laplace transform for the IC-enabled scenario. Here, $\phi _1(s)=\frac{1}{2}(sp_d)^{\frac{2}{\alpha }}\varGamma (1+\frac{2}{\alpha })\varGamma (1-\frac{2}{\alpha }), \phi _2(s)=\frac{1}{\alpha }(sp_d)^{\frac{2}{\alpha }}\varGamma (1+\frac{2}{\alpha })\varGamma (-\frac{2}{\alpha },s\tau )$, and $\phi _3=\frac{1}{\alpha }(\tau ^{-1}p_d)^{\frac{2}{\alpha }}\varGamma (\frac{2}{\alpha })$.

As a result, the secrecy outage probability of CU$_c$ can be derived as follows,

$$\begin{aligned} \begin{aligned} P_{\mathrm {SOP}}^{(\mathrm {I})}&=1-\int _{0}^{\infty }\mathrm {Pr}^{\mathrm {(I)}}(\gamma _{c}>\mathrm {Th}(\max \gamma _{e}))\mathrm {d}G(M)\\&=1-\frac{2B}{\alpha \lambda _{c,d}}\int _{0}^{\infty }P e^{-\frac{B}{\lambda _{c,d}}x^{-\frac{2}{\alpha }}}x^{-1-\frac{2}{\alpha }}\mathrm {d} x, \end{aligned} \end{aligned}$$

(18)

where $P=\mathrm {Pr}^{\mathrm {(I)}}(\gamma _c > \mathrm {Th}(x))$. And this completes the proof of Lemma 2.

Appendix C: Proof of Lemma 3

Assuming $T=2^{R_t}-1$ and $M=2^{R_t-R_s}-1$ in (14) and (15), then the transmission constraint and the security constraint can be rewritten as $P_{\mathrm {TC}}=\frac{1-e^{-\hat{A}\lambda _{c,d}}}{\hat{A}\lambda _{c,d}}$ and $P_{\mathrm {SC}}=e^{-\frac{\hat{B}}{\lambda _{c,d}}}$. Then, an extremum of $P_{\mathrm {STP}}$ can be computed by its first derivative of $\lambda _{c,d}$, i.e.,

$$\begin{aligned} \lambda _{c,d}^*\triangleq \arg \left\{ \frac{\mathrm {d} P_{\mathrm {STP}}^{(\mathrm {N})}}{\mathrm {d} \lambda _{c,d}}=0\right\} =\arg \left\{ f(\lambda _{c,d})=0\right\} , \end{aligned}$$

(19)

where $f(\lambda _{c,d})=e^{\hat{A}\lambda _{c,d}}-\frac{\hat{A}\lambda _{c,d}^2}{\lambda _{c,d}-\hat{B}}-1$. Then, We analyze the existence of the extremum and explain that the extremum is the maximum value.

Existence: Considering the properties of continuous function, we analyse two cases of $f(\lambda _{c,d})$. Because $\frac{\mathrm {d} f(\lambda _{c,d})}{\mathrm {d} \lambda _{c,d}}=\hat{A}\left[ e^{\hat{A}\lambda _{c,d}}-1+(\frac{\hat{B}}{\lambda _{c,d}-\hat{B}})^2 \right] >0$ holds and $f(\lambda _{c,d})$ is continuous, $f(\lambda _{c,d})$ is larger than zero with $\lambda _{c,d}\in (0,\hat{B})$. Similarly, there must exists only one solution $\lambda _{c,d}^*$ to ensure $f(\lambda _{c,d}) =0$ with $\lambda _{c,d}\in (\hat{B},+\infty )$.

The Maximum Value: It’s easy to know that $\frac{\mathrm {d} P_{\mathrm {STP}}^{(\mathrm {N})}}{\mathrm {d} \lambda _{c,d}}>0$ with $\lambda _{c,d}\in (0,\hat{B})\cap (\hat{B},\lambda _{c,d}^* )$. For the full range of $\lambda _{c,d}$, we still need to consider $\frac{\mathrm {d} P_{\mathrm {STP}}^{(\mathrm {N})}(\hat{B})}{\mathrm {d} \lambda _{c,d}}=\frac{\hat{A}}{\hat{B}}e^{-1-\hat{A}\hat{B}}>0$. Similarly, $\frac{\mathrm {d} P_{\mathrm {STP}}^{(\mathrm {N})}}{\mathrm {d} \lambda _{c,d}}<0$ with $\lambda _{c,d}\in (\lambda _{c,d}^*,+\infty )$.

According to the above analysis of the extremum of $P_{\mathrm {STP}}$, we know that $P_{\mathrm {STP}}^{(\mathrm {N})}$ is a unimodal function of $\lambda _{c,d}$. And this completes the proof of Lemma 3.