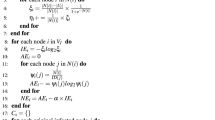Keywords

1 Introduction

Epidemic dynamical behavior can be observed in different scenarios and fields, such as computer worms spreading in networks and rumor propagation on the Internet. If not under control, epidemic outbreaks will bring great negative effects to economy and society. Therefore, how to model, analyze and contain the dynamics of epidemic outbreaks in social networks has been receiving considerable attention. Whereas the prediction of the diffusion process has attracted a considerable number of works (e.g., [1, 2]), the inverse problem of estimating the original source has been studied only recently [3]. The task of source localization is inherently challenging because of the stochastic nature of infection propagation. Indeed, different initial conditions can lead to the same observed results, and the epidemic outbreak can be explained by multiple and possibly very different dynamical processes.

Researchers have proposed various models and algorithms for source localization, and these studies can be roughly divided into two categories, i.e., graph-centrality measures and maximum likelihood methods. Graph-centrality measures quantify the influence of nodes based on the network topological structure, and select the most influential node as an estimator for the actual epidemic source. Besides, graph-centrality measures could be applied to estimating a set of origins by using spectral methods [4]. Examples include the closeness centrality [5], betweenness centrality [6], or the Jordan center of a graph [7]. In general, graph-centrality measures focus on exploiting the information about infected nodes, i.e., the nodes which recieved and spread the harmful content (e.g., rumor or computer worm) in the spreading process. The advantage of graph-centrality measures is that they are easy to implement; however, their precision is limited. Graph-centrality measures take advantage of the network topology for estimation, whereas maximum likelihood methods require much more detailed information, thereby supporting more precise estimation. For instance, Lokhov et al. proposed a fast Dynamic Message-Passing method (DMP) to compute the probability of a given node in the network to be the origin of the epidemic [8]. To construct the DMP estimator that locates the most probable origin, the infection rate of each node and the terminal time slot need to be given in advance. Other Bayes inference approaches also employ extra information about the epidemic process such as the exact infection time of some given infected nodes to calculate the probability [9, 10]. However, information collection is never free, and it is not realistic to obtain too much node information in large-scale social networks.

In order to improve the performance of localization without extra information, we focus on making better use of the information about susceptible nodes, which are neglected in graph-centrality measures. Susceptible nodes are the ones which the epidemic propagation did not spread to, but information about them is also valuable. In our model, we take both susceptible and infected nodes into account, and propose a novel metric called Classifying Quality (CQ) centrality for source localization. Inspired by Fisher criterion [11], CQ centrality views infected nodes and susceptible nodes as two different classes, and quantifies the property of a node to separate the two classes. All observed infected (respectively, susceptible) sensor nodes constitute the infected (respectively, susceptible) set, and our target is to find the node which achieves the optimal separation between the two sets, i.e., the node which has the maximum CQ centrality.

As far as our knowledge goes, our study is the first to connect source localization with classification criterion. Due to the efficient use of the information about the susceptible nodes, the proposed metric outperforms other centrality measures. CQ centrality only utilizes length of the shortest path between nodes, so it can still work even if there was no extra information about the epidemic outbreak. Moreover, if the infection rates of edges are already known, the proposed metric can be improved by using effective distances [12].

The rest of the paper is organized as follows. First, we briefly review related works in Sect. 2. Then, we give details of our approach of CQ centrality in Sect. 3. Next, we present our experimental results and the corresponding analysis in Sect. 4. Finally, conclusions and discussions are given in Sect. 5.

2 Related Works

Many different methods have been proposed to estimate the rumor (or worm) source, and they mainly fall into two categories: graph-centrality measures and maximum likelihood methods. In this section, some important works are introduced.

2.1 Graph-Centrality Measures

Graph-centrality measures use a topological index to score the importance of nodes in a network. The index reflects some of the characteristics of the network topological structures and is generally referred to as the centrality. The nodes with high centrality are probable suspects of the real source. The earliest centrality used for scoring is the degree, which represents the number of neighboring nodes adjacent to a node [13]. The idea is that the importance of one node is closely related to the neighboring nodes directed towards it. Since the spread of rumor or virus relies heavily on the distance between nodes, in subsequent studies, researchers proposed various distance-based centrality indicators. The Closeness Centrality (CC) indicator is one of them, which describes how fast a node can propagate information to other nodes in the network [14]. Its value is defined as the inverse of the sum of the distances between a node and all other nodes, given by: \(CC(u)=\frac{1}{\sum \limits _{v\ne u} {d_{uv}}}\), where \(d_{uv}\) is the minimum hop required from node u to node v. Betweenness Centrality (BC) is another metric based on shortest paths, proposed by Freeman et al. [15]. The principle is that if a node is located closer to the information center, then the node is more likely to be on the shortest path between other nodes, reflecting the node’s ability to control the flow of information. BC is one of the most common centrality indicators and is a core concept in social network analysis. The definition of BC is given by: \(BC(u)=\displaystyle \sum \limits _{s\ne v\ne u} \displaystyle \frac{\sigma _{sv}(u)}{\sigma _{sv}}\), where \(\sigma _{sv}\) is the number of shortest paths between node s and node v, and \(\sigma _{sv}(u)\) counts the shortest paths in which node u is included. Another important centrality, which is widely used in source localization, is the Jordan centrality. The Jordan centrality of a node is the maximum of the minimum distances with respect to a given infected node set [16]. Generally, the node with the minimal Jordan centrality is called the Jordan center, which is an estimator for the actual source. Studies have shown that the Jordan Center method can achieve good performance in different network structures and has strong robustness [7].

2.2 Maximum Likelihood Methods

Maximum likelihood methods solve the problem of localization with probability theory. For instance, according to Bayes rule, the probability that node u is the source \(s^{*}\) given some observations O about the diffusion process is in proportion to the joint probability of observations given the source, i.e., \(P(u=s^{*}|O)\propto P(O|u=s^{*})\). This idea is very naive and its key point lies in the construction of likelihood probability formula. The solution proposed by Dong et al. was to construct a posteriori estimator [9], while Zheng and Tan carried out a probabilistic analysis of the propagation boundary by using the connected nature of spreading subgraph and the infection time of observed infected nodes [10]. However, their methods are only suitable for tree structure. Jiang et al. did more detailed work. They considered different network topologies with time delays, and gave log-likelihood probability formulas under three categories of observations (WaveFront, Snapshot, Sensor) [17].

The time delays on different edges are expected to be inconsistent, and many researches focus on studying the influence of distribution types. For example, Spencer and Srikant assumed that rumor propagation conforms to the SI model and the time delay on each edge complies with the exponential distribution [18]. Based on their assumptions, they proposed an explicit, non-iterative, maximum likelihood estimator for the source. The aforementioned works mostly rely on the assumption that there is only one single source node, and there are also many pioneer works studying multi-source locating problem. For example, Zang et al. presented an approximate multi-source locating algorithm, which involves three principal steps [19]. Firstly, they introduced a reverse propagation model to detect all infected nodes, which were then clustered into multiple infected communities by employing a community detection method. At last, they computed the maximum likelihood estimate in each infected community and obtained all the source nodes.

3 Proposed Approach

In the following subsections, we present our assumptions, localization algorithm and various notations used throughout this paper.

3.1 Assumptions

We make the following assumptions.

  • The graph topology of the underlying social network is already known.

  • The epidemic process follows the SI model in which each node keeps in one of the two possible states: susceptible (s), infected (i). Once a node receives the harmful content (e.g., rumor or computer worm), it is infected. After that, it will remain in state i forever and try to infect its susceptible neighbors with the same probability at any following time. This is a common assumption widely adopted [8, 16, 20].

  • Time can be divided into discrete slots and the spread follows a Markov process. Specifically, there is only one node \(s^{*}\) in state i at initial time slot \(T_0=0\), which is called the epidemic source.

3.2 Notations and Definitions

We model the connections across which an epidemic can spread with a binary group \(G=(V,E)\), where V is the set of all nodes and E is the set of all links. The problem of source-localization can be abstracted as follows: Which node in V is the most probable origin, given some current knowledge about the state of a subset of V? The subset is denoted by M and the nodes in it are called sensors. A sensor gives information about which state it keeps in. If it reveals that it is in state i (respectively, s), we say that the sensor gives a positive (respectively, negative) observation. It is reasonable that an observation contributes to the localization process even if it is negative. For simplicity sake, we divide M into two subsets, and denote the set of sensors who give positive (respectively, negative) observations by \(M^+\) (respectively, \(M^-\)). Both \(M^+\) and \(M^-\) are assumed to be nonempty. After that, two important indexes, the spectral radius and the centre distance, are introduced.

Definition 1

(spectral radius). Let d(u, v) be the length of the shortest path between node u and node v in the network G (i.e., the shortest distance between them). For any set of nodes \(V_0\subset {V}\) in G, the spectral radius \(\widetilde{d}(u,V_0)\) of u with respect to (w.r.t.) \(V_0\) is defined as the maximum distance from u to any node v in \(V_0\), given by:

$$\begin{aligned} \widetilde{d}(u,V_0)=\max \limits _{v\in V_0} d(u,v) \end{aligned}$$
(1)

Definition 2

(centre distance). Given all the distance d(u, v) \((v\in V_0)\), let the centre distance \(\bar{d}(u,V_0)\) of u w.r.t. \(V_0\) be the mean of them, represented as:

$$\begin{aligned} \bar{d}(u,V_0)=\frac{1}{|V_0|} \sum \limits _{v\in V_0} d(u,v) \end{aligned}$$
(2)

3.3 CQ Centrality for Source Locating

Inspired by Fisher’s linear discriminant [11], which is a classical approach to dimensionality reduction for classification, we put forward a backward diffusion method to locate the epidemic source in social networks by calculating the CQ centrality of nodes w.r.t. M.

The objective of CQ centrality is to give a function that quantifies the property of a node to separate the \(M^+\) from \(M^-\) in terms of the spectral radius and the centre distance. The simplest measure of the separation of the two sets is the separation of the distance means, i.e., the centre distances, based on the consideration that infected nodes should be close to the epidemic source, whereas susceptible nodes should locate relatively distant from the epidemic source so that they could have survived the infection transmission. This idea is naive and the difference between the two centre distances is called inter-class distance in analogy to the between-class variance in the Fisher criterion. Besides, the smaller the spectral radius of a node w.r.t. \(M^+\) is, the less expected time is needed for the node to infect \(M^+\), thus increasing the likelihood of the node being the epidemic source. This thesis has been proved in [7] and is frequently used for source localization. From another point of view, if we use u as the center to form a circle to cover all the nodes in \(V_0\), the spectral radius \(\widetilde{d}(u,V_0)\) gives the minimum radius. A smaller \(\widetilde{d}(u,V_0)\) implies that the area of the circle is also smaller, meaning that the circle is denser. Hence, \(\widetilde{d}(u,V_0)\) can reflect the clustering coefficient of \(V_0\) w.r.t. u. In the spreading process, the epidemic source is the information center of \(M^+\), rather than \(M^-\), so we only consider the spectral radius w.r.t. \(M^+\), i.e., \(\widetilde{d}(u,M^+)\). For uniformity, \(\widetilde{d}(u,M^+)\) is named the inner-class distance, versus the inter-class distance. The CQ centrality of node u is defined to be the ratio of the inter-class distance to the inner-class distance and is given by

$$\begin{aligned} CQ(u)=\frac{\bar{d}(u,M^-)-\bar{d}(u,M^+)}{\widetilde{d}(u,M^+)} \end{aligned}$$
(3)

CQ centrality provides in-depth information w.r.t. both the structural characteristics of the network and propagation features of the diffusion process. Thus, we can utilize CQ centrality to locate the source. Our locating algorithm contains the following three steps:

  1. (i)

    Because the graph topology is known, we can calculate the shortest distances from any node u to sensors. This problem can be solved by means of Dijkstra algorithm [21] or Floyd-Warshall algorithm [22].

  2. (ii)

    For any node u, compute \(\bar{d}(u,M^-)\), \(\bar{d}(u,M^+)\), and \(\widetilde{d}(u,M^+)\) with Eqs. (1) and (2).

  3. (iii)

    Calculate the CQ centrality of each node w.r.t. M using Eq. (3), and the node with the maximum value is considered to be the source.

The key and difficult part of this method lies in calculating the shortest distance between every pair of nodes. Generally, we view the number of hops needed as the distance. But when the infection rate is known, we improve our method by using the effective distance instead, a concept proposed by Brockmann and Helbing [12]. The effective distance from node u to its neighboring node v is defined as

$$\begin{aligned} \hat{d}(u,v)=1-\ln {P_{uv}} \end{aligned}$$
(4)

where \(P_{uv}\) is the fraction of a propagation with destination v emanating from u. In our experiments, we replace the fraction with the infection rate from u to v.

4 Experimental Results

4.1 Experiment Setup

In our experiments, we use the Jordan center (JD), optimized Jordan center with effective distances (JD-E), and Dynamic Message-Passing (DMP) estimators as benchmarks to compare with our two CQ centrality based algorithm, i.e., one that regards hops as the distance (CQ), and one that utilizes the effective distance instead (CQ-E). We evaluate the performance of these different approaches in terms of the error distance, which is the number of hops between the estimated source and the actual source. The results are averaged over 1000 simulation runs, in which the position of the epidemic source is chosen randomly.

4.2 Network Topologies

We conduct experiments on both synthetic and real-world networks, and the statistics of these networks are presented in Table 1. Diameter represents the length of the longest shortest path between node pairs, and avg distance is the average length of all shortest paths. Avg clustering indicates the average clustering coefficient of the given network.

Table 1. Statistics for the networks used in our experiments.
Full size table

Synthetic Datasets. We generated synthetic networks for experiments from the following classes: Regular Graph of degree 3 (RG), Barabasi-Albert network (BA) [23], Erdos-Renyi random network (ER) [24] and Watts-Strogatz small world network (WS) [25]. For each network class, we generated connected weighted instances of size 100 or 200, in which the weight on each edge represents the infection rate between the adjacent node pair.

Fig. 1.
figure 1

An example of snapshot on a random ER network with \(|V|=30\) nodes. The epidemic source is the blue node. All green nodes appear in state s, while all red nodes and the blue node appear in state i. The epidemic is generated under a uniform distribution in the interval (0.2, 0.8); the snapshot is obtained at time \(T = 5\). (Color figure online)

Full size image
Fig. 2.
figure 2

Average error distances in various networks under different distributions

Full size image

Real-World Datasets. We use three kinds of real-world networks, which are listed below:

  • In the General Relativity and Quantum Cosmology collaboration network (GR-QC), nodes represent scientists, while edges represent collaborations, i.e., co-authoring a paper. This dataset was obtained from the e-print arXiv, covering papers submitted in the period from January 1993 to April 2003.

  • The Facebook network (Fb), which is a typical online social network, was collected from survey participants using the Facebook app. This network consists of ‘friend lists’. To be specific, if there were interactions among user a and user b, the network contains an undirected edge between a and b.

  • The Bitcoin Alpha trust network (BitA) is a who-trusts-whom network of people who trade using Bitcoin on a platform called Bitcoin Alpha [26]. We preprocess this network by converting it to an undirected graph, and then select the maximal connected subgraph.

We refer the readers to [27] for more detailed information of these three datasets.

4.3 Experiments on Synthetic Networks

For each synthetic network class, the infection rates of the edges are assumed to obey a truncated normal distribution with mean 0.5 and variance 0.25 in the scope (0, 1), or a uniform distribution in the interval (0.2, 0.8). Since these networks are relatively small, we just observe the state of all nodes at time slot \(T=3\) for source localization. In other words, we set all nodes as sensors and estimate the location of the actual epidemic source based on the snapshot at \(T=3\). An example of snapshot is given in Fig. 1, and the simulation results are shown in Fig. 2.

Fig. 3.
figure 3

Average error distances with different sensor proportions

Full size image

From Fig. 2, we can see that our proposed estimators CQ and CQ-E perform consistently better than the benchmarks JD, JD-E and DMP in all synthetic networks. Clearly, these benchmark localization methods are sensitive to network topology. The JD and JD-E methods perform well in RG network, but achieve bad results in the other three networks. The performance of the DMP method is not good, as its average error distance is more than 1 in all considered networks. The CQ and CQ-E methods outperform these three methods, but they are also sensitive to network topology. In the ER network, they get their worst results and the error distances are around 1. Moreover, by comparing the results shown in Fig. 2(a) and (b), we can find that these methods behave similarly under the uniform distribution and the truncated normal distribution, which indicates that the distribution type has little effect on the performance of these source localization approaches.

4.4 Experiments on Real-World Networks

Since the computation cost for DMP estimator in large-scale networks is too high to be accepted, we only compare the performance of the JD, JD-E, CQ and CQ-E methods in terms of the fraction of sensors, i.e., the value of |M|/|V|. Sensors are randomly sampled from V, and the infection rates of edges are set to follow the truncated normal distribution. Observations of sensors are obtained at the time when there are more than \(20\%\) nodes get infected in the whole network.

In Fig. 3, we present the average error distances in three real-world networks w.r.t. different sensor proportions, which range from \(5\%\) to \(50\%\). Results show that a higher proportion of sensors dramatically reduces the average error distance in GR-QC. This is because a higher proportion of sensors implies that there is more information for source localization, which decreases the estimated deviation. However, the impact of sensor fraction is not obvious in Fb and BitA. We believe the cause lies in the selection strategy of sensors. As shown in Table 1, the average distances between nodes is much shorter in these two networks than in GR-QC, which means that the difference between shortest paths is less significant in Fb and BitA. Hence, valuable information about shortest paths hardly increases when we improve the ratio of random sampling in Fb and BitA. From Fig. 3, we can see that CQ, CQ-E outperform JD and JD-E in all three real-world networks, which is consistent with the results on synthetic networks.

5 Conclusions and Future Work

In this paper, we propose a novel metric of centrality measurement, Classifying Quality (CQ) centrality, to estimate the most probable source of an infectious outbreak in social networks. One superiority of our method, compared to existing algorithms, is that our metric makes efficient use of the information about susceptible nodes which the epidemic did not spread to. As is usual for graph-centrality measures, our approach only utilizes statistics of shortest paths for estimation, thus is easy to be realized. Importantly, if the infection rates of edges are already known, the proposed metric can be improved by using effective distances. We use the SI model to simulate the dissemination of information and evaluate the performance of our CQ, CQ-E methods against JD, JD-E and DMP estimators. Experimental results on both synthetic and real-world networks reveal that CQ, CQ-E outperform the other three approaches because they have smaller average error distances.

Let us mention a few possibilities of extension of our approach, the study of which is left for future work. First, in our source localization method, the information spreading process is modeled by the SI model, meaning there are only two types of nodes. However, the patterns of nodes are more complex in social networks. Thus, it is important to combine CQ centrality with more sophisticated models such as the SIR model in future work. Second, in this paper, the topologies of networks are static, whereas the structure of a social network usually changes dynamically in real life. How to apply CQ centrality to time-changing networks is a significant topic of future study. Third, if we select sensors with better strategies, rather than random selection, we can boost the performance of CQ. Potential solutions include stratified sampling, systematic sampling and selecting sensors according to their centralities (e.g., degree). Finally, when it comes to multi-source scenario, whether the CQ algorithm remains useful has to be investigated further.